© Intel Corporation 2021

J. Reinders et al.Data Parallel C++https://doi.org/10.1007/978-1-4842-5574-2_14

14. Common Parallel Patterns

James Reinders¹ , Ben Ashbaugh², James Brodman³, Michael Kinsner⁴, John Pennycook⁵ and Xinmin Tian⁶

(1)

Beaverton, OR, USA

(2)

Folsom, CA, USA

(3)

Marlborough, MA, USA

(4)

Halifax, NS, Canada

(5)

San Jose, CA, USA

(6)

Fremont, CA, USA

 

When we are at our best as programmers, we recognize patterns in our work and apply techniques that are time proven to be the best solution. Parallel programming is no different, and it would be a serious mistake not to study the patterns that have proven to be useful in this space. Consider the MapReduce frameworks adopted for Big Data applications; their success stems largely from being based on two simple yet effective parallel patterns—map and reduce.

There are a number of common patterns in parallel programming that crop up time and again, independent of the programming language that we’re using. These patterns are versatile and can be employed at any level of parallelism (e.g., sub-groups, work-groups, full devices) and on any device (e.g., CPUs, GPUs, FPGAs). However, certain properties of the patterns (such as their scalability) may affect their suitability for different devices. In some cases, adapting an application to a new device may simply require choosing appropriate parameters or fine-tuning an implementation of a pattern; in others, we may be able to improve performance by selecting a different pattern entirely.

Developing an understanding of how, when, and where to use these common parallel patterns is a key part of improving our proficiency in DPC++ (and parallel programming in general). For those with existing parallel programming experience, seeing how these patterns are expressed in DPC++ can be a quick way to spin up and gain familiarity with the capabilities of the language.

This chapter aims to provide answers to the following questions:

• Which patterns are the most important to understand?

• How do the patterns relate to the capabilities of different devices?

• Which patterns are already provided as DPC++ functions and libraries?

• How would the patterns be implemented using direct programming?

Understanding the Patterns

The patterns discussed here are a subset of the parallel patterns described in the book Structured Parallel Programming by McCool et al. We do not cover the patterns related to types of parallelism (e.g., fork-join, branch-and-bound) but focus on the algorithmic patterns most useful for writing data-parallel kernels.

We wholeheartedly believe that understanding this subset of parallel patterns is critical to becoming an effective DPC++ programmer. The table in Figure 14-1 presents a high-level overview of the different patterns, including their primary use cases, their key attributes, and how their attributes impact their affinity for different hardware devices.

Figure 14-1

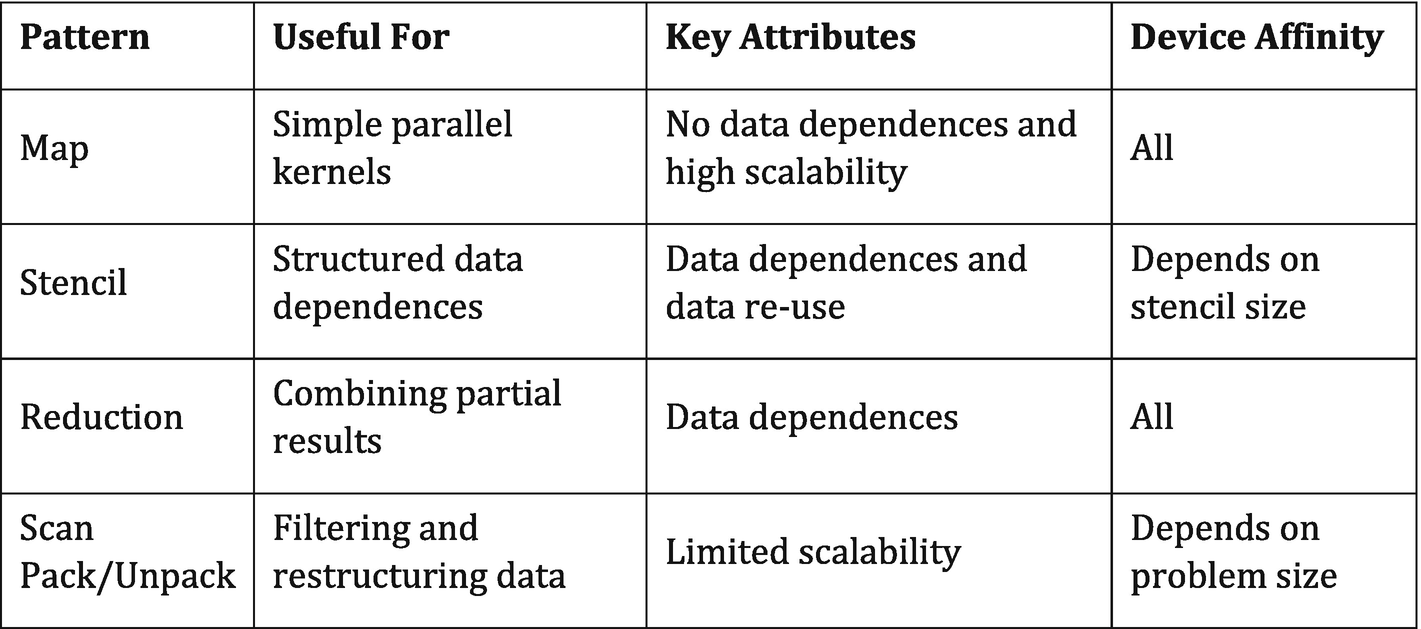
Parallel patterns and their affinity for different device types

Map

The map pattern is the simplest parallel pattern of all and will be immediately familiar to readers with experience of functional programming languages. As shown in Figure 14-2, each input element of a range is independently mapped to an output by applying some function. Many data-parallel operations can be expressed as instances of the map pattern (e.g., vector addition).

Figure 14-2

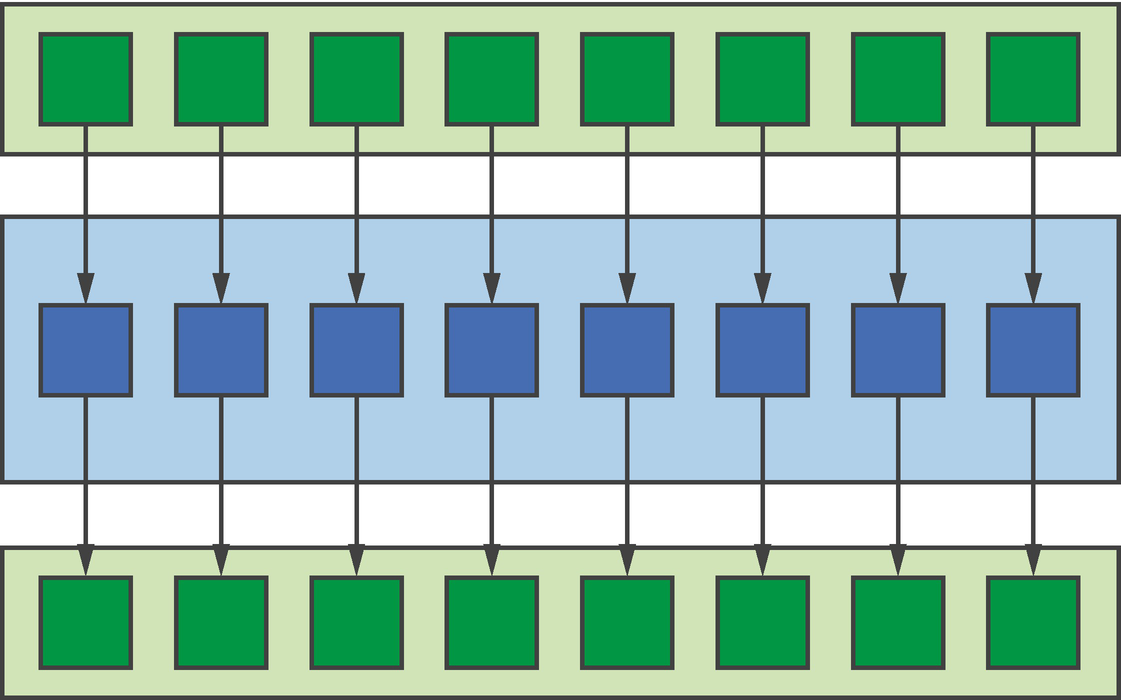
Map pattern

Since every application of the function is completely independent, expressions of map are often very simple, relying on the compiler and/or runtime to do most of the hard work. We should expect kernels written to the map pattern to be suitable for any device and for the performance of those kernels to scale very well with the amount of available hardware parallelism.

However, we should think carefully before deciding to rewrite entire applications as a series of map kernels! Such a development approach is highly productive and guarantees that an application will be portable to a wide variety of device types but encourages us to ignore optimizations that may significantly improve performance (e.g., improving data reuse, fusing kernels).

Stencil

The stencil pattern is closely related to the map pattern. As shown in Figure 14-3, a function is applied to an input and a set of neighboring inputs described by a stencil to produce a single output. Stencil patterns appear frequently in many domains, including scientific/engineering applications (e.g., finite difference codes) and computer vision/machine learning applications (e.g., image convolutions).

Figure 14-3

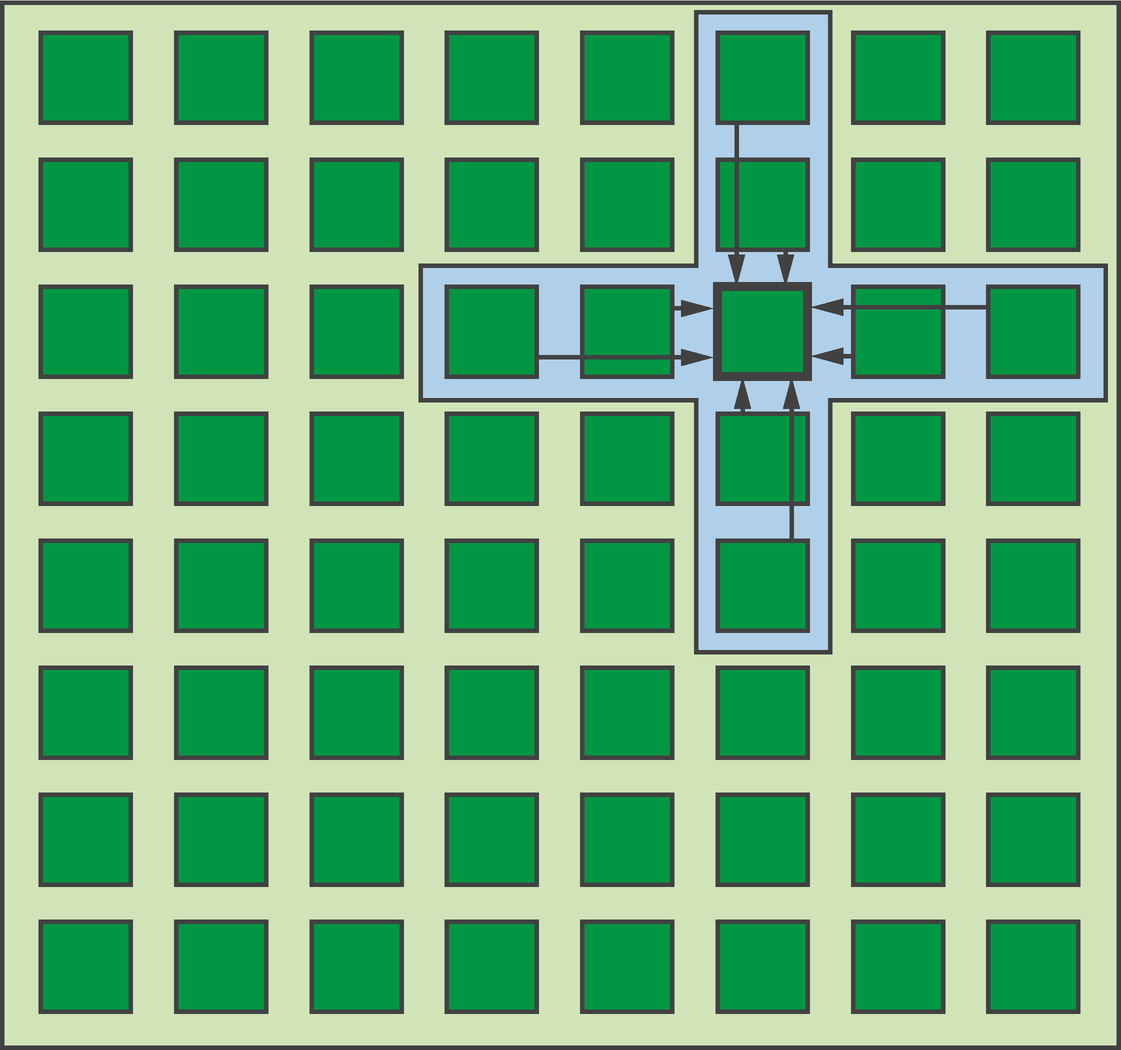
Stencil pattern

When the stencil pattern is executed out-of-place (i.e., writing the outputs to a separate storage location), the function can be applied to every input independently. Scheduling stencils in the real world is often more complicated than this: computing neighboring outputs requires the same data, and loading that data from memory multiple times will degrade performance; and we may wish to apply the stencil in-place (i.e., overwriting the original input values) in order to decrease an application’s memory footprint.

The suitability of a stencil kernel for different devices is therefore highly dependent on properties of the stencil and the input problem. As a rule of thumb:

• Small stencils can benefit from the scratchpad storage of GPUs.

• Large stencils can benefit from the (comparatively) large caches of CPUs.

• Small stencils operating on small inputs can achieve significant performance gains via implementation as systolic arrays on FPGAs.

Since stencils are easy to describe but complex to implement efficiently, stencils are one of the most active areas of domain-specific language (DSL) development. There are already several embedded DSLs leveraging the template meta-programming capabilities of C++ to generate high-performance stencil kernels at compile time, and we hope that it is only a matter of time before these frameworks are ported to DPC++.

Reduction

A reduction is a common parallel pattern which combines partial results from each instance of a kernel invocation using an operator that is typically associative and commutative (e.g., addition). The most ubiquitous examples of reductions are computing a sum (e.g., while computing a dot product) or computing the minimum/maximum value (e.g., using maximum velocity to set time-step size).

Figure 14-4 shows the reduction pattern implemented by way of a tree reduction, which is a popular implementation requiring log₂(N) combination operations for a range of N input elements. Although tree reductions are common, other implementations are possible—in general, we should not assume that a reduction combines values in a specific order.

Figure 14-4

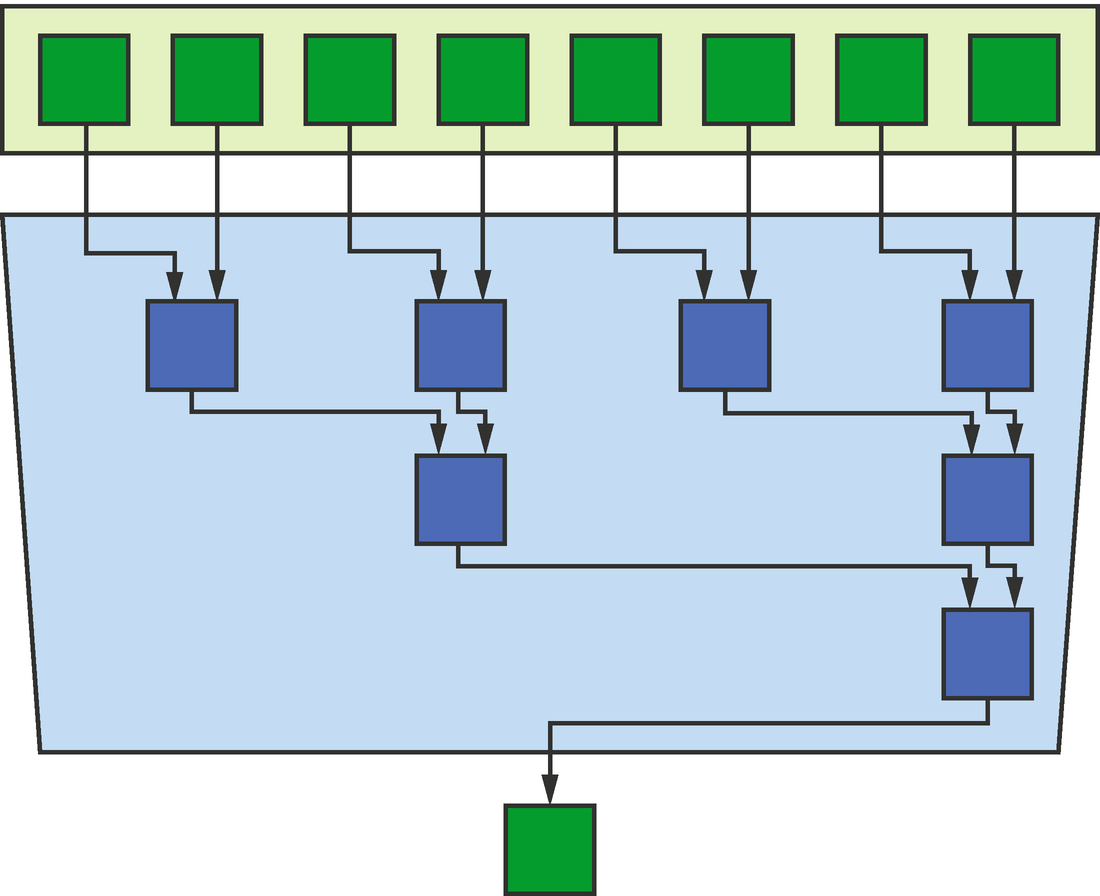
Reduction pattern

Kernels are rarely embarrassingly parallel in real life, and even when they are, they are often paired with reductions (as in MapReduce frameworks) to summarize their results. This makes reductions one of the most important parallel patterns to understand and one that we must be able to execute efficiently on any device.

Tuning a reduction for different devices is a delicate balancing act between the time spent computing partial results and the time spent combining them; using too little parallelism increases computation time, whereas using too much parallelism increases combination time.

It may be tempting to improve overall system utilization by using different devices to perform the computation and combination steps, but such tuning efforts must pay careful attention to the cost of moving data between devices. In practice, we find that performing reductions directly on data as it is produced and on the same device is often the best approach. Using multiple devices to improve the performance of reduction patterns therefore relies not on task parallelism but on another level of data parallelism (i.e., each device performs a reduction on part of the input data).

Scan

The scan pattern computes a generalized prefix sum using a binary associative operator, and each element of the output represents a partial result. A scan is said to be inclusive if the partial sum for element i is the sum of all elements in the range [0, i] (i.e., the sum including i). A scan is said to be exclusive if the partial sum for element i is the sum of all elements in the range [0, i]) (i.e., the sum excluding i).

At first glance, a scan appears to be an inherently serial operation, since the value of each output depends on the value of the previous output! While it is true that scan has less opportunities for parallelism than other patterns (and may therefore be less scalable), Figure 14-5 shows that it is possible to implement a parallel scan using multiple sweeps over the same data.

Figure 14-5

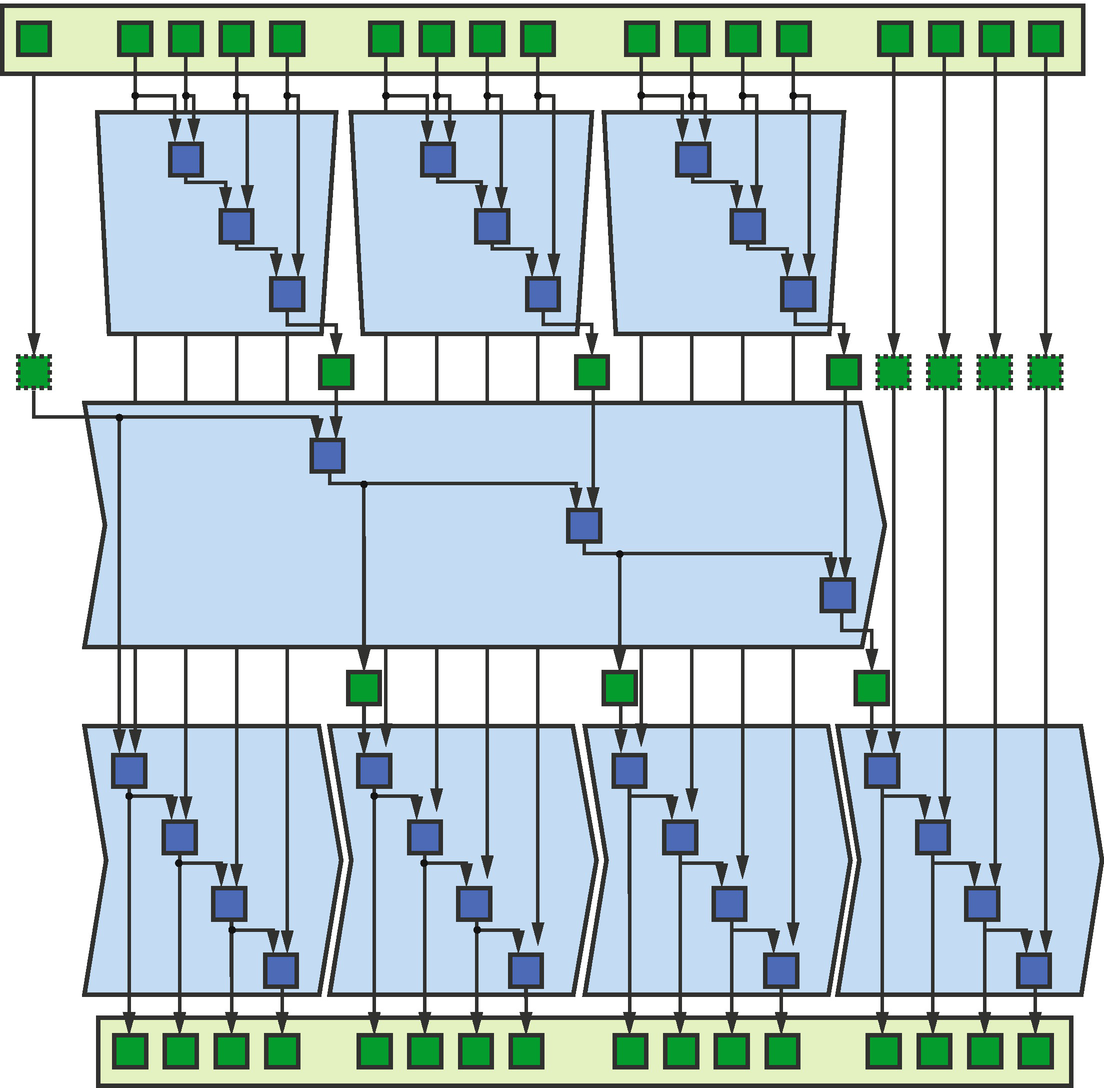
Scan pattern

Because the opportunities for parallelism within a scan operation are limited, the best device on which to execute a scan is highly dependent on problem size: smaller problems are a better fit for a CPU, since only larger problems will contain enough data parallelism to saturate a GPU. Problem size is less of a concern for FPGAs and other spatial architectures, since scans naturally lend themselves to pipeline parallelism. As in the case of a reduction, a good rule of thumb is to execute the scan operation on the same device that produced the data—considering where and how scan operations fit into an application during optimization will typically produce better results than focusing on optimizing the scan operations in isolation.

Pack and Unpack

The pack and unpack patterns are closely related to scans and are often implemented on top of scan functionality. We cover them separately here because they enable performant implementations of common operations (e.g., appending to a list) that may not have an obvious connection to prefix sums.

Pack

The pack pattern , shown in Figure 14-6, discards elements of an input range based on a Boolean condition, packing the elements that are not discarded into contiguous locations of the output range. This Boolean condition could be a pre-computed mask or could be computed online by applying some function to each input element.

Figure 14-6

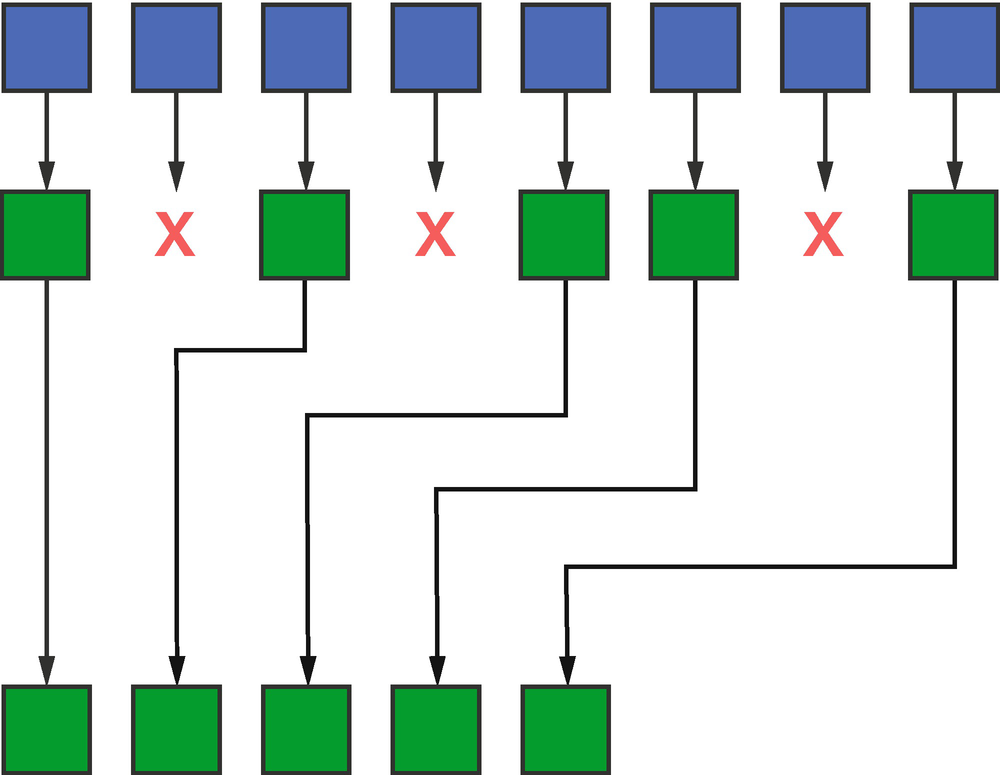
Pack pattern

Like with scan, there is an inherently serial nature to the pack operation. Given an input element to pack/copy, computing its location in the output range requires information about how many prior elements were also packed/copied into the output. This information is equivalent to an exclusive scan over the Boolean condition driving the pack.

Unpack

As shown in Figure 14-7 (and as its name suggests), the unpack pattern is the opposite of the pack pattern. Contiguous elements of an input range are unpacked into non-contiguous elements of an output range, leaving other elements untouched. The most obvious use case for this pattern is to unpack data that was previously packed, but it can also be used to fill in “gaps” in data resulting from some previous computation.

Figure 14-7

Unpack pattern

Using Built-In Functions and Libraries

Many of these patterns can be expressed directly using built-in functionality of DPC++ or vendor-provided libraries written in DPC++. Leveraging these functions and libraries is the best way to balance performance, portability, and productivity in real large-scale software engineering projects.

The DPC++ Reduction Library

Rather than require that each of us maintain our own library of portable and highly performant reduction kernels, DPC++ provides a convenient abstraction for describing variables with reduction semantics. This abstraction simplifies the expression of reduction kernels and makes the fact that a reduction is being performed explicit, allowing implementations to select between different reduction algorithms for different combinations of device, data type, and reduction operation.

The kernel in Figure 14-8 shows an example of using the reduction library . Note that the kernel body doesn’t contain any reference to reductions—all we must specify is that the kernel contains a reduction which combines instances of the sum variable using the plus functor. This provides enough information for an implementation to automatically generate an optimized reduction sequence.

Figure 14-8

Reduction expressed as an ND-range data-parallel kernel using the reduction library

At the time of writing, the reduction library only supports kernels with a single reduction variable. Future versions of DPC++ are expected to support kernels which perform more than one reduction simultaneously, by specifying multiple reductions between the nd_range and functor arguments passed into parallel_for and taking multiple reducers as arguments to the kernel functor.

The result of a reduction is not guaranteed to be written back to the original variable until the kernel has completed. Apart from this restriction, accessing the result of a reduction behaves identically to accessing any other variable in SYCL : accessing a reduction result stored in a buffer requires the creation of an appropriate device or host accessor, and accessing a reduction result stored in a USM allocation may require explicit synchronization and/or memory movement.

One important way in which the DPC++ reduction library differs from reduction abstractions found in other languages is that it restricts our access to the reduction variable during kernel execution—we cannot inspect the intermediate values of a reduction variable, and we are forbidden from updating the reduction variable using anything other than the specified combination function. These restrictions prevent us from making mistakes that would be hard to debug (e.g., adding to a reduction variable while trying to compute the maximum) and ensure that reductions can be implemented efficiently on a wide variety of different devices.

The reduction Class

The reduction class is the interface we use to describe the reductions present in a kernel. The only way to construct a reduction object is to use one of the functions shown in Figure 14-9.

Figure 14-9

Function prototypes of the reduction function

The first version of the function allows us to specify the reduction variable and the operator used to combine the contributions from each work-item. The second version allows us to provide an optional identity value associated with the reduction operator—this is an optimization for user-defined reductions, which we will revisit later.

Note that the return type of the reduction function is unspecified, and the reduction class itself is completely implementation-defined. Although this may appear slightly unusual for a C++ class, it permits an implementation to use different classes (or a single class with any number of template arguments) to represent different reduction algorithms. Future versions of DPC++ may decide to revisit this design in order to enable us to explicitly request specific reduction algorithms in specific execution contexts.

The reducer Class

An instance of the reducer class encapsulates a reduction variable, exposing a limited interface ensuring that we cannot update the reduction variable in any way that an implementation could consider to be unsafe. A simplified definition of the reducer class is shown in Figure 14-10. Like the reduction class, the precise definition of the reducer class is implementation-defined—a reducer's type will depend on how the reduction is being performed, and it is important to know this at compile time in order to maximize performance. However, the functions and operators that allow us to update the reduction variable are well-defined and are guaranteed to be supported by any DPC++ implementation.

Figure 14-10

Simplified definition of the reducer class

Specifically, every reducer provides a combine() function which combines the partial result (from a single work-item) with the value of the reduction variable. How this combine function behaves is implementation-defined but is not something that we need to worry about when writing a kernel. A reducer is also required to make other operators available depending on the reduction operator; for example, the += operator is defined for plus reductions. These additional operators are provided only as a programmer convenience and to improve readability; where they are available, these operators have identical behavior to calling combine() directly.

User-Defined Reductions

Several common reduction algorithms (e.g., a tree reduction) do not see each work-item directly update a single shared variable, but instead accumulate some partial result in a private variable that will be combined at some point in the future. Such private variables introduce a problem: how should the implementation initialize them? Initializing variables to the first contribution from each work-item has potential performance ramifications, since additional logic is required to detect and handle uninitialized variables. Initializing variables to the identity of the reduction operator instead avoids the performance penalty but is only possible when the identity is known.

DPC++ implementations can only automatically determine the correct identity value to use when a reduction is operating on simple arithmetic types and the reduction operator is a standard functor (e.g., plus). For user-defined reductions (i.e., those operating on user-defined types and/or using user-defined functors), we may be able to improve performance by specifying the identity value directly.

Support for user-defined reductions is limited to trivially copyable types and combination functions with no side effects, but this is enough to enable many real-life use cases. For example, the code in Figure 14-11 demonstrates the usage of a user-defined reduction to compute both the minimum element in a vector and its location.

Figure 14-11

Using a user-defined reduction to find the location of the minimum value with an ND-range kernel

oneAPI DPC++ Library

The C++ Standard Template Library (STL) contains several algorithms which correspond to the parallel patterns discussed in this chapter. The algorithms in the STL typically apply to sequences specified by pairs of iterators and—starting with C++17—support an execution policy argument denoting whether they should be executed sequentially or in parallel.

The oneAPI DPC++ Library (oneDPL) leverages this execution policy argument to provide a high-productivity approach to parallel programming that leverages kernels written in DPC++ under the hood. If an application can be expressed solely using functionality of the STL algorithms, oneDPL makes it possible to make use of the accelerators in our systems without writing a single line of DPC++ kernel code!

The table in Figure 14-12 shows how the algorithms available in the STL relate to the parallel patterns described in this chapter and to legacy serial algorithms (available before C++17) where appropriate. A more detailed explanation of how to use these algorithms in a DPC++ application can be found in Chapter 18.

Figure 14-12

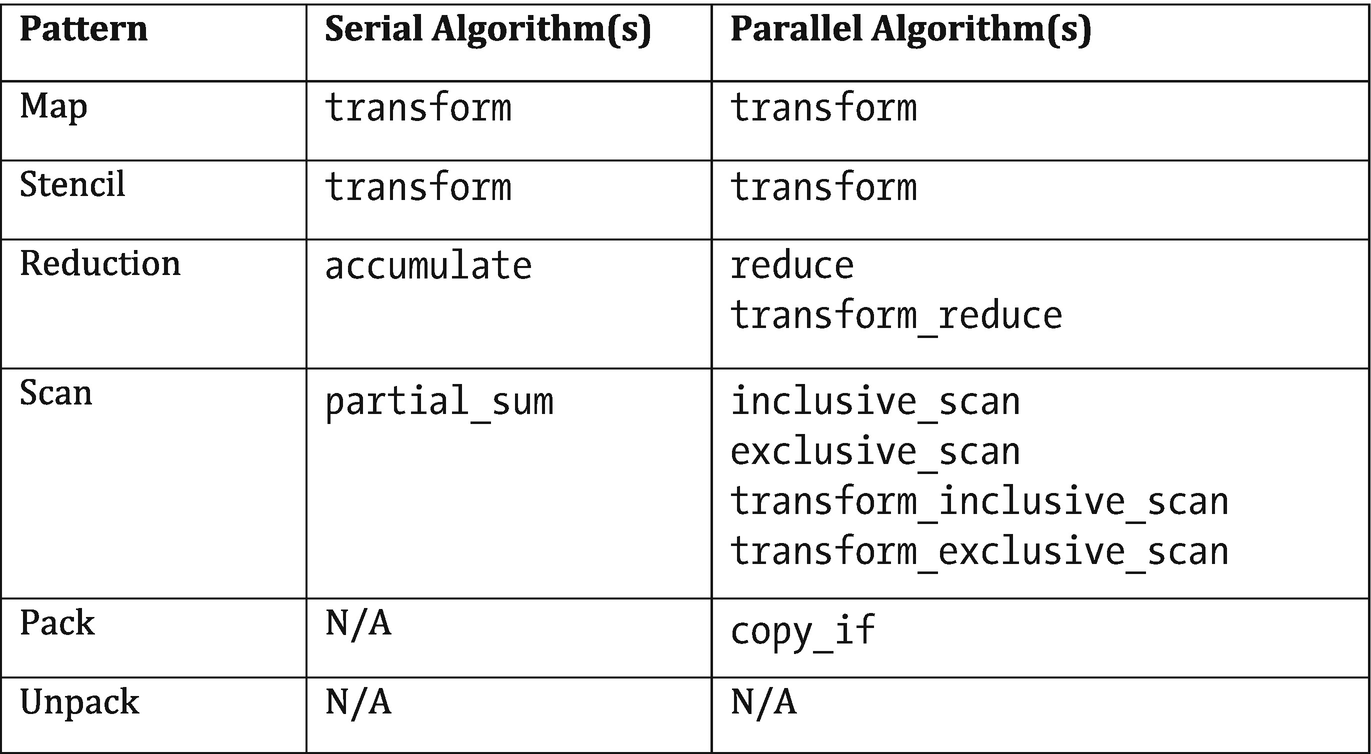
Relating parallel patterns with the C++17 algorithm library

Group Functions

Support for parallel patterns in DPC++ device code is provided by a separate library of group functions. These group functions exploit the parallelism of a specific group of work-items (i.e., a work-group or a sub-group) to implement common parallel algorithms at limited scope and can be used as building blocks to construct other more complex algorithms.

Like oneDPL, the syntax of the group functions in DPC++ is based on that of the algorithm library in C++. The first argument to each function accepts a group or sub_group object in place of an execution policy, and any restrictions from the C++ algorithms apply. Group functions are performed collaboratively by all the work-items in the specified group and so must be treated similarly to a group barrier—all work-items in the group must encounter the same algorithm in converged control flow (i.e., all work-items in the group must similarly encounter or not encounter the algorithm call), and all work-items must provide the same function arguments in order to ensure that they agree on the operation being performed.

At the time of writing, the reduce, exclusive_scan, and inclusive_scan functions are limited to supporting only primitive data types and the most common reduction operators (e.g., plus, minimum, and maximum). This is enough for many use cases, but future versions of DPC++ are expected to extend collective support to user-defined types and operators.

Direct Programming

Although we recommend leveraging libraries wherever possible, we can learn a lot by looking at how each pattern could be implemented using “native” DPC++ kernels.

The kernels in the remainder of this chapter should not be expected to reach the same level of performance as highly tuned libraries but are useful in developing a greater understanding of the capabilities of DPC++—and may even serve as a starting point for prototyping new library functionality.

USE VENDOR-PROVIDED LIBRARIES!

When a vendor provides a library implementation of a function, it is almost always beneficial to use it rather than re-implementing the function as a kernel!

Map

Owing to its simplicity, the map pattern can be implemented directly as a basic parallel kernel. The code shown in Figure 14-13 shows such an implementation, using the map pattern to compute the square root of each input element in a range.

Figure 14-13

Implementing the map pattern in a data-parallel kernel

Stencil

Implementing a stencil directly as a multidimensional basic data-parallel kernel with multidimensional buffers, as shown in Figure 14-14, is straightforward and easy to understand.

Figure 14-14

Implementing the stencil pattern in a data-parallel kernel

However, this expression of the stencil pattern is very naïve and should not be expected to perform very well. As mentioned earlier in the chapter, it is well-known that leveraging locality (via spatial or temporal blocking) is required to avoid repeated reads of the same data from memory. A simple example of spatial blocking, using work-group local memory, is shown in Figure 14-15.

Figure 14-15

Implementing the stencil pattern in an ND-range kernel, using work-group local memory

Selecting the best optimizations for a given stencil requires compile-time introspection of block size, the neighborhood, and the stencil function itself, requiring a much more sophisticated approach than discussed here.

Reduction

It is possible to implement reduction kernels in DPC++ by leveraging language features that provide synchronization and communication capabilities between work-items (e.g., atomic operations, work-group and sub-group functions, sub-group shuffles). The kernels in Figures 14-16 and 14-17 show two possible reduction implementations: a naïve reduction using a basic parallel_for and an atomic operation for every work-item; and a slightly smarter reduction that exploits locality using an ND-range parallel_for and a work-group reduce function, respectively. We will revisit these atomic operations in more detail in Chapter 19.

Figure 14-16

Implementing a naïve reduction expressed as a data-parallel kernel

Figure 14-17

Implementing a naïve reduction expressed as an ND-range kernel

There are numerous other ways to write reduction kernels, and different devices will likely prefer different implementations, owing to differences in hardware support for atomic operations, work-group local memory size, global memory size, the availability of fast device-wide barriers, or even the availability of dedicated reduction instructions. On some architectures, it may even be faster (or necessary!) to perform a tree reduction using log₂(N) separate kernel calls.

We strongly recommend that manual implementations of reductions be considered only for cases that are not supported by the DPC++ reduction library or when fine-tuning a kernel for the capabilities of a specific device—and even then, only after being 100% sure that the reduction library is underperforming!

Scan

As we saw earlier in this chapter, implementing a parallel scan requires multiple sweeps over the data, with synchronization occurring between each sweep. Since DPC++ does not provide a mechanism for synchronizing all work-items in an ND-range, a direct implementation of a device-wide scan must be implemented using multiple kernels that communicate partial results through global memory.

The code, shown in Figures 14-18, 14-19, and 14-20, demonstrates an inclusive scan implemented using several kernels. The first kernel distributes the input values across work-groups, computing work-group local scans in work-group local memory (note that we could have used the work-group inclusive_scan function instead). The second kernel computes a local scan using a single work-group, this time over the final value from each block. The third kernel combines these intermediate results to finalize the prefix sum. These three kernels correspond to the three layers of the diagram in Figure 14-5.

Figure 14-18

Phase 1 for implementing a global inclusive scan in an ND-range kernel: Computing across each work-group

Figure 14-19

Phase 2 for implementing a global inclusive scan in an ND-range kernel: Scanning across the results of each work-group

Figure 14-20

Phase 3 (final) for implementing a global inclusive scan in an ND-range kernel

Figures 14-18 and 14-19 are very similar; the only differences are the size of the range and how the input and output values are handled. A real-life implementation of this pattern could use a single function taking different arguments to implement these two phases, and they are only presented as distinct code here for pedagogical reasons.

Pack and Unpack

Pack and unpack are also known as gather and scatter operations. These operations handle differences in how data is arranged in memory and how we wish to present it to the compute resources.

Pack

Since pack depends on an exclusive scan, implementing a pack that applies to all elements of an ND-range must also take place via global memory and over the course of several kernel enqueues. However, there is a common use case for pack that does not require the operation to be applied over all elements of an ND-range—namely, applying a pack only across items in a specific work-group or sub-group.

The snippet in Figure 14-21 shows how to implement a group pack operation on top of an exclusive scan.

Figure 14-21

Implementing a group pack operation on top of an exclusive scan

The code in Figure 14-22 demonstrates how such a pack operation could be used in a kernel to build a list of elements which require some additional postprocessing (in a future kernel). The example shown is based on a real kernel from molecular dynamics simulations: the work-items in the sub-group assigned to particle i cooperate to identify all other particles within a fixed distance of i, and only the particles in this “neighbor list” will be used to calculate the force acting on each particle.

Figure 14-22

Using a sub-group pack operation to build a list of elements needing additional postprocessing

Note that the pack pattern never re-orders elements—the elements that are packed into the output array appear in the same order as they did in the input. This property of pack is important and enables us to use pack functionality to implement other more abstract parallel algorithms (such as std::copy_if and std::stable_partition). However, there are other parallel algorithms that can be implemented on top of pack functionality where maintaining order is not required (such as std::partition).

Unpack

As with pack , we can implement unpack using scan. Figure 14-23 shows how to implement a sub-group unpack operation on top of an exclusive scan.

Figure 14-23

Implementing a sub-group unpack operation on top of an exclusive scan

The code in Figure 14-24 demonstrates how such a sub-group unpack operation could be used to improve load balancing in a kernel with divergent control flow (in this case, computing the Mandelbrot set). Each work-item is assigned a separate pixel to compute and iterates until convergence or a maximum number of iterations is reached. An unpack operation is then used to replace completed pixels with new pixels.

Figure 14-24

Using a sub-group unpack operation to improve load balancing for kernels with divergent control flow

The degree to which an approach like this improves efficiency (and decreases execution time) is highly application- and input-dependent, since checking for completion and executing the unpack operation both introduce some overhead! Successfully using this pattern in realistic applications will therefore require some fine-tuning based on the amount of divergence present and the computation being performed (e.g., introducing a heuristic to execute the unpack operation only if the number of active work-items falls below some threshold).

Summary

This chapter has demonstrated how to implement some of the most common parallel patterns using DPC++ and SYCL features, including built-in functions and libraries.

The SYCL and DPC++ ecosystems are still developing, and we expect to uncover new best practices for these patterns as developers gain more experience with the language and from the development of production-grade applications and libraries.

For More Information

• Structured Parallel Programming: Patterns for Efficient Computation by Michael McCool, Arch Robison, and James Reinders, © 2012, published by Morgan Kaufmann, ISBN 978-0-124-15993-8

• Intel oneAPI DPC++ Library Guide, https://software.intel.com/en-us/oneapi-dpcpp-library-guide

• Algorithms library, C++ Reference, https://en.cppreference.com/w/cpp/algorithm

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.