1. Three questions about the dynamics of single species
3. Endogenous population variability
4. Exogenous population variability
5. Returning to the three questions
In ecology, population dynamics refers to how populations of a species change through time. The study of single-species population dynamics encompasses three general questions: (1) What explains the average abundance of a population? (2) What explains the fluctuations in abundance of a population through time? and (3) How do average abundances and fluctuations in abundance vary among populations in different geographic locations? Any of these questions can be asked of any population of any species, yet some populations pose particularly interesting challenges for one or more of the questions. Thus, ecologists often focus on populations that are remarkably large (pests) or small (endangered species), that have dramatic fluctuations through time, or that vary markedly from one location to another.
density dependence. Density-dependent population growth occurs when the per capita population growth rate changes as the population density changes. Because it changes with population density, density-dependent growth is not exponential.
dynamics. The dynamics of a population consists of the changes through time in the population size or a related measure such as density.
endogenous variability. Endogenous population variability is driven by density-dependent factors that involve interactions among individuals in the system specified by a researcher. The system could consist of a single population or populations of interacting species.
exogenous variability. Exogenous population variability is driven by factors outside the system that are not themselves influenced by population fluctuations within the system. Examples include not only environmental factors such as weather but also the abundances of other species if the dynamics of these species is not affected by the focal species within the system.
exponential population growth and decline. When the per capita population growth rate remains constant, the population experiences exponential growth or decline. Exponential population growth can also occur when the per capita population growth rate varies through time provided its average remains constant.
intrinsic rate of increase. The intrinsic rate of increase is the maximum per capita population growth rate for a population with a stable age structure (i.e., the proportions of the population in different age groups remain the same). The intrinsic rate of increase is often achieved when the population is at low density.
per capita population growth rate. The per capita population growth rate is the rate at which a population changes per individual in the population. It is often expressed as the natural logarithm of the ratio of population densities at consecutive sample times, logex(t + 1)/x(t).
population. A population is a group of individuals of the same species occupying a specified geographic area over a specified period of time. The area may be ecologically relevant (an island) or irrelevant (political districts), and the boundaries may be porous, with individuals immigrating to and emigrating from the population.
stability. Stability is defined in many ways in ecology. In models of population dynamics, stability is generally used in two ways. First, when there is no environmental stochasticity, stability describes how populations change when they are around points or cycles. A stable point, for example, is one in which, if the population density is initially near the point, it will move generally closer to the point through time. Second, when there is environmental stochasticity, a more stable system is one in which population variability is small for a given level of environmental variability in the per capita population growth rate. There are additional ways that stability can be defined in model and real systems, which necessitate care in using the word stability.
stochasticity. Stochasticity is random (unpredictable) variability that is described by a probability distribution giving the mean, variance, and other properties of the random process.
The three broad questions about single-species population dynamics boil down to: What explains the abundance of a population and changes in abundance through time and space? As an example of the first question, we could ask why, unfortunately, there are more mosquitoes than moose in Wisconsin. The answer might seem simple; moose are so much bigger than mosquitoes, they simply occupy more space and need more food. The question becomes more difficult, however, when asking why the roughly 60 species of mosquitoes in Wisconsin differ hugely in abundance. One species, Aedes vexans, is many times more common than most other species. Is this because A. vexans is more flexible in its breeding requirements and capable of breeding in more diverse habitats than other species? Is it because the females have more catholic tastes for the hosts that unwillingly give up a blood meal that the females convert to eggs? Or is it because A. vexans somehow is more adept at avoiding the many predators that turn mosquitoes into lunch? This set of questions poses a real challenge to ecologists, and a challenge of possible practical importance. Along with being common, A. vexans females also include humans in their range of suitable hosts, and if we understood why it is so common, we might also be able to change this situation.
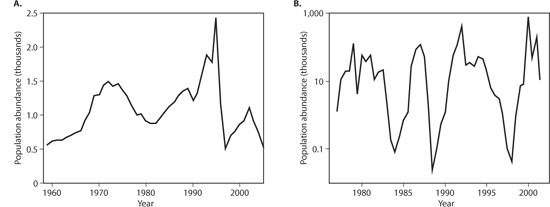
The second question is best illustrated with a figure showing two example populations (figure 1). The first, the moose population on Isle Royale in Lake Superior, fluctuates over the 45 years of data, showing a peak of 2500 individuals followed by a crash in the late 1990s to 500 individuals. This fivefold variation, however, is small in comparison to the 500,000-fold variation in the abundance of midges in Lake Myvatn, Iceland. The root causes of the fluctuations of both populations are the same: a combination of depleted food resources (balsam fir trees for moose, algae for midges) and predation (by wolves on moose and a variety of species on midges). Despite having the same general causes, however, why are the fluctuations in midges so much more dramatic?
Finally, an example of the third question is posed by the pattern of population dynamics shown by many small rodent species such as voles. Many populations at high latitudes show strong fluctuations, often exceeding two orders of magnitude, whereas populations of the same species fluctuate much less dramatically at lower latitudes. A tempting explanation for this pattern is simply that populations at higher latitudes have to contend with a more severe climate, in particular hard winters, and the severe climate drives greater population fluctuations. This answer cannot be the sole explanation, however, because the fluctuations in rodent populations at high latitudes do not match the fluctuations in weather conditions. In fact, some peaks in rodent abundances occur in winter instead of summer. Ecolo-gists suspect that predators are involved in the high population fluctuations of rodents at high latitudes and that the importance of these predators for some reason diminishes for populations closer to the equator.
Figure 1. Population abundances of (A) moose on Isle Royale (http://www.isleroyalewolf.org) and (B) the midge Tanytarsus gracilentus in Lake Myvatn, Iceland (Ives et al., 2008). Note the log10 scale in B.
This chapter is about single-species population dynamics, so a discussion of what is a single-species population is in order. In ecology, what is meant by a population is often given by the context of the discussion or study. In the examples above, the moose population on Isle Royale is clearly delineated; it is the number of individuals on the island, and Lake Superior gives a clear, ecologically relevant boundary through which moose do not easily pass (despite being excellent swimmers). In other cases, the boundaries might be clear but ecologically irrelevant. For example, the population of moose in Wisconsin is delineated by political, not ecological boundaries. For issues of population management, political boundaries make sense, but not so for ecological concerns. Furthermore, the boundaries are porous, with moose obliviously crossing from Michigan to Wisconsin and back again. Nonetheless, the moose population of Wisconsin can still be delineated and counted, making it clear what the population is.
Obviously, single-species populations consist of a single species, although no species lives on an island unto itself. Population dynamics of any species will be affected by other species—species that it consumes, species that consume it, species that compete, and species that might in some way help (such as pollinators helping plants). Although ecologists recognize the importance of interactions among species, very often studies are conducted on a single focal species, with other species considered only to the extent that they affect the dynamics of the focal species. In this way, other species are treated somewhat like the weather. Often, the reason for focusing on a single species is simply pragmatic. If there is a single species that is of applied or academic interest, it is necessary to limit the ecological extent of the investigation to what can sensibly be studied with the resources available.
The other topic of this chapter is density dependence, and explaining this requires an entire section.
The easiest way to explain density dependence is to consider when it is absent. In particular, consider European rabbits. Rabbits have remarkable reproductive proclivity. At 3 months of age, the females start to breed, and a single pair can produce up to 40 offspring per year. The consequence of this breeding ability was seen when Thomas Austin introduced 24 rabbits for sport hunting onto his property in the state of Victoria, Australia, on Christmas Day, 1859. Within 10 years, the descendants of these rabbits reached a population numbering in the millions that spread throughout much of eastern Australia. By the early twentieth century, the population plateaued at about 200 million.
The population growth of rabbits can described by a simple mathematical formula,
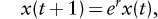
where x(t) is the population size of rabbits in year t, and r is a biological parameter called the intrinsic rate of increase, which gives the maximum rate at which the rabbit population can increase. Studies have shown that r for invading European rabbits is roughly 2.5 year-1, which when plugged into this equation means the population can increase by a factor of e2.5 = 12 each year. This reproductive potential is impressive, the more so when the equation above is used to predict the growth of the rabbit population. Starting with 24 rabbits, assuming they and their descendants maintain the intrinsic rate of increase of 2.5 year-1, in 5 years the population would be over 250,000, and in 10 years it would be almost 100 billion (1011). Following this exponential growth a little longer, in about 21 years the mass of rabbits would exceed that of the Earth (6x1024kg).
This did not happen. The reason is that rabbits experienced density-dependent reductions in their per capita population growth rate. The per capita population growth rate is the natural logarithm of the number of individuals in a population at some time t +1 divided by the number at time t, logex(t +1)/x(t), where time is measured in units appropriate for the species (years for rabbits, minutes for bacteria, etc.). The per capita population growth rate integrates both reproduction and survival, and when the per capita population growth rate is density dependent, the birth and/or death rates change with density. For rabbits in Australia, when densities became very high, birthrates declined and death rates increased as rabbits suffered food shortages.
Like rabbits, all populations cannot maintain their intrinsic rate of increase indefinitely. Eventually, densities will become high enough that birthrates decline and/or death rates increase. Eventually, the per capita population growth rate will drop to zero. Populations that persist for long periods of time must have negative per capita population growth rates at high densities that stop unbounded increases and positive per capita population growth rates at low densities to stop population extinction. In fact, in the long run, a population must have an average per capita population growth rate of zero.
Although all persisting populations must have density-dependent population dynamics, the factors leading to density dependence are often multiple, complex, and not easily identified and understood. For example, the exotic dynamics shown by midges in Lake Myvatn (figure 1B), with fluctuations of over five orders of magnitude, involves density dependence that causes populations to crash from very high densities. But what explains the timing of the crashes, why do the midges crash for several generations in a row, and what saves the population at low density so that the species does not become extinct? Detailed answers to these questions about midges, and similar questions for other species, are often extremely hard to answer. Much of the study of population ecology revolves around explaining the factors causing density dependence and the consequences they have for population dynamics.
Density dependence not only bounds a population above and below but also sets the character of the population dynamics. To illustrate this, it is easiest to use another mathematical model that includes a density-dependent per capita population growth rate, specifically
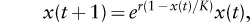
where, as before, r is the intrinsic rate of increase, and K is often called the carrying capacity. Here, the per capita population growth rate, r(1 — x(t)/K), decreases as the population size x(t) increases, reaching zero when x(t) = K. Thus, K for the rabbits in Australia would be around 200 million. Because the per capita population growth rate is positive when x(t) is less than K and negative when x(t) is greater than K, it seems reasonable to expect that the population will eventually settle close to K. Although this is the case sometimes, it is not always so. This is because density dependence itself can generate population variability.
Before we proceed, a disclaimer is needed. Simple models such as the one above are extremely helpful in understanding basic ecological phenomena, such as the possible consequences of density dependence. Nonetheless, they are not very realistic and do not necessarily do a good job describing the dynamics of any real species. But it is in fact their unrealistic simplicity that makes these models didactically valuable; the point is not that real populations act exactly like the model but instead that the general types of phenomena shown by the model may in fact have counterparts in real systems.
Figure 2 illustrates the population dynamics generated by the simple model with density-dependent per capita population growth rates for three values of the intrinsic rate of increase, r. When r is low (r = 0.1), the population can increase only slowly, so a graph of x(t + 1) versus x(t) is nearly a straight line (figure 2A). Nonetheless, the line curves down slightly, showing that the population is increasing when x(t) is below the carrying capacity K and decreasing when x(t) is above K. When r is intermediate (r = 1), there is a higher per capita population growth rate when densities are low, yet the per capita population growth rate declines more rapidly so that x(t + 1) = x(t) again when x(t) = K (figure 2B). Finally, when r is high (r = 2.2), the population increases very rapidly from low densities and declines rapidly from high densities (figure 2C). In fact, it increases so rapidly that the relationship between x(t + 1) and x(t) is strongly hump-shaped; when the population density starts at some intermediate value, say K/2, the resulting population at the next time step is higher than K, whereas if the population starts at high values, say 2 K, the population subsequently crashes to very low levels.
Plots of the model populations over time reflect these patterns. When r is low, the population rises slowly toward the carrying capacity K (figure 2D), whereas when r is intermediate, the population attains K rapidly (figure 2E). However, when r is high, the population experiences perpetual booms and busts; when populations are initially low, they bounce to high densities in the next time step and then drop down again in the time step after that. In this case, the formerly stable carrying capacity becomes unstable; even if the population started very close to K, it would exhibit cycles of increasing amplitude until it settled down to the perpetual cycle. Thus, although the carrying capacity K is unstable, the cycle is stable. Such stable boom-and-bust cycles are rarely seen so starkly in real populations, but this in no way diminishes the lesson from the simple model that density dependence can itself generate population fluctuations. There is no environmental variability in the model, so the only factor creating these cycles is endogenous.
Do purely endogenously driven population fluctuations occur in nature? Certainly, although not necessarily as clearly and simply as in the model. In laboratory systems, sustained fluctuations have been created for flies and beetles that involve either populations that reach high enough densities to consume all their food, or cannibalism in which high densities of adults consume large numbers of juveniles. In nature, sustained cycles consistent with a single-species population model have been observed for fish species in which a few, large adult individuals dominate the population by consuming most of the juveniles. This domination is punctuated by bursts of juvenile success when the current large adults senesce and die, and the burst of juvenile recruitment establishes the next dominant cohort of adults. These types of endogenous fluctuations involve species that have distinct stage structures, a topic discussed in chapter Even more complex possibilities occur when there are strong interactions among two or more species, another topic described in chapter II.3.
Figure 2. Hypothetical population dynamics generated by the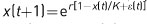 
for values of the intrinsic rate of increase r = 0.1, 1, and 2.2. Panels A-C plot the population abundance at time step t+1 against the abundance in the previous time step t. The gray line gives the one-to-one line; therefore, x(t+1) crosses the dashed line at K, because at K, x(t+1) = x(t). Panels D-F give trajectories of population abundance, x(t), through time t when there is no environmental stochasticity, ε (t) = 0. Panels G–I give population trajectories with environmental stochasticity starting from K; each trajectory is subjected to the same sequence of environmental fluctuations given by values of ε(t).
In the models so far, the only source of population fluctuations has been density dependence, but real populations are buffeted by purely environmental forces. The consequences of these exogenous sources of population variability on population dynamics depend on density dependence. To illustrate the importance of density dependence, the population model can be modified to include environmental stochasticity— variability that is unpredictable. Specifically, let the per capita population growth rate be r (1 — x(t)/K) + ε(t), where ε(t) is selected at random from a normal probability distribution. Thus, the per capita population growth rate includes density dependence and environmental stochasticity.
Figure 2G–I illustrates examples of population trajectories generated by the new stochastic model. Even though the environmental stochasticity [the values of ε(t)] is the same for all examples, the impact it has on population fluctuations is markedly different. These differences can be understood by comparing populations with and without environmental stochasticity (figure 2D-F). When the intrinsic rate of increase, r, is low, population densities are brought very slowly toward the carrying capacity K (figure 2D). Therefore, in the presence of environmental stochasticity (figure 2G), the weak endogenous force of density dependence does little to counteract the environmental fluctuations that buffet populations away from their initial abundance at K. In contrast, for intermediate r (figure 2E), population densities away from K are returned rapidly, so in the stochastic case, the environmentally driven fluctuations are more rapidly damped out (figure 2H). Finally, for the high value of r there are sustained fluctuations driven by endogenous processes alone (figure 2F). Environmental stochasticity adds to this variability, creating cycles that tend to have higher booms and lower busts (figure 2I).
This simple model with environmental stochasticity illustrates the dual nature of density dependence. Density dependence can reduce the magnitude of population fluctuations if it acts to bring the population rapidly to some stable point (K in the simple model). Conversely, density dependence can itself generate endogenous population variability by driving a point unstable. Thus, understanding population fluctuations requires understanding the interactions between density-dependent per capita population growth rates and exogenous stochasticity.
The three questions concerning singlespecies population dynamics—what explains the abundance of a population, and how its abundance changes through time and space—intimately involve density dependence. Density dependence sets the average population abundance because the average abundance is where the average per capita population growth rate is zero. Density dependence also determines the characteristics of the fluctuations in population abundance through time because it can generate endogenous population fluctuations. Furthermore, density dependence determines the impact of environmental stochasticity on population dynamics, either damping out environmental stochasticity rapidly or allowing it to produce large fluctuations in population abundance. Finally, when populations in different geographic locations differ in either average abundance or the characteristics of their dynamics, then density dependence somehow differs among populations.
Although density dependence is fundamental to population dynamics, determining how per capita population growth rates depend on density for a specific species is often very difficult. To measure how per capita population growth rates depend on density, it is necessary to observe populations at both very low and very high abundances. Some populations fluctuate sufficiently violently that they naturally occur at both very low and very high abundances, but other populations do not. Experiments designed to perturb population abundances are often the best way to measure density dependence, although for many species, such manipulative experiments are impossible or unethical. Another difficulty is that species dynamics are generally affected by those of other species, such as species that are eaten by the focal species, compete with the focal species, or eat the focal species. For species with strong and close interactions, the dynamics of one cannot be separated from those of the other species.
Despite these difficulties, we know a lot about the dynamics and density dependence of a large number of plant and animal species. This is not a random selection of species. Some species were studied because they have practical significance, either being pests that we want to eliminate or endangered species that we want to protect. Other well-studied species were selected because they are particularly easy to study, at least relative to related species in other areas. For example, the study of moose on Isle Royale has the advantage that the population is well defined and isolated from factors (such as deer and elk populations) that could complicate its dynamics. A final set of well-studied species consists of those whose dynamics is sufficiently dramatic to beg an explanation that an ecologist cannot resist, for example, the hugely fluctuating midge population in Lake Myvatn. To understand the population dynamics of any species requires long-term study into the many facets of the species ecology that affect its per capita population growth rate.
Gotelli, Nicholas J. 2001. A Primer of Ecology, 3rd ed. Sunderland, MA: Sinauer Associates.
Gurney, W.S.C., and R. M. Nisbet. 1998. Ecological Dynamics. New York: Oxford University Press.
Ives, Anthony R. 1998. Population ecology. In S. I. Dodson, T.F.H. Allen, S. R. Carpenter, A. R. Ives, R. L. Jeanne, J. F. Kitchell, N. E. Langston, and M. G. Turner, eds. Ecology. New York: Oxford University Press, 235–314.
Turchin, Peter. 2003. Complex Population Dynamics: A Theoretical/Empirical Synthesis. Princeton, NJ: Princeton University Press.
