PART II

ARISTARCHUS OF SAMOS ON THE SIZES AND DISTANCES OF THE SUN AND MOON

I

ARISTARCHUS OF SAMOS

WE are told that Aristarchus of Samos was a pupil of Strato of Lampsacus,1 a natural philosopher of originality,² who succeeded Theophrastus as head of the Peripatetic school in 288 or 287 B.C. and held that position for eighteen years. Two other facts enable us to fix Aristarchus’s date approximately. In 281/280 B.C. he made an observation of the summer solstice;³ and the book in which he formulated his heliocentric hypothesis was published before the date of Archimedes’ Psammites or Sandreckoner, a work written before 216 B.C. Aristarchus therefore probably lived circa 310–230 B.C., that is, he came about 75 years later than Heraclides and was older than Archimedes by about 25 years.

Aristarchus was called ‘the mathematician’, doubtless in order to distinguish him from the many other persons of the same name; he is included by Vitruvius among the few great men who possessed an equally profound knowledge of all branches of science, geometry, astronomy, music, &c. ‘Men of this type are rare, men such as were, in times past, Aristarchus of Samos, Philolaus and Archytas of Tarentum, Apollonius of Perga, Eratosthenes of Cyrene, Archimedes and Scopinas of Syracuse, who left to posterity many mechanical and gnomonic appliances which they invented and explained on mathematical (lit. numerical) and natural principles.’4 That Aristarchus was a very capable geometer is proved by his extant work On the sizes and distances of the sun and moon, translated in this volume: in the mechanical line he is credited with the discovery of an improved sun-dial, the so-called , which had, not a plane, but a concave hemispherical surface, with a pointer erected vertically in the middle throwing shadows and so enabling the direction and the height of the sun to be read off by means of lines marked on the surface of the hemisphere.⁵ He also wrote on vision, light, and colours.⁶ His views on the latter subjects were no doubt largely influenced by his master Strato; thus Strato held that colours were emanations from bodies, material molecules, as it were, which imparted to the intervening air the same colour as that possessed by the body,⁷ while Aristarchus said that colours are ‘shapes or forms stamping the air with impressions like themselves as it were’,⁸ that ‘colours in darkness have no colouring’,⁹ and that light is^c the colour impinging on a substratum’.¹⁰ It does not appear that Strato can be credited with any share in his astronomical discoveries: of Strato we are only told (1) that, like Metrodorus before him, he held that the stars received their light from the sun (Metrodorus alleged this of ‘all the fixed stars’, and it is not stated that Strato made any limitation);¹¹ (2) that he held a comet to be ‘the light of a star enclosed in a thick cloud, just as happens with (torches)’;¹² (3) that, like Parmenides and Heraclitus, he considered the heaven to be of fire;¹³ (4) that he regarded time as^l quantity in (i.e. expressed by) things in motion and at rest’;¹⁴ (5) that he said the divisions of the universe were without limit;¹⁵ and (6) that he maintained that there was no void outside the universe, though there might be within it.¹⁶

The Heliocentric Hypothesis.

There is not the slightest doubt that Aristarchus was the first to put forward the heliocentric hypothesis. Ancient testimony is unanimous on the point, and the first witness is Archimedes, who was a younger contemporary of Aristarchus, so that there was no possibility of a mistake. Copernicus himself admitted that the theory was attributed to Aristarchus, though this does not seem to be generally known. Thus Schiaparelli quotes two passages from Copernicus’s work in which he refers to the opinions of the ancients about the motion of the earth. One is in the dedicatory letter to Pope Paul III, where Copernicus mentions that he first found out from Cicero that one Nicetas (i.e. Hicetas) had attributed motion to the earth, and that he afterwards read in Plutarch that certain others held that opinion; he then quotes the Placita, according to which ‘Philolaus the Pythagorean asserted that the earth moved round the fire in an oblique circle, in the same way as the sun and moon.17 The other passage is in Book I, c. 5, where, after an allusion to the views of Heraclides, Ecphantus, and Nicetas (Hicetas), who made the earth rotate about its own axis at the centre of the universe, he goes on to say that it would not be very surprising if any one should attribute to the earth another motion besides rotation, namely revolution in an orbit in space; ‘atque etiam (terram) pluribus motibus vagantem et unam ex astris Philolaus Pythagoricus sensisse fertur, Mathematicus non vulgaris.’ Here, however, there is no question of the earth revolving round the sun, and there is no mention of Aristarchus. But it is a curious fact that Copernicus did mention the theory of Aristarchus in a passage which he afterwards suppressed: ‘Credibile est hisce similibusque causis Philolaum mobilitatem terrae sensisse, quod etiam nonnulli Aristarchum Samium ferunt in eadem fuisse sentential.’¹⁸

I will now quote the whole passage of Archimedes in which the allusion to Aristarchus’s heliocentric hypothesis occurs, in order to show the whole context.¹⁹

‘You are aware [‘you’ being King Gelon] that “universe” is the name given by most astronomers to the sphere, the centre of which is the centre of the earth, while its radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account , as you have heard from astronomers. But Aristarchus brought out a book consisting of certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than the “universe” just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun in the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface. Now it is easy to see that this is impossible; for, since the centre of the sphere has no magnitude, we cannot conceive it to bear any ratio whatever to the surface of the sphere. We must, however, take Aristarchus to mean this: since we conceive the earth to be, as it were, the centre of the universe, the ratio which the earth bears to what we describe as the “universe” is equal to the ratio which the sphere containing the circle in which he supposes the earth to revolve bears to the sphere of the fixed stars. For he adapts the proofs of the phenomena to a hypothesis of this kind, and in particular he appears to suppose the size of the sphere in which he makes the earth move to be equal to what we call the “universe”.’

We shall come back to the latter part of this passage; at present we are concerned only with the italicized words. The heliocentric hypothesis is stated in language which leaves no room for dispute as to its meaning. The sun, like the fixed stars, remains unmoved and forms the centre of a circular orbit in which the earth revolves round it;20 the sphere of the fixed stars has its centre at the centre of the sun. But a question arises as to the form in which Aristarchus’s hypotheses were given out. The expression used by Archimedes is , ‘put out of certain hypotheses.’ I take it in the sense of bringing out a tract or tracts consisting of or stating certain hypotheses; for one of the meanings of the word is a ‘writing’ or a written ‘description’. Heiberg takes in this sense, but regards as the title of the book (‘libros quosdam edidit, qui hypotheses inscribuntur’21). Hultsch,²² however, takes in its other possible sense of ‘drawings’ or figures constructed to represent the hypotheses; and Schiaparelli²³ suggests that the word here used seems not only to signify a verbal description but to include also the idea of explanatory drawings. I agree that it is probable enough that Aristarchus’s tract or tracts included geometrical figures illustrating the hypotheses, but I still think that the word here does not itself mean ‘figures’ but means written statements of certain hypotheses. This seems to me clear from the words immediately following , namely ., ‘in which it results from the assumptions made that the universe is many times greater than our “universe” above mentioned’; ‘in which’ can only refer to or and it cannot refer to because what follows from the assumptions made cannot be in those assumptions which are nothing but the hypotheses themselves; therefore ‘in which’ refers to , but a result following from assumptions does not follow in figures illustrating those assumptions but in the course of a description of them or an argument about them. The words ‘in which it results . . .’ also show clearly enough that the tract or tracts did not merely state the hypothesis but also included some kind of geometrical proof.²⁴ I need only add that there are other cases of the use of in the sense of ‘writing’; cf. an expression in Eutocius, ‘I have come across writings of many famous men which give this problem [that of the two mean proportionals].25

Our next evidence is a passage of Plutarch²⁶:

‘Only do not, my good fellow, enter an action against me for impiety in the style of Cleanthes, who thought it was the duty of Greeks to indict Aristarchus of Samos on the charge of impiety for putting in motion the Hearth of the Universe, this being the effect of his attempt to save the phenomena by supposing the heaven to remain at rest and the earth to revolve in an oblique circle, while it rotates, at the same time, about its own axis.’

Here we have the additional detail that Aristarchus followed Heraclides in attributing to the earth the daily rotation about its axis; Archimedes does not state this in so many words, but it is clearly involved by his remark that Aristarchus supposed that the fixed stars as well as the sun remain unmoved in space. When Plutarch makes Cleanthes say that Aristarchus ought to be indicted for the impiety of ‘putting the Hearth of the Universe in motion’, he is probably quoting the exact words used by Cleanthes, who doubtless had in mind the passage in Plato’s Phaedrus where ‘Hestia abides alone in the House of the Gods’. A similar expression is quoted by Theon of Smyrna from Dercyllides, who ‘says that we must suppose the earth, the Hearth of the House of the Gods according to Plato, to remain fixed, and the planets with the whole embracing heaven to move, and rejects with abhorrence the view of those who have brought to rest the things which move and set in motion the things which by their nature and position are unmoved, such a supposition being contrary to the hypotheses of mathematics’;²⁷ the allusion here is equally to Aristarchus, though his name is not mentioned. A tract ‘Against Aristarchus’ is mentioned by Diogenes Laertius among Cleanthes’ works; and it was evidently published during Aristarchus’s lifetime (Cleanthes died about 232 B.C.).

Other passages bearing on our present subject are the following.

‘Aristarchus sets the sun among the fixed stars and holds that the earth moves round the sun’s circle (i.e. the ecliptic) and is put in shadow according to its (i. e. the earth’s) inclinations.’28

One of the two versions of this passage has ‘the disc is put in shadow’, and it would appear, as Schiaparelli says, ‘that the words “the disc” were interpolated by some person who thought that the passage was an explanation of solar eclipses.’ It is indeed placed under the heading ‘Concerning the eclipse of the sun’; but this is evidently wrong, for we clearly have here in the concisest form an explanation of the phenomena of the seasons according to the system of Copernicus.²⁹

‘Yet those who did away with the motion of the universe and were of opinion that it is the earth which moves, as Aristarchus the mathematician held, are not on that account debarred from having a conception of time.’³⁰

‘Did Plato put the earth in motion, as he did the sun, the moon, and the five planets, which he called the instruments of time on account of their turnings, and was it necessary to conceive that the earth “which is globed about the axis stretched from pole to pole through the whole universe” was not represented as being held together and at rest, but as turning and revolving , as Aristarchus and Seleucus afterwards maintained that it did, the former stating this as only a hypothesis , the latter as a definite opinion ?’³¹

‘Seleucus the mathematician, who had written in opposition to the views of Crates, and who himself too affirmed the earth’s motion, says that the revolution of the moon resists the rotation [and the motion]³² of the earth, and, the air between the two bodies being diverted and falling upon the Atlantic ocean, the sea is correspondingly agitated into waves.’³³

When Plutarch refers to Aristarchus as only putting forward the double motion of the earth as a hypothesis, he must presumably be basing himself on nothing more than the word hypotheses used by Archimedes, and his remark does not therefore exclude the possibility of Aristarchus having supported his hypothesis by some kind of argument; nor can we infer from Plutarch that Seleucus went much further towards proving it. Plutarch says that Seleucus declared the hypothesis to be true , but it is not clear how he could have attempted to prove it. Schiaparelli suggests that Aristarchus’s attitude may perhaps be explained on the basis of the difference between the rôles of the astronomer and the physicist as distinguished by Geminus in the passage quoted above (pp. 275–6). Aristarchus, as the astronomer and mathematician, would only be concerned to put forward geometrical hypotheses capable of accounting for the phenomena; he may have left it to the physicists to say ‘which bodies ought from their nature to be at rest and which to move’. But this is only a conjecture.

Seleucus, of Seleucia on the Tigris, is described by Strabo34 as a Chaldaean or Babylonian; he lived about a century after Aristarchus and may have written about 150 B.C. The last of the above quotations is Aetius’s summary of his explanation of the tides, a subject to which Seleucus had evidently given much attention;³⁵ in particular, he controverted the views held on this subject by Crates of Mallos, the ‘grammarian’, who wrote on geography and other things, as well as on Homer. The other explanations of the tides summarized by Aetius include those ot Aristotle and Heraclides, who sought the explanation in the sun, holding that the sun sets up winds, and that these winds, when they blow, cause the high tide and, when they cease, the low tide; Dicaearchus who put the tides down to the direct action of the sun according to its position; Pytheas and Posidonius who connected them with the moon, the former directly, the latter through the setting up of winds; Plato who posited a certain general oscillation of the waters, which pass through a hole in the earth;³⁶ Timaeus who gave as the reason the unequal flow of rivers from the Celtic mountains into the Atlantic; then, immediately before Seleucus, are mentioned Crates ‘the grammarian’ and Apollodorus of Corcyra, the account of whose views is vague enough, the former attributing the tides to ‘the counter-movement of the sea,’37 and the latter to ‘the refluxes from the Ocean’. When Aëtius adds, in introducing Seleucus’s views, that ‘he too made the earth move’, we should expect that he had just before mentioned some one else who had done the same. But Crates adhered to the old view and did not make the earth move;³⁸ nor is there anything to suggest that Apollodorus attributed motion to the earth. Consequently Bergk supposes that, just before the notice of Seleucus’s explanation of the tides with reference to the earth’s motion, there must have been a notice of a different explanation of them by a person who also attributed motion to the earth, and that, as we know of no other person by name who adopted Aristarchus’s views, except Seleucus, the notice which has dropped out must have given a different explanation of the tides by Aristarchus himself.³⁹ But, as the motion of the earth referred to in Seleucus’s explanation may be rotation only ( or ), it seems possible that Heraclides (who made the earth rotate) is the other person referred to in the collection of notices as having ‘made the earth move’, although he is mentioned some way back. To judge by Seleucus’s explanation of the tides, he would seem to have supposed that the atmosphere about the earth extended as far as the moon and rotated with the earth in 24 hours, and that the resistance of the moon acted upon the rotating atmosphere either by virtue of the relative slowness of the moon’s revolution about the earth or of its motion perpendicular to the equator;⁴⁰ Strabo tells us that Seleucus had discovered periodical inequalities in the flux and reflux of the Red Sea which he connected with the position of the moon in the zodiac.⁴¹

No one after Seleucus is mentioned by name as having accepted the doctrine of Aristarchus, and if other Greek astronomers refer to it, they do so only to denounce it, as witness Dercyllides.⁴² The rotation of the earth is, however, mentioned as a possibility by Seneca.

‘It will be proper to discuss this, in order that we may know whether the universe revolves and the earth stands still, or the universe stands still and the earth rotates. For there have been those who asserted that it is we whom the order of nature causes to move without our being aware of it, and that risings and settings do not occur by virtue of the motion of the heaven, but that we ourselves rise and set. The subject is worthy of consideration, in order that we may know in what conditions we live, whether the abode allotted to us is the most slowly or the most quickly moving, whether God moves everything around us, or ourselves instead.’43

Hipparchus, himself a contemporary of Seleucus, reverted to the geocentric system, and it was doubdess his great authority which sealed the fate of the heliocentric hypothesis for so many centuries. The reasons which weighed with Hipparchus were presumably (in addition to the general prejudice in favour of maintaining the earth in the centre of the universe) the facts that the system in which the earth revolved in a circle of which the sun was the exact centre failed to ‘save the phenomena’, and in particular to account for the variations of distance and the irregularities of the motions, which became more and more patent as methods of observation improved; that, on the other hand, the theory of epicycles did suffice to represent the phenomena with considerable accuracy; and that the latter theory could be reconciled with the immobility of the earth.

We revert now to the latter part of the passage quoted above from Archimedes, in which he comments upon the assumption of Aristarchus that the sphere of the fixed stars is so great that the ratio in which the earth’s orbit stands to the said sphere is such a ratio as that which the centre of the sphere bears to its surface. If this is taken in a strictly mathematical sense, it means of course that the sphere of the fixed stars is infinite in size, a supposition which would not suit Archimedes’ purpose, because he is undertaking to prove that he can evolve a system for expressing large numbers which will enable him to state easily in plain words the number of grains of sand which the whole universe could contain; hence, while he wishes to base his estimate of the maximum size of the universe upon some authoritative statement which will be generally accepted, and takes the statement of Aristarchus as suitable for his purpose, he is obliged to interpret it in an arbitrary way which he can only justify by somewhat sophistically pressing the mathematical point that Aristarchus could not have meant to assert that the sphere of the fixed stars is actually infinite in size and therefore could not have wished his statement to be taken quite literally; consequently he suggests that a reasonable interpretation would be to take it as meaning that

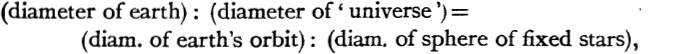
instead of

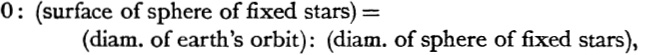
and he explains that the ‘universe’ as commonly conceived by the astronomers of his time (he refers no doubt to the adherents of the system of concentric spheres) is a sphere with the earth as centre and radius equal to the distance of the sun from the earth, and that Aristarchus seems to regard the sphere containing (as a great circle) the orbit in which the earth revolves about the sun as equal to the ‘universe’ as commonly conceived, so that the second and third terms of the first of the above proportions are equal.

While it is clear that Archimedes’ interpretation is not justified, it may be admitted that Aristarchus did not mean his statement to be taken as a mathematical fact. He clearly meant to assert no more than that the sphere of the fixed stars is incomparably greater than that containing the earth’s orbit as a great circle; and he was shrewd enough to see that this is necessary in order to reconcile the apparent immobility of the fixed stars with the motion of the earth. The actual expression used is similar to what was evidently a common form of words among astronomers to express the negligibility of the size of the earth in comparison with larger spheres. Thus, in his own tract On the sizes and distances of the sun and moon, Aristarchus lays down as one of his assumptions that ‘the earth is in the relation of a point and centre to the sphere in which the moon moves’. In like manner Euclid proves, in the first theorem of his Phaenomena, that ‘the earth is in the middle of the universe and holds the position of centre relatively to the universe’. Similarly Geminus44 describes the earth as ‘in the relation of a centre to the sphere of the fixed stars’; Ptolemy⁴⁵ says that the earth is not sensibly different from a point in relation to the radius of the sphere of the fixed stars; according to Cleomedes⁴⁶ the earth is ‘in the relation of a centre’ to the sphere in which the sun moves, and a fortiori to the sphere of the fixed stars, but not to the sphere in which the moon moves.

In Aristarchus’s extant treatise On the sizes and distances of the sun and moon there is no hint of the heliocentric hypothesis, but the sun and moon are supposed to move in circles round the earth as centre. From this we must infer either (1) that the work in question was earlier than the date at which he put forward the hypotheses described by Archimedes, or (2) that, as in the tract the distances of the sun from the earth and of the moon from the earth are alone in question, and therefore it was for the immediate purpose immaterial which hypothesis was taken, Aristarchus thought it better to proceed on the geocentric hypothesis which was familiar to everybody. Schiaparelli⁴⁷ suggests that one of the reasons which led Aristarchus to place the sun in the centre of the universe was probably the consideration of the sun’s great size in comparison with the earth. Now in the treatise referred to Aristarchus finds the ratio of the diameter of the sun to the diameter of the earth to lie between 19:3 and 43:6; this makes the volume of the sun something like 300 times the volume of the earth, and, although the principles of dynamics were then unknown, it might even in that day seem absurd to make the body which was so much larger revolve round the smaller.

There is no reason to doubt that, in his heliocentric system, Aristarchus retained the moon as a satellite of the earth revolving round it as a centre; thus even in his system there was one epicycle, that described by the moon about the earth as centre.

The apparent diameter of the sun.

Another passage of the Sand-reckoner of Archimedes states that

‘Aristarchus discovered that the sun’s apparent size is about one 720th part of the zodiac circle.’48

This, again, is a valuable contribution to our knowledge of Aristarchus, for in the treatise On the sizes and distances of the sun and moon he makes the apparent diameter not of the zodiac circle, or , but one-fifteenth part of a sign, that is to say 2°, which is a gross over-estimate. The nearest estimate to this which we find recorded appears to be that mentioned by Macrobius,⁴⁹ who describes an experiment madé with a hemispherical dial by marking the points on which the shadow of the upright needle fell at the moments respectively when the first ray of the sun as it began to rise fell on the instrument and when the sun just cleared the horizon respectively. The result showed that the interval of time was of an hour, which gave as the apparent diameter of the sun of 360° or . Macrobius would apparently have us believe that this very inaccurate estimate was due to the Egyptians. We have, however, seen reason to believe that Macrobius probably attributed to the ‘Egyptians’ the doctrines of certain Alexandrian astronomers,⁵⁰ and in the present case it would seem that we have to do with an observation very unskilfully made by some even less competent person.⁵¹ The Babylonians had, however, many centuries before arrived at a much closer approximation; they made the time which the sun takes to rise of an hour, and, even if the hour is the double hour (one-twelfth of a day and night), this gives 1° as the apparent diameter of the sun. How, then, did Aristarchus in his extant work come to take 2° as the value? Tannery has an interesting suggestion, which is however perhaps too ingenious.⁵² ‘If Aristarchus chose for the apparent diameter of the sun a value which he knew to be false, it is clear, that his treatise was mainly intended to give a specimen of calculations which require to be made on the basis of more exact experimental observations, and to show at the same time that, for the solution of the problem, one of the data could be chosen almost arbitrarily. He secured himself in this way against certain objections which might have been raised. According to the testimony of Macrobius, it seems that in fact the Egyptians had, by observations completely erroneous, fixed the apparent diameter of the sun at of the circumference, i.e. . Aristarchus seems to have deliberately chosen to assign it a still higher value; but it is beyond question that he was perfectly aware of the consequences of his hypothesis.’ Manitius⁵³ suggests that the ‘one-fifteenth part ’ of a sign of the zodiac in Aristarchus’s treatise should be altered into ‘one-fiftieth part’ , which would give the quite acceptable value of o° 36′. But the propositions in the treatise in which the hypothesis is actually used seem to make it clear that ‘one-fifteenth’ is what Aristarchus really wrote. Unless therefore we accept Tannery’s suggestion, we seem to be thrown back once more on the supposition that the treatise was an early work written before Aristarchus had made the more accurate observation recorded by Archimedes. From the statement of Archimedes that Aristarchus discovered the value of , I think we may infer with safety that Aristarchus was at least the first Greek who had given it, and we have therefore an additional reason for questioning the tradition which credits Thales with the discovery. How Aristarchus obtained his result we are not told, but, seeing that he is credited with the invention of an improved sun-dial , it is possible that it was by means of this instrument that he made his observations. Archimedes himself seems to have been the first to think of the better method of using an instrument for measuring angles; by the use of a rough instrument of this kind he made the apparent angular diameter of the sun lie between the limits of and of a right angle. Hipparchus used for the same purpose a more elaborate instrument, his dioptra, the construction of which is indicated by Ptolemy,⁵⁴ and is more fully described by Pappus in his commentary on Book V of Ptolemy, quoted by Theon of Alexandria;⁵⁵ Proclus describes it somewhat differently.⁵⁶ Though we gather that Hipparchus made many observations of the apparent diameters of the sun and moon,⁵⁷ only one actual result is handed down; he found that the diameter of the moon was contained about 650 times in the circle described by it.⁵⁸ This would no doubt be the mean of the different observations of the moon at its varying distances; it is of course equivalent to nearly o° 33′ 14″. Ptolemy complains that the requisite accuracy could not be secured by the dioptra; he therefore checked the observations as regards the moon by means of ‘certain lunar eclipses’, and found Hipparchus’s values appreciably too high. Ptolemy⁵⁹ himself made the apparent diameter of the moon to be (a) at the time when it is furthest from the earth o° 31′ 20″, and (b) at its least distance o° 35′ 20″. The mean of these figures being o° 33′ 20″, and the true values corresponding to Ptolemy’s figures being 29′ 26″ and 32′ 51″, it follows that Hipparchus’s mean value is actually nearer the true mean value than Ptolemy’s.⁶⁰ Aristarchus, as we shall see, took the apparent diameters of the sun and moon to be the same. Sosigenes (2nd c. A. D.) showed that they are not always equal by adverting to the phenomenon of annular eclipses of the sun,⁶¹ and doubtless Hipparchus had observed the differences; Ptolemy found that the apparent diameter of the sun was approximately constant, whenever observed, its value being the same as that of the moon when at its greatest distance, not (‘as supposed by earlier astronomers‘) when at its mean distance.⁶² Another estimate of the apparent diameter of the sun, namely of the complete circle described by the sun, or 29′, is given by Cleomedes as having been obtained by means of a water-clock; he adds that the Egyptians are said to have been the first to discover this method.⁶³ Yet another valuation appears in Martianus Capella;⁶⁴ the diameter of the moon is there estimated as of its orbit or 36′. This estimate was probably quoted from Varro, and belongs to a period anterior to Hipparchus.⁶⁵

The Year and the Great Year of Aristarchus.

We are told by Censorinus that Aristarchus added of a day to Callippus’s figure of days for the solar year,66 and that he gave 2,484 years as the length of the Great Year, or the period after which the sun, the moon, and the five planets return to the same position in the heavens.⁶⁷ Tannery⁶⁸ shows that 2,484 years is probably a mistake for 2,434 years, and he gives an explanation, which seems convincing, of the way in which Aristarchus arrived at his figures. They were doubtless derived from the Chaldaean period of 223 lunations and the multiple of this by 3, which was called , a period defined by Geminus as the shortest time containing a whole number of days, a whole number of months (synodic), and a whole number of anomalistic months.⁶⁹ The Greeks were by Aristarchus’s time fully acquainted with these periods, which were doubtless known through the Chaldaean Berosus, who flourished about 280 B.C., in the time of Alexander the Great, and founded an astronomical school on the island of Cos opposite Miletus. Ptolemy,⁷⁰ too, says of the first of the two periods (which he attributes to ‘the ancients’, not the Chaldaeans specifically) that it was estimated at days, containing 223 lunations, 239 ‘restorations of anomaly’ (i.e. anomalistic months), 242 ‘restorations of latitude’ (i.e. draconitic months, the draconitic month–a term not used by Ptolemy–meaning the period after which the moon returns to the same position with respect to the nodes), and 241 sidereal revolutions phus which the sun describes in the time in addition to 18 sidereal revolutions. The exeligmus then, which was three times this period, consisted of 19,756 days, containing 669 lunations, 717 anomalistic months, 726 draconitic months, and 723 sidereal revolutions plus 32L described by the sun in the period over and above 54 sidereal revolutions.

It follows that the number of days in the sidereal year is

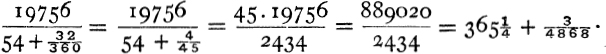
Now . Thus, in replacing the complementary by Aristarchus followed the fashion of only admitting fractions with unity as numerator, and thereby only neglected the insignificant fraction or .

It is clear that Aristarchus multiplied by 45 so as to avoid all fractions, and so arrived at 889,020 days containing 2,434 sidereal years, 30,105 lunations, 32,265 anomalistic months, 32,670 draconitic months, and 32,539 sidereal months.

Tannery gives good reason for thinking that this evaluation of the solar year at days was really a sort of argument in a circle and was therefore worthless. The Chaldaean period was obtained from the observation of eclipses; those which were similar were classified, and it was recognized that they returned at the end of a period estimated at days. If the theory of the sun had been sufficiently established, or if the difference of longitude between the positions of two similar eclipses had been observed and allowance made for the solar anomaly, it would have been possible to evaluate with precision the number of degrees traversed during the period by the sun over and above the whole number of its revolutions. But this precision was beyond the powers of the Chaldaeans, and the estimate of the excess of was probably obtained by means of the simple difference between days and 18 years of days or days. This difference is days, and, if this is turned into degrees by multiplying by , we have about ; the complementary fraction would then be neglected as unimportant. Thus Aristarchus’s estimate of days was valueless, as the Chaldaean period itself depended on a solar year of days.

The question remaining is whether Aristarchus’s Great Year was intended to be the period which brings all the five planets as well as the sun and moon back again to the same places, as appears to be implied by Censorinus, who mentions different estimates of the Great Year (including Aristarchus’s) just after an explanation that ‘there is also a year which Aristotle calls the greatest rather than the great year, which is completed by the sun, the moon, and the five planets when they return together to the same sign in which they were once before simultaneously found’. As Tannery observes, if Aristarchus’s Great Year corresponded to an effective determination of the periods of the revolutions of the planets, it would have a particular interest because Aristarchus would have, in accordance with his system, to treat the revolution of Mercury and Venus as heliocentric, whereas in the earlier estimates of Great Years, e.g. that of Oenopides, the revolution of these planets was geocentric and of the same mean duration as that of the sun, so that they could be left out of account. But, just as we were obliged to conclude that Oenopides could not have maintained that his Great Year of 59 years contained a whole number of the periods of revolution of the several planets, so it seems clear that Aristarchus could hardly have maintained that his Great Year exactly covered an integral number of the periods of revolution of the five planets. For suppose that his Great Year of 889,020 days is divided by the respective periods of their sidereal revolutions, and that we take the nearest whole numbers to the quotients—say 10,106 for Mercury, 3,950 for Venus, 1,294 for Mars, 206 for Jupiter, 83 for Saturn—the errors as regards the positions at the end of the period would amount, according to Tannery’s calculation, to 133° for Saturn, 70° for Jupiter, 25° for Mars, 171° for Venus, and 11° for Mercury. This being so, it is difficult to believe that the period of Aristarchus is anything more than a luni-solar cycle.71

---

¹ Aëtius, i. 15. 5 (D. G. p. 313).

² Galen, Histor. Philos, 3 (D. G. p. 601. 1).

³ Ptolemy, Syntaxis, iii. 2 (i, pp. 203, 206, ed. Heib.).

⁴ Vitruvius, De architectura, i. 1. 16.

⁵ Ibid. ix. 8 (9). I.

⁶ Aet. i. 15. 5 (A G. p. 313), iv. 13–8 (D. G. pp. 404 and 853).

⁷ Aet. iv. 13. 7 (D. G. p. 403).

⁸ Ibid. iv. 13. 8 (D. G, pp. 404 and 853).

⁹ Ibid. i. 15. 9 (D. G. p. 314).

¹⁰ Ibid. i. 15. 5 (D. G. p. 313).

¹¹ Ibid. ii. 17. 1–2 (D. G. p. 346).

¹² Ibid. iii. 2. 4 (D. G. p. 366).

¹³ Ibid. ii. 11. 4 (D. G. p. 340).

¹⁴ Ibid. i. 22. 4 (D. G. p. 318).

¹⁵ Epiphanius, Adv. haeres. iii. 33 (D. G. p. 592).

¹⁶ Aet. i. 18. 4 (D.G. p. 316).

¹⁷ Ps. Plutarch, De plac. phil. = Aët. iii. 13. 2 (D. G. p. 378).

¹⁸ De Revolutionibus Caelestibus, ed. Thorun., 1873, p. 34 note, quoted in Gomperz, Griechische Denker, i³, p. 432.

¹⁹ Archimedes, ed. Heiberg, vol. ii, p. 244 (Arenarius 1. 4–7); The Works of Archimedes, ed. Heath, pp. 221, 222.

²⁰ There is only one slight awkwardness in the language. The sentence is and it would be natural to suppose that the relative would refer to the masculine substantive nearest to it, i.e. ‘circle,’ rather than ‘the sun’; but ‘which is situated in the middle of the (earth’s) course’ cannot possibly refer to the circle, i. e. to the course itself, and must refer to the sun. The awkwardness suggested to Bergk (Fünf Abhandlungen, 1883, p. 162) that Archimedes wrote , ‘which is in the middle of the heaven.’ This would enable to refer to the ‘circle’, but there seems to be no sufficient ground for changing the reading .

²¹ Archimedes, ed. Heiberg, vol. ii, p. 245.

²² Hultsch, art. ‘Aristarchus’ in Pauly-Wissowa’s Real-Encyclopädie, p. 875.

²³ Schiaparelli, Origine del sistemaplanetario eliocentrico presso i Greet, p. 95.

²⁴ Bergk (Fünf Abhandlungen, p. 160) thinks that ‘ cannot be taken as synonymous with : this would be a somewhat otiose circumlocution: but it means the “outline” (Umriss), like . Archimedes chooses this expression because Aristarchus had rather indicated his hypotheses than worked them out and established them.’ I do not think this inference necessary; may be quite colourless without being otiose, a sufficient reason for its insertion being the fact that some word other than is necessary as an antecedent to the relative sentence ‘in which it follows from the assumptions made, &c.’

²⁵ Archimedes, ed. Heiberg, vol. iii, p. 66. 9.

²⁶ Plutarch, De facie in orbe lunae, c. 6, pp. 922 F - 923 A.

²⁷ Theon of Smyrna, p. 200. 7–12, ed. Hiller.

²⁸ Aët. ii. 24. 8 (D. G. p. 355. 1–5).

²⁹ Schiaparelli, I precursori, p. 50.

³⁰ Sextus Empiricus, Adv. Mathematicos, x. 174, p. 512. 19, Bekker.

³¹ Plutarch, Plat, quaest. viii. 1, 1006 C.

³² The Ps. Plutarch version has the words ‘and the motion,’ after ; Stobaeus omits them, and has instead of .

³³ Aet. iii. 17. 9 (D. G. p. 383).

³⁴ Strabo, xvi. 1. 6, i. 1. 9.

³⁵ Cf. Strabo, iii. 5. 9.

³⁶ Cf. Phaedo 111 c sqq.

³⁷ Some details of Crates’ views are also given in Strabo, i. 1.8.

³⁸ Bergk (Fünf Abhandlungen, p. 166) quotes from Strabo, i. 2. 24, the words, .

³⁹ Bergk, op. cit., p. 167.

⁴⁰ Schiaparelli, I precursori, p. 36.

⁴¹ Strabo, iii. 5. 9.

⁴² Theon of Smyrna, p. 200. 7–12: see above (p. 304).

⁴³ Seneca, Nat. Quaest. vii. 2. 3.

⁴⁴ Geminus, Isagoge, 18. 16, p. 186. 16, ed. Manitius.

⁴⁵ Ptolemy, Syntaxis, i. 6, p. 20. 5, Heib.

⁴⁶ Cleomedes, De motu circulari, i. 11.

⁴⁷ Schiaparelli, I precursori, p. 33.

⁴⁸ Archimedes, ed. Heiberg, ii, p. 248. 19; The Works of Archimedes, ed. Heath, p. 223.

⁴⁹ Macrobius, In somn. Scip. i. 20. 26–30.

⁵⁰ See p. 259 above.

⁵¹ Hultsch, Poseidonios über die Grösse und Entfernung der Sonne, p. 43.

⁵² Tannery, ‘Aristarque de Samos’ in Mém. de la Soc. des sciences phys. et nat. de Bordeaux, 2^e sér. v. 1883, p. 241; Mémoires scientifiques, ed. Heiberg and Zeuthen, i, pp. 375–6.

53 Proclus, Hypotyposis, ed. Manitius, note on p. 292.

⁵⁴ Ptolemy, Syntaxis, v. 14, p. 417. 2–3 and 20–23, ed. Heib.

55 Theon, in Ptolem. magn. construct. p. 262,

⁵⁶ Proclus, Hypotyposis, ed. Manitius, pp. 126. 13–128. 13,

⁵⁷ Ptolemy, Syntaxes, loc. cit.

⁵⁸ Ptolemy, Syntaxis, iv. 9, p. 327. 1–3, Heib.

⁵⁹ Ptolemy, v. 14, p. 421. 3–5; Pappus, ed. Hultsch, vi, p. 556. 17–19.

⁶⁰ On the whole of this subject see Hultsch, ‘Winkelmessungen durch die Hipparchische Dioptra’ in Abhandlungen zur Gesch. d. Math. ix (Cantor-Festschrift), 1899, pp. 193–209.

⁶¹ Simplicius on De caelo, p. 505. 7–9, Heib.

⁶² Ptolemy, Syntaxis, v. 14, p. 417. 3–11, Heib.

⁶³ Cleomedes, De motu circulari, ii. 1, pp. 136–8, ed. Ziegler.

⁶⁴ Martianus Capella, De nuptiis philologiae et Mercurii, viii. 860.

⁶⁵ Tannery, Recherches sur l’histoire de l’astronomie ancienne, p. 334.

⁶⁶ Censorinus, De die natali, c. 19. 2.

⁶⁷ Ibid., c. 18. 11.

⁶⁸ Tannery, ‘La Grande Année d’Aristarque de Sarnos’ in Mém. de la Soc. des sciences phys. et naturelles de Bordeaux, 3^e série, iv. 1888, pp. 79–96.

⁶⁹ Geminus, Isagoge, c. 18, pp. 2co sqq., ed. Manitius.

⁷⁰ Ptolemy, Syntaxis, iv. 2. pp.269. 21–270. 18, Heib.

⁷¹ Tannery, loc. cit., pp. 93–4.