for the time when the moon is at its mean distance in the conjunctions; Ptolemy chose the time when the moon is at its greatest distance, and made the ratio insensibly less than 
(a little too large).3THE style of Aristarchus is thoroughly classical, as befits an able geometer intermediate in date between Euclid and Archimedes, and his demonstrations are worked out with the same rigour as those of his predecessor and successor. The propositions of Euclid’s Elements are, of course, taken for granted, but other things are tacitly assumed which go beyond what we find in Euclid. Thus the transformations of ratios defined in Eucl. V and indicated by the terms inversely, alternately, componendo, convertendo, &c., are regularly and naturally used in dealing with unequal ratios, whereas in Euclid they are only used in proportions, i. e. cases of equality of ratios. But the propositions of Aristarchus are also of particular mathematical interest because the ratios of the sizes and distances which have to be calculated are really trigonometrical ratios, sines, cosines, &c., although at the time of Aristarchus trigonometry had not been invented, while no reasonably close approximation to the value of π, the ratio of the circumference of a circle to its diameter, had been made (it was Archimedes who first obtained the value 22/7). Exact calculation of the trigonometrical ratios being therefore impossible for Aristarchus, he set himself to find upper and lower limits for them, and he succeeded in locating those which emerge in his propositions within tolerably narrow limits, though not always the narrowest within which it would have been possible, even for him, to confine them. In this species of approximation to trigonometry he tacitly assumes propositions comparing the ratio between a greater and a less angle in a figure with the ratio between two straight lines in the figure, propositions which are formally proved by Ptolemy at the beginning of his Syntaxis. Here, again, we have a proof that text-books containing such propositions existed before Aristarchus’s time, and probably much earlier, although they have not survived.
One of the assumptions or hypotheses at the beginning of the treatise, the grossly excessive estimate of 2° for the apparent angular diameter of the moon, has already been discussed (pp. 311, 312 above). We proceed to Hypotheses 4 and 5, giving values for a certain ratio and a certain other angle respectively.
In Hypothesis 5, Aristarchus takes the diameter of the earth’s shadow (at the place where the moon passes through it at the time of an eclipse) to be twice that of the moon. The figure 2 for this ratio was presumably based on the observed length of the longest eclipses on record.1 Hipparchus, as we learn from Ptolemy,2 made the ratio for the time when the moon is at its mean distance in the conjunctions; Ptolemy chose the time when the moon is at its greatest distance, and made the ratio insensibly less than (a little too large).3
Tannery4 shows in an interesting way the connexion between (1) the estimate (Hypothesis 4) that the angular distance between the sun and moon viewed from the earth at the time when the moon appears halved is 87°, the complement of 3°, (2) the estimate (Hypothesis 5) of 2 for the ratio of the diameter of the earth’s shadow to that of the moon, and (3) the ratio (greater than 18 to 1 and less than 20 to 1) of the diameter of the sun to the diameter of the moon as obtained in Props. 7 and 9 of our treatise.
The diagram overleaf (Fig. 14) will serve to indicate very roughly the relative positions of the sun, the earth, and the moon at the moment during a lunar eclipse when the moon is in the middle of the earth’s shadow.
Fig. 14.
Let S be the radius of the sun’s orbit,
L moon’s orbit,
s the radius of the sun,
l . . . moon,
t . . . earth,
D the distance from the centre of the earth to the vertex of the cone of the earth’s shadow,
and d the radius of the earth’s shadow at the distance of the moon.
Then we have, approximately, by similar triangles,
whence, if we suppose that 
, and put 
, we easily derive
and
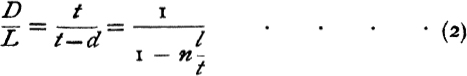
Now, since eclipses of the sun occur through the interposition of the moon, S > L, so that s > l. The ancients knew, too, that the sun is larger than the earth, so that s > t. It follows from (1) that 
, so that the moon is smaller than the earth.
Now suppose δ to be the angle subtended at the centre of the sun by the distance between the moon and the earth at the time when the moon appears halved, i.e. when the earth, sun, and moon form a right-angled triangle with its right angle at the centre of the moon.
Let 
We have then from (1), substituting s/x for l,
and, substituting lx for s, we have
Fig. 15.
Now if 
is taken at 19, Aristarchus’s mean value, and n = 2, these formulae give
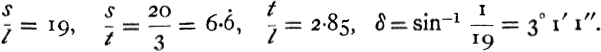
Tannery’s object is to prove that the method of our treatise was not invented by Aristarchus but by Eudoxus. We know in the first place, from Aristotle, that by the middle of the fourth century mathematical speculations on the sizes and distances of the sun and moon had already begun. Aristotle5 says:
‘Besides, if the facts as shown in the theorems of astronomy are correct, and the size of the sun is greater than that of the earth, while the distance of the stars from the earth is many times greater than the distance of the sun, just as the distance of the sun from the earth is many times greater than that of the moon, the cone marking the convergence of the sun’s rays (after passing the earth) will have its vertex not far from the earth, and the earth’s shadow, which we call night, will therefore not reach the stars, but all the stars will necessarily be in the view of the sun, and none of them will be blocked out by the earth.’
Now Eudoxus was the first person to develop scientifically the hypothesis that the sun and moon remain at a constant distance from the earth respectively, and this is the hypothesis of Aristarchus. Further, we are told by Archimedes that Eudoxus had estimated the ratio of the sun’s diameter to that of the moon at 9:1, Phidias, Archimedes’ father, at 12:1, and Aristarchus at a figure between 18:1 and 20:1. Accordingly, on the assumption that Eudoxus and Phidias took n = 2 in the above formulae, as Aristarchus did, we can make out the following table:
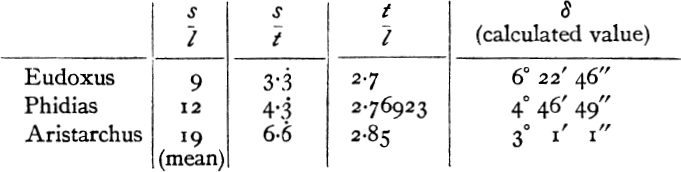
Hence, says Tannery, while Aristarchus took 3° as the value of δ, Eudoxus probably took 6° or 
of a sign of the zodiac, and Phidias 5° or 
of a sign. ‘I cannot believe that these values were deduced from direct observations of the angular distance. The necessary instruments were in all probability not in existence in the fourth century. But Eudoxus could, on the day of the dichotomy, mark the positions of the sun and the moon in the zodiac, and try to observe at what hour the dichotomy took place. The evaluations involve an error of about twelve hours for Eudoxus, ten for Phidias, and six for Aristarchus. It seems that all of them sought upper limits for δ. It will be noticed that the value of δ especially affects the values of the ratios s/l, s/t; the ratio t/l on the contrary depends mostly on the value of n.’6 Seeing, however, that the only figures in the above tables which are actually attested are the three in the first column, the 3° of Aristarchus, and the results obtained by Aristarchus on the basis of his assumptions, it seems a highly speculative hypothesis to suppose that Eudoxus started with 6°, and Phidias with 5°, as Aristarchus did with 3°, and then deduced the ratio of the diameter of the sun to that of the moon by precisely Aristarchus’s method.
Besides the formal Assumptions laid down at the beginning of the treatise, there lie at the root of Aristarchus’s reasoning certain propositions assumed without proof, presumably because they were generally known to mathematicians of the day. The most general of these propositions are the equivalent of the statements that—
If α is what we call the circular measure of an angle, and α is less than 
, then
(1) The ratio sin α/α decreases as α increases from 0 to 
, but (2) the ratio tan α/α increases as α increases from 0 to 
.
Tannery7 took pains to set out the trigonometrical equivalents of the particular results obtained by Aristarchus in the several propositions.
If we bear in mind that
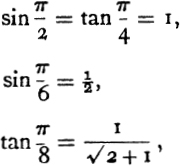
and if we substitute for 
the approximate value 
which is assumed by Aristarchus, we can deduce the following inequalities:
or
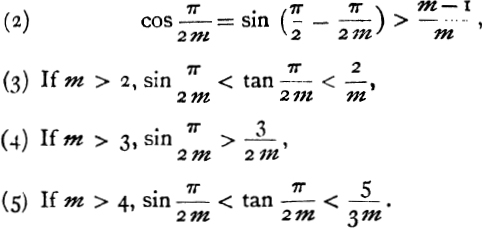
The narrowest limits for sin 
obtained by means of these inequalities are
whereas, if Aristarchus had known the approximate value 
for π, he could have obtained the closer upper limit
Now, for example, in Prop. 7, Aristarchus has to find limits for sin 3°, that is to say sin 
; thus m = 30, and the formula (6) above gives his
In Prop. 4 Aristarchus proves the negligibility of the maximum angle 
subtended at the centre of the earth by a certain arc (α) on the surface of the moon subtended at the centre of the moon by an angle equal to half the apparent angular diameter of the moon. From the figure of the proposition it is easy to see that, taking the radius of the moon to be unity,
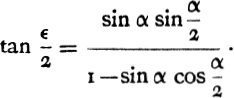
For, if M be the foot of the perpendicular from H on AB,
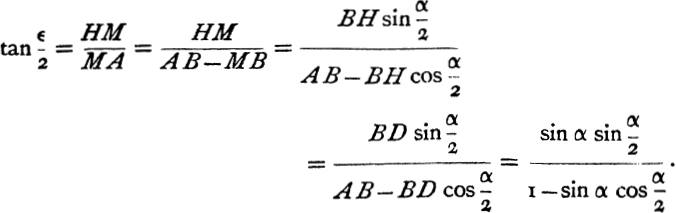
This would give, for α = 1°, 
.
What Aristarchus in fact does is to prove that
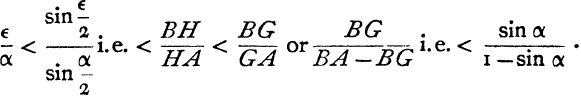
Now, if α = π/2m (m > 4), formula (5) above would give
but Aristarchus is content with the equivalent of using formula (3) which gives
In Prop. 11 Aristarchus uses the equivalent of formulae (3) and (4), proving that
Prop. 12 is the equivalent of using formula (2) to prove that
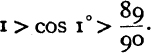
From formula (2) we deduce
and, for m = 90, this gives the equivalent of the first part of Prop. 13, namely
In Prop. 14 Aristarchus determines a lower limit for the ratio L/c, where L is the radius of the moon’s orbit and c the distance of the centre of the moon from the centre of the circle of the shadow at the middle of an eclipse. The arithmetical value of the limit depends of course on the particular assumptions which he makes as to the angles subtended at the centre of the earth by the diameter of the moon and by the diameter of the circle of the shadow. If these angles be 2α, 2γ respectively, we see from the figure of Prop. 14 that
Therefore, ex aequali,
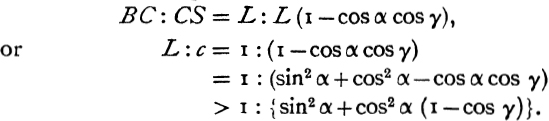
If γ = 2α, as assumed by Aristarchus, this becomes
The corresponding inequality obtained by Aristarchus, who assumes that α = 1°, is
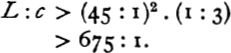
The generalized trigonometrical equivalent of Prop. 15 is more complicated and need not be given here. Tannery has an interesting remark, which was however anticipated by Fortia d’Urban,8 upon one of the arithmetical results obtained by Aristarchus in that proposition. If y be the ratio of the sun’s radius to the earth’s radius, his result is
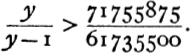
He replaces this value by 
, merely remarking that ‘71755875 has to 61735500 a ratio greater than that which 43 has to 37’. It is difficult, says Tannery, not to see in 
the expression
, which suggests that 
was obtained by developing 
or 
as a continued fraction. ‘We have here an important proof of the employment by the ancients of a method of calculation, the theory of which unquestionably belongs to the moderns, but the first applications of which are too simple not to have originated in very remote times.’
1 Tannery, Recherches sur l’histoire de l’astronomie ancienne, p. 225.
2 Ptolemy, Syntaxis, iv. 9, p. 327. 3–4, Heib.
3 Ibid., v. 14, p. 421. 12–13.
4 Tannery in Mémoires de la Société des sciences physiques et naturelles de Bordeaux, 2e série, v, 1883, PP. 241–3; Mémoires scientifiques, ed. Heiberg and Zeuthen, i, 1912, pp. 376–9.
5 Arist. Me!eorologica, i. 8, 345 b 1–9.
6 Tannery, Mémoires de la Société des sciences phys. et nat, de Bordeaux, 2e série, v, 1883, pp. 243–4; Mémoires saentifiques, ed. Heiberg and Zeuthen, i, P. 379.
7 Tannery, Mémoires de la Soc. des sciences phys. et nat. de Bordeaux, 2e série, v, 1883, pp. 244 sq.; Mémoires scientiftques, i, pp. 380 sqq.
8 Fortia d’Urban, Traité d’Aristarque de Samos, 1823, p. 86, note.
