WHILE it would not be consistent with the plan of this work to carry the history of Greek astronomy beyond Aristarchus, it will be proper, I think, to conclude this introduction with a few particulars of the improvements which later Greek astronomers made upon Aristarchus’s estimates of sizes and distances.
We have already spoken of Aristarchus’s assumption of 87° as the angle subtended at the centre of the earth by the line joining the centres of the sun and moon at the time when the moon appears halved. The true value of this angle is 89° 50′, so that Aristarchus’s estimate was decidedly inaccurate; no direct estimate of the angle seems to have been made by his successors. Aristarchus himself, as we have seen, afterwards corrected to 
the estimate of 2° for the apparent angular diameter of the sun and moon alike. His assumption of 2 as the ratio of the diameter of the circle of the earth’s shadow to the diameter of the moon was improved upon by Hipparchus and Ptolemy. Hipparchus made it 
at the moon’s mean distance at the conjunctions;1 Ptolemy made it at the moon’s greatest distance ‘inappreciably less than 
’.2
Coming now to estimates of absolute and relative sizes and distances, we find some data in Archimedes;3 according to him Eudoxus had declared the diameter of the sun to be nine times the diameter of the moon, and Phidias (Archimedes’ father) twelve times; most astronomers, he says, agreed that the earth is greater than the moon, and ‘some have tried to prove that the circumference of the earth is about 300,000 stades and not greater’. It seems probable that it was Dicaearchus who (about 300 B.C.) arrived at this value,4 and that it was obtained by taking 24° (1/15th of the whole meridian circle) as the difference of latitude between Syene and Lysimachia (on the same meridian), and 20,000 stades as the actual distance between the two places,5 Archimedes’ own estimates are scarcely estimates at all; they are intentionally exaggerated, as, his object being to measure the number of grains of sand that would fill the universe, he adopts what he considers maximum values in order to be on the safe side. Thus he says that, whereas Aristarchus tried to prove that the ratio of the diameter of the sun to that of the moon is between 18:1 and 20: 1, he himself will take the ratio to be 30:1 and not greater, in order that his thesis may be proved ‘beyond all cavil’; in the case of the earth he actually multiplies the estimate of the perimeter by 10, making it 3,000,000 instead of 300,000 stades.
Before passing on to later writers, it will be convenient to recapitulate Aristarchus’s figures; and for brevity I shall use the letters by which Tannery denotes the various distances and radii, namely S for the distance of the centre of the sun, L for the distance of the centre of the moon, from the centre of the earth, and s, l, t for the radii of the sun, moon, and earth respectively. Aristarchus’s figures then are as follows :
We may with Hultsch,6 for convenience of comparison with other calculations, take figures approximating to the mean between the higher and lower limits; and it will be convenient to express the various diameters and distances in terms of the diameter of the earth. We may say then, roughly, that
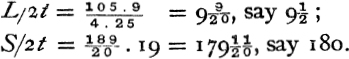
We are not told what size Aristarchus attributed to the earth, but presumably, like Archimedes, he would have accepted Dicaearchus’s estimate of 300,000 stades for its circumference.
Eratosthenes (born about eleven years after Archimedes, say 276 B.C.) is famous for a measurement of the earth based on scientific principles. He found that at noon at the summer solstice the sun threw no shadow at Syene, while at the same hour at Alexandria (which he took to be on the same meridian) it made the gnomon in the scaphe cast a shadow showing an angle equal to one-fiftieth of the whole meridian circle; assuming, further, that the sun’s rays at Syene and Alexandria are parallel in direction, and that the known distance from Syene to Alexandria is 5,000 stades (doubtless taken as a round figure), Eratosthenes arrived by an easy geometrical proof at 50 times 5,000 or 250,000 stades as the circumference of the earth. This is the figure given by Cleomedes;7 but Strabo quite definitely says that, according to Eratosthenes, the circumference is 252,000 stades,8 and this is the figure which is most generally quoted in antiquity. The reason for the discrepancy has been the subject of a good deal of discussion;9 it is difficult, in view of Cleomedes’ circumstantial account, to suppose that 252,000 was the original figure arrived at by Eratosthenes; it seems more likely that Eratosthenes himself corrected 250,000 to 252,000 for some reason, perhaps in order to get a figure divisible by 60 and, incidentally, a round number (700) of stades for one degree. There is some question as to the length of the particular stade used by Eratosthenes, but, if Pliny is right in saying that Eratosthenes made 40 stades equal to the Egyptian 
,10 then, taking the 
at 12,000 Royal cubits of 0.525 metres,11 we get 300 such cubits, or 157.5 metres, as the length of the stade, which is thus equal to 516.73 feet. The circumference of the earth, being 252,000 times this length, works out to about 24,662 miles, and the diameter of the earth on this basis is about 7,850 miles, only 50 miles shorter than the true polar diameter, a surprisingly close approximation, however much it owes to happy accidents in the calculation.12
We have no trustworthy information as to evaluations by Eratosthenes of other dimensions and distances. The Doxographi, it is true, say that Eratosthenes made L, the distance of the moon from the earth, to be 78 myriads of stades, and S, the distance of the sun, to be 80,400 myriads of stades13 (the versions of Stobaeus and Joannes Lydus admit of 408 myriads of stades as an alternative interpretation, but this figure obviously cannot be right). Tannery14 considers that none of these figures can be correct. He suggests that L was put by Eratosthenes at 278 myriads of stades, not 78; but I am not clear that 78 is wrong. We have seen that, if we take mean figures, Aristarchus made the distance of the moon from the earth to be about 
times the earth’s diameter. Now 252,000/π, approximately 
, is about 80,180, or roughly 8 myriads of stades; 
times this is 76 myriads, and Eratosthenes’ supposed figure of 780,000 is sufficiently close to this. According to Tannery’s conjecture of 2,780,000 stades, the ratio L/2t would be nearly 34·7, which is greater than the values given to it by Hipparchus, Posidonius, and Ptolemy, and also greater than the true value. With regard to Eratosthenes’ estimate of S, Tannery points to Macrobius’s statement that Eratosthenes said that ‘the measure (mensura) of the earth multiplied 27 times will make the measure of the sun’.15 The question here arises whether it is the solid contents of the two bodies or their diameters which are compared. Tannery takes the latter to be the meaning. If this is right, and if Eratosthenes took the value of 
for the apparent angular diameter of the sun discovered by Aristarchus, the circumference 2πS of the sun’s orbit would be equal to 27.2t.720, which, if we put 
for π, would give
But Hultsch16 shows reason for believing that ‘mensura’ in the statement of Macrobius means solid content. One ground is the further statement of Macrobius that Posidonius’s estimate of the size of the sun in terms of the earth was ‘many many times’ greater than that of Eratosthenes (‘multo multoque saepius’, sc. ‘multiplicata’). But we shall find that Posidonius’s figures lead to only about 
as the ratio of the diameter of the sun to that of the earth, which is not ‘many many times’ greater than 27. It seems therefore necessary to conclude, if Macrobius is to be trusted, that according to Eratosthenes s/t was equal to 3, not 27. This would divide the value of S by 9, and S/2t would be equal to 
instead of 
.
We are much better informed on the subject of Hipparchus’s estimates of sizes and distances, thanks to the investigations of Hultsch,17 who found in the commentaries of Pappus and Theon on chapter 2 of Book V of Ptolemy’s Syntaxis particulars as to which Ptolemy himself leaves us entirely in the dark. Ptolemy states that there are certain observed facts with regard to the sun and moon which make it possible, when the distance of one of them from the centre of the earth is known, to calculate the distance of the other, and that Hipparchus first found the distance of the sun on certain assumptions as to the solar parallax, and then deduced the distance of the moon. According to the value assumed for the solar parallax (and Ptolemy says that there was doubt as to whether it was the smallest appreciable amount or actually negligible), Hipparchus deduced, of course, different figures for the distance of the moon.18 Ptolemy does not state these figures, but Pappus supplies the deficiency. Pappus begins by saying that Hipparchus’s calculation, depending mainly on the sun, was ‘not exact’. Next, he observes that, if the apparent diameter of the sun is taken to be very nearly the same as that of the moon at its greatest distance at the conjunctions, and if we are given the relative sizes of the sun and moon and the distance of one of them, the distance of the other is also given; then, after paraphrasing Ptolemy’s remarks above quoted, he proceeds as follows: ‘In his first book about sizes and distances Hipparchus starts from this observation: there was an eclipse of the sun which was exactly total in the region about the Hellespont, no portion of the sun being seen, whereas at Alexandria in Egypt about four-fifths only of its diameter was obscured.19 From the facts thus observed he proves in his first book that, if the radius of the earth be the unit, the least distance of the moon contains 71, and the greatest 83 of these units; the mean therefore contains 77. After proving these propositions, he says at the end of the first book : “In this treatise I have carried the argument to this point. Do not, however, suppose that the theory of the distance of the moon has ever yet been worked out accurately in every respect; for even in this question there is an investigation remaining to be carried out, in the course of which the distance of the moon will be proved to be less than the figure just calculated,” so that he himself admits that he is not quite in a position to state the truth about the parallaxes. Then, again, he himself, in the second book about sizes and distances, proves from many considerations that, if we take the radius of the earth as the unit, the least distance of the moon contains 62 of these units, and its mean distance 
, while the distance of the sun contains 2,490. It is clear from the former figures that the greatest distance of the moon contains 
of these units.’ The figure of 2,490 for the distance of the sun has to be obtained by a correction of the Greek text. The later MSS. have c or 90, but one MS. has 
or 490. The 2,490 is credibly restored by Hultsch on the following grounds. Adrastus20 and Chalcidius21 tell us that Hipparchus made the sun nearly 1880 times the size of the earth,22 and the earth about 27 times the size of the moon. The size means the solid content, and, the cube root of 1880 being approximately 
, we have approximately
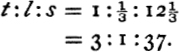
Now the mean distance of the moon is, according to Hipparchus, 
times the earth’s radius; assuming then that the apparent angular diameter of the sun and moon as seen from the earth is about the same, we find that
That is to say, S = 2490 t, nearly. It is clear, therefore, that 
has fallen out of the text before 
, and the true number arrived at by Hipparchus was 2490.
Thus Hipparchus made the distance of the moon equal, at the mean, to 
times the diameter of the earth, and the distance of the sun equal to 1,245 times the diameter of the earth. As we said above, Ptolemy does not mention these figures of Hipparchus, much less does he make any use of them. Yet they are remarkable, because not only are they far nearer the truth than Aristarchus’s estimates, but the figure of 1,245 for the distance of the sun is much better than that of Ptolemy himself, namely 605 times the earth’s diameter, or less than half the figure obtained by Hipparchus. Yet Hipparchus’s estimate remained unknown, and Ptolemy’s held the field for many centuries; even Copernicus only made the distance of the sun to be equal to 750 times the earth’s diameter, and it was not till 1671–3 that a substantial improvement was made, observations of Mars carried out in those years by Richer enabling Cassini to conclude that the sun’s parallax was about 9″·5, corresponding to a distance of the sun from the earth of 87,000,000 miles.23
Hultsch shows that the particular solar eclipse referred to by Hipparchus was probably that of 20th November in the year 129 B.C.,24 and he concludes that the following year (128 B.C.) was the date of Hipparchus’s treatise in two books ‘On the sizes and distances of the sun and moon’.
Hipparchus, in his Geography, definitely accented the estimate of 252,000 stades obtained by Eratosthenes for the circumference of the earth;25 if there is any foundation for the statement of Pliny26 that he added a little less than 26,000 stades to this estimate, making nearly 278,000, the explanation must apparently be that he stated this number as a maximum, allowing for possible errors resulting from Eratosthenes’ method;27 but Berger considers that Pliny’s statement is based on a misapprehension.28
Posidonius of Rhodes (135–51 B.C.) cannot be reckoned among astronomers in the strict sense of the term, but he dealt with astronomical questions in his work on Meteorology, and he wrote a separate tract on the size of the sun.29 It was presumably in the latter work that he put forward a bold hypothesis as to the distance of the sun, which has the distinction of coming far nearer to the truth than the estimates of Hipparchus and all other ancient waiters had done.30 Cleomedes tells us that Posidonius supposed the circle in which the sun apparently moves round the earth to be 10,000 times the size of a circular section of the earth through its centre. With this hypothesis he combined (says Cleomedes) the assumption which he took from Eratosthenes that at Syene (which is under the summer tropic) and throughout a circle round it with a diameter of 300 stades the upright gnomon throws no shadow (at noon). It follows from this that the diameter of the sun occupies a portion of the sun’s circle 3,000,000 stades in length; in other words, the diameter of the sun is 3,000,000 stades.31 If we only knew the fraction of the circumference of the sun’s circle occupied by the sun itself, we could calculate the circumference of the earth, and the absolute distance of the centre of the sun from the centre of the earth; but Cleomedes gives us no information on this, and we have to go elsewhere for what we want—in this case to Pliny. Now Pliny says that according to Posidonius there is round the earth a height of not less than 40 stades, which is the region of winds and clouds, and beyond which there is pure air; the distance from the belt of clouds, &c., to the moon is 2,000,000 stades, and the further distance from the moon to the sun is 500,000,000 stades.32 This would give
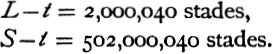
Dividing the latter figure by 10,000 we obtain, approximately, for the radius of the earth
Hultsch gives reason for thinking that the 500,000,000 stades should be the distance from the centre of the earth to the centre of the sun, not the distance from the moon to the sun; the 40 stades representing the depth of the region of clouds, &c., is clearly negligible; and, as Posidonius dealt in round figures, we may infer that his estimate of the earth’s diameter would be 100,000 stades. If now we use the Archimedean approximation of 
for π, the circumference of the earth would on this basis be 314,285 stades; but we may, with some probability, suppose that Posidonius would take the round figure of 300,000 stades corresponding to π = 3, an approximation used by Cleomedes in another place.33
On the other hand, Cleomedes gives 240,000 stades as Posidonius’s estimate of the earth’s circumference based on the following assumptions, (1) that the star Canopus, invisible in Greece, was just seen to graze the horizon at Rhodes as it rose and set again immediately, whereas its meridian altitude at Alexandria was ‘a fourth part of a sign, that is, one forty-eighth part of the zodiac circle’, (2) that the distance between the two places was considered to be 5,000 stades.34 The circumference of the earth was thus made out to be 48 times 5,000 or 240,000 stades. But the estimate of the difference of latitude at 1/48th of a great circle, or 
, was very far from correct (the true difference of latitude is 
only); indeed the effects of refraction at the horizon would inevitably vitiate the result of such an attempt at measurement of the angle in question as Posidonius was in a position to make. Moreover, the estimate of 5,000 stades for the distance was also incorrect; it was the maximum estimate put upon it by mariners, while some put it at 4,000 only, and Eratosthenes, by observations of the shadows cast by gnomons, found it to be 3,750 stades only.35 The existence of the latter estimate of the distance between Rhodes and Alexandria seems to account for Strabo’s statement that Posidonius favoured ‘the latest of the measurements which gave the smallest dimensions to the earth’, namely about 180,000 stades;36 for 180,000 is 48 times 3,750, just as 240,000 is 48 times 5,000. Now Eratosthenes must presumably have arrived at his distance of 3,750 stades by means of a calculation based on his own estimate of the total circumference of the earth (250,000 or 252,000) and the observed angle representing the difference of the inclination of the shadows thrown by the gnomon at the two places respectively.37 We are not told what the angle was, but it can be inferred that it was 
or 
, because
It is nothing short of extraordinary that Posidonius should have used the 3,750 stades without a thought of its origin and then calculated the circumference of the earth by combining the 3,750 with an estimate of the corresponding angle which is so grossly erroneous 
. It may seem not less extraordinary that Ptolemy (following Marinus of Tyre) should have accepted without any argument or question Posidonius’s figure of 180,000 stades. But the explanation doubtless is that Ptolemy’s stades were Royal stades of 210 metres (nearly 
th of a Roman mile) instead ot Eratosthenes’ stades of 
metres; for Ptolemy in his Geography says that the length of a degree is 500 stades,38 whereas Eratosthenes made a degree contain about 700 stades. Thus, as Ptolemy’s stades were to Eratosthenes’ as 4 to 3, Ptolemy’s estimate of the circumference of the earth would, in stades of Eratosthenes, be 240,000, the same as the estimate attributed by Cleomedes to Posidonius.
As we have seen, Pliny’s account of Posidonius’s estimates of the distances of the sun and moon leads to about 300,000 stades, and not 240,000, as the circumference of the earth. What is the explanation of the discrepancy ? Hultsch takes the 300,000 stades and the assumption that the sun’s circle is 10,000 times as large as the circumference of the earth to be part of a calculation of the minimum distance of the sun, on the ground that Cleomedes goes on to say that ‘it is indeed plausible that the sun’s circle is not less than 10,000 times the circumference of the earth, seeing that the earth is to it in the relation of a point; but it may also be greater still without our knowing it’.39 But it is somewhat awkward to suppose with Hultsch that Posidonius is arguing, ‘I take the earth to be of the size attributed to it by Dicaearchus, namely 300,000 stades in circumference, although this figure exceeds the truth; but I am satisfied that, even if I take the circumference to be fully 300,000 stades, I shall yet arrive at an estimate of the sun’s distance which is less than the true distance.’ The italics are mine, and represent the part of Hultsch’s argument which seems to me doubtful. The use of an exaggerated estimate of the earth’s circumference with a view to a minimum estimate of the sun’s distance is so strange that I prefer to suppose that, in the development of the hypothesis about the sun’s distance, Posidonius simply used Dicaearchus’s figure for the earth’s circumference without any arrière-pensée at all.
In considering the origin of the bold hypothesis of Posidonius with regard to the sun’s distance, it is necessary to refer to the hypotheses of Archimedes with regard to the size of the universe, on which in his Sand-reckoner he bases his argument that it is possible to formulate a system for expressing numbers as large as we please, say a number such as the number of the grains of sand which would be required to fill an empty space as large as our ‘universe’. For the purpose which he has in view, Archimedes has of course to take what he considers to be outside or maximum measurements. Thus, whereas his predecessors had tried to prove the perimeter of the earth to be 300,000 stades, he will allow it to be as much as ten times that ‘and not greater’, viz. 3,000,000 stades. Next, whereas Aristarchus had made the sun between 18 and 20 times as large as the moon, he will take it to be 30 times, but not greater, so that (the earth being greater than the moon) the sun will be less than 30 times the size of the earth. Archimedes proceeds to consider the size of the so-called ‘universe’ and of the sun. He has explained that the ‘universe’ as commonly understood by astronomers is the sphere which has for its centre the centre of the earth and for its radius the distance between the centre of the earth and the centre of the sun, but that the sphere of the fixed stars is much greater than this so-called ‘universe’. Considering now the sun in relation to its orbit, a great circle of the so-called ‘universe’, Archimedes found by a rough experiment (in confirmation of Aristarchus’s discovery that the apparent angular diameter of the sun is 
th of four right angles) that the angle subtended by the sun’s diameter is between 
th and 
th part of a right angle, or between 
th and 
th part of four right angles. By means of this result he proves that the diameter of the sun is greater than the side of a chiliagon (or a regular polygon with 1,000 sides) inscribed in its orbit. The proof of this is very interesting because we there see Archimedes abandoning the traditional view that the earth is a point in relation to the sphere in which the sun moves40 (Aristarchus assumed it to be so in relation even to the moon’s sphere), and recognizing parallax in the case of the sun, apparently for the first time; for, from the fact that the apparent diameter of the sun, as seen at its rising by an observer on the surface of the earth, subtends an angle less than 
th and greater than 
th of four right angles, he proves geometrically that the arc of the sun’s orbit subtended by a chord equal to the diameter of the sun subtends at the centre of the earth an angle greater than 
th and a fortiori greater than 
th of four right angles.
Now, says Archimedes, since
while the perimeter of any regular polygon of more than six sides is greater than 3 times the diameter of the circle in which it is described, it follows that
Posidonius assumed, not that the diameter of the sun’s orbit was less than 10,000 times the diameter of the earth, but that it was equal to (or not less than) 10,000 times the earth’s diameter. But the origin of his ratio of 10,000 : 1 is sufficiently clear; he took it from Archimedes. Similarly, the combination of the estimate of 300,000 stades for the circumference of the earth with Eratosthenes’ assumption that the shadowless circle at Syene was 300 stades in diameter suggests that Posidonius likewise adopted from Archimedes the 
th part of four right angles as the apparent angular diameter of the sun, being satisfied to take Archimedes’ minimum estimate as the actual figure.
It remains to express Posidonius’s estimates of the sun’s and moon’s sizes and distances in terms of the earth’s diameter. On the basis of his estimate of 240,000 stades for the circumference of the earth, the earth’s diameter, which we will call D, is 240,000/π stades, or about 76,400 stades.
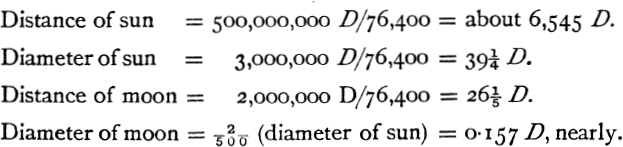
As Ptolemy gives none of the estimates which Pappus’s commentary on the Syntaxis quotes from Hipparchus’s treatise on the sizes and distances of the sun and moon, it was not unnatural to suppose, as Wolf did,41 that the elaborate calculations in Ptolemy (v. 13–16) were referable to Hipparchus. This cannot be so as regards the results, as Hultsch has shown by means of Pappus’s commentary, though doubtless Ptolemy may have been at least partially indebted to Hipparchus for the methods which he followed. The following are Ptolemy’s results :
It follows that
the diam. of the sun = about 
times the diam. of the earth.
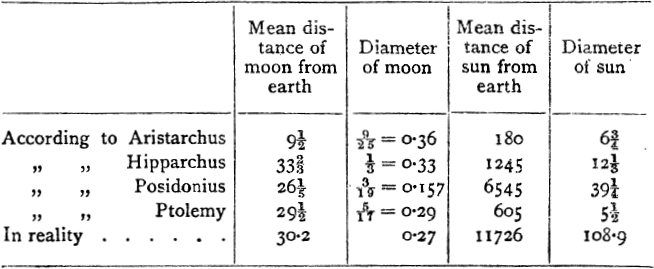
I will conclude with Hultsch’s final comparative table44 of sizes and distances in terms of the earth’s mean diameter (=1,716 geographical miles):
1 Ptolemy, Syntaxis, iv. 9, vol. i, p. 327. 3–4, Heib.
2 Ibid. v. 14, vol. i, p. 421. 12–14, Heib.
3 Archimedes, Sand-reckoner (Archimedis opera, ed. Heib., vol. ii, p. 246 sqq) : The Works of Archimedes, pp. 222, 223.
4 Berger, Geschichte der wissenschaftlichen Erdkunde der Griechen, pp. 370 sqq.
5 Cf. Cleomedes, De motu circulari, i. 8, p. 78, Ziegler.
6 Hultsch, Poseidonios über die Grösse und Entfernung der Sonne, 1897, p. 5.
7 Cleomedes, De motu circulari i. 10, especially p. 100. 15–23, ed. Ziegler.
8 Strabo, ii. 5. 7, p. 113 Cas.
9 Berger, op. cit., pp. 410, 411.
10 Pliny, N. H. xii. c. 13, § 53.
11 Hultsch, Griechische u. römische Metrologie (Berlin, 1882), p. 364. Cf. Tannery, Recherches sur l’histoire de l’astronomie ancienne, pp. 109, 110.
12 Cf. Dreyer, Planetary Systems, p. 175.
13 Aët. ii. 31. 3 (D. G. 362–3).
14 Tannery, ‘Aristarque de Samos’ in Mém. de la Soc. des sci. phys. et nat, de Bordeaux, 2θ sér., v, 1883, pp. 254, 255; Mémoires scientifiques, ed. Heiberg and Zeuthen, i, pp. 391–2.
15 Macrobius, In somn. Scip. i. 20. 9.
16 Hultsch, Poseidonios über die Grösse und Entfernung der Sonne, pp. 5, 6.
17 Hultsch, ‘Hipparchos über die Grösse und Entfernung der Sonne’ (Berichte der philologisch-historischen Classe der Kgl. Sächs. Gesellschaft der Wissenschaften zu Leipzig, 7. Juli 1900).
18 Ptolemy, Syntaxis, v. 2, vol. i, p. 402, Heib.
19 This same eclipse is also mentioned by Cleomedes, De motu circulari, ii. 3, pp. 172. 22 and 178. 14, ed. Ziegler.
20 Theon of Smyrna, p. 197. 8–12, ed. Hiller.
21 Chalcidius, Timaeus, c. 91, p. 161.
22 A less trustworthy authority, Cleomedes (De motu circulari, ii. 1, p. 152. 5–7), mentions a tradition that Hipparchus made the sun 1050 times as large as the earth.
23 Berry, A Short History of Astronomy, 1898, pp. 205–7.
24 Cf. Boll, Art. ‘Finsternisse’ in Pauly-Wissowa’s Real-Encyclopädie, vi. 2, 1909, p. 2358.
25 Strabo, ii. 5. 34, p. 132 Cas.
26 Pliny, N. H. ii. c. 108, § 247.
27 Tannery, Recherches sur l’hist. de l’astronomie ancienne, p. 116.
28 Berger, Gesch. der wissenschaftlichen Erdkunde der Griechen, pp. 413–14.
29 Cleomedes, De motu circulari, i. II, p. 118. 4–6.
30 On the whole of this subject, see Hultsch, ‘Poseidonios über die Grösse und Entfernung der Sonne’ (Abh. der Kgl. Gesellschaft der Wissenschaflen zu Göttingen, Phil.-hist. Klasse, Neue Folge, Bd. I, Nr. 5), 1897.
31 Cleomedes, ii. 1, p. 144. 22–146. 16; ibid. i. 10, pp. 96. 28–98. 5.
32 Pliny, ii, c. 23, § 85.
33 Cleomedes, De motu circulari, i. 8, p. 78. 22–3.
34 Ibid. i. 10, pp. 93. 26–94. 22.
35 Strabo, ii. 5.24, pp. 125–6 Cas.; Berger, Gesch. der wissenschaftlichen Erdkunde der Griechen, p. 415.
36 Strabo, ii. 2. 2, p. 95 Cas.
37 Berger, op. cit., pp. 579, 580.
38 Ptolemy, Geography, vii. 5. 12.
39 Cleomedes, ii. 1, p. 146. 12–16. The text has 
, ‘it may be greater, or again it may be less’; Hultsch rejects 
as a gloss inconsistent with the trend of Cleomedes’ argument.
40 Cf. Cleomedes, De motu circulari, i. n, pp. 108–12, ed. Ziegler.
41 Wolf, Geschichte der Astronomie, pp. 174 sqq.
42 Ptolemy, Syntaxis, v. 15, p. 425. 17–20, Heib.
43 Ibid., v. 16, p. 426. 12–15, Heib.
44 Hultsch, Hipparchos über die Grösse und Entfernung der Sonne, p. 199.
