20

Unification ♥ SUSY

When we expand the equations of physics to include supersymmetry, we enrich the Grid. Thus we must recalibrate our calculation of how the Grid distorts our view of unification. When we make the correction, a sharp image of unification comes into focus.

 

 

BY PERFECTING OUR EQUATIONS, we enlarge the world.

In the 1860s, James Clerk Maxwell assembled the equations for electricity and magnetism as they were understood at the time, and found that they led to contradictions.⁵¹ He saw that he could make them consistent if he added a new term. The new term, of course, corresponds to a new physical effect. Some years before, Michael Faraday (in England) and Joseph Henry (in the United States) had discovered that when magnetic fields change in time, they create electric fields. Maxwell’s new term embodied the converse effect: changing electric fields produce magnetic fields. Combining those effects, we get a dramatic new possibility: changing electric fields produce changing magnetic fields, which produce changing electric fields, which produce changing magnetic fields, . . . . You can have a self-renewing disturbance that takes on a life of its own. Maxwell saw that his equations had solutions of this kind. He could calculate the speed at which these disturbances would move through space. And he found that they move at the speed of light.

Being a very bright fellow, Maxwell leaped to the conclusion that these electromagnetic disturbances are light. That idea has held up to this day, with many many fruitful applications. It remains the foundation of our deepest understanding of the nature of light. But there’s more. Maxwell’s equations also have solutions with smaller wavelengths than those of visible light, and with larger wavelengths. So the equations predicted the existence of new kinds of things—new kinds of matter, if you like—that weren’t known at the time. These are what we now know as radio waves, microwaves, infrared, ultraviolet, x-rays, γ-rays—each a significant contributor to modern life, each an immigrant from concept world to physical world (c-world to p-world).

In the late 1920s, Paul Dirac was working to improve the equation that describes electrons in quantum mechanics. A few years before, Erwin Schrödinger had formulated an electron equation that worked very well in many applications. But theoretical physicists were not entirely satisfied with Schrödinger’s electron equation, because it does not obey the special theory of relativity. It is a quantum-mechanical version of Newton’s force law; it obeys the old mechanical relativity rather than Einstein’s electromagnetic relativity. Dirac found that to make an equation consistent with special relativity, he had to use a larger equation than Schrödinger’s. Like Maxwell’s perfected equations for electricity and magnetism, Dirac’s perfected equation for electrons had new kinds of solutions: besides the solutions that correspond to electrons moving with different velocities and spinning in different directions, there were others. After some struggles and false starts, and with some help from Hermann Weyl, by 1931 Dirac had deciphered the meaning of these strange new solutions. They represent a new kind of particle, with the same mass as the electron but opposite charge. Just such a particle was discovered soon thereafter, in 1932, by Carl Anderson. We call it the antielectron, or positron. Nowadays we use positrons to monitor what’s happening inside brains (via the PET scan, a.k.a. positron-electron tomography).

There are many other recent examples where new forms of matter appeared in our equations before they appeared in our laboratories. In fact, it’s become the usual case. Quarks (both as a general concept, and the specific c, b, and t flavor varieties), color gluons, W and Z bosons, and all three kinds of neutrinos were seen first as solutions of equations, and only later as physical realities.

The search is on for other talented inhabitants of c-world that we’d like to recruit into p-world, notably Higgs particles and axions. It breaks my heart not to describe them in detail here, but that would require two major digressions, just as we’re building to a climax. You can find more information and references on them in the glossary and endnotes and, for the Higgs particle, also in Appendix B.

For our story, the most important proposed expansion of the equations of physics is supersymmetry, often fondly called SUSY. Supersymmetry, as the name suggests, proposes that we should use equations with larger symmetry.

SUSY’s new symmetry is related to the boost symmetry of special relativity. As you may recall, boost symmetry says that the basic equations don’t change when you impart a common, constant velocity to all the components of the system you’re describing. (Dirac had to modify Schrödinger’s equation to give it that property.) Supersymmetry likewise says that the equations don’t change when you impart a common motion to all the components of the system you’re describing. But it’s a very different kind of motion from what’s involved in boost symmetry. Instead of motion through ordinary space with a constant velocity, supersymmetry involves motion into new dimensions!

Before you get carried away with visions of spirit worlds and wormholes through hyperspace, let me hasten to add that the new dimensions have a very different character from the familiar dimensions of space and time. They’re quantum dimensions. What happens to a body when it moves in the quantum dimensions isn’t that it gets displaced—there’s no notion of distance out there—instead, its spin changes. The “superboosts” turn particles with a given amount of intrinsic spin into particles with a different amount of spin. Because the equations are supposed to stay the same, supersymmetry relates properties of particles with different spin. SUSY allows us to see them as the same particle, moving in different ways through the quantum dimensions of superspace.

You can visualize the quantum dimensions as new layers of the Grid. When a particle hops into these layers its spin changes, and so does its mass. Its charges—electric, color, and weak—stay the same.

SUSY might allow us to complete the work of unifying the Core. Unification of the different charges, using the symmetry SO(10), united all the gauge bosons into a common cluster, and all the quarks and leptons into a common cluster. But no ordinary symmetry is capable of joining those two clusters, for they describe particles with different spins. Supersymmetry is the best idea we have for connecting them.

Correcting the Correction

After expanding the equations of physics to include supersymmetry, we find that they have more solutions. Just as with Maxwell’s and Dirac’s equations, the new solutions represent new forms of matter—new kinds of fields and, as their excitations, new kinds of particles.

Supersymmetry requires us, roughly speaking, to double the number of fields we have in our equations. Alongside every field we know about, off in the quantum dimensions, is a new partner field describing activity in the new layer of Grid. The particles associated with these new fields have the same charges (of all kinds) as their known partners, but different masses and spins.

It may sound reckless and extravagant to infer a doubling of the world based on esthetic considerations.⁵² Maybe it is. But Dirac’s introduction of antimatter involved a similar doubling, and Maxwell’s enlargement of the world of light from the visible band to the infinite expanse of the electromagnetic spectrum was even larger. Both were—at the time of their conception—essentially esthetic gambits. So physicists have learned to be bold. It is more blessed to ask forgiveness than permission. Thus endeth the apology; now back to business.

The new, partner particles must be heavier than their observed siblings, or else they’d already have been observed. But we’ll assume that they’re not too much heavier, and see where that leads.⁵³

Fluctuations in these new fields permeate the Grid. They are new kinds of virtual particles, which contribute to the screening and antiscreening of strong, weak, and electromagnetic sources. To see our way to the basics, at short distances or high energy, we have to correct our vision, to remove the distorting effect of that bubbly medium. We tried to make such a correction before, in Chapter 18, without taking into account these possible new contributions. Now we must correct the corrections.

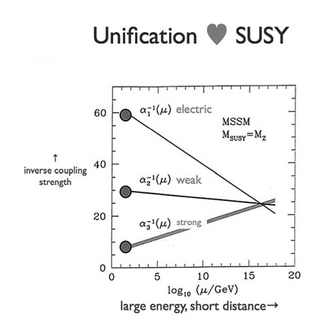
Figure 20.1 displays the result. With SUSY on board, it works.

Gravity Too

We can also bring gravity into the game. Gravity, as we’ve seen, starts out ridiculously feebler than the other forces. Looking at Figure 20.1, at the left-hand side, corresponding to the distances and energies we can access in practice, we see that the difference in power between the strong and electromagnetic forces is roughly a factor of 10. So they fit easily, together with the weak interaction, into a nice tidy plot. Gravity doesn’t come close to fitting in. Because it’s feebler and we’re plotting inverse power, gravity should appear up higher than the others. But to include it at this scale, we’d need to make our figure far larger than the known universe!

Figure 20.1 Supersymmetry requires expanding the equations of physics to include new fields. Grid fluctuations due to these new fields distort our view of the most basic, underlying physical process. After we correct for those distortions, we find accurate unification at short distances or, equivalently, at high energies.

 

On the other hand . . .

For the Core forces—the strong, weak, and electromagnetic forces—the corrections as we go to the right, toward much shorter distances or higher energies, are fairly modest (and remember, each tick on the horizontal axis represents a factor of 10). Those corrections, after all, arose from a subtle quantum-mechanical effect: screening (or antiscreening) due to Grid fluctuations. When we look at gravity at very short distances, by transferring very large amounts of energy, the change is much more drastic. As we discussed way back in Chapter 3, gravity responds directly to energy. Its power, as defined here, is proportional to energy squared. Allowing for that effect, we can calculate the power of gravity at short distances and compare it with the other interactions. Figure 20.2 displays the result. From well outside the known universe, the inverse power of gravity descends to join the other interactions, pretty nearly.

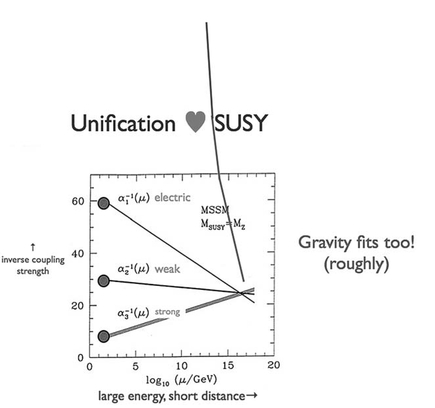
Figure 20.2 Gravity starts ridiculously feeble, but at short distances it approaches the other interactions in power; and they all come together, pretty nearly.