Einer der wichtigsten Spezialfälle in der Newton'schen Mechanik ist das Gravitationsfeld einer kugelsymmetrischen Massenverteilung, denn damit lassen sich in sehr guter Näherung z. B. die Himmelskörper im Sonnensystem beschreiben. Dieser Fall ist einer der wenigen, für den auch die Einstein'schen Feldgleichungen analytisch gelöst werden können. Dabei betrachten wir aber nur den Außenraum, d. h. Regionen innerhalb der Massenverteilung sind im Folgenden ausgenommen. In Abschn. 21.4.1 kommen wir auf den Innenraum im Rahmen der Behandlung von Neutronensternen zu sprechen.
13.1 Herleitung der Schwarzschild-Metrik
Die Herleitung der entsprechenden Metrik für eine kugelsymmetrische Massenverteilung gelang Schwarzschild bereits 1916 [1], weshalb sie heute seinen Namen trägt.



 hängt von den sphärischen Winkelkoordinaten 𝜗 ∈ [0, π] und φ ∈ [0, 2π) ab und beschreibt das gewohnte Flächenelement einer Einheitskugel.
hängt von den sphärischen Winkelkoordinaten 𝜗 ∈ [0, π] und φ ∈ [0, 2π) ab und beschreibt das gewohnte Flächenelement einer Einheitskugel.
Da wir uns im Folgenden zunächst nur auf statische Metriken beschränken wollen, gibt es in (13.3) keine explizite Abhängigkeit von der Zeitkoordinate t (s. Abschn. 11.3.3).













 verpackt haben. Nach Exponentieren und mit der Abkürzung
verpackt haben. Nach Exponentieren und mit der Abkürzung  gelangen wir zu
gelangen wir zu


 und
und  erfolgt über die Betrachtung des nichtrelativistischen Grenzfalls und des Grenzfalls r → ∞. Für r → ∞ soll gμν in die Minkowski-Metrik übergehen, da im Unendlichen die Massenverteilung keinen Einfluss mehr auf die Metrik haben sollte. Es folgt dann die Bedingung
erfolgt über die Betrachtung des nichtrelativistischen Grenzfalls und des Grenzfalls r → ∞. Für r → ∞ soll gμν in die Minkowski-Metrik übergehen, da im Unendlichen die Massenverteilung keinen Einfluss mehr auf die Metrik haben sollte. Es folgt dann die Bedingung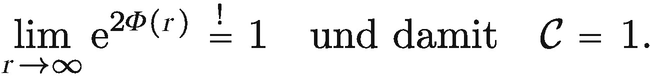



 hergeleitet.
hergeleitet.Die Beschränkung, dass die Funktionen Φ(r) und Ψ(r) alleine von der Radialkoordinate r abhängen sollen, ist eigentlich zu eng gefasst. Jebsen1 zeigte 1921 [2], dass auch ein allgemeinerer Ansatz, wo die beiden Funktionen auch von der Zeitkoordinate t abhängen dürfen, ebenfalls zur Schwarzschild-Metrik führt. Sie ist daher die eindeutige Lösung der Vakuum-Feldgleichungen mit sphärischer Symmetrie und verschwindender kosmologischer Konstante. Das Theorem, dass die statische Schwarzschild-Metrik die Lösung für jede beliebige sphärisch-symmetrische Massenverteilung ist, wurde jedoch lange Zeit Birkhoff 2 alleine zugeschrieben, der das nach ihm benannte Birkhoff'sche-Theorem [3] 1923 fand, siehe auch [4].
13.2 Eigenschaften der Schwarzschild-Metrik
Im Folgenden wollen wir auf einige erste physikalische Eigenschaften der Schwarzschild-Metrik eingehen.
13.2.1 Singularitäten
 aus (11.104) zur Charakterisierung der Problemstellen. Für die Schwarzschild-Metrik gilt
aus (11.104) zur Charakterisierung der Problemstellen. Für die Schwarzschild-Metrik gilt



Bei Annäherung an den Schwarzschild-Radius rs verengen sich die Lichtkegel immer weiter. Am Schwarzschild-Radius sind sie zu einer Linie entartet und öffnen sich innerhalb des Schwarzschild-Radius entlang der Raumachse. Der dunkelgraue Bereich kennzeichnet den Zukunftslichtkegel
Die Lichtkegel verengen sich bei Annäherung an den Schwarzschild-Radius. Für r > rs sind sie entlang der Zeitachse geöffnet, für r < rs öffnen sich die Lichtkegel entlang der Raumachse, d. h. r wird eine zeitartige und t eine raumartige Koordinate. Unterhalb des Horizonts bewegt sich alles unausweichlich auf die Singularität bei r = 0 zu.
13.2.2 Messung der Radialkoordinate


Über die Messung der Fläche oder des Umfangs kann man also, zumindest theoretisch, die Radialkoordinate bestimmen.
13.2.3 Radialabstand von Punkten



![$$ \Delta s={r}_{\mathrm{s}}\sqrt{\frac{r}{r_{\mathrm{s}}}\left(\frac{r}{r_{\mathrm{s}}}-1\right)}+\frac{r_{\mathrm{s}}}{2}\ln \left[2\frac{r}{r_{\mathrm{s}}}-1+2\sqrt{\frac{r}{r_{\mathrm{s}}}\left(\frac{r}{r_{\mathrm{s}}}-1\right)}\right]. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ33.png)
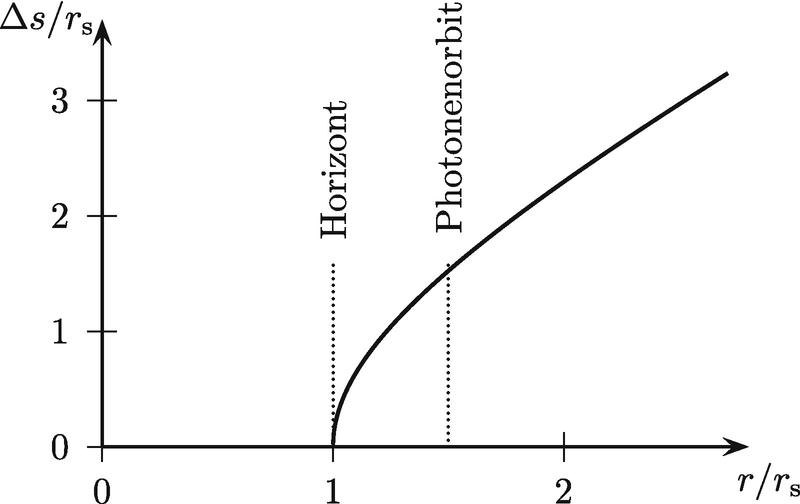
Eigenradialabstand Δs zum Ereignishorizont eines Schwarzen Lochs in Abhängigkeit von der Radialkoordinate r, normiert bezüglich des Schwarzschild-Radius rs. Zur Orientierung ist der Photonenorbit r = 3rs∕2 eingezeichnet (s. Abschn. 13.2.6). Dort wird Licht bereits so stark abgelenkt, dass es auf einer Kreisbahn um das Schwarze Loch läuft
13.2.4 Bedeutung der Koordinatenzeit


13.2.5 Radiale lichtartige Geodäten

13.2.6 Photonenorbit in der Schwarzschild-Metrik








13.2.7 Qualitatives Verhalten von Geodäten

 auftauchen. Aus der Euler-Lagrange-Gleichung (11.135) folgt dann
auftauchen. Aus der Euler-Lagrange-Gleichung (11.135) folgt dann

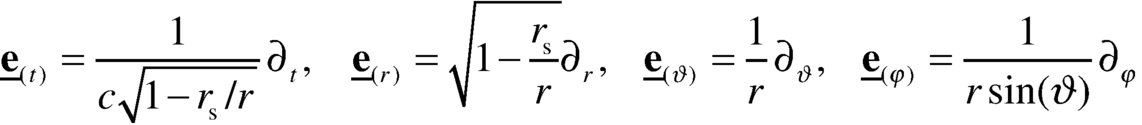
 bezogen auf diese Tetrade von
bezogen auf diese Tetrade von
 (s. (11.137)) folgt dann
(s. (11.137)) folgt dann
Lichtartige Geodäten

Effektives Potential für eine lichtartige Geodäte. Das Maximum Vmax liegt stets an der Position rpo = 3rs∕2 und repräsentiert den Photonenorbit
 für den Umkehrpunkt der Geodäten. Auflösen nach dem Radius führt auf
für den Umkehrpunkt der Geodäten. Auflösen nach dem Radius führt auf![$$ {r}_{\mathrm{min}}=\frac{2\varepsilon }{\sqrt{3}}\cos \left[\frac{1}{3}\operatorname{arccos}\left(-\frac{3\sqrt{3}{r}_{\mathrm{s}}}{2\varepsilon}\right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ51.png)
 , wobei wir ρ = 1 wählen konnten.
, wobei wir ρ = 1 wählen konnten.
Zeitartige Geodäten

 negativ, so gibt es keine Extremalstelle. Im Fall
negativ, so gibt es keine Extremalstelle. Im Fall  handelt es sich um eine indifferente Extremalstelle und für
handelt es sich um eine indifferente Extremalstelle und für  gibt es zwei Extremalstellen. Daraus folgt auch, dass r+ und r− nur in den Bereichen
gibt es zwei Extremalstellen. Daraus folgt auch, dass r+ und r− nur in den Bereichen

Effektives Potential für eine zeitartige Geodäte mit zwei Extremalstellen
 und den Radius der Kreisbahn in das Minimum des Potentials bei r+ setzen. Die Konstanten der Bewegung lauten dann
und den Radius der Kreisbahn in das Minimum des Potentials bei r+ setzen. Die Konstanten der Bewegung lauten dann
 bezogen auf seine Eigenzeit t zuordnen, wobei
bezogen auf seine Eigenzeit t zuordnen, wobei
 und daraus
und daraus  . Entsprechend können wir die Zeiten für einen vollen Umlauf berechnen und erhalten t2π = 2π∕ω bzw. T2π = 2π∕Ω. Um dem Objekt auch eine Geschwindigkeit v = cβ zuordnen zu können, die ein Beobachter an dessen aktueller Position misst, müssen wir zunächst die Vierergeschwindigkeit
. Entsprechend können wir die Zeiten für einen vollen Umlauf berechnen und erhalten t2π = 2π∕ω bzw. T2π = 2π∕Ω. Um dem Objekt auch eine Geschwindigkeit v = cβ zuordnen zu können, die ein Beobachter an dessen aktueller Position misst, müssen wir zunächst die Vierergeschwindigkeit  bestimmen. Daraus folgt dann
bestimmen. Daraus folgt dann
13.2.8 Einstein-Ring

Das punktförmige Objekt bei x = −8rs erscheint dem Beobachter bei x = 20rs als Einstein-Ring mit dem Öffnungswinkel ξ ≈ 11,9473° (Ring erster Ordnung) bzw. ξ ≈ 7,279793° (Ring zweiter Ordnung)



![$$ {x}_{\mathrm{min}}=\frac{r_{\mathrm{s}}}{r_{\mathrm{min}}}=\frac{\sqrt{3}a}{2}{\left\{\cos \left[\frac{1}{3}\operatorname{arccos}\left(-\frac{3\sqrt{3}a}{2}\right)\right]\right\}}^{-1}. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ61.png)
13.3 Schwarze Löcher
Die Schwarzschild-Metrik gilt für alle sphärisch-symmetrischen Massenverteilungen mit verschwindender kosmologischer Konstante. Befindet sich diese Massenverteilung vollständig unterhalb des Schwarzschild-Radius, so beschreibt sie auch eines der außergewöhnlichsten Objekte in der ART – ein statisches Schwarzes Loch. Wie bereits im vorherigen Abschn. 13.2 diskutiert, trennt der Ereignishorizont den Innenbereich vom Außenbereich vollkommen ab. Dies bedeutet aber auch, dass nicht einmal Licht aus dem Innenbereich nach außen gelangen kann, weshalb dieser Bereich schwarz ist. Stark vereinfacht haben wir diesen Fall bereits in Abschn. 1.4.4 angesprochen.
In den folgenden Abschnitten wollen wir weitere Eigenschaften der Schwarzschild-Metrik untersuchen, die ihr Extremum im Fall von Schwarzen Löchern besitzen.
13.3.1 Freier Fall auf ein Schwarzes Loch
In diesem Abschnitt wollen wir den freien Fall eines Teilchens in ein Schwarzes Loch untersuchen. Dabei interessiert uns besonders, wie ein Beobachter, der mit dem Teilchen mitfällt, und wie ein Beobachter, der sich weit entfernt befindet, die Situation jeweils beurteilen. Wir lassen dabei das Teilchen bei r = R > rs aus der Ruhe heraus starten.

 . Setzen wir diese in die Lagrange-Funktion (13.51) ein und formen um, so gelangen wir zu den Bewegungsgleichungen
. Setzen wir diese in die Lagrange-Funktion (13.51) ein und formen um, so gelangen wir zu den Bewegungsgleichungen

Mitfallender Beobachter

 ermitteln. Setzen wir diese in das Integral von (13.53) ein, so gelangen wir zu dem Ausdruck
ermitteln. Setzen wir diese in das Integral von (13.53) ein, so gelangen wir zu dem Ausdruck
 mit der Ableitung
mit der Ableitung  und erhalten mit den substituierten Integrationsgrenzen
und erhalten mit den substituierten Integrationsgrenzen  und xf = π∕2,
und xf = π∕2,![$$ \tau (r)=\frac{2{R}^{3/ 2}}{c\sqrt{r_{\mathrm{s}}}}\underset{x_i}{\overset{x_f}{\int }}{\sin}^2(x)\, \mathrm{d}x=\frac{R^{3/ 2}}{c\sqrt{r_{\mathrm{s}}}}{\left[x-\frac{1}{2}\sin (2x)\right]}_{\arcsin \left(\sqrt{r/ R}\right)}^{\pi / 2}. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ67.png)

![$$ \tau (r)=\frac{R^{3/ 2}}{c\sqrt{r_{\mathrm{s}}}}\left[\sqrt{\frac{r}{R}}\sqrt{1-\frac{r}{R}}+\operatorname{arccos}\left(\sqrt{\frac{r}{R}}\right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ69.png)
![$$ \tau \left({r}_{\mathrm{s}}\right)=\frac{R^{3/ 2}}{c\sqrt{r_{\mathrm{s}}}}\left[\sqrt{\frac{r_{\mathrm{s}}}{R}}\sqrt{1-\frac{r_{\mathrm{s}}}{R}}+\operatorname{arccos}\left(\sqrt{\frac{r_{\mathrm{s}}}{R}}\right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ70.png)
 , dass das Teilchen auch die Singularität des Schwarzen Lochs nach endlicher Zeit
, dass das Teilchen auch die Singularität des Schwarzen Lochs nach endlicher Zeit
![$$ r=\frac{R}{2}\left[1+\cos \left(\eta \right)\right], $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ72.png)
![$$ \tau \left(\eta \right)=\frac{R^{3/ 2}}{2c\sqrt{r_{\mathrm{s}}}}\left[\eta +\sin \left(\eta \right)\right]. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ73.png)
Weit entfernter Beobachter
![$$ \frac{\mathrm{d}t}{\mathrm{d}r}=\frac{\dot{t}}{\dot{r}}=-\frac{k}{c^2}{\left(1-\frac{r_{\mathrm{s}}}{r}\right)}^{-1}{\left[\frac{k^2}{c^2}-{c}^2\left(1-\frac{r_{\mathrm{s}}}{r}\right)\right]}^{-1/ 2}. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ74.png)

 bei rʹ = rs singulär wird. Zur genauen Auswertung des Integrals verwenden wir wieder die Zykloidenkoordinate. Mit dem bereits gefundenen Ausdruck (13.61) für τ(η) und dessen Ableitung
bei rʹ = rs singulär wird. Zur genauen Auswertung des Integrals verwenden wir wieder die Zykloidenkoordinate. Mit dem bereits gefundenen Ausdruck (13.61) für τ(η) und dessen Ableitung![$$ \mathrm{d}\tau =\frac{R^{3/ 2}}{2c\sqrt{r_{\mathrm{s}}}}\left[1+\cos \left(\eta \right)\right]\, \mathrm{d}\eta $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ76.png)
![$$ \mathrm{d}t=\frac{R^{3/ 2}}{2c\sqrt{r_{\mathrm{s}}}}\sqrt{1-\frac{r_{\mathrm{s}}}{R}}\frac{{\left[1+\cos \left(\eta \right)\right]}^2}{1+\cos \left(\eta \right)-2{r}_{\mathrm{s}}/ R}\, \mathrm{d}\eta $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ77.png)
![$$ t\left(\eta \right)=\frac{r_{\mathrm{s}}}{c}\left\{\ln \left[\frac{\sqrt{R/ {r}_{\mathrm{s}}-1}+\tan \left(\frac{\eta }{2}\right)}{\sqrt{R/ {r}_{\mathrm{s}}-1}-\tan \left(\frac{\eta }{2}\right)}\right]+\sqrt{\frac{R}{r_{\mathrm{s}}}-1}\left[\eta +\frac{R}{2{r}_{\mathrm{s}}}\left(\eta +\sin \left(\eta \right)\right)\right]\right\} $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ78.png)
 . Mit der trigonometrischen Relation
. Mit der trigonometrischen Relation  folgt daraus
folgt daraus
Da nun die Koordinatenzeit t der Eigenzeit für einen weit entfernten Beobachter entspricht, würde dieser berechnen, dass das Teilchen den Horizont nie erreicht. Um zu ermitteln, was er sehen würde, müssen wir noch zusätzlich die Lichtlaufzeit Δt(r, R) vom aktuellen Ort des Teilchens zum Beobachter einbeziehen (s. Abschn. 13.2.5). Diese divergiert jedoch ebenfalls im Grenzfall r → rs. Zusammengenommen sieht der Beobachter das Teilchen am aktuellen Ort r zu seiner Zeit tobs(r) = t(r) + Δt(r, R). Für den weit entfernten Beobachter erreicht das Teilchen den Horizont sowohl rechnerisch als auch visuell niemals.
13.3.2 Erweiterung der Schwarzschild-Metrik
Bei Betrachtung der Schwarzschild-Metrik in (13.16) erkennt man zwei Singularitäten, eine bei r = rs und eine bei r = 0. Wie bereits in Abschn. 13.2.1 diskutiert, haben diese aber unterschiedlichen Charakter, wie es mehrere Autoren, unter anderen auch Einstein, in verschiedenen Arbeiten ab 1921 gezeigt haben (siehe z. B. [6]).
Man kann sich die Tatsache, dass bei r = rs keine physikalische Singularität auftritt, am besten klarmachen, indem man auf Koordinaten transformiert, in denen diese Singularität nicht auftritt. Einen ersten Schritt in diese Richtung kann man durch die Einführung der Eddington-Finkelstein-Koordinaten machen.
Eddington-Finkelstein-Koordinaten
 eingeführt über
eingeführt über

 > lautet die Metrik
> lautet die Metrik


 Für radial nach außen laufende Photonen tritt allerdings bei r = rs immer noch eine Singularität auf. Analog kann man statt
Für radial nach außen laufende Photonen tritt allerdings bei r = rs immer noch eine Singularität auf. Analog kann man statt  die Koordinate
die Koordinate  zur Beschreibung radial auslaufender Photonen einführen. Hier tritt dann bei r = rs eine Singularität für einlaufende Photonen auf.
zur Beschreibung radial auslaufender Photonen einführen. Hier tritt dann bei r = rs eine Singularität für einlaufende Photonen auf.Kruskal-Szekeres-Koordinaten







![$$ r={r}_{\mathrm{s}}\left[\mathcal{W}\left(\frac{u^2-{v}^2}{\mathrm{e}}\right)+1\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ92.png)
Die durch das Linienelement (13.78) beschriebene Kruskal-Raumzeit erweitert die Schwarzschild-Raumzeit nun wie folgt. Im Fall r ≥ rs gilt  . Kurven mit konstanter Zeit t = const führen also auf v∕u = const und sind daher Geraden im (u, v)-Diagramm. Kurven konstanter Radialkoordinate r = const sind dagegen Hyperbeln im (u, v)-Diagramm, wie man aus (13.76) unmittelbar sieht. Speziell folgt für r = rs, dass u2 − v2 = 0. Hieraus ergibt sich also der Spezialfall von Geraden, u = ±v. Für r = 0 ist hingegen u2 − v2 = −1 bzw.
. Kurven mit konstanter Zeit t = const führen also auf v∕u = const und sind daher Geraden im (u, v)-Diagramm. Kurven konstanter Radialkoordinate r = const sind dagegen Hyperbeln im (u, v)-Diagramm, wie man aus (13.76) unmittelbar sieht. Speziell folgt für r = rs, dass u2 − v2 = 0. Hieraus ergibt sich also der Spezialfall von Geraden, u = ±v. Für r = 0 ist hingegen u2 − v2 = −1 bzw.  .
.
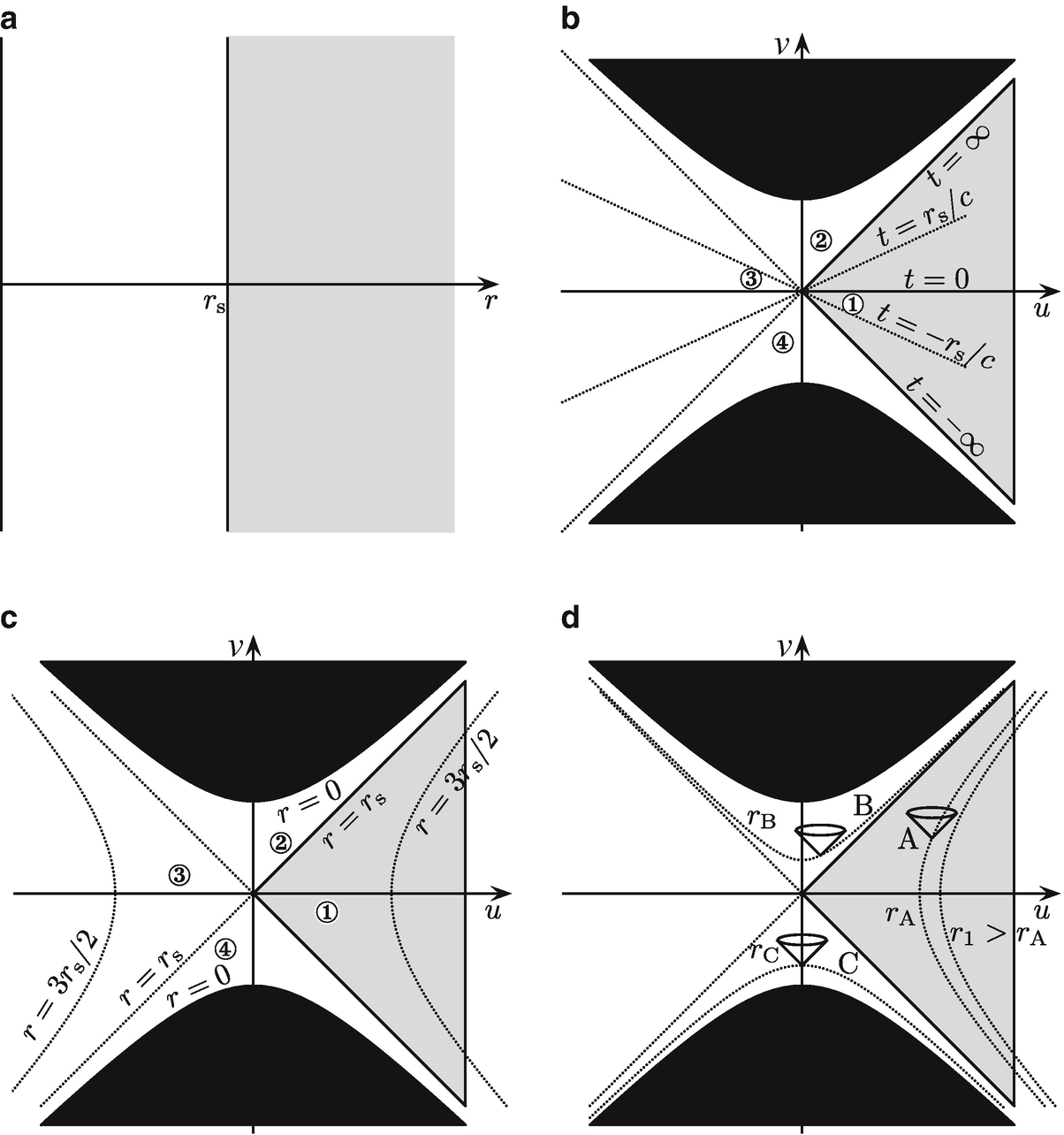
Die Schwarzschild-Koordinaten decken nur den in (a) grau markierten Teil der Raumzeit ab. In Kruskal-Koordinaten wird die Schwarzschild-Raumzeit um drei weitere Bereiche erweitert. Der ursprüngliche Bereich ist in den weiteren Abbildungen ebenfalls grau eingezeichnet. (b) Linien konstanter Zeit t, (c) Linien konstanter Radialkoordinate r, (d) Zukunftslichtkegel verschiedener Beobachter. Beobachter B befindet sich im Schwarzen Loch (Bereich ②), C im weißen Loch (Bereich ④)
Abb. 13.6b zeigt Geraden konstanter Zeit t. Die Geraden mit Steigung ±1 entsprechen t = ±∞. Die dunkelgrau untermalten Bereiche entsprächen r < 0 und sind nicht Teil der Raumzeit. Abb. 13.6c zeigt die Hyperbeln konstanter Raumkoordinate r. Die Geraden r = rs liegen im (u, v)-Diagramm exakt auf den t = ±∞ Geraden. Für unendliche Zeiten wird der Ereignishorizont also auf diese Geraden abgebildet, während sämtliche Punkte der Raumzeit mit r = rs für endliche Zeiten auf den Punkt u = v = 0 abgebildet werden.
Abb. 13.6d zeigt die Lichtkegel von drei Beobachtern A, B und C. Beobachter A befindet sich im Schwarzschild-Teil der Raumzeit bei rA > rs. Sein Zukunftslichtkegel enthält Weltlinien, die zu größeren Radialkoordinaten r1 laufen. Beobachter B dagegen befindet sich bei rB < rs. Alle von dort ausgehenden Weltlinien enden bei r = 0 in der Singularität. Jedes Teilchen, das den Schwarzschild-Radius durchquert (r < rs), wird deshalb immer in der Singularität bei r = 0 enden! Dieser Bereich heißt deshalb Schwarzes Loch. Kein Objekt, das in diesen Bereich kommt, kann ihn wieder verlassen; es endet unweigerlich bei r = 0. Gleichzeitig sieht man, dass alle Objekte, die in das Schwarze Loch gelangen wollen, die Zeitlinie t = ∞ überqueren müssen. Dies ist konform zu der bereits gezeigten Aussage, dass ein weit entfernter Beobachter das Objekt nie hinter den Ereignishorizont laufen sieht.
Beobachter C schließlich befindet sich bei rC < rs in Bereich ④. Alle Weltlinien von dort laufen zu größeren Radialkoordinaten hin. In diesen Bereich kann also kein Objekt eindringen und alle dort befindlichen Objekte wandern von dort heraus. Man spricht in diesem Fall deshalb von einem weißen Loch . Die Weltlinien überqueren dabei allerdings die Zeitlinie t = −∞. Wenn weiße Löcher also existieren sollten, dann hätte es sie bereits vor der Entstehung des Universums geben müssen, die Anfangsbedingung für die Existenz eines weißen Lochs ist daher in einem endlich alten Universum nicht zu erfüllen. Abschließend sei erwähnt, dass Bereich ③ wiederum einer Schwarzschild-Raumzeit entspricht. Allerdings zeigt dort der Zeitpfeil in Richtung kleiner werdender Zeit t. Dies wird klar, wenn man bedenkt, dass von Beobachter C kommende Lichtstrahlen die Gerade t = ∞ überqueren, um in Bereich ③ zu kommen, und die Weltlinien von Objekten, die ins Schwarze Loch fallen, über die Linie t = −∞ wandern.
13.4 Tests der ART in der Schwarzschild-Metrik
In den folgenden Abschnitten diskutieren wir einige Folgen der ART, die sich im Rahmen der Schwarzschild-Metrik ergeben und auch zu ersten experimentellen Tests der ART genutzt wurden.
13.4.1 Gravitative Frequenzverschiebung









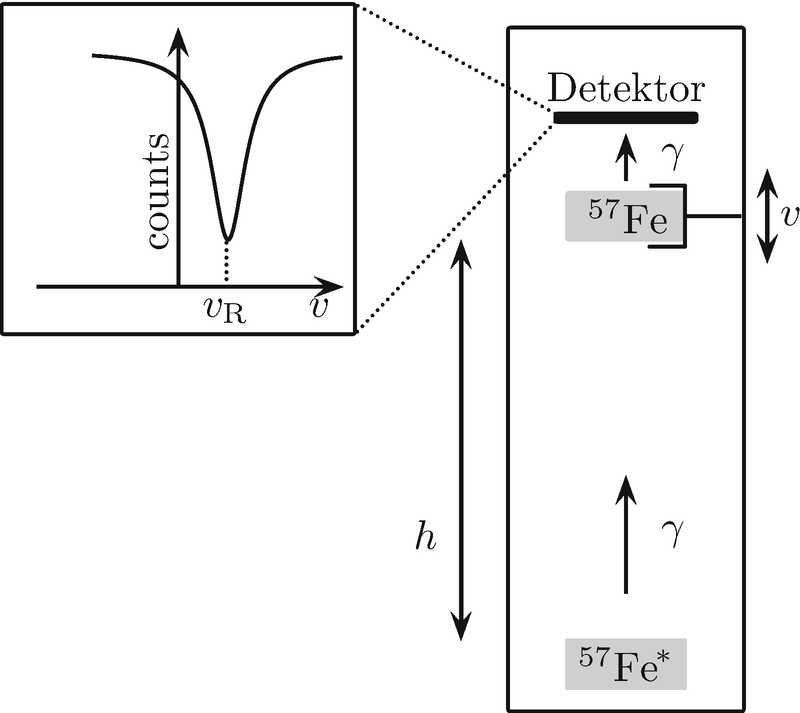
Nachweis der gravitativen Rotverschiebung: Eine angeregte Probe 57Fe emittiert γ-Strahlung mit  Eine um die Strecke h höher gelegene Probe 57Fe kann die γ-Strahlung aufgrund der Rotverschiebung zuerst nicht absorbieren. Durch Bewegen der Probe und den dadurch auftretenden Dopplereffekt kann die Rotverschiebung bei einer bestimmten Geschwindigkeit vR kompensiert und über den Wert von vR bestimmt werden. In diesem Fall beträgt vR ≈ 7,5 · 10−7 ms−1
Eine um die Strecke h höher gelegene Probe 57Fe kann die γ-Strahlung aufgrund der Rotverschiebung zuerst nicht absorbieren. Durch Bewegen der Probe und den dadurch auftretenden Dopplereffekt kann die Rotverschiebung bei einer bestimmten Geschwindigkeit vR kompensiert und über den Wert von vR bestimmt werden. In diesem Fall beträgt vR ≈ 7,5 · 10−7 ms−1
13.4.2 Periheldrehung
In der Newton’schen Mechanik sind die Bahnen von Teilchen im gravitativen Zentralpotential ϕm(r) = −GM∕r Kegelschnitte, also z. B. Kepler-Ellipsen. In diesem Abschnitt untersuchen wir, wie sich der Bahnverlauf in der ART ändert.
Aufstellen der Bewegungsgleichungen



 bedeutet hier die Ableitung nach der Eigenzeit τ. Unser Ziel ist die Bestimmung der Bahnkurve r(φ). Dazu führen wir zunächst die Substitutionen
bedeutet hier die Ableitung nach der Eigenzeit τ. Unser Ziel ist die Bestimmung der Bahnkurve r(φ). Dazu führen wir zunächst die Substitutionen



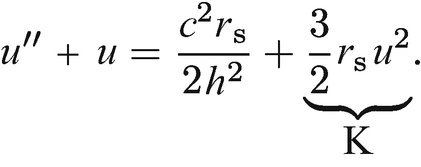
Behandlung mit klassischer Störungstheorie


![$$ {u}_0\left(\varphi \right)=\frac{c^2{r}_{\mathrm{s}}}{2{h}^2}\left[1+\varepsilon \cos \left(\varphi \right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ112.png)

![$$ {u}_1^{\prime \prime }+{u}_1\approx \frac{c^2{r}_{\mathrm{s}}}{2{h}^2}+\frac{3}{2}{r}_{\mathrm{s}}{u}_0^2=\frac{c^2{r}_{\mathrm{s}}}{2{h}^2}+\frac{3{c}^4{r}_{\mathrm{s}}^3}{8{h}^4}\left[1+2\varepsilon \cos \left(\varphi \right)+{\varepsilon}^2{\cos}^2\left(\varphi \right)\right]. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ114.png)
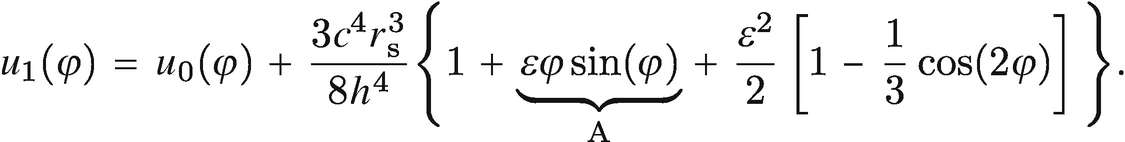
![$$ {\displaystyle \begin{array}{rll}{u}_1\left(\varphi \right)& \approx \frac{c^2{r}_{\mathrm{s}}}{2{h}^2}\left[1+\varepsilon \cos \left(\varphi \right)+\varepsilon \frac{3{c}^2{r}_{\mathrm{s}}^2}{4{h}^2}\varphi \sin \left(\varphi \right)+\dots \, \right]& \\ {}& \approx \frac{c^2{r}_{\mathrm{s}}}{2{h}^2}\left\{1+\varepsilon \cos \left[\left(1-\frac{3{c}^2{r}_{\mathrm{s}}^2}{4{h}^2}\right)\varphi \right]\right\}.\end{array}} $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ116.png)
![$$ \cos \left[\left(1-\delta \right)\varphi \right]\approx \cos \left(\varphi \right)+\sin \left(\varphi \right)\, \delta \varphi +\mathcal{O}\left({\delta}^2\right). $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ117.png)



Die Störung durch die Wechselwirkung mit den anderen Planeten war im 19. Jahrhundert bereits quantitativ bekannt. Für Merkur beträgt sie 531,5 ± 0,3ʺ pro Jahrhundert. Langjährige Beobachtungen lieferten aber 574,3 ± 0,4ʺ. Es wurden erfolglos verschiedene Erklärungen vorgeschlagen, um die Differenz von 42,7 ± 0,5ʺ zu deuten. Beispielsweise postulierte der Astronom Le Verrier10 1859 den Planeten Vulkan innerhalb der Merkur-Bahn, der für die Abweichung verantwortlich sein sollte.



Effekt der Periheldrehung: Durch die Abweichung vom 1∕r-Potential ist die Bahnkurve des Planeten nicht geschlossen. Die Punkte Pi sind die aufeinander folgenden sonnennächsten Punkte (Perihel), die Punkte Ai die sonnenfernsten (Aphel)
Ganz im Gegensatz dazu ist die entsprechende Periastrondrehung bei Pulsarsystemen um vieles größer, wie wir in Abschn. 21.5.2 sehen werden. Beim Doppelpulsarsystem PSR B1913+16 (s. Tab. 21.1) beträgt die mittlere Periastrondrehung etwa 4,23° pro Jahr.
Ich war einige Tage fassungslos vor freudiger Erregung.
13.4.3 Lichtablenkung im Gravitationsfeld
In diesem Abschnitt diskutieren wir die Lichtablenkung im Gravitationsfeld. Dazu stellen wir zuerst analog zur Periheldrehung die Bewegungsgleichungen für lichtartige Geodäten auf und lösen diese mit Hilfe der Störungsrechnung. Anschließend diskutieren wir eine alternative Berechnung basierend auf der Darstellung der Schwarzschild-Metrik in isotropen Koordinaten.
Untersuchung analog zur Periheldrehung

 für die Ableitung bezüglich des affinen Parameters λ steht. Einsetzen der Konstanten der Bewegung k und h aus (13.35) und Substitution analog zu (13.92) führt auf die Differentialgleichung
für die Ableitung bezüglich des affinen Parameters λ steht. Einsetzen der Konstanten der Bewegung k und h aus (13.35) und Substitution analog zu (13.92) führt auf die Differentialgleichung

 . Wieder benutzen wir die klassische Störungstheorie und lösen zuerst die Gleichung
. Wieder benutzen wir die klassische Störungstheorie und lösen zuerst die Gleichung  ohne Störungsterm. Dies führt auf
ohne Störungsterm. Dies führt auf

Zur Lichtablenkung im Schwerefeld: Eine in der (𝜗 = π∕2)-Ebene laufende Gerade wird in sphärischen Polarkoordinaten durch die Gleichung r (φ) = R∕sin(φ) beschrieben

![$$ {u}_1\left(\varphi \right)=\frac{1}{R}\sin \left(\varphi \right)+\frac{3{r}_{\mathrm{s}}}{4{R}^2}\left[1+\frac{1}{3}\cos \left(2\varphi \right)\right]. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ128.png)
![$$ \frac{1}{R}\sin \left(\varphi \right)+\frac{3{r}_{\mathrm{s}}}{4{R}^2}\left[1+\frac{1}{3}\cos \left(2\varphi \right)\right]=0. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ129.png)
 und
und  verwenden und erhalten
verwenden und erhalten

Resultat in Newton'scher Theorie
![$$ \frac{1}{r\left(\varphi \right)}=u\left(\varphi \right)=\frac{c^2{r}_{\mathrm{s}}}{2{h}^2}\left[1+\varepsilon \sin \left(\varphi \right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ132.png)

 bei φ = π∕2. Aufgelöst nach ε erhält man
bei φ = π∕2. Aufgelöst nach ε erhält man
![$$ 0=\frac{r_{\mathrm{s}}}{2{R}^2}\left[1+\varepsilon \sin \left({\varphi}_{\infty}\right)\right] $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ135.png)


Isotrope Schwarzschild-Metrik
 über
über

 und der Koordinatentransformation
und der Koordinatentransformation  . Es folgt dann für Photonen aus ds2 = 0 die Beziehung
. Es folgt dann für Photonen aus ds2 = 0 die Beziehung
 , d. h. auch für
, d. h. auch für 
![$$ \left|\frac{\mathrm{d}\overset{\sim }{\boldsymbol{x}}}{\mathrm{d}t}\right|=\frac{1-{r}_{\mathrm{s}}/ \left(4\overset{\sim }{r}\right)}{{\left[1+{r}_{\mathrm{s}}/ \left(4\overset{\sim }{r}\right)\right]}^3}c\approx \left(1-\frac{r_{\mathrm{s}}}{\overset{\sim }{r}}\right)c={v}_{\mathrm{Licht}}<c. $$](../images/331389_2_De_13_Chapter/331389_2_De_13_Chapter_TeX_Equ141.png)


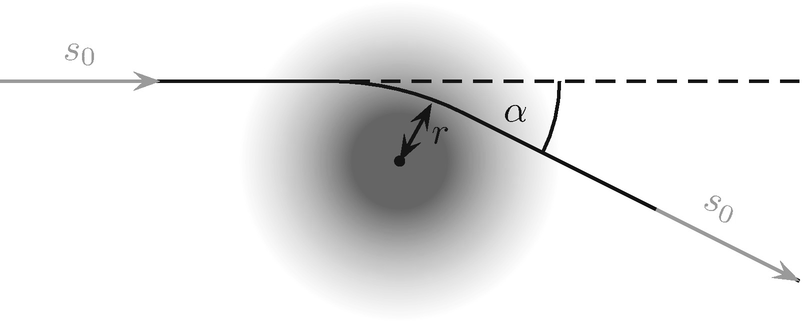
Die Wirkung von Massen kann beschrieben werden als scheinbarer ortsabhängiger Brechungsindex der Raumzeit. Die Änderung des Tangentialvektors s0 ist durch die Eikonal-Gleichung gegeben


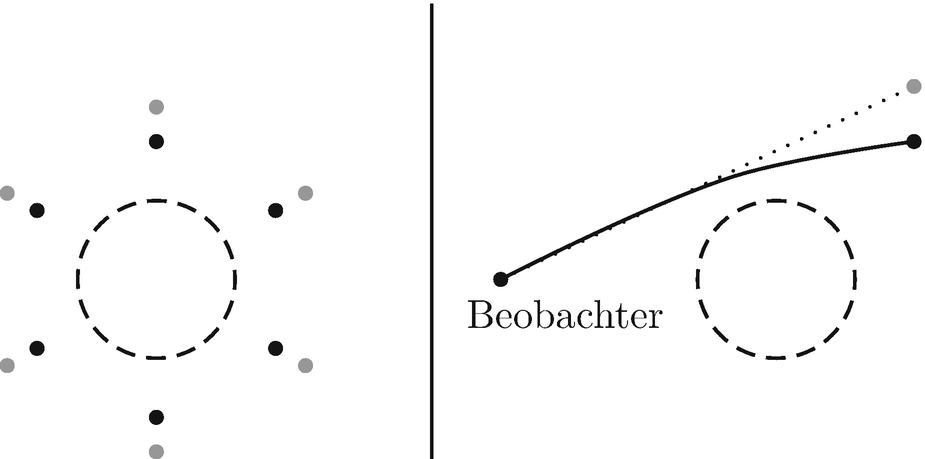
Während einer Sonnenfinsternis erscheinen Sterne, die am Himmel der Sonne nah sind, aufgrund der Lichtablenkung scheinbar weiter entfernt von der Sonne (grau) als ihre tatsächliche Position ist (schwarz)
Durch Messungen während der Sonnenfinsternis am 29. Mai 1919 konnte von Eddington die Lichtablenkung erstmals nachgewiesen und die Newton’sche Vorhersage ausgeschlossen werden [14]. Heutzutage gibt es allerdings Zweifel daran, ob mit Eddington’s Versuchsanordnung dieser Nachweis überhaupt möglich war und er nicht bei ihm auftretende systematische Fehler weit unterschätzte.
Der Effekt der Lichtablenkung wird auch als Gravitationslinseneffekt bezeichnet, da das massive Objekt, in diesem Fall die Sonne ähnlich wie eine Linse wirkt. Es besteht allerdings ein wichtiger Unterschied: Bei einer Linse wird das Licht umso stärker abgelenkt, je weiter es vom Mittelpunkt der Linse entfernt auf sie auftrifft. Die Lichtablenkung im Gravitationsfeld dagegen wird dann immer kleiner. Eine ,,Gravitationslinse“ hat daher keinen Brennpunkt.Lights all askew in the Heavens – Men of science more or less agog over results of eclipse observations – Einstein's Theory triumphs.
Eine sehr gute und leicht verständliche Abhandlung über die Lichtablenkung im Schwerefeld auch unter einem geschichtlichen Aspekt findet sich in [15].
Im Rahmen des 100-jährigen Jubiläums zur Entdeckung der Lichtablenkung an der Sonne entstand ein kurzes Vollkuppel-Video, das die Lichtablenkung demonstriert und zeigt, wie die Situation ausgesehen hätte, wenn ein Schwarzes Loch vor den Sternhaufen der Hyaden und Plejaden vorbeigezogen wäre [16].
Lichtablenkung außerhalb des Sonnensystems
Mit den leistungsfähigsten Teleskopen ist es heutzutage möglich, die Lichtablenkung auch außerhalb des Sonnensystems zu beobachten. Läuft etwa Licht einer weit entfernten Galaxie an einem sehr massiven Objekt, etwa einem Galaxienhaufen, vorbei, bevor es die Erde erreicht, so tritt hier wiederum eine Lichtablenkung auf. Durch die viel größeren Massen kann die Lichtablenkung hier noch deutlich größer sein. Licht, das vom selben Gebiet der beobachteten Galaxie in verschiedene Richtungen ausgesandt wurde, kann so abgelenkt werden, dass es bei uns aus verschiedenen Richtungen ankommt. Im Idealfall erscheint uns das betrachtete Objekt als Einstein-Ring.
Durch quantitative Messungen dieses Effekts kann wiederum Rückschluss auf die Masse des ablenkenden Objekts gezogen werden. Durch Vergleich mit Berechnungen anhand der sichtbaren Masse in diesem Objekt zeigt sich, dass viel mehr Masse für die beobachtete Lichtablenkung nötig ist, als sichtbar ist. Dies ist einer der aktuellen Hinweise auf dunkle Materie (s. Abschn. 26.4).
13.4.4 Laufzeitverzögerung
Neben der Lichtablenkung erfährt ein Lichtstrahl auch eine Laufzeitverzögerung beim Durchqueren eines Gravitationsfeldes. Dies wollen wir anhand von Radiowellen, die an den Planeten Merkur und Venus reflektiert werden, untersuchen. Für einen maximalen Effekt sollen die Planeten in Konjunktion stehen. Dabei sind Planeten und Sonne in Konjunktion, wenn sie vereinfacht gesagt auf einer Linie stehen.

 (s. Abb. 13.12). Da r ≫ rs gilt, können wir den Ausdruck in (13.132) entwickeln und erhalten
(s. Abb. 13.12). Da r ≫ rs gilt, können wir den Ausdruck in (13.132) entwickeln und erhalten
Zur Lichtlaufzeitverzögerung im Schwerefeld: Um die Verzögerung zu bestimmen, muss der Ausdruck r(l) bekannt sein, der sich elementar herleiten lässt

 und lP der Erde und des entsprechenden Planeten zur Sonne dann
und lP der Erde und des entsprechenden Planeten zur Sonne dann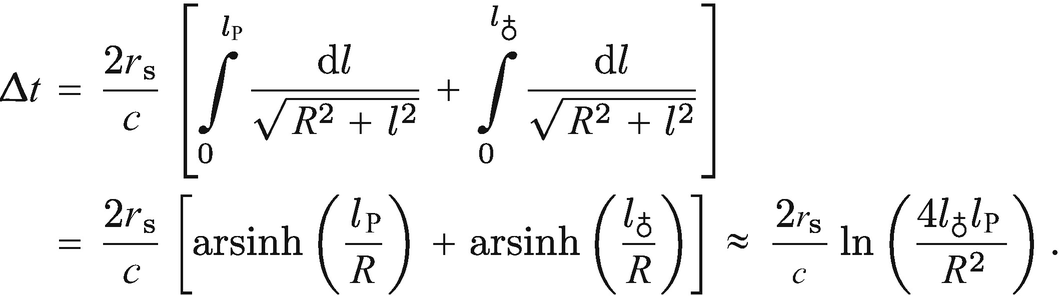

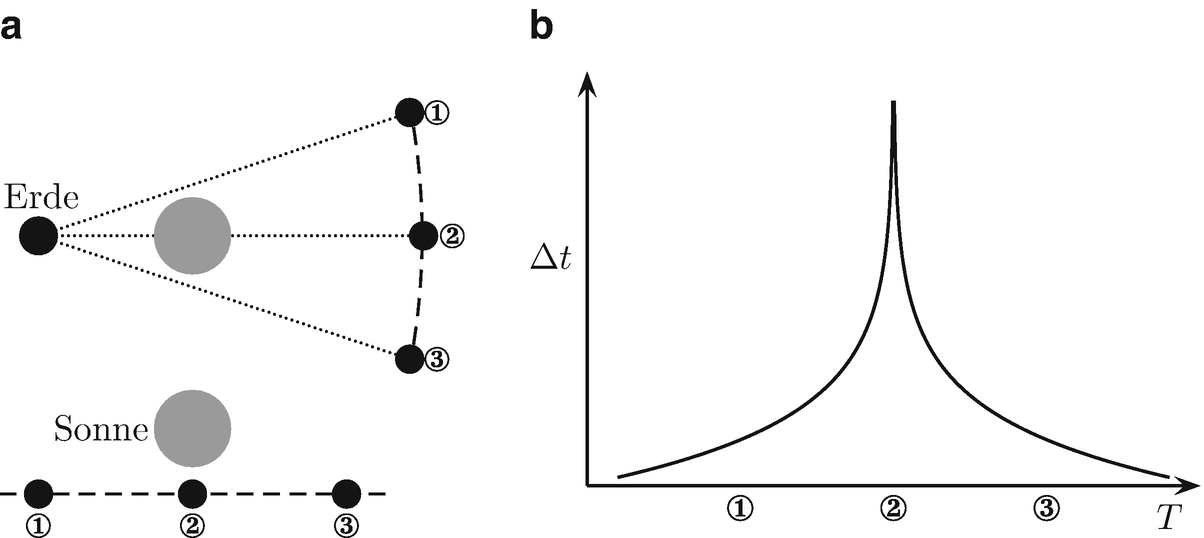
Laufzeitverzögerung des Lichts: (a) In den drei Konstellationen ①–③ ändert sich jeweils der Parameter b und damit die Laufzeitverzögerung (oben: Blick auf die Bahnebene der Erde, unten: Blick aus Erdperspektive). (b) zeigt skizzenhaft die zeitliche Entwicklung der Laufzeitverzögerung, wie man sie in einer Messung erwarten würde (s. Abb. 21.17)


Neuere Messung mit Hilfe der Cassini-Raumsonde

13.4.5 Geodätische Präzession
 -Richtung der bewegten lokalen Tetrade
-Richtung der bewegten lokalen Tetrade  zur Eigenzeit τ und die grauen Pfeile geben die
zur Eigenzeit τ und die grauen Pfeile geben die  - und
- und  -Richtung der Referenztetrade
-Richtung der Referenztetrade  an der momentanen Position an. Der momentane Rotationswinkel von
an der momentanen Position an. Der momentane Rotationswinkel von  ergibt sich jedoch nicht aus dem Winkel zur radialen Richtung
ergibt sich jedoch nicht aus dem Winkel zur radialen Richtung  des Referenzsystems, wie in Abb. 13.14 durch die grau schraffierten Kreissegmente angedeutet, sondern bezogen auf den ,,unendlichen Fixsternhimmel“. Nach einem Umlauf ist daher der Rotationswinkel α ≈ 105,44° zwischen der ursprünglichen Richtung
des Referenzsystems, wie in Abb. 13.14 durch die grau schraffierten Kreissegmente angedeutet, sondern bezogen auf den ,,unendlichen Fixsternhimmel“. Nach einem Umlauf ist daher der Rotationswinkel α ≈ 105,44° zwischen der ursprünglichen Richtung  und der aktuellen Richtung
und der aktuellen Richtung  . Die Umlaufzeit τ2π = 2π∕ω ergibt sich dabei aus der Winkelgeschwindigkeit ω bezogen auf die Eigenzeit t des Objekts (s. (13.45)).
. Die Umlaufzeit τ2π = 2π∕ω ergibt sich dabei aus der Winkelgeschwindigkeit ω bezogen auf die Eigenzeit t des Objekts (s. (13.45)).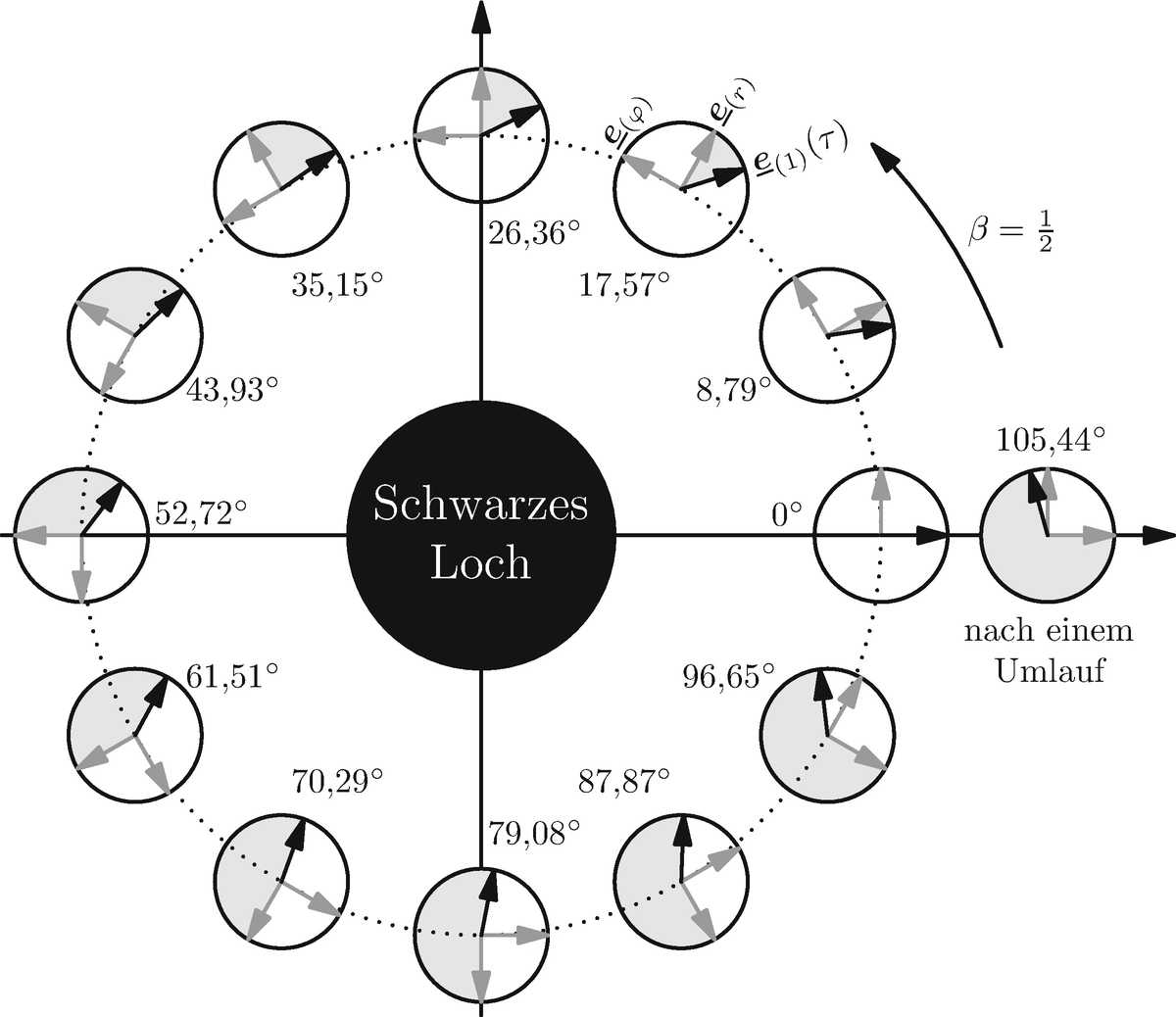
Geodätische Präzession entlang des letzten stabilen Orbits innerhalb der Schwarzschild-Raumzeit. Der Rotationswinkel an der momentanen Position bezieht sich auf den ,,unendlichen Fixsternhimmel“
13.4.6 Global Positioning System
Für den Betrieb des Global Positioning System (GPS) sind sowohl speziell- als auch allgemein-relativistische Effekte sehr wichtig, weshalb wir hier kurz darauf eingehen wollen. GPS besteht aus 24 Satelliten, die auf 6 Bahnen mit jeweils 4 Satelliten kreisen und einigen Satelliten zur Reserve. Die Satelliten befinden sich in einer Höhe von etwa 20.200 km über der Erdoberfläche und umrunden die Erde zweimal pro Tag. Aufgrund der großen Entfernung zur Erde, und der damit einhergehenden schwächeren Gravitation, gehen die Uhren der Satelliten pro Tag etwa um 45 μs vor.

13.5 Das massereiche Schwarze Loch im Zentrum der Milchstraße
Zwei Beobachtungsgruppen, die eine geführt von Reinhard Genzel13 am Max-Planck-Institut für Extraterrestrische Physik in Garching [19, 20], die andere von Andrea Ghez14 an der University of California, Los Angeles [21], haben seit 1994 die Bahnen von Sternen um das Zentrum der Milchstraße im Detail vermessen und dadurch nicht nur die Existenz eines massereichen Schwarzen Lochs im Zentrum der Milchstraße nachgewiesen, sondern auch seine Masse und seine Entfernung genau bestimmen können. Die unabhängig voneinander bestimmten Massen sind miteinander konsistent: (4,31 ± 0,36) ∙ 106 Sonnenmassen [19] bzw. (4,5 ± 0,4) ∙ 106 Sonnenmassen [21]. Der Abstand des Zentrums des Galaktischen Schwarzen Lochs konnte zuletzt mit einer Unsicherheit von nur 0,3 % zu R0 = 8178 pc (26.670 Lichtjahre) bestimmt werden [22]. Für diese Entdeckungen teilen sich Genzel und Ghez eine Hälfte des Nobelpreises für Physik 2020 [23, 24].
Das Schwarze Loch im Zentrum der Milchstraße verbirgt sich hinter dichten Vorhängen aus Gas und interstellarem Staub. Dies verhindert seine Beobachtung bei optischen Wellenlängen, da nur etwa eines von 109 Photonen den Staub in Richtung der Sichtlinie zur Erde durchdringen kann. Für Infrarot- und Radiostrahlung hingegen ist der Staub um einen Faktor 10 durchlässiger.
Entsprechend begann die Suche nach dem Schwarzen Loch zunächst mit Radioteleskopen. Balick15 und Brown16 entdeckten 1974 im Sternbild Schütze (lat. Sagitarius) bei Wellenlängen von 3,7 cm und 11 cm eine recht intensive, sehr kompakte Quelle nichtthermischer Synchrotronstrahlung, deren Position innerhalb weniger Lichtjahre mit dem vermuteten Zentrum der Milchstraße übereinstimmte [25]. Sie nannten die Quelle Sagitarius A∗ (Sgr A∗) . Der Name kam zustande, da Brown eine Theorie präsentierte, in der er Sgr A∗ als eine angeregte Radioquelle interpretierte und in Analogie zur Kennzeichnung angeregter Zustände in der Atomphysik ein Asterisk ,,∗“ hinzufügte. Die Theorie erwies sich als falsch, aber der Name blieb.
Die Gruppen von Genzel und Ghez führten ihre Beobachtungen bei Wellenlängen im nahen Infrarotbereich aus, und zwar zentriert um λ = 2,2 μm. Die von Genzel geleitete GRAVITY-Kollaboration [26] nutzte für ihre Beobachtungen das in der Atacama-Wüste im Norden Chiles gelegene Very Large Telescope (VLT) der Europäischen Südsternwarte (ESO). Dieses besteht aus vier identischen 8,2 m-Teleskopen, die zur Interferenz zusammengeschlossen werden können und dadurch ein ,,Superteleskop“ von effektiv 130 m Durchmesser ergeben, das Very Large Telescope Interferometer (VLTI). Die Gruppe von Ghez beobachtete von dem auf Hawaii stehenden Keck-Observatorium aus mit den beiden Teleskopen Keck-I und Keck-II, mit Spiegeldurchmessern von jeweils 10,4 m. Zur Interferenz zusammengeschlossen entsteht ein Teleskop mit einem effektiven Durchmesser von 85 m.
Die für die Bahnverfolgung von Sternen in der Nähe von Sgr A∗ nötige hohe räumliche Auflösung konnte durch die Technik der ,,Adaptiven Optik“ erreicht werden. Turbulenzen in der Erdatmosphäre verschmieren die Bahnen der von Sternen kommenden Photonen auf einer Zeitskala kürzer als etwa eine Sekunde (,,das Funkeln der Sterne“). Um dies auszugleichen, benutzt die Technik der Adaptiven Optik entweder einen hellen Referenzstern in der Nähe des zu beobachtenden Objekts oder einen künstlichen ,,Stern“, der durch Anregung von Natriumatomen in der oberen Atmosphäre (90 km) durch einen Laserstrahl erzeugt wird. Ein Wellenfrontsensor misst die durch die Luftunruhe aktuell verursachte Verzerrung der Wellenfronten des Referenzobjekts, ein Computer berechnet die erforderliche Rekonstruktion der Wellenfronten, diese Information wird in einer Rückkopplungsschleife auf einen verformbaren Zweitspiegel des Teleskops weitergegeben, der in Echtzeit so ,,verbogen“ wird, dass die durch die Luftunruhe verursachten Störungen im Bild des beobachteten Objekts komplett korrigiert werden können. Dies ermöglichte lange Belichtungszeiten und lieferte Bilder so scharf, als ob sie vom Weltall aus aufgenommen worden wären. Diese technische Revolution gestattete es auch, die Spektren der Sterne zu messen. Aus der Position der Spektrallinien konnte auf diese Weise zum einen auf die chemische Zusammensetzung der Atmosphären der Sterne geschlossen werden. Zum andern konnten über die Dopplerverschiebung der Linien die Radialgeschwindigkeiten der Sterne bestimmt werden.
Einer der über die Jahre verfolgten Sterne (von Genzels Gruppe S2 bezeichnet), ragt aus den beobachteten Sternen heraus. Seine Umlaufzeit um Sgr A∗ beträgt knapp unter 16 Jahren. Zum Vergleich: Für eine volle Bahn um das Galaktische Zentrum benötigt die Sonne etwas über 200 Millionen Jahre. S2 besitzt eine hochelliptische Bahn mit einer Exzentrizität von e = 0,88. Zweimal konnte die Passage von S2 durch das Perizentrum17 gemessen werden, nämlich 2002 und besonders genau im Mai 2018. Der Abstand im Perizentrum zu Sgr A∗ beträgt nur 17 Lichtstunden (oder 120 AE). Die Bahn ist um 46° relativ zur Himmelsebene geneigt.

Zusammenfassung der Beobachtungsergebnisse der Bahnverfolgung des Sterns S2 um Sgr A∗ von 1992 bis 2018 [27]. Die Farbskala gibt das Jahr der Beobachtung an. Links: Die auf die Himmelsebene projizierte Bahn von S2 relativ zu der kompakten Radioquelle Sgr A∗ (braunes Kreuz am Ursprung). Die radiale Dopplergeschwindigkeit (rechts oben) variiert zwischen −2000 und 4000 km∕s. Die Bahn von S2 während der Passage des Perizentrums im Mai 2018 wurde von GRAVITY hochgenau bestimmt (rechts unten). Um den besten Fit für den Orbit von S2 zu finden (durchgezogene Kurve) müssen Effekte sowohl der Speziellen als auch der Allgemeinen Relativitätstheorie berücksichtigt werden. Man beachte die Längenskala, die das 5000-fache des Schwarzschild-Radius von Sgr A∗ angibt, also etwa 400 Astronomische Einheiten. (Credit: GRAVITY collaboration [27], reproduced with permission ⒸESO)
Aus der Neigung der Bahnebene kann auf die dreidimensionale Geschwindigkeit geschlossen werden. Für die Gesamtgeschwindigkeit im Perizentrum ergibt sich ein Wert von etwa 7650 km∕s, was einem Geschwindigkeitsparameter von β = v∕c = 2,55 ∙ 10−2 entspricht. Dies bedeutet, dass der transversale Dopplereffekt der Speziellen Relativitätstheorie bei der Analyse der Beobachtungsdaten berücksichtigt werden muss. Bei der Annäherung an das Perizentrum ist S2 zunehmend dem starken Schwerefeld des Galaktischen Schwarzen Lochs ausgesetzt. Die dadurch bewirkte Gravitationsrotverschiebung der Infrarotstrahlung musste ebenfalls mit einbezogen werden, um den in Abb. 13.15 gezeigten besten Fit für den Orbit von S2 in der Umgebung des Perizentrums zu erhalten.
Seit 2016 hat das Instrument GRAVITY am Very Large Telescope die Infrarotastronomie noch einmal um einen gewaltigen Sprung vorangebracht. Es kombiniert, wie schon erwähnt, die Signale aller vier, interferometrisch effektiv bis zu 130 m voneinander entfernten VLT-Teleskope und erreicht eine Winkelauflösung, die etwa 16-mal besser ist als die eines einzelnen Teleskops. Dadurch konnten allgemeinrelativistische Effekte wie die Gravitationsrotverschiebung [27] und sogar die Schwarzschild-Präzession nachgewiesen werden: In [28] wird berichtet, dass das Perizentrum von S2 pro Umlauf um 12 Bogensekunden weiterwandert. Dies ist genau der Wert, den man in der Schwarzschild-Metrik bei der gegebenen Masse von etwa 4 Millionen Sonnenmassen erwartet. Außerdem konnten mit GRAVITY Ausbrüche (Flares) von Infrarotstrahlung beobachtet werden, die aus der Akkretionsscheibe von Sgr A∗ stammen [29]. Ein Gürtel aus Gas mit etwa 10 Lichtminuten Durchmesser umkreist Sgr A∗ nahe dem (aus Abschn. 13.5 bekannten) letzten stabilen Orbit. Dabei wirbelt das Gas mit einem Tempo von 30 % der Lichtgeschwindigkeit um das Schwarze Loch herum. Material, das unter den letzten stabilen Orbit gerät, stürzt auf das Schwarze Loch und erzeugt die Flares.
Eine Gruppe an der Universität Köln hat am VLT Sterne mit noch kürzerer Umlaufszeit um Sgr A∗ als S2 entdeckt [30]. Der erste, S62, benötigt 9,9 Jahre, und der allerschnellste, S4711 (benannt nach dem Parfüm aus Köln) nur 7,6 Jahre [30]. Seine Geschwindigkeit im Perizentrum beträgt 24.000 km∕s, entsprechend β = 0,08. Ein weiterer Stern, S4714, hat eine Bahnperiode von 12 Jahren, die Bahnellipse weist die extreme Exzentrizität von 0,985 auf. Diese Sterne mit noch kürzeren Umlaufzeiten sind weitere ideale Kandidaten, um Gravitationsverschiebung und Perizentrum-Drehung in der Schwarzschild-Metrik zu beobachten.
13.6 Übungsaufgaben
13.6.1 Dopplereffekt beim Pound-Rebka-Experiment
Wir haben in Abschn. 13.4.1 das Pound-Rebka-Experiment diskutiert. Dabei kamen wir auf eine Größenordnung v ≈ 7,5 · 10−7 ms−1, mit der der Absorber bewegt werden muss, um resonante Absorption zu erreichen.
Bestätigen Sie diese Größenordnung.
13.6.2 Zeitdifferenzen bei GPS
In Abschn. 13.4.6 haben wir die Zeitdifferenz angegeben, die ein GPS-Satellit gegenüber einer Uhr auf der Erdoberfläche besitzt. Diese setzt sich aus der speziell-relativistischen und der gravitativen Zeitdilatation zusammen.
Bestätigen Sie die angegebenen Werte.
13.6.3 Geschwindigkeit des frei fallenden Beobachters
In Abschn. 13.3.1 haben wir den auf ein Schwarzes Loch frei fallenden Beobachter und dessen aktuelle Position in Abhängigkeit seiner Eigenzeit diskutiert. Bestimmen Sie dessen Geschwindigkeit β am aktuellen Ort r bezogen auf die lokale Tetrade (13.37) eines Beobachters, der an diesem Ort ruht.
13.6.4 Geodätische Präzession
In Abschn. 13.4.5 haben wir die geodätische Präzession eines Vektors für einen Umlauf auf dem letzten stabilen Orbit um ein Schwarzes Loch angegeben. Berechnen Sie die geodätische Präzession für eine zeitartige Kreisbahn mit beliebigem Radius.