© Springer-Verlag GmbH Deutschland, ein Teil von Springer Nature 2022
S. Boblest et al.Spezielle und allgemeine Relativitätstheoriehttps://doi.org/10.1007/978-3-662-63352-6_2

2. Weg zur speziellen Relativitätstheorie

Sebastian Boblest1  , Thomas Müller2   und Günter Wunner3  
(1)
Dürnau, Deutschland
(2)
Max-Planck-Institut für Astronomie, Haus der Astronomie, Heidelberg, Deutschland
(3)
Universität Stuttgart, 1. Institut für Theoretische Physik, Stuttgart, Deutschland
 
 
Sebastian Boblest (Korrespondenzautor)
Email: sebastian.boblest@googlemail.com
 
Thomas Müller (Korrespondenzautor)
Email: tmueller@mpia.de
 
Günter Wunner (Korrespondenzautor)
Email: wunner@itp1.uni-stuttgart.de

Die Veröffentlichung der speziellen Relativitätstheorie (SRT) durch Albert Einstein1 1905 [2] fällt in eine Zeit, in der die Physik durch revolutionäre Umbrüche, neben der speziellen durch die allgemeine Relativitätstheorie und die Quantenmechanik, innerhalb weniger Jahrzehnte komplett verändert wurde. Die SRT revolutionierte unser Bild von Raum und Zeit. Während zuvor Zeit und Raum strikt getrennte unabhängige Entitäten waren, wurden sie innerhalb der SRT zur Raumzeit verknüpft. Die ART, die Einstein in den folgenden 10 Jahren erarbeitete, verallgemeinert dieses Konzept noch weiter. Es liegt außerhalb des Rahmens und ist nicht Ziel dieses Textes, Einsteins Arbeit in den historischen Kontext der Arbeiten anderer Wissenschaftler einzubetten, auch wenn eine solche Einordnung sehr interessant ist. Zu diesem Thema sei der Leser z. B. auf einen Artikel von Darrigol [1] verwiesen.

Wir möchten aber in einer nicht chronologisch korrekten Form einige zentrale Experimente und theoretische Ergebnisse aufzeigen, deren Probleme und Widersprüche die Formulierung der SRT motiviert haben und die durch sie aufgelöst wurden.

2.1 Modell der Lichtausbreitung im 19. Jahrhundert

Wir wissen, dass Schall ein Wellenphänomen ist. Dichte- bzw. Druckvariationen breiten sich wellenförmig durch Luft, Wasser oder andere Medien aus. Man kann es auch so auffassen, dass Schall durch Vibrationen des jeweiligen Trägermediums erzeugt wird. Durch die Interferenzversuche von Hertz war man im 19. Jahrhundert schließlich davon überzeugt, dass auch Licht ein Wellenphänomen ist. Nur was ist dann das Trägermedium, dessen Vibrationen Licht erzeugen, insbesondere, wenn man weiß, dass etwa das Licht der Sonne oder von Sternen durch das Vakuum zu uns gelangt?

Um dieses Problem zu lösen, postulierte man ein solches Medium, den Weltäther oder Lichtmedium , wie er von Einstein bezeichnet wurde. Die Existenz dieses Lichtmediums wurde fast schon als gegeben vorausgesetzt. Zu den konkreten Eigenschaften des Lichtmediums gab es aber verschiedene Hypothesen. Maxwell etwa nahm an, dass Äther und Materie eine Einheit bildeten, so sollte sich bewegende, auch sehr dünne, Materie den Äther vollständig mit sich mitziehen. Dies ist die sogenannte Mitnahme-Hypothese (engl. ether-drag). Diese Vorstellung stand aber im Widerspruch zur in Abschn. 1.​5.​5 besprochenen Aberration von Sternlicht. Aus diesem Widerspruch heraus entwickelte sich die Alternativvorstellung, dass die Erde sich durch den ruhenden Äther hindurchbewegt. Der dadurch auf der Erdoberfläche auftretende ,,Ätherwind“ hätte sich allerdings wiederum in optischen Experimenten feststellen lassen müssen, was nicht gelang. Um dieses Problem zu lösen, postulierte Fresnel2 eine partielle Äthermitnahme.

Ein großes Ziel der Experimentalphysik des 19. Jahrhunderts war es nun, experimentell die richtige unter diesen Hypothesen zu finden. Bei diesen Versuchen tat sich besonders Michelson3 hervor.

2.2 Michelson-Morley-Experiment

Das von Michelson 1881 [3] und in verbesserter Form zusammen mit Morley 1887 [5] durchgeführte Experiment ist sicherlich der berühmteste Versuch, dessen Ergebnis die Hypothese der Existenz eines Lichtmediums in große Schwierigkeiten brachte. Das eigentliche Ziel des Experiments war es aber, die Geschwindigkeit der Erde relativ zum Lichtmedium zu finden. Ausgangspunkt für das Experiment ist, dass die Zeit, die Licht auf der Erde benötigt, um eine bestimmte Strecke zurückzulegen, von der Laufrichtung des Lichts abhängen sollte. Nehmen wir an, ein Lichtstrahl soll von einem Punkt A zu einem anderen Punkt B laufen, der in der Entfernung l liegt. Dabei soll die Strecke parallel zur Bewegungsrichtung der Erde relativ zum Lichtmedium sein, die wir allerdings nicht kennen. Wenn sich die Erde mit der Geschwindigkeit v relativ zum Lichtmedium bewegt, so verringert sich die Lichtgeschwindigkeit effektiv um den Anteil v, mit dem der Punkt B sich von der Lichtfront entfernt, und es ergibt sich die Laufzeit
$$ {t}_{AB}=\frac{l}{c-v}. $$
(2.1)
In Gegenrichtung läuft der Punkt B der Lichtfront mit der Geschwindigkeit v entgegen, und wir erhalten die Laufzeit
$$ {t}_{BA}=\frac{l}{c+v}. $$
(2.2)
Für Hin- und Rückweg zusammen ergibt sich also
$$ {t}_{ABA}=2l\frac{c}{c^2-{v}^2}. $$
(2.3)
Wenn sich die Erde dagegen relativ zum Lichtmedium in Ruhe befindet, so haben wir für Hin- und Rückreise jeweils einfach
$$ {t}_0=\frac{l}{c}. $$
(2.4)
Wenn man nun experimentell entweder die Differenz tABA − 2t0 oder die Differenz tAB − tBA bestimmen kann, so erhält man daraus die Geschwindigkeit v wegen
$$ {t}_{AB}-{t}_{BA}=2l\frac{v}{c^2-{v}^2}\approx 2\frac{vl}{c^2}\left[1+\mathcal{O}\left(\frac{v^2}{c^2}\right)\right]\approx 2{t}_0\frac{v}{c}, $$
(2.5)
wobei c und t0 bekannt sind. Michelson erkannte nun, dass mit Hilfe eines Interferometers die Messung dieser Zeitdifferenz möglich sein sollte.
Sein Experiment bestand aus einem Interferometer mit aufeinander senkrecht stehenden Armen. Abb. 2.1 zeigt eine stark vereinfachte Skizze des Versuchsaufbaus. Von einer Lichtquelle wird ein Lichtstrahl auf einen Strahlteiler geleitet. Ein Teil des Lichts wird am Strahlteiler reflektiert, läuft die Strecke l auf den Spiegel S1, wird reflektiert und trifft wieder auf den Strahlteiler. Ein Teil durchläuft nun den Strahlteiler und trifft auf ein Teleskop, der jetzt reflektierte Teil ist für das Experiment nicht von Bedeutung. Gleichzeitig durchläuft ein Teil des Lichts beim ersten Auftreffen auf den Strahlteiler diesen, trifft nach einer gleich langen Strecke l auf den Spiegel S2, wird reflektiert und trifft wieder auf den Strahlteiler. Derjenige Teil des Lichts, der jetzt am Strahlteiler reflektiert wird, trifft mit dem anderen Lichtstrahl im Teleskop zusammen, und die beiden Teilstrahlen können dort miteinander interferieren. Der gesamte Aufbau ist um eine Achse senkrecht zur Bildebene drehbar. Bei der Rotation sollten sich die beobachteten Interferenzringe dann verändern. Um das zu verstehen, fangen wir mit dem Fall an, dass der Aufbau mit der Achse von der Lichtquelle zum Spiegel S2 genau parallel zur Bewegung der Erde ausgerichtet ist. Der Lichtstrahl, der vom Strahlteiler zum Spiegel S2 und zurück läuft, benötigt dafür genau die oben berechnete Zeit tABA = 2lc∕(c2 − v2). Die in dieser Zeit bezüglich des Lichtmediums zurückgelegte Strecke ist dann
Abb. 2.1

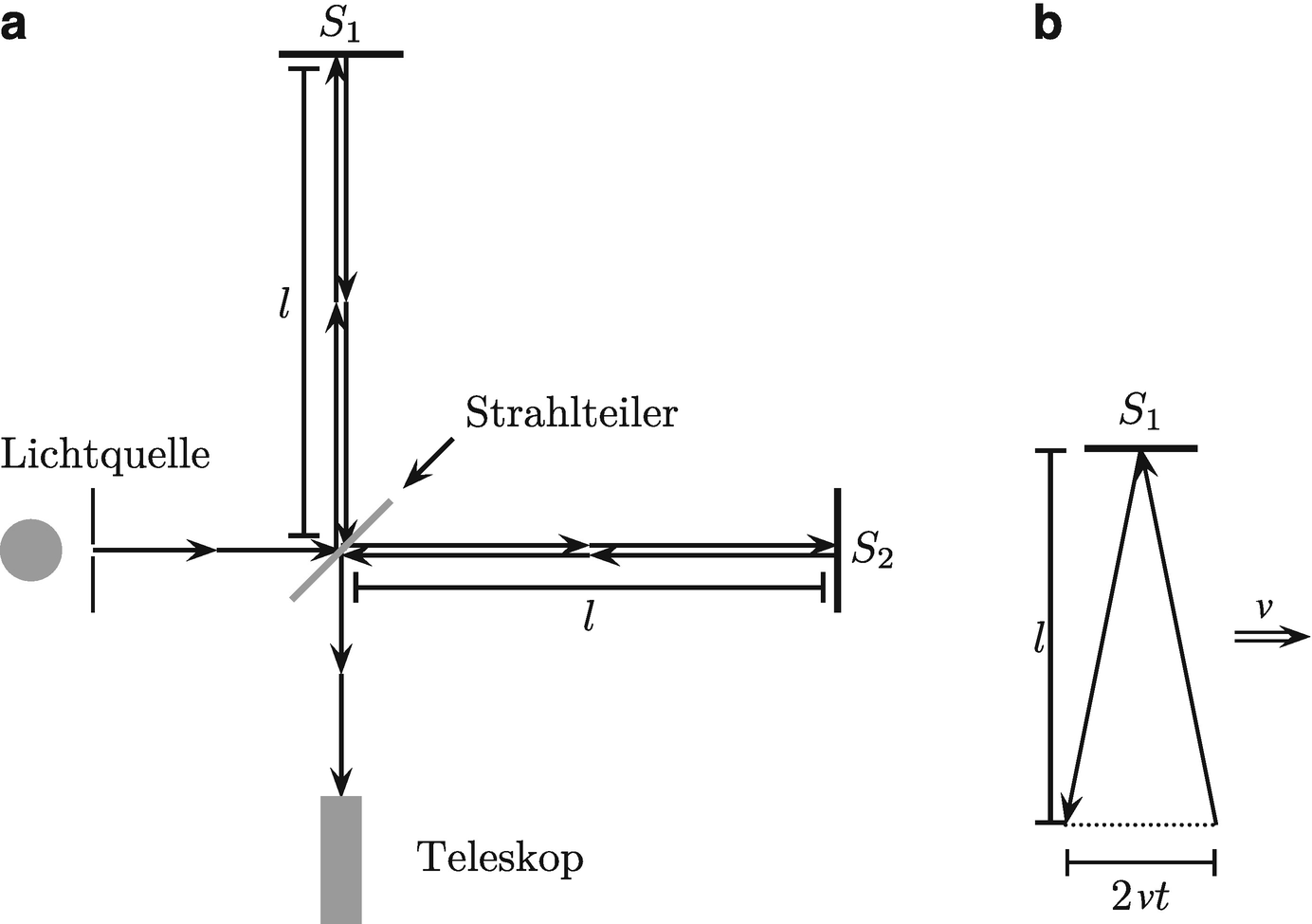
Skizze zum Michelson-Morley-Experiment. a Vereinfacht besteht der Aufbau aus einer Lichtquelle, von der ein Lichtstrahl durch einen Stahlteiler aufgeteilt wird und die beiden Teilstrahlen je auf einen von zwei Spiegeln S1 und S2 geleitet werden. Danach interferieren die Teilstahlen in einem Teleskop und man kann Interferenzringe beobachten. b Da sich das Interferometer gegen das Lichtmedium bewegt, ergibt sich auch für den senkrecht zur Bewegungsrichtung stehenden Arm eine verlängerte Wegstrecke

$$ {d}_{\parallel }=2l\frac{c^2}{c^2-{v}^2}\approx 2l\left(1+\frac{v^2}{c^2}\right)+\mathcal{O}\left(\frac{v^4}{c^4}\right). $$
(2.6)
Für den Interferometerarm senkrecht zur Bewegungsrichtung ergibt sich ebenfalls eine Korrektur der Wegstrecke. Dies ist anhand von Abb. 2.1b leicht einzusehen. Da sich der Versuchsaufbau mit der Erde bezüglich des Lichtmediums bewegt, läuft der Lichtstrahl nicht gerade zum Spiegel S1, sondern leicht schräg. Wenn er in der Zeit t bis zum Spiegel kommt, so hat sich der Versuchsaufbau um die Strecke vt weiterbewegt. Für die vom Lichtstrahl zurückgelegte Strecke haben wir daher zwei Relationen, die wir gleichsetzen können, um t zu eliminieren:
$$ d= ct=\sqrt{l^2+{v}^2{t}^2}. $$
(2.7)
Daraus berechnen wir leicht
$$ t=\frac{l}{c}\frac{1}{\sqrt{1-{v}^2 / {c}^2}}. $$
(2.8)
Die auf Hin- und Rückweg zurückgelegte Strecke ist also
$$ {d}_{\perp }=2l\frac{1}{\sqrt{1-{v}^2 / {c}^2}}\approx 2l\left(1+\frac{1}{2}\frac{v^2}{c^2}\right)+\mathcal{O}\left(\frac{v^4}{c^4}\right). $$
(2.9)
Der Effekt der Bewegung auf die Laufstrecke ist beim senkrechten Fall also nur um die Hälfte kleiner als beim parallel laufenden Lichtstrahl. Dies erschwert die Detektion der Differenz zusätzlich. Diese beträgt dann nur
$$ \Delta d=\mid {\mathrm{d}}_{\perp }-{d}_{\parallel}\mid =l\frac{v^2}{c^2}+\mathcal{O}\left(\frac{v^4}{c^4}\right). $$
(2.10)
Nimmt man als Abschätzung der Geschwindigkeit der Erde relativ zum Lichtmedium ihre Bahngeschwindigkeit aus (1.​74) an, so ergibt sich eine Differenz Δd ≈ 10−8 m. Bei einer Armlänge von l = 1,2 m und bei Verwendung von Licht mit einer Wellenlänge λ ~ 600 nm ist l ≈ 2 · 106 λ und damit Δd ≈ 0,02 λ.
Nach einer Drehung um 90° sind die Verhältnisse gerade umgekehrt, der Lichtlaufweg ist jetzt beim anderen Interferometerarm entsprechend länger. Während einer Viertelumdrehung erhalten wir daher eine Gesamtverschiebung
$$ \Delta d\approx 0,04\ \lambda . $$
(2.11)
Die Korrektur der Laufzeit wurde von Michelson bei der Auswertung seines ersten Experiments 1881 übersehen, er ging also von der doppelten Differenz aus. Dieses Experiment war sehr ähnlich der Skizze in Abb. 2.1 aufgebaut. Als Michelson auf seinen Fehler aufmerksam gemacht wurde, war klar, dass bei der Wiederholung des Experiments ein weiterentwickelter Aufbau nötig sein würde, um die entsprechenden Effekte nachweisen zu können.
Abb. 2.2 zeigt den Aufbau, den Michelson und Morley dann 1887 verwendeten. Durch Verwendung mehrerer Spiegel konnte der Lichtlaufweg vervielfacht und damit die Wegdifferenz im Vergleich zu (2.11), bzw. die Messgenauigkeit, dementsprechend erhöht werden. Die Erfahrungen mit dem ersten Aufbau hatten gezeigt, dass der kritische Punkt des Experiments die möglichst störungsfreie Drehung des Experiments war. Um so wenig Erschütterungen wie möglich zu verursachen, war der neue Aufbau auf Quecksilber schwimmend montiert. Der ganze Aufbau wurde dann kontinuierlich, mit einer Geschwindigkeit von einer Umdrehung in 6 Minuten, gedreht. Es wurde erwartet, dass sich während der Rotation des Apparates die beobachteten Interferenzringe periodisch verschieben würden. Trotz all dieser Bemühungen konnten Michelson und Morley keine Verschiebung der Interferenzringe beobachten. Die Hypothese eines ruhenden Lichtmediums, durch das sich die Erde bewegt, war damit nicht mehr zu halten. Michelson erhielt für seine Arbeiten zur Spektroskopie 1907 den Nobelpreis.
Abb. 2.2

Aufbau des Michelson-Morley-Experiments. a Perspektivische Ansicht, b Strahlenverlauf in Draufsicht. Das Interferometer ist auf einem quadratischen Stein der Seitenlänge a = 1,5 m angebracht. Der Stein ist auf einem ringförmigen Holzstück aufgestellt, das wiederum in Quecksilber schwimmt. Diese Anordnung ermöglicht es, das Experiment möglichst störungsfrei zu rotieren. Das eigentliche Interferometer besteht aus einer Anordnung von mehreren Spiegeln in den Ecken des Steins, um den Lichtweg zu maximieren.Aus Michelson und Morley [5], mit freundlicher Genehmigung

2.3 Fizeau-Versuch zur Äthermitbewegung

Der in diesem Abschnitt vorgestellte Versuch wurde erstmals 1850 von Fizeau4 durchgeführt und ist nach ihm benannt. In verbesserter Form wurde auch dieser Versuch von Michelson und Morley 1886 [4] wiederholt. Ziel dieses Experiments war es, die Mitbewegung des Äthers in optisch transparenten Medien zu testen. Abb. 2.3 zeigt eine Skizze des Versuchsaufbaus. Durch ein Rohr wird Wasser durch vier 90°-Kurven geleitet. Es entstehen so zwei parallele Teilabschnitte, in denen das Wasser in entgegengesetzter Richtung fließt. Dann wird ein Lichtstrahl durch einen Strahlteiler in zwei Teilstrahlen unterteilt, diese durchlaufen in entgegengesetzter Richtung diese beiden Teilabschnitte des Wasserlaufes. Dadurch läuft einer der Strahlen jeweils in und der andere entgegen der Fließrichtung des Wassers. Anschließend läuft ein Teil beider Lichtstrahlen durch den Strahlteiler zum Beobachter, wo die Teilstrahlen zur Interferenz gebracht werden.
Abb. 2.3

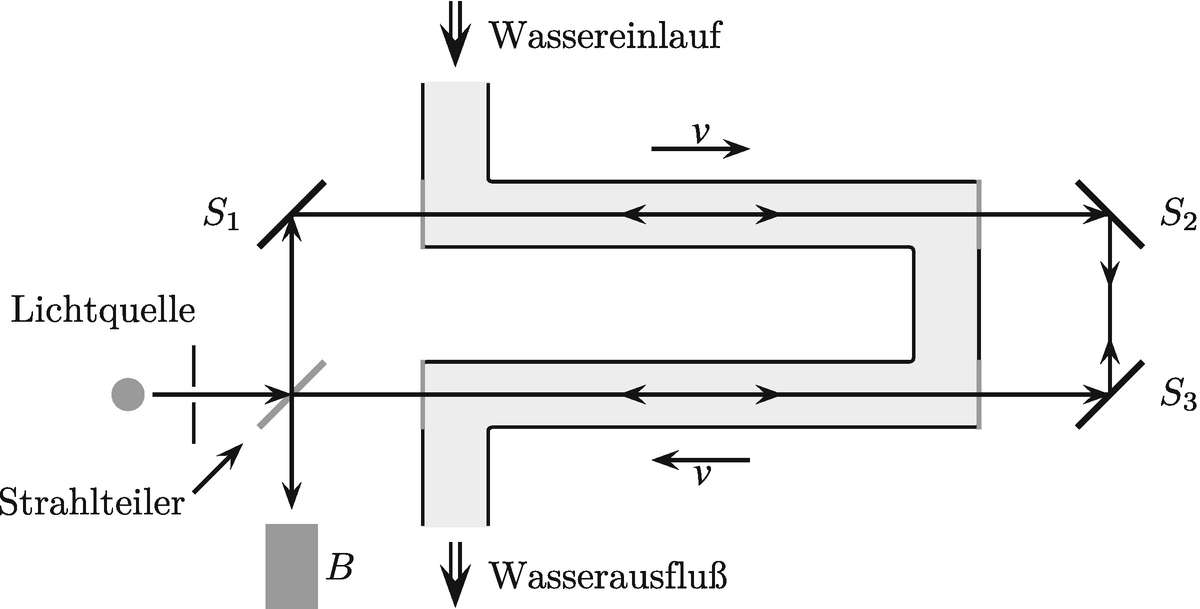
Skizze des Fizeau-Experiments. Der Lichtstrahl einer Lichtquelle wird durch einen Strahlteiler in zwei Teilstrahlen aufgeteilt. Beide Teilstrahlen durchlaufen danach einen Aufbau von Wasserrohren. In diesen Rohren fließt das Wasser mit Geschwindigkeit v. Einer der Strahlen durchläuft das Wasser in, der andere gegen die Fließrichtung. Anschließend interferieren die Teilstrahlen beim Beobachter

Die Lichtgeschwindigkeit in einem Medium mit Brechungsindex n ist
$$ {c}_{\mathrm{Med}}=\frac{c}{n}. $$
(2.12)
Wenn wir davon ausgehen, dass das Licht vom Wasser ,,mitgenommen“ wird, so erwarten wir in, bzw. entgegen der Fließrichtung die Geschwindigkeiten
$$ {c}_{\mathrm{Med}\pm }=\frac{c}{n}\pm v. $$
(2.13)
Stattdessen fanden Fizeau und auch Michelson und Morley aber
$$ {c}_{\mathrm{Med}\pm }=\frac{c}{n}\pm v\left(1-\frac{1}{n^2}\right). $$
(2.14)
Dieses Resultat passte zwar zu Fresnels Ansatz der partiellen Äthermitnahme, der eine teilweise Äthermitführung im Medium angenommen hatte, diese Annahme steht aber wiederum im Widerspruch zum Michelson-Experiment. Im Rahmen der SRT lässt sich das Ergebnis des Fizeau-Experiments zwanglos erklären (s. Übung 3.​6.​1).

2.4 Relativitätsprinzip und Inertialsysteme

Das wiederholte Scheitern, den Weltäther experimentell nachzuweisen, führte Einstein zu dem Schluss, dass es gar keinen Weltäther gibt und die Lichtgeschwindigkeit für jeden Beobachter gleich groß ist, unabhängig von seiner Bewegung relativ zur Lichtquelle.

Wenn es einen Weltäther geben würde, könnte man damit Bewegung absolut definieren. Die Geschwindigkeit eines Körpers wäre dann Null, wenn er sich relativ zum Weltäther in Ruhe befände. Wenn wir nun mit Einstein davon ausgehen, dass es keinen Weltäther gibt, so müssen wir auch das Konzept der absoluten Bewegung aufgeben. Nehmen wir z. B. einen Raumfahrer an, der sich in einem Bereich des Universums befindet, in dem es keine Sterne gibt, die nahe genug sind, damit er sie beobachten kann. Die Triebwerke seines Raumschiffes sollen ausgeschaltet sein, er beschleunigt also nicht. Wie soll er entscheiden, mit welcher Geschwindigkeit er reist und relativ zu was? Nur die Relativbewegung zu einem anderen Körper lässt sich feststellen.

Einstein fasste dieses Relativitätsprinzip so zusammen [2]:

[…] die mißlungenen Versuche, eine Bewegung der Erde relativ zum ,,Lichtmedium“ zu konstatieren, führen zu der Vermutung, dass dem Begriffe der absoluten Ruhe nicht nur in der Mechanik, sondern auch in der Elektrodynamik keine Eigenschaften der Erscheinungen entsprechen, sondern dass vielmehr für alle Koordinatensysteme, für welche die mechanischen Gleichungen gelten auch die gleichen elektrodynamischen und optischen Gesetze gelten […]

In Kap. 29 werden wir die kosmische Mikrowellenhintergrundstrahlung (cosmic microwave background radiation, CMB) kennenlernen. Sie ist ein Hinweis darauf, dass das Universum früher in einem Zustand sehr hoher Dichte war und sich seitdem ausgedehnt hat. Die CMB ist bis auf kleine Abweichungen sehr isotrop, aber z. B. auf der Erde aufgrund ihrer Bewegung und des dadurch hervorgerufenen Dopplereffektes, den wir in Abschn. 8.​1 besprechen, auf Teilen der Himmelskugel rot- und auf anderen blauverschoben, siehe auch die Diskussion in Abschn. 29.​1. Wir könnten den CMB also benutzen, um eine absolute Ruhe zu definieren. Um dem gegenüber zu treten, könnten wir von unserem Raumfahrer fordern, dass er in seinem geschlossenen Raumschiff durch ein physikalisches Experiment entscheiden soll, ob er in Ruhe ist oder sich mit einer konstanten Geschwindigkeit, etwa relativ zum CMB, bewegt. Die Aussage des Relativitätsprinzips ist, dass er an dieser Aufgabe scheitern wird.
Einer der wichtigsten Begriffe der Newton'schen Mechanik ist der des Inertialsystems . Diese sind darüber definiert, dass in ihnen das erste Newton'sche Axiom gilt:

Jeder Körper verharrt im Zustand der Ruhe, bzw. der geradlinig-gleichförmigen Bewegung, solange keine äußere Kraft auf ihn wirkt.

Diese Aussage gilt z. B. nicht für die Erdoberfläche, auf der Scheinkräfte wie die Corioliskraft auftreten. Das Relativitätsprinzip sagt nun, dass wir kein Inertialsystem besonders auszeichnen können, nämlich solch eines, das in absoluter Ruhe ist. Somit sind alle Inertialsysteme gleich gut geeignet, um physikalische Gesetze zu formulieren, und sie nehmen auch in allen Inertialsystemen die gleiche Form an.

Mit dem Vorwissen zum Relativitätsprinzip und zur Beobachterunabhängigkeit der Lichtgeschwindigkeit können wir uns in den folgenden Kapiteln jetzt mit den Grundlagen der SRT eingehend befassen.