Unsere bisherige mathematische Notation war ausreichend, um die Grundzüge der speziellen Relativitätstheorie und ihre Folgen nachvollziehen zu können. Im Hinblick auf die relativistische Mechanik, aber vor allem für die kovariante Formulierung der Elektrodynamik und später der allgemeinen Relativitätstheorie, müssen wir uns einer kompakteren und allgemeineren Notation widmen. Vieles in diesem Kapitel wird einem als eine ,,Übermathematisierung“, als eine fast zwanghafte Einführung einer abstrakten mathematischen Notation, vorkommen. Sie ist jedoch für spätere Anwendungen unumgänglich.
Wir haben bereits Vierervektoren in der Form xμ = (x0, x1, x2, x3) = (ct, x, y, z) mit einem griechischen Index geschrieben und eingeführt, dass xμ je nach Kontext den Vektor  oder eine Komponente dieses Vektors bezeichnen kann. Die Transformation in ein anderes Bezugssystem ist dann eine einfache Matrix-Vektor-Multiplikation.
oder eine Komponente dieses Vektors bezeichnen kann. Die Transformation in ein anderes Bezugssystem ist dann eine einfache Matrix-Vektor-Multiplikation.
Ab jetzt schreiben wir die Matrizen der Lorentz-Transformation ebenfalls als indexbehaftete Größen. Wenn ein Vektor einen Index hat, ist es anschaulich, dass eine Matrix entsprechend mit zwei Indizes gekennzeichnet wird, wobei ein Index die Zeile und ein Index die Spalte kennzeichnet, d. h. aus Λ wird Λμν.
Weiterhin führen wir die
Einstein'sche Summenkonvention
ein, um Schreibarbeit zu sparen. Diese besagt, dass über doppelt vorkommende Indizes in einem Ausdruck summiert wird. Eine Lorentz-Transformation in ein anderes Inertialsystem schreiben wir dann als
5.1 Minkowski-Raum
Wir haben bei der Einführung der Lorentz-Transformation die Forderung aufgestellt, dass die Größe
darunter invariant bleiben soll und auch schon auf die formale Ähnlichkeit mit dem Abstandsquadrat
im euklidischen Raum hingewiesen. Jede Drehmatrix
D im euklidischen Raum lässt den Abstand
l zwischen zwei Punkten invariant. Entsprechend lässt die Lorentz-Transformation den ,,Abstand“
s invariant. Dieser ist aber kein Abstand im euklidischen Sinn. Die SRT ist also in einem nicht-euklidischen Raum definiert, in dem der ,,Abstand“ zwischen Punkten anders definiert ist. Mathematisch sagen wir, dieser Raum hat eine andere
Metrik
als der euklidische. Die zur SRT gehörende Metrik ist die
Minkowski-Metrik
und der zugehörige Raum heißt entsprechend
Minkowski-Raum
.
5.1.1 Definition des Minkowski-Raumes
Der Minkowski-Raum ist ein vierdimensionaler, reeller Vektorraum mit folgendem
Skalarprodukt
: Seien

und

Vierervektoren mit den Komponenten
aμ und
bμ. Das Skalarprodukt

ist gegeben durch:
mit der
Minkowski-Metrik
Die Größe
bμ mit hochgestelltem Index heißt
kontravarianter Vektor
,
aμ mit tiefgestelltem Index heißt
kovarianter Vektor
. Diese Begriffe präzisieren wir in Abschn.
5.2. Die Matrix
ημν =
ημν ermöglicht im Minkowski-Raum das Herauf- und
Herunterziehen von Indizes. Darüber sind etwa die Größen
aμ und
aμ verknüpft, d. h. wir haben
Das Abstandsquadrat
s2 können wir unter Verwendung der Minkowski-Metrik dann analog als
schreiben.
Im euklidischen Raum gilt
Das Skalarprodukt eines Vektors mit sich selbst ist also größer Null, wenn der Vektor nicht der Nullvektor ist, und nur genau für den Nullvektor ebenfalls Null, d. h. es ist positiv definit. Im Gegensatz dazu ist das Skalarprodukt im Minkowski-Raum nicht positiv definit, wie man an der Definition sofort erkennt. Wie bereits diskutiert heißen Vektoren mit
 zeitartig
zeitartig
, solche mit
 raumartig
raumartig
und solche mit
 lichtartig
lichtartig
.
5.1.2 Definition der Lorentz-Transformation
Unter Verwendung der Minkowski-Metrik können wir jetzt die notwendige Eigenschaft für eine Matrix herleiten, die sie zu einer Lorentz-Transformation macht, d. h. den Abstand s invariant lässt. Wieder betrachten wir zwei Inertialsysteme S und S′ und einen Vierervektor mit Koordinaten xν in S und x′μ in S′, sowie eine Lorentz-Transformation, die von S nach S′ transformiert, d. h. es ist x′μ = Λμνxν.
Aus der Invarianz von
s2 =
xμxμ unter Lorentz-Transformationen folgt dann
Wir setzen für
x′μ den durch die Lorentz-Transformation definierten Ausdruck ein und erhalten
Dieses Ergebnis verwenden wir in (
5.9) und bringen alle Ausdrücke auf die linke Seite. Dann haben wir
Da aber
ξαβ xα xβ = 0 für beliebige
xα und
xβ gelten soll, muss
sein. Dabei haben wir die Reihenfolge der Faktoren auf der linken Seite vertauscht. Die erste Multiplikation in dieser Gleichung ist keine Matrizenmultiplikation, da
μ sowohl in der Lorentz-Transformation als auch in der Minkowski-Metrik ein Spaltenindex ist. In Einstein'scher Summenkonvention dargestellte mathematische Operationen können nicht immer oder nicht direkt als Matrixgleichung dargestellt werden. Um diese Gleichung als Matrizenmultiplikation darzustellen, muss die erste Lorentz-Matrix transponiert werden. Es ergibt sich dann die Bedingungsgleichung
für Lorentz-Transformationen. Diese Gleichung ist analog zur Definition der orthogonalen Drehmatrizen
DT1D =
1 im euklidischen Raum. Anstelle der Minkowski-Metrik
η steht hier die Identität
1.
Wenn wir die Determinante von (
5.13) bilden, so ergibt sich
Mit

und

erhalten wir
Wenden wir die Minkowski-Metrik nochmals von links auf (
5.12)
an, so führt dies auf
Mit

und
ηκαΛμαημν =
Λνκ folgt dann
wobei

für das
Kronecker-Symbol steht. Die Größe
ist also die Inverse der Lorentz-Transformation
Λμα. Wichtig hierbei ist, auf die Stellung der Indizes zu achten.
Wir werten diese Gleichung explizit für den Lorentz-Boost in
x-Richtung aus (s. (
3.20)). Hochziehen des zweiten Index geschieht über
In Matrixdarstellung ausgeschrieben lautet diese Gleichung
Herunterziehen des ersten Index erfolgt weiter durch
Diese Gleichung können wir wiederum in Matrixschreibweise darstellen und erhalten
Damit können wir (
5.17)
nun für den
x-Boost in Matrixdarstellung auswerten. Es ergibt sich dann
wie gefordert. Die inverse Lorentz-Transformation zu einem Boost ist also, wie man erwarten konnte, ein Boost mit der negativen Geschwindigkeit −
β. Für eine reine Raumdrehung
ΛR aus (
3.20) ist mit
DDT =
DTD =
1 ebenfalls
Die Menge aller Drehmatrizen bildet die Drehgruppe
SO(3) (
speziell orthogonale Gruppe), die Menge aller Lorentz-Matrizen die
Lorentz-Gruppe O(3, 1). Dabei sind aber reine Verschiebungen des Koordinatenursprungs
xμ ↦
xμ +
aμ noch nicht berücksichtigt. Wenn wir diese miteinbeziehen, dann gelangen wir zur
Poincaré-Gruppe,
1 die wie die Gruppe der Galilei-Transformationen 10 freie Parameter be
sitzt: drei Rotationen, drei Boosts, drei Verschiebungen und eine Zeittranslation. Die entsprechenden Transformationen sind dann die
Poincaré-Transformationen.
5.2 Kontra- und kovariante Vektoren
Wir müssen die Zusammenhänge zwischen Größen mit Index oben und unten noch präzisieren. Sei
aμ ∈
V ein kontravarianter Vektor im Vektorraum
V. Dann ist
aμ =
ημνaν ∈
V∗ ein kovarianter Vektor und ein Element des
Dualraumes
V∗ der 1-Formen, d. h.
Jede vierkomponentige Größe
aμ, die sich unter Lorentz-Transformation mit der Lorentz-Matrix gemäß
transformiert, nennt man einen
kontravarianten Tensor 1. Stufe
. Sei
aμ kontravarianter Vektor mit
a′
μ =
Λμνaν, dann gilt
mit der inversen Lorentz-Transformation
Λμβ. Im zweiten Schritt haben wir dabei
aν =
ηνβaβ eingesetzt. Damit haben wir das Transformationsverhalten der Größe
aβ hergeleitet. Jede vierkomponentige Größe, die sich mit der inversen Lorentz-Matrix transformiert gemäß
heißt
kovarianter Tensor 1. Stufe
.
5.2.1 Transformationsverhalten der Differentiale und Koordinatenableitungen
Sei
xμ ein kontravarianter Vektor. Es gilt dann
Die Differentiale d
xμ tranformieren sich also wie kontravariante Vektoren.
Sei weiter
f =
f(
xμ) eine skalare Funktion, dann gilt für ihr Differential
Mit
x′
μ =
Λμνxν bzw.
xν =
Λμνx′
μ folgt
Ab jetzt schreiben wir für die Koordinatenableitungen verkürzt
und
mit dem
Nabla-Operator
∇ = (
∂x,
∂y,
∂z)
T. Ein Vergleich der verschiedenen Ausdrücke in (
5.31) zeigt, dass die Koordinatenableitungen
∂μ sich wie kovariante Vektoren transformieren, d. h.
und entsprechend
∂μ wie ein kontravarianter Vektor, d. h.
Dieser Eigenschaft trägt auch die Notation der Koordinatenableitungen mit Index unten Rechnung.
5.2.2 Tensoralgebra
Wir kommen in der SRT nicht mit ko- und kontravarianten Vektoren, also Tensoren 1. Stufe aus, wenn wir alle Phänomene beschreiben wollen. Die bisherigen Definitionen von kontra- und kovarianten Tensoren müssen wir deshalb verallgemeinern. Ein
Tensor vom Typ (
r,
s)
ist eine multilineare Abbildung
Dabei bezeichnen griechische Buchstaben Elemente des Dualraumes
V∗, also kovariante Vektoren, und lateinische Buchstaben Elemente von
V, d. h. kontravariante Vektoren. Die Größe
T heißt
r-fach kontra- und
s-fach kovarianter Tensor. Gl. (
5.34) ist die Verallgemeinerung des Skalarproduktes in (
5.25).
Unter Multilinearität versteht man die Eigenschaft, linear in jedem Argument (bei Festhalten der übrigen) zu sein. Ein Tensor
χ lässt sich also zerlegen in
mit den Koeffizienten
a,

in unserem Fall. Die Menge aller Tensoren des Typs (
r,
s) bildet einen
Vektorraum

. In Indexschreibweise kann diese Abbildung in der Form
dargestellt werden. Dabei sind


…,

kovariante Vektoren und


…,

kontravariante Vektoren.
Wir können Tensoren auch so kombinieren, dass ein weiterer Tensor von anderem Typ dabei entsteht. Seien

und

, dann können wir einen neuen Tensor
definieren, d. h. aus einem Tensor vom Typ (
r,
s) und einem Tensor (
r′,
s′) wird ein Tensor vom Typ (
r +
r′,
s +
s′) gebildet. Wir können diesen Zusammenhang auch in Indexschreibweise darstellen:
Die Operation ,,⊗“ heißt
Tensorprodukt
oder
direktes Produkt
.
Sei

wieder ein Tensor vom Typ (
r,
s). Indem in Komponentenschreibweise der
k-te kovariante und der
j-te kontravariante Index das gleiche Symbol bekommen und über diese zwei Indizes aufsummiert wird, erhält man einen Tensor aus

:
Diese Operation heißt
Tensorverjüngung oder
Kontraktion
.
Wir betrachten diese Definitionen an einigen Beispielen. Seien
aμ und

kontravariante Vierervektoren. Dann ist
 ein kovarianter Vektor,
ein kovarianter Vektor,
 ein direktes Produkt und kontravarianter Tensor 2. Stufe,
ein direktes Produkt und kontravarianter Tensor 2. Stufe,
 ein direktes Produkt und einfach kontra-, einfach kovarianter Tensor,
ein direktes Produkt und einfach kontra-, einfach kovarianter Tensor,
 eine Kontraktion und Tensor 0. Stufe, d. h. ein Skalar (s. Abschn. 5.2.4)
eine Kontraktion und Tensor 0. Stufe, d. h. ein Skalar (s. Abschn. 5.2.4)
Mehr zur Tensorrechnung besprechen wir in Abschn.
11.2 im Rahmen der allgemeinen Relativitätstheorie.
5.2.3 Tensoreigenschaft des Differentialoperators
Der Begriff ,,Tensor“ ist abstrakt. Einigen Tensoren sind wir bereits begegnet, so sind Vierervektoren, d. h. Vektoren aus  Tensoren, und natürlich sind auch die Lorentz-Transformationen Λμν und
Tensoren, und natürlich sind auch die Lorentz-Transformationen Λμν und  Tensoren.
Tensoren.
Neu hingegen ist die Tensoreigenschaft des
Differentialoperators
:
welcher auch
Vierergradient
heißt. Bei Anwendung des Vierergradienten auf einen Lorentz-Skalar
φ ergibt sich ein kovarianter Vektor:
Dabei haben wir an dieser Stelle die Schreibweise
X,μ für die Differentiation nach den Koordinaten eingeführt, die im Folgenden parallel zur Notation
∂μX benutzt wird. Bei Anwendung auf einen Vierervektor
aμ ergibt sich dagegen ein Lorentz-Skalar:
Dieser Ausdruck wird auch als
Viererdivergenz
bezeichnet. Weiter ist
ein antisymmetrischer, kovarianter Tensor 2. Stufe und heißt
Viererrotation
.
5.2.4 Eigenzeit
Betrachten wir im Minkowski-Raum nur infinitesimale Abstände, so lautet das daraus resultierende infinitesimale Abstandsquadrat
mit den raumartigen Abständen d
x, d
y, d
z, und dem zeitartigen Abstand d
t (s. a. (
5.7)). Der Ausdruck d
s2 = d
xμd
xμ =
ημνd
xμd
xν mit
xμ = (
ct,
x,
y,
z) wird auch als infinitesimales Weg- bzw. Linienelement bezeichnet und ist ebenfalls invariant unter Lorentz-Transformationen.
Für einen Beobachter, der sich entlang einer Weltlinie mit Geschwindigkeit
v(
t) bewegt, gilt insbesondere d
x =
v(
t)d
t. Das Linienelement (
5.44)
lautet damit
Ist seine Geschwindigkeit
β = 0, so entspricht d
s2 = −
c2d
t2. Da man immer ein instantanes Ruhsystem für den Beobachter findet, gilt allgemein d
s2 = −
c2d
τ2 mit der
Eigenzeit τ, die selber wiederum ein Lorentz-Skalar ist.
Vergleicht man die Eigenzeit
τ eines Beobachters, der sich momentan mit Geschwindigkeit
β bezogen auf ein System ruhender synchronisierter Uhren bewegt, mit der Zeit dieser Uhren, so können wir aus (
5.45) schließen, dass
Da
γ ≥ 1 ist, vergeht die Zeit für den bewegten Beobachter langsamer als für das System ruhender synchronisierter Uhren.
 oder eine Komponente dieses Vektors bezeichnen kann. Die Transformation in ein anderes Bezugssystem ist dann eine einfache Matrix-Vektor-Multiplikation.
oder eine Komponente dieses Vektors bezeichnen kann. Die Transformation in ein anderes Bezugssystem ist dann eine einfache Matrix-Vektor-Multiplikation.


 und
und  Vierervektoren mit den Komponenten aμ und bμ. Das Skalarprodukt
Vierervektoren mit den Komponenten aμ und bμ. Das Skalarprodukt  ist gegeben durch:
ist gegeben durch:




 zeitartig
, solche mit
zeitartig
, solche mit  raumartig
und solche mit
raumartig
und solche mit  lichtartig
.
lichtartig
.




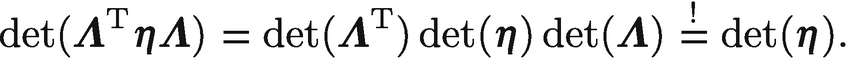
 und
und  erhalten wir
erhalten wir

 und ηκαΛμαημν = Λνκ folgt dann
und ηκαΛμαημν = Λνκ folgt dann
 für das Kronecker-Symbol steht. Die Größe
für das Kronecker-Symbol steht. Die Größe












![$$ \mathrm{d}f=\frac{\partial f}{\partial {x}^{\prime \mu }}\mathrm{d}{x}^{\prime \mu }=\frac{\partial f}{\partial {x}^{\nu }}\frac{\partial {x}^{\nu }}{\partial {x}^{\prime \mu }}\mathrm{d}{x}^{\prime \mu }=\left[{\varLambda_{\mu}}^{\nu}\frac{\partial }{\partial {x}^{\nu }}\right]f\mathrm{d}{x}^{\prime \mu }. $$](../images/331389_2_De_5_Chapter/331389_2_De_5_Chapter_TeX_Equ31.png)






 in unserem Fall. Die Menge aller Tensoren des Typs (r, s) bildet einen Vektorraum
in unserem Fall. Die Menge aller Tensoren des Typs (r, s) bildet einen Vektorraum
 . In Indexschreibweise kann diese Abbildung in der Form
. In Indexschreibweise kann diese Abbildung in der Form

 …,
…,  kovariante Vektoren und
kovariante Vektoren und 
 …,
…,  kontravariante Vektoren.
kontravariante Vektoren. und
und  , dann können wir einen neuen Tensor
, dann können wir einen neuen Tensor

 wieder ein Tensor vom Typ (r, s). Indem in Komponentenschreibweise der k-te kovariante und der j-te kontravariante Index das gleiche Symbol bekommen und über diese zwei Indizes aufsummiert wird, erhält man einen Tensor aus
wieder ein Tensor vom Typ (r, s). Indem in Komponentenschreibweise der k-te kovariante und der j-te kontravariante Index das gleiche Symbol bekommen und über diese zwei Indizes aufsummiert wird, erhält man einen Tensor aus  :
:
 kontravariante Vierervektoren. Dann ist
kontravariante Vierervektoren. Dann ist ein kovarianter Vektor,
ein kovarianter Vektor, ein direktes Produkt und kontravarianter Tensor 2. Stufe,
ein direktes Produkt und kontravarianter Tensor 2. Stufe, ein direktes Produkt und einfach kontra-, einfach kovarianter Tensor,
ein direktes Produkt und einfach kontra-, einfach kovarianter Tensor, eine Kontraktion und Tensor 0. Stufe, d. h. ein Skalar (s. Abschn. 5.2.4)
eine Kontraktion und Tensor 0. Stufe, d. h. ein Skalar (s. Abschn. 5.2.4) Tensoren, und natürlich sind auch die Lorentz-Transformationen Λμν und
Tensoren, und natürlich sind auch die Lorentz-Transformationen Λμν und  Tensoren.
Tensoren.





