Chapter 16. Appendix C: Analysis Topics Overview
16.1. Introduction to Metric Spaces*
Introduction
In may courses, concepts such as continuity and convergence are invoked without much discussion of their formal definitions, instead relying on the reader's intuitive understanding of these matters. However, for purposes of proofs, including some in the main body of material for this course, a greater rigor is required. This module will discuss metric spaces, a mathematical construct that provide a framework for the study continuity, convergence, and other related ideas in their most concrete but still formal senses. This is accomplished by formalizing a notion of the distance between two elements in a set. The intent in this and subsequent modules in this chapter is not to give a complete overview of the basic topics of analysis but to give a short introduction to those most important to discussion of signal processing in this course.
Metric Spaces
A Notion of Distance
In many situations in signal processing it is often useful to have a concept of distance between the points in a set. This notion is mathematically formalized through the idea of a metric space. A metric space (M,d) is a set M together with a function d : M × M → R that assigns distances between pairs of elements in M while satisfying three conditions. First, for every x,y ∈ M , d(x,y) ≥ 0 with d(x,y) = 0 if and only if x = y . Second, for every x,y ∈ M , d(x,y) = d(y,x) symmetrically. Third, for every x,y,z ∈ M , d(x,y) + d(x,z) ≥ d(y,z), which is known as the triangle inequality.
There are, of course, several different possible choices of definitions for distances in a given set. Our typical intuitive understanding of distance in R n fits within this framework as the standard Euclidean metric
as does the taxicab or Manhatten metric
that sums individual components of vectors, representing, for example, distances traveled walking around city blocks. Another simple yet more exotic example is provided by the discrete metric on any set defined by
in which all pairs of distinct points are equidistant from eachother but every point is distance zero from itself. One can check that these satisfy the conditions for metric spaces.
Relationship with Norms
It is not surprising that norms, which provide a notion of size, and metrics, which provide a notion of distance, would have a close relationship. Intuitively, one way of defining the distance between two points in a metric space could be the size of their difference. In other words given a vector space V over the field F with norm || · ||, we might ask if the function
for every x,y ∈ V satisfies the conditions for (V,d) to be a metric space.
Let V be a vector space over the field F with norm || · ||, and let d(x,y) = ||x – y||. Recall that since || · || is a norm, ||x|| = 0 if and only if x = 0 and ||a x|| = |a|||x|| for all a ∈ F and x ∈ V . Hence ||x – y|| ≥ 0 for all x,y ∈ V and ||x – y|| = 0 if and only if x = y . Since y – x = – (x – y) and || – (x – y)|| = ||x – y|| it follows that ||x – y|| = ||y – x|| for all x,y ∈ V . Finally, ||x|| + ||y|| ≥ ||x + y|| by the properties of norms, so ||x – y|| + ||x – z|| ≥ ||y – z|| for all x,y,z ∈ V . Thus, (V,d) does indeed satisfy the conditions to be a metric space and is discussed as the metric space induced by the norm || · ||.
Metric Spaces Summary
Metric spaces provide a notion of distance and a framework with which to formally study mathematical concepts such as continuity and convergence, and other related ideas. Many metrics can be chosen for a given set, and our most common notions of distance satisfy the conditions to be a metric. Any norm on a vector space induces a metric on that vector space and it is in these types of metric spaces that we are often most interested for study of signals and systems.
16.2. Convergence of Sequences*
Introduction
Insert paragraph text here.
Sequences
- Definition: sequence
A sequence is a function g n defined on the positive integers ' n '. We often denote a sequence by
Example .
A real number sequence:
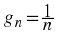
Example .
A vector sequence:
Example .
A function sequence:
Note
A function can be thought of as an infinite dimensional vector where for each value of ' t ' we have one dimension
Convergence of Real Sequences
- Definition: limit
A sequence
converges to a limit
g ∈ ℝ
if for every
ε > 0
there is an integer
N
such that
|g
i
− g| < ε ,
i ≥ N
We usually denote a limit by writing
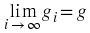or
g
i
→ g
The above definition means that no matter how small we make ε , except for a finite number of g i 's, all points of the sequence are within distance ε of g .
Example 16.4.
We are given the following convergent sequence:
Intuitively we can assume the following limit:
Let us prove this rigorously. Say that we are given a
real number
ε > 0
. Let us choose
, where
⌈x⌉
denotes the smallest integer larger than
x
. Then for
n ≥ N
we have
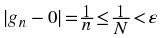Thus,
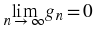
Example 16.5.
Now let us look at the following non-convergent sequence
This sequence oscillates between 1 and -1, so it will
therefore never converge.
16.3. Convergence of Sequences of Vectors*
Convergence of Vectors
We now discuss pointwise and norm convergence of vectors. Other types of convergence also exist, and one in particular, uniform convergence, can also be studied. For this discussion , we will assume that the vectors belong to a normed vector space.
Pointwise Convergence
A sequence
converges pointwise to the limit
g
if each element of
converges to the corresponding element in
g
.
Below are few examples to try and help illustrate this idea.
Example 16.6.
First we find the following limits for our two
g
n
's:
Therefore we have the following,
pointwise, where
.
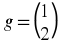Example 16.7.
As done above, we first want to examine the limit
where
t
0 ∈ ℝ
. Thus
pointwise where
g(t) = 0
for all
t ∈ ℝ
.
Norm Convergence
The sequence
converges to
g
in
norm if
. Here
∥ ˙ ∥
is the norm of the
corresponding vector space of
's. Intuitively this means the distance between
vectors
and
g
decreases to 0.
Example 16.8.
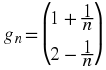Let
Thus
Therefore,
in norm.
Example 16.9.
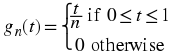Let
g(t) = 0
for all
t
.
Thus
Therefore,
g
n
(t) → g(t)
in norm.
Pointwise vs. Norm Convergence
Theorem 16.1.
For ℝ m , pointwise and norm convergence are equivalent.
Proof: Pointwise ⇒ Norm
g
n
[i] → g[i]
Assuming the above, then
Thus,
Proof: Norm ⇒ Pointwise
Since each term is greater than or equal zero, all
'
m
' terms must be zero.
Thus,
forall
i
. Therefore,
Note
In infinite dimensional spaces the above theorem is no longer true. We prove this with counter examples shown below.
Counter Examples
Example 16.10. Pointwise ⇏ Norm
We are given the following function:
Then
This means that,
g
n
(t) → g(t)
where for all
t
g(t) = 0
.
Now,
Since the function norms blow up, they cannot converge to
any function with finite norm.
Example 16.11. Norm ⇏ Pointwise
We are given the following function:
Then,
where
g(t) = 0
for all
t
. Therefore,
g
n
→ g
in norm
However, at
t = 0
,
g
n
(t)
oscillates between -1 and 1, and so it does not
converge. Thus,
g
n
(t)
does not converge pointwise.
16.4. Uniform Convergence of Function Sequences*
Uniform Convergence of Function Sequences
For this discussion, we will only consider functions with g n where ℝ → ℝ
- Definition: Uniform Convergence
The sequence
converges uniformly to function
g
if for every
ε > 0
there is an integer
N
such that
n ≥ N
implies
|g
n
(t) − g(t)| ≤ ε
for all
t ∈ ℝ
.
Obviously every uniformly convergent sequence is pointwise convergent. The difference between pointwise and uniform convergence is this: If {g n } converges pointwise to g , then for every ε > 0 and for every t ∈ ℝ there is an integer N depending on ε and t such that Equation holds if n ≥ N . If {g n } converges uniformly to g , it is possible for each ε > 0 to find one integer N that will do for all t ∈ ℝ .
Example 16.12.
Let
ε > 0
be given. Then choose
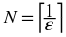. Obviously,
|g
n
(t) − 0| ≤ ε ,
n ≥ N
for all
t
. Thus,
g
n
(t)
converges uniformly to
0.
Example 16.13.
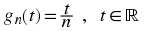Obviously for any
ε > 0
we cannot find a single function
g
n
(t)
for which Equation holds
with
g(t) = 0
for all
t
. Thus
g
n
is not uniformly convergent. However we do have:
g
n
(t) → g(t)
pointwise
Conclusion
Uniform convergence always implies pointwise convergence, but pointwise convergence does not guarantee uniform convergence.