CHAPTER 10
Redox and Electrochemistry
Have you ever bitten into an apple and set it down on a countertop? After a while the apple turns brown. The same thing happens to a potato that has been peeled; it too will turn brown. Why does this occur? Have you ever used a cleaning agent that has the term “ox” in it? Read on for the answers to these questions.
Redox Defined
Redox, a term not often found in the spell-check option in word processors, is short for reduction and oxidation. The previous chapter looked at the loss and gain of the protons. This chapter focuses on the movement of electrons. Just like protons, electrons can be gained and lost in a chemical reaction. The loss and gain of electrons, of course, will involve ions as well. Before you go any further, you will need to learn a set of rules about oxidation numbers.
Oxidation Numbers
Oxidation numbers can be thought of as the charge of an ion or the charge that an atom “feels.” You can expect ionic compounds to contain charged particles, but the atoms in covalently bonded compounds do not normally carry charges as ions do. However, the nonmetals in a neutral covalently bonded compound can still have an oxidation state or charge that they “feel.” You can find the oxidation state of an element by understanding and applying the following rules:
1. Free elements have an oxidation number of zero. That is, any element bonded to itself or by itself has no oxidation number. This is because there will be an equal sharing of the electrons in the compound. Examples are Cl2, Na, O3, and S8.
2. Group 1 metals will have an oxidation number of 1+ when bonded in compounds. For example, Na in NaCl, K in K2O, and Li in LiOH all have oxidation states of 1+.
3. Group 2 metals will have an oxidation number of 2+ when bonded in compounds. For example, Ca in CaCl2 and MgO both have oxidation states of 2+.
4. Hydrogen will have an oxidation state of 1+ when bonded in compounds. For example, H in HCl will have an oxidation state of 1+. An exception to this rule is when hydrogen is bonded in a metal hydride. Examples are NaH and KH. In a metal hydride the hydrogen will have an oxidation state of 1−.
5. Fluorine will have an oxidation state of 1− when bonded in compounds. This is the only oxidation state (other than zero) for fluorine.
6. Oxygen will have an oxidation state of 2−. An example is CaO. In this compound the oxygen has an oxidation state of 2− to balance the 2+ charge of Ca. When bonded to fluorine, oxygen has a positive oxidation number. When bonded in a peroxide, general formulas of X2O2, oxygen will have an oxidation state of 1−. Examples of this are H2O2 and Na2O2.
7. The oxidation number of an ion is the charge that the ion carries. For example, Fe3+ has an oxidation state of 3+.
Problems:
Find the oxidation numbers for O in H2O, K in KI, Ca in CaS, H in MgH2, F in HF, and Fe in Fe(s).
Solutions: Oxygen will be 2− as it is quite often. Potassium is located in group 1 and will have an oxidation number of 1+. Calcium is in group 2 and will have a charge of 2+. Hydrogen is bonded with a metal in a metal hydride and will have an oxidation number of 1−. Fluorine will have an oxidation number of 1−. Iron is a lone element and will have an oxidation state of zero.
What if you were asked to find the oxidation state of an element that has not been listed in the rules above? For example, how do you know the oxidation state of Cr in K2Cr2O7? This is a case where conservation of charge comes into play. Although you do not have oxidation state rules for Cr, you do know rules for K and O and you can apply conservation of charge to help find the oxidation state for chromium. Looking at the compound potassium chromate, you see that there is no overall charge on the compound. This means that the sum of all the oxidation states is zero. You can set up a solution that allows you to mathematically work out the oxidation states for the elements. A helpful method for solving for an unknown oxidation state is to write out the compound, find the oxidation numbers for the elements in which it is known, and work out the math to agree with the Law of Conservation of Charge. The oxidation states are always written above the elements in the compound and the math is worked out below the elements. Start by putting in the oxidation numbers for oxygen and potassium:
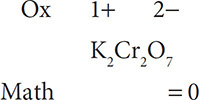
Then multiply the oxidation state by the number of atoms of the element present:
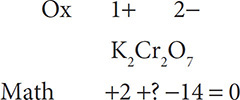
Next solve for the unknown number in the equation:
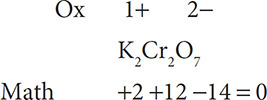
Finally, solve for the oxidation number for Cr. Because two Cr ions contribute a total of +12 to the math, each individual Cr ion has a charge of 6+:

When finding the oxidation state of an element in a polyatomic ion, remember that, mathematically, the oxidation states must equal the total charge on the polyatomic ion. For example, SO42− must be set up as:
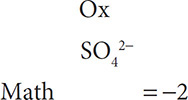
Now include the oxidation number and math for oxygen:
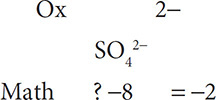
Finally, solve for the oxidation number for the sulfur:

The oxidation state for sulfur is 6+.
Problems:
Find the oxidation states for Mn in KMnO4, Cl in HClO4, P in H3PO3, and C in HCO31−.
Solutions: In short, the oxidation states are as follows:

Writing Half Reactions
Once you have a firm grasp on the rules for oxidation numbers and solving problems involving oxidation numbers, you can use oxidation numbers to determine the substance that undergoes a reduction and an oxidation in a redox reaction. You can tell that a substance has been reduced if it has gained electrons (electrons are a reactant). A substance that has been oxidized has lost electrons (electrons are a product). After the substances that have changed oxidation states in a redox reaction are identified, you then write separate half reactions. Half reactions are two separate reactions that show the oxidation and reduction reactions separately. An example follows.
When determining which substances were oxidized and reduced in a redox reaction, first assign the oxidation numbers to all the elements in the reaction. The formation for magnesium chloride serves as an example:
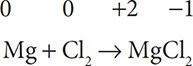
In this equation, the free elements have oxidation states of zero and the oxidation states have been assigned to Mg and Cl in magnesium chloride. Next, separate the two elements that have undergone a change in oxidation state:

Next, add electrons to balance the charges and obey the Law of Conservation of Charge. A student once pointed out to me that the electrons always go on the more positive side of the equation. To this day, my students are taught this rule religiously. This means that two electrons will be written as a product for the magnesium half reaction and two electrons will be written as a reactant for the chlorine half reaction:
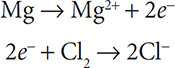
Because the Mg lost electrons, it was the substance oxidized and it is called the reducing agent. Because the Cl gained electrons, it was the substance reduced and it is called the oxidizing agent. A good mnemonic device to use is “LEO the lion says GER” (Loss of Electrons is Oxidation, Gain of Electrons is Reduction). The so-called agents are always one of the reactants in a redox reaction. Finally, notice that the number of electrons lost is the same number of electrons gained. You might think that four electrons were transferred in this reaction. Actually, only two electrons were transferred because oxidation and reduction occur simultaneously. The two electrons lost are the same two that were gained.
Write the two half reactions for: 2H2O → 2H2 + O2. First, assign oxidation numbers:
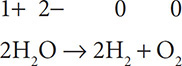
Next, separate the reactions for the elements that changed oxidation numbers:
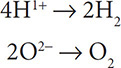
Now add electrons to balance the charges. Electrons go on the more positive side of the half reaction.
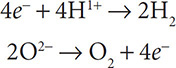
The substance oxidized (reducing agent) is O2− because it is the reactant that lost electrons. The substance reduced (oxidizing agent) is H1+ because it is the reactant that gained electrons.
Problem:
Write two half reactions for 2Na + Cl2 → 2NaCl. Which substances were oxidized and reduced?
Solutions: Assign oxidation numbers and separate the substances that had a change in oxidation state:
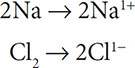
Now write in the electrons to the more positive side of the equation to balance the charge:
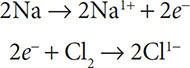
Na was oxidized and is the reducing agent. Cl2 was reduced (notice the oxidation number was reduced from 0 to 1−) and is the oxidizing agent.
Strength of Oxidizing and Reducing Agents
It is often difficult to find the strongest or weakest oxidizing or reducing agent in a redox reaction. To answer such questions, go back to the basics: electronegativity. A highly electronegative element like fluorine will gain electrons (will be reduced). What does this say about fluorine? Fluorine is the best oxidizing agent. At the other end of the spectrum is lithium. Lithium has a very low electronegativity and will give away its electrons (will be oxidized). Therefore, lithium is a very good reducing agent.
THINK ABOUT THIS 
Balancing Half Reactions
Look at the following redox reaction and write two half reactions for it:
Cu + Ag1+ → Ag + Cu2+
The Cu and Ag have oxidation states of 0 and the ions have oxidation numbers equal to their charge:
Cu0 → Cu2+
Ag1+ → Ag0
Finally, add in the electrons:
Cu0 → Cu2+ + 2e−
1e− + Ag1+ → Ag0
Here is a situation where the number of electrons lost is not equal to the number of electrons gained—processes that must occur simultaneously with an equal number of electrons. To remedy the situation, you must call upon the distributive property of mathematics. Multiply the silver half reaction by 2 to get an equal number of electrons lost and gained, and at the same time, correct the coefficients for the silver atom and ion in the equation.
2(1e− + Ag1+ → Ag0) = 2e− + 2Ag1+ → 2Ag0
Next, add up the two reactions:

Because the electrons appear on both sides of the equation in equal amounts, you can cancel them out and have a balanced equation: Cu + 2Ag1+ → 2Ag + Cu2+.
Just in case you were wondering, Cu0 was oxidized and is the reducing agent, while Ag1+ was reduced and is the oxidizing agent.
Problem:
Balance the following: Zn + Fe3+ → Zn2+ + Fe
Solutions: After placing the electrons on the more positive side of the half reactions, the half reactions will look like this:
Zn → Zn2+ + 2e−
3e− + Fe3+ → Fe
Multiply to get:
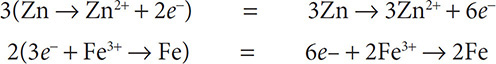
Add up the two equations and drop out the electrons that are in equal amounts on both sides of the equation to get: 3Zn + 2Fe3+ → 3Zn2+ + 2Fe.
Balancing other types of redox reactions can be more complicated and require more work. Fortunately, there is a set method for solving the complex balancing of redox reactions. These steps must be learned if you are to be successful in balancing a complex redox reaction. We will first consider the reaction: As + ClO31− → H3AsO3 + HClO.
1. First, write separate half reactions for the As and Cl. It is important to carry along the H and O that appear in the compounds:
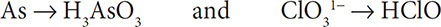
2. Then balance the elements other than H and O. The As and Cl atoms are already balanced in the two half reactions, so you still have:
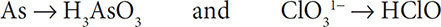
3. Add water molecules to the half reactions to balance the oxygen atoms:
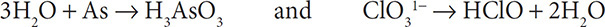
4. Add H1+ ions to the half reactions to balance the hydrogen atoms:
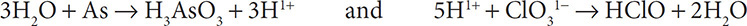
5. Obey conservation of charge by adding electrons to the more positive side of the half reactions:

6. Use the distributive property of mathematics to multiply the half reactions so that the number of electrons lost is equal to the number gained:
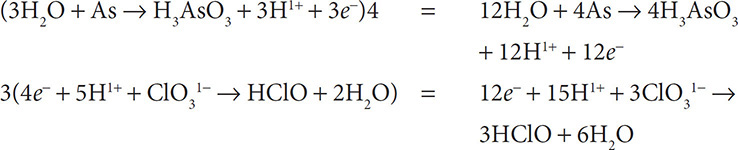
7. Finally, add the two half reactions and cancel out substances that appear on both sides of the equation:
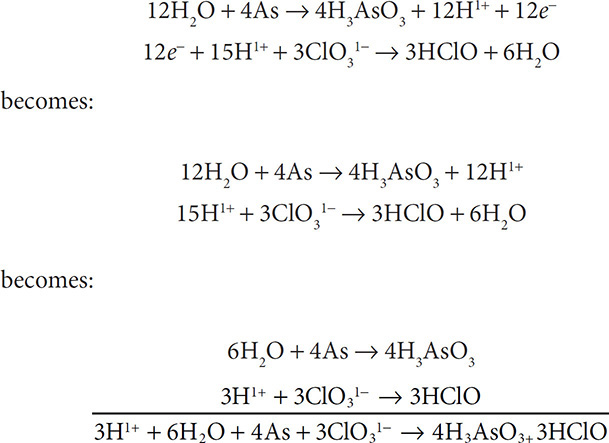
Redox reactions can be balanced in basic solutions as well. This task will require an additional step, but it can still be done following the steps shown above. To balance the redox reaction: H2O2 + ClO31− → ClO21− + O2 in a basic solution, do as follows:
1. First write separate half reactions for the O and Cl. It is important to carry along the H and O that appear in the compounds:
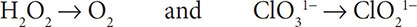
2. Then balance the elements other than H and O. The Cl atoms are already balanced, so you still have:
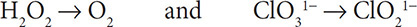
3. Add water molecules to the half reactions to balance the oxygen atoms:
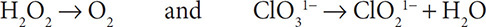
4. Add H1+ ions to the half reactions to balance the hydrogen atoms:
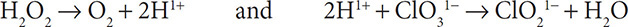
5. Obey conservation of charge by adding electrons to the more positive side of the half reactions:
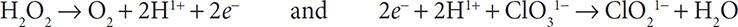
6. Because hydroxide ions neutralize hydronium ions in a basic solution, replace all of the H1+ ions with water and add an equal number of OH1− ions to the other side of the half reaction:

7. Balance the number of electrons by using the distributive property of mathematics:
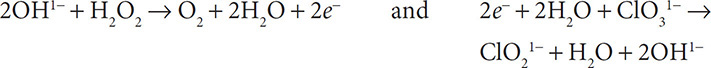
8. Finally, cancel out substances that appear on both sides of the equation:

Problem:
Balance the following reaction in an acidic solution: Cu + NO31− → NO2 + Cu2+.
Solution:
1. First write separate half reactions for the Cu and N. It is important to carry along the H and O that appear in the compounds:
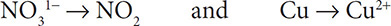
2. Then balance the elements other than H and O. The Cl and N atoms are already balanced, so you still have:
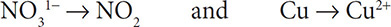
3. Add water molecules to the half reactions to balance the oxygen atoms:

4. Add H1+ ions to the half reactions to balance the hydrogen atoms:
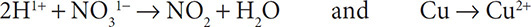
5. Obey conservation of charge by adding electrons to the more positive side of the half reactions:
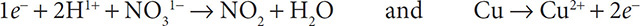
6. Balance the number of electrons by using the distributive property of mathematics:
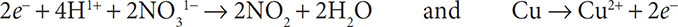
7. Finally, cancel out substances that appear on both sides of the equation:
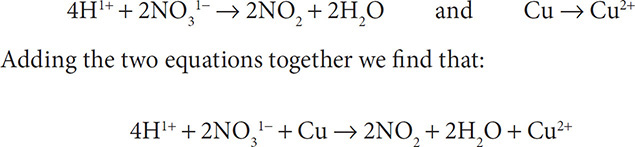
The Voltaic Cell
Because redox reactions can make electrons move from one substance to another, it is possible to create a setup so that the electrical energy produced in a redox reaction can be channeled to do work. There is a way to harvest the electrons produced by a redox reaction. Today these devices are called batteries. The first device that could do this was called a voltaic cell. In a voltaic cell a redox reaction occurs spontaneously so that the electrons can be used to do work. A typical voltaic cell is shown in Figure 10.1.
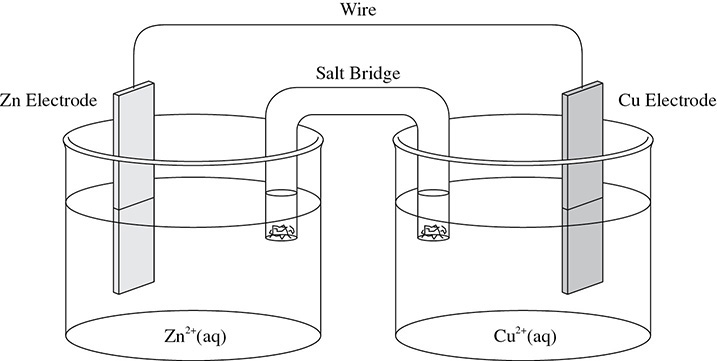
Figure 10.1 The Voltaic Cell
The wire in the voltaic cell carries the electrons from one half cell to another. The salt bridge allows ions to migrate from one half cell to the other so that there is no buildup of charge as the electrons are transferred from one half cell to the other. The electrodes are the sites of oxidation and reduction in the voltaic cell. These processes will occur on the surfaces of the cathode (electrode where reduction occurs) and the anode (electrode where oxidation occurs).
In order to understand in which direction electrons will flow in the voltaic cell, you must first get an idea of the activity of certain elements. This will tell you which elements want to lose their electrons more than others and force their electrons on these other elements. Figure 10.2 shows select metals and nonmetals sorted from most active to least active.

Figure 10.2 Activity Series
A more careful examination of the elements’ electronegativity values shows a correlation (for the most part) between electronegativity and ability to lose or gain electrons.
Look back at Figure 10.1 showing the Zn and Cu electrodes set up in the voltaic cell. For simplicity, the setup can be abbreviated by writing: Zn / Zn2+ // Cu / Cu2+. The electrons will flow spontaneously from the Zn electrode to the Cu electrode because according to the activity series, Zn is a more active metal than Cu. This means that Zn behaves more like a metal and loses electrons easily. The half reaction for Zn in this half cell will be: Zn → Zn2+ + 2e−.
The electrons lost from the Zn half cell travel through the wire (and possibly an electrical device) and remain on the surface of the Cu electrode. The negatively charged electrons will attract the positively charged Cu2+ ions and react to give: Cu2+ + 2e− → Cu.
Because the Zn electrode lost electrons (oxidation), it is called the anode (remember the mnemonic device “AN OX”). The Cu electrode gained electrons (reduction) and is called the cathode (remember the mnemonic device “RED CAT”). The anode is considered to be the negative electrode in the voltaic cell and the cathode is considered to be the positive electrode.
Finally, there is the issue of ion movement. The cations in the salt bridge will move toward the cathode half cell while the anions in the salt bridge move toward the anode half cell. Figure 10.3 shows the voltaic cell labeled to reflect the discussion above.

Figure 10.3 The Zinc/Copper Voltaic Cell
Problem:
For the voltaic cell Al / Al3+ // Co / Co2+, write the two half reactions and determine which electrode is the anode and which is the cathode.
Solutions: Looking at the activity series shows that Al is a more active metal than Co. This means that Al will lose electrons and Co will have to gain them. The half reaction for the oxidation is Al → Al3+ + 3e−. The half reaction for the reduction is 2e− + Co2+ → Co. The Al electrode is the anode and the Co electrode is the cathode.
E° Values and Spontaneous Reactions
The activity series tells the likelihood of a metal or a nonmetal to lose or gain electrons, but it does not quantify exactly how much more likely a metal or a nonmetal is to lose or gain an electron. You can examine the electrode potentials of certain elements to determine exactly how much voltage can be produced from the loss and gain of electrons between two substances. The electrode potentials can be found in Appendix 4, Reference Tables. For convenience, all reactions have been written as reduction reactions. Upon inspection of these values, you will notice a highly positive value for fluorine gas to gain electrons. Because of its high electronegativity, fluorine will gain electrons. This means that highly positive potential values (E°) for a half reaction are spontaneous half reactions. Looking under Metals in the reference table in Appendix 4 you see that the gaining of an electron by lithium has an E° value of −3.05. This indicates that the reduction of a lithium ion will not occur. Instead the opposite is most likely to happen, Li → Li1+ + 1e−. The oxidation reaction, because it is reversed, will have an E° of +3.05, again showing that positive E° values indicate half reactions that occur spontaneously.
Look back at the Zn / Zn2+ // Cu / Cu2+ voltaic cell shown in Figure 10.3. What is the E° value for this reaction? First look at the half reactions that occur in this voltaic cell:

Because the half reaction for Zn is written as an oxidation, you will need to reverse the sign of the electrode potential for this half reaction:

Problem:
Will the reaction 2KCl → 2K + Cl2 occur spontaneously?
Solutions: Start with the two half reactions: 2K1+ + 2e− → 2K and 2Cl1− → 2e− + Cl2. Now find the electrode potentials for each (remember to reverse the sign for the oxidation reaction):
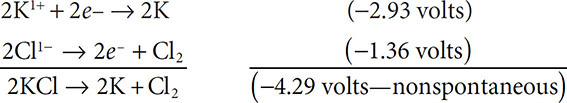
One last word about the electrode potentials before moving on. Notice that when you multiply the half reaction by a coefficient to balance the equation, you do not multiply the electrode potential for the reaction by the coefficient. The electrode potential stays the same as printed in the reference tables and is never multiplied by any coefficient.
THINK ABOUT THIS 
As redox reactions occur, the reactants are used and eventually reach completion. This is better known as “batteries dying.” When this happens, the E° value is zero and the reaction has reached equilibrium.
Because conditions under which a battery is operating (such as temperature and concentration of reactants) can change, different potentials can be reached. The new electrode potential, E, can be calculated using the Nernst equation:

This equation includes the standard electrode potential E° and the familiar constant R. The Q in the equation is the concentration of the products divided by the concentration of the reactants. The variable n stands for the number of moles of electrons transferred. The equation also introduces a new symbol, the faraday. A faraday, ƒ, is the charge on one mole of electrons, or about 96,352 coulombs of charge. For convenience it is rounded off as 96,500 C of charge. Because R and ƒ are constants and most reactions occur at 298 K, the equation can be simplified to look like this:
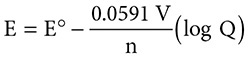
Consider the familiar voltaic cell: Zn + Cu2+ → Zn2+ + Cu. If you create a battery that has [Cu2+] = 3.0 M and [Zn2+] = 0.1 M, what will be the potential of this battery? Start with the Nernst equation and substitute:
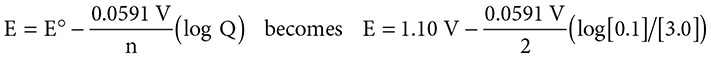
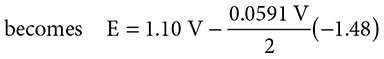
The new voltage becomes +1.144 volts, a voltage greater than that at standard conditions.
The Electrolytic Cell
Earlier you saw that the decomposition of 2KCl → 2K + Cl2 is not a spontaneous reaction. Does that mean that it is impossible to achieve this reaction? Remember that any reaction that is nonspontaneous can be made to be spontaneous if enough energy is added. The device that can help achieve this is called the electrolytic cell. While the voltaic cell spontaneously generates its own electricity, the electrolytic cell requires an outside source of current to make a nonspontaneous reaction occur. If the KCl undergoes electrolysis (literally meaning “electricity split”) the K and Cl can be split up into their original elements.
The electrolytic cell is set up with an external source of current. The electrons will flow from the negative terminal in the battery into the electrode. If the KCl is going to carry a current, it must be molten so that the ions can move freely and carry the current needed to complete the electrolysis. This can be seen in Figure 10.4. Once the current flows into the molten KCl electrons on the negative electrode, reduction will occur at this electrode, the cathode. The equation for the reaction between the negative electrons and the positive potassium ions is K1+ + 1e− → K(s). To complete the circuit, the electrons must return to the power source. This is done by the loss of electrons from the chlorine: 2Cl1− → 2e− + Cl2.

Figure 10.4 The Electrolysis of KCl
As shown in Figure 10.4, the anode is still the site of oxidation while the cathode is the site of reduction. One major change is that in the electrolytic cell the anode is now positive and the cathode is negative.
The electrolytic cell can also be used for electroplating an object with a metal. In Figure 10.5 the ring is being plated with silver. As the silver ions in solution are being attracted to the electrons on the ring to coat the ring with silver, the silver electrode is replenishing the silver that is being taken from the solution.

Figure 10.5 Electroplating with Silver
The reaction at the ring (the cathode) is Ag1+ + 1e− → Ag(s). (Why does this make sense?) The reaction at the silver electrode (the anode) is Ag(s) → Ag1+ + 1e−.
The final example of electrolysis is that of water. When water undergoes hydrolysis, hydrogen gas and oxygen gas are the products: 2H2O → 2H2 + O2. What is so special about this reaction is how the hydrogen and oxygen can be separated and captured. When the electricity from the external source reaches the cathode, reduction occurs and hydrogen gas is formed: 4e– + 4H1+ → 2H2. At the anode the oxygen from the water loses electrons to form oxygen gas: 2O2− → 4e– + O2. This is shown in Figure 10.6.
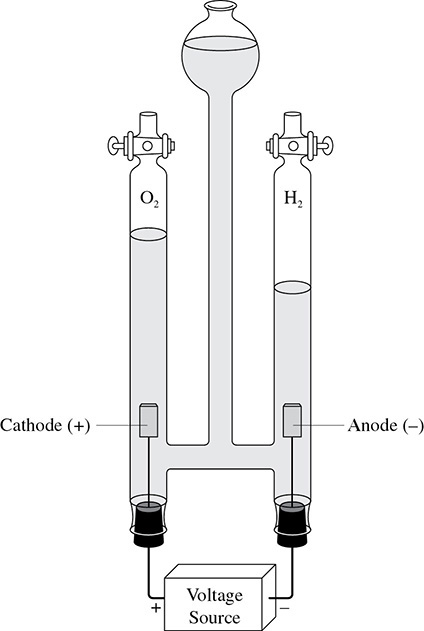
Figure 10.6 Electrolysis of Water
The apparatus also allows the gases to be captured for everyday use and experimentation.
REVIEW QUESTIONS
1. The oxidation number for hydrogen in NaH is
(A) 1+
(B) 2+
(C) 0
(D) 1−
(E) 2−
2. Of the compounds below, in which one does chlorine have the highest oxidation number?
(A) HCl
(B) KClO3
(C) HClO2
(D) KClO4
(E) CaCl2
3. In the reaction Al + Fe3+ → Al3+ + Fe, the oxidizing agent is
(A) Al
(B) Fe
(C) Al3+
(D) Fe3+
(E) none of the above
4. In the chemical cell reaction 2Cr + 3Ni2+ → 2Cr3+ + 3Ni, which species is reduced?
(A) Cr
(B) Ni2+
(C) Cr3+
(D) Ni
(E) none of the above
5. When Fe2+ is oxidized to Fe3+, the Fe2+ ion
(A) loses 1 electron
(B) loses 1 proton
(C) gains 1 electron
(D) gains 1 proton
(E) gains 1 neutron
6. Which half reaction demonstrates conservation of mass and conservation of charge?
(A) Cl2 + e− → Cl1−
(B) Cl2 + 2e− → Cl1−
(C) Cl2 → 2Cl1− + e−
(D) Cl2 + e− → 2Cl1−
(E) Cl2 + 2e− → 2Cl1−
7. When the equation Co + Ni2+ → Co3+ + Ni is balanced, the sum of the coefficients is
(A) 2
(B) 3
(C) 5
(D) 10
(E) 15
8. What is the purpose of the salt bridge in an electrochemical cell?
(A) It allows ion migration.
(B) It allows neutron migration.
(C) It allows electron migration.
(D) It prevents ion migration.
(E) It prevents neutron migration.
9. Making reference to electronegativity values, which substance is most easily reduced?
(A) Br2
(B) Cl2
(C) F2
(D) I2
(E) At2
10. When nonspontaneous redox reactions occur by use of an external current, the process is called
(A) neutralization
(B) esterification
(C) electrolysis
(D) hydrolysis
(E) voltaic ion
Questions 11–14 refer to the following;
(A) 0
(B) 1+
(C) 2+
(D) 1−
(E) 2−
11. Oxidation number of O in hydrogen peroxide
12. Oxidation number of O in OF2
13. Oxidation number of O in hydroxide ion
14. Oxidation number of O in O2
ANSWERS AND EXPLANATIONS
1. (D) The hydrogen of a metal hydride will have an oxidation number of 1− as the metal will be positive, forcing the hydrogen to be negative.
2. (D) Chlorine has an oxidation number of 7+ in choice D.
3. (D) The oxidizing agent is the substance that was reduced. This is the substance that gained electrons and saw a reduction in the oxidation number. The iron (III) ion was reduced in this reaction.
4. (B) The substance reduced in this reaction is the nickel (II) ion because the oxidation number is reduced from 2+ to 0.
5. (A) The oxidation of the iron (II) ion to form the iron (III) ion means that it lost one electron.
6. (E) All chemical reactions must show conservation of mass, charge, and energy. The reaction in choice E shows two chlorine atoms reacting and two becoming products. The reaction also shows a charge of 2− on the left side of the equation and the right side of the equation.
7. (D) To balance the reaction you first need to write two half reactions: Co → Co3+ + 3e− and Ni2+ + 2e− → Ni. Then the electrons need to be balanced:
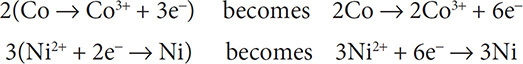
The six electrons will cancel out and the remaining coefficients will add up to 10.
8. (A) The salt bridge in a reaction allows for ion migration. Electrons migrate through the wire.
9. (C) The substance most easily reduced is the one that likes to gain electrons. The best gainer of electrons on the list is fluorine.
10. (C) The method for making a nonspontaneous reaction occur is called electrolysis. In this process, electricity is added to force a reaction to occur. An example is recharging your cell phone battery. This is a process that does not normally occur, but will occur when an electric current forces it to occur.
11. (D) The oxidation number of an oxygen atom in hydrogen peroxide, or any peroxide, is 1–. This is an exception to the usual rule for oxygen.
12. (C) The oxidation number of oxygen in this case is 2+ to balance the 1– of each of the fluorine atoms. This is an exception to the usual rule that governs oxygen.
13. (E) This is a case where there is no exception to the oxidation rules for oxygen.
14. (A) The oxidation number of an element in its free state is zero.