CHAPTER 3
Atomic Structure
A Brief History of the Atom
Our idea of the atom has come a long way over the last several thousand years. The early Greek idea of the substances was that everything was made up of earth, wind, fire, or water. The idea of an indivisible particle arrived later on, and the word “atom” was derived from the Greek word “atomos,” which means “indivisible.”
In the early 1800s John Dalton formulated his Atomic Theory, which can be summarized as follows:
• All matter is composed of atoms.
• All atoms of a given element are alike (however, in Chapter 3 this will be disputed).
• Compounds are made up of atoms combining in fixed proportions.
• A chemical reaction involves the rearrangement of atoms. The atoms are not created or destroyed in a chemical reaction.
In the early 1900s a scientist named Robert Millikan performed an experiment using drops of oil that carried a charge. Although the details of the experiment can be quite extensive, essentially the drops were allowed to fall through an electric field at a certain rate. From this experiment Millikan was able to determine the mass and charge of the electrons that were on the oil drops.
Also in the early 1900s Ernest Rutherford performed his famous Gold Foil Experiment. Rutherford set up an experiment in which a radioactive substance released alpha particles. These particles were aimed at a thin sheet of gold foil. A screen coated with zinc sulfide was set up around the gold foil to detect the alpha particles when they hit the screen. Rutherford’s experiment showed that while some of the alpha particles were deflected and bounced back, the majority of the alpha particles were able to go through the gold foil. This is demonstrated in Figure 3.1.
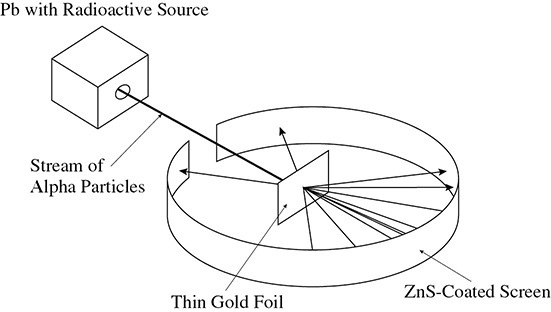
Figure 3.1 Rutherford’s Gold Foil Experiment
The next question to answer is: Why can this take place? How can an alpha particle, a particle that has mass, go through the gold foil, another substance with mass? Because the gold was hammered into a thin sheet (some say about 100 atoms thick), many alpha particles were able to pass through the gold foil. Not every alpha particle was able to pass through, however, and some were bounced back at the source of radiation. Rutherford drew the following conclusions from this experiment:
• The atom is mainly empty space. (This conclusion is often referred to as the “empty space concept.”)
• The size of the nucleus of the atom is small compared to the size of the entire atom.
• The mass of the atom is concentrated in the nucleus of the atom.
• The nucleus has a positive charge.
Subatomic Particles
A better understanding of the structure of the atom came about through additional experiments in the early 1900s. The discovery of the subatomic particles was a major breakthrough in atomic structure. These particles were classified as electrons and nucleons. The nucleons were later found to be neutrons and protons. The properties of these particles can be compared side by side:
This summarizes just the very basics of atomic structure. As time went on, more about the structure of the atom was revealed.
Isotopes
Quite often you encounter an element’s symbol written with a few numbers. These numbers tell quite a bit about the nucleus of the element in question. Look at this common example:
126C
The number 12, shown as a superscript, is called the mass number for the element. The mass number is the sum of the protons and neutrons in the nucleus of the atom. Recall from Rutherford’s experiment that the nucleus contains the atom’s mass. Because protons and neutrons are the particles in the nucleus of the atom, they make up the mass of the atom because the masses of the electrons are minimal in comparison. The number 6, shown as a subscript, is called the atomic number. This can be defined as the number of protons in the nucleus, the nuclear charge (protons are the only nucleons with a charge), or the number of electrons in a neutral atom. How many neutrons are in carbon-12? To find the number of neutrons in the atom, subtract the atomic number from the mass number. In this case there are 6 neutrons in this atom.
There exist other carbon atoms with different mass numbers: carbon-13 and carbon-14. Here is a comparison of these carbon atoms:
Notice that there is something different about the nucleus of these carbon atoms. These atoms are isotopes of one another. The similarities and differences are shown below:
Isotopes can help determine the atomic mass (not mass number) of an element. The atomic mass for an element can be found on the periodic table. The atomic mass is a number that contains decimal places. Why? Can there be a fraction of a proton or neutron? The atomic mass is not a whole number because the atomic mass takes into account all of the masses of the isotopes of an atom and their relative abundance. For example, bromine has two isotopes, bromine-79 and bromine-81. It has been discovered that 50% of all bromine atoms are bromine-79 and 50% are bromine-81. From this you can calculate why the atomic mass of bromine is 80:
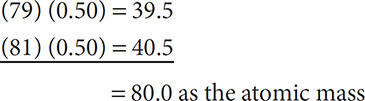
Problem:
Chlorine has two isotopes: 75% of all chlorine atoms are chlorine-35 and 25% are chlorine-37. How many neutrons are in these isotopes? What is the atomic mass of chlorine?
Solution: Both isotopes of chlorine have 17 protons. Chlorine-35 will have 18 neutrons to make the total mass number of 35. Chlorine-37 will have 20 neutrons to make a total mass number of 37. Multiply the masses of the two isotopes by their relative abundances:
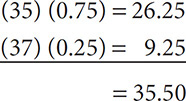
Checking the periodic table in Appendix 3 shows that this is close to the mass listed for chlorine, 35.45.
The Bohr Model of the Atom
Niels Bohr proposed a model of the atom in which the electrons move around the nucleus in fixed orbits. In this model, each orbit is at a fixed distance from the nucleus and the electrons in these orbits each have a certain amount of energy. The electrons have to be in one of the orbits; they cannot be in-between. Low-energy electrons orbit closer to the nucleus while higher-energy electrons orbit farther from the nucleus. When the electrons are in their lowest energy state they are said to be in the ground state. In this state they are orbiting as close to the nucleus as possible. When energy is added to atoms, for example in the form of heat or electricity, the electrons move to a higher energy level called the excited state. Because nature prefers a lower energy state, the electrons give off their added energy in the form of light. This allows the electrons to return to their ground state as diagrammed in Figure 3.2.
Figure 3.2 Ground and Excited States of the Atom
The light given off from an excited element can be passed through a prism or diffraction gradient to determine the exact wavelengths of light being given off by the excited atom. These exact wavelengths of light are what are called an element’s line spectrum. The line spectrum for hydrogen is shown in Figure 3.3.
Figure 3.3 Line Spectrum for Hydrogen
Each element has its own line spectrum. This is why the line spectrum for an element is also considered to be a “fingerprint” for that particular element. Because the amounts of light given off by the excited atoms were in fixed amounts, Bohr termed them “quantized” amounts of light. These fixed amounts of energy proved that the electrons could only make certain jumps between the orbits that were at fixed distances in the atom. Because of these fixed, circular orbits, Bohr’s model of the atom is often referred to as the “solar system model” of the atom (see Figure 3.4).
Figure 3.4 Solar System Model of the Atom
Wave-Mechanical Model
The wave-mechanical model of the atom shows a more complex structure of the atom and the way electrons configure themselves in the principal energy levels. Principal energy levels are divided into sublevels, each with its own distinct set of orbitals. This more complex structure is outlined with the help of this diagram. The principal energy levels in the atom are numbered 1 through 7.
The first principal energy level has just one subshell, the second principal energy level has two, the third has three, etc. Now the outline can be enhanced:
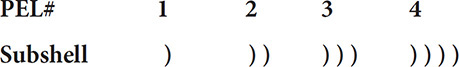
The first subshell in each principal energy level is given the letter “s.” The second sublevel is given the letter “p,” the third “d,” and the fourth “f.” Now the model is labeled even further:
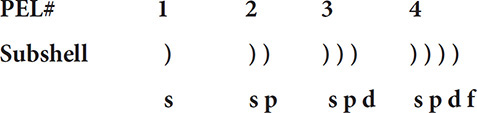
The s subshell contains one orbital or region where an electron can be found. The p sublevel has three orbitals, while the d and f levels have five and seven orbitals, respectively. The shapes of the s and p orbitals are shown in Figure 3.5.
Figure 3.5 Shapes of s and p Orbitals
Each orbital is allowed to carry a maximum of two electrons and, according to the Pauli Exclusion Principle, the electrons must have opposite spins.
How do electrons fill these principal energy levels? Consider the simplest example, hydrogen and its one electron. Because electrons want to be in the lowest energy state possible, the one electron will be located in the 1s orbital. This can be diagrammed by simply writing 1s1 or by drawing a diagram as follows: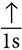 
.
Because the 1s orbital can hold up to two electrons, the electron configuration for helium would look like this: 1s2 or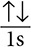 
. Notice that the arrows are pointing in different directions. This shows the opposite spins of the electrons. The next example will show how Hund’s rule works. Consider the electron configuration of nitrogen in its ground state. Nitrogen has seven electrons total. The first two electrons will fill the 1s orbital. Looking at the diagrams above, after the 1s orbital is full, the 2s orbital then takes in electrons. The remaining three electrons will go in the 2p orbital. The electron configuration looks like this: 1s22s22p3. What is of concern here is how the electrons orient themselves in the 2p orbitals. There are two possibilities:
According to Hund’s rule, the electrons fill their orbitals singly and then they begin to pair up. This means that the second situation shown above is the correct filling order for the electrons.
Problem:
Give the electron configurations for S and Ca.
Solution: Sulfur has 16 electrons. The shorthand notation is 1s22s22p63s23p4 or
Ca has 20 electrons and has the configuration that looks like this: 1s22s22p63s23p64s2.
Notice that in the previous problem the 3d orbital has been skipped over. The 3d orbital fills up after the 4s orbital has filled up. This is because the 4s orbital actually has less energy than the 3d orbital (unusual but true). This means that the filling order through element number 36, Kr, is 1s22s22p63s23p64s23d104p6. Also note the maximum number of electrons that can be held in a principal energy level. The first principal energy level can hold up to 2 electrons (1s2), the second up to 8 (2s22p6), and the third up to 18 (3s23p63d10). This pattern follows the equation 2n2, where n is the number for the principal energy level. For example, to find the maximum number of electrons that can be held in the fourth principal energy level you can say that 2(4)2 = 32 electrons maximum.
Valence Electrons and Dot Diagrams
Valence electrons play a huge role in bonding, as will be shown later. Valence electrons are the electrons that are in the outermost principal energy level (not to be confused with the outermost subshell). These electrons are important because they are the electrons that are lost, gained, or shared when forming chemical bonds. The valence electrons of an atom are the electrons that interact with the valence electrons of another atom to form these bonds.
Problem:
How many valence electrons are in the elements Na, P, Cl, and Ca?
Solution: Look at the electron configurations first.
When diagramming the shapes and structures of atoms it is important to have correct valence dot diagrams. These diagrams are easy to draw because they follow a simple pattern. There are two rules you need to remember when drawing valence dot diagrams (see Figure 3.6):
Figure 3.6 Valence Dot Diagrams
• The first two electrons go together on the same side of the symbol, as if they were filling the s orbital.
• The next six electrons fill singly then pair up according to Hund’s rule, as if they were filling the p orbital. A good way to remember this rule is to say to yourself, “Single, single, single, then paired, paired, paired.”
Problem:
Give the valence dot diagram for N, Ne, O, and Ca.
Solution: Determine the electron configurations and find the valence electrons:
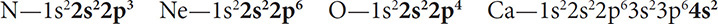
Then draw the diagrams as in Figure 3.7.
Figure 3.7 Valence Dot Solutions
Effective Nuclear Charge—Zeff
All electrons in an atom experience an attraction to the positively charged nucleus. However, at the same time, there is a repulsion felt between the electrons because of their negative charge. The effective nuclear charge acting upon an electron or set of electrons can be calculated using the following:
Zeff = Z − S
where Z is the number of protons in the nucleus and S is the number of electrons between the valence electrons and the nucleus. If we were to calculate the effective nuclear charge for the valence electron in a sodium atom we would find that value would be 1+. Looking at the electron configuration of sodium we find that there are 10 electrons between the nucleus and the valence electron: 1s22s22p63s1. Z in this case is 11 and S is 10, giving Zeff = 1+.
Problem:
What is the effective nuclear charge on the eight electrons in the second principal energy level of sodium?
Solution: The eight electrons in principal energy level two would feel a +9 effective nuclear charge because the nucleus has a +11 charge and there are two electrons in principal energy level one.
Quantum Numbers
To help keep track of each electron present in an atom, four quantum numbers are assigned to each electron. The rules for assigning quantum numbers are as follows:
• The first number is called the principal quantum number, n, and it can be any whole number integer. The first quantum number, n, represents the principal energy level that the electron in question is in. For example, the one electron in H is 1s1 and n will equal 1. The valence electron of Li, 1s22s1, will have n equal to 2.
• The second number is called the angular momentum quantum number, l, and it can be an integer from 0 to n – 1. The second quantum number represents the sublevel that the electron is in. If the electron is in the s orbital, then l = 0. An electron in the p orbital will have l = 1, and so on.
• The third number is called the magnetic quantum number, ml, and it can be an integer that ranges from – l to + l. The third quantum number helps us identify in which region of each sublevel the electron in question is located. These regions are specific orbitals.
• The fourth quantum number is ms and it can only be a value of +1/2 or –1/2. The fourth quantum number represents the direction of the electron’s spin. The opposite signs represent the opposite spins.
Assigning quantum numbers to the electrons of a few simple atoms will help us learn how to assign these numbers.
Problem:
An atom of hydrogen has one electron and it is labeled 1s1. What will the quantum number be?
Solution: In this case n will be equal to 1 because the electron is in principal energy level 1.
l must be 0 because l is a number from 0 to n – 1.
ml is equal to 0 because the value of l is 0.
ms is equal to +1/2.
The quantum numbers are 1, 0, 0, +1/2.
Problem:
Assign quantum numbers to the valence electron of a lithium atom.
Solution: The sole valence electron for lithium has an electron configuration of [He]2s1. From this we can see that:
n = 2 because the valence electron is in the second principal energy level.
l can be either 0 or 1 (2 – 1 = 1). We assign the 0 first as l = 1 because it will not be used until we start to fill the p orbitals.
ml is equal to 0 because the value of l is 0.
ms is equal to +1/2.
The quantum numbers are 2, 0, 0, +1/2.
Problem:
Assign quantum numbers for the tenth electron to fill a neon atom.
Solution: n = 2, l = 1, ml = 1 and ms = –1/2.
Hybridization
Carbon is an exception to the rules for writing valence dot diagrams as described above. A close examination of carbon and its valence electrons shows a different story, the proof being that carbon can make four bonds. Carbon has six electrons and its electron configuration is 1s22s22p2. The valence dot diagram according to this arrangement should look like:
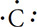
According to this dot diagram, carbon should make only two bonds. However, this is not the case as all. Instead, carbon has an arrangement that is 1s22s12p3 or
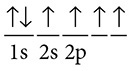
This is called the sp3 hybridization of the carbon atom. One of the electrons has moved from the 2s orbital to the 2p orbital. This now gives carbon four single electrons rather than two paired electron and two unpaired electrons. It is the single electrons that bond in an effort to become paired up. Because there are four single electrons in the sp3 hybridized carbon atom, carbon can bond four different atoms to its four single electrons. In order to have the four electrons as unpaired electrons, the sp3 hybridization also changes the shapes of the s and p orbitals that are involved in the bonding. This change is shown in Figure 3.8.
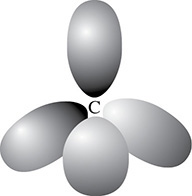
Figure 3.8 sp3 Hybridized Carbon Atom
The new arrangement is called a tetrahedral shape because the atoms are at 109.5-degree angles to each other. This can be seen in the three-dimensional shape of methane, a molecule with a tetrahedral molecular geometry. Should only three atoms bond to the sp3 hybridized atom, then the molecular geometry is said to be trigonal pyramidal. Ammonia is an example of this. Finally, in water the oxygen is sp3 hybridized but because only two atoms have bonded to the oxygen, the molecular geometry is said to be bent (see Figure 3.9).
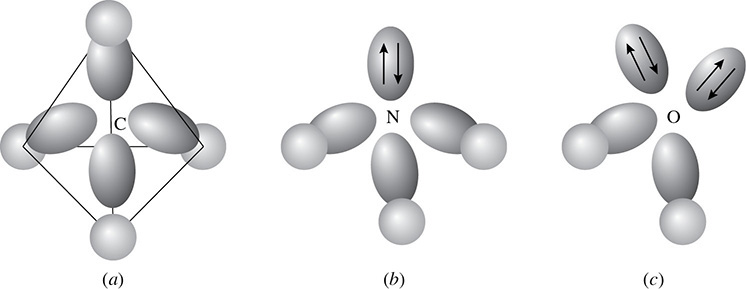
Figure 3.9 Tetrahedral, Trigonal Pyramidal, and Bent Molecular Geometries
In an sp2 hybridization one 2s and two 2p orbitals combine to form a new shape as shown in Figure 3.10.
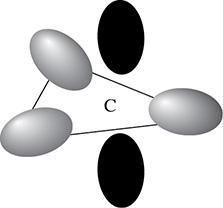
Figure 3.10 The sp2 Hybridized Carbon Atom
In this hybridized state the carbon will make two single bonds and one double bond. This will allow the carbon atom to bond to three different atoms. The orientation of these atoms around the carbon atom will be trigonal planar molecular geometry. The angle of these atoms to one another is 120 degrees. This is demonstrated in the diagram of ethene shown in Figure 3.11.
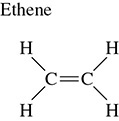
Figure 3.11 Molecular Geometry of Ethene
When an atom is sp hybridized, one s orbital combines with one p orbital. This allows an atom like carbon to make two double bonds or one single and one triple bond. The two atoms that bond to the carbon atom in this case will orient themselves 180 degrees apart. This is called a linear molecular geometry (see Figure 3.12).
Figure 3.12 sp Hybridized Carbon Atoms
Here is a side-by-side comparison of the three states of hybridization:
Problems:
What is the hybridization of carbon in CCl4, in HCN, and in CH2O?
Solution: In CCl4 the carbon atom forms all single bonds. The carbon is sp3 hybridized and the chlorine atoms will be 109.5 degrees apart. The carbon in HCN has a single bond with the hydrogen atom and a triple bond with the nitrogen atom. This carbon atom is sp hybridized. The carbon atom in CH2O has a double bond with the oxygen atom and single bonds with the hydrogen atoms. This carbon atom is sp2 hybridized.
Ions and the Octet Rule
The number of electrons in an atom can be found by looking at the atomic number, provided the atom is neutral. In a neutral atom the number of protons is equal to the number of electrons. The balancing of the positive and negative charge is what makes the atom neutral. But what happens if an atom gains or loses electrons? When an atom loses or gains electrons it becomes an ion. The atom now has an unequal number of protons and electrons (the number of protons does not change). When an atom loses electrons, it loses negative charges. In this case, the protons outnumber the electrons and the ion is positively charged. An ion with a positive charge is called a cation. When an atom gains electrons it gains negative charges. In this case, the electrons outnumber the protons and the ion is negatively charged. An ion with a negative charge is called an anion.
THINK ABOUT THIS 
Just how many electrons will an atom gain or lose? How much of a charge will an ion take on? There is a simple pattern to follow but in the end you will see that it all depends upon the number of valence electrons that an atom has. There is one thing that all ions have in common: They form so that they have eight valence electrons in the outermost principal energy level. This is called the octet rule. Having eight electrons in the valence shell gives the atom a stable electron configuration. Once eight valence electrons have been achieved, it is very difficult to modify this stable configuration.
To determine the charge an atom will take on as an ion, first look at the electron configuration of the atom. Sodium, for example, has 11 electrons and the electron configuration of 1s22s22p63s1. In order to achieve an octet, sodium has two options—gain seven electrons or lose just one. Losing one electron is a much easier task than gaining seven electrons. When the sodium atom loses one electron (loses a negative charge), the sodium ion has a charge of 1+ and the atom is written as Na1+. After the one electron has been lost, the new electron configuration of sodium is 1s22s22p6. The eight valence electrons are shown in bold to emphasize the octet rule.
Another example would be the ion formed for sulfur. Sulfur has the electron configuration of 1s22s22p63s23p4. Sulfur has six valence electrons as shown in bold. For sulfur to achieve a stable octet it could either lose six electrons or gain two electrons. Gaining two electrons is a more feasible task, and the gain of two electrons will give sulfur ion a 2− charge. The new electron configuration for sulfur is 1s22s22p63s23p6. Again, the eight valence electrons have been emphasized.
Problem:
What will be the charges of the following elements when they form an ion: Ca, Al, F, N, Ne?
Solution: Start with the electron configurations for each atom:
Now look at the configurations and decide which is the easiest way to obtain a stable octet. Calcium will lose two electrons and become Ca2+. Aluminum will lose three electrons and become Al3+. Fluorine will gain one electron and become F1−. Nitrogen will gain three electrons and become N3−. Neon will not lose or gain any electrons because of its stable octet.
Exceptions to the Octet Rule
There are exceptions to the octet rule. Helium, for example, is incredibly stable with just two valence electrons in its outermost principal energy level. The same holds true for lithium and beryllium ions as well. This indicates that it isn’t so much having an octet that stabilizes the atom, as it is the issue of having a full outermost principal energy level.
One last exception to the octet rule lies in the bonding of the atom boron. Boron prefers six electrons in its outermost principal energy level. This allows compounds containing boron to make three bonds in a trigonal planar arrangement. Two examples are BH3 and BF3 as shown in Figure 3.13.
Figure 3.13 The Trigonal Planar Geometry of Boron
Isoelectronic Series
Atoms will gain, lose, or share valence electrons as to achieve an octet (in most cases) or electron configuration that is similar to that of a noble gas. For example, all of the following atoms and ions have 18 electrons and an electron configuration similar to that of a noble gas, argon: S2-, Cl1-, Ar, K1+, and Ca2+. All of these atoms/ions have an electron configuration of 1s22s22p63s23p6.
Knowing the information just presented, we can now predict the relative size of the atoms and ions presented. Because they all have 18 electrons we can look at the number of protons present as well. The ion with the greatest number of protons, Ca, will have the smallest radius because it has the greatest nuclear “pull” on the 18 electrons. Sulfur, with just 16 protons, will have the least nuclear attraction for the 18 electrons that it has. This helps explain why nonmetal atoms are smaller than their respective ions. Just the same, it also explains why metal atoms are larger than their respective ions.
REVIEW QUESTIONS
1. Which of the following isotopes has the greatest number of neutrons?
(A) 35Cl
(B) 31P
(C) 40Ar
(D) 41Ca
(E) 14C
2. An atom has eight electrons in a 3d subshell. How many orbitals in this subshell have an unpaired electron?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
3. Which principal energy level has exactly four subshells?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
4. An atom in the ground state has seven valence electrons. Which electron configuration could represent the valence electron configuration of this atom in the ground state?
(A) 3s13p6
(B) 3s63p1
(C) 3s13p43d2
(D) 3s23p43d1
(E) 3s23p5
Questions 5–6 refer to the following:
(A) 1s22s1
(B) 1s22s22p4
(C) 1s22s2
(D) 1s22s22p63s2
(E) 1s22s23s1
5. Has six valence electrons.
6. Is in the excited state.
7. Which pair of symbols below show different isotopes of the same element?
(A) 3918A and 3919R
(B) 6027X and 5928Y
(C) 126L and 146L
(D) 3717X and 3717X
(E) 32E and 31G
8. Which of the following is not a conclusion Rutherford made from his experiment with alpha particles being shot at a thin sheet of gold foil?
(A) An atom has a very small, compact nucleus.
(B) An atom is mainly empty space.
(C) An atom’s mass is concentrated in the nucleus.
(D) An atom has a very dense nucleus.
(E) An atom has a negatively charged nucleus.
9. Which atom is not paired with its correct ion and ionic charge?
(A) Rb / Rb1−
(B) Mg / Mg2+
(C) F / F1−
(D) Li / Li1+
(E) Br / Br1−
10. Which of the following statements is false regarding sub-atomic particles?
(A) The proton has a positive one charge.
(B) The neutron has no charge.
(C) The electrons are found in regions of the atom called orbitals.
(D) The electrons have a greater mass than the protons.
(E) Protons and neutrons are the nucleons of the atom.
11. Which is inconsistent with the concept of an isotope?
(A) Same atomic number
(B) Different number of neutrons
(C) Same mass number
(D) Same name of the element
(E) Same number of protons
12. A mysterious element has the following relative abundances:
X-34 15% X-35 20% X-36 65%
Which of the following is true?
(A) The atomic mass of this element is closer to 34.1.
(B) The atomic mass of this element is closer to 34.9.
(C) The atomic mass of this element cannot be determined without knowing exactly what X is.
(D) A mass spectrometer would not be helpful in determining the percentages of the isotopes.
(E) The atomic mass of this element is approximately 35.5.
13. Which of the following ions will be the smallest in the isoelectronic series?
(A) O2–
(B) F1–
(C) Ne
(D) Na1+
(E) Mg2+
14. What is the correct set of quantum numbers for the eighth electron that fills the orbitals in an atom of oxygen?
(A) n = 2, l = 1, ml = –1, ms = –1/2
(B) n = 2, l = 1, ml = +1, ms = –1/2
(C) n = 2, l = 1, ml = +1, ms = +1/2
(D) n = 2, l = 0, ml = –1, ms = +1/2
(E) n = 1, l = 1, ml = +1, ms = –1/2
ANSWERS AND EXPLANATIONS
1. (C) Filling in the number of protons for each element we get: 3717Cl, 3115P, 4018Ar, 4120Ca, 146C. The difference in the mass number and the atomic number will give the number of neutrons. The greatest difference in this case is the Ar with 22.
2. (B) There are five orbitals in the d subshells. The first five valence electrons will be singly placed in the orbitals. But when the remaining three are added, three of the five orbitals will be paired with electrons and two will not.
3. (D) The fourth principal energy level has four subshells. They are designated s, p, d, and f.
4. (E) All of the choices show seven electrons. However, only choice E shows them filling in a proper order that demonstrates the ground state.
5. (B) Choice B is the electron configuration for oxygen, an element that has six valence electrons in the 2s and 2p orbitals.
6. (E) The excited state in this question is demonstrated by choice E as the entire 2p orbital was skipped over.
7. (C) Isotopes will have the same atomic number and a different mass number. The mass number of element “L” differs but the atomic number is the same.
8. (E) The nucleus has a positive charge because of the protons that are present. The other choices are factual with regards to the nucleus of an atom.
9. (A) As a Group 1 metal with just one valence electron, rubidium will lose one electron to form a 1+ charge.
10. (D) Electrons have a mass that is about 1/1836 of that of a proton.
11. (C) Isotopes will have all this is described by choices A, B, D, and E. However, because choice B holds true, the mass number of the isotopes must differ.
12. (E) Because X-36 is the most abundant isotope of this element, the atomic mass will be closest to 36.
13. (E) In an isoelectronic series all of the ions have the same number of electrons. As the number of protons for that element increases the ion will decrease in size. All of the ions in this problem have 10 electrons. Because magnesium has 12 protons, it will have a smaller ion.
14. (A) Because the eighth electron must have the configuration of 1s22s22p4, n = 2 and l = 1. Because we are adding the eighth electron to the 2p orbital and pairing up a previously single electron, ml = –1. Because the first electron in that orbital has a positive spin, the second one must have a negative spin, ms = –1/2.
15. (T, T, CE) There is a Zeff of +11 on the electrons in the first principal energy level of a sodium atom. There are no other electrons to shield those two electrons from the charges of the 11 protons present.