CHAPTER 8
Reaction Rates and Chemical Equilibrium
Reaction Rates
In sports there are certain times when contact is required between two players. Consider a situation in a game of football where a big linebacker wants to tackle a quarterback. Does the linebacker walk up to the quarterback and tap him lightly in hopes that the quarterback will fall down? Think about a hockey player who couldn’t check the opposing players into the boards and keep them out of the play. That’s not exactly a great way to defend one’s own goal!
If substances are going to react with each other, there must be frequent contact between the substances. However, as in the two situations just mentioned, contact isn’t always enough. Reactants need to collide effectively and frequently if a reaction is going to occur. That is, not only do they need to make contact, but they must also make contact with enough energy or at a certain angle or a certain orientation. As this occurs, the rate of the reaction will increase, meaning that there will be a greater change in the concentration of the reactants and products over time.
There are a number of ways conditions can be modified to make molecules collide more effectively. These cases can be examined in the outline below:

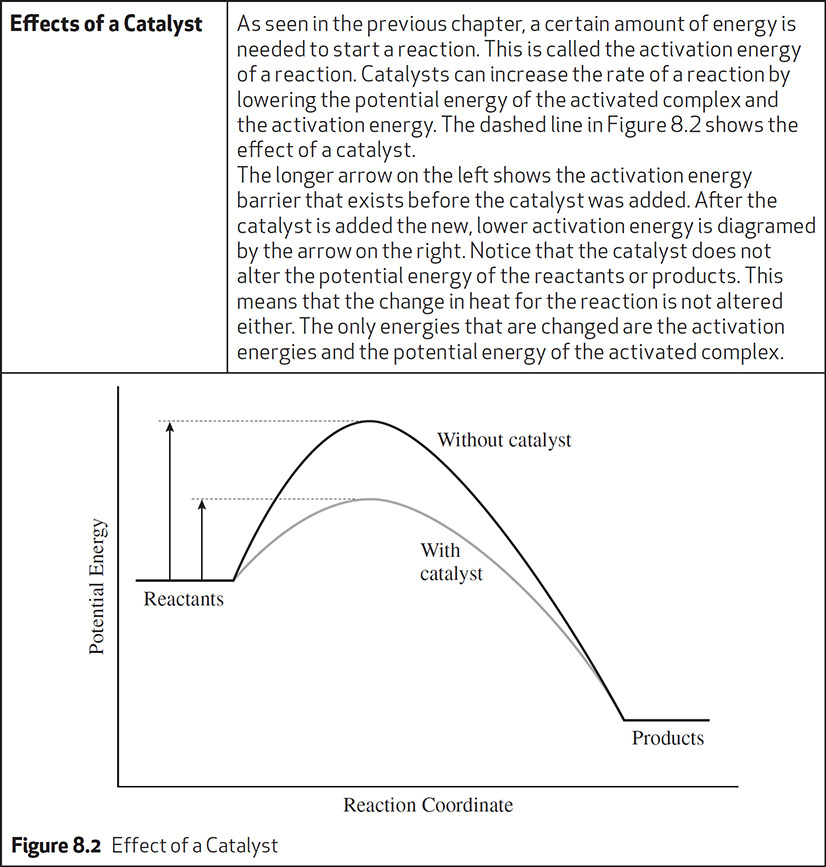
THINK ABOUT THIS 
Reverse Reactions and Potential Energy Diagrams
The reactions considered up to this point have had only a single arrow in their chemical equation. An example is the following reaction: 2Na(s) + Cl2(g) → 2NaCl(s). What does it mean when there is a double arrow in a chemical equation? Here is an equation with a double arrow: A + B ←→ C + D. Reactions with a double arrow mean that the reaction is a reversible reaction. As substances A and B react to form the products C and D (the forward reaction), the products C and D can form the original reactants (the reverse reaction). It sounds counterproductive, but it happens. Later you will see how conditions can be manipulated to make a reaction favor the products, but for now the focus is only on what a reversible reaction means for the enthalpy changes during the reaction.
The enthalpy of a reaction can be found using the equation ΔH = PEP − PER, but this equation has been used only for a forward reaction. What happens to the enthalpy of reaction in a reverse reaction? Consider the following reaction: A + B ←→ C + D + energy. The potential energy diagram in Figure 8.3 shows the energy changes involved in the reaction.
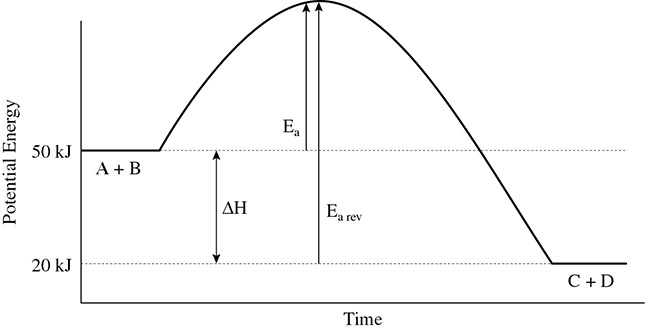
Figure 8.3 Potential Energy Diagram for a Reverse Reaction
In the reverse reaction you can now consider C + D to be the reactants and A + B the products. Using the equation ΔH = PEP − PER, the value for the reverse reaction is 50 kJ − 10 kJ = +40 kJ. How does this compare to the forward reaction? Again use ΔH = PEP − PER, but in the forward reaction C + D are the products, so you get 10 kJ − 50 kJ = −40 kJ. Comparing the two values for ΔH shows that the heat of reaction for the forward reaction and the heat of reaction for the reverse reaction have the same magnitude but a different sign. Finally, notice the differences in the activation energies of the forward and reverse reactions. These values will be different in magnitude.
Problem:
Given the reaction A + B ←→ C + D + 30 kJ, what is ΔH for the reverse reaction?
Solution: This reaction is exothermic in the forward direction and it releases 30 kJ of energy. This means that ΔH in the forward reaction is −30 kJ. For the reverse reaction we change the sign of ΔH, making the reaction endothermic and the value of ΔH = +30 kJ.
Equilibrium
When two reactions oppose each other, they will eventually reach a point where the amount of product formed is equal to the amount of reactant formed. This situation of an equal “give and take” is called a state of equilibrium. Equilibrium is defined as a state of balance between two opposing reactions that are occurring at the same rate. Notice that the definition says nothing about the amounts or concentrations of any reactants or products. The only factors that are equal at equilibrium are the rates of the forward and reverse reactions.
Phase equilibrium is one type of equilibrium. Consider the following closed system at equilibrium (see Figure 8.4):

Figure 8.4 Phase Equilibrium
At first, the container is sealed with only liquid water and as time goes on, more water vapor begins to form. Eventually the space above the water becomes saturated with water vapor. The system now has the conditions for phase equilibrium to occur; the system is closed and saturation has been achieved. Once the space above the water becomes saturated with water vapor, for every water molecule that evaporates into the gas phase, one gas molecule will condense into liquid water. Because of this, the level of water in the container will remain constant.
When a reversible chemical reaction is put into action, we initially start with all reactants and no products. However, as the reaction proceeds, we eventually reach an equilibrium where the reactants and products remain at a constant concentration. Because the rates of the forward and reverse reactions were equal right from the start, we can say that, at equilibrium “rates are equal and concentrations remain constant.”
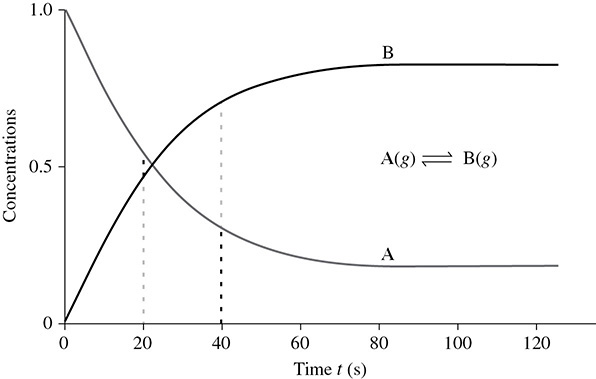
There are a number of methods for identifying a chemical reaction that has reached equilibrium. One is to perform an experiment to measure the rates of reaction. Another method is to check if the concentrations are remaining constant. It is much easier, however, just to make sure that no further changes are occurring in temperature, pressure, volume, and/or color. What if a reaction does have a color change occurring? In this case equilibrium has not been established because there is a change in conditions that is causing a stress upon the point of equilibrium. A stress, or changes in conditions, can force the point of equilibrium to change. However, stresses can also be used to manipulate a reaction and force it in a particular direction.
Le Châtelier’s Principle
Le Châtelier’s Principle regarding changes in the point of equilibrium was stated by Le Châtelier in the late 1800s. Le Châtelier’s Principle states that if a stress or change in conditions is applied to a system at equilibrium, the point of equilibrium will shift in such a manner as to relieve the applied stress. There are several conditions that can change the point of equilibrium. These are detailed in the table below.

Problem:
Given the following reaction: 3H2(g) + N2(g) ←→ 2NH3(g) + 22 kcal heat energy. What is the heat of reaction for the reverse reaction? What would you do to the temperature, pressure, and concentrations of the reactants and products to shift the equilibrium so that more ammonia is made?
Solution: The ΔH for the reverse reaction will have a positive sign because the reverse reaction is endothermic. The ΔH is equal to + 22 kcal. To shift the equilibrium to make more ammonia, start by adding more hydrogen gas and nitrogen gas because having more reactants present will make more products. Because the heat energy is a product, you do not want to add heat. You would have to lower the temperature to remove the heat so that the reaction will shift to the right in an effort to replace the heat. Because there is a total of four volumes of gas on the left and two volumes of gas on the right, an increase in pressure will favor the production of ammonia because it is the side with fewer volumes of gas.
Equilibrium Constants and Mass Action Equations
Looking again at the equation: A + B ←→ C + D, if C and D react to form the original reactants, and the original reactants form more products, who wins the battle? How can you tell if the reaction favors the formation of reactants or the formation of products? A mathematical expression can be set up to calculate just how much the reaction favors the formation of products. This mathematical expression is used to calculate the equilibrium constant for a particular reaction. For the reaction aA + bB ←→ cC + dD the mathematical expression can be written as

This expression is called a mass action equation. The brackets in the equation represent the concentration of the products and reactants. Notice that the products are placed in the numerator while the reactants are placed in the denominator. Also notice that the coefficients are now the powers of the concentration of each substance. The mnemonic device used to remember these rules is “Products Over Reactants, Coefficients Become Powers.” One other rule that you need to know is that you do not include substances that are in the liquid or solid phases. These concentrations are written as the number “1” in the equation.
Values for Keq that are greater than 1.0 indicate a reaction that favors the products, as the value of the numerator (products) outweighs that of the denominator (reactants). Values less than 1.0 indicate that the denominator is greater in value than the numerator and the reactants are favored.
Problem:
Write the mass action equation for W(aq) + X(s) ←→ 3Y(aq) + 2Z(l). At equilibrium the concentration of W is 0.1 M and the concentration of Y is 0.1 M. What is the value of the equilibrium constant? Does this reaction favor the formation of reactants or products?
Solution: Remember the rule, “Products Over Reactants, Coefficients Become Powers.” Leave out the solids and liquids from the reaction and get:

Substitution and solving gives:

Problem:
At equilibrium, a 1.00 liter flask is found to contain 0.01 moles H2(g) and 0.02 moles of I2(g) that have reacted according to the equation: H2(g) + I2(g) ←→ 2HI(g). The Keq for this reaction at a particular temperature is 50.5. What is the concentration of HI inside the flask?
Solution: Because the gases are in a 1.00-liter flask, the concentrations of the reactants are [H2] = 0.01 M and [I2] = 0.02 M. Write the mass action equation as:
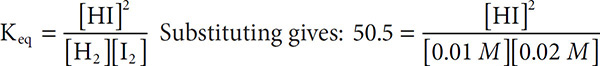
Solving gives 50.5[0.01][0.02] = x2 and x = 0.10 M.
Problem:
Given the following reaction: A + B ←→ C. Calculate the equilibrium constant in a reaction where the initial concentration of A is 1.5 M, the initial concentration of B is 1.3 M, and, after A and B react and come to equilibrium, the concentration of C is 1.2 M.
Solution: Unlike in the previous problem you are not given the concentrations of reactants at equilibrium. Instead you are given the initial concentrations of reactants.
Set up a chart to organize the changes in concentration as the reaction proceeds. First put in the initial concentrations of A and B. Put in C also because you know its final concentration.

Next, add the changes in concentration. These changes are in the same 1:1 ratio as the coefficients in the balanced equation.

Calculate the final concentrations.

Place the final concentrations into the mass action equation and calculate the equilibrium constant:
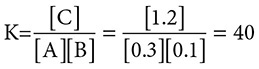
showing that this reaction greatly favors the formation of the product, C.
Solubility Product Constants
Recall from previous chapters that solubility is the amount of a solid that it takes to saturate the solution that it is in. Also remember that not every salt is completely soluble in water. The solubility product constant helps determine how soluble a salt is in solution at a particular temperature. The values for these constants can be found in Appendix 4, Reference Tables, in the back of this book.
One salt to examine is PbSO4. Lead sulfate dissolves according to the following equation: PbSO4(s) ←→ Pb2+(aq) + SO42−(aq). The solubility product constant for lead sulfate can be written as Ksp = [Pb2+][SO42−] / 1. Notice that the solid was not included in the equilibrium constant expression. What concentration of lead and sulfate ions will you find in a saturated solution of lead sulfate at 298 K? The solubility product constant for lead sulfate is 1.6 × 10−8. This means that the concentration of lead ions and sulfate ions is each 1.26 × 10−4 M.
Problem:
Magnesium hydroxide has a solubility product constant of 1.8 × 10−11 at 298 K. Write the equilibrium constant expression for this salt. What is the concentration of magnesium and hydroxide ions in a saturated solution of magnesium hydroxide? Which salt is more soluble in water, Mg(OH)2 or PbSO4?
Solution: The equation looks like Mg(OH)2(s) ←→ Mg2+(aq) + 2OH1−(aq). The solubility product constant expression is written as: Ksp = [Mg2+][OH1−]2 / 1. Because for each magnesium ion formed, two hydroxide ions form, substitution gives: 1.8 × 10−11 = [x][x]2 = x3.
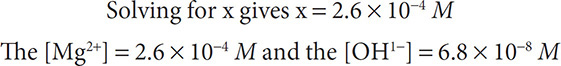
PbSO4 is more soluble because it has a greater solubility product constant than that of magnesium hydroxide.
Common Ion Effect
Consider the chemical equation for AgCl dissolved in water to make a saturated solution: AgCl(s) ←→ Ag1+(aq) + Cl1−(aq). At 298 K the solubility product constant is 1.8 × 10−10, which indicates that is a slightly soluble salt. There is a way of making AgCl even less soluble, via the common ion effect. Consider the following, when an ion that is already present is added to the solution, the equilibrium will shift to consume the increase in concentration of the ion.
If NaCl(aq) were added to a solution of silver chloride, the NaCl would introduce more Cl1− ions and shift the equilibrium to the left. This would favor the production of more AgCl(s). Adding the common ion, Cl1−, actually decreases the solubility of AgCl by forming more of its solid.
Reactions That Go to Completion
Why isn’t every reaction reversible? Why don’t reactions such as Mg + 2HCl → MgCl2 + H2 have a reversible reaction? Inserting the phases into the chemical equation will help to answer this question: Mg(s) + 2HCl(aq) → MgCl2(aq) + H2(g). This reaction produces a gas—a gas that, according to the laws of entropy, loves to escape from the reaction so that it can spread out. Because the reaction is constantly losing one of its products to the atmosphere, the reactants work feverishly to replace the missing hydrogen gas. This attempt to replace the missing hydrogen gas drives the reaction completely to the right.
In addition to reactions that form a gas, reactions that form a precipitate also go to completion. Consider the following reaction: Pb(NO3)2(aq) + 2KI(aq) → PbI2(s) + 2KNO3(aq). This reaction forms a solid precipitate that removes itself from the reaction and settles to the bottom of the reaction vessel. Again, because the reaction is constantly losing one of its products, the reactants work feverishly to replace the missing lead iodide. This attempt to replace the missing lead iodide drives the reaction completely to the right. Finally, reactions that form water tend to go to completion.
REVIEW QUESTIONS
1. Given the reaction: Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)
Why is the reaction slower when a single piece of zinc is used than when powdered zinc of the same mass is used?
(A) The powdered zinc is more concentrated.
(B) The single piece of zinc is more reactive.
(C) The powdered zinc requires less activation energy
(D) The powdered zinc generates more heat energy.
(E) The powdered zinc has a greater surface area.
2. Which takes place when a catalyst is added to a reaction at equilibrium?
(A) The point of equilibrium is shifted to the right.
(B) The point of equilibrium is shifted to the left.
(C) The forward and reverse reactions rates are increased unequally.
(D) The forward and reverse reactions rates are increased equally.
(E) The value of ΔH has the same magnitude but a different sign.
3. As the frequency and the number of effective collisions between reacting particles increases, the rate of the reaction
(A) increases
(B) decreases
(C) remains the same
(D) approaches zero
(E) none of the above
4. Which factors are equal in a reversible chemical reaction that has reached equilibrium?
(A) The number of moles of the reactants and products
(B) The potential energies of the reactants and products
(C) The activation energies of the forward and reverse reactions
(D) The rates of reaction for the forward and reverse reactions
(E) The concentrations of the reactants and products
5. A catalyst is added to a system at equilibrium. The concentration of the reactants will then
(A) decrease
(B) increase
(C) remain constant
(D) approach zero
(E) none of the above
6. Given the following reaction that has reached equilibrium: NaCl(s)←→NaCl(aq). For the phase equilibrium to exist, the NaCl(aq) must be a solution that is
(A) concentrated
(B) saturated
(C) dilute
(D) heated
(E) unsaturated
7. In an effort to speed up a reaction between a solid and a gas one would not:
(A) make an effort to concentrate the reactants as best as possible
(B) add a catalyst
(C) cool the reaction down
(D) increase the pressure on the system
(E) use a powdered solid instead of one big lump of the same solid
8. Which reaction below is expected to go to completion?
I. Zn + HCl
II. HCl + NaOH
III. Ag1+(aq) + Cl1–(aq)
(A) II only.
(B) III only.
(C) I and II only.
(D) II and III only.
(E) I, II, and III.
9. Which salt listed in Appendix 4 of this book has the greatest solubility in water under equal conditions?
(A) lead iodide
(B) lead sulfate
(C) magnesium hydroxide
(D) silver chloride
(E) The salts are all equally soluble.


I. The final concentration of B is 0.1 M.
II. The change in concentration of C is 0.3 M.
III. The final concentration of A is 0.3 M.
Which of the above statements are correct?
(A) I only
(B) II only
(C) II and III only
(D) I and II only
(E) I, II, and III
ANSWERS AND EXPLANATIONS
1. (E) A substance that has more surface area will react faster than being one larger, solid piece.
2. (D) When a catalyst is added to a reaction, the reaction will speed up by creating an alternative pathway for the products to form. This alternative pathway has a lower activation energy involved and a lower potential energy of its activated complex.
3. (A) As molecules, ions, etc., collide more frequently the rate of a reaction will increase.
4. (D) At equilibrium the rates will be equal and all concentrations will be constant.
5. (C) When a system is at equilibrium, the concentrations of product and reactant will be constant.
6. (B) For a phase equilibrium to exist, the solution has to be saturated so that when one particle of solute dissolves, one particle of solute will precipitate.
7. (C) A lower temperature will mean a slower rate of reaction.
8. (E) All of the reactions go to completion. Reaction I forms a gas that leaves the system and cannot be recovered. Reaction II forms water, which doesn’t readily ionize. Reaction III forms a precipitate that does not dissolve, blocking the reverse reaction from occurring.
9. (B) Lead sulfate has the greatest Ksp of the salts listed. Remember that 10−8 is bigger than the other number values present.
10. (T, F) Lead iodide is more soluble than silver chloride because the Ksp value for lead iodide is greater.
11. (D) The chart shows that the concentration of C increased by 0.3 M. Because the reaction shows that all of the reactants and products are in a 1:1:1 ratio, any loss or gain in concentration for one substance has to be equal to that of the other substances. Both A and B will go down by 0.3 M and C will go up by 0.3 M.