Chapter Six. A Computing Machine

6.1 Representing Information

6.2 TOY Machine

6.3 Machine-Language Programming

6.4 TOY Virtual Machine

Our goal in this chapter is to show you how simple the computer that you’re using really is. We will describe in detail a simple imaginary machine that has many of the characteristics of real processors at the heart of the computational devices that surround us.

You may be surprised to learn that many, many machines share these same properties—even some of the very first computers that were developed. Accordingly, we are able to tell the story in historical context. Imagine a world without computers, and which sort of device might be received with enthusiasm, and that is not far from what we have! We tell our story from the standpoint of scientific computing—but there is an equally fascinating story from the standpoint of commercial computing that we touch on just briefly.

Next, our aim is to convince you that the basic concepts and constructs that we covered in Java programming are not so difficult to implement on a simple machine, using its own machine language. We will consider in detail conditionals, loops, functions, arrays, and linked structures. Since these are the same basic tools that we examined for Java, it follows that several of the computational tasks that we addressed in the first part of this book are not difficult to address at a lower level.

This simple machine is a link on the continuum between your computer and the actual hardware circuits that change state to reflect the action of your programs. As such it is preparation for learning how those circuits work, in the next chapter.

And that still is only part of the story. We end the chapter with a profound idea: we can use one machine to simulate the operation of another one. Thus, we can easily study imaginary machines, develop new machines to be built in future, and work with machines that may never be built.

6.1 Representing Information

The first step in understanding how a computer works is to understand how information is represented within the computer. As we know from programming in Java, everything suited for processing with digital computers is represented as a sequence of 0s and 1s, whether it be numeric data, text, executable files, images, audio, or video. For each type of data, standard methods of encoding have come into widespread use: the ASCII standard associates a 7-bit binary number with each of 128 distinct characters; the MP3 file format rigidly specifies how to encode each raw audio file as a sequence of 0s and 1s; the .png image format specifies the pixels in digital images ultimately as a sequence of 0s and 1s; and so forth.

---

6.1.1 Number conversion

6.1.2 Floating-point components

Programs in this section

---

Within a computer, information is most often organized in words, which are nothing more than a sequence of bits of a fixed length (known as the word size). The word size plays a critical role in the architecture of any computer, as you will see. In early computers, 12 or 16 bits was the typical word size; for many years, 32-bit words were widely used; and nowadays 64-bit words are the norm.

The information content within every computer is nothing more nor less than a sequence of words, each consisting of a fixed number of bits, each either 0 or 1. Since we can interpret every word as a number represented in binary, all information is numbers, and all numbers are information.

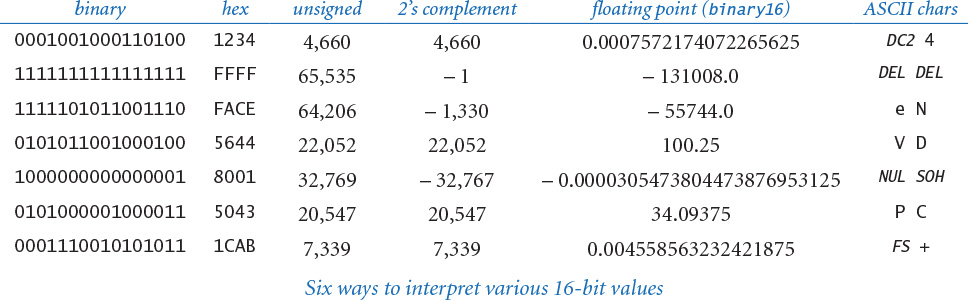
The meaning of a given sequence of bits within a computer depends on the context. This is another of our mantras, which we will repeat throughout this chapter. For example, as you will see, depending on the context, we might interpret the binary string 1111101011001110 to mean the positive integer 64,206, the negative integer –1,330, the real number –55744.0, or the two-character string "eN".

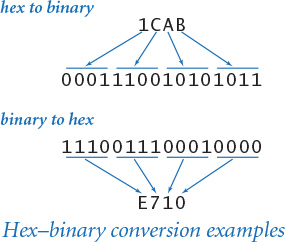
Convenient as it may be for computers, the binary number system is extremely inconvenient for humans. If you are not convinced of this fact, try memorizing the 16-bit binary number 1111101011001110 to the point that you can close the book and write it down. To accommodate the computer’s need to communicate in binary while at the same time accommodating our need to use a more compact representation, we introduce in this section the hexadecimal (base 16) number system, which turns out to be a convenient shorthand for binary. Accordingly, we begin by examining hexadecimal in detail.

Binary and Hexadecimal

For the moment, consider non-negative integers, or natural numbers, the fundamental mathematical abstraction for counting things. Since Babylonian times, people have represented integers using positional notation with a fixed base. The most familiar of these systems is certainly decimal, where the base is 10 and each positive integer is represented as a string of digits between 0 and 9. Specifically, d_nd_n–1...d₂d₁d₀ represents the integer

d_n10ⁿ + d_n–110^n–1 + ... + d₂10² + d₁10¹ +d₀10⁰

For example, 10345 represents the integer

10,345 = 1·10,000 + 0·1,000 + 3·100 + 4·10 +5·1

We can replace the base 10 by any integer greater than 1 to get a different number system where we represent any integer by a string of digits, all between 0 and 1 less than the base. For our purposes, we are particularly interested in two such systems: binary (base 2) and hexadecimal (base 16).

Binary

When the base is 2, we represent an integer as a sequence of 0s and 1s. In this case, we refer to each binary (base 2) digit—either 0 or 1—as a bit, the basis for representing information in computers. In this case the bits are coefficients of powers of 2. Specifically, the sequence of bits b_nb_n–1...b₂b₁b₀ represents the integer

b_n 2ⁿ + b_n–12^n–1 + ... + b₂ 2² + b₁ 2¹ + b₀ 2⁰

For example, 1100011 represents the integer

99 = 1·64 + 1·32 + 0·16 + 0·8 + 0·4 + 1·2 +1·1

Note that the largest integer that we can represent in an n-bit word in this way is 2ⁿ – 1, when all n bits are 1. For example, with 8 bits, 11111111 represents

2⁸ – 1 = 255 = 1·128 + 1·64 + 1·32 + 1·16 + 1·8 + 1·4 + 1·2 +1·1

Another way of stating this limitation is to say that we can represent only 2ⁿ non-negative integers (0 through 2ⁿ – 1) in an n-bit word. We often have to be aware of such limitations when processing integers with a computer. Again, a big disadvantage of using binary notation is that the number of bits required to represent a number in binary is much larger than, for example, the number of digits required to represent the same number in decimal. Using binary exclusively to communicate with a computer would be unwieldy and impractical.

Hexadecimal

In hexadecimal (or just hex from now on), the sequence of hex digits h_nh_n–1...h₂h₁h₀ represents the integer

h_n16ⁿ + h_n–116^n–1 + ... + h₂16² + h₁16¹ + h₀16⁰

The first complication we face is that, since the base is 16, we need digits for each of the values 0 through 15. We need to have one character to represent each digit, so we use A for 10, B for 11, C for 12, and so forth, as shown in the table at right. For example, FACE represents the integer

64,206 = 15·16³ + 10·16² + 12·16¹ + 14·16⁰

This is the same integer that we represented with 16 bits earlier. As you can see from this example, the number of hex digits needed to represent integers in hexadecimal is only a fraction (about one-fourth) of the number of bits needed to represent the same integer in binary. Also, the variety in the digits makes a number easy to remember. You may have struggled with 1111101011001110, but you certainly can remember FACE.

Conversion between hex and binary

Given the hex representation of a number, finding the binary representation is easy, and vice versa, as illustrated in the figure at left. Since the hex base 16 is a power of the binary base 2, we can convert groups of 4 bits to hex digits, and vice versa. To convert from hex to binary, replace each hex digit by the four binary bits corresponding to its value (see the table at right). Conversely, given the binary representation of a number, add leading 0s to make the number of bits a multiple of 4, then group the bits 4 at a time and convert each group to a single hex digit. You can do the math to prove that these conversions are always correct (see EXERCISE 6.1.8), but just a few examples should serve to convince you. For example, the hex representation of the integer 39 is 27, so the binary representation is 00100111 (and we can drop the leading zeros); the binary representation of 228 is 11100100, so the hex representation is E4. This ability to convert quickly from binary to hex and from hex to binary is important as an efficient way to communicate with the computer. You will be surprised at how quickly you will learn this skill, once you internalize the basic knowledge that A is equivalent to 1010, 5 is equivalent to 0101, F is equivalent to 1111, and so forth.

A hex number 1CAB is converted to binary as 0001 1100 1010 1011 and a binary number 1110 0111 0001 0000 is converted to hex as E710.

decimal	binary	hex
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
Representations of integers from 0 to 15

Conversion from decimal to binary

We have considered the problem of computing the string of 0s and 1s that represent the binary number corresponding to a given integer as an early programming example. The following recursive program (the solution to EXERCISE 2.3.15) does the job, and is worthy of careful study:

Click here to view code image

public static String toBinaryString(int n)
{
    if (n == 0) return "";
    if (n % 2 == 0)
       return toBinaryString(n/2) + '0';
    else
       return toBinaryString(n/2) + '1';
}

It is a recursive method based on the idea that the last digit is the character that represents n % 2 ('0' if n % 2 is 0 and '1' if n % 2 is 1) and the rest of the string is the string representation of n/2. A sample trace of this program is shown at right. This method generalizes to handle hexadecimal (and any other base). In addition, we are interested in converting string representations to Java data-type values. In the next section, we consider a program that accomplishes such conversions.

Click here to view code image

toBinaryString(109)
   toBinaryString(54)
      toBinaryString(27)
         toBinaryString(13)
            toBinaryString(6)
               toBinaryString(3)
                  toBinaryString(1)
                     toBinaryString(0)
                        return ""
                     return "1"
                  return "11"
               return "110"
            return "1101"
         return "11011"
      return "110110"
   return "1101101"

Call trace for toBinaryString(109)

When we talk about what is happening within the computer, our language is hex. The contents of an n-bit computer word can be specified with n/4 hex digits and immediately translated to binary if desired. You likely have observed such usage already in your daily life. For example, when you register a new device on your network, you need to know its media access control (MAC) address. A MAC address such as 1a:ed:b1:b9:96:5e is just hex shorthand (using some superfluous colons and lowercase a-f instead of the uppercase A-F that we use) for a 48-bit binary number that identifies your device for the network.

dec	binary	hex	dec	binary	hex	dec	binary	hex	dec	binary	hex
0	00000000	00	32	00100000	20	64	01000000	40	96	01100000	60
1	00000001	01	33	00100001	21	65	01000001	41	97	01100001	61
2	00000010	02	34	00100010	22	66	01000010	42	98	01100010	62
3	00000011	03	35	00100011	23	67	01000011	43	99	01100011	63
4	00000100	04	36	00100100	24	68	01000100	44	100	01100100	64
5	00000101	05	37	00100101	25	69	01000101	45	101	01100101	65
6	00000110	06	38	00100110	26	70	01000110	46	102	01100110	66
7	00000111	07	39	00100111	27	71	01000111	47	103	01100111	67
8	00001000	08	40	00101000	28	72	01001000	48	104	01101000	68
9	00001001	09	41	00101001	29	73	01001001	49	105	01101001	69
10	00001010	0A	42	00101010	2A	74	01001010	4A	106	01101010	6A
11	00001011	0B	43	00101011	2B	75	01001011	4B	107	01101011	6B
12	00001100	0C	44	00101100	2C	76	01001100	4C	108	01101100	6C
13	00001101	0D	45	00101101	2D	77	01001101	4D	109	01101101	6D
14	00001110	0E	46	00101110	2E	78	01001110	4E	110	01101110	6E
15	00001111	0F	47	00101111	2F	79	01001111	4F	111	01101111	6F
16	00010000	10	48	00110000	30	80	01010000	50	112	01110000	70
17	00010001	11	49	00110001	31	81	01010001	51	113	01110001	71
18	00010010	12	50	00110010	32	82	01010010	52	114	01110010	72
19	00010011	13	51	00110011	33	83	01010011	53	115	01110011	73
20	00010100	14	52	00110100	34	84	01010100	54	116	01110100	74
21	00010101	15	53	00110101	35	85	01010101	55	117	01110101	75
22	00010110	16	54	00110110	36	86	01010110	56	118	01110110	76
23	00010111	17	55	00110111	37	87	01010111	57	119	01110111	77
24	00011000	18	56	00111000	38	88	01011000	58	120	01111000	78
25	00011001	19	57	00111001	39	89	01011001	59	121	01111001	79
26	00011010	1A	58	00111010	3A	90	01011010	5A	122	01111010	7A
27	00011011	1B	59	00111011	3B	91	01011011	5B	123	01111011	7B
28	00011100	1C	60	00111100	3C	92	01011100	5C	124	01111100	7C
29	00011101	1D	61	00111101	3D	93	01011101	5D	125	01111101	7D
30	00011110	1E	62	00111110	3E	94	01011110	5E	126	01111110	7E
31	00011111	1F	63	00111111	3F	95	01011111	5F	127	01111111	7F
Decimal, 8-bit binary, and 2-digit hex representations of integers from 0 to 127

dec	binary	hex	dec	binary	hex	dec	binary	hex	dec	binary	hex
128	10000000	80	160	10100000	A0	192	11000000	C0	224	11100000	E0
129	10000001	81	161	10100001	A1	193	11000001	C1	225	11100001	E1
130	10000010	82	162	10100010	A2	194	11000010	C2	226	11100010	E2
131	10000011	83	163	10100011	A3	195	11000011	C3	227	11100011	E3
132	10000100	84	164	10100100	A4	196	11000100	C4	228	11100100	E4
133	10000101	85	165	10100101	A5	197	11000101	C5	229	11100101	E5
134	10000110	86	166	10100110	A6	198	11000110	C6	230	11100110	E6
135	10000111	87	167	10100111	A7	199	11000111	C7	231	11100111	E7
136	10001000	88	168	10101000	A8	200	11001000	C8	232	11101000	E8
137	10001001	89	169	10101001	A9	201	11001001	C9	233	11101001	E9
138	10001010	8A	170	10101010	AA	202	11001010	CA	234	11101010	EA
139	10001011	8B	171	10101011	AB	203	11001011	CB	235	11101011	EB
140	10001100	8C	172	10101100	AC	204	11001100	CC	236	11101100	EC
141	10001101	8D	173	10101101	AD	205	11001101	CD	237	11101101	ED
142	10001110	8E	174	10101110	AE	206	11001110	CE	238	11101110	EE
143	10001111	8F	175	10101111	AF	207	11001111	CF	239	11101111	EF
144	10010000	90	176	10110000	B0	208	11010000	D0	240	11110000	F0
145	10010001	91	177	10110001	B1	209	11010001	D1	241	11110001	F1
146	10010010	92	178	10110010	B2	210	11010010	D2	242	11110010	F2
147	10010011	93	179	10110011	B3	211	11010011	D3	243	11110011	F3
148	10010100	94	180	10110100	B4	212	11010100	D4	244	11110100	F4
149	10010101	95	181	10110101	B5	213	11010101	D5	245	11110101	F5
150	10010110	96	182	10110110	B6	214	11010110	D6	246	11110110	F6
151	10010111	97	183	10110111	B7	215	11010111	D7	247	11110111	F7
152	10011000	98	184	10111000	B8	216	11011000	D8	248	11111000	F8
153	10011001	99	185	10111001	B9	217	11011001	D9	249	11111001	F9
154	10011010	9A	186	10111010	BA	218	11011010	DA	250	11111010	FA
155	10011011	9B	187	10111011	BB	219	11011011	DB	251	11111011	FB
156	10011100	9C	188	10111100	BC	220	11011100	DC	252	11111100	FC
157	10011101	9D	189	10111101	BD	221	11011101	DD	253	11111101	FD
158	10011110	9E	190	10111110	BE	222	11011110	DE	254	11111110	FE
159	10011111	9F	191	10111111	BF	223	11011111	DF	255	11111111	FF
Decimal, 8-bit binary, and 2-digit hex representations of integers from 128 to 255

Later in this chapter, we will be particularly interested in integers less than 256, which can be specified with 8 bits and 2 hex digits. For reference, we have included on the previous two pages a complete table of their representations in decimal, binary, and hex. A few minutes studying this table is worth your while, to give you confidence in working with such integers and understanding the relationships among these representations. If you believe, after doing so, that the table is a waste of space, then we have achieved our goal!

Parsing and string representations

Converting among different representations of integers is an interesting computational task, which we first considered in PROGRAM 1.3.7 and then revisited in EXERCISE 2.3.15. We have also been making use of Java’s methods for such tasks throughout. Next, to cement ideas about positional number representations with various bases, we will consider a program for converting any number from one base to another.

Parsing

Converting a string of characters to an internal representation is called parsing. Since SECTION 1.1, we have been using Java methods like Integer.parseInt() and our own methods like StdIn.readInt() to convert numbers from the strings that we type to values of Java’s data types. We have been using decimal numbers (represented as strings of the characters between 0 and 9), now we look at a method to parse numbers written in any base. For simplicity, we limit ourselves to bases no more than 36 and extend our convention for hex to use the letters A though Z to represent digits from 10 to 35. Note: Java’s Integer class has a two-argument parseInt() method that has similar functionality, except that it also handles negative integers.

i	n	characters seen
0	1	1
1	3	11
2	6	110
3	13	1101
4	27	11011
5	54	110110
6	109	1101101
Trace of parseInt(1101101, 2)

One of the hallmark features of modern data types is that the internal representation is hidden from the user, so we can use only defined operations on data type values to accomplish the task. Specifically, it is best to limit direct reference to the bits that represent a data type value, and to use data-type operations instead.

The first primitive operation that we need to parse a number is a method that converts a character into an integer. EXERCISE 6.1.12 gives a method toInt() that takes a character in the range 0-9 or A-Z as an argument and returns an int value between 0 and 35 (0–9 for digits and 10–35 for letters). With this primitive, the rather simple method parseInt() in PROGRAM 6.1.1 parses the string representation of an integer in any base b from 2 to 36 and returns the Java int value for that integer. As usual, we can convince ourselves that it does so by reasoning about the effect of the code in the loop. Each time through the loop, the int value n is the integer corresponding to all the digits seen so far. To maintain this invariant, all we need to do is multiply by the base and add the value of the next digit. The trace shown here illustrates the process: each value of n is the base times the previous value of n plus the next digit (in blue). To parse 1101101, we compute 0·2 + 1 = 1, 1·2 + 1 = 3, 3·2 + 0 = 6, 6·2 + 1 = 13, 13·2 + 1 = 27, 27·2 + 0 = 54, and 54·2 + 1 = 109. To parse FACE as a hex number, we compute 0·16 + 15 = 15, 15·16 + 10 = 250, 250·16 + 12 = 4,012, and 4,012·16 + 14 = 64,206. This is a special case of polynomial evaluation via Horner’s method (see EXERCISE 2.1.31).

---

Program 6.1.1 Converting a natural number from one base to another

Click here to view code image

public class Convert
{
    public static int toInt(char c)
    {  /* See Exercise 6.1.12. */  }
    public static char toChar(int i)
    {  /* See Exercise 6.1.13. */  }
    public static int parseInt(String s, int d)
    {
        int n = 0;
        for (int i = 0; i < s.length(); i++)
            n = d*n + toInt(s.charAt(i));
        return n;
    }
    public static String toString(int n, int d)
    {
        if (n == 0) return "";
        return toString(n/d, d) + toChar(n % d);
    }
    public static void main(String[] args)
    {
        while (!StdIn.isEmpty())
        {
            String s = StdIn.readString();
            int baseFrom = StdIn.readInt();
            int baseTo = StdIn.readInt();
            int n = parseInt(s, baseFrom);
            StdOut.println(toString(n, baseTo));
        }
    }
}

---

% java Convert
1101101 2 10
109

FACE 16 10
64206

FACE 16 2
1111101011001110

109 10 2
1101101

64206 10 16
FACE

64206 10 32
1UME

1UME 32 10
64206

This general-purpose conversion program reads strings and pairs of bases from standard input and uses parseInt() and toString() to convert the string from a representation of an integer in the first base to a representation of the same integer in the second base.

---

i	n	characters seen
0	15	"F"
1	250	"FA"
2	4012	"FAC"
3	64206	"FACE"
Trace of parseInt(FACE, 16)

For simplicity, we have not included error checks in this code. For example, parseInt() should raise an exception if the value returned by toInt() is not less than the base. Also, it should throw an exception on overflow, as the input could be a string that represents a number larger than can be represented as a Java int.

String representation

Using a toString() method to compute a string representation of a data-type value is also something that we have been doing since the beginning of this book. We use a recursive method that generalizes the decimal-to-binary method (the solution to EXERCISE 2.3.15) that we considered earlier in this section. Again, it is instructive to look at a method to compute the string representation of an integer in any given base, even though Java’s Integer class has a two-argument toString() method that has similar functionality.

toString(64206, 16)
   toString(4012, 16)
      toString(250, 16)
         toString(15, 16)
            toString(0, 16)
               return ""
            return "F"
         return "FA"
      return "FAC"
   return "FACE"

Call trace for toString(64206, 16)

Again, the first primitive operation that we need is a method that converts an integer into a character (digit). EXERCISE 6.1.13 gives a method toChar() that takes an int value between 0 and 35 and returns a character in the range 0-9 (for values less than 10) or A-Z (for values from 10 to 35). With this primitive, the toString() method in PROGRAM 6.1.1 is even simpler than parseInt(). It is a recursive method based on the idea that the last digit is the character representation of n % d and the rest of the string is the string representation of n / d. The computation is essentially the inverse of the computation for parsing, as you can see from the call trace shown at the bottom of the previous page.

When discussing the contents of computer words, we need to include leading zeros, so that we are specifying all the bits. For this reason, we include a three-argument version of toString() in Convert, where the third argument is the desired number of digits in the returned string. For example, the call toString(15, 16, 4) returns 000F and the call toString(14, 2, 16) returns 0000000000001110. Implementation of this version is left as an exercise (see EXERCISE 6.1.15).

Putting all of these ideas together, PROGRAM 6.1.1 is a general-purpose tool for computing numbers from one base to another. While the standard input stream is not empty, the main loop in the test client reads a string from standard input, followed by two integers (the base in which the string is expressed and the base in which the result is to be expressed); it performs the specified conversion and prints the result. To accomplish this task, it uses parseInt() to convert the input string to a Java int, then it uses toString() to convert that Java int to a string representation of the number in the specified base. You are encourage to download and make use of this tool to familiarize yourself with number conversion and representation.

Integer arithmetic

The first operations that we consider on integers are basic arithmetic operations like addition and multiplication. Indeed, the primary purpose of early computing devices was to perform such operations repeatedly. In the next chapter, we will be studying the idea of building computational devices that can do so, since every computer has built-in hardware for performing such operations. For the moment, we illustrate that the basic methods you learned in grade school for decimal work perfectly well in binary and hex.

Addition

In grade school you learned how to add two decimal integers: add the two least significant digits (rightmost digits); if the sum is more than 10, then carry a 1 and write down the sum modulo 10. Repeat with the next digit, but this time include the carry bit in the addition. The same procedure generalizes to any base. For example, if you are working in hex and the two summand digits are 7 and E, then you should write down a 5 and carry a 1 because 7 + E is 15 in hex. If you are working in binary and the two summand bits are 1 and the carry is 1, then you should write down a 1 and carry the 1 because 1+1+1 = 11 in binary. The examples at left illustrate how to compute the sum 4567₁₀ + 366₁₀ = 4933₁₀ in decimal, hex, and binary. As in grade school, we suppress leading zeros.

decimal	binary
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
4-bit integers (unsigned)

Unsigned integers

If we want to represent integers within a computer word, we are immediately accepting a limitation on the number and size of integers that we can represent. As already noted, we can represent only 2ⁿ integers in an n-bit word. If we want just nonnegative (or unsigned) integers, the natural choice is to use binary for the integers 0 through 2ⁿ – 1, with leading 0s so that every word corresponds to an integer and every integer within the defined range corresponds to a word. The table at right shows the 16 unsigned integers we can represent in a 4-bit word, and the table at left shows the range of representable integers for the 16-bit, 32-bit, and 64-bit word sizes that are used in typical computers.

bits	smallest	largest
4	0	15
16	0	65,535
32	0	4,294,967,295
64	0	18,446,744,073,709,551,615
Representable unsigned integers

Overflow

As you have already seen with Java programming in SECTION 1.2, we need to pay attention to ensure that the value of the result of an arithmetic operation does not exceed the maximum possible value. This condition is called overflow. For addition in unsigned integers, overflow is easy to detect: if the last (leftmost) addition causes a carry, then the result is too large to represent. Testing the value of one bit is easy, even in computer hardware (as you will see), so computers and programming languages typically include low-level instructions to test for this possibility. Remarkably, Java does not do so (see the Q&A in SECTION 1.2).

Multiplication

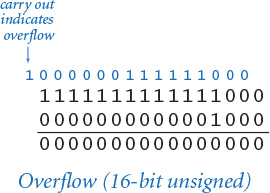
Similarly, as illustrated in the diagram at right, the grade-school algorithm for multiplication works perfectly well with any base. (The binary example is difficult to follow because of cascading carries: if you try to check it, add the numbers two at a time.) Actually, computer scientists have discovered multiplication algorithms that are much better suited to implementation in a computer and much more efficient than this method. In early computers, programmers had to do multiplication in software (we will illustrate such an implementation much later, in EXERCISE 6.3.35). Note that overflow is a much greater concern when developing a multiplication algorithm than for addition, as the number of bits in the result can be twice the number of bits in the operands. That is, when you multiply two n-bit numbers, you need to be prepared for a 2n-bit result.

In this book, we certainly cannot describe in depth all of the techniques that have been developed to perform arithmetic operations with computer hardware. Of course, you want your computer to perform division, exponentiation, and other operations efficiently. Our plan is to cover addition/subtraction in full detail and to offer just some brief information about other operations.

You also want to be able to compute with negative numbers and real numbers. Next, we briefly describe standard representations that allow for these operations.

Negative numbers

Computer designers discovered early on that it is not difficult to modify the integer data type to include negative numbers, using a representation known as two’s complement.

The first approach that you might think of would be to use a sign-and-magnitude representation, where the first bit is the sign and the rest of bits indicate the magnitude of the number. For example, with 4 bits in this representation, 0101 would represent +5 and 1101 would represent –5. By contrast, in n-bit two’s complement, we represent positive numbers as before, but we represent each negative number –x with the (positive, unsigned) binary number 2ⁿ – x. For example, the table at left shows the 16 two’s complement integers we can represent in a 4-bit word. You can see that 0101 still represents +5 but 1011 represents –5, because 2⁴ – 5 = 11₁₀ = 1011₂.

decimal	binary
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001
10	1010
11	1011
12	1100
13	1101
14	1110
15	1111
4-bit integers (unsigned)

With one bit reserved for the sign, the largest two’s complement number that we can represent is about half the largest unsigned integer that we could represent with the same number of bits. As you can see from the 4-bit example, there is a slight asymmetry in two’s complement: we represent the positive numbers 1 through 7 and the negative numbers – 8 through –1, and we have a single representation of 0. In general, in n-bits two’s complement, the smallest possible negative number is – 2^{n – 1} and the largest possible positive number is 2^{n – 1} – 1. The table at left shows the smallest and largest (in absolute value) 16-bit two’s complement integers.

decimal	binary
0	0000000000000000
1	0000000000000001
2	0000000000000010
3	0000000000000011
...	...
32765	0111111111111101
32766	0111111111111110
32767	0111111111111111
-32768	1000000000000000
-32767	1000000000000001
-32766	1000000000000010
-32765	1000000000000011
...	...
-3	1111111111111101
-2	1111111111111110
-1	1111111111111111
16-bit integers (two’s complement)

There are two primary reasons that two’s complement evolved as the standard over sign-and-magnitude. First, because there is only one representation of 0 (the binary string that is all 0s), testing whether a value is 0 is as easy as possible. Second, arithmetic operations are easy to implement—we discuss this for addition later in this section. Moreover, as with sign-and-magnitude, the leading bit indicates the sign, so testing whether a value is negative is as easy as possible. Building computer hardware is sufficiently difficult that achieving these simplifications just by adopting a convention on how we represent numbers is compelling.

Addition

Adding two n-bit two’s complement integers is also easy: add them as if they were unsigned integers. For example, 2 + (– 7) = 0010 + 1001 = 1011 = –5. Proving that this is the case when result is within range (between – 2^{n – 1} and 2^{n – 1} – 1) is not difficult:

• If both integers are non-negative, then standard binary addition as we have described it applies, as long as the result is less than 2^{n – 1}.

• If both integers are negative, then the sum is

(2ⁿ – x) + (2ⁿ – y) = 2ⁿ + 2ⁿ – (x + y)

• If x is negative, y is positive, and the result is negative, then we have

(2ⁿ – x) + y = 2ⁿ – (x – y)

• If x is negative, y is positive, and the result is positive, then we have

(2ⁿ – x) + y = 2ⁿ + (y – x)

In the second and fourth cases, the extra 2ⁿ term does not contribute to the n-bit result (it is the carry out), so a standard binary addition (ignoring the carry out) gives the result. Detecting overflow is a bit more complicated than for unsigned integers—we leave that for the Q&A.

Subtraction

To compute x – y, we compute x + (– y). That is, we can still use standard binary addition, if we know how to compute – y. It turns out that negating a number is very easy in two’s complement: flip the bits and then add 1. Three examples of this process are shown at left—we leave the proof that it works for an exercise.

Knowing two’s complement is relevant for Java programmers because short, int, and long values are 16-, 32-, and 64-bit two’s complement integers, respectively. This explains the bounds on values of these types that Java programmers have to recognize (shown in the table at the top of the next page).

Moreover, Java’s two’s complement representation explains the behavior on overflow in Java that we first observed in SECTION 1.2 (see the Q&A in that section, and EXERCISE 1.2.10). For example, we saw that, for any of Java’s integer types, the result of adding 1 to the largest positive integer, is the largest negative integer. In 4-bit two’s complement, incrementing 0111 gives 1000; in 16-bit two’s complement, incrementing 0111111111111111 gives 1000000000000000. (Note that this is the only case where incrementing a two’s complement integer does not produce the expected result.) The behavior of the other cases in EXERCISE 1.2.10 is also easily explained. For decades, such behavior has bewildered programmers who do not take the time to learn about two’s complement. Here is one convincing example: in Java, the call Math.abs(-2147483648) returns -2147483648, a negative integer!

16-bit	smallest	– 32,768
largest	32,767
32-bit	smallest	– 2,147,483,648
largest	2,147,483,647
64-bit	smallest	– 9,223,372,036,854,775,808
largest	9,223,372,036,854,775,807
Representable two’s complement integers

Real numbers

How do we represent real numbers? This task is a bit more challenging than representing integers, as many choices must be made. Early computer designers tried many, many options and numerous competing formats evolved during the first few decades of digital computation. Arithmetic on real numbers was actually implemented in software for quite a while, and was quite slow by comparison with integer arithmetic.

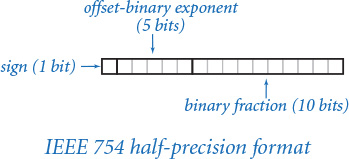
By the mid-1980s, the need for a standard was obvious (different computers might get slightly different results for the same computation), so the Institute for Electrical and Electronic Engineers (IEEE) developed a standard known as IEEE 754—a standard that is still under development to this day. The standard is extensive—you may not want to know the full details—but we can describe the basic ideas briefly here. We illustrate with a 16-bit version known as the IEEE 754 half-precision binary floating-point format, or binary16 for short. The same essential ideas apply to the 32-bit and 64-bit versions used in Java.

Floating point

The real-number representation that is commonly used in computer systems is known as floating point. It is just like scientific notation, except that everything is represented in binary. In scientific notation, you are used to working with numbers like + 6.0221413 × 10²³, which consist of a sign, a coefficient, and an exponent. Typically the number is expressed such that the coefficient is one (nonzero) digit. This is known as a normalization condition. In floating point, we have the same three elements.

The expression reads plus 2 to the power 6 multiplied with 1.1001000100, where the plus symbol is enclosed in a box representing it as “sign.” The number 6 is enclosed in a box representing it as an exponent. The number before the decimal point is mentioned as always 1 and the numbers after the decimal point are enclosed in a box representing it as a fraction.

Sign

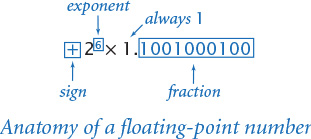
The first bit of a floating-point number is its sign. Nothing special is involved: the sign bit is 0 is the number is positive (or zero) and 1 if it is negative. Again, checking whether a number is positive or negative is easy.

decimal	binary
-15	00000
-14	00001
-13	00010
-12	00011
-11	00100
-10	00101
-9	00110
-8	00111
-7	01000
-6	01001
-5	01010
-4	01011
-3	01100
-2	01101
-1	01110
0	01111
1	10000
2	10001
3	10010
4	10011
5	10100
6	10101
7	10110
8	10111
9	11000
10	11001
11	11010
12	11011
13	11100
14	11101
15	11110
16	11111
5-bit integers (offset binary)

Exponent

The next t bits of a floating-point number are devoted to its exponent. The numbers of bits used for binary16, binary32, and binary64 are 5, 8, and 11, respectively. The exponent of a floating-point number is not expressed in two’s complement, but rather in offset binary, where we take R = 2 ^{t – 1} – 1 (15, 127, and 1,023 for t = 5, 8, and 11, respectively) and represent any decimal number x between –R and R + 1 with the binary representation of x + R. The table at right shows the 5-bit offset binary representations of the numbers between –15 and +16. In the standard, 0000 and 1111 are used for other purposes.

Fraction

The rest of the bits in a floating-point number are devoted to the coefficient: 10, 23, and 53 bits for binary16, binary32, and binary64, respectively. The normalization condition implies that the digit before the decimal place in the coefficient is always 1, so we need not include that digit in the representation!

A horizontal rectangle with sixteen boxes is shown. The first box represents sign (1 bit) and the consecutive five boxes next to it represent offset-binary exponent (5 bits). The remaining ten boxes represent binary fraction (10 bits).

Given these rules, the process of decoding a number encoded in IEEE 754 format is straightforward, as illustrated in the top example in the figure at the top of the next page. According to the standard, the first bit in the given 16-bit quantity is the sign, the next five bits are the offset binary encoding of the exponent (– 6₁₀), and the next 10 bits are the fraction, which defines the coefficient 1.101₂. The process of encoding a number, illustrated in the bottom example, is more complicated, due to the need to normalize and to extend binary conversion to include fractions. Again, the first bit is the sign bit, the next five bits are the exponent, and the next 10 bits are the fraction. These tasks make for a challenging programming exercise even in a high-level language like Java (see EXERCISE 6.1.25, but first read about manipulating bits in the next subsection), so you can imagine why floating-point numbers were not supported in early computer hardware and why it took so long for a standard to evolve.

The first section shows IEEE 754 to decimal conversion and the IEEE 754 number 1010011010000000 is converted where 1 at the leading position is converted to -, 01001 is converted to superscript 9-15 and 1010000000 is converted to .101. The line below shows the calculation: "product of minus 2 superscript 9 minus 15 and 1.101 subscript 2 equals the product of minus 2 superscript minus 6 and 1 plus 2 superscript minus 1 plus 2 superscript minus three which gives the resultant decimal value as -0.0253906250 subscript 10." Decimal to IEEE 754 conversion is shown below where the decimal number 100.25 subscript 10 is converted to floating point. The line below shows the calculation that reads: "100.25 subscript 10 equals product of 2 superscript 6 and 1 plus 2 superscript minus 1 plus 2 superscript minus 4 plus 2 superscript minus 8 that equals plus 2 superscript 21 minus 15 multiplied with 1.10010001 subscript 2 where plus represents 0, 21 represents 10101 and 10010001 represents 1001000100, thus bringing the output as 0101011001000100.

Java’s Float and Double data types include a floatToIntBits() method that you can use to check floating-point encoding. For example, the call

Click here to view code image

Convert.toString(Float.floatToIntBits(100.25), 2, 16)

prints the result 0101011001000100 as expected from the second example above.

Arithmetic

Performing arithmetic on floating-point numbers also makes for an interesting programming exercise. For example, the following steps are required to multiply two floating-point numbers:

• Exclusive or the signs.

• Add the exponents.

• Multiply the fractions.

• Normalize the result.

If you are interested, you can explore the details of this process and the corresponding process for addition and for multiplication by working EXERCISE 6.1.25. Addition is actually a bit more complicated than multiplication, because it is necessary to “unnormalize” to make the exponents match as the first step.

Computing with floating-point numbers is often challenging because they are most often approximations to the real numbers of interest, and errors in the approximation can accumulate during a long series of calculations. Since the 64-bit format (used in Java’s double data type) has more than twice as many bits in the fraction as the 32-bit format (used in Java’s float data type), most programmers choose to use double to lessen the effects of approximations errors, as we do in this book.

Java code for manipulating bits

As you can see from floating-point encoding of real numbers, encoding information in binary can get complicated. Next, we consider the tools available within Java that facilitate the development of programs to encode and decode information. These tools are made possible because Java defines integer values to be two’s complement integers, and makes explicit that the values of the short, int, and long data types are 16-, 32-, and 64-bit binary two’s complement, respectively. Not all languages do so; some instead leave such code to a lower-level language, define an explicit data type for bit sequences, and/or perhaps require difficult or expensive conversion. We focus on 32-bit int values, but the operations also work for short and long values.

Binary and hex literals

In Java, it is possible to specify integer literal values in binary (by prepending 0b) and in hex (by prepending 0x). This strategy substantially clarifies code that is working with binary values. You can use literals like this anywhere that you can use a decimal literal; it is just another way of specifying an integer value. If you assign a hex literal to an int variable and specify fewer than 8 digits, Java will fill in the leading zeros. A few examples are shown in the table at right.

binary literal	hex literal	shorter form
0b01000000010101000100111101011001	0×40544F59
0b11111111111111111111111111111111	0×0000000F	0×F
0b00000000000000000001001000110100	0×00001234	0×1234
0b00000000000000001000101000101011	0×00008A2B	0×8A2B

Shifting and bitwise operations in Java code

To allow clients to manipulate the bits in an int value, Java supports the operations shown in the table at the bottom of this page. We can complement the bits (change the 0s to 1s and the 1s to 0s), do bitwise logical operations (apply the and, or, and xor functions defined at the bottom of the next page to the corresponding pairs of bits), and shift left or right a given number of bit positions. For shift right, there are two options: logical shift, where 0s are filled in at the left, and arithmetic shift, where vacated positions are filled with the sign bit (see the Q&A at the end of this section). Examples of these operations are shown at right.

values	32-bit integers
typical literals	0b00000000000000000000000000001111 0b1111 0xF 0x1234
operations	bitwise complement	bitwise and	bitwise or	bitwise xor	shift left	shift right (logical)	shift right (arithmetic)
operators	~	&	|	^	<<	>>>	>>
Bit manipulation operators for Java’s built-in int data type

Shifting and masking

One of the primary uses of such operations is masking, where we isolate a bit or a group of bits from the others in the same word. Usually we prefer to specify masks as hex constants. For example, the mask 0x80000000 can be used to isolate the leftmost bit in a 32-bit word, the mask 0x000000FF can be used to isolate the rightmost 8 bits, and the mask 0x007FFFFF can be used to isolate the rightmost 23 bits.

Going a bit further, we often do shifting and masking to extract the integer value that a contiguous group of bits represents, as follows:

• Use a shift right instruction to put the bits in the rightmost position.

• If we want k bits, create a literal mask whose bits are all 0 except its k rightmost bits, which are 1.

• Use a bitwise and to isolate the bits. The 0s in the mask lead to zeros in the result; the 1s in the mask give the bits of interest in the result.

This sequence of operations enables us to use the result as we would any other int value, which is often what is desired. Later in this chapter we will be interested in shifting and masking to isolate hex digits, as shown in the example at right.

x	y	AND(x,y)	OR(x,y)	XOR(x,y)
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0
Truth-table definitions for bitwise functions

expression	value
0x00008A2B >> 8	0x0000008A
(0x00008A2B >> 8) & 0xF	0x0000000A
Shifting and masking example

---

Program 6.1.2 Extracting the components of a floating-point number

Click here to view code image

public class ExtractFloat
{
   public static void main(String[] args)
   {
      float x = Float.parseFloat(args[0]);
      int t = Float.floatToIntBits(x);

      if ((t & 80000000) == 1) StdOut.println("Sign:     -");
      else                     StdOut.println("Sign:     +");

      int exponent = ((t >> 23) & 0xFF) - 127;
      StdOut.println("Exponent: " + exp);

      double fraction =  1.0 * (t & 0x007FFFFF) / (1 << 23);
      double mantissa =  1.0 + fraction;
      StdOut.println("Mantissa: " + mantissa);

      StdOut.println(mantissa * (1 << exponent));
   }
}

This program illustrates the use of Java bit manipulation operations by extracting the sign, exponent, and fraction fields from float values entered as the command-line argument, then using the exponent and fraction to recompute the absolute value of the number.

---

% java ExtractFloat -100.25
    Sign: -
Exponent: 6
Mantissa: 1.56640625
100.25

---

As an example of a practical application of bitwise operations, PROGRAM 6.1.2 illustrates the use of shifting and masking to extract the sign, exponent, and fraction from a floating-point number. Most computer users are able to work comfortably without dealing with data representations at this level (indeed, we have hardly needed it so far in this book), but, as you will see, bit manipulation plays an important role in all sorts of applications.

Characters

To process text, we need a binary encoding for characters. The basic method is quite simple: a table defines the correspondence between characters and n-bit unsigned binary integers. With 6 bits, we can encode 64 different characters; with 7 bits, 128 different characters; with 8 bits, 256 different characters; and so forth. As with floating-point numbers, many different schemes evolved as computers came into use, and people still use different encodings in different situations.

ASCII

The American Standard Code for Information Interchange (ASCII) code was developed as a standard in the 1960s, and has been in widespread use ever since. It is a 7-bit code, though in modern computing it most often is used in 8-bit bytes, with the leading bit being ignored.

One of the primary reasons for the development of ASCII was for communication via teletypewriters that could send and receive text. Accordingly, many of the encoded characters are control characters for such machines. Some of the control characters were part of communications protocols (for example, ACK means “acknowledge”); others controlled the printing aspect of the machine (for example, BS means “backspace” and CR means “carriage return”).

The table at right is a definition of ASCII that provides the correspondence that you need to convert from 8-bit binary (equivalently, 2-digit hex) to a character and back. Use the first hex digit as a row index and the second hex digit as a column index to find the character that it encodes. For example, 31 encodes the digit 1, 4A encodes the letter J, and so forth. This table is for 7-bit ASCII, so the first hex digit must be 7 or less. Hex numbers starting with 0 and 1 (and the numbers 20 and 7F) correspond to nonprinting control characters such as CR, which now means “newline” (most of the others are rarely used in modern computing).

A table with 16 columns has the headers, from left to right: _0, _1, _2, _3, _4, _5, _6, _7, _8, _9, _A, _B, _C, _D, _E, _F, 8. Rows are present in the table with the headers, from the top to bottom: 0_, 1_, 2_, 3_, 4_, 5_, 6_ , 7_. The first row reads “NUL,” SOH,” “STX,” “ETX,” “ENQ,” “ACK,” “BEL,” “BS,” “HT,” “LF,” “VT,” “FF,” “CR,” “SO,” and “SI.” The second row reads “DLE,” “DC1,” “DC2,” “DC3,” “DC4,” “NAK,” “SYN,” “ETB,” “CAN,” “EM,” “SUB,” “ESC,” “FS,” “GS,” “RS,” and “US.” The third row reads “SP,” “!,” “”,” “#,” “$,” “%,” “&,” “’,” “(,” “),” “*,” “+,” “,,” “-,” “.,” and “/.” The fourth row reads “0,1,2,3,4,5,6,7,8,9,:,;,<,=,>,?.” The fifth row reads “@, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O.” The sixth row reads “P, Q, R, S, T, U, V, W, X, Y, Z, [, \, ], ^,_.” The seventh row reads “’,a, b, c, d, e, f, g, h, I, j, k, l, m, n and o. The eight row reads “p, q, r, s, t, u, v, w, x, y, z, {, |, }, ~ and DEL.

Unicode

In the connected world of the 21st century, it is necessary to work with many more than the 100 or so ASCII characters from the 20th century, so a new standard known as Unicode is emerging. By using 16 bits for most characters (and up to 24 or 32 bits for some characters), Unicode can support tens of thousands of characters and a broad spectrum of the world’s languages. The UTF-8 encoding (from sequences of characters to sequences of 8-bit bytes, and vice versa, with most characters mapping to two bytes) is rapidly emerging as a standard. The rules are complicated but comprehensive, and they are implemented in most modern systems (such as Java) so programmers generally need not worry much about the details. ASCII survives within Unicode: all ASCII characters map to 1 byte, so ASCII files are special cases of UTF-8 files (and backward compatible).

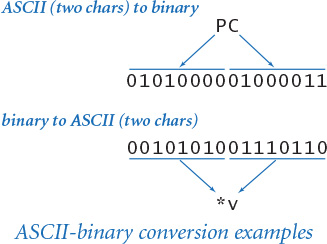
We generally pack as much information as possible into a computer word, so it is possible to encode two ASCII characters in 16 bits (as shown in the example at right), four characters in 32 bits, eight characters in 64 bits, and so forth. In high-level languages such as Java, such details and UTF-8 encoding and decoding are implemented in the String data type, which we have been using throughout the book. Nevertheless, it is often important for Java programmers to understand some basic facts about the underlying representation, as it can certainly affect the resource requirements of programs. For example, many programmers discovered that the memory usage of their programs suddenly doubled when Java switched from ASCII to Unicode in the 2000s, and began using a 16-bit char to encode each ASCII character. Experienced programmers know how to pack two ASCII characters per char to save memory when necessary.

An ASCII number PC (two chars) is converted to binary, where P is converted to 01010000 and C is converted to 01000011. A binary number 0010101001110110 is converted to ASCII (two chars), where 00101010 is converted to * and 01110110 is converted to v.

Summary

Generally, it is wise to write programs that function properly independent of the data representation. Many programming languages fully support this point of view. Unfortunately, this approach can stand in direct opposition to the idea of taking full advantage of the capability of a computer, by using its hardware the way it was designed to be used. Java’s primitive types are intended to support this point of view. For example, if the computer has hardware to add or multiply 64-bit integers, then we would like each add or multiply operation to reduce to a single instruction so that our program can run as fast as possible. For this reason, it is wise for the programmer to try to match data types that have performance-critical operations with the primitive types that are implemented in the computer hardware. Achieving the actual match might involve deeper understanding of your system and its software, but striving for optimal performance is a worthwhile endeavor.

You have been writing programs that compute with various types of data. Our message in this section is that since every sequence of bits can be interpreted in many different ways, the meaning of any given sequence of bits within a computer depends on the context. You can write programs to interpret bits any way that you want. You cannot tell from the bits alone which type of data they represent, or even whether they represent data at all, as you will see.

To further emphasize this point, the table below gives several different 16-bit values, along with their values if interpreted as binary integers, hex integers, unsigned integers, two’s complement integers, binary16 floating-point numbers, and pairs of ASCII characters. These are but a few early examples of the myriad available ways of representing information within a computer.

Q&A

Q. How do I find out the word size of my computer?

A. You need to find out the name of its processor, then look for the specifications of that processor. Most likely, you have a 64-bit processor. If not, it may be time to get a new computer.

Q. Why does Java use 32 bits for int values when most computers have 64-bit words?

A. That was a design decision made a long time ago. Java is unusual in that it completely specifies the representation of an int. The advantage of doing so is that old Java programs are more likely to work on new computers than programs written in languages where machines might use different representations. The disadvantage is that 32 bits is often not enough. For example, in 2014 Google had to change from a 32-bit representation for its view count after it became clear that the video Gangham Style would be watched more than 2,147,483,647 times. In Java, you can switch to long.

Q. This seems like something that could be taken care of by the system, right?

A. Some languages, such as Python, place no limit on the size of integers, leaving it to the system to use multiple words for integer values when necessary. In Java, you can use the BigInteger class.

Q. What’s the BigInteger class?

A. It allows you to compute with integers without worrying about overflow. For example, if you import java.math.BigInteger, then the code

Click here to view code image

BigInteger x = new BigInteger("2");
StdOut.println(x.pow(100));

prints 1267650600228229401496703205376, the value of 2¹⁰⁰. You can think of a BigInteger as a string (the internal representation is more efficient than that), and the class provides methods for standard arithmetic operations and many other operation. For example, this method is useful in cryptography, where arithmetic operations on numbers with hundreds of digits play a critical role in some systems. The implementation works with many digits as necessary, so overflow is not a concern. Of course, operations are much more expensive than built-in long or int operations, so Java programmers do not use BigInteger for integers that fit in the range supported by long or int.

Q. Why hexadecimal? Aren’t there other bases that would do the job?

A. Base 8, or octal, was widely used for early computer systems with 12-bit, 24-bit, or 36-bit words, because the contents of a word could be expressed with 4, 8, or 12 octal digits, respectively. An advantage over hex in such systems was that only the familiar decimal digits 0–7 were needed, so primitive I/O devices like numeric keypads could be used both for decimal numbers and octal numbers. But octal is not convenient for 32-bit and 64-bit word sizes, because those word sizes are not divisible by 3. (They are not divisible by 5 or 6 either, so no switch to a larger base is likely.)

Q. How can I guard against overflow?

A. It is not so easy, as a different check is needed for each operation. For example, if you know that x and y are both positive and you want to compute x + y, you could check that x < Integer.MAX_VALUE - y.

A. Another approach is to “upcast” to a type with a bigger range. For example, if you are calculating with int values, you could convert them to long values, then convert the result back to int (if it is not too big).

A. In Java 8, you can use Math.addExact(), which throws an exception on overflow.

Two examples are displayed with carry out being different from carry represented first with two arrows pointing to 1 and 0 in the number 1000000000000000. Two binary numbers 1111111111111000 and 1000000000000100, representing decimal equivalents -8 and -32764, are added. The resultant of the addition is another binary number 1111111111111100 that represents decimal equivalent -4 with a cross mark next to it. Carry out being different from carry in is represented in the second example, where two arrows point to 0 and 1 in the number 0111111111111000. Two binary numbers 0000000000010000 and 0000000000001000, representing decimal equivalents 32760 and 8, are added resulting in another binary number 1000000000000000 which is a decimal equivalent of -32768 and a cross mark is present next to the decimal equivalent.

Q. How might hardware detect overflow for two’s complement addition?

A. The rule is simple, though it is a bit tricky to prove: check the values of the carry in to the leftmost bit position and the carry out of the leading bit position. Overflow is indicated if they are different (see the examples at right).

Q. What is the purpose of the arithmetic shift?

A. For two’s complement integers, arithmetic shifting right by 1 is the same as integer division by 2. For example, the value of (-16) >> 3 is -2, as illustrated at right. To test your understanding of this operator, figure out the values of (-3) >> 1 and (-1) >> 1. This convention is called “sign extension,” as opposed to “zero extension” for logical shifts.

Positive number is defined first with x as 0000000000010000 which is equivalent to 16 in decimal notation and x greater than greater than 3 as 0000000000000010 which is equivalent to 2 in decimal notation where the first three zeroes in x greater than greater than 3 are highlighted with an arrow labeled “fill with 0s” pointing toward it. Arrows point from the binary values in x to the values in x greater than greater than 3 except the last three zeroes. Negative number is defined with x as 1111111111110000 which is equivalent to -16 in decimal notation and x greater than greater than 3 as 1111111111111110 which is equivalent to -2 in decimal notation where the first three ones are highlighted with an arrow labeled “fill with 1s” pointing toward it. Arrows point from the binary values in x to the values in x greater than greater than 3 except the last three zeroes.

Q. What is x >> y if y is negative or greater than 31?

A. Java uses only the five low-order bits of the second operand. This behavior coincides with the physical hardware on typical computers.

Q. I never really understood the examples in the Q&A in SECTION 1.2 that claim that (0.1 + 0.1 == 0.2) is true but (0.1 + 0.1 + 0.1 == 0.3) is false. Can you elaborate, now?

A. A literal like 0.1 or 0.3 in Java source code is converted to the nearest 64-bit IEEE 754 number (the one whose least significant bit is 0 in case of a tie), a Java double value. Here are the values for the literals 0.1, 0.2, and 0.3:

As you can see, 0.1 + 0.1 is equal to 0.2, but 0.1 + 0.1 + 0.1 is greater than 0.3. The situation is not so different from noticing that, for integers, 2/5 + 2/5 is equal to 4/5 (they are both 0), but 2/5 + 2/5 + 2/5 is not equal to 6/5.

Q. System.out.println(0.1) prints 0.1, not the value in the table on the previous page. Why?

A. Few programmers need that much precision, so println() truncates for readability. There must be at least one digit to represent the fractional part, and beyond that as many—but only as many—more digits as are needed to uniquely distinguish the argument value from adjacent values of type double. You can use printf() for more precise control over the format, and BigDecimal for extended precision. For example, if you import java.math.BigDecimal, then the code

Click here to view code image

double x = 0.1;
StdOut.println(new BigDecimal(x));

prints 0.1000000000000000055511151231257827021181583404541015625.

Exercises

6.1.1 Convert the decimal number 92 to binary.

Solution. 1011100.

6.1.2 Convert the octal number 31415 to binary.

Solution. 011001100001101.

6.1.3 Convert the octal number 314159 to decimal.

Solution. That is not an octal number! You can do the computation, even with Convert, to get the result 104561, but 9 is just not a legal octal digit. The version of Convert on the booksite includes such legality checks. It is not unusual for a teacher to try this trick on a test, so beware!

6.1.4 Convert the hexadecimal number BB23A to octal.

Solution. First convert to binary 1011 1011 0010 0011 1010, then consider the bits three at a time 10 111 011 001 000 111 010, and convert to octal 2731072.

6.1.5 Add the two hexadecimal numbers 23AC and 4B80 and give the result in hexadecimal. Hint: Add directly in hex instead of converting to decimal, adding, and converting back.

6.1.6 Assume that m and n are positive integers. How many 1 bits are there in the binary representation of 2^m+n?

6.1.7 What is the only decimal integer whose hexadecimal representation has its digits reversed?

Solution. 53 is 35 in hex.

6.1.8 Prove that converting a hexadecimal number one digit at a time to binary, and vice versa, always gives the correct result.

6.1.9 IPv4 is the protocol developed in the 1970s that dictates how computers on the Internet communicate. Each computer on the Internet needs it own Internet address. IPv4 uses 32-bit addresses. How many computers can the Internet handle? Is this enough for every mobile phone and every toaster to have its own?

6.1.10 IPv6 is an Internet protocol in which each computer has a 128-bit address. How many computers would the Internet be able to handle if this standard is adopted? Is this enough?

Solution. 2¹²⁸. That at least enough for the short term—5,000 addresses per square micrometer of the Earth's surface!

6.1.11 Fill in the values of the expressions in this table:

6.1.12 Develop an implementation of the toInt() method specified in the text for converting a character in the range 0-9 or A-Z into an int value between 0 and 35.

Solution.

Click here to view code image

public static int toInt(char c)
{
    if ((c >= '0') && (c <= '9')) return c - '0';
    return c - 'A' + 10;
}

6.1.13 Develop an implementation of the toChar() method specified in the text for converting an int value between 0 and 35 into a character in the range 0-9 or A-Z.

Solution.

Click here to view code image

public static char toChar(int i)
{
    if (i < 10) return (char) ('0' + i);
    return (char) ('A' + i - 10);
}

6.1.14 Modify Convert (and the answers to the previous two exercises) to use long, test for overflow, and check that the digits in the input string are within the range specified by the base.

Solution. See Convert.java on the booksite.

6.1.15 Add to Convert a version of the toString() method that takes a third argument, which specifies the length of the string to be produced. If the specified length is less than needed, return only the rightmost digits; if it is greater, fill in with leading 0 characters. For example, toString(64206, 16, 3) should return "ACE" and toString(15, 16, 4) should return "000F". Hint: First call the two-argument version.

6.1.16 Compose a Java program TwosComplement that takes an int value i and a word size w from the command line and prints the w-bit two’s complement representation of i and the hex representation of that number. Assume that w is a multiple of 4. For example, your program should behave as follows:

Click here to view code image

% java TwosComplement -1 16
1111111111111111 FFFF
% java TwosComplement 45 8
00101101 2D
% java TwosComplement -1024 32
11111111111111111111110000000000 FFFFFC00

6.1.17 Modify ExtractFloat to develop a program ExtractDouble that accomplishes the same task for double values.

6.1.18 Write a Java program EncodeDouble that takes a double value from the command line and encodes it as a floating-point number according to the IEEE 754 binary32 standard

6.1.19 Fill in the blanks in this table.

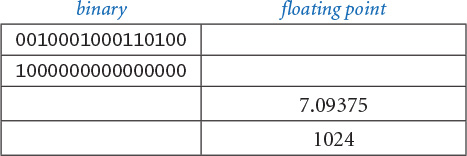
6.1.20 Fill in the blanks in this table.

Creative Exercises

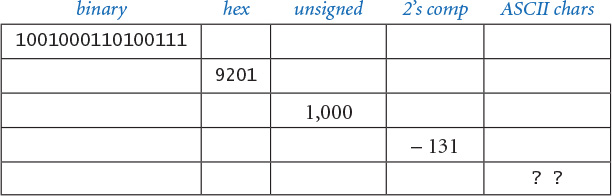
6.1.21 IP addresses and IP numbers An IP address (IPV4) consists of integers w, x, y, and z and is typically written as the string w.x.y.z. The corresponding IP number is given by 16777216w + 65536x + 256y + z. Given an IP number n, the corresponding IP address is derived from w = (n / 16777216) mod 256, x = (n / 65536) mod 256, y = (n / 256) mod 256, z = n mod 256. Write a function that takes an IP number and returns a String representation of the IP address. and another function that takes an IP address and returns a int corresponding to the IP number. For example, given 3401190660, the first function should return 202.186.13.4.

6.1.22 IP address. Write a program that takes a 32-bit string as a command-line argument and prints the corresponding IP address in dotted decimal form. That is, take the bits 8 at a time, convert each group to decimal, and separate each group with a dot. For example, the binary IP address 010100000001000000000000000000 01 should be converted to 80.16.0.1.

6.1.23 MAC address. Write functions to convert back and forth between MAC addresses and 48-bit long values.

6.1.24 Base64 encoding. Base64 encoding is a popular method for sending binary data over the Internet. It converts arbitrary data to ASCII text, which can be emailed back between systems without problems. Write a program to read in a arbitrary binary file and encode it using Base64.

6.1.25 Floating-point software. Write a class FloatingPoint that has three instance variables sign, exponent, and fraction. Implement addition and multiplication. Include toString() and parseFloat(). Support 16-, 32-, and 64-bit formats.

6.1.26 DNA encoding. Develop a class DNA that supports an efficient representation of strings that are composed exclusively of A, T, C, or G characters. Include a constructor that converts a string to the internal representation, a toString() method that converts the internal representation to a string, a charAt() method that returns the character at the specified index, and an indexOf() method that takes a String pattern as an argument and returns the first occurrence of pattern in the represented string. For the internal representation, use an array of int values, packing 16 characters in each int (two bits per character).

6.2 TOY Machine

To help you better understand the nature of computation on your computer, we introduce in this section TOY, an imaginary machine designed for this book that is very similar to the computers that first came into widespread use in the 1970s. We study it today because it also shares the essential characteristics of the modern day microprocessors found in your mobile device and your computer and everywhere else, not to mention countless other computing devices developed in the intervening years. The figure at the bottom of this page depicts a PDP-8, a real computer from the 1970s, and TOY, our imaginary computer.

---

6.2.1 Your first TOY program

6.2.2 Euclid’s algorithm

6.2.3 Self-modifying code

Programs in this section

---

TOY demonstrates that simple computational models can perform useful and nontrivial calculations, and also serves a reference point that can help you understand the basic characteristics of your own computer. One of the remarkable facts of the evolution of computation over the past several decades is that all computers share the same basic architecture, an approach that was widely adopted almost immediately after it was first articulated by John von Neumann in 1945.

We begin by introducing the basic constituent parts of the TOY machine. There are only a few, and the purpose of each is easy to understand. All computers are made up of similar components.

Then we describe how to use and program the TOY machine. Starting with the basic ways of representing information that we covered in the previous section, we look at operations on such information. In other words, we are working with the data types that the TOY machine hardware implements: sets of values and operations on those values. Working at this level is known as machine-language programming. Studying programming at the machine language level will help you better understand the relationship between your Java programs and your computer, as well as the nature of computation itself. Machine-language programming is actually still used today in performance-critical applications such as video processing, audio processing, and scientific computing. As you will see, it is not difficult to learn how to program in machine language.

PDP-8 from the 1970's is shown at the left which has a tuner and a list of switches at the bottom. A TOY, timeless system is shown on the right with four options at the top that read, "LOAD, LOOK, RUN and ON/OFF." There are two boxes with four switches and four LED lights, each, with ADDR written at the left. There are four boxes below with four switches and four LED lights on each box with DATA written on the left.

In CHAPTER 7, we describe how to build such a machine in hardware. This will be the final step in demystifying your computer, helping you to better understand the connection between your Java programs and the physical world.

This essential layer of abstraction is found in all computers. A complete description of precisely what a processor can do provides a target language for translating a program written in a high-level language like Java while at the same time providing a blueprint for building a circuit that can implement the machine.

Brief historical note

It is perhaps a bit difficult for you to imagine a modern world without computers. To pick a point in time, consider the 1950s, when the world was becoming industrialized after World War II. At that time, there were cars, airplanes, satellites, and all sorts of other technological developments that are recognizable today, but there were no computers available to the average person or even the average scientist or engineer.

The original motivation for building computers was to be able to perform calculations for applications of all sorts in science, engineering, and commerce. World War II itself proved the point, from the ballistics tables computed by John von Neumann to the code-breaking machine developed by Alan Turing, not to mention the calculations done at Los Alamos that enabled the development of the atomic bomb. And imagine running a bank or building a car without a computer.

The most important tool used for calculations by a typical science or engineering student before the 1970s was the slide rule, a decidedly non-electronic and non-digital device that nonetheless was very useful, particularly for computing logarithms and doing multiplications. Another tool in common use was a book of tables of functions; for example, to compute sin(x), you would look it up in the book!

Once computers did start to become available, they were generally shared by a group of people and were cumbersome to use, as you will see. Still, it was immediately apparent that computing would be a vast improvement over slide rules and function tables. Within a very short amount of time, people were sharing large computers in ways that made slide rules and tables of functions obsolete. For many years people used calculators, based on the same technology as computers but specialized for calculations, and handheld. For simple calculations, calculators persist.

For complex calculations, scientists, engineers, and applications developers wrote computer programs, then as now. It is quite remarkable that the basic design of the first devices that were created for such purposes has persisted to the present day and still supports the ocean of applications that have transformed the world.

TOY components

We begin with an overview of the basic design components that have been found in virtually all computers for more than half a century, but are reduced to their essentials in our TOY machine.

Memory

The memory is a critical component of any computer. It holds not only data to be processed and the results of the computation, but also any program that the machine is to run. TOY’s memory consists of 256 words, each 16 bits. That certainly is not much by today’s standards, but you will be surprised at the range of calculations it can support. And here is a sobering thought: Those 256 × 16 = 4,096 bits have 2^4,096 different possible values, so the vast majority of things that TOY can do will never be observed in this universe.

Click here to view code image

     0_   1_   2_   3_   4_   5_   6_   7_   8_   9_   A_   B_   C_   D_   E_   F_
_0  7A10 8A15 8A2B 7101 7101 7800 8AFF 7101 7101 BB0E 0000 0000 0000 0000 0000 0000
_1  7BEF 8B16 8B2C 75FF 7A00 8CFF 8BFF A90A A90A 1EE1 0000 0000 0000 0000 0000 0000
_2  9AFF 1CAB 2CAB 7901 7B01 CC55 7101 140A 180A 900E 0000 0000 0000 0000 0000 0000
_3  9BFF 9C17 CC29 2C59 894C 188C 7900 7B00 C98F 1EE1 0000 0000 0000 0000 0000 0000
_4  7101 0000 DC27 CC3B C94B C051 22B9 C97C AC09 900E 0000 0000 0000 0000 0000 0000
_5  7900 0008 2BBA 1991 9AFF 98FF C26B 2991 2CBC 1EE1 0000 0000 0000 0000 0000 0000
_6  22B9 0005 C022 1A09 1CAB 0000 1CA9 2441 CC96 EF00 0000 0000 0000 0000 0000 0000
_7  C200 0000 EF00 8B3D 1AB0 0000 8DFF AC04 1991 0000 0000 0000 0000 0000 0000 0000
_8  1CA9 0000 0000 FF22 1BC0 0000 BD0C 2EBC 1809 0000 0000 0000 0000 0000 0000 0000
_9  AD0C 0000 00C3 2AA1 2991 0000 1991 DE7B A909 0000 0000 0000 0000 0000 0000 0000
_A  9DFF 0000 0111 CA36 C044 0000 C064 1B0C DCBE 0000 0000 0000 0000 0000 0000 0000
_B  1441 0000 0000 9B3E 0000 0000 1AA9 C074 1981 0000 0000 0000 0000 0000 0000 0000
_C  C006 0000 0000 0000 000C FF60 BB0A EF00 1809 0000 0000 0000 0000 0000 0000 0000
_D  0000 0000 0000 005B 0000 FF70 EF00 0000 A909 0000 0000 0000 0000 0000 0000 0000
_E  0000 0000 0000 0000 0000 9BFF 0000 0000 C083 0000 0000 0000 0000 0000 0000 0000
_F  0000 0000 0000 0000 0000 0000 0000 0000 BE08 0000 0000 0000 0000 0000 0000 0000

TOY memory dump (256 16-bit words)

With hex notation, we can specify the contents of a memory word with 4 hex digits. Furthermore, we consider the words to be numbered from 0 to 255, so that we can refer to each word with 2-digit hex number known as its address. For example, we might say that “the value of the word at address 1E is 0FA2” or just “memory location 1E is 0FA2.” For economy, we often just use array notation and say that “M[1E] is 0FA2.” We can specify the contents of the TOY memory using a 16-row table like the one at the bottom of the previous page. The first column gives values for locations 00 to 0F; the second column gives values for locations 10 to 1F, and so forth. Such a table is known as a memory dump. In this case, the memory contains all the programs that we consider in this chapter (!)

Instructions

A critical characteristic of the TOY machine (and virtually all other computers) is that the contents of a memory word might be interpreted either as data or as an instruction, depending on the context. For example, you know from the previous section that the value 1234 might be interpreted as representing the integer 4660₁₀ or the real number 0.00302886962890625; in this section you will learn that it might also represent a machine instruction that adds two numbers. It is up to the programmer to ensure that data is treated as data, and that instructions are treated as instructions. We will examine how all TOY instructions are encoded shortly, so that you will know how to decode any 16-bit value as an instruction (and how to encode any instruction as a 16-bit value).

Registers

A register is a machine component that holds a sequence of bits, much like a word in main memory. Registers serve the function of holding intermediate results during computation. You can think of them as playing the role of variables in TOY programming. TOY has 16 registers, numbered from 0 through F. As with memory, we use array notation and refer to the registers with the designations R[0] through R[F]. Since they are 16 bits, the same as memory words, we represent the contents of each register with a 4-digit hex value, and the contents of all the registers with a table of 16 4-digit hex numbers. The table at right shows the contents of the registers during a typical computation, which we examine later. By convention, R[0] is always 0000.

R[0] 0000
R[1] 0001
R[2] 000A
R[3] 0000
R[4] 0000
R[5] 0000
R[6] 0030
R[7] 0000
R[8] 003A
R[9] 0000
R[A] 0A23
R[B] 0B44
R[C] 0C78
R[D] 0000
R[E] 0000
R[F] 0000

TOY registers

Arithmetic logic unit

The arithmetic logic unit (ALU) is TOY’s computational engine—the workhorse of the machine that performs all its calculations. Typically, a TOY instruction directs the ALU to compute some function that takes two registers as arguments and put the result in a third register. For example, the TOY instruction 1234 says to direct the contents of R[2] and R[3] to the ALU, add them, and then direct the result to R[4]. Later in this section, we will describe how to compose TOY programs based upon such instructions.

Program counter and instruction register

The 8-bit program counter (PC) is an internal register that holds the address of the next instruction to be executed. The 16-bit instruction register (IR) is an internal register that contains the current instruction being executed. These registers are central to the operation of the machine. The IR is not directly accessed by programs, but programmers are always aware of its contents.

The diagram at the bottom of this page is a schematic that includes these basic components. In Chapter 7, we will consider how to create a circuit that implements all of them. For the rest of this chapter, we will consider how they operate and how a programmer can control them to get them to perform a desired computation.

Fetch–increment–execute cycle

The TOY machine executes instructions by taking a specific sequence of actions, repeatedly. First it checks the value of the PC and fetches (copies) the contents of this memory location into the IR. Next, it increments the program counter by 1. (For example, if the program counter is 10, it gets incremented to 11.) Finally, it interprets the 16-bit value in the IR as an instruction and executes it according to the rules that characterize the TOY machine, which we will describe shortly. Each instruction can modify the contents of various registers, main memory, or even the program counter itself. After executing the instruction, the machine repeats the whole fetch–increment–execute cycle, using the new value of the program counter to find the next instruction. This process continues forever, or until the machine executes a halt instruction. As with Java, it is possible to write programs that go into infinite loops. To stop the TOY machine in an infinite loop, a programmer would have to turn it off, or perhaps even to unplug it.

There are two boxes at the left, where the box at the top represents “ALU” and the box at the bottom represents “REGISTERS.” There are two boxes at the center where the box at the top represents "PC” and the bottom represents “IR.” A box on the right represents “MEMORY.”

The text “Fetch” is shown on the left and a curved arrow points from this text to the text “increment” on the right. A curved arrow from this text points to "Fetch."

Instructions

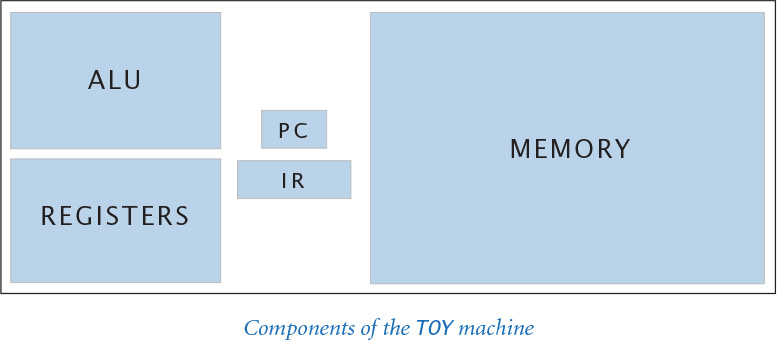
Any 16-bit value (the contents of any memory word) can be interpreted as a TOY instruction. The purpose of each instruction is to modify the state of the machine (the value of a memory word, a register, or the PC) in some way. To describe the operation of the instructions, we use pseudo-code, which is much like Java code except that it refers to memory words, registers, and the PC directly.

RR format is shown at the top with four boxes. The contents of the boxes are op, d, s, and t, respectively. "A" format below has three boxes op, d and st, respectively. OP represents 4 bit opcode, d, s, and t represent 4 bit registers, and st represents 8 bit address.

Anatomy of an instruction

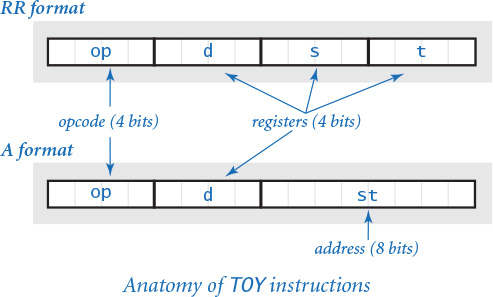
We use hex to encode instructions: each 16-bit instruction is four hex digits. The first digit of an instruction is its opcode, which specifies the operation it performs. There are 16 different instructions, so one hex digit suffices to specify one of them. The second digit of an instruction specifies a register—each instruction uses or changes the value of some register. Since there are 16 registers, one hex digit suffices to specify one of them. Most of the instructions are coded in one of two instruction formats, which tell us how to interpret the third and fourth hex digits. In RR-format instructions, each of the two remaining hex digits refers to a register. In A-format instructions, the third and fourth hex digits (together) specify a memory address.

Instruction set

On the next page is a table that describes all of TOY’s instructions. This table is a complete reference guide to programming in TOY, to be consulted when you compose TOY programs. Next, we describe the instructions in detail.

Halt

Opcode 0, the most basic instruction, simply directs the machine to halt—that is, to stop the fetch–increment–execute cycle. At this point, the programmer can examine the contents of memory to see the results of the computation. TOY ignores the other three hex digits of a halt, so 0000, 0123, and 0FFF are all halt instructions.

There are four columns and sixteen rows in the table, with the column headers “opcode, description, format, and pseudo-code.” The first row reads "0," "halt," "-," and the fourth column is left blank. The second row reads "1," "add," "RR," and "R[d] <- R[s] + R[t]." The third row reads “2,” “subtract,” “RR,” and “R[d] <- R[s] – R[t].” The fourth row reads “3,” “bitwise and,” “RR,” and “R[d] <- R[S] & R[t].” The fifth row reads “4,” “bitwise xor,” “RR,” and “R[d] <- R[s] ^ R[t].” The sixth row reads “5,” “left shift,” “RR,” and “R[d] <- R[s] << R[t].” The seventh row reads “6,” “right shift,” “RR,” and “R[d] <- R[s] >> R[t].” The eighth row reads “7,” “load address,” “A,” and “R[d] <- M[addr].” The ninth row reads “8,” “load,” “A,” and “R[d] <- M[addr].” The tenth row reads “9,” “store,” “A,” and “M[addr] <- R[d].” The eleventh row reads “A,” “load indirect,” “RR,” and “R[d] <- M[R[t]].” The twelfth row reads “B,” “store indirect,” “RR,” and “M[R[t]] <- R[d].” The thirteenth row reads “C,” “branch zero,” “A,” and “if (R[d] == 0) PC <- addr.” The fourteenth row reads “D,” “branch positive,” “A,” and “if (R[d] > 0) PC <- addr.” The fifteenth row reads “E,” “jump register,” “-, “ and “PC<- R[d].” The sixteenth row reads “F,” “jump and link,” “A,” and “R[d] <- PC; PC <- addr.”

Arithmetic instructions

Opcodes 1 and 2 are arithmetic instructions, which invoke the ALU to perform an arithmetic operation on two registers (R[s] and R[t]), putting the result in a third register (R[d]). For example, the instruction 1234 means “add R[3] to R[4] and put the result in R[2]” and 2AAC means “subtract R[C] from R[A] and put the result in R[A].” These instructions might be said to implement TOY’s integer data type: the set of values is the 16-bit integers and the operations are add and subtract.

Memory address instructions

Opcodes 7, A, and B are memory address instructions, which we use to manipulate addresses in TOY. For example, the instruction 7423 means “set R[4] to the value 0023” or just R[4] = 0023 (note the leading 0s). Then opcodes A and B can be used to reference memory indirectly via the address in a register. Understanding these instructions is a helpful way to better understand references in Java. We will examine their use in more detail later when we look at implementing arrays and linked structures.

Another important use of opcode 7 is as an integer-data-type instruction: once the bits are loaded into the register, we can use them in an arithmetic instruction (interpret them as representing an integer). For example, we use the instruction 7C01 to set R[C] to 0001 (R[C] = 0001).

Logical instructions

Opcodes 3 through 6 are logical instructions, which invoke the ALU to perform operations on the bits in the registers, like the operations that we considered for Java in SECTION 5.1. Opcode 3 is “bitwise and,” where each bit in R[d] is set to 1 if the corresponding bits in R[s] and R[t] are both 1; otherwise, it is set to 0. Similarly, opcode 4 is “bitwise xor,” where each bit in R[d] is set to 1 if the corresponding bits in R[s] and R[t] are different; otherwise, it is set to 0. Opcode 5 leaves in R[d] the result of shifting the bits in R[s] left by the number of bit positions given in R[t], discarding the bits shifted out and shifting in 0 bits as needed. Opcode 6 is similar, but bits are shifted right and the bits shifted in match the sign bit (see the Q&A in SECTION 6.1). The logical instructions complete the implementation of TOY’s int data type in a manner that corresponds to Java. In TOY, as in Java, we sometimes bend data abstraction rules by treating the values just as sequences of 16 bits, rather than as integers. Shift and bitwise logical instructions are useful in implementing and decoding all types of data, just as in Java code.

Four types of instructions are listed. A section labeled “bitwise and” shows the "bitwise and" operation on the numbers 101000111010111 and 0011000101101110 that results in 0001000101000110. A section labeled "bitwise xor" shows the "bitwise xor" operation on the numbers 0101000111010111 and 0011000101101110 that results in 0110000010111001. A section labeled "shift left 6" shows the left shift operation of the numbers 0001000111010111 and 0000000000000110 that results in 0111010111000000. A section labeled "shift right 3 (arithmetic)" shows the right shift operation of the numbers 0000000111010111 and 0000000000000011 that results in 0001000000111010. Another right shift operation is shown on the numbers 1000000111010111 and 0000000000000011 that result in 1111000000111010.

Memory instructions

Opcodes 8 and 9 are memory instructions, which transfer data between memory and the registers. For example, the instruction 8234 means “load into R[2] the value of memory word M[34],” or R[2] = M[34] for short; and the instruction 9234 means “store into memory word M[34] the value of R[2],” or M[34] = R[2].

Flow of control instructions

Opcodes C through F are flow of control instructions, which modify the PC and are essential for implementing flow-of-control constructs like conditionals, loops, and functions that are fundamental in programming. For example, the instruction C212 means “set the PC to 12 if R[2] is 0” and D212 means “set the PC to 12 if R[2] is positive.” Note in particular that C0xx means “set the PC to xx,” since R[0] is always zero. This operation is known as an unconditional branch. Changing the value of the PC has the effect of changing the flow of control because the next instruction is always taken from the memory address given by the PC. We will examine opcodes E and F in more detail later when we look at implementing functions.

Your first reaction to this set of instructions might be that it is minimal at best. That is certainly true, but one of the goals of this chapter is to convince you that a small set of instructions like this suffices to write programs equivalent to the Java programs that you learned in the first half of this book, or any program. For the moment, the most important thing to remember is that you now have the information you need to decode any 16-bit value as a TOY instruction.

Your first TOY program

“Hello, World” for TOY is a program that adds two integers, shown in PROGRAM 6.2.1 on the opposite page. As with HelloWorld.java, in SECTION 1.1, we start with such a simple program to allow us to focus on the details of running the program. The code in PROGRAM 6.2.1, known as machine code, illustrates the various conventions that we use for TOY programs:

• All data and code relevant to a given program are included.

• Each line gives a 2-digit (hex) memory address and the 4-digit (hex) value of the word at that address.

• The starting value for the PC is always the address of the first instruction, highlighted in blue.

• The third column gives pseudo-code for each instruction.

The program itself is just the five 4-digit hex numbers stored in memory locations 10-14. The pseudo-code makes this program very easy to understand—it reads much like a Java program.

To trace a TOY program, we simply write down the PC and IR values for each instruction executed and the value of any affected register or memory word after execution. The table below the code gives such a trace for PROGRAM 6.2.1. To specify the result of the computation, we list the contents of memory when the halt instruction is reached, with the halt instruction itself and any memory locations whose values have changed highlighted in blue. In this case, only one memory value changes: location 17 gets the computed result 000D.

This process seems exceedingly simple, but we still have not described the process of actually getting the program to run. For Java, we were able to describe how you would use an editor to create a file containing the program, then use a compiler and the Java Virtual Machine to execute it and view the results in the terminal window. For TOY, you have to consider that there is no operating system, no applications, certainly no editor, terminal emulator, compiler, or runtime—not even a keyboard or a display.

Indeed, the picture at the bottom of the facing page shows the “result” of running PROGRAM 6.2.1: the lights at the bottom of the front panel of the computer display the computed result 000D, in binary—0000000000001101. Next, we consider, step by step, the process of getting this program to run on the TOY machine and to achieve this result.

---

Program 6.2.1 Your first TOY program

Click here to view code image

20:  8A15  R[A] <- M[15]           load first summand into a
11:  8B16  R[B] <- M[16]           load second summand into b
12:  1CAB  R[C] <- R[A] + R[B]     c = a + b
13:  9C17  M[17] <- R[C]           store result
14:  0000  halt

15:  0008  integer value 8₁₀
16:  0005  integer value 5₁₀
17:  0000  result

Started with the PC at 10, this program adds the two numbers at memory locations 15 and 16 and puts the result 000D in memory location 17.

---

The TOY machine consists of the LOAD, LOOK, RUN and ON/OFF options. Two boxes, representing ADDR, at the top have four switches and an LED light under each switch where the last switch in the first box and last three switches in the second box are in ON position. LED lights are illuminated wherever switches are in ON position. Four boxes, representing DATA, is present, where each box has four switches and an LED light below each switch. LED lights under the first, second, and fourth switches in the fourth box are illuminated. Binary result 0000 0000 0000 1101 and the hex result 0 0 0 D are present below the boxes of DATA.

Operating the machine

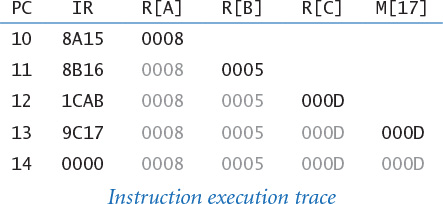
You communicate with your computer though I/O devices like the keyboard, display, and trackpad. TOY has I/O devices, too—in a sense. Next, we describe how programmers would communicate with machines like TOY, to actually run programs. At left is a depiction of the front panel of our imaginary TOY machine. It has just three simple devices for control, input, and output: pushbuttons, switches, and lights. All of them are simple on/off mechanisms, but there are very few of them: just 24 switches and lights and just 4 pushbuttons. Nothing else. No keyboard, printer, or display. No Internet connection, wireless card, speakers, or touchpad. Just buttons for control, switches for input, and lights for output. Still, this is enough to perform worthwhile computations with a general-purpose computer with the same basic characteristics as your own, as we now describe.

The TOY machine consists of the LOAD, LOOK, RUN and ON/OFF options. ADDR section in the machine contains two boxes with four switches and four LED lights each below it and DATA section in the machine contains four such boxes. A text “TOY, A COMPUTING MACHINE” on the machine at top right.

Pushbuttons

Perhaps the most basic control for a computer is to turn it on or off. The PDP-8 had a key for this purpose; TOY has a pushbutton. The first thing a programmer would do is to turn the machine on (and the last thing would be to turn it off). Additionally, three other basic functions are controlled by pushbuttons:

• Load a word into the computer’s memory.

• Look at the value of a word in the computer’s memory.

• Run a program.

We will discuss each of these functions in context shortly.

Switches

Programmers using such machines specify binary values with on/off switches. A switch in the up position denotes 1; a switch in the down position denotes 0. The TOY machine has two banks of switches: an 8-switch bank for specifying a location in the memory and a 16-switch bank for specifying a memory-word value. These switches are TOY’s input devices.

Lights

TOY’s output devices are the banks of lights under the switches. Again, an 8-light bank specifies a location in the memory and a 16-light bank specifies a memory-word value.

Running a program

To run a program on a machine such as TOY, a programmer would typically reserve time with the machine and show up at the appointed time with the program written down on a piece of paper. To fix ideas, we consider in full detail the steps needed to run our first program. For brevity, we “think in hex” by specifying hex values for switches and lights, when in reality each switch or light corresponds to a bit. For example, when we say “set the DATA switches to 1CAB” we mean “turn on the DATA switches corresponding to 1s in the bitstring 0001110010101011.” That said, here is how a programmer would implement and run PROGRAM 6.2.1:

• Turn on the machine (press the ON/OFF button).

• Set the ADDR switches to 10 and the DATA switches to 8A15, then press LOAD.

• Set the ADDR switches to 11 and the DATA switches to 8B16, then press LOAD.

• Set the ADDR switches to 12 and the DATA switches to 1CAB, then press LOAD.

• Set the ADDR switches to 13 and the DATA switches to 9C01, then press LOAD.

• Set the ADDR switches to 14 and the DATA switches to 0000, then press LOAD.

• Set the ADDR switches to 15 and the DATA switches to 0008, then press LOAD.

• Set the ADDR switches to 16 and the DATA switches to 0005, then press LOAD.

• Set the ADDR switches to 10, then press the RUN button.

• Set the ADDR switches to 17, then press the LOOK button.

• Write down the computed answer, shown in the DATA lights (000D).

• (Typically) repeat the previous five steps with other data values.

• Turn off the machine (press the ON/OFF button).

In summary, when we turn the machine on, we cannot assume anything about the values in the memory, registers, and PC (except that R[0] is 0000), so we need to load the program and the data (the seven steps after turning the machine on) before we can run the program. After running the program, we need to examine the memory location containing the result to learn the answer.

It is worthwhile to reflect on the truly fundamental nature of this interface. Essentially, programmers would communicate with the machine one bit at a time. Crude as this process was, people put up with it because developing programs was far superior to doing calculations with pencil and paper, slide rules, or mechanical calculators, the only other widely available alternatives at the time. We will soon see many examples where short programs yield computed values that would otherwise be very difficult to learn.

Better input/output devices such as keyboards, printers, paper tapes, and magnetic tapes soon followed, of course, but this method of programming was certainly a starting point for many scientists, engineers, and students (yes, this is how students at universities would learn to program in the early 1970s).

Conditionals and loops

To consider increasingly interesting TOY programs, we are following a similar approach to the one we used when you first learned programming, in CHAPTER 1. We have considered data types and basic operations in our description of machine instructions; now we move to control constructs.

The first control flow constructs that you learned in CHAPTER 1 were conditionals and loops. Accordingly, we next consider implementations of these constructs with TOY’s branch statements.

As an example, we consider Euclid’s algorithm for computing the greatest common divisor (gcd) of two positive integers a and b. We studied a version of this algorithm in SECTION 2.3 that is based on integer division (with remainder). Since TOY has no division instruction, we will start with the following version, implemented in Java:

Click here to view code image

public static int gcd(int a, int b)
{
    while (a != b)
        if (b > a) b = b - a;
        else       a = a - b;
    return a;
}

This code is based on a simple idea: if b is greater than a, any number that divides both a and b also divides both a and b - a (in particular, the gcd); and if a is greater than b, any number that divides both a and b also divides both b and a - b. When a and b are positive, each iteration of the loop decreases the larger of the two (but it stays positive), so the process must eventually end with a and b equal—to the gcd of all the numbers encountered, including the original a and b. A trace of the values of a and b for sample inputs is shown at right.

a	b
7215	6123
1092	6123
1092	5031
1092	3939
1092	2847
1092	1755
1092	663
429	663
429	234
195	234
195	39
156	39
117	39
78	39
39	39
Trace of Euclid’s algorithm

Euclid’s algorithm was first articulated more than 2,000 years ago, and many versions of it have been studied since. This particular version can sometimes be slow: for example, you may have noticed in the trace that 1,092 is subtracted six times before a becomes less than b. (Taking the remainder accomplishes the same task with one division.) If one of the numbers is very small, then the algorithm can take time proportional to the magnitude of the other. For example, the algorithm takes 7,214 iterations to find that the greatest common divisor of 7,215 and 7,214 is 1. Rest assured that versions of Euclid’s algorithm that are much more efficient than this have been studied in quite some detail, even for machines like TOY (see EXERCISE 6.2.19).

For the moment, we will concentrate on implementing the code in the body of this function, assuming that the programmer will enter the input data in specified memory locations, as in PROGRAM 6.2.1. In the next section, we will discuss how to package the code as a function.

The key to the implementation is effective use of TOY’s branch statements to implement loops and conditionals, as illustrated by the diagrams on this page.

A Java code at the top states “while (<expression>) <statements>” and the flowchart below it starts with a flow reading “is <expression> false?” If yes, it leads to the TOY code below. If no, the arrow points to another flow that says “<statements>” which reverts back to the previous flow. The TOY code at the bottom has “yy:” at the left of a box which reads “code for <expression> leaving 0 in R[1] iff false” followed by C1xx with an arrow pointing to it from the text “branch to xx if R[1] is 0.” Another box below reads “code for <statements>” followed by the text C0yy below with an arrow pointing toward it from the text “branch to yy” with the text “xx:” below the box.

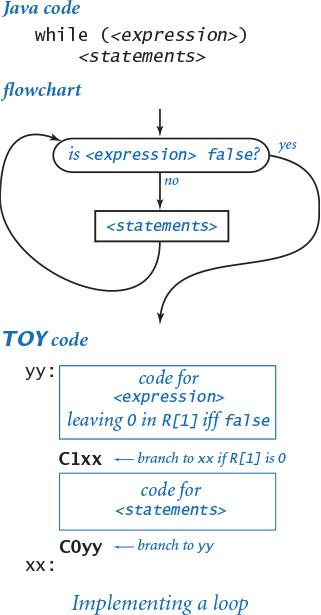
To implement a while loop (diagram at right), we put the code that computes the value of the expression starting at some memory location yy and implement the loop with the instruction C0yy, an unconditional branch to yy. Within the loop, we put the code for evaluating the expression, arranging that it leave zero in some register (say R[1]) if and only if the value is false. Then we use the conditional branch C0xx to transfer control to the instruction after the loop (at address xx) if the register is zero. The implementation of an if statement, illustrated at left, is similar.

A java code reads “if (<expression>) <statements for true> else <statements for false>" followed by a flowchart where the first flow reads “is <expression> false?” If yes, an arrow points to another flow that reads “<statements for false>." If no, it redirects to “<statements for true>.” A flow line points out from the statements for true and false. The TOY code is stated in a box at the bottom which reads “code for <expression> leaving 0 in R[1] iff false” followed by Clyy with an arrow pointing to it from the text “branch to yy if R[1] is 0." Another box right below reads “code for <statements for true>” followed by C0zz with an arrow pointing towards it from the text “branch to zz.” Another box below it says “code for <statements for false>” which has “yy:” to its left and “zz:” below it.

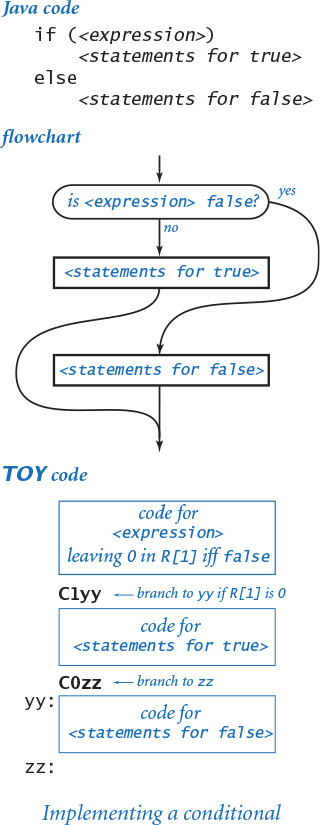
From these constructions, it is clear that any loop or conditional in a Java program can be directly implemented in a TOY program. Each line of Java code corresponds to just a few TOY branches. As further evidence, several of the exercises at the end of this section address implementations of Java programs that you learned early in this book. As with Java, conditionals and loops take us from a world of programming where we execute only a few instructions to one where we can execute thousands or millions of instructions, or more.

With TOY programs, we are not even limited to these ways of implementing conditionals and loops. For example, the implementation in PROGRAM 6.2.2 actually happens to evaluate just one conditional expression for both the while loop and the if statement. Indeed, programmers can use branch instructions to set up flow-of-control structures in TOY that cannot be naturally expressed with conditionals and loops. It took many years for people to become comfortable with the idea that it is best to use just the few building blocks (conditionals, loops, and nesting) that we use in modern programming. For clarity, we take a middle-of-the road approach in this book, where we are guided by the constructs just considered (and we use Java-like code as documentation), but we take shortcuts that simplify the code when appropriate.

Thus, a programmer could use the switches to enter PROGRAM 6.2.2 and its data in memory locations 20 through 2D, then set the address switches to 20, press RUN, and observe the result in the lights by examining location 2D. The program computes the gcd of 195 and 273, which is 39. The programmer could run the program as often as desired, entering new pairs of numbers in 2B and 2C, resetting the address switches to 20, pressing RUN, and observing the result in 2D.

Following the trace is a worthwhile way to develop more comfort with TOY programming. First, the program loads 195 (00C3) into R[A] and 273 (0111) into R[B]. Then it subtracts them, putting the result –78 (FFC3) into R[C]. Since this value is not zero, it enters the loop, and then tests whether the difference is negative or positive. Since it is negative, it subtracts R[A] from R[B], leaving 78 (004E) in R[B], and then goes back for another iteration of the loop. In the next iteration of the loop, it subtracts R[B] from R[A], leaving 117 (0075) in R[A]. Then it subtracts R[B] from R[A] again, leaving 39 (0027) in R[A]. The last iteration of the loop subtracts R[A] from R[B], leaving the result 39 (0027) in both registers.

This is a classic computation, and we can imagine the excitement experienced by early programmers upon realizing that such computations could so easily be relegated to the computer. Would anyone rather perform such computations by hand? The ability to quickly implement algorithms like this appealed to the mathematicians and scientists who became early programmers, stimulated the search for faster algorithms, and unleashed research into developing efficient algorithms that continues to this day.

---

Program 6.2.2 Conditionals and loops: Euclid’s algorithm

Click here to view code image

20:  8A2B  R[A] <- M[2B]             a = p
21:  8B2C  R[B] <- M[2C]             b = q
22:  2CAB  R[C] <- R[A] - R[B]       while (a != b)
23:  CC29  if (R[C] == 0) PC <- 29   {
24:  DC27  if (R[C]  > 0) PC <- 27      if (b > a)
25:  2BBA  R[B] <- R[B] - R[A]             b = b - a
26:  C022  PC <- 22                     else
27:  2AAB  R[A] <- R[A] - R[B]             a = a - b
28:  C022  PC <- 22                  }
29:  9A2D  return a (= b = GCD)      return a
2A:  0000  halt

2B:  00C3  integer value 195₁₀        p
2C:  0111  integer value 273₁₀        q
2D:  0000  result

Started with the PC at 20, this program finds the greatest common divisor of the two numbers at memory locations 2B and 2C and puts the result in memory location 2D.

---

The TOY machine with LOAD, LOOK, RUN and ON/OFF options at the top has LOAD and RUN selected. There are two boxes, representing ADDR, right below it with four switches and LED lights on each box where the third slider from the left on the first box is switched on and all switches except the third from the left of the second box are switched on. LED lights are illuminated wherever switches are in ON position. Four similar boxes with switches and LEDs, representing DATA, are present, where LED lights are illuminated under the third switch on the third box and on the second, third, and fourth switches on the fourth box. Binary result 0000 0000 0010 0111 and the hex result 0 0 2 7 are present below the boxes of DATA.

Stored-program computing

One of the essential characteristics of the TOY machine is that it stores computer programs as numbers, and both data and programs are stored in the same main memory. This is a profound idea with a fascinating history that is crucial to understanding the basic nature of computation.

Instructions as data and data as instructions

As an illustration of the fundamental idea, consider PROGRAM 6.2.3, which adds a sequence of numbers. The sequence could be of any length, terminated by 0000. A trace of the operation of this program is shown at right, and is worthy of careful study (R[1] and M[1B] are omitted from the trace because each of their values changes only once). The computation starts out in a manner similar to PROGRAM 6.2.1, but then does something quite different. After adding the first two numbers, and leaving the result in R[A], the program loads the instruction 8B1D at location 12 into R[D], adds 1 to it, then stores the result 8B1E back into location 12. Then, it branches back to location 12, where that instruction loads into R[B] the next number to be added to R[A], continuing in a loop until it encounters 0000 in the data.

Such code is known as self-modifying code. We have included this program because it succinctly illustrates the fundamental concept of stored-program computing. Is the content of memory location 12 an instruction or data? It is both! When we add 1 to it, it is data, but when the PC refers to it and it is loaded into the IR, it is an instruction. Since the program and data share the same memory, the machine can modify its data or the program itself while it is executing. That is, code and data are the same, or at least they can be. The memory is interpreted as an instruction when the program counter references it, and as data when an instruction references it.

Self-modifying code liked this is rarely used in modern computing because it is difficult to understand, debug, and maintain. We will consider an alternative method of adding a sequence of numbers in the next section. But the ability to process instructions as data is fundamental in computing, as discussed next and throughout the rest of this chapter.

Some implications

On reflection, you can see that the ability to treat the program as data is crucial and essential in our modern computational infrastructure:

• Any application is treated as data while you are downloading or installing it, but as a program once you launch it.

• Compilers are programs that read in other programs as input data and produce machine-language programs as output data, so all programming languages depend on this capability.

• Modern cloud computing is based on the concept of a virtual machine, where one computer runs a program written for another computer. Indeed, TOY itself is a virtual machine, as you will see in SECTION 6.4.

---

Program 6.2.3 Self-modifying code: Compute a sum

Click here to view code image

10:  7101  R[1] <- 0001
11:  8A1C  R[A] <- M[1C]          load first number into a
12:  8B1D  R[B] <- M[1D]          while (b != 0)
13:  CB19  if (R[B]==0) PC <- 19  {
14:  1AAB  R[A] <- R[A] + R[B]        a = a + b
15:  8D12  R[D] <- M[12]              modify instruction at M[12]
16:  1D1D  R[D] <- R[D] + 1             to load next number into
17:  9D12  M[12] <- R[D]                b on next iteration
18:  C012  PC <- 12               }
19:  9A1B  store result
1A:  0000  halt

1B:  0000  result
1C:  0001  data
1D:  0008  integer value  8₁₀
1E:  001B  integer value 27₁₀
1F:  0040  integer value 64₁₀
20:  0000

Started with the PC at 10, this program adds the sequence of numbers at memory locations 1C through 1F (terminated by 0000) and stores the result in memory location 1B.

---

The TOY machine has LOAD, LOOK, RUN, and ON/OFF buttons at the top with LOAD and RUN selected. Two boxes, representing ADDR, at the top have four switches and an LED light under each switch where the third switch from the left in the first box is upward and all switches except the third switch from the left are upward in the second box. LED lights are lit wherever switches are placed upward. Four boxes, representing DATA, is present, where each box has four switches and an LED light below each switch. LED lights are lit under the third switch on the third box and under last three switches on the fourth box. Binary result 0000 0000 0010 0111 and the hex result 0 0 2 7 are present below the boxes of DATA.

These are but a few examples, and we will be revisiting this concept throughout this chapter.

Treating programs as data is not without its perils. For example, computer viruses are (malicious) programs that propagate by writing new programs or modifying existing ones. And, as we saw in CHAPTER 5, it is a consequence of Turing’s theory that there is no effective way in general to tell the difference between a malicious virus, a useful application, or data. This practical downside is an inescapable consequence of the stored-program model. We will examine a specific example in the context of our TOY machine in the next section.

Von Neumann machines

As already mentioned, by the 1940s and 1950s scientists and engineers were performing extensive calculations, not just for wartime applications such as ballistics, atomic weapons and cryptography, but also for peacetime applications like space flight and meteorology. The idea that electronic components could be much faster than mechanical ones was a powerful one.

Many early computers, however, emulated mechanical calculators. Operators had to “program” the computer by plugging cables and setting banks of switches, which was tedious, time-consuming, and error-prone. Any memory was devoted to data. One such machine was the ENIAC, being developed in the mid-1940s at the University of Pennsylvania by Eckert and Mauchly.

At the same time (actually a bit earlier, in the 1930s) there was great excitement in the field of mathematics because Alan Turing had developed the ingenious theoretical constructs that we just considered in CHAPTER 5. Turing’s work provided deep insights into the true nature of computation.

Princeton scholar John von Neumann worked as a consultant with Eckert and Mauchly on the ENIAC project and its planned successor, the EDVAC. He was interested both in the ballistics calculations that were the primary purpose of the machine and in the extensive calculations that were needed for the development of the atom bomb.

In 1945, while on a train from Princeton to Los Alamos, von Neumann wrote up his report on planned improvements to ENIAC. This memo, First Draft of a Report on the EDVAC, is a complete description of the stored-program model of computing. Since von Neumann was a professor at Princeton while Turing was a graduate student there, he certainly was influenced by Turing’s ideas, and he was in a unique position to bridge the gap between Turing’s theories and the practical challenges faced by Eckert and Mauchly. Soon after von Neumann’s arrival at Los Alamos, a young lieutenant named Herman Goldstine recognized that there would be intense interest in the idea, and he circulated the memo widely. Scientists around the world immediately saw the value of the stored-program model, and computers based on the model (virtually all computers) have been called von Neumann machines ever since. Many historians believe that Eckert and Mauchly deserve credit for the idea (as did Turing!), but von Neumann’s memo was certainly the spark that made it happen around the world.

The stored-program model enables computers to perform any type of computation, without requiring the user to physically alter or reconfigure the hardware. This simple but fundamental model has been used in virtually every computer since von Neumann first articulated it.

In hindsight, the von Neumann architecture may seem obvious. However, plenty of research groups were working in a different direction at the time, and the question of whether a computer built around a stored program model can be as powerful as a computer that can be rewired and reconfigured was debated. In fact, Turing’s theory shows that the ability to physically reconfigure a computer does not enable it to solve more problems, so long as the basic instruction set is rich enough (as is the case even with our TOY machine). Other than Turing himself, von Neumann was one of the few people in the world in a position to appreciate this point. His ability to fully articulate the idea in a practical context on a long train ride was a serendipitous development that profoundly changed the world.

Q&A

Q. Did programmers really flip switches to enter programs?

A. Yes. Many, many people learned this skill. Even when better input/output devices became available, it was necessary to enter a program through switches that could drive one of the devices.

Q. What’s the difference between a register and a memory word?

A. Both store 16-bit integers, but they play different roles within the computer. The purpose of the memory is to hold programs and data—we want the memory to be as large as possible. The purpose of the registers is to provide an intermediate staging ground to get data to and from the ALU—only a limited number of registers are really needed. Typically, computers use more expensive technology for registers because they are involved in virtually every instruction. The number of registers in a computer is a design decision.

Q. Are special-purpose computers or microprocessors still fabricated today?

A. Yes, because it is possible to do simple things faster in hardware than in software.

Q. It’s hard to imagine programming without thinking in terms of loops and conditionals. Did people really work that way?

A. Most certainly. Programmers designed their logic with flowcharts, and early high-level languages had a “goto” statement that translated to a machine-language branch. The idea of “structured programming” using just loops, conditionals, and functions emerged in academia but was not taken seriously by many programmers until the 1970s. One famous turning point was a letter to the editor of the Communications of the ACM by E. W. Dijkstra in 1968, entitled “Goto considered harmful.” In this letter he argued for the “goto” statement to be abolished in all higher-level programming languages because programs that use it are too difficult to understand, debug, and maintain. This point of view was universally embraced within a decade, and structured programming has been taken for granted since.

Exercises

6.2.1 How many bits of memory does TOY have? Include all registers (including the PC) and main memory.

6.2.2 TOY uses 8-bit memory addresses, which means that it is possible to access 256 words of memory. How many words of memory can we address with 32-bit addresses? 64-bit addresses?

6.2.3 Suppose that we want to use the same instruction format as TOY, but with 32-bit addresses. What word size would we need? Describe a problem with this design.

6.2.4 Give a single instruction that changes the program counter to memory address 15 regardless of the contents of any registers or memory cells.

Solution. C015 or F015. Both instructions rely on the fact that R[0] is always 0000.

6.2.5 List seven instructions (all having different opcodes) that put 0000 into register A.

Solution. 1A00, 2Axx, 3A0x, 4Axx, 5A0x, 6A0x, 7A00, where x is any hex digit.

6.2.6 List three ways (different opcodes) to set the program counter to 00 without changing the contents of any register or memory cell.

Solution. C000, E0xy, F000.

6.2.7 List five instructions (all having different opcodes) that are no-ops. Exclude cases where the second digit is 0.

Solution. 1xx0, 1x0x, 2xx0, 3xxx, 5xx0, 6xx0, or D0xx, where x is any hex digit other than 0.

6.2.8 List six ways to assign the contents of R[B] into R[A].

Solution. 1AB0, 1A0B, 2AB0, 3ABB, 4A0B, 4AB0, 5AB0, and 6AB0.

6.2.9 There is no branch if non-negative operator in TOY. Explain how to jump to memory address 15 if R[A] is greater than or equal to 0.

Solution. Use branch if positive and branch if zero, one after the other: CA15 DA15.

6.2.10 Fill in the blanks in this table:

6.2.11 There is no absolute value function in TOY. Give a sequence of TOY instructions that sets R[d] to the absolute value of R[s].

6.2.12 There is no bitwise NOR operator in TOY. Give a sequence of three TOY instructions that sets each bit of Rd to 1 if and only if either or both of the corresponding bits in R[s] and R[t] are 0.

6.2.13 There is no bitwise OR operator in TOY. Give a sequence of three TOY instructions that sets each bit of R[d] to 0 if and only if either or both of the corresponding bits in R[s] and R[t] are 1.

Solution. 3DAB 4EAB 1CDE.

6.2.14 There is no bitwise NAND operator in TOY. Give a sequence of three TOY instructions that sets each bit of R[d] to 0 if and only if both of the corresponding bits in R[s] and R[t] are 1.

6.2.15 There is no bitwise NOT operator in TOY. Give a sequence of three TOY instructions that sets each bit of R[d] to the opposite of the corresponding bit value in R[s].

Solution. 7101 2B01 4BAB or 7101 2B01 2BBA.

6.2.16 Show that the subtract operator is redundant. That is, explain how to compute Rd = Rs - Rt by using a sequence of TOY instructions that do not involve opcode 2.

6.2.17 Which of the 16 TOY instructions do not use all 16 bits?

Solution. Halt (only uses first 4 bits), load indirect (does not use third hex digit), store indirect (does not use third hex digit), jump register (does not use two hex digits).

6.2.18 We interpret some TOY integers to be negative according to two’s complement notation. What are the only instructions for which this matters?

Solution. The branch positive instruction treats integers between 0001 and 7FFF as positive. The right shift instruction is an arithmetic shift so that if the leftmost bit is 1, then vacated positions are filled with 1s. All other instructions (even subtract!) do not depend on whether TOY has negative integers.

6.2.19 Improve the TOY function for computing the gcd given in the text by including a variable c initialized at 0 and modifying the while loop as follows:

• If a and b are even, gcd(a, b) = 2 gcd(a / 2, b / 2), so divide both a and b by 2 and increment c by 1.

• If a is even and b is odd, gcd(a, b) = gcd(a / 2, b) so divide a by 2.

• If a is odd and b is even, divide b by 2 (same reasoning).

• Otherwise, both a and b are odd, so proceed as before (replacing the larger by their difference, which, by the way, is even).

At the end, shift the result left by c positions to account for the factors of 2 cast out. Include a client that reads in two integers from standard input and punches their greatest common divisor to standard output. (Analysis beyond the scope of this book shows that the worst-case running time of this algorithm is quadratic in the number of bits in the numbers—much faster than the version given in the text.)