We now prove

THEOREM 9.19.   Let R be a compact open subring of D such that (31) holds for P the radical of R. Then R is a valuation ring in the sense that if a ∈ D, R, then a^–1 ∈ R. R is a maximal compact open subring of D and is the only subring having these properties.

Proof.   If a R, there exists a b₁ ∈ P such that ab₁ P. If ab₁ R, we repeat the process. Eventually we obtain n elements b_i ∈ P such that ab₁ … b_n ∈ R, P. Otherwise, we get an infinite sequence {b_k} ⊂ P such that ab₁ … b_k R. On the other hand, {Pⁿ} is a base for the neighborhoods of 0, so lim b₁ … b_k = 0, which implies that lim ab₁ … b_k = 0. This contradicts ab₁ … b_k R for all k. Thus we have an n such that ab₁ … b_n ∈ R, P. Then ab₁…b_n = u is a unit in R and a^–1 = b₁ … b_nu^–1 ∈ P ⊂ R. Hence R is a valuation ring in D. We have shown also that if a R, then a^–1 ∈ P, and since bⁿ → 0 for every b ∈ P, aⁿ → ∞ if a R. If u ∈ R, P, we have uⁿ ∞ and u^–n 0. In fact, since R – P is a compact set, every sequence of powers {u^n_k} contains a convergent subsequence with limit in R – P and hence ≠ 0. It is clear from these results on powers that P = {b ∈ D|bⁿ → 0}, R = {a ∈ D|aⁿ ∞}, D – R = {a ∈ D|aⁿ → ∞}. If R′ is any compact open subring of D, then R′ ∩(D – R) = ϕ so R′ ⊂ R. This shows that R is maximal and it is the only maximal compact open subring of D.

We can use the valuation ring R to define an absolute value on D (defined as for fields). We have Pⁿ = 0. Hence given any a ≠ 0 in R, there exists a k ≥ 0 such that a ∈ P^k, a P^{k + 1} where we put P⁰ = R. Then we define v(a) = k. If a R, then a^–1 ∈ P and we define v(a) = –v(a^–1). Also we define v(0) = ∞ and |a| = c^v(a) where c is a fixed real number such that 0 < c < 1. Then we have

THEOREM 9.20. | | is a non-archimedean absolute value on D: |a| ≥ 0, |a| = 0 if and only if a = 0, |a + b| ≤ max(|a|, |b|), |ab| = |a| | b|.

Proof. It suffices to prove the corresponding statements on the map v from D into , namely, v(a) = ∞ if and only if a = 0, v(a + b) ≥ min (v(a),v(b)), v(ab) = v(a) + v(b). The first is clear from the definition of v. Let a,b ∈ D satisfy v(a) = v(b) = k ≥ 0. If ab^–1 ∈ P, a ∈ Pb ⊂ P^{k + 1} contrary to v(a) = k. Hence ab^–1 P and similarly ba^–1 P. Then ab^–1 ∈ R – P and v(ab^–1) = 0. If v(a) = v(b) = k < 0, then v(a^–1) = v(b^–1) = –k > 0 and again v(ab^–1) = 0. Now choose π ∈ P, P². Then π^k ∈ P^k for k > 0, so v(π^k) ≥ k. If v(π^k) = l > k, then where b_i^(j) ∈ P and every b₁^(j) P², so v(b₁^(j)) = 1 = v(π). Then and π^–1b₁^(j) ∈ R – P. Hence v(π^{k – 1}) > k – 1. This leads to the contradiction that v(π) > 1. Thus v(π^k) = k. This and our earlier result show that if v(a) = k ≠ ∞, then there exists a u ∈ R – P such that a = uπ^k. We observe next that the characterization of the sets P, R – P, and D – R by the properties of the power sequences of the elements in these sets shows that these sets are stabilized by inner automorphisms of D. Now let a ≠ 0, b ≠ 0, and let v(a) = k, v(b) = l ≥ k. Then a = uπ^k, b = vπ^l where u and v are units in R. We have a + b = (u + vπ^{l – k})π^k and u + vπ^{l – k} ∈ R, so v(a + b) ≥k = min(v(a),v(b)). We have ab = uπ^kvπ^l = uv′π^{k + 1} where v′ = π^kvπ^–k ∈ R – P. If k + l > 0, we have seen that π^{k + 1} ∈ P^{k + 1} P^{k + l + 1}. Then the same relations hold for ab, so v(ab) = k + l = v(a) + v(b). This is clear also if k + l = 0. On the other hand, if k + l < 0, then (ab)^–1 = b^–1a^–1 = π^{–(k + l)}w with W ∈ R – P. Then v((ab)^–1)= –(k + l) and again v(ab) = k + l = v(a) + v(b). Hence in all cases v(ab) = v(a) + v(b). We therefore have v(a + b) ≥ min(v(a) v(b)) and v(ab) = v(a) + v(b) if a ≠ 0 and b ≠ 0. These relations are evident if either a = 0 or b = 0. Hence we have the required relations for all a, b.

The definition of | | shows that the spherical neighborhood of 0 defined by |a| ≤c^k, k ≥ 0, is P^k. Hence it is clear that the topology defined by the valuation is the same as the given topology on D. It follows also that D is complete relative to | |.

Let F be a closed subfield of D such that P_F = P ∩ F ≠ 0. Then the absolute value | | is non-trivial on F and F is complete. Moreover, if R_F = R ∩ F, then R_F/P_F is isomorphic to a subfield of R/P. Hence R_F/P_F is finite and F is a local field. Then the results of section 9.12 are available.

Let p be the characteristic of = R/P. Then || = q = p^m for m ≥ 1. Let ζ₀ be an element of R such that ₀ = ζ₀ + P is a primitive (q – 1)-st root of 1. We shall now show that R contains an element ζ such that ζ^{q – 1} = 1 and = ₀. Then ζ will be a primitive (q – 1)-st root of unity in R. Now ζ₀^{q – 1} – 1 ∈ P and if ζ₀^{q – 1} = 1, we can take ζ = ζ₀. Otherwise, let F be the closure in D of C(ζ₀) where C is the center of D. Then P_F = P ∩ F contains ζ₀^{q – 1} – 1 ≠, so P_F ≠ 0, and if R_F = F ∩ R, then _F = R_F/P_F contains ζ₀ + P_F and this is a primitive (q – 1)-st root of unity. The results of the previous section show that R_F contains an element ζ such that ζ^{q – 1} = 1 and ζ + P_F= ζ₀ + P_F. Then = ₀.

We have seen that R and P are stabilized by the inner automorphisms of D. Hence any inner automorphism determines an automorphism of = R/P. In particular, if π ∈ P – P², then we have the automorphism

of = R/P. Since || = q = p^m, this has the form

On the other hand, if u ∈ R – P, then and . Hence the corresponding automorphism in is the identity. Since π is determined up to a multiplier in R – P by the condition that π ∈ P – P², it is clear that is independent of the choice of π in P – P².

We shall now show that π can be chosen so that

Let G = <ζ>, the subgroup of D* generated by ζ. Then if π₀ ∈ P – P² and λ ∈ G, then and hence and . Then

satisfies μ^–sπμ = π for μ ∈G. Moreover, π ≡ (q – 1)π₀ (mod P²) and since q1 ∈ P,π ≡ – π₀ (mod P²) and hence π ∈ P – P². Then μ^–sπμ = π gives πμπ^–1 = μ^s for μ ∈ G, so in particular we have (34).

The inner automorphism a πaπ^–1 stabilizes G and induces the automorphism in . Since λ is an isomorphism of G onto the multiplicative group *, it is clear that the order of the restriction of a πaπ^–1 to G is the order r of . Then π^r commutes with every λ ∈ G and this is the smallest power of π with this property.

The proof given on pp. 571–572 shows that every element of D has a representation as a power series in π with coefficients in K = {0} ∪ G. Thus we can show that any non-zero element of D can be written in one and only one way as a series

where the λ_i ∈ K, λ₀ ≡ 0, and k ≥ 1. It is clear from this that an element a is in the center if and only if it commutes with π and with every λ ∈ G. It follows that the center C is the set of elements

where the μ_i are elements of K such that μ_i^s = μ_i. Evidently C ≠ P ≡ 0 and C is a local field. The extension field W = C(ζ) is stabilized by the inner automorphism determined by π. If σ is the induced automorphism in W/C, then C is the set of elements fixed under σ. Hence W/C is cyclic with Galois group <σ>. It is clear also that σ has order r. Hence [W : C] = r. Since W is the set of elements

where the λ_i ∈ R, it is clear that the ramification index of W over C is 1, so W is an unramified extension of C. Comparison of (36) and (38) shows that every element of D can be written in one and only one way in the form

where the w_i ∈ W. The multiplication in D is determined by that in W and the following relations for w ∈ W:

Thus D is a cyclic algebra D = (W, σ, π^r) and [D: C] = r². We have therefore obtained the following structure theorem for totally disconnected locally compact division rings.

THEOREM 9.21.   Let D be a totally disconnected locally compact division ring. Then the center C of D is a local field and D is a cyclic algebra D =(W, σ, γ) over C where W is unramified and γ is a generator of the maximal ideal P_c of the valuation ring of C.

Of course, this shows that D is a finite dimensional algebra over a local field. We have seen also that a local field is either a Laurent series field over a finite field or a finite dimensional extension field of a field of p-adic numbers (Theorem 9.16, p. 597). Hence D is either a finite dimensional division algebra over a field of formal Laurent series F₀((x)), F₀ finite, or a finite dimensional division algebra over some p-adic field _p. The first case holds if and only if the characteristic of D is a prime. We have seen also that the topology is given by the absolute value | | defined by the unique maximal compact and open subring R of D. It is easily seen that this topology is the same as the product topology obtained by regarding D as a product of a finite number of copies of F₀((x)) or of _p.

It is not difficult to prove the following converse of Theorem 9.21. Let D be a finite dimensional division algebra over F₀((x)) or _p. Then we can introduce a topology in D so that D becomes a non-discrete totally disconnected locally compact division ring. We sketch the argument. Let F = F₀((x)) or _p. We have the topology on F given by an absolute value defined as before and the valuation ring R and the maximal ideal P (R = F₀[[x]] in the first case and the ring of p-adic integers in the second). Now R can be regarded as the inverse limit of the set of finite rings R/P^k (see p. 73) and its topology can be identified with the topology of the inverse limit of finite sets. Hence R is compact and totally disconnected. It follows that F is locally compact totally disconnected and not discrete. The fact that the map x x^–1 of F* into itself is continuous can be proved as in the case of the field .

Now let A be a finite dimensional algebra over F and endow A with the product topology. Then A is locally compact totally disconnected and not discrete. It is readily seen that A is a topological ring. Let N(a) denote the determinant of the matrix ρ(a) in a regular representation of A. Then a N(a) is a continuous map of A into F, and the set U of invertible elements of A is the open subset defined by N(u) ≠ 0. It is easy to see that u u^–1 is a continuous map of U into U. In the special case in which A = D is a division algebra over F, U = D* and A is a topological division ring in the sense defined at the outset.

9.14   THE BRAUER GROUP OF A LOCAL FIELD

We shall now apply Theorem 9.21, the remarks following it, and the results on cyclic algebras given in section 8.5 (p. 484) to determine the Brauer group Br(F) of a local field F. We recall that if E is a cyclic extension of a field F, then the subgroup Br(F, E) of the Brauer group of F consisting of the classes of finite dimensional central simple algebras A having E as splitting field is isomorphic to F*/N(E*) where N(E*) is the group of norms N_E/F(a) of the non-zero elements a ∈ E. The isomorphism is implemented by choosing a generator s of G = Gal E/F and defining the cyclic algebra (E, s, γ), γ ∈ F*. Then the map γ(N(E*)) [(E,s,γ)], the similarity class of (E,s,γ), is an isomorphism of F*/N(E*) onto Br(E/F). Let K be a subfield of E/F and let be the restriction of s to K. Then is a generator of the Galois group of K/F. The order of is [K : F] = r and we have n = rm where m = [E : K]. Any central simple algebra split by K is split by E and we have the monomorphism of Br(K/F) into Br(E/F) sending the class of (K,,γ) into that of (E, s, γ^m) (p. 485).

Now let F be a local field. We determine first the group F*/N(W*) where W is an unramified extension of F. We shall need the following result.

LEMMA.   Let F_q be a finite field with q elements, F_qⁿ an extension field with qⁿ elements. Then any a ∈ F*_q is a norm of an element b ∈ F*_qⁿ that is not contained in any proper subfield of F_qⁿ.

Proof.   The automorphism x x^q generates the Galois group of F_qⁿ/F_q. Hence the norm map of F*_qⁿ is

The kernel of this map is the set of elements such that N_{Fqⁿ Fq}(x) = 1 and this has order (qⁿ– 1)/(q – 1). Hence the image has order q – 1. Since the image is contained in F*_q, which has order q – 1, it is clear that the norm map of F*_qⁿ is surjective on F*_q. Moreover, for any a ∈ F*_q there exist (qⁿ – 1)/(q – 1) elements b such that N_Fqⁿ/Fq(b) = a. On the other hand, the elements b contained in proper subfields of F_qⁿ are contained in maximal proper subfields. The cardinality of any of these is of the form q^m where m is a maximal proper divisor of n, and distinct subfields have distinct orders. It follows that the number of non-zero elements contained in proper subfields does not exceed (q^m – 1) where the summation is taken over the maximum proper divisors m of n. Evidently this number is < (qⁿ – 1)/(q – 1) = 1 + q + … + q^{n – 1}. Hence we have a b ∈ F_qⁿ not in any proper subfield such that N_{Fqⁿ/ Fq}(b) = a.

The requirement that b is not contained in any proper subfield of F_qⁿ is equivalent to F_q(b) = F_qⁿ. This occurs if and only if the degree of the minimum polynomial of b over F_q is n. We can now prove

PROPOSITION 9.8.   Let W be an unramified extension field of the local field F, R_F the valuation ring of F, P_F its ideal of non-units. Then any element u ∈ R_F – P_F is a norm in W.

Proof.   Let _F be the residue field R_F/P_F and similarly let _w = R_w/P_w where R_w is the valuation ring of W, P_w its ideal of non-units. Since W is unramified, we have [_w : _F] = n = [W: F]. By the lemma, if a = = u + P_F, then there exists a b ∈ _w such that the minimum polynomial of b over _F has degree n and . If σ ∈ Gal W/F, then the map , x ∈ R_w, is in Gal _W/_F and is an isomorphism between these Galois groups. Hence for any v ∈ R_w we have , so if we choose v ∈ R_w such that = b, then . We can choose a monic polynomial f(x)∈ R_F[x] of degree n such that is the minimum polynomial of = b. Since deg = n, this is the characteristic polynomial of b (in a regular representation) and its constant term is Hence we may assume that the constant term of f(x) is (–1)ⁿu. Since is a separable polynomial, we can apply Hensel’s lemma to conclude that there exists a v ∈ R_w such that f(v) = 0. Since is irreducible in _F, f(x) is irreducible in F[x] and so this is the minimum polynomial over F of v. Since its degree is n, it is also the characteristic polynomial. Hence its constant term (–1) ⁿu = (–1)ⁿN_w/F(v). Then u = N_w/F(v) as required.

Since W is unramified over F, we can choose π ∈ F such that π ∈ P_w – (P_w)². Then any w ∈ W has the form uπ^k where u ∈ R_w – P_w and k ∈ . Then and N_W/F(u) ∈ R_F – P_F. Conversely, if v = uπ^kn where u ∈ R_F – P_F, then π^kn = N_W/F(π^k) and Proposition 9.8 shows that u is a norm. Hence v is a norm. It is clear from these results that F*/N(W*) is a cyclic group of order n with generator πN(W*). Then Br(W/F) is a cyclic group of order n. We can obtain an isomorphism between F*/N(W*) and Br(W/F) by mapping the coset π^kN(W*), 0 ≤ k ≤ n – 1, onto the class of central simple algebras over F determined by the cyclic algebra (W, σ, π^k) where σ is the Frobenius automorphism of W/F.

We can combine this result with the results of the previous section to obtain a determination of Br(F), namely, we have

THEOREM 9.22 (Hasse).   The Brauer group of a local field is isomorphic to the additive group of rational numbers modulo 1 (that is, /).

Proof.   We have seen that any finite dimensional central division algebra D over the local field F is a totally disconnected locally compact division ring. Hence Theorem 9.21 shows that D has an unramified (hence cyclic) extension field W/F as splitting field. It follows that any class [A] in Br(F) is contained in Br(W/F) for some W. Then A ~ (W, σ, π^k) where σ is the Frobenius automorphism and 0 ≤ k < n = [W : F]. Once W has been chosen, then k is uniquely determined. We now map [A] into the rational number r = k/n. We wish to show that the rational number thus determined is independent of the choice of the splitting field. It is readily seen by using the results of section 9.12 that for any positive integer n there exists a unique (up to isomorphism) unramified extension W/F with [W : F] = n. Moreover, if W′/F is unramified and [W′ : F] = m, then W′ ⊂ W is isomorphic to a subfield of W if and only if m|n. It follows that it suffices to show that if W′ ⊂ W is a splitting field for A, then the rational number determined by W′ is the same as that determined by W. Now the restriction of the Frobenius automorphism σ of W/F is the Frobenius automorphism of W′/F. Hence A ~ (W′, , π^l) where 0 ≤ l < m and so the rational number determined by A and W′ is l/m. Since (W′, , π^l) ~ (W, π, π^ln/m) = (W, σ, π^k), we have ln/m = k and k/n = l/m. It is clear also that our map is surjective on rational numbers satisfying 0 ≤ r < 1. For r = k/n with 0 ≤ k < n and if we take W to be the unramified extension of degree n over F, then the cyclic algebra (W, σ, π^k) is central simple with W as splitting field and this maps into r = k/n. If we have two central simple algebras A and B over F, we can choose an unramified extension field W that is a splitting field for both. Then A ~ (W, σ, π^k) and B ~ (W, σ, π^l) where 0 ≤ k, l < n, and A B ~ (W, σ, π^{k + l}) ~ (W, σ, π^m) where 0 ≤ m < n and m/n ≡ (k + l)/n (mod ). It follows that the map {A} (k/n)+ is an isomorphism of Br(F) onto /.

Another important consequence of our results is

THEOREM 9.23.   The exponent of a finite dimensional central simple algebra over a local field coincides with its index.

Proof.   We have to show that if D is a central division algebra over a local field F such that [D : F] = n², then the order of {D} is n. By Theorem 9.21, D = (W, τ, π) where τ is a generator of the Galois group of W/F and τ ∈P_F – P_F². Then the exponent of D is the order of πN(W*). This is evidently n.

9.15   QUADRATIC FORMS OVER LOCAL FIELDS

We shall first define an invariant, the Hasse invariant, of a non-degenerate quadratic form on a finite dimensional vector space over an arbitrary field F of characteristic ≠ 2. In this we follow a method due to Witt that appeared in a beautiful paper of his on quadratic forms in vol. 176 (1937) of Crelle’s Journal.

The definition and properties of the Hasse invariant are based on quaternion algebras and Clifford algebras. We need to recall some results on quaternion algebras and develop some formulas for tensor products of these algebras. We have denoted the quaternion algebra generated by two elements i, j satisfying the relations

where a and b are non-zero elements of F, as (a, b) (p. 232). In dealing with tensor products of quaternion algebras we abbreviate (a, b) _F (c, d) to (a, b)(c, d) and as usual we write ~ for similarity of central simple algebras. Evidently we have

It is clear also that

for any s ≠ 0, t ≠ 0.

A quaternion algebra (a,b) is either a division algebra or (a, b) M₂(F), that is, (a, b) ~ 1 in the Brauer group Br(F). Evidently (1, b) ~ 1 and hence

The algebra (a, b) has the base (1, i, j, k = ij). If x = x₀ + x₁i + x₂j + x₃k and

then x² – T(x)x + N(x) = 0. Let (a, b)₀ denote the subspace of elements of trace 0: T(x) = 0. This has the base (i,j,k) and has the quadratic norm form N(x) = – ax₁² – bx₂² + abx₃². It is clear that (a,b)~ 1 if and only if (a, b) contains an element z ≠ 0 such that z² = 0. This is the case if and only if T(z) = 0 = N(z). Hence (a, b) ~ 1 if and only if the quadratic norm form on (a, b)₀ is a null form, that is, – ax₁ ² – bx₂² + abx₃² = 0 has a solution ≡ (0, 0,0). Evidently this implies

Since (a, b)₀ can be characterized as the set of elements x ∈ (a, b) such that x F but x² ∈ F, it is clear that an isomorphism of (a, b) onto (c, d) maps (a, b)₀ onto (c, d)₀. It follows that if (a, b) (c,d), then the quadratic forms – ax₁ ² – bx₂² + abx₃² and – cx₁² – dx₂² + cdx₃² are equivalent. It is quite easy to apply the theory of composition algebras to prove the converse (see exercise 2, page 450 of BAI).

If a is a non-square, then we have the field , which has the automorphism σ such that . Then the quaternion algebra (a, b) is the same thing as the cyclic algebra (Z, σ, b) (p. 480). Hence the multiplication formula for cyclic algebras (p. 475) gives the formula

if a is a non-square. Evidently this holds also if a is a square, since in this case all three algebras are ~1. Since (a, b)(a, b) ~ 1, (a, a).(b, b) ~ (a, a)(a, b)(b, b)(a, b) ~ (a, ab)(b, ab) ~ (ab, ab). Hence we have

Iteration of this gives

We now consider a quadratic form Q on an n-dimensional vector space V over a field F of characteristic≠ 2. The associated symmetric bilinear form B is defined by B(x, y) = Q(x + y) – Q(x) – Q(y). Then Q(x) = B(x, x). We assume throughout that Q is non-degenerate in the sense that B is nondegenerate. We now define the discriminant of Q to be the discriminant of B. Thus if (v₁,…, v) is an orthogonal base of V relative to Q (= relative to B) then the discriminant d = d(Q) defined by this base is .

We shall now define the Hasse invariant of Q as a certain element of the Brauer group Br(F). If n = 1, the element is the unit 1 of Br(F) and if n > 1, we define the Hasse invariant of Q relative to an orthogonal base (v₁,…,v_n) as the element of Br(F) determined by the tensor product

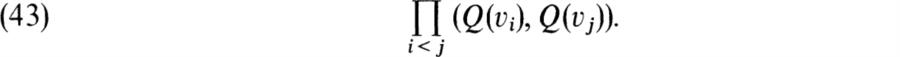
We proceed to show that this is independent of the choice of the orthogonal base.

PROPOSITION 9.9.   Let (v… ,v_n),(v′ _l, …,v′ _n) be orthogonal bases of V relative to Q. Then

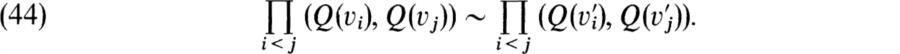
Proof (Witt). Let U be an n-dimensional vector space equipped with a quadratic form P for which we have an orthogonal base (u_l, …,u_n) such that P(U_i) = – 1, 1 ≤ i ≤ n Form W = U V and define a quadratic form R on W by R(u + v) = P(u) + Q(v), u ∈ U,v ∈ V. Then W = U V and the restrictions of R to U and Vare P and Q respectively. We shall show that for any orthogonal base (v ₁…, v_n) for V we have

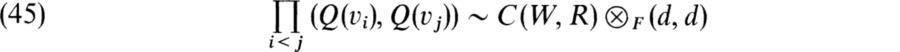
where C(W, R) is the Clifford algebra of R and d is a discriminant of Q. Evidently this will imply (44). Put . We show first that

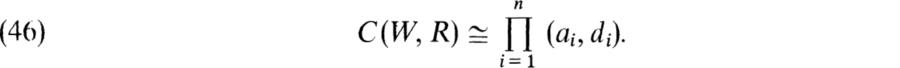
We know that C(W, R) is a central simple algebra generated by the elements u_i, v_i 1 = ≤ i ≤ n, and we have the relations u_i² = – 1, v_i² = a_i, U_iU_j = –U_jU_i, v_iv_j = – V_jV_i if i ≠ j, u_iv_k = – V_kU_i for all i, k (pp. 229–230). Put

Since , and v_nw₂ = – w₂ u_n, we have

Hence the subalgebra generated by W₁ and w₂ is (a_n,d_n) and C(W, R) ≅ (a_n,d_n) _FC′ where C′ is the centralizer in C(W, R) of the subalgebra generated by w₁ and w₂ (p. 233). The elements u_i v_i 1 ≤ i ≤ n – l, commute with w₁ and w₂ and the subalgebra generated by these elements is isomorphic to the Clifford algebra C(W′ R′ ) where and R′ is the restriction of R to W′ . Since [C(W′ R′ : F] = 2 ^{2(n – 1}} and [C′ : F] 2²ⁿ/4 = 2^{2(n – 1)}, we have C C(W′ R′ ) and C(W, R) (a_n, d_n) C(W′ R′ ). The formula (46) now follows by induction on n. This and (v) and (vi′ ) give

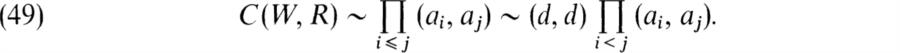
Hence

In view of Proposition 9.9 it makes sense to define the Hasse invariant s(Q) of Q to be the unit of Br(F) if n = 1 and the element of Br(F) defined by (43) if > 1.

The Hasse invariant is either 1 or an element of order two in the Brauer group. If F is algebraically closed or is finite, then Br(F) = 1, so in this case the Hasse invariant is trivial for any quadratic form over F. If F = or a local field, then there is a unique element of order two in Br(F). We denote this as – 1. Let Q⁺ and Q^– be positive definite and negative definite quadratic forms respectively on an n-dimensional vector space over . Then the Hasse invariant (mod 4), then s(Q⁺) = s(Q^–), but these forms are inequivalent. On the other hand, we shall show that the discriminant and Hasse invariant constitute a complete set of invariants for quadratic forms over local fields: Two such forms are equivalent if and only if they have the same discriminant and the same Hasse invariant.

We develop first some results for arbitrary base fields (of characteristic ≠ 2).

PROPOSITION 9.10.   Let n ≤ 3. Then two non-degenerate quadratic forms on an n-dimensional vector space are equivalent if and only if they have the same discriminant and Hasse invariant.

Proof.   The necessity of the condition is clear and the sufficiency is clear if n = 1. Now let n = 2 and let diag {a, b}, diag {a′ , b′ } be diagonal matrices for the two quadratic forms. We are assuming that (a, b) ~ (a′ b′ ) and ab and a′ b′ differ by a square. Then (a, b) (a′ , b′ ) and we may assume that ab = a′ b′ . The condition (a,b) ≅ (a′ b′ ) implies that the quadratic forms and are equivalent. Since ab = a′ b′ we have the equivalence of by Witt’s cancellation theorem (BAI, p. 367). Next let n = 3 and assume that . The hypotheses are and d = abc and d′ = a′ b′ c′ differ by a square, so we may assume that d = d′ . It suffices to show that – dQ and – dQ′ which have discriminant – 1, are equivalent. A simple calculation, which we leave as an exercise, shows that , so it suffices to prove the result for Q and Q′ of discriminant – 1. Then we may assume that . Then s(Q) = . Since Q arid Q′ are the negatives of the norm forms on (a, b)₀ and (a′ , b′ )₀ respectively, it follows that Q and Q′ are equivalent.

We prove next

PROPOSITION 9.11.   Let F be a field such that every quadratic form on a five-dimensional vector space over F is a null form. Then any two non-degenerate quadratic forms on a vector space V over F are equivalent if and only if they have the same discriminant and the same Hasse invariant.

Proof. The necessity of the condition is clear and the sufficiency holds by Proposition 9.10 if dim V ≤ 3. Hence assume n ≥4. The hypothesis implies that any non-degenerate quadratic form P on a four-dimensional vector space U/F is universal, that is, represents every non-zero element of F. For if a ≠ 0 we can form U Fx, x ≠ 0, and define a quadratic form R on U Fx by . The fact that R is a null form implies that we have a u + α x ≠ 0 such that P(u) = α²a. If α = 0 then u ≠ 0, so P is a null form and hence P is universal. If α ≠ 0 then P(α^{– 1} u) = a. Thus P is universal. The universality of non-degenerate quadratic form on four-dimensional spaces implies that if Q is a non-degenerate quadratic form on an n-dimensional vector space V, n ≥ 4, then we have an orthogonal base (v_l,…,v_n) with Q(v_i) = 1 for i > 3. If R denotes the restriction of Q to Fv₁ + Fv₂ + Fv₃, then the definitions and the formula (l,a) ~ 1 show that Q and R have the same discriminant and Hasse invariant. If Q′ is a second non-degenerate quadratic form on an _n-dimensional vector space, then we have an orthogonal base (v′ _l,…,v′ _n) with Q(v′ _i) = 1 for i > 3. The conditions that s(Q) = s(Q′ ) and Q and Q′ have the same discriminant imply the same conditions on the restrictions of Q and Q′ to Fv₁ + Fv₂ + Fv₃ and Fv′ ₁ + Fv′ ₂ + _{Fv′ 3}. Hence these restrictions are equivalent and so Q and Q′ are equivalent.

We require one further result for general fields.

PROPOSITION 9.12.   The quadratic form with d = a₁a₂a₃a₄. ≠ 0 is a null form if and only if is a splitting field for ( – a₃a₄, – a₂a₄).

Proof. Put a = – a₃a₄, b = – a₂a₄, c = a₂a₃a₄. Then cQ is equivalent to is the norm form on (a, b)₀ = ( – a₃a₄, – a₂a₄)₀. Suppose first that . In this case cQ is equivalent to , the norm form of (a,b), and (a, b) ~ 1 if and only if this norm form and hence Q is a null form. Thus the result holds in this case. Next assume . Then is a splitting field of (a,b) if and only if is a subfield of (a,b) (p. 221). The condition for this is that (a, b)₀ contains an element u such that u² = d. This is the case if and only if cQ and hence Q is a null form. Hence the result holds in this case also.

We now suppose that F is a local field. Then the results of the previous section show that there is a unique element of order two in Br(F). This has a representative that is a cyclic algebra (W, σ, π) where W is an unramified quadratic extension of F, σ the automorphism ≠ 1 of W/F, and π is any element of F such that π ∈ P – P² where P is the ideal of non-units in the valuation ring R of W. Since we are assuming that char F ≠ 2, W = F and hence (W, σ, π) = (a, n). We have

PROPOSITION 9.13.   Let F be a local field of characteristic ≠ 2 and let A be a quaternion division algebra over F. Then any quadratic extension field E/F is a splitting field for A.

Proof.   We have A = (W,σ, π) = (a, π). The extension field E/F is either unramified or completely ramified. In the first case E W, so A contains a subfield isomorphic to E and hence E is a splitting field. Next assume that E is completely ramified. Then E = F(b) where b is a root of a quadratic Eisenstein polynomial. By completing the square we may assume that b² = π′ ∈ P – P². We can construct the division algebra (W′ ,σ′ ,π′ ) where W′ is unramified and σ′ is an automorphism of period two. Then (W′ , σ′ , π′ ) ≅ (W, σ, π) = A, so again A contains a subfield isomorphic to E and E is a splitting field.

The next result we shall need on quaternion algebras requires the stronger hypothesis that the residue field R/P is of characteristic ≠ 2. This is

PROPOSITION 9.14.   If F is a local field such that char R/P ≠ 2, then (–1, – 1 )/F~ 1.

(This does not always hold if char R/_P = 2. For example ( – 1, – 1)/₂ ~ 1. See exercise 5 below.)

Proof.   The result is clear if – 1 is a square in F. Hence we assume Now W is unramified since the reducibility of x² + 1 in (R/P)[x] implies by Hensel’s lemma the existence of in F. Thus [(R_w/P_w):(R/P] = 2 so the residue degree of W/F is two and hence the ramification index is 1, that is _W/F is unramified. It follows that if (– 1, – 1) ~ 1 then (– 1, – 1) ≅ (– l,π) where π ∈ P_w –P_w². This implies that – π ∈ N(W*). This contradicts the determination of N(W*) given on p. 610. Hence ( – 1, – 1)~1.

We can now prove

PROPOSITION 9.15.   If F is a local field of characteristic ≠ 2, then any non-degenerate quadratic form Q on a five-dimensional vector space over F is a null form.

Proof.   We may assume that and if multiply Q by ∏ a_i we may assume that ∏a_i; is a square. Suppose that Q is not a null form. Then ∑⁴₁ a_jx_j² is not a null form. By Proposition 9.12 F is not a splitting field for (– a₃a₄, – a₂a₄). Then (– a₃a₄, – a₂a₄)~ 1, so by Proposition 9.13, a₁a₂a₃ a₄ is a square. Hence a₅ is a square. Similarly every a_i is a square and hence we may assume that . by Proposition again. This contradicts Proposition 9.14 if the characteristic of the residue field of F ≠ 2. Now suppose this is 2. Then F contains the field ₂ of 2-adic numbers and ₂ contains . To see this we note that, by Hensel’s lemma, x² + x + 2 is reducible in l₂. Hence ₂ contains contains . Then is a null form in ₂ and hence in F. This completes the proof.

By Proposition 9.11 and 9, 15 we have

THEOREM 9.24.   If F is a local field of characteristic ≠ 2, then any two non-degenerate quadratic forms on an n-dimensional vector space V/F are equivalent if and only if they have the same discriminant and Hasse invariant.

We show next that if n ≥ 3, the two invariants are independent. The proof of Proposition 9.11 shows that it suffices to prove this for n = 3. Then a calculation indicated in the proof of Proposition 9.10 shows that if Q = ax ² + bx₂² + cx₃², then s(Q) ~ ( – da, –db)( – x, –d) where d = abc. It is clear from this formula that for a given d, a and b can be chosen so that s(Q) = ±1. Hence a, b, c can be chosen so that the discriminant is any d and s(Q) = ± 1. This result and Theorem 9.24 imply that the number of equivalence classes of non-degenerate quadratic forms over F with n ≥ 3 is 2|F*/F*²| where F*² is the subgroup of squares in F*. It is easy to see, using an argument based on Hensel’s lemma as in the proof of Proposition 9.8 on norms, that if the characteristic of the residue field is ≡ 2, then |F*/F*²| = 4. Accordingly, the number of equivalence classes of non-degenerate quadratic forms for a given n ≥ 3 is 8. Some information on the case n < 3 and the case in which the residue class has characteristic two is indicated in the exercises.

EXERCISES

        1. Show that ax₁² + bx₂², ab ≠ 0, is a null form if and only if ab = –d² and that ax₁² + bx₂² + cx₃² is a null form if and only if s(Q) ~ ( – d, – d), d = abc.

        2. Let F be a finite dimensional extension of ₂. Show that |F*/F*²| = 2^{[F Q₂]}.

        3. Determine the number of equivalence classes of non-degenerate quadratic forms with n = 2 over a local field.

        4. Let F be a field such that (a, b) ~ 1 for every quaternion algebra over F. Show that two non-degenerate quadratic forms on an n-dimensional space over F are equivalent if and only if they have the same discriminant.

        5. Show that the quadratic form x₁² + x₂² + x₃² on a three-dimensional vector space over ₂ is not a null form. Hence conclude that (– 1, – 1)₂ 1.

REFERENCES

S. Kürschak, Über Limesbildung und allgemeine Körpertheorie, Journal für die reine und angewandete Mathematik, vol. 142 (1913), 211–253.

E. Witt, Theorie der quadratischen Formen in beliebigen Körpern, Journal für die reine und angewandete Mathematik, vol. 176 (1937), 31–44.

O. F. G. Schilling, The Theory of Valuations, American Mathematical Society Surveys, Providence, R.I., 1950.

O. Zariski and P. Samuel, Commutative Algebra II, New printing, Springer, New York, 1960.

E. Artin, Algebraic Numbers and Algebraic Functions, Gordon and Breach, New York, 1967.

 

* An example in which n ≠ ∑ e_ι f_ι has been given by F. K. Schmidt in “Über die Erhaltund der Kettensatz der Ideal theorie bei beliebigen endliche Körpereweiterungen,” Mathematische Zeitschrift vol. 41 (1936), pp. 443–450.

* A good bibliography of the early literature on topological algebra appears in H.Freudenthals’s review of this book in Nieuw Archief voor Wiskunde, vol. 20(1940), pp.311–316.