8 A Keynes—Marx theory of investment

Jonathan P. Goldstein


Introduction

The theory of investment lies at the center of an integrated heterodox macro model.1 Yet, heterodox theories of investment have not advanced beyond simplistic expressions of the investment function. In particular, Keynesian investment functions have focused on capacity utilization as the primary determinant of investment, while Marxian approaches have concentrated on the profit rate. These simplistic theories are inadequate for understanding the complex macroeconomic dynamics of the capitalist growth process in the era of the Neoliberal regime. Thus, the purpose of this chapter is to extend the basic theory of investment in order to better explain the macro dynamics of the global economy.

Based on the work of Crotty (1993) and Crotty and Goldstein (1992a, 1992b, 1992c), I develop a microfoundation for the firm’s investment decision. This theory integrates both Keynesian and Marxian insights in order to produce a more flexible and realistic investment function. In particular, the theory further incorporates the external financing of investment based upon uncertain future profit flows, the irreversibility of investment, and the coercive role of competition on investment. The investment function is extended to depend on the profit rate, long-term and short-term heuristics for the firm’s financial robustness and the intensity of competition. The interaction of these factors fundamentally alters the nature of the investment function, particularly the typical role assigned to capacity utilization.2

This chapter is organized in the following manner. In the first section, I present an overview of the model. This is followed by sections on the details of the model, the optimal investment strategy, and a constrained version of the model that highlights the crucial Marxian competition effect. The final section elaborates how the theory is useful for understanding the macro dynamics of the Neoliberal regime.


Model overview

In this section, I outline a Keynesian—Marxian theory of the firm’s investment decision. The Keynesian aspects of the model include true/Keynesian uncertainty and the possibility of financially fragile outcomes in such an environment, the illiquid nature of capital, endogenous expectations and preferences, and the potential for misaligned interests between firm management and shareholder/ owners and creditors. The Marxian attributes include the Marxian competitive environment, as distinct from the neoclassical concept of competition, including critical regime shifts in the form of competition, transitions between different modes of accumulation, the imperative to accumulate capital through the progressive maximization of surplus value/profits and endogenous expectations and preferences.

It is assumed that managers control the firm subject to constraints made on their decision-making autonomy by owners and finance capitalists. Managers pursue the objectives of the growth and financial safety of the firm and in doing so maximize their own goals (utility). Within both of these objectives are constraints imposed by owners and creditors in the form of dividends, interest payments3 and the expectation of continued credit-worthiness. Failure to meet historically determined marks for these categories can possibly set off stockholder revolts, bankruptcy proceedings or creditor interference4 with firm decision-making.

The Marxian competitive environment emphasizes the importance of the growth objective of the firm and at times acts as an additional constraint on the firm’s investment strategy. For Marx, competition was a coercive force that compelled individual capitalists to continually investment as a survival strategy.5 Thus, growth is essential to reproduction. Here, competition has anarchic and war-like attributes that force firms to take an offensive position with respect to investment as a means of generating enough profit to ultimately defend the firm from competitive onslaughts in the form of innovation by competitors. Firms that have ineffective investment strategies or do not keep pace with competitors are either marginalized or fail. Thus, competition can create an “invest or die” situation for the firm.6 When competition intensifies to this point, investment must become defensive by focusing on new cost-cutting production methods as a means of shoring up the firm’s market share. In this defensive situation, investment acts as an overarching constraint on the firm that trumps the constraints imposed by shareholders and creditors.7 In this manner, competition-induced defensive investment can become an imperative that must be undertaken despite its impacts on the financial position of the firm. In this coerced situation, a competitive criteria—the imperative to revive the firm’s competitive position irrespective of its consistency with other firm objectives—dominates.8 In addition, regime shifts between two forms of competition (co-respective and coercive) can be used to explain transitions in investment behavior from an offensive form (widening of capital) to a defensive form (deepening of capital).

While investment in either of its forms is an imperative of the firm, a successful firm in a cyclically unstable environment, predicted by Marxian crisis theory, must also know when not to invest. Profit squeeze or under-consumption crises that periodically result in declining aggregate demand must be forecasted as best as possible in an uncertain environment. New investment mistakenly undertaken in such circumstances is likely to further exacerbate the firm’s profit and cash flow positions and increase the likelihood of not meeting debt obligations and earnings expectations. Thus, investment, while necessary, is also risky. In addition, investment can also be mandatory (a competitive criteria dominates) and thus it can induce further reliance on debt at inopportune times or the generation of further excess capacity.

The incorporation of Keynesian uncertainty, irreversible investment and a dependency on external finance adds a new and deeper dimension to the potential financial fragility associated with investment. In such an environment, finance can both enhance and impinge on capital accumulation. With external finance, firms take on certain debt obligations that are to be paid from uncertain future profit flows without the cushion of being able to effectively sell capital assets when profit expectations are disappointed. It is this risk of reductions in the firm’s financial security and as a result its decision-making autonomy that underlies an investment-induced growth—safety tradeoff. The severity of the firm’s financial difficulties can also lead to a change in management’s relative preferences for its growth and safety objectives. In periods of financial crisis, the firm is likely to shift its focus to solving security problems. In the case where the competitive constraint on the firm’s behavior is binding, preferences are shifted back to growth based on an investment-induced cost-cutting strategy irrespective of the firm’s financial condition.

In light of the model’s main attributes and the firm’s operating environment, the firm’s optimization problem can be specified. Managers maximize a utility function, O, that is a function of the growth, G, and safety, S, objectives of the firm subject to a competitive constraint on the firm’s market share, M, by choosing an optimal investment strategy from two forms of investment—offensive investment, I, and defensive investment, ID. Thus, the firm’s optimization problem is

Maximize

O[G(I, ID), S(I, ID)](1a)

subject to

M(ID) ≥ M*(1b)

where M* is a critical market share level below which the firm must undertake defensive investment in order to shore up its competitive position for long-run survival.9

Two aspects of the model require clarification. First, the model is static, while standard investment models are dynamic. Second there exists a dichotomy in the implementation of the two investment strategies. If the competitive constraint is non-binding, the firm only uses I, offensive investment—the expansion of output via investment that replicates the existing technology or makes minor improvements in technology. When the competitive constraint is binding, the firm solely relies on ID which constitutes investment in new cost-cutting technology.

Under a realistic set of three assumptions that are consistent with the Keynesian—Marxian environment elaborated above and a specification of the S function that includes both short-term and long-term security concerns, it can readily be shown that the firm’s dynamic optimization problem reduces to the problem specified in Equations 1a and 1b.10

The dichotomy in the implementation of the two forms of investment is justified by the disruptive nature of defensive investment. An ID strategy is both dangerous and costly. It might entail a disastrous confrontation with labor and tension between management and short-sighted shareholders and has enormous “costs of adjustment” that are proportional to the level of ID such that it will never appear to be optimal over an intermediate-length investment horizon. However, when competitive pressure threatens long-term survival, the firm has no choice but to adopt an ID strategy and absorb the costs in the short-run—the competitive criteria dominates the profit or O maximization objective.


Model details

I keep the level of model detail to the minimum necessary to lay bare the fundamental workings of the model. Full details of model components are contained in Crotty and Goldstein (1992c) and in an appendix available upon request from the author.

The growth objectives of the firm depend on the present value of expected future earnings designated as R–expected net revenues. R depends on the pattern of expected future demand and cost conditions and the present value of debt and dividend payments. The firm’s price-cost markup, α, is an important index of how demand and cost factors influence R.

A fuller specification of the R function: demand and cost structures, financing mechanisms and the firm’s dividend policy is contained in the above referenced appendix. Here, I briefly touch on demand and cost conditions.

I assume a fixed-coefficient, constant variable cost production function and a downward-sloping demand curve: Q = Q(I, ID; K, KD), P = P(Q(I, ID; K, KD)) and U = Ū where Q is output, P is expected output price, U is expected variable cost, Ū is a constant, K and KD are the initial levels of offensive and defensive capital stocks and the relations between K and I and KD and ID are implicitly incorporated.11 I further assume that PQ < 0 and PQQ ≤ 0 where subscripts denote partial derivatives. Integrating the firm’s price-variable cost markup (α), gross profits, π, can be expressed as π(I, ID) = α(I, ID) Q(I, ID) where α = (P–U).12 This implies that R, which is a function of π, depends on α.

Explicitly considering the role of international competition on market shares, Q = M(ID, P; PF) QW(P; PF, YW) where PF is the foreign competitor’s price, QW is a world demand curve and YW is a world demand shift parameter, such as world GDP. Thus, the firm has a share (M) of the world demand curve. The incorporation of international competition in this manner does not necessitate any change in our demand curve assumptions.13

In order to capture both the short-term and long-term aspects of the firm’s financial security, the S function is comprised of two security sub-goals. In the current period, the firm can lessen impingements on its decision-making autonomy by maintaining a comfortable margin between its expected gross profits, π, and x defined as the interest plus dividend payments necessary to preserve managerial autonomy. Given the uncertain nature of π, there exists an expected probability distribution of π, conditional on the current level of the two distinct capital stocks, defined as f. Thus, the perceived likelihood of an autonomy crisis is given by F, the cumulative probability that π < x. It should also be recognized that R ≡ π–x.14

Given the static treatment of the investment decision, it is necessary to ensure that the firm also considers its long-run financial position. I define D′ as an index of the firm’s current perception of its long-term financial vulnerability. In particular, 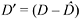, where D is the current level of debt and is the maximum debt level that management is comfortable carrying into its uncertain future based on conjunctional expectations of financial institutions. The inclusion of D′ in S forces the firm’s current investment decision to be consistent with its long-term safety objective. Both F and reflect managerial optimism or pessimism over short and long periods and both can shift endogenously as optimism and confidence in forecasts ebb and flow. The use of a conventional, rule-of-thumb variable such as constitutes a very Keynesian solution to this long-term aspect of the uncertainty problem (Crotty 1994). Integrating these two security subgoals, the security function takes the following form: S(F(I, ID), D′(I, ID)).

Finally, the firm’s market share constraint can be written as M(PF–αU(ID) ≥ M* where PF is the price of competing foreign goods, and P = αU. The firm’s market share depends on its output price relative to competitors’ prices and only the ID form of investment can lower unit cost.

Key parameters of the model that are revealed in current and more detailed specifications of the above functions include: the firm’s mark-up, the initial levels of both types of capital stock, the mean and variance of the firm’s subjective probability distribution for π and the form of that distribution, initial debt levels, the maximum acceptable debt level, the price of capital, the price of competing foreign goods, the firm’s target market share, the interest rate, the dividend payout rate and a constant rate of depreciation.

Given this partial detail, the firm’s optimization problem can be rewritten as:

maximize

O[G(R(I, ID;PF)), S(F(I, ID), D′ (I, ID))](2a)

subject to

M(PF–αU(ID)) ≥ M*(2b)

Given the dichotomous treatment of I and ID strategies, I first examine the firm’s optimal decision for the case where the market share constraint is not binding. Thus, I explore the firm’s offensive investment strategy. The case where the constraint binds when coercive competition forces a transition to a defensive investment strategy—the Marxian competition effect—is subsequently analyzed.


The optimal investment strategy

At the heart of the unconstrained model is an investment-induced G–S tradeoff. The G–S tradeoff is best understood by examining GI = GR RI and SI = SFFI + SD′D′I where GR > 0, SF < 0 and SD′ < 0 are preference weights for the R, F and D′ sub-objectives.

The sign indeterminacy of FI and thus SI imply that the nature of the G-S tradeoff is undetermined.15 However, it is shown in an available appendix that the first order conditions for (2) and the assumptions that PQ < 0 and PQQ ≤ 0, restrict SI < 0 and GI > 0 in the neighborhood of equilibrium: an investmentinduced G—S tradeoff is operational. The mechanics of the tradeoff are straightforward. A one unit increase in I increases G, and thus utility, through an increase in net revenues as security concerns force the firm to under-invest in general (PDV > 0 compared to conventional solutions where PDV = 0). At the same time, marginal I decreases S either through a simultaneous increase in the probability of short-term financial strife (RI < 0) and long-term debt dependency or an increase in long-term debt dependency that outweighs, in utility units, the decline in F (RI > 0).

The dependence of O in Equation (2a) on multiple objectives ( G and S) and sub-objectives (R, F and D') requires that management’s relative subjective ranking of these objectives and sub-objectives be made explicit. For simplicity, it is assumed that S and G are linear in their arguments: SFF = SD'D' = SFD', = GRR = 0. In Keynesian and Marxian traditions, the relative preference ordering for G and S is variable and thus endogenous. It is assumed that OGG = OGS = 0, while OSS < 0: the firm’s imperative to grow is a constant unyielding commitment that is independent of the size of the firm, while the firm’s response to financial security, and uncertainty is variable. At lower levels of financial security, management responds by choosing an investment/debt strategy which focuses on restoring financial security even at the expense of maintaining or promoting the firm’s growth objective. A financially fragile firm will sacrifice potential growth to lower the probability of crisis. Thus, that the intensity of the G–S tradeoff is variable. Ceteris paribus, at higher levels of I (and thus higher levels of G and lower levels of S) the relative preference for security increases.

The first order condition for an interior solution to maximization problem (2) is OGGI = OSSI or alternatively OG[GRRI] + OS[SF FI + SD'D′I] = 0.

The firm invests to the point where the marginal utility gains (losses) from growth are exactly offset by the marginal utility losses (gains) from financial security/autonomy. In equilibrium sgn(–SI) = sgn(GI)–the firm faces a G–S tradeoff.

The second order condition for a maximum requires that:

OGGII + GI OGI + OSSII + SIOSI < 0.

 

Recognizing that OSI = OSSSI and that OGI = OGGGI = 0, the second order condition can be stated as:

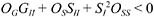(3)

This condition is met under the assumptions that PQ < 0, PQQ ≤ 0 and additionally that QII = 0.16

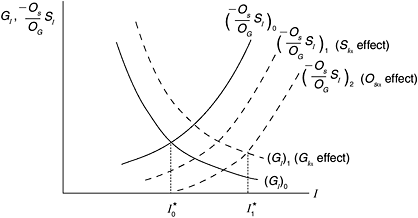
The managerial firm’s optimal I decision is depicted in Figure 8.1. In finding the I* that ensures , management must resolve the G–S tradeoff. At levels of I < I1, marginal increases in I increase gross profits by enough to:


  1. offset the marginal increments in the costs of autonomy and thus ensure that G rises (GI > 0);
  2. ensure that F declines by enough, despite the increase in financial obligations, to offset the increase in D', thus S increases and;
  3. increase the relative preference weight, assigned to the G objective as safety increases and thus OS declines.

Thus for I < I1, OI > 0: total utility increases with I. For I1 < I < I2 marginal increases in investment result in smaller increases in gross profits as the firm’s profit per unit decreases at higher levels of output. As a result, 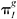offsets the marginal increments in the costs of autonomy by less–GI declines—and is no longer capable of reducing F by enough to offset the rise in D'–SI becomes negative. In addition, declines. Thus G continues to rise but at the expense of a decline in S(SI < 0): the G-S tradeoff is operable. As long as 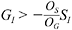marginal increments in I will increase O. But, given that 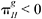(which ensures that SII < 0), GII < 0, and OSS < 0, beyond I* marginal increments to I will no longer generate enough profits to ensure that the appropriately weighted increase in G offsets the increasingly more heavily weighted declines in S.

Figure 8.1 The optimal solution and G—S tradeoff.


Comparative statics

In this section, the comparative static effects of model parameters are discussed for the unconstrained model. These results are used later to establish the macro dynamics of the Neoliberal paradox (Crotty (2003a, 2003b, 2005). Detailed derivations are contained in an available appendix.

In general the effect on I* and K* of a one unit change in any parameter, p (with the exception of K0) can be expressed as

 

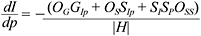
where OGG = 0 is invoked, |H| is the second order condition in Equation (3), and OSp is written as SPOSS. Given that |H| < 0, the sign of depends on the sign of three separate effects: OGGIp, OSSIp and SISpOSS. These effects respectively represent:


  1. the change in investment-induced increases in growth objectives evaluated in utility terms by OG;
  2. the change in investment-induced reductions in financial security evaluated in utility terms by OS; and
  3. the change in the evaluation of the investment-induced reduction in financial security (SI) as a result of changes in the preference weight OSp = (SpOSS) that occur as S changes.

Given that OG > 0, OS > 0, OSS < 0 and SI < 0 in the neighborhood of equilibrium, the sign of depends on the signs of GIp, SIp and SP.

The comparative static results are best understood by recognizing that each of these three effects alters the intensity of the G-S tradeoff. Unambiguous increases in the intensity of the tradeoff (any combination of GIp < 0 or SIp < 0 or SP < 0) will result in less I and conversely.

To show how the model works, we consider in detail a change in α, the firm’s profit markup. Changes in α are the primary channel through which real sector developments directly affect the pace of accumulation in the model. dI/dα can be expressed as:

 

where 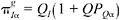and β is the divided payout rate. If demand increases such that PQα ≥ 0 and 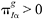, then GIα > 0, SIα > 0 and Sα > 0 implying that .

A rise in α stimulates I in three ways. First, it increases the marginal return to growth—marginal gross profits are increased because the additional output is sold at a higher α, marginal costs remain the same, and the marginal decline in price when Q grows is either unaffected or reduced. Second, it reduces the marginal decline in safety because F is reduced. Third, it increases the level of S through higher gross profits that reduce F, and thereby lower the weight on the investment-induced decline in S. All three effects reduce the intensity of the G-S tradeoff and result in optimal trades of investment-induced reductions in S in favor of investment-induced increases in G. Thus, I increases. As can be seen in Figure 8.2, the first (or demand) effect shifts the GI curve to the right while the latter effects (SIα > 0 and Sα > 0) both shift the curve to the right.

This result is important on both the micro and macro levels. On the micro level, it shows how shifts in demand and cost functions (changes in profitability) alter I demand. On the macro level, it provides a feedback mechanism through which macroeconomic variables, including the distribution of income, shift the firm’s demand and cost functions and thus influence microeconomic profitability and I.

Other comparative static results are summarized in Table 8.1.


The constrained model: the Marxian competition effect

When coercive competition erodes or is expected to erode the firm’s market share below the critical M* level, the firm faces an invest-or-die situation. The firm must either defend its illiquid capital, be marginalized by the competition or forced to sell off its assets to satisfy the demands of finance capitalists and shareholders. In this situation, investment goes from a necessary, but risky, activity to a required activity. Here, a competitive criteria dominates the maximization of combined growth and safety objectives and as a result financial security objectives are abandoned in the intermediate run. The firm can only improve its market share through the implementation of a qualitatively distinct form of investment referred to as defensive investment.

Figure 8.2 The effect of dα on optimal I.


Table 8.1 Comparative static results*


It is important to note that the abandonment of safety concerns can be accompanied by different circumstances that underlie the violation of the market share constraint. Declining market shares can be caused by:


  1. rising mark-ups;
  2. intensified competition during periods of stagnant demand growth including price wars (destructive competition); and
  3. intensified rivalries during periods of normal demand growth.

While these three scenarios produce the same defensive competitive response on the micro level, the particular combination of circumstances have important implications for the resulting macroeconomics environment (discussed below, pp. 123–4).

The Marxian competition effect and the firm’s transition from an offensive to a defensive investment strategy are depicted in Figure 8.3 where each curve represents a linearized version of the locus of mark-up (α)–offensive investment (I) combinations for a fixed market share (M) that maximize the firm’s unconstrained G-S objective function. Along each curve, only one of the two forms of price competition is operable—the impact of rising prices/mark-ups on the international demand for the firm’s product is abstracted from so that it can be properly included as a shift parameter with other changes affecting the firm’s market share. The positive relation between α and I reflects the comparative static result discussed above.

Starting from point A (I0, α0, M0), a ceteris paribus increase in α to α1 results in an increase in optimal I to I1 when international competition is not considered and more appropriately to a smaller rise in I to I2 due to the reduction in market share to M1 when all forms of competition are considered.

Figure 8.3 The Marxian competition effect.

Any combination of individual increases in α, increases in U, or declines in PF that reduces the firm’s market share below M* such as at point D, sets off a transition to a defensive investment strategy. Given that the transition to a production process with a new cost-cutting technology requires significant amounts of defensive investment, investment demand rises significantly to say point E with an initial defensive investment level of . Point E represents both a constrained optimum and a disequilibrium point with respect to the firm’s unconstrained G–S equilibrium.

In the disequilibrium sense of point E, the firm is forced to undertake a level of investment that is far greater and is associated with far more financial risk then it would normally assme at equilibrium point D. While a discussion of disequilibrium dynamics from point E back to an unconstrained G–S equilibrium is beyond the scope of this chapter, particularly due to the potential macro crisis tendencies (discussed below, pp. 123–4) embedded in such micro decisions, some points can be made. Abstracting from crisis generating mechanisms, the ID strategy, if successful, will improve the firm’s market share and after a transition period, the new production techniques become the accepted technology implying that further investment in these methods constitutes the next generation of offensive investment. Thus, the movement from point E will be back to an unconstrained G–S equilibrium. If we assume for simplicity that restores the firm’s market share to M0 and the firm maintains its markup at α, then the movement will be from point E to B. Of course, other paths are possible depending on how the firm negotiates the tradeoff between its markup and market share (Goldstein 1985)

An ID strategy can be set off in a variety of ways. Any mechanism that raises the firm’s price relative to their competitor’s price will lower the firm’s market share—increases in competition (lower competitor’s prices), or increases in the firm’s mark-up. The latter can occur from defending the markup against a profit squeeze (Goldstein 1985) or from increases in the rate of exploitation when capital has the upper hand in the capital—labor relation. In addition, price wars either within the domestic industry or the entire industry can lead to ID. In this situation, either the market share is expected to decline from this form of destructive competition or if firms resist ID and match competitor’s price declines, then the decline in the profit rate may lead financial capitalists to pressure firms to increase their earnings. In this case, the most viable response would be to use ID.

When the competitive constraint is binding there are also some situations in which an ID strategy may not be pursued. The firm can always opt out of the industry—the die option—or finance capitalists with control over the firm can decide to sell off the assets of the firm to maximize the wealth of the stockholders. While these are possible outcome, the more typical response is to defend the firm’s illiquid capital. Thus, from a representative agent perspective, the ID strategy is the dominant outcome.


The Keynes—Marx theory of investment and the Neoliberal paradox

Given that the theory of investment lies at the core of an integrated heterodox macroeconomic theory, the Keynes—Marx theory of investment should be capable of explaining some of the key macro dynamics of the Neoliberal regime. In this section, I use the model to capture the Neoliberal paradox—a tendency to chronic global excess capacity—developed by Crotty (2003a, 2003b, 2005).

In the Neoliberal era, free trade and financial liberalization have led to increases in international competition, particularly as firms in developing nations enter established markets and direct investment across developed nations increases. A decline in market shares for firms in advanced countries reduces their relative demand growth shifting the G curve to the left and the S curve to the left as net revenues are reduced on the margin and simultaneously making the competitive constraint more binding. At the same time, one of the hallmarks of the Neoliberal regime has been macro policies and firm low road labor strategies that shift income away from the working class and slow global aggregate demand growth. This general erosion of demand growth would have the same effects as increased competition on the G and S curves, but would not further tighten the competitive constraint as market share should remain relatively constant from this general decline in demand growth. The impact of these two factors on the firm’s optimal investment strategy would be for offensive investment to be reduced. If the described shifts in the G and S curves are large enough, the curves could meet in the northwest quadrant of Figure 8.1 where I is negative implying that the optimal capital stock exceeds the initial capital stock—excess capacity exists. This excess capacity would exist at the same time that the firm’s competitive constraint is closer to being violated. If the constraint is not yet violated, then destructive competition in the form of price wars is likely to break out. This represents one strategy by which the firm can defend its illiquid capital with the hopes of emerging as one of the remaining firms after the industry shake-out settles. In addition, international competition from developing areas is likely to increase. Both of these tendencies will result in the tightening or ultimate violation of the market share constraint. In the case of a price war, either the firm’s market share is expected to decline if it does not reciprocate with price cuts, or the reduction in profits from successive price declines will trigger finance capitalists and shareholders to demand increased earnings. The firm’s best strategy in both of these cases is to engage in defensive investment and to pursue low road labor strategies.

Increases in defensive investment will further exacerbate the excess capacity crisis. While low road labor strategies will further slow aggregate demand growth and reproduce the excess capacity problem that started this dynamic process. Hence the excess capacity problem has a chronic and global dimension.


Notes

1 See Chapter 3 in this volume.

2 Capacity utilization does not explicitly enter as a determinant of investment because it is subsumed in the capital-output ratio component of the profit rate.

3 While not formally addressed, legacy labor (retiree) costs and stock buy backs to buoy the stock price can be readily included.

4 Creditor interference has become more relevant in the current period of a finance-led accumulation regime.

5 See Crotty (1993) on the relation between investment and competition.

6 See Crotty (1993) for a discussion and extension of the Marxian concept of competition, particularly as it relates to the firm’s investment decision. Crotty’s contribution includes distinguishing forms of Marxian competition, particularly a co-respective form and a coercive form.

7 Unless, these groups decide it is in their best interests to force a sale of the firm’s assets.

8 Shaihk (1978) is the first to mention a competitive criteria as distinct from a profit maximization objective. Goldstein (2006) discusses the use of competitive constraints in Marxian microfoundations. Shaihk (1978) discussed a “switch or die” imperative for the firm with respect to a transition to a new cost-cutting technology, while Crotty (1993) considers a similar “invest or die” transition in investment strategy.

9 An alternative constraint could entail reductions in the firm’s earnings as a result of destructive competition that sets off finance capitalist demands for improved earnings. These demands can be met through a defensive investment strategy.

10 An appendix that demonstrates the reduction of the firm’s dynamic problem to the problem in equations (1a and 1b) is available upon request from the author.

11 Given the dichotomy in the firm’s usage of I and ID, it is assumed that the production function retains these properties separately with respect to both forms of capital. After a transition period associated with a shift to an ID strategy, the new technology exhibits the assumed production function characteristics. In the remainder of the chapter, the initial values of both types of capital stock is suppressed in the notation. Thus every time I or ID appears in functional notation, they should respectively be followed by K and KD.

12 In this model, the firm’s mark-up is treated exogenously for a given level of investment. Goldstein (1985) develops a microfoundation for a variable mark-up pricing strategy for the firm. Ideally, the pricing and investment decisions of the firm should be integrated. Given the complexities of the current model, I treat the markup exogenously.

13 PQ is qualitatively the same. Quantitatively, there are now two determinants of the elasticity of demand. Ceteris paribus, as the firm raises its price, both domestic and foreign competitors capture a portion of the firm’s demand.

14 It is argued, in the available appendix, that the use of such a subjective probability distribution is consistent with the notion of Keynesian uncertainty. In particular, the firm is only able to effective use such a distribution in the current period. Future distributions are not knowable. Thus, long-term financial vulnerability is treated through a separate sub-objective of the firm to ensure that the firm does not make short-run decisions that are inconsistent with its long-run objectives.

15 In this model with the inclusion of S, the firm acts in a risk—averse fashion setting PDV > 0. Thus, RI > 0. For FI, an increase in investment can increase expected gross profit flows by either more or less than the increase in current autonomy payments.

16 All derivations and proofs that are subsequently applied hold for the more general case where QII ≤ 0.


References

Crotty, J. (1993) “Rethinking Marxian Investment Theory: Keynes—Minsky Instability, Competitive Regime Shifts and Coerced Investment,” Review of Radical Political Economics, 25(1): 1–26.

——(1994) “Are Keynesian Uncertainty and Macrotheory Compatible? Conventional Decision Making, Institutional Structures, and Conditional Stability in Keynesian Macromodels,” in G. Dymski and R. Pollin (eds.) New Perspectives in Monetary Macroeconomics: Explorations in the Tradition of Hyman P. Minsky, 105–39, Ann Arbor: University of Michigan Press.

——(2003a) “Core Industries, Coercive Competition and the Structural Contradictions of Global Neoliberalism,” in N. Phelps and P. Raines (eds.) The New Competition for Inward Investment: Companies, Institutions and Territorial Development, 9–37, Northampton, MA: Edward Elgar.

——(2003b) “The Neoliberal Paradox: The Impact of Destructive Product Market Competition and Impatient Finance on Nonfinancial Corporations in the Neoliberal Era,” Review of Radical Political Economics, 35(3): 271–9.

——(2005) “The Neoliberal Paradox: The Impact of Destructive Product Market Competition and ‘Modern’ Financial Markets on Nonfinancial Corporation Performance in the Neoliberal Era,” in G. Epstein (ed.) Financialization and the World Economy, 77–110, Cheltenham, UK and Northampton, MA: Edward Elgar.

Crotty, J., and Goldstein, J. (1992a) “A Marxian—Keynesian Theory of Investment Demand: Empirical Evidence,” in F. Moseley and E. Wolff (eds.) International Perspectives on Profitability and Accumulation, 197–234, Brookfield: Edward Elgar.

——(1992b) “The Impact of Profitability, Financial Fragility and Competitive Regime Shifts on Investment Demand: Empirical Evidence,” Levy Economics Institute of Bard College, Working Paper No. 81, September.

——(1992c) “The Investment Decision of the Post-Keynesian Firm: A Suggested Microfoundation for Minsky’s Investment Instability Thesis,” Levy Economics Institute of Bard College, Working Paper No. 79, September.

Goldstein, J. (1985) “The Cyclical Profit Squeeze: A Marxian Microfoundation,” Review of Radical Political Economics, 17(1–2): 103–28.

——(2006) “Marxian Microfoundations: Contribution or Detour?” Review of Radical Political Economics, 38(4): 569–94.

Shaikh, A. (1978) “Political Economy and Capitalism: Notes on Dobb’s Theory of Crisis,” Cambridge Journal of Economics, 2(2): 233–51.