
Metrics covered in this chapter:
Price Premium
Reservation Price
Percent Good Value
Price Elasticity of Demand
Optimal Prices, Linear and Constant Demand
“Own,” “Cross,” and “Residual” Price Elasticity
“The cost of . . . lack of sophistication in pricing is growing day by day. Customers and Competitors operating globally in a generally more complex marketing environment are making mundane thinking about pricing a serious threat to the firm’s financial well being.”1
A full-fledged evaluation of pricing strategies and tactics is well beyond the scope of this book. However, there are certain key metrics and concepts that are fundamental to the analysis of pricing alternatives, and this chapter addresses them.
First we describe several of the more common methods of calculating price premiums—also called relative prices.
Next, we discuss the concepts that form the foundation of price-quantity schedules—also known as demand functions or demand curves. These include reservation prices and percent good value.
In the third section, we explain the definition and calculation of price elasticity, a frequently used index of market response to changes in price. This relatively simple ratio of percentage changes in volumes and prices is complicated in practice by variations in measure and interpretation.
For managers, the purpose of understanding price elasticity is to improve pricing. With this in mind, we’ve devoted a separate section to determining optimal prices for the two main types of demand functions: linear and constant elasticity. The final portion of this chapter addresses the question of whether elasticity has been calculated in a manner that incorporates likely competitive reactions. It explains three types of elasticity—“own,” “cross,” and “residual” elasticity. Although these may seem at first glance to rest upon subtle or pedantic distinctions, they have major pragmatic implications. The familiar concept of the prisoner’s dilemma helps explain their import.



Price premium, or relative price, is the percentage by which a product’s selling price exceeds (or falls short of) a benchmark price.
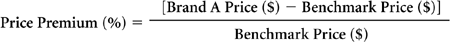
Marketers need to monitor price premiums as early indicators of competitive pricing strategies. Changes in price premiums can also be signs of product shortages, excess inventories, or other changes in the relationships between supply and demand.
Although there are several useful benchmarks with which a manager can compare a brand’s price, they all attempt to measure the “average price” in the marketplace. By comparing a brand’s price with a market average, managers can gain valuable insight into its strength, especially if they view these findings in the context of volume and market share changes. Indeed, price premium—also known as relative price—is a commonly used metric among marketers and senior managers. Fully 63% of firms report the Relative Prices of their products to their boards, according to a recent survey conducted in the U.S., UK, Germany, Japan, and France.2
Price Premium: The percentage by which the price charged for a specified brand exceeds (or falls short of) a benchmark price established for a similar product or basket of products. Price premium is also known as relative price.
In calculating price premium, managers must first specify a benchmark price. Typically, the price of the brand in question will be included in this benchmark, and all prices in the benchmark will be for an equivalent volume of product (for example, price per liter). There are at least four commonly used benchmarks:
• The price of a specified competitor or competitors.
• Average price paid: The unit-sales weighted average price in the category.
• Average price displayed: The display-weighted average price in the category.
• Average price charged: The simple (unweighted) average price in the category.
Price of a Specified Competitor: The simplest calculation of price premium involves the comparison of a brand’s price to that of a direct competitor.
Ali’s company sells “gO2” mineral water in its EU home market at a 12% premium over the price of its main competitor. Ali would like to know whether the same price premium is being maintained in the Turkish market, where gO2 faces quite different competition. He notes that gO2 mineral water sells in Turkey for 2 (new) Lira per liter, while its main competitor, Essence, sells for 1.9 Lira per liter.

When assessing a brand’s price premium vis à vis multiple competitors, managers can use as their benchmark the average price of a selected group of those competitors.
Average Price Paid: Another useful benchmark is the average price that customers pay for brands in a given category. This average can be calculated in at least two ways: (1) as the ratio of total category revenue to total category unit sales, or (2) as the unit-share weighted average price in the category. Note that the market Average Price Paid includes the brand under consideration.
Note also that changes in unit shares will affect the average price paid. If a low-price brand steals shares from a higher-priced rival, the average price paid will decline. This would cause a firm’s price premium (calculated using the average price paid as a benchmark) to rise, even if its absolute price did not change. Similarly, if a brand is priced at a premium, that premium will decline as it gains share. The reason: A market share gain by a premium-priced brand will cause the overall average price paid in its market to rise. This, in turn, will reduce the price differential between that brand and the market average.
Ali wants to compare his brand’s price to the average price paid for similar products in the market. He notes that gO2 sells for 2.0 Lira per liter and has 20% of the unit sales in market. Its up-market competitor, Panache, sells for 2.1 Lira and enjoys 10% unit market share. Essence sells for 1.9 Lira and has 20% share. Finally, the budget brand, Besik, sells for 1.2 Lira and commands 50% of the market.

To calculate the price premium using the average price paid benchmark, managers can also divide a brand’s share of the market in value terms by its share in volume terms. If value and volume market shares are equal, there is no premium. If value share is greater than volume share, then there is a positive price premium.

Average Price Charged: Calculation of the average price paid requires knowledge of the sales or shares of each competitor. A much simpler benchmark is the average price charged—the simple unweighted average price of the brands in the category. This benchmark requires knowledge only of prices. As a consequence, the price premium calculated using this benchmark is not affected by changes in unit shares. For this reason, this benchmark serves a slightly different purpose. It captures the way a brand’s price compares to prices set by its competitors, without regard to customers’ reactions to those prices. It also treats all competitors equally in the calculation of the benchmark price. Large and small competitors are weighted equally when calculating average price charged.
Using the previous data, Ali also calculates the average price charged in the mineral water category as (2 + 2.1 + 1.9 + 1.2)/4 = 1.8 Lira.
Using the average price charged as his benchmark, he calculates gO2’s price premium as

Average Price Displayed: One benchmark conceptually situated between average price paid and average price charged is the average price displayed. Marketing managers who seek a benchmark that captures differences in the scale and strength of brands’ distribution might weight each brand’s price in proportion to a numerical measure of distribution. Typical measures of distribution strength include numeric distribution, ACV (%), and PCV (%).
Ali calculates the average price displayed using numeric distribution. Ali’s brand, gO2, is priced at 2 Lira and is distributed in 500 of the 1,000 stores that carry bottled water. Panache is priced at 2.1 Lira and stocked by 200 stores. Essence is priced at 1.9 Lira and sold through 400 stores. Besik carries a price of 1.2 Lira and has a presence in 900 stores. Ali calculates relative weighting on the basis of numeric distribution. The total number of stores is 1,000. The weightings are therefore, for gO2, 500/1,000 = 50%; for Panache, 200/1,000 = 20%; for Essence, 400/1,000 = 40%; and for Besik, 900/1,000 = 90%. As the weightings thus total 200%, in calculating average price displayed, the sum of the weighted prices must be divided by that figure, as follows:

There are several practical aspects of calculating price premiums that deserve mention. Managers may find it easier to select a few leading competitors and focus their analysis and comparison on these. Often, it is difficult to obtain reliable data on smaller competitors.
Managers must exercise care when interpreting price premiums. Different benchmarks measure different types of premiums and must be interpreted accordingly.
Can a price premium be negative? Yes. Although generally expressed in terms that imply only positive values, a price premium can be negative. If one brand doesn’t command a positive premium, a competitor will. Consequently, except in the unlikely event that all prices are exactly equal, managers may want to speak in terms ofpositive premiums. When a given brand’s price is at the low end of the market, managers may want to say that the competition holds a price premium of a certain value.
Should we use retail, manufacturer, or distributor pricing? Each is useful in understanding the market dynamics at its level. When products have different channel margins, their price premiums will differ, depending on the channel under consideration. When stating a price premium, managers are advised to specify the level to which it applies.
Prices at each level can be calculated on a gross basis, or net of discounts, rebates, and coupons. Especially when dealing with distributors or retailers, there are likely to be substantial differences between manufacturer selling prices (retail purchase prices), depending on whether they are adjusted for discounts and allowances.
Theoretical Price Premium: This is the price difference that would make potential customers indifferent between two competing products. It represents a different use of the term “price premium” that is growing in popularity. The theoretical price premium can also be discovered through a conjoint analysis using brand as an attribute. The theoretical price premium is the point at which consumers would be indifferent between a branded and an unbranded item, or between two different brands. We have termed this a “theoretical” price premium because there is no guarantee that the price premiums observed in the market will take this value. (Refer to Section 4.5 for an explanation of conjoint analysis.)
The reservation price is the value a customer places on a product. It constitutes an individual’s maximum willingness to pay. Percent good value represents the proportion of customers who believe a product is a “good value” at a specific price.
These are useful metrics in marketers’ evaluation of pricing and customer value.
Reservation prices provide a basis for estimating products’ demand functions in situations where other data are not available. They also offer marketers insight into pricing latitude. When it is not possible or convenient to ask customers about their reservation prices, percent good value can provide a substitute for that metric.
Reservation Price: The price above which a customer will not buy a product. Also known as the maximum willingness to pay.
Percent Good Value: The proportion of customers who perceive a product to represent a good value, that is, to carry a selling price at or below their reservation price.
By way of example, let’s posit a market consisting of 11 individuals with reservation prices for a given product of $30, $40, $50, $60,$70, $80, $90, $100, $110, $120, and $130. The manufacturer of that product seeks to decide upon its price. Clearly, it might do better than to offer a single price. For now, however, let’s assume tailored prices are impractical. The variable cost to produce the product is $60 per unit.
With these reservation prices, the manufacturer might expect to sell 11 units at $30 or less, 10 units at a price greater than $30 but less than or equal to $40, and so on. It would make no sales at a unit price greater than $130. (For convenience, we have assumed that people buy at their reservation price. This assumption is consistent with a reservation price being the maximum an individual is willing to pay.)
Table 7.1 shows this price-quantity relationship, together with the contribution to the firm at each possible price.
Table 7.1. Price-Quantity Relationship
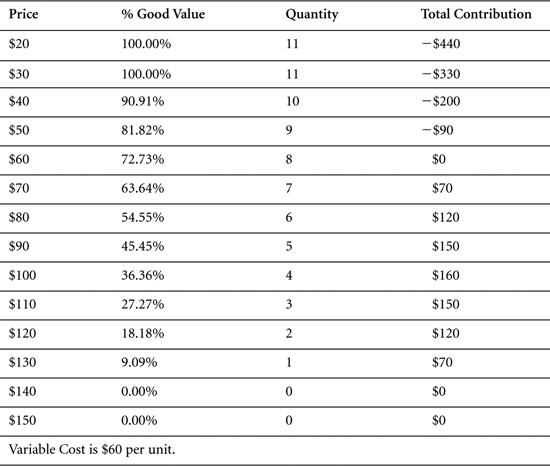
A table of quantities expected at each of several prices is often called a demand schedule (or curve). This example shows that one way to conceptualize a demand curve is as the accumulation of individual reservation prices. Although it will clearly be difficult in practice to measure individual reservation prices, the point here is simply to illustrate the use of reservation prices in pricing decisions. In this example, the optimal price—that is, the price that maximizes total contribution—is $100. At $100, the manufacturer expects to sell four units. Its contribution margin is $40, yielding a total contribution of $160.
This example also illustrates the concept of consumer surplus. At $100, the manufacturer sells three items at a price point below customers’ reservation prices. The consumer with the reservation price of $110 enjoys a surplus of $10. The consumer with the reservation price of $120 receives a surplus of $20. Finally, the consumer with the highest reservation price, $130, receives a surplus of $30. From the manufacturer’s perspective, the total consumer surplus—$60—represents an opportunity for increased contribution if it can find a way to capture this unclaimed value.
Finding reservation prices is no easy matter. Two techniques that are frequently used to gain insight into this metric are as follows:
• Second-price auctions: In a second-price auction, the highest bidder wins but pays only the second-highest bid amount. Auction theory suggests that when bidding on items of known value in such auctions, individuals have an incentive to bid their reservation prices. Certain survey techniques have been designed to mimic this process. In one of these, customers are asked to name their prices for an item, with the understanding that these prices will then be subjected to a lottery. If the price drawn in the lottery is less than the price named, the respondent gains an opportunity to purchase the item in question at the drawn price.
• Conjoint analysis: In this analytical technique, marketers gain insight into customer perceptions regarding the value of any set of attributes through the trade-offs they are willing to make.
Such tests can, however, be difficult to construct and impractical in many circumstances. Consequently, as a fallback technique, marketers can measure percent good value. Rather than seeking to learn each customer’s reservation price, they may find it easier to test a few candidate prices by asking customers whether they consider an item a “good value” at each of those prices.
The quantity-price schedule formed by an accumulation of reservation prices can take a variety of shapes. When the distribution of reservation prices is uniform—when reservation prices are equally spaced, as in our example—the demand schedule will be linear (see Figure 7.1). That is, each increment in price will reduce quantity by an equal amount. As the linear function is by far the most commonly used representation of demand, we provide a description of this function as it relates to the distribution of underlying reservation prices.
Figure 7.1. Maximum Willing to Buy and Maximum Reservation Price

It takes only two points to determine a straight line. Likewise, it takes only two parameters to write an equation for that line. Generally, that equation is written as Y =mX + b, in which m is the slope of the line and b is its Y-intercept.
A line, however, can also be defined in terms of the two points where it crosses the axes. In the case of linear demand, these crossing points (intercepts) have useful managerial interpretations.
The quantity-axis intercept can be viewed as a representation of the maximum willing to buy (MWB). This is the total number of potential customers for a product. A firm can serve all these customers only at a price of zero. Assuming that each potential customer buys one unit, MWB is the quantity sold when the price is zero.
The price-axis intercept can be viewed as the maximum reservation price (MRP). The MRP is a number slightly greater than the highest reservation price among all those willing to buy. If a firm prices its product at or above MRP, no one will buy.
Maximum Reservation Price: The lowest price at which quantity demanded equals zero.
Maximum Willing to Buy (MWB): The quantity that customers will “buy” when the price of a product is zero. This is an artificial concept used to anchor a linear demand function.
In a linear demand curve defined by MWB and MRP, the equation for quantity (Q) as a function of price (P) can be written as follows:

Erin knows that the demand for her soft drink is a simple linear function of price. She can sell 10 units at a price of zero. When the price hits $5 per unit, demand falls to zero. How many units will Erin sell if the price is $3 (see Figure 7.2)?
Figure 7.2. Simple Linear Demand (Price-Quantity) Function

For Erin’s soft drink, the MRP (Maximum Reservation Price) is $5 and the MWB (Maximum Willing to Buy ) is 10 units. At a price of $3, Erin will sell 10 * (1 - $3/$5), or 4 units.
When demand is linear, any two points on the price-quantity demand function can be used to determine MRP and MWB. If P1 and Q1 represent the first price-quantity point on the line, and P2 and Q2 represent the second, then the following two equations can be used to calculate MWB and MRP.


Early in this chapter, we met a firm that sells five units at a price of $90 and three units at a price of $110. If demand is linear, what are MWB and MRP?
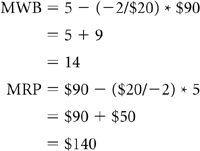
The equation for quantity as a function of price is thus:

The market in this example, as you may recall, comprises 11 potential buyers with reservation prices of $30, $40, ..., $120, $130. At a price of $130, the firm sells one unit. If we set price equal to $130 in the previous equation, our calculation does indeed result in a quantity of one. For this to hold true, the MRP must be a number slightly higher than $130.
A linear demand function often yields a reasonable approximation of actual demand only over a limited range of prices. In our 11-person market, for example, demand is linear only for prices between $30 and $130. To write the equation of the linear function that describes demand between $30 and $130, however, we must use an MWB of 14 and an MRP of $140. When we use this linear equation, we must remember that it reflects actual demand only for prices between $30 and $130, as illustrated in Figure 7.3.
Figure 7.3. Example of Linear Demand Function

Price elasticity measures the responsiveness of quantity demanded to a small change in price.

Price elasticity can be a valuable tool, enabling marketers to set an optimal price.
Price elasticity is the most commonly employed measure of market responsiveness to changes in price. Many marketers, however, use this term without a clear understanding of what it entails. This section will help clarify some of the potentially dangerous details associated with estimates of price elasticity. This is challenging material but is well worth the effort. A strong command of price elasticity can help managers set optimal prices.
Price Elasticity: The responsiveness of demand to a small change in price, expressed as a ratio of percentages. If price elasticity is estimated at –1.5, for example, then we expect the percentage change in quantity to be approximately 1.5 times the percentage change in price. The fact that this number is negative indicates that when price rises, the quantity demanded is expected to decline, and vice versa.
If we raise the price of a product, do we expect demand to hold steady or crash through the floor? In markets that are unresponsive to price changes, we say demand is inelastic. If minor price changes have a major impact on demand, we say demand is elastic. Most of us have no trouble understanding elasticity at a qualitative level. The challenges come when we quantify this important concept.
The first challenge in elasticity is to agree on its sign. Elasticity is the ratio of the percentage change in quantity demanded to the percentage change in price, for a small change in price. If an increase in price leads to a decrease in quantity, this ratio will be negative. Consequently, by this definition, elasticity will almost always be a negative number.
Many people, however, simply assume that quantity goes down as price goes up, and jump immediately to the question of “by how much.” For such people, price elasticity answers that question and is a positive number. In their eyes, if elasticity is 2, then a small percentage increase in price will yield twice that percentage decrease in quantity.
In this book, under that scenario, we would say price elasticity is –2.
For a linear demand function, the slope is constant, but elasticity is not. The reason: Elasticity is not the same as slope. Slope is the change in quantity for a small change in price. Elasticity, by contrast, is the percentage change in quantity for a small percentage change in price.
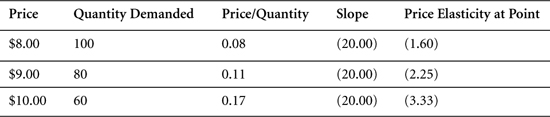
Consider three points on a linear demand curve: ($8, 100 units), ($9, 80 units), and ($10, 60 units) (see Figure 7.4). Each dollar change in price yields a 20-unit change in quantity. The slope of this curve is a constant –20 units per dollar.
Figure 7.4. Linear Demand Function
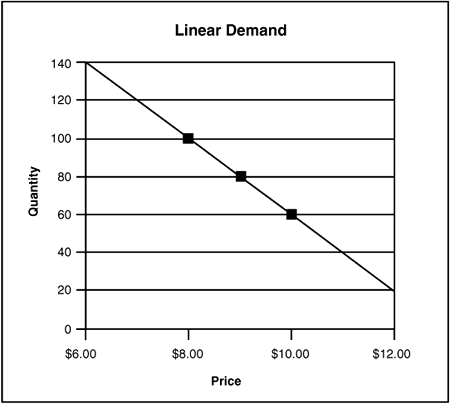
As price rises from $8 to $9 (a 12.5% increase), quantity declines from 100 to 80 (a 20% decrease). The ratio of these percentages is 20%/12.5%, or –1.6. Similarly, as price rises from $8 to $10 (a 25% increase), quantity declines from 100 to 60 (a 40% decrease). Once again, the ratio (40%/25%) is –1.6. It appears that the ratio of percentage change in quantity to percentage change in price is –1.6, regardless of the size of the change made in the $8 price.
Consider, however, what happens when price rises from $9 to $10 (an 11.11% increase). Quantity declines from 80 to 60 (a 25% decrease). The ratio of these figures, 25%/ 11.11%, is now -2.25. A price decline from $9 to $8 also yields an elasticity ratio of -2.25. It appears that this ratio is -2.25 at a price of $9, regardless of the direction of any change in price.
Exercise: Verify that the ratio of percentage change in quantity to percentage change in price at the price of $10 is –3.33 for every conceivable price change.
For a linear demand curve, elasticity changes with price. As price increases, elasticity gains in magnitude. Thus, for a linear demand curve, the absolute unit change in quantity for an absolute dollar change in price (slope) is constant, while the percentage change in quantity for a percentage change in price (elasticity) is not. Demand becomes more elastic—that is, elasticity becomes more negative—as price increases.
For a linear demand curve, the elasticity of demand can be calculated in at least three ways:

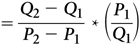
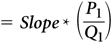
To emphasize the idea that elasticity changes with price on a linear demand curve, we write “Elasticity (P),” reflecting the fact that elasticity is a function of price. We also use the term “point elasticity” to cement the idea that a given elasticity applies only to a single point on the linear demand curve.
Equivalently, because the slope of a linear demand curve represents the change in quantity for a given change in price, price elasticity for a linear demand curve is equal to the slope, multiplied by the price, divided by the quantity. This is captured in the third equation here.
Revisiting the demand function from earlier, we see that the slope of the curve reflects a 20-unit decline in demand for each dollar increase in price. That is, slope equals -20.
The slope formula for elasticity can be used to verify our earlier calculations. Calculate price/quantity at each point on the curve, and multiply this by the slope to yield the price elasticity at that point (see Table 7.2).
Table 7.2. Elasticities at a Point Calculated from the Slope of a Function
For example, at a price of $8, quantity sold is 100 units. Thus:
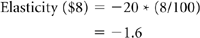
In a linear demand function, point elasticities can be used to predict the percentage change in quantity to be expected for any percentage change in price.
Xavi manages the marketing of a toothpaste brand. He knows the brand follows a linear demand function. At the current price of $3.00 per unit, his firm currently sells 60,000 units with an elasticity of -2.5. A proposal is floated to raise the price to $3.18 per unit in order to standardize margins across brands. At $3.18, how many units would be sold?
The proposed change to $3.18 represents a 6% increase over the current $3 price. Because elasticity is -2.5, such an increase can be expected to generate a decrease in unit sales of 2.5 * 6, or 15%. A 15% reduction in current sales of 60,000 units would yield a new quantity of 0.85 * 60,000, or 51,000.
A second common form of function used to estimate demand entails constant elasticity.3 This form is responsible for the term “demand curve” because it is, indeed, curved. In contrast with the linear demand function, the conditions in this scenario are reversed: Elasticity is constant, while the slope changes at every point.
The assumption underlying a constant elasticity demand curve is that a small percentage change in price will cause the same percentage change in quantity, regardless of the value of the initial price. That is, the rate of change in quantity versus price, expressed as a ratio of percentages, is equal to a constant throughout the curve. That constant is the elasticity.
In mathematical terms, in a constant elasticity demand function, slope multiplied by price divided by quantity is equal to a constant (the elasticity) for all points along the curve (see Figure 7.5). The constant elasticity function can also be expressed in an equation that is easily calculated in spreadsheets:
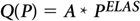
Figure 7.5. Constant Elasticity
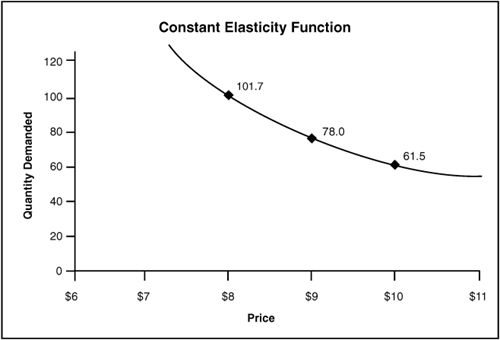
In this equation, ELAS is the price elasticity of demand. It is usually a negative number. A is a scaling factor. It can be viewed as the quantity that would be sold at a price of $1 (assuming that $1 is a reasonable price for the product under consideration).
Plot a demand curve with a constant elasticity of -2.25 and a scaling factor of 10,943.1. For every point on this curve, a small percentage increase in price will yield a percentage decrease in quantity that is 2.25 times as great. This 2.25 ratio holds, however, only for the very smallest percentage changes in price. This is because the slope changes at every point. Using the 2.25 ratio to project the results of a finite percentage increase in price is always approximate.
The curve traced in this example should look like the constant elasticity curve in Figure 7.5. More exact figures for demand at prices $8, $9, and $10 would be 101.669, 78.000, and 61.538 units.
In its way, constant elasticity is analogous to the continuous compounding of interest. In a constant elasticity function, every small percentage increase in price generates the same percentage decrease in quantity. These percentage decreases compound at a constant rate, leading to an overall percentage decrease that does not precisely equal the continuous rate.
For this reason, given any two points on a constant elasticity demand curve, we can no longer calculate elasticity using finite differences as we could when demand was linear. Instead, we must use a more complicated formula grounded in natural logarithms:

Taking any two points from the previous constant elasticity demand curve, we can verify that elasticity is -2.25.
At $8, for example, the quantity is 101.669. Call these P1 and Q1
At $9 the quantity is 78.000. Call these P2 and Q2
Inserting these into our formula, we determine that

If we had set P2 equal to $8, and P1 equal to$9, we would have arrived at the same figure for elasticity. In fact, regardless of which two points we select on this constant elasticity curve, and regardless of the order in which we consider them, elasticity will always be -2.25.
In summary, elasticity is the standard measure of market responsiveness to changes in price. In general, it is the “percentage slope” of the demand function (curve) obtained by multiplying the slope of the curve for a given price by the ratio of price to quantity.
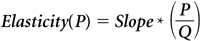
Elasticity can also be viewed as the percentage change in quantity for a small percentage change in price.
In a linear demand function, the slope is constant, but elasticity changes with price. In this scenario, marketers can use elasticity estimates to calculate the result of an anticipated price change in either direction, but they must use the elasticity that is appropriate for their initial price point. The reason: In a linear demand function, elasticity varies across price points, but projections based on these elasticities are accurate.
In a constant elasticity demand function, elasticity is the same at all price points, but projections based on these elasticities will be approximate. Assuming they are estimated with precision, using the constant elasticity demand function itself to make sales projections on the basis of price changes will be more accurate.
Price elasticity is generally estimated on the basis of available data. These data can be drawn from actual sales and price changes observed in the market, conjoint studies of customer intentions, consumer surveys about reservation prices or percent good value, or test-market results. In deriving elasticity, price-quantity functions can be sketched on paper, estimated from regressions in the form of linear or constant elasticity equations, or estimated through more complex expressions that include other variables in the marketing mix, such as advertising or product quality.
To confirm the validity and usefulness of these procedures, marketers must thoroughly understand the implications of the resulting elasticity estimate for customer behavior. Through this understanding, marketers can determine whether their estimate makes sense or requires further validation. That done, the next step is to use it to decide on pricing.
The optimal price is the most profitable price for any product. In a linear demand function, the optimal price is halfway between the maximum reservation price and the variable cost of the product.

Generally, the gross margin on a product at its optimal price will be the negative inverse of its price elasticity.

Although it can be difficult to apply, this relationship offers a powerful insight: In a constant elasticity demand function, optimal margin follows directly from elasticity. This greatly simplifies the determination of the optimal price for a product of known variable cost.
Although “optimal price” can be defined in a number of ways, a good starting point is the price that will generate the greatest contribution by a product after deducting its variable cost—that is, the most profitable price for the product.
If managers set price too low, they forego revenue from customers who would willingly have paid more. In addition, a low price can lead customers to value a product less than they otherwise might. That is, it causes them to lower their reservation prices.
By contrast, if managers set price too high, they risk losing contribution from people who could have been served profitably.
For linear demand, the optimal price is the midpoint between the maximum reservation price and the variable cost of the product.
In linear demand functions, the price that maximizes total contribution for a product is always precisely halfway between the maximum reservation price (MRP) and the variable cost to produce that product. Mathematically, if P* represents the optimal price of a product, MRP is the X-intercept of its linear demand function, and VC is its variable cost per unit:

Jaime’s business sells goods that cost $1 to produce. Demand is linear. If priced at $5, Jaime believes he won’t sell anything. For every dollar decrease in price, Jaime believes he will sell one additional unit.
Given that the variable cost is $1, the maximum reservation price is $5, and the demand function is linear, Jaime can anticipate that he’ll achieve maximum contribution at a price midway point between VC and MRP. That is, the optimal price is ($5 +$1)/2, or $3.00 (see Figure 7.6).4
Figure 7.6. Optimal Price Midway Between Variable Cost and MRP
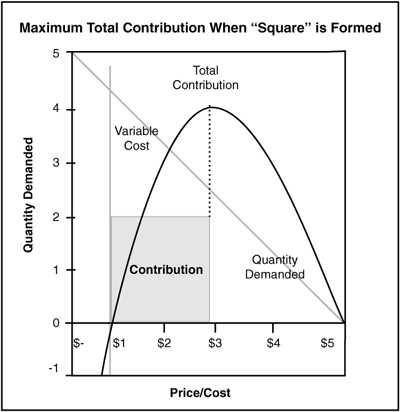
In a linear demand function, managers don’t need to know the quantity of a product demanded in order to determine its optimal price. For those who seek to examine Jaime’s contribution figures, however, please find the details in Table 7.3.
Table 7.3. Optimal Price =1/2 (MRP + Variable Cost)

The previous optimal price formula does not reveal the quantity sold at a given price or the resulting contribution. To determine optimal contribution, managers can use the following equation:

Jaime develops a new but similar product. Its demand follows a linear function in which the maximum willing to buy (MWB) is 200 and the maximum reservation price (MRP) is $10. Variable cost is $1 per unit. Jaime knows that his optimal price will be midway between MRP and variable cost. That is, it will be ($1 + $10)/2 = $5.50 per unit. Using the formula for optimal contribution, Jaime calculates total contribution at the optimal price:

Jaime builds a spreadsheet that supports this calculation (see Table 7.4).
Table 7.4. Contribution Maximized at the Optimal Price

This relationship holds across all linear demand functions, regardless of slope. For such functions, it is therefore possible to calculate the optimal price for a product on the basis of only two inputs: variable cost per unit and the maximum reservation price.
Brands A, B, and C each have a variable cost of $2 per unit and follow linear demand functions as shown in Table 7.5.
Table 7.5. The Optimal Price Formula Applies to All Linear Demand Functions
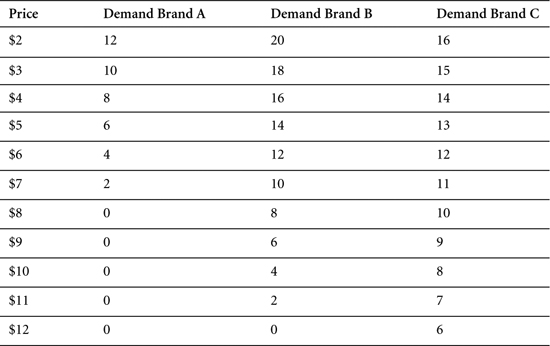
On the basis of these inputs, we can determine the maximum reservation price—the lowest price at which demand is zero. For Brand C, for example, we know that demand follows a linear function in which quantity declines by one unit for each dollar increase in price. If six units are demanded at $12, then $18 will be the lowest price at which no one will buy a single unit. This is the maximum reservation price. We can make similar determinations for Brands A and B (see Table 7.6).
Table 7.6. In Linear Demand Functions, the Determination of Optimal Price Requires Only Two Inputs

To verify that the optimal prices so determined will generate the maximum attainable contribution, please see Table 7.7.
Table 7.7. The Optimal Prices for Linear Demand Functions Can Be Verified

Because slope doesn’t influence optimal price, all demand functions with the same maximum reservation price and variable cost will yield the same optimal price.
A manufacturer of chair cushions operates in three different markets—urban, suburban, and rural. These vary greatly in size. Demand is far higher in the city than in the suburbs or the country. Variable cost, however, is the same in all markets at $4 per unit. The maximum reservation price, at $20 per unit, is also the same in all markets. Regardless of market size, the optimal price is therefore $12 per unit in all three markets (see Figure 7.7 and Table 7.8).
Figure 7.7. Linear Demand Functions with the Same MRP and Variable Cost
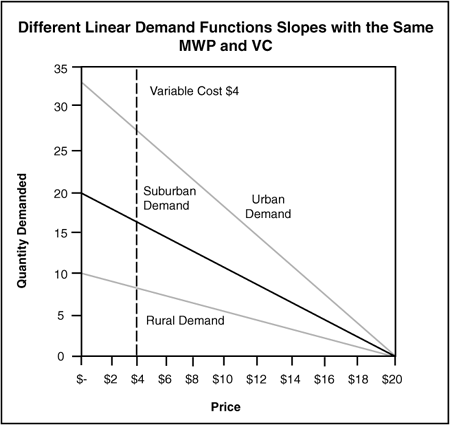
Table 7.8. The Slope Doesn’t Influence Optimal Price

The optimal price of $12 is verified by the calculations in Table 7.9.
Table 7.9. Linear Demand Functions with Different Slopes

In this example, it might help to think of the urban, suburban, and rural markets as groups of people with identical, uniform distributions of reservation prices. In each, the reservation prices are uniform between $0 and the maximum reservation price (MRP). The only difference between segments is the number of people in each. That number represents the maximum willing to buy (MWB). As might be expected, the number of people in a segment doesn’t affect optimal price as much as the distribution of reservation prices in that segment. As all three segments here show the same distribution of reservation prices, they all carry the same optimal price.
Another useful exercise is to consider what would happen if the manufacturer in this example were able to increase everyone’s reservation price by $1. This would raise the optimal price by half that amount, or $0.50. Likewise, the optimal price would rise by half the amount of any increase in variable cost.
When demand is linear, we have an easy-to-use formula for optimal price. Regardless of the shape of the demand function, there is a simple relationship between gross margin and elasticity at the optimal price.
Optimal Price, Relative to Gross Margin: The optimal price is the price at which a product’s gross margin is equal to the negative of the reciprocal of its elasticity of demand.5

A relationship such as this, which holds at the optimal price, is called an optimality condition. If elasticity is constant, then we can easily use this optimality condition to determine the optimal price. We simply find the negative of the reciprocal of the constant elasticity. The result will be the optimal gross margin. If variable costs are known and constant, then we need only determine the price that corresponds to the calculated optimal margin.
The manager of a stall selling replica sporting goods knows that the demand for jerseys has a constant price elasticity of -4. To price optimally, she sets her gross margin equal to the negative of the reciprocal of the elasticity of demand. (Some economists refer to the price-cost margin as the Lerner Index.)

If the variable cost of each jersey is $5, the optimal price will be $5/(1 - 0.25), or $6.67.
The optimal margins for several price elasticities are listed in Table 7.10.
Table 7.10. Optimal Margins for Sample Elasticities

Thus, if a firm’s gross margin is 50%, its price will be optimal only if its elasticity at that price is -2. By contrast, if the firm’s elasticity is -3 at its current price, then its pricing will be optimal only if it yields a gross margin of 33%.
This relationship between gross margin and price elasticity at the optimal price is one of the principal reasons that marketers take such a keen interest in the price elasticity of demand. Price elasticities can be difficult to measure, but margins generally are not. Marketers might now ask whether their current margins are consistent with estimates of price elasticity. In the next section, we will explore this issue in greater detail.
In the interim, if elasticity changes with price, marketers can use this optimality condition to solve for the optimal price. This condition applies to linear demand functions as well. Because the optimal price formula for linear demand is relatively simple, however, marketers rarely use the general optimality condition in this instance.
The shortcuts for determining optimal prices from linear and constant elasticity demand functions rest on an assumption that variable costs hold constant over the range of volumes considered. If this assumption is not valid, marketers will likely find that a spreadsheet model will offer the easiest way to determine optimal price.
We have explored these relationships in detail because they offer useful perspectives on the relationship between margins and the price elasticity of demand. In day-to-day management, margins constitute a starting point for many analyses, including those of price. One example of this dynamic would be cost-plus pricing.
Cost-plus pricing has received bad press in the marketing literature. It is portrayed not only as internally oriented, but also as naïve, in that it may sacrifice profits. From an alternate perspective, however, cost-plus pricing can be viewed as an attempt to maintain margins. If managers select the correct margin—one that relates to the price elasticity of demand—then pricing to maintain it may in fact be optimal if demand has constant elasticity. Thus, cost-plus pricing can be more customer-oriented than is widely perceived.
Price Tailoring—a.k.a. Price Discrimination: Marketers have invented a variety of price discrimination tools, including coupons, rebates, and discounts, for example. All are designed to exploit variations in price sensitivity among customers. Whenever customers have different sensitivities to price, or different costs to serve, the astute marketer can find an opportunity to claim incremental value through price tailoring.
The demand for a particular brand of sunglasses is composed of two segments: style-focused consumers who are less sensitive to price (more inelastic), and value-focused consumers who are more sensitive to price (more elastic) (see Figure 7.8). The style-focused group has a maximum reservation price of $30 and a maximum willing to buy of 10 units. The value-focused group has a maximum reservation price of $10 and a maximum willing to buy of 40 units.
Figure 7.8. Two Segments Form Demand


ALTERNATIVE A: ONE PRICE FOR BOTH SEGMENTS
Suppose the sunglasses manufacturer plans to offer one price to both segments. Table 7.11 shows the contribution of several candidate prices. The optimal single price (to the nearest cent) is $6.77, generating a total contribution of $98.56.
Table 7.11. Two Segments: One Price for Both Segments

ALTERNATIVE B: PRICE PER SEGMENT
If the manufacturer can find a way to charge each segment its own optimal price, it will increase total contribution. In Table 7.12, we show the optimal prices, quantities, and contributions attainable if each segment pays a distinct optimal price.
Table 7.12. Two Segments: Price Tailoring

These optimal prices were calculated as the midpoints between maximum reservation price (MRP) and variable cost (VC). Optimal contributions were calculated with the formula

In the style-focused segment, for example, this yields
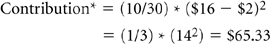
Thus, through price tailoring, the sunglasses manufacturer can increase total contribution from $98.56 to $129.33 while holding quantity constant.
Where variable costs differ between segments, as in an airline’s costs of service in business class versus economy class, the fundamental calculations are the same. To determine optimal prices, marketers need only change the variable cost per unit in each segment to correspond to actual costs.
In most industrial economies, governments have passed regulations concerning price discrimination. In the United States, the most important of these is the Robinson-Patman Act. According to Supreme Court interpretations of this statute (as of mid-2005), Robinson-Patman forbids price discrimination only to the extent that it threatens to injure competition. There are two main types of injury contemplated by the Act:
In the United States, price discrimination is often lawful, particularly if it reflects different costs of dealing with diverse buyers, or if it results from a seller’s attempts to meet a competitor’s prices or services.6 Clearly, this is not intended to be a legal opinion, however. Legal advice should be sought for a company’s individual circumstances.
The concept of residual price elasticity introduces competitive dynamics into the pricing process. It incorporates competitor reactions and cross elasticity. This, in turn, helps explain why prices in daily life are rarely set at the optimal level suggested by a simpler view of elasticity. Marketers consciously or unconsciously factor competitive dynamics into their pricing decisions.
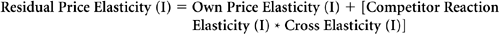
The greater the competitive reaction anticipated, the more residual price elasticity will differ from a company’s own price elasticity.
Often, in daily life, price elasticity doesn’t quite correspond to the relationships discussed in the prior section. Managers may find, for example, that their estimates of this key metric are not equal to the negative of the reciprocal of their margins. Does this mean they’re setting prices that are not optimal? Perhaps.
It is more likely, however, that they’re including competitive factors in their pricing decisions. Rather than using elasticity as estimated from current market conditions, marketers may estimate—or intuit—what elasticity will be after competitors respond to a proposed change in price. This introduces a new concept, residual price elasticity—customers’ elasticity of demand in response to a change in price, after accounting for any increase or decrease in competitors’ prices that may be triggered by the initial change.
Residual price elasticity is the combination of three factors:
These factors and their interactions are illustrated in Figure 7.9.
Figure 7.9. Residual Price Elasticity

Own Price Elasticity: How customers in the market react to our price changes.
Competitive Reaction Elasticity: How our competitors respond to our price changes.
Cross Elasticity: How our customers respond to the price changes of our competitors.
The distinction between own and residual price elasticity is not made clear in the literature. Some measures of price elasticity, for example, incorporate past competitive reactions and thus are more indicative of residual price elasticity. Others principally reflect own price elasticity and require further analysis to determine where sales and income will ultimately settle. The following sequence of actions and reactions is illustrative:
Due to this dynamic, if a firm measures price elasticity only through customer response to its initial actions, it will miss an important potential factor: competitive reactions and their effects on sales. Only monopolists can make pricing decisions without regard to competitive response. Other firms may neglect or decline to consider competitive reactions, dismissing such analyses as speculation. But this generates a risk of shortsightedness and can lead to dangerous surprises. Still other firms may embrace game theory and seek a Nash Equilibrium to anticipate where prices will ultimately settle. (In this context, the Nash Equilibrium would be the point at which none of the competitors in a market have a profit-related incentive to change prices.)
Although a detailed exploration of competitive dynamics is beyond the scope of this book, we offer a simple framework for residual price elasticity next.
To calculate residual price elasticity, three inputs are needed:

The percentage change in a firm’s sales can be approximated by multiplying its own price change by its residual price elasticity:
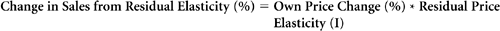
Forecasts of any change in sales to be generated by a price change thus should take into account the subsequent competitive price reactions that can be reasonably expected, as well as the second-order effects of those reactions on the sales of the firm making the initial change. The net effect of adjusting for such reactions might be to amplify, diminish, or even reverse the direction of the change in sales that was expected from the initial price change.
A company decides to reduce price by 10% (price change =-10%). It has estimated its own price elasticity to be -2. Ignoring competitive response, the company would expect a 10% price reduction to yield an approximately 20% increase in sales (-2 * -10%). (Note: As observed in our earlier discussion of elasticity, projections based on point elasticity are accurate only for linear demand functions. Because this example does not specify the shape of the demand function, the projected 20% increase in sales is an approximation.)
The company estimates competitor reaction elasticity to be 1. That is, in response to the firm’s action, competitors are expected to shift pricing in the same direction and by an equal percentage.
The company estimates cross elasticity to be 0.7. That is, a small percentage change in competitors’ prices will result in a change in the firm’s own sales of 0.7 percent. On this basis,

Competitor reactions and cross elasticity are expected to reduce the firm’s initially projected sales increase from 20% to 13%.
Accounting for potential competitive reactions is important, but there may be simpler and more reliable methods of managing price strategy in a contested market. Game theory and price leadership principles offer some guidance.
It is important for managers to distinguish between price elasticity measures that are inherently unable to account for competitive reactions and those that may already incorporate some competitive dynamics. For example, in “laboratory” investigations of price sensitivity—such as surveys, simulated test markets, and conjoint analyses—consumers may be presented with hypothetical pricing scenarios. These can measure both own price elasticity and the cross elasticities that result from specific combinations of prices. But an effective test is difficult to achieve.
Econometric analysis of historical data, evaluating the sales and prices of firms in a market over longer periods of time (that is, annual or quarterly data), may be better able to incorporate competitive changes and cross elasticities. To the extent that a firm has changed price somewhat randomly in the past, and to the extent that competitors have reacted, the estimates of elasticity that are generated by such analyses will measure residual elasticity. Still, the challenges and complexities involved in measuring price elasticity from historical data are daunting.
By contrast, short-term test market experiments are unlikely to yield good estimates of residual price elasticity. Over short periods, competitors might not learn of price changes or have time to react. Consequently, elasticity estimates based on test markets are much closer to own price elasticity.
Less obvious, perhaps, are econometric analyses based on transactional data, such as scanner sales and short-term price promotions. In these studies, prices decline for a short time, rise again for a longer period, decline briefly, rise again, and so forth. Even if competitors conduct their own price promotions during the study period, estimates of price elasticity derived in this way are likely to be affected by two factors. First, competitors’ reactions likely will not be factored into an elasticity estimate because they won’t have had time to react to the initial firm’s pricing moves. That is, their actions will have been largely motivated by their own plans. Second, to the extent that consumers stock up during price deals, any estimates of price elasticity will be higher than would be observed over the course of long-term price changes.
Prisoner’s dilemma pricing describes a situation in which the pursuit of self-interest by all parties leads to sub-optimal outcomes for all. This phenomenon can lead to stability at prices above the expected optimal price. In many ways, these higher-than-optimal prices have the appearance of cartel pricing. But they can be achieved without explicit collusion, provided that all parties understand the dynamics, as well as their competitors’ motivations and economics.
The prisoner’s dilemma phenomenon derives its name from a story illustrating the concept. Two members of a criminal gang are arrested and imprisoned. Each prisoner is placed in solitary confinement, with no means of speaking to the other. Because the police don’t have enough evidence to convict the pair on the principal charge, they plan to sentence both to a year in prison on a lesser charge. First, however, they try to get one or both to confess. Simultaneously, they offer each prisoner a Faustian bargain. If the prisoner testifies against his partner, he will go free, while the partner is sentenced to three years in prison on the main charge. But there’s a catch ... If both prisoners testify against each other,both will be sentenced to two years in jail.7 On this basis, each prisoner reasons that he’ll do best by testifying against his partner, regardless of what the partner does.
For a summary of the choices and outcomes in this dilemma, please see Figure 7.10, which is drawn in the first person from the perspective of one of the prisoners. First-person outcomes are listed in bold. Partner outcomes are italicized.
Figure 7.10. Prisoner’s Dilemma Pay-off Grid

Continuing the first-person perspective, each prisoner reasons as follows: If my partner testifies, I’ll be sentenced to two years in prison if I testify as well, or three years if I don’t. On the other hand, if my partner refuses to testify, I’ll go free if I testify, but serve one year in prison if I don’t. In either case, I do better if I testify. But this raises a dilemma. If I follow this logic and testify—and my partner does the same—we end up in the lower-left cell of the table, serving two years in prison.
Figure 7.11 uses arrows to track these preferences—a dark arrow for the first-person narrator in this reasoning, and a light arrow for his partner.
Figure 7.11. Pay-off Grid with Arrows Representing Preferences for Prisoners
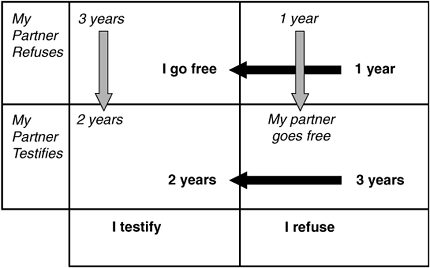
The dilemma, of course, is that it seems perfectly logical to follow the arrows and testify. But when both prisoners do so, they both end up worse off than they would have if they’d both refused. That is, when both testify, both are sentenced to two years in prison. If both had refused, they both could have shortened that term to a single year.
Admittedly, it takes a good deal of time to grasp the mechanics of the prisoner’s dilemma, and far longer to appreciate its implications. But the story serves as a powerful metaphor, encapsulating a wide range of situations in which acting in one’s own best interest leads to outcomes in which everyone is worse off.
In pricing, there are many situations in which a firm and its competitors face a prisoner’s dilemma. Often, one firm perceives that it could increase profits by reducing prices, regardless of competitors’ pricing policies. Simultaneously, its competitors perceive the same forces at work. That is, they too could earn more by cutting prices, regardless of the initial firm’s actions. If both the initial firm and its competitors reduce prices, however—that is, if all parties follow their own unilateral best interests—they will, in many situations, all end up worse off. The industry challenge in these situations is to keep prices high despite the fact that each firm will benefit by lowering them.
Given a choice between high and low prices a firm faces a prisoner’s dilemma pricing situation when the following conditions apply:
As shown in Table 7.13, my firm faces one main competitor. Currently my price is $2.90, their price is $2.80, and I hold a 40% share of a market that totals 20 million units. If I reduce my price to $2.60, I expect my share will rise to 55%—unless, of course, they also cut their price. If they also reduce price by $0.30—to $2.50—then I expect our market shares to remain constant at 40/60. On the other hand, if my competitor cuts its price but I hold steady at $2.90, then I expect they’ll increase their market share to 80%, leaving me with only 20%.
Table 7.13. Scenario Planning Pay-off Table


If we both have variable costs of $1.20 per unit, and market size remains constant at 20 million units, we face four possible scenarios with eight contribution figures—four for my firm and four for the competition:
Are we in a prisoner’s dilemma situation?
Figure 7.12 shows the four contribution possibilities for both my firm and my competitor.
Figure 7.12. Pay-off Grid with Expected Values (Values Are in the Millions of Dollars)

Let’s check to see whether the conditions for the prisoner’s dilemma are met:
The conditions for the prisoner’s dilemma are met (see Figure 7.13).
Figure 7.13. Pay-off Grid with Expected Values and Preference Arrows (Values Are in the Millions of Dollars)

The implication for my firm is clear: Although it is tempting to lower my price, seeking increased share and a $15.4 million contribution, I must recognize that my competitor faces the same incentives. They, too, have an incentive to cut price, grab share, and increase their contribution. But if they lower their price, I’ll probably lower mine. If I lower my price, they’ll probably lower theirs. If we both reduce our prices, I’ll earn only $11.2m in contribution—a sharp decline from the $13.6m I make now.
Managerial Note: To determine whether you face a prisoner’s dilemma situation, project the dollar contributions for both your firm and your competition at four combinations of high and low prices. Projections may require assumptions about your competitors’ economics. These, in turn, will require care. If competitors’ economics differ greatly from your projections, they may not face the decisions or motivations ascribed to them in your model. Additionally, there are a number of reasons why the logic of the prisoner’s dilemma won’t always hold, even if all assumptions are correct.
Applying the lessons of the prisoner’s dilemma, we see that optimal price calculations based on own price elasticity may lead us to act in our own unilateral best interest. By contrast, when we factor residual price elasticity into our calculations, competitive response becomes a key element of our pricing strategy. As the prisoner’s dilemma shows, over the long term, a firm is not always best served by acting in its apparent unilateral best interest.
Dolan, Robert J., and Hermann Simon. (1996). Power Pricing: How Managing Price Transforms the Bottom Line, New York: Free Press, 4.
Roegner, E. V., M. V. Marn, and C. C. Zawada. (2005). “Pricing,” Marketing Management, 14(1), 23–28.