Chapter 29

European Mathematics: 1200–1500

In the previous chapter, we mentioned the emperor Frederick II, whose court was located in Sicily. His encouragement of arts and sciences gave a voice to one of the most remarkable mathematicians of the Middle Ages, Leonardo of Pisa, with whom we begin our discussion of late Medieval mathematics.

29.1 Leonardo of Pisa (Fibonacci)

As soon as translations from Arabic into Latin became generally available in the twelfth and thirteenth centuries, Western Europeans began to learn about algebra. The first work translated (by Robert of Chester in 1145) was al-Khwarizmi's Algebra. Several talented mathematicians appeared early on who were able to make original contributions to the development of algebra. In some cases the books that they wrote were not destined to be published for many centuries, but at least one of them formed part of an Italian tradition of algebra that continued for several centuries. That tradition begins with Leonardo, who wrote several mathematical works, the best known of which is the Liber abaci.¹

29.1.1 The Liber abaci

Many of the problems in the Liber abaci (Book of Computation) reflect the routine computations that must be performed when converting currencies. These are applications of the Rule of Three that we have found in Brahmagupta and Bhaskara. Many of the other problems are purely fanciful. Leonardo's indebtedness to Arabic sources was detailed by Levey (1966), who listed 29 problems in the Liber abaci that are identical to problems in the Algebra of Abu Kamil. In particular, the problem of separating the number 10 into two parts satisfying an extra condition occurs many times. For example, one problem is to find x such that .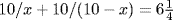

29.1.2 The Fibonacci Sequence

The most famous (not the most profound) of Leonardo's achievements is a problem from his Liber abaci, whose second edition appeared in 1202: How many pairs of rabbits can be bred from one pair in one year, given that each pair produces a new pair each month, beginning two months after its birth?

By enumeration of cases, the author concludes that there will be 377 pairs, and “in this way you can do it for the case of infinite numbers of months.” The reasoning is simple. Each month, those pairs that were alive two months earlier produce duplicates of themselves. Hence the total number of rabbits after n + 2 months is the number alive after n + 1 months plus the number alive after n months. That is, each term in the sequence is the sum of the two preceding numbers.

Assuming the original pair was a mature pair, ready to reproduce, the sequence generated in this way—starting at the beginning of the year, when 0 months have elapsed—is (1, 2, 3, 5, 8,. . .), and its 13th term is 377. This sequence has been known as the Fibonacci sequence since the printing of the Liber abaci in the nineteenth century. The Fibonacci sequence has been an inexhaustible source of identities. Many curious representations of its terms have been obtained, and there is a mathematical journal, the Fibonacci Quarterly, named in its honor and devoted to its lore.

A Practical Application

In 1837 and 1839 the crystallographer Auguste Bravais (1811–1863) and his brother Louis (1801–1843) published articles on the growth of plants.² In these articles they studied the spiral patterns in which new branches grow out of the limbs of certain trees and classified plants into several categories according to this pattern. For one of these categories they gave the amount of rotation around the limb between successive branches as 137° 30′ 28”. Now, one could hardly measure the limb of a tree so precisely. To measure within 10° would require extraordinary precision. To refine such crude measurements by averaging to the claimed precision of 1”, that is, 1/3600 of a degree, would require thousands of individual measurements. In fact, the measurements were carried out in a more indirect way, by counting the total number of branches after each full turn of the spiral. Many observations convinced the brothers Bravais that normally there were three branches in a little less than two turns, five in a little more three turns, eight in a little less than five turns, and thirteen in a little more than eight turns. For that reason they took the actual amount of revolution between successive branches to be the number we call 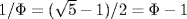of a complete (360°) revolution, since

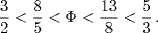
Observe that 360° ÷ Φ ≈ 222 . 4922359° ≈ 222° 29′ 32 ” = 360° − (137° 30′ 28 ”). An illustration of this kind of growth is shown in Fig. 29.1. The picture shows three views of a branch of a flowering crab apple tree with the twigs cut off and the points from which they grew marked by pushpins. When these pins are joined by string, the string follows a helical path of nearly constant slope along the branch. By simply counting, one can get an idea of the average number of twigs per turn. For example, the fourth intersection is between pins 6 and 7, indicating that the average number of pins per turn up to that point is between 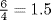and . 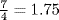One can see that the pins that fall nearest to the intersection of this helical path with the meridian line marked along the length of the branch are pins numbered 3, 5, 8, and 13, which are Fibonacci numbers, and that the intersections they are near come at the end of 2, 3, 5, and 8 revolutions, respectively, also Fibonacci numbers. 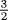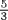Thus the average number of twigs per turn is approximately or 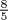or or 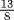. The brothers Bravais knew that the ratios of successive Fibonacci numbers are the terms in the continued-fraction expansion of the Golden Ratio 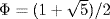, and hence they chose this elegant way of formulating what they had observed. By looking at the side of the intersection where the corresponding pins are in Fig. 29.1, you can see that the first and third of these approximations are underestimates and the second and fourth are overestimates. You can also see that the approximation gets better as the number of turns increases.

Figure 29.1 Three views of a branch of a flowering crab apple tree.

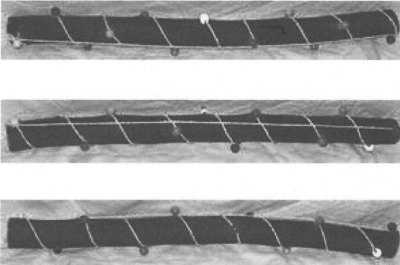
This pattern is not universal among plants, although the brothers Bravais were able to find several classes of plants that exhibit a pattern of this type, with different values for the first two terms of the sequence.

29.1.3 The Liber quadratorum

In his Liber quadratorum [Book of Squares (Sigler, 1987)] Leonardo speculated on the difference between square and nonsquare numbers. In the prologue, addressed to the Emperor Frederick II, Leonardo says that he had been inspired to write the book because a certain John of Palermo, whom he had met at Frederick's court, had challenged him to find a square number such that if 5 is added to it or subtracted from it, the result is again a square.³ This question inspired him to reflect on the difference between square and nonsquare numbers. He then notes his pleasure on learning that Frederick had actually read one of his previous books and uses that fact as justification for writing on the challenge problem.

The Liber quadratorum is written in the spirit of Diophantus and shows a keen appreciation of the conditions under which a rational number is a square. Indeed, the ninth of its 24 propositions is a problem of Diophantus: Given a nonsquare number that is the sum of two squares, find a second pair of squares having this number as their sum. This problem is Problem 9 of Book 2 of Diophantus, as discussed in Section 4 of Chapter 9. Leonardo's solution of this problem, like that of Diophantus, involves a great deal of arbitrariness, since the problem does not have a unique solution. The resemblance in some points is so strong that one is inclined to think that Leonardo saw a copy of Diophantus, or, more likely, an Arabic work commenting and extending the work of Diophantus. This question is discussed by the translator of the Liber quadratorum (Sigler, 1987, pp. xi–xii), who notes that strong resemblances have been pointed out between the Liber quadratorum and a book by Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji (953–1029) called the Fakhri,⁴ parts of which were copied from the Arithmetica, but that there are also parts of the Liber quadratorum that are original.

One advance in the Liber quadratorum is the use of general letters in an argument. Although in some proofs Leonardo argues much as Diophantus does, using specific numbers, he becomes more abstract in others. For example, Proposition 5 requires finding two numbers, the sum of whose squares is a square that is also the sum of the squares of two given numbers. He says to proceed as follows. Let the two given numbers be. a . and. b . and the sum of their squares. g . . Now take any other two numbers. de . and. ez . [not proportional to the given numbers] the sum of whose squares is a square. These two numbers are arranged as the legs of a right triangle. If the square on the hypotenuse of this triangle is. g ., the problem is solved. If the square on the hypotenuse is larger than. g ., mark off the square root of. g . on the hypotenuse. The projections (as we would call them) of this portion of the hypotenuse on each of the legs are known, since their ratios to the square root of. g . are known. Moreover, that ratio is rational, since they are the same as the ratios of. a . and. b . to the hypotenuse of the original triangle. These two projections therefore provide the new pair of numbers. Being proportional to. a . and. b ., which are not proportional to the two numbers given originally, they must be different from those numbers.

This argument is more convincing, because it is more abstract, than proofs by example, but the geometric picture plays an important role in making the proof comprehensible.

29.1.4 The Flos

Leonardo's approach to algebra begins to look modern in other ways as well. In one of his works, called the Flos super solutionibus quarumdam questionum ad numerum et ad geometriam vel ad utrumque pertinentum [The Full Development⁵ of the Solutions of Certain Questions Pertaining to Number or Geometry or Both (Boncompagni 1854, p. 4)] he reports the challenge from John of Palermo mentioned above, which was to find a number satisfying x³ + 2x² + 10x = 20 using the methods given by Euclid in Book 10 of the Elements, that is, to construct a line of this length using straightedge and compass. In working on this question, Leonardo made two important contributions to algebra, one numerical and one theoretical. The numerical contribution was to give the unique positive root in sexagesimal notation correct to six places. The theoretical contribution was to show by using divisibility properties of numbers that there cannot be a rational solution or a solution obtained using only rational numbers and square roots of rational numbers.

29.2 Hindu–Arabic numerals

The Liber abaci advocated the use of the Hindu–Arabic numerals that we are familiar with. Partly because of the influence of that book, the advantages of this system came to be appreciated, and within two centuries these numerals were winning general acceptance. In 1478, an arithmetic was published in Treviso, Italy, explaining the use of Hindu–Arabic numerals and containing computations in the form shown in Fig 26.1 of Chapter 26. In the sixteenth century, scholars such as Robert Recorde (1510–1558) in Britain and Adam Ries (1492–1559) in Germany, advocated the use of the Hindu–Arabic system and established it as a universal standard.

The system was explained by the Flemish mathematician and engineer Simon Stevin (1548–1620) in his 1585 book De Thiende (Decimals). Stevin took only a few pages to explain, in essentially modern terms, how to add, subtract, multiply, and divide decimal numbers. He then showed the application of this method of computing in finding land areas and the volumes of wine vats. He wrote concisely, as he said, “because here we are writing for teachers, not students.” His notation appears slightly odd, however, since he put a circled 0 where we now have the decimal point, and thereafter he indicated the rank of each digit by a similarly encircled number. For example, he would write 13.4832 as 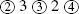. Here is his explanation of the problem of expressing 0.07 ÷ 0.00004:

When the divisor is larger [has more digits] than the dividend, we adjoin to the dividend as many zeros as desired or necessary. For example, if 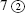is to be divided by 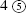, I place some 0s next to the 7, namely 7000. This number is then divided as above, as follows:

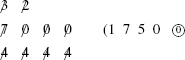
Hence the quotient is 1750 ; 0 (Gericke and Vogel, 1965, p. 19).

From a 1535 illustration to theMargarita philosophica (Philosophical Pearl) published byGregor Reisch (1467–1525) in 1503. Copyright © FotoMarburg/Art Resource.

Except for the location of the digits and the cross-out marks, this notation is essentially what is now used by school children in the United States. In other countries—Russia, for example—the divisor would be written just to the right of the dividend and the quotient just below the divisor.

Stevin also knew what to do if the division does not come out even. He pointed out that when is divided by , the result is an infinite succession of 3s and that the exact answer will never be reached. He commented, “In such a case, one may go as far as the particular case requires and neglect the excess. It is certainly true that 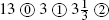, or 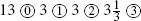, and so on, are exactly equal to the required result, but our goal is to work only with whole numbers in this decimal computation, since we have in mind what occurs in human business, where [small parts of small measures] are ignored.” Here we have a clear case in which the existence of infinite decimal expansions is admitted, without any hint of the possibility of irrational numbers. Stevin was an engineer, not a theoretical mathematician. His examples were confined to what is of practical value in business and engineering, and he made no attempt to show how to calculate with an actually infinite decimal expansion.

Stevin did, however, suggest a reform in trigonometry that was ignored until the advent of hand-held calculators, remarking that, “if we can trust our experience (with all due respect to Antiquity and thinking in terms of general usefulness), it is clear that the series of divisions by 10, not by 60, is the most efficient, at least among those that are by nature possible.” On those grounds, Stevin suggested that degrees be divided into decimal fractions rather than minutes and seconds. Modern hand-held calculators now display angles in exactly this way, despite the scornful remark of a twentieth-century mathematician that this mixture of sexagesimal and decimal notation proves that“it required four millennia to produce a system of angle measurement that is completely absurd.”

29.3 Jordanus Nemorarius

The translator and editor of Jordanus' book De numeris datis (On Given Numbers, Hughes, 1981, p. 11) says, “It is reasonable to assume. . .that Jordanus was influenced by al-Khwarizmi's work.” This conclusion was reached on the basis of Jordanus' classification of quadratic equations and his order of expounding the three types, among other resemblances between the two works.

De numeris datis is the algebraic equivalent of Euclid's Data. Where Euclid says that a line is given (determined) if its ratio to a given line is given, Jordanus Nemorarius says that a number is given if its ratio to a given number is given. The well-known elementary fact that two numbers can be found if their sum and difference are known is generalized to the theorem that any set of numbers can be found if the differences of the successive numbers and the sum of all the numbers is known. This book contains a large variety of data sets that determine numbers. For example, if the sum of the squares of two numbers is known, and the square of the difference of the numbers is known, the numbers can be found. The four books of De numeris datis contain about 100 such results. These results admit a purely algebraic interpretation. For example, in Book 4 Jordanus Nemorarius writes:

If a square with the addition of its root multiplied by a given number makes a given number, then the square itself will be given. [p. 100]⁶

Where earlier mathematicians would have proved this proposition with examples, Jordanus Nemorarius uses letters representing abstract numbers. The assertion is that there is only one (positive) number x such that x² + αx = β, and that x can be found if α and β are given.

29.4 Nicole d'Oresme

A work entitled Tractatus de latitudinibus formarum (Treatise on the Latitude of Forms) was published in Paris in 1482 and ascribed to Oresme, but probably written by one of his students. It contains descriptions of the graphical representation of “intensities.” This concept finds various expressions in physics, corresponding intuitively to the idea of density. In Oresme's language, an “intensity” is any constant of proportionality. Velocity, for example, is the “intensity” of motion.

We think of analytic geometry as the application of algebra to geometry. Its origins in Europe, however, antedate the high period of European algebra by a century or more. The first adjustment in the way mathematicians think about physical dimensions, an essential step on the way to analytic geometry, occurred in the fourteenth century. The crucial idea found in the representation of distance as the “area under the velocity curve” was that since the area of a rectangle is computed by multiplying length and width and the distance traveled at constant speed is computed by multiplying velocity and time, it follows that if one line is taken proportional to time and a line perpendicular to it is proportional to a (constant) velocity, the area of the resulting rectangle is proportional to the distance traveled.

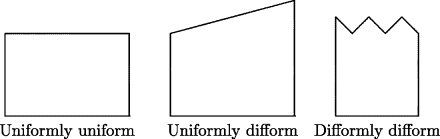
Oresme considered three forms of qualities, which he labeled uniform, uniformly difform, and difformly difform. We would call these classifications constant, linear, and nonlinear. Examples are shown in Fig. 29.2, which can be found in another of Oresme's works. Oresme (or his students) realized that the “difformly difform” constituted a large class of qualities and mentioned specifically that a semicircle could be the representation of such a quality.

Figure 29.2 Nicole Oresme's classification of motions.

The advantage of representing a distance by an area rather than a line appeared in the case when the velocity changed during a motion. In the simplest nontrivial case the velocity was uniformly difform. This is the case of constant acceleration. In that case, the distance traversed is what it would have been had the body moved the whole time with the velocity it had at the midpoint of the time of travel. This is the case now called uniformly accelerated motion. According to Clagett (1968, p. 617), this rule was first stated by William Heytesbury (ca. 1313–ca. 1372) of Merton College, Oxford around 1335 and was well known during the Middle Ages. Boyer (1949, p. 83) says that the rule was stated around this time by another fourteenth-century Oxford scholar named Richard Suiseth,⁷ known as Calculator for his book Liber calculatorum. Suiseth shares with Oresme the credit for having proved that the harmonic series (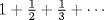) diverges.

The rule just stated is called the Merton rule. In his book De configurationibus qualitatum et motuum, Oresme applied these principles to the analysis of such motion and gave a simple geometric proof of the Merton Rule. He illustrated the three kinds of motion by drawing a figure similar to Fig. 29.2. He went on to say that if a difformly difform quality was composed of uniform or uniformly difform parts, as in the example in Fig. 29.2, its quantity could be measured by (adding) its parts. He then pushed this principle to the limit, saying that if the quality was difform but not made up of uniformly difform parts, say being represented by a curve, then “it is necessary to have recourse to the mutual measurement of curved figures” (Clagett, 1968, p. 410). This statement must mean that the distance traveled is the “area under the velocity curve” in all three cases. Oresme unfortunately did not give any examples of the more general case, but he could hardly have done so, since the measurement of figures bounded by curves was still very primitive in his day.

29.5 Trigonometry: Regiomontanus and Pitiscus

In the late Middle Ages, the treatises translated into Latin from Arabic and Greek were made the foundation for ever more elaborate mathematical theories.

29.5.1 Regiomontanus

Analytic geometry as we know it today would be unthinkable without plane trigonometry. Latin translations of Arabic texts of trigonometry, such as the text of Nasir al-Din al-Tusi, began to circulate in Europe in the late Middle Ages. These works provided the foundation for such books as De triangulis omnimodis (On General Triangles) by Regiomontanus, published in 1533, more than half a century after the author's death. This book contained trigonometry almost in the form still taught. Book 2, for example, contains as its first theorem the law of sines for plane triangles, which asserts that the sides of triangles are proportional to the sines of the angles opposite them. The main difference between this trigonometry and ours is that a sine remains a line rather than a ratio. It is referred to an arc rather than to an angle. It was once believed that Regiomontanus discovered the law of sines for spherical triangles (Proposition 16 of Book 4) as well,⁸ but we now know that this theorem was known at least 500 years earlier to Muslim mathematicians whose work Regiomontanus must have read.

29.5.2 Pitiscus

A more advanced book on trigonometry, which reworked the reasoning of Heron on the area of a triangle given its sides, was Trigonometriæ sive de dimensione triangulorum libri quinque (Five Books of Trigonometry, or, On the Size of Triangles), published in 1595 and written by the Calvinist theologian Bartholomeus Pitiscus (1561–1613). This was the book that established the name trigonometry for this subject even though the basic functions are called circular functions (Fig. 29.3). Pitiscus showed how to determine the parts into which a side of a triangle is divided by the altitude, given the lengths of the three sides, or, conversely, to determine one side of a triangle knowing the other two sides and the length of the portion of the third side cut off by the altitude. To guarantee that the angles adjacent to the side were acute, he stated the theorem only for the altitude from the vertex of the largest angle.

Figure 29.3 The three basic trigonometric functions: The secant OB, which cuts the circle; the tangent AB, which touches the circle; the sine CD, which is half of a chord.

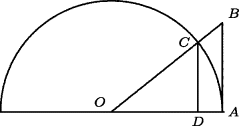
Pitiscus' way of deriving his fundamental relation was as follows. If the shortest side of the triangle ABC is AC and the longest is BC, let the altitude to BC be AG, as in Fig. 29.4. Draw the circle through C with center at A, so that B lies outside the circle, and let the intersections of the circle with AB and BC be E and F, respectively. Then extend BA to meet the circle at D, and connect CD. Then ∠BFE is the supplement of ∠CFE. But ∠EDC is also supplementary to ∠CFE, since the two are inscribed in arcs that partition the circle. Thus, ∠BFE = ∠ CDB, and so the triangles BCD and BEF are similar. It follows that 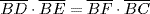, and since 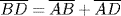, , 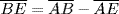, 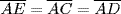and 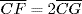, we find

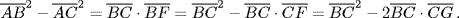
Observe that 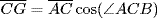. When this substitution is made, we obtain what is now known as the law of cosines:

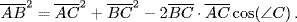
Figure 29.4 Pitiscus' derivation of the proportions in which an altitude divides a side of a triangle.

Pitiscus also gave an algebraic solution of the trisection problem discovered by an earlier mathematician named Jobst Bürgi (1552–1632). The solution had been based on the fact that the chord of triple an angle is three times the chord of the angle minus the cube of the chord of the angle. This relation makes no sense in terms of geometric dimension; it is a purely numerical relation. It is interesting that it is stated in terms of chords, since Pitiscus surely knew about sines.

29.6 A Mathematical Skill: ProsthaphÆresis

Pitiscus needed trigonometry in order to do astronomy, especially to solve spherical triangles. Since the computations in such problems often become rather lengthy, Pitiscus discovered (probably in the writings of other mathematicians) a way to shorten the labor. While the difficulty of addition and subtraction grows at an even, linear rate with the number of digits being added, multiplying two n-digit numbers requires on the order of 2n² separate binary operations on integers. Thus the labor becomes excessive and error-prone for integers with any appreciable number of digits. As astronomy becomes more precise, of course, the number of digits to which quantities can be measured increases. Thus a need arose some centuries ago for a shorter, less error-prone way of doing approximate computations.

The ultimate result of the search for such a method was the subject of logarithms. That invention, however, required a new and different point of view in algebra. Before it came along, mathematicians had found a way to make a table of sines serve the purpose that was later fulfilled by logarithms. Actually, the process could be greatly simplified by using only a table of cosines, but we shall follow Pitiscus, who used only a table of sines and thus was forced to compute the complement of an angle where we would simply look up the cosine. The principle is the same: converting a product to one or two additions and subtractions—hence the name prosthaphæresis, from prosthæresis (taking forward, that is, addition) and aphæresis (taking away, that is, subtraction).

As just pointed out, the amount of labor involved in multiplying two numbers increases in direct proportion to the product of the numbers of digits in the two factors, while the labor of adding increases in proportion to the number of digits in the smaller number. Thus, multiplying two 15-digit numbers requires over 200 one-digit multiplications, and another 200 or so one-digit additions, while adding the two numbers requires only 15 such operations (not including carrying). It was the large number of digits in the table entries that caused the problem in the first place, but the key to the solution turned out to be in the structural properties of the sine function.

There are hints of this process in several sixteenth-century works, but we shall quote just one example. In his Trigonometria, first published in Heidelberg in 1595, Pitiscus posed the following problem: To solve the proportion in which the first term is the radius, while the second and third terms are sines, avoiding multiplication and division. The problem here is to find the fourth proportional x, satisfying r : a = b : x, where r is the radius of the circle and a and b are two sines (half-chords) in the circle. We can see immediately that x = ab/r, but as Pitiscus says, the idea is to avoid the multiplication and division, since in the trigonometric tables the time a and b might easily have seven or eight digits each.

The key to prosthaphæresis is the well-known formula

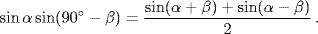
This formula is applied as follows: If you have to multiply two large numbers, find two angles having the numbers as their sines. Replace one of the two angles by its complement. Next, add the angles and take the sine of their sum to obtain the first term; then subtract the angles and take the sine of their difference to obtain a second term. Finally, divide the sum of these last two sines by 2 to obtain the product. To take a very simple example, suppose that we wish to multiply 155 by 36. A table of trigonometric functions shows that sin (8° 55 ') = 0.15500 and sin (90° − 68° 54 ') = 0.36000. Hence, since we moved the decimal points a total of five places to the left in the two factors, we obtain

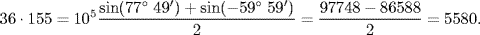
In general, some significant figures will be lost in this kind of multiplication. Obviously, no labor is saved in this simple example, but for large numbers this procedure really does make things easier. In fact, multiplying even two seven-digit numbers would tax the patience of most modern people, since it would require about 100 separate multiplications and additions. A further advantage is that prosthaphæresis is less error-prone than multiplication. Its advantages were known to the Danish astronomer Tycho Brahe (1546–1601),⁹ who used it in the astronomical computations connected with the precise observations he made at his observatory during the latter part of the sixteenth century.

This process could be simplified by using the addition and subtraction formula for cosines rather than sines. That formula is

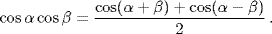
29.7 Algebra: Pacioli and Chuquet

The fourteenth century, in which Nicole d'Oresme made such remarkable advances in geometry and nearly created analytic geometry, was also a time of rapid advance in algebra, epitomized by Antonio de’ Mazzinghi (ca. 1353–1383). His Trattato d'algebra (Treatise on Algebra) contains some complicated systems of linear and quadratic equations in as many as three unknown (Franci, 1988). He was one of the earliest algebraists to move the subject toward the numerical and away from the geometric interpretation of problems.

29.7.1 Luca Pacioli

In the fifteenth century, Luca Pacioli wrote Summa de arithmetica, geometrica, proportioni et proportionalita (Encyclopedia of Arithmetic, Geometry, Proportion, and Proportionality), which was closer to the elementary work of al-Khwarizmi and more geometrical in its approach to algebra than was the work of Mazzinghi. Actually, (Parshall, 1988) the work was largely a compilation of the works of Leonardo of Pisa, but it did bring the art of abbreviation closer to true symbolic notation. For example, what we now write as 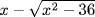was written by Pacioli as

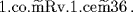
Here co means cosa (thing), the unknown. It is a translation of the Arabic word used by al-Khwarizmi. The abbreviation ce means censo (power), and Rv is probably a printed version of Rx, from the Latin radix, meaning root.¹⁰ Pacioli's work was both an indication of how widespread knowledge of algebra had become by this time and an important element in propagating that knowledge even more widely. The sixteenth-century Italian algebraists who moved to the forefront of the subject and advanced it far beyond where it had been up to that time had all read Pacioli's treatise thoroughly.

29.7.2 Chuquet

According to Flegg (1988), on whose work the following exposition is based, there were several new things in the Triparty. One is a superscript notation similar to the modern notation for the powers of the unknown in an equation. The unknown itself is called the premier or “first,” that is, power 1 of the unknown. In this work, algebra is called the rigle des premiers “rule of firsts.” Chuquet listed the first 20 powers of 2 and pointed out that when two such numbers are multiplied, their indices are added. Thus, he had a clear idea of the laws of integer exponents. A second innovation in the Triparty is the free use of negative numbers as coefficients, solutions, and exponents. Still another innovation is the use of some symbolic abbreviations. For example, the square root is denoted R² (R for the Latin radix, or perhaps the French racine). The equation we would write as 3x² + 12 = 9x was written 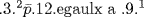. Chuquet called this equation impossible, since its solution would involve taking the square root of −63.

His instructions are given in words. For example (Struik, 1986, p. 62), consider the equation

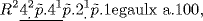
which we would write

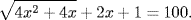
Chuquet says to subtract 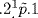from both sides, so that the equation becomes

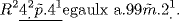
Next he says to square, getting

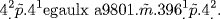
Subtracting 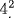(that is, 4x²) from both sides and adding 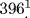to both sides then yields

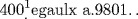
Thus x = 9801/400.

Chuquet's approach to algebra and its application can be gathered from one of the illustrative problems in the second part (Problem 35). This problem tells of a merchant who buys 15 pieces of cloth, spending a total of 160 ecus. Some of the pieces cost 11 ecus each, and the others 13 ecus. How many were bought at each price?

If x is the number bought at 11 ecus apiece, this problem leads to the equation 11x + 13(15 − x) = 160. Since the solution is 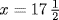, this means the merchant bought 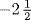pieces at 13 ecus. How does one set about buying a negative number of pieces of cloth? Chuquet said that these 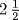pieces were bought on credit!

Problems and Questions

Mathematical Problems

29.1 Carry out Leonardo's description of the way to find two numbers the sum of whose squares is a square that is the sum of two other given squares in the particular case when the given numbers are. a . = 5 and. b . = 12 (the sum of whose squares is 169 = 13²). Take. de . = 8 and. ez . = 15. Draw the right triangle described by Leonardo, and also carry out the numerical computation that produces the new pair for which the sum of the squares is again 169.

29.2 Use Pitiscus' law of cosines to find the third side of a triangle having sides of length 6 cm and 8 cm and such that the altitude to the side of length 8 cm divides it into lengths of 5 cm and 3 cm. (There are two possible triangles, depending on the orientation.)

29.3 Use prosthaphæresis to find the product 829.038 × 66.9131. (First write this product as 10⁵ × 0.829038 × 0.669131. Find the angles that have the last two numbers as cosines, and use the addition and subtraction formula for cosines given above.)

Historical Questions

29.4 What parts of the algebraic work of Leonardo of Pisa were compilations of work in earlier sources, and what parts were advances on that earlier work?

29.5 In what ways did the geometric work of Nicole of Oresme prefigure modern analytic geometry?

29.6 How did Regiomontanus and Pitiscus change the way mathematicians thought about trigonometry? How did their trigonometry continue to differ from what we use today?

Questions for Reflection

29.7 Was there scientific value in making use of the real (irrational, infinitely precise) number Φ, as the Bravais brothers did, even though no actual plant grows exactly according to the rule they stated? Why wouldn't a rational approximation have done just as well?

29.8 How did the notion of geometric dimension (length, area, volume) limit the use of numerical methods in geometry? How did Oresme's latitude of forms help to overcome this limitation?

29.9 Does it make sense to interpret the purchase of a negative number of items as an amount bought on credit? Would it be better to interpret such a “purchase” as returned merchandise?

Notes

1. Devlin (2011), who has looked at the old manuscripts of this work, says that it is properly spelled Liber abbaci. The spelling we are using merely preserves a long-standing traditional usage.

2. See the article by I. Adler, D. Barabe, and R. V. Jean, “A history of the study of phyllotaxis,” Annals of Botany, 80 (1997), pp. 231–244, especially p. 234. The articles by Auguste and Louis Bravais are “Essai sur la disposition générale des feuilles curvisériées,” Annales des sciences naturelles, 7 (1837), pp. 42–110, and “Essai sur la disposition générale des feuilles rectisériées,” Congrès scientifique de France, 6 (1839), pp. 278–330.

3. Leonardo gave a general discussion of problems of this type, asking when m² + kn² and m₂ + 2kn² can both be squares.

4. Apparently, this word means something like glorious and the full title might be translated as The Glory of Algebra.

5. The word flos means bloom and can used in the figurative sense of “the bloom of youth.” That appears to be its meaning here.

6. This translation is my own and is intended to be literal; Hughes gives a smoother, more idiomatic translation on p. 168.

7. Also known as Richard Swyneshed and as Swineshead with a great variety of first names. There is uncertainty whether the works ascribed to this name are all due to the same person.

8. This law says that the sines of the sides of spherical triangles are proportional to the sines of their opposite angles. (Both sides and angles in a spherical triangle are measured in great-circle degrees.)

9. The formula for the product of two sines had been discovered in 1510 by Johann Werner (1468–1522). This formula and the similar formula for cosines were first published in 1588 in a small book entitled Fundamentum astronomicum written by Nicolai Reymers Baer (dates uncertain), known as Ursus, which is the Latin translation of Baer. Brahe, however, had already noticed their application in spherical trigonometry and had been using them during the 1580s. He even claimed credit for developing the technique himself. The origin of the technique of prosthaphæresis is complicated and uncertain. A discussion of it was given by Thoren (1988).

10. The symbol Rx should not be confused with the same symbol in pharmacy, which comes from the Latin recipe, meaning take.