Chapitre 7

Vous le voulez pour quand, ce projet ?

Dans ce chapitre :

Analyser et exploiter un diagramme réseau
Construire le calendrier de votre projet

Les projets ont toujours une date limite. Même si vous ne savez pas avec certitude ce que votre nouveau projet est censé produire, il faut savoir pour quelle date il doit être terminé. Malheureusement, lorsque vous prenez connaissance de cette date limite, vous avez souvent une réaction de panique : « Mais, je n’aurai jamais assez de temps ! »

À vrai dire, quand la mission de mener à bien votre projet vous échoit, vous n’avez généralement aucune idée du temps qu’il vous faudra pour y parvenir. Les premières actions ont tendance à s’inscrire dans le registre de la peur et de l’anxiété plutôt que de s’appuyer sur des faits, surtout quand vous essayez de jongler entre de multiples responsabilités et que le projet paraît complexe.

Pour vous aider à effectuer une estimation plus réaliste du temps que vous prendra ce projet, il faut opter pour une approche organisée rendant limpide le déroulement des activités du projet, les calendriers possibles et la façon de respecter les délais qui vous paraissaient intenables de prime abord. Ce chapitre décrit une technique vous aidant à développer avec un sens de l’initiative certain un calendrier réaliste (tout en maîtrisant votre anxiété).

L’utilisation de diagrammes réseau pour établir des calendriers est le thème le plus technique du présent ouvrage. Même s’il faut seulement dix minutes pour maîtriser cette technique, les explications et illustrations peuvent paraître déroutantes dans un premier temps. Si vous rencontrez pour la première fois ces bêtes curieuses que sont les schémas fonctionnels, nous vous suggérons de faire d’abord le tour des principaux points de ce chapitre, puis de lire plusieurs fois les différentes sections. Plus vous lirez le texte, plus les explications vous paraîtront logiques. Cependant, si les détails techniques vous agacent, mettez le livre de côté et soufflez avant de le reprendre plus tard. Vous découvrirez avec surprise que les détails sont beaucoup plus clairs à la deuxième ou troisième lecture ! Mais, rassurez-vous, si vous utilisez un progiciel de gestion de projet, quel qu’il soit, tous les calculs présents dans cette section seront faits pour vous automatiquement !

Le diagramme réseau

Pour déterminer le temps nécessaire pour n’importe quel projet, vous devez disposer des deux informations suivantes :

La séquence : l’ordre dans lequel vous réalisez les activités ;
La durée : le temps que dure chaque activité.

Par exemple, supposons que votre projet comprenne dix activités et qu’il faille compter une semaine de travaux pour chacun. Combien de temps vous faudra-t-il pour achever votre projet ? La vérité, c’est que vous ne pouvez pas le dire. Vous pouvez boucler le projet en une semaine si les dix activités peuvent être menées de front et si vous disposez des ressources pour y parvenir. Vous pouvez avoir besoin de dix semaines s’il faut mener les activités l’une après l’autre. La réalisation du projet peut très bien prendre entre une et dix semaines s’il n’est pas nécessaire de faire toutes les activités dans un ordre donné.

Illustrer un plan de travail à l’aide d’un diagramme réseau

Pour établir le calendrier d’un petit projet, vous pouvez probablement visualiser les nécessités relatives à la durée et à l’ordre des activités. Mais, avec des projets comprenant 15 à 20 activités, voire plus, dont bon nombre sont réalisables simultanément, il faut une certaine organisation pour mener votre analyse.

Cette section vous aide à créer des calendriers réalistes en vous montrant comment dessiner des diagrammes de réseau, puis comment choisir le meilleur pour votre projet.

Définir les éléments d’un diagramme de réseau

Un diagramme de réseau est un schéma fonctionnel illustrant l’ordre dans lequel vous allez réaliser les activités. Peut-être avez-vous déjà entendu parler de diagramme PERT (Program Evaluation and Review Technique). Dans le même état d’esprit, c’est le laboratoire d’essai de votre projet. Il vous permet de tester les différentes stratégies avant d’entamer l’exécution des travaux. Il vous permet aussi, d’utiliser la méthode du chemin critique ou CPM (Critical Path Method), nous le verrons plus loin.

Quelle que soit la complexité de votre projet, le diagramme de réseau présente les trois éléments suivants : jalons, activités et durée.

Les jalons : un jalon, aussi appelé « milestone » ou « événement », il s’agit d’un moment important dans la vie du projet. Les jalons ne prennent pas de temps et ne consomment aucune ressource puisqu’ils se produisent instantanément. Considérez-les comme des poteaux matérialisant une étape dans le périple devant vous conduire à l’achèvement du projet. Les jalons marquent le début ou la fin d’une ou plusieurs activités. Voici des exemples : la version de travail approuvée et conception démarrée ;
Les activités : une activité, ou tâche, est le composant d’un travail réalisé au cours d’un projet. Les activités prennent du temps et sont consommatrices de ressources. Voici des exemples d’activités : rédiger un rapport et réaliser une enquête.

Veillez à définir avec clarté jalons et activités. Plus vous serez clair, plus vous pourrez évaluer avec précision le temps et les ressources nécessaires pour les mener à bien, plus l’affectation de personnes sera simple et plus votre rapport sur l’avancement des travaux et le déroulement du calendrier sera pertinent et exact ;

La durée : la durée est le total des périodes de travail nécessaires pour mener une activité à son terme. La quantité de travail à fournir, la disponibilité du personnel et la possibilité ou non pour ce dernier d’exécuter simultanément les tâches sont autant de facteurs qui influent sur la durée de l’activité. La capacité des ressources non humaines (par exemple, la vitesse de traitement d’un ordinateur et d’impression à la minute d’une imprimante) et la disponibilité de ces ressources conditionnent également la durée. En outre, un retard peut également allonger la durée d’une activité. Par exemple, si votre chef passe une heure à lire votre note alors que cela fait quatre jours et sept heures qu’elle est arrivée dans sa boîte de réception, la durée de l’activité sera de cinq jours, même si la lecture ne prend qu’une petite heure.
Comprendre une estimation de durée vous aide à trouver des moyens de la réduire. Par exemple, supposons que vous estimiez la durée des tests d’un logiciel sur un ordinateur à 24 heures. Si vous ne pouvez utiliser cet ordinateur que six heures par jour, vos tests dureront donc quatre jours. Ce n’est pas en doublant le nombre de personnes affectées aux tests que vous ramènerez ce délai à deux jours. En revanche, vous y parviendrez si vous obtenez l’autorisation d’utiliser l’ordinateur 12 heures par jour.

Il existe une confusion extrêmement fréquente entre durée et effort !

Les unités de temps décrivent en effet deux caractéristiques liées mais différentes.

La durée est le nombre de périodes de travail nécessaires pour mener une activité à son terme, tandis que l’effort ou charge de travail est le temps qu’il faut à une personne pour achever une activité en s’y consacrant à plein-temps. (Le chapitre 8 approfondit la question de la charge de travail.) Par exemple, supposons que quatre personnes doivent travailler ensemble à plein-temps pendant cinq jours pour mener une activité à son terme.

La durée de l’activité sera donc de cinq jours, alors que la charge de travail sera de 20 jours-personne (4 personnes X 5 jours).

Dessiner un diagramme de réseau

Pour fixer la date de fin de votre projet, il faut choisir les dates de début et de fin de chaque activité et la date à laquelle chaque jalon est atteint. Un diagramme de réseau vous y aide.

La technique de représentation nodale (également appelée méthode des antécédents) pour dessiner un diagramme de réseau emploie trois symboles pour décrire les trois éléments du diagramme :

Cases : les cases représentent les activités et jalons. Si la durée est 0, il s’agit d’un jalon. Si elle est supérieure à 0, il s’agit d’une activité. Vous remarquerez que les cases des jalons ont parfois une double bordure ou une bordure en gras ;
Lettre t : la lettre t représente la durée ;
Flèches : les flèches représentent le sens du travail d’une activité ou d’un jalon au suivant. Lorsqu’une activité est terminée ou un jalon atteint, vous pouvez passer au jalon suivant ou directement à une autre activité, selon ce qu’indique(nt) la ou les flèche(s) partant de l’activité ou du jalon précédent. On appelle aussi ces liens des dépendances entre tâches.

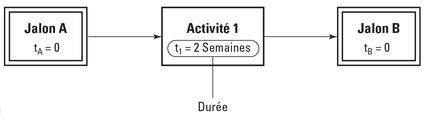
La figure 7-1 présente un exemple simple de diagramme de réseau avec représentation nodale. Lorsque vous atteignez le jalon A (la case de gauche), vous pouvez réaliser l’activité 1 (la case du milieu), dont vous estimez qu’elle vous demandera deux semaines de travail. Une fois l’activité 1 terminée, vous atteignez le jalon B (la case de droite). Les flèches indiquent le sens du flux.

Figure 7-1 : Les trois symboles d’un diagramme de réseau avec représentation nodale, le t illustrant la durée.

Ceux d’entre vous qui ont déjà utilisé des diagrammes de réseau connaissent peut-être un autre format appelé représentation vectorielle, approche classique évoquée plus haut, diagramme en flèche ou graphique PERT (une explication de l’analyse PERT figure dans la section « Améliorer l’estimation de durée des activités ». Avec ce format, les jalons sont représentés par un cercle et les activités par une flèche. Mais, dans la mesure où c’est aujourd’hui la technique de la représentation nodale la plus utilisée, nous avons choisi de l’employer dans ce livre.

Analyser un diagramme de réseau

Considérez votre projet comme un voyage que vous et vos amis envisagez d’effectuer. Chacun de vous possède une voiture et empruntera un chemin différent pour rallier la destination finale. Pendant le voyage, plusieurs itinéraires se croiseront en certains endroits. Vous convenez ensemble que toutes les personnes passant par un même point doivent attendre que tout le monde y soit parvenu avant de se diriger vers la prochaine étape. Le voyage est considéré comme terminé une fois que tout le monde a atteint la destination finale.

Vous ne souhaiterez certainement pas entreprendre un voyage d’une telle complexité sans le planifier d’abord à l’aide d’une carte routière. Après tout, la planification du voyage vous permet :

De fixer la durée du voyage ;
D’identifier les difficultés potentielles qui vous attendent en cours de route ;
De prévoir des itinéraires de remplacement pour atteindre plus vite la destination finale.

Cette section vous aide à établir le calendrier de votre projet en vous indiquant comment lire et interpréter une carte routière (votre diagramme de réseau), afin que vous puissiez déterminer les conséquences potentielles des diverses approches.

Lire un diagramme de réseau

Utilisez les deux règles suivantes pour dessiner et interpréter votre diagramme de réseau. Une fois ces règles comprises, l’analyse du diagramme est un jeu d’enfant :

Règle nº 1 : une fois une activité terminée ou un jalon atteint, vous pouvez passer à l’activité ou au jalon suivant, conformément à ce qu’indique(nt) la ou les flèche(s) ;
Règle nº 2 : avant de démarrer une activité ou d’atteindre un jalon, vous devez d’abord terminer toutes les activités et atteindre tous les jalons dotés de flèches pointant vers le prochain jalon ou l’activité suivante.

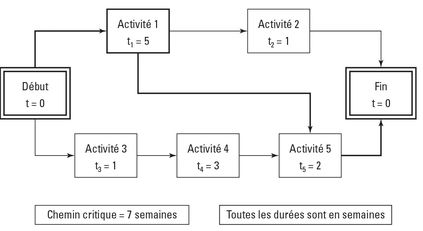
La figure 7-2 illustre un diagramme de réseau. Selon la règle n° 1, quand vous êtes au début, vous pouvez démarrer l’activité 1 ou l’activité 3. Cela signifie que vous réalisez l’activité 1 ou l’activité 3 seule ou les deux activités en même temps. Autrement dit, ces deux activités sont indépendantes l’une de l’autre.

Figure 7-2 : Un exemple de diagramme de réseau.

Vous pouvez aussi choisir de ne faire aucune des deux activités. La règle n° 1 est une dépendance optionnelle et non une dépendance obligatoire. Autrement dit, vous pouvez entamer n’importe quelle activité vers laquelle mène une flèche partant de la case début, mais ce n’est pas une obligation.

Par exemple, supposons qu’une partie de votre plan comprenne deux activités visant à fabriquer un appareil : recevoir les pièces et assembler les pièces. Dès que vous avez reçu les pièces, vous pouvez commencer à les assembler. En fait, vous ne pouvez entamer l’assemblage avant d’avoir reçu les pièces (vous êtes d’accord ?). Mais, une fois reçues toutes les pièces commandées, aucune règle ne vous impose de les assembler immédiatement. Vous pouvez le faire si vous le souhaitez, ou attendre.

Bien entendu, si vous attendez, la fin de l’assemblage sera retardée. Mais, c’est votre choix.

Selon la règle n° 2, vous pouvez commencer l’activité 2 de la figure 7-2 dès que vous avez terminé l’activité 1 car la flèche de l’activité 1 est la seule qui mène à l’activité 2. La règle n° 2 est donc une dépendance obligatoire. Si des flèches de trois activités pointaient vers l’activité 2, vous devriez terminer ces trois activités avant de démarrer l’activité 2. (Le diagramme n’indiquerait pas que vous pouvez entamer l’activité 2 après avoir uniquement terminé une ou deux activités sur les trois.)

Interpréter un diagramme de réseau

Vous pouvez utiliser votre diagramme de réseau pour savoir quand commencer et terminer des activités et quand vous bouclerez le projet si vous vous y prenez de cette façon. Pour déterminer le calendrier applicable en fonction de votre approche, vous avez besoin des informations suivantes :

Chemin critique : séquence d’activités la plus longue. Tout retard d’une tâche sur le chemin critique entraînera le recul de la date de fin du projet ;
Chemin non critique : séquence d’activités autorisant le retard de certaines activités et qui vous permet toujours de terminer votre projet dans le plus court délai possible ;
Marge : durée maximale pendant laquelle vous pouvez retarder une activité tout en terminant toujours votre projet dans le plus court délai possible ;
Date de début au plus tôt : date la plus précoce à laquelle vous pouvez démarrer une activité ;
Date de fin au plus tôt : date la plus précoce à laquelle vous pouvez terminer une activité ;
Date de début au plus tard : date la plus éloignée à laquelle vous pouvez démarrer une activité, tout en terminant toujours votre projet dans le plus court délai possible ;
Date de fin au plus tard : date la plus éloignée à laquelle vous pouvez terminer une activité, tout en bouclant toujours votre projet dans le plus court délai possible.

Vous pouvez employer la méthode du chemin critique pour déterminer ces informations et bâtir le calendrier général de votre projet. Les sections à suivre détaillent le fonctionnement de cette méthode.

L’importance du chemin critique

La longueur du ou des chemins critiques de votre projet sur votre diagramme de réseau conditionne sa durée (d’où la méthode du chemin critique pour établir le calendrier de votre projet). Si vous souhaitez que votre projet soit bouclé plus rapidement, envisagez des moyens de raccourcir votre chemin critique.

Surveillez attentivement la réalisation des activités du chemin critique car tout retard les concernant risque de repousser la fin de votre projet. Ayez bien à l’œil également les activités se situant sur des chemins proches d’être critiques, car le moindre retard peut également remettre la fin du projet à plus tard.

Votre projet peut présenter simultanément plusieurs chemins critiques. En fait, tout chemin peut s’avérer critique si parcourir chacun d’eux prend le même temps. Cependant, quand chaque chemin est critique, vous êtes face à une situation à haut risque. Un retard concernant n’importe quelle activité repousse immédiatement la date de fin du projet.

Les chemins critiques peuvent évoluer en cours de route. Il arrive que des activités situées sur un chemin critique finissent si tôt que ce dernier devient plus court qu’un ou plusieurs autres considérés au départ comme non critiques. Il se peut également que des activités situées au départ sur un chemin non critique soient retardées au point que la somme des durées de réalisation devienne supérieure à la longueur du chemin critique actuel (ce qui transforme en chemin critique le chemin préalablement non critique).

Le calcul au plus tôt : fixer les chemins critiques, chemins non critiques et les dates de début et de fin au plus tôt

La première étape de l’analyse du diagramme de réseau de votre projet est de commencer par le début et de voir dans quel délai vous pouvez mener les activités à leur terme pour chaque chemin. On appelle cette analyse le calcul au plus tôt.

Pour aider à la compréhension du calcul au plus tôt, vous pouvez l’effectuer sur le diagramme de la figure 7-2. Selon la règle n° 1, vous pouvez envisager d’entamer l’activité 1 ou l’activité 3 (ou les deux ensemble) dès le démarrage du projet (pour en savoir plus sur les deux règles de l’analyse d’un diagramme de réseau, reportez-vous à la section « Lire un diagramme de réseau », plus haut dans ce chapitre). Prenez d’abord les activités 1 et 2 du chemin supérieur :

Vous pouvez débuter au plus tôt l’activité 1 au moment du démarrage du projet (début de la semaine 1) ;
Vous pouvez finir l’activité 1 au plus tôt à la fin de la semaine 5 (vous ajoutez la durée prévue de cinq semaines à sa date de début au plus tôt, laquelle correspond au démarrage du projet) ;
Selon la règle n° 2, vous pourrez commencer l’activité 2 au plus tôt en début de semaine 6 car une seule flèche mène à l’activité 2, celle provenant de l’activité 1 ;
Vous pouvez finir l’activité 2 au plus tôt à la fin de la semaine 6 (vous ajoutez la durée prévue d’une semaine à sa date de début au plus tôt, à savoir le début de la semaine 6).

Jusqu’ici tout va bien. Prenons maintenant les activités 3, 4 et 5 situées sur le chemin inférieur du diagramme :

Vous pouvez débuter au plus tôt l’activité 3 au moment du démarrage du projet (début de la semaine 1) ;
Vous pouvez finir l’activité 3 au plus tôt à la fin de la semaine 1 ;
Vous pouvez commencer l’activité 4 au plus tôt au début de la semaine 2 ;
Vous pouvez finir l’activité 4 au plus tôt à la fin de la semaine 4.

Vous devez faire très attention au moment de fixer la date de début au plus tôt de l’activité 5. Selon la règle n° 2, les deux flèches pointant vers l’activité 5 indiquent que vous devez terminer à la fois l’activité 1 et l’activité 4 avant de démarrer l’activité 5. Même si vous parvenez à finir l’activité 4 à la fin de la semaine 4, vous ne pouvez terminer l’activité 1 avant la fin de la semaine 5. En conséquence, vous pouvez démarrer l’activité 5 au plus tôt en début de semaine 6.

Si plusieurs activités ou jalons mènent à la même activité, vous pourrez démarrer au plus tôt celle-ci à la date de fin au plus tôt la plus tardive des activités ou jalons précédents.

Vous avez la tête qui tourne ? Courage, la fin est proche :

Vous pouvez commencer l’activité 5 au plus tôt au début de la semaine 6 ;
Vous pouvez finir l’activité 5 au plus tôt à la fin de la semaine 7 ;
Vous pouvez finir l’activité 2 au plus tôt à la fin de la semaine 6. Par conséquent, vous pourrez finir le projet au plus tôt (et atteindre le jalon nommé fin) à la fin de la semaine 7.

Vous disposez pour l’heure des informations suivantes sur votre projet :

La longueur du chemin critique (le délai le plus court pour achever le projet) est de sept semaines. Un seul chemin critique prend sept semaines : il comprend le jalon début, l’activité 1, l’activité 5 et le jalon fin ;
L’activité 1, l’activité 3 et l’activité 4 ne figurent pas sur des chemins critiques.

Le calcul au plus tard : fixer les dates de début et de fin au plus tard et les marges

Vous êtes à mi-chemin du but. Si jamais des conflits de ressources ou des retards imprévus vous empêchent de démarrer toutes les activités aux dates de début au plus tôt, vous souhaiterez savoir de combien de temps vous pouvez les retarder, sur chaque chemin, tout en pouvant toujours terminer le projet le plus tôt possible. Cette analyse s’appelle un calcul au plus tard.

Reprenons l’exemple de la section précédente : le calcul au plus tôt vous a révélé que vous pouviez atteindre le jalon fin au plus tôt à la fin de la semaine 7. Cependant, la règle n° 2 de la précédente section « Lire un diagramme de réseau » stipule que vous ne pouvez atteindre le jalon fin tant que vous n’avez pas bouclé les activités 2 et 5. Ainsi, pour que votre projet soit achevé à la fin de la semaine 7, vous pouvez terminer les activités 2 et 5 au plus tard à la fin de la semaine 7. Reprenez le chemin inférieur du diagramme de la figure 7-2, avec les activités 3, 4 et 5 :

Vous devez démarrer l’activité 5 en début de semaine 6 et la finir en fin de semaine 7 (car l’activité 5 est prévue pour durer deux semaines) ;
Selon la règle n° 2, vous ne pouvez démarrer l’activité 5 tant que vous n’avez pas terminé les activités 1 et 4. Les activités 1 et 4 doivent donc être terminées à la fin de la semaine 5 ;
Vous devez démarrer l’activité 4 au début de la semaine 3 ;
Vous devez terminer l’activité 3 avant de passer à l’activité 4. Par conséquent, vous devez terminer l’activité 3 à la fin de la semaine 2 ;
Vous devez démarrer l’activité 3 au début de la semaine 2.

Enfin, prenez le chemin supérieur du diagramme de réseau de la figure 7-2 :

Vous devez démarrer l’activité 2 au début de la semaine 7 ;
Vous ne pouvez travailler sur l’activité 2 tant que vous n’avez pas terminé l’activité 1. Par conséquent, vous devez terminer l’activité 1 à la fin de la semaine 6.

Là encore, vous devez être prudent dans vos calculs. Vous devez terminer l’activité 1 à la fin de la semaine 5 pour pouvoir démarrer l’activité 5 en début de semaine 6. Mais, pour commencer l’activité 2 au début de la semaine 7, vous devez terminer l’activité 1 à la fin de la semaine 6. Ainsi, en finissant l’activité 1 à la fin de la semaine 5, vous respectez les deux conditions.

Si plusieurs flèches partent d’un même jalon ou activité, vous pourrez terminer au plus tard cette activité ou atteindre ce jalon à la date de fin au plus tard à laquelle vous devez démarrer les activités ou atteindre les jalons suivants.

Sur la figure 7-2, les dates de début au plus tard des activités 2 et 5 correspondent respectivement au début de la semaine 6 et de la semaine 7. Résultat, la date de fin au plus tard de l’activité 1 est la fin de la semaine 5. Le reste est simple : vous devez démarrer l’activité 1 au plus tard au début de la semaine 1.

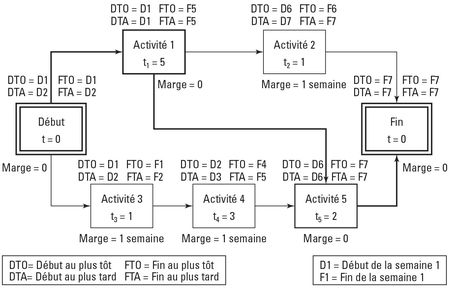
Pour organiser les dates lors des calculs au plus tôt et au plus tard, pensez à inscrire au-dessus de la case de chaque jalon ou activité du diagramme de réseau du projet les dates de début au plus tôt et au plus tard ainsi que les dates de fin au plus tôt et au plus tard. La figure 7-3 vous montre ce que cela donne pour l’exemple de la figure 7-2.

Figure 7-3 : Un exemple de diagramme de réseau avec les dates de début et de fin au plus tôt et au plus tard.

Maintenant que vous connaissez toutes les dates de début et de fin au plus tôt et au plus tard de vos jalons et activités, vous devez déterminer la marge dont vous disposez pour chaque activité ou jalon. (La marge d’une activité est la période pendant laquelle vous pouvez la retarder sans repousser la date d’achèvement du projet.) Il existe deux façons de déterminer la marge :

Soustraire la date de début au plus tôt de la date de début au plus tard autorisée ;
Soustraire la date de fin au plus tôt de la date de fin au plus tard autorisée.

Vous découvrez ainsi que les activités 2, 3 et 4 ont des marges d’une semaine, tandis que les activités 1 et 5 ne présentent aucune marge. La figure 7-3 présente ces informations.

Remarque : si la marge d’une activité est de zéro, l’activité figure sur un chemin critique.

Bien que la marge se définisse comme la période pendant laquelle vous pouvez retarder l’achèvement d’une activité ou l’atteinte d’un jalon sans repousser la date de fin de projet, elle est en fait associée à une séquence d’activités et non à une seule activité. Les informations de la figure 7-3 indiquent que l’activité 3 et l’activité 4 (qui figurent sur le même chemin) bénéficient d’une marge d’une semaine. Cependant, si l’activité 2 est retardée d’une semaine, l’activité 3 ne bénéficiera d’aucune marge.

Exploiter le diagramme de réseau de son projet

Les sections précédentes expliquent les règles et procédures générales pour dessiner et analyser un diagramme de réseau. La présente section vous indique comment créer et analyser le diagramme de réseau de votre projet.

Déterminer les antécédents

Avant de dessiner le diagramme de réseau de votre projet, vous devez d’abord déterminer l’ordre de réalisation des activités. Cette section détaille les raisons pour lesquelles les activités doivent parfois être menées à bien dans un certain ordre.

Étudier les facteurs touchant les antécédents

L’antécédent d’une activité (l’activité A, par exemple) est une activité ou un jalon qui fixe le moment où peut démarrer cette activité A. Il existe quatre liaisons entre un antécédent et l’activité ou le jalon qui vient juste après (appelé successeur) :

Liaison fin-début : l’activité antécédente doit se terminer pour que l’activité successeur puisse démarrer ;
Liaison fin-fin : l’activité antécédente doit se terminer pour que l’activité successeur puisse se terminer ;
Liaison début-début : l’activité antécédente doit démarrer pour que l’activité successeur puisse démarrer ;
Liaison début-fin : l’activité antécédente doit démarrer pour que l’activité successeur puisse se terminer.

La liaison fin-début étant la relation d’antériorité la plus couramment utilisée, c’est celle que nous traitons dans ce livre. Autrement dit, dans cet ouvrage, une activité antécédente est une activité qui doit être achevée avant que son successeur puisse démarrer ou être atteint (s’il s’agit d’un jalon).

Il arrive qu’une activité ne puisse démarrer immédiatement après la fin de l’activité antécédente. Un décalage avec retard est le temps d’attente nécessaire avant de démarrer l’activité suivante. Un décalage avec avance est la période pendant laquelle il est possible de démarrer une activité avant la fin de l’activité antécédente. Dans ce livre, nous n’exposons que des situations où les décalages avec retard et avance sont de zéro.

Une activité est dite immédiatement antécédente à l’activité A s’il n’existe aucune autre activité entre elle et l’activité A. Lorsque vous déterminez les activités immédiatement antécédentes à chaque activité, vous disposez de toutes les informations nécessaires pour dessiner le diagramme de réseau de votre projet. Les facteurs suivants influent sur l’ordre dans lequel vous devez réaliser les activités de votre projet :

Les dépendances obligatoires : ces liens doivent être observés pour que les travaux du projet soient un succès. Elles englobent :
- • Les exigences juridiques : des lois ou règlements nationaux ou locaux vous obligent parfois à réaliser certaines activités avant d’autres. Prenez par exemple un laboratoire pharmaceutique qui a développé un nouveau médicament et démontré son efficacité et l’absence de danger grâce à des essais cliniques. Le fabricant souhaiterait démarrer la production et la commercialisation immédiatement, mais ça lui est interdit car il doit d’abord obtenir une autorisation de mise sur le marché accordée par l’Agence française de sécurité sanitaire des produits de santé ;
- • Les exigences techniques : les procédures et politiques des entreprises stipulent que certaines activités ne peuvent être réalisées avant certaines autres. Supposons que vous développiez un logiciel pour votre entreprise. vous avez terminé la conception et souhaitez démarrer la programmation. Cependant, votre entreprise a mis en place une méthode de développement selon laquelle un comité de surveillance doit approuver officiellement votre conception avant d’autoriser le développement ;
- • La logique forte : certains processus doivent logiquement intervenir avant d’autres. Par exemple, pour construire une maison, vous devez d’abord construire les fondations avant d’ériger la structure.
Les dépendances optionnelles : vous pouvez choisir d’établir ces liens entre les activités, mais sachez qu’elles ne sont pas obligatoires. Elles comprennent :
- • Les liens logiques : la réalisation de certaines activités avant d’autres tombe parfois sous le sens. Imaginons que vous rédigiez un rapport. Dans la mesure où le contenu du chapitre 3 dépend de ce que vous écrivez dans le chapitre 2, vous décidez de rédiger d’abord le chapitre 2. Vous pourriez vous consacrer d’abord au chapitre 3 ou rédiger les deux en même temps, mais cette tactique augmenterait le risque de devoir réécrire une partie du chapitre 3 une fois le chapitre 2 terminé ;
- • Les choix stratégiques : il arrive que vous preniez la décision arbitraire de commencer par certaines activités. Supposons que vous deviez réaliser l’activité C et l’activité D. Vous ne pouvez les mener en même temps et il n’existe aucune obligation légale ni logique vous incitant à en privilégier une d’abord. Vous décidez de commencer par l’activité C.
Les dépendances externes : le démarrage d’une activité peut être conditionné par l’achèvement d’une activité extérieure au projet. Par exemple, imaginons que votre projet englobe le test de l’appareil que vous développez. Vous souhaitez démarrer les tests immédiatement mais vous ne pouvez pas tant que le laboratoire de votre entreprise n’a pas reçu et installé le nouvel équipement commandé.

Choisir les antécédents immédiats

Il existe deux façons de déterminer les antécédents immédiats des activités d’un projet :

Avant-arrière : entamez les activités que vous pouvez réaliser dès que votre projet a démarré et progressez jusqu’à la fin. Pour employer cette méthode, procédez comme suit :
1. Sélectionnez la ou les premières activités à réaliser dès le démarrage du projet ;
2. Déterminez à quelle(s) activité(s) vous pouvez passer une fois les premières (de l’étape 1) achevées ;
3. Continuez ainsi jusqu’à ce que toutes les activités du projet aient été prises en compte.
Arrière-avant : choisissez la ou les activités qui seront exécutées en dernier, puis poursuivez à rebours jusqu’au début. Pour employer cette méthode, procédez comme suit :
1. Identifiez la ou les dernières activités du projet que vous mènerez ;
2. Décidez de la (ou des) activité(s) à boucler juste avant d’entamer les dernières activités (de l’étape 1) ;
3. Continuez ainsi jusqu’à avoir pris en compte toutes les activités de votre projet.

Quelle que soit la méthode employée pour trouver les antécédents immédiats de votre projet, consignez-les dans un simple tableau tel que celui-ci. (Il récapitule les antécédents immédiats de l’exemple illustré par la figure 7-2.)

Tableau 7-1 : Antécédents immédiats de la figure 7-2

Code de l’activité	Description de l’activité	Antécédents immédiats
1	Activité 1	Aucun
2	Activité 2	1
3	Activité 3	Aucun
4	Activité 4	3
5	Activité 5	1, 4

Déterminez l’antécédence en fonction de la nature et des exigences des activités et non en fonction des ressources potentiellement disponibles. Supposons qu’il vous soit possible de réaliser en même temps les activités A et B de votre projet mais que vous prévoyiez de les affecter à la même personne. Dans ce cas, ne faites pas de l’activité A l’antécédent immédiat de l’activité B en partant du principe que cette personne ne peut être que sur une activité à la fois. Indiquez plutôt sur votre diagramme que A et B peuvent être effectuées en même temps. Plus tard, si vous disposez d’une autre personne capable de participer à ces travaux, vous pourrez évaluer l’impact d’une réalisation simultanée des activités A et B. (Le chapitre 8 vous dit comment savoir si quelqu’un est surchargé et comment remédier à ces situations.)

Au moment de la création du diagramme de réseau d’un projet simple, écrivez le nom des activités et jalons sur des Post-it que vous collez ensuite sur un mur. Pour les projets plus complexes, envisagez l’utilisation d’un logiciel de gestion de projet.

Utiliser un diagramme de réseau pour analyser un exemple simple

Nous allons prendre l’exemple de la préparation d’un pique-nique pour illustrer l’utilisation d’un diagramme de réseau qui permettra d’estimer la durée des opérations tout en répondant aux attentes du projet et en prenant en compte les contraintes identifiées.

Choisir les activités

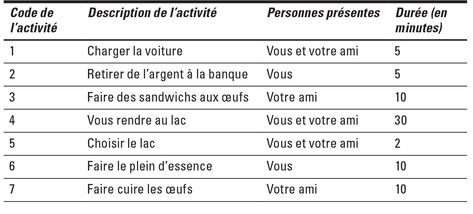
Nous sommes vendredi soir et vous et votre ami réfléchissez à ce que vous pourriez faire ce week-end pour vous détendre. On annonce un samedi doux et ensoleillé et vous décidez donc d’aller pique-niquer en forêt. Souhaitant passer un moment le plus agréable possible, vous décidez de planifier minutieusement la sortie à l’aide d’un diagramme de réseau. Le tableau 7-2 illustre les sept activités que vous jugez nécessaires de réaliser afin de préparer votre pique-nique et de vous rendre au lac.

Tableau 7-2 : Activités concernant votre pique-nique

En outre, vous décidez de respecter les contraintes suivantes :

Vous et votre ami allez démarrer ce projet chez vous samedi à 8 heures. Vous ne pouvez rien faire avant ;
Vous devez réaliser les sept activités pour terminer votre projet ;
Vous ne pouvez modifier l’affectation des personnes aux différentes activités ;
Les deux forêts auxquelles vous avez pensé sont dans des directions opposées à partir de votre maison. Vous devez donc décider de la destination avant de prendre la voiture.

Déterminer l’ordre de réalisation des activités

Maintenant que toutes les activités ont été listées, vous devez établir l’ordre dans lequel vous les mènerez. Autrement dit, il faut déterminer les antécédents immédiats de chaque activité. Voici les dépendances obligatoires : votre ami doit faire cuire les œufs avant de faire les sandwichs (non, sans blague !) et vous devez tous deux charger la voiture et choisir la destination avant de partir.

Vous avez tout loisir de choisir l’ordre des autres activités. Voici une possibilité :

Choisir la forêt avant de faire quoi que ce soit d’autre ;
Une fois que vous vous êtes mis d’accord sur la forêt, vous allez retirer de l’argent à la banque ;
Après avoir retiré de l’argent, vous allez faire le plein de la voiture ;
Pendant ce temps-là, votre ami commence à faire cuire les œufs ;
Une fois les œufs cuits, votre ami fait les sandwichs ;
Une fois que vous êtes revenu de la station-service et que votre ami a fait les sandwichs, vous chargez tous les deux la voiture ;
Une fois la voiture chargée, vous prenez la route, direction le lac.

Le tableau 7-3 décrit les liaisons antécédentes.

Tableau 7-3 : Liaisons antécédentes des activités liées à votre pique-nique au lac

Code de l’activité	Description de l’activité	Antécédents immédiats
1	Charger la voiture	3, 6
2	Retirer de l’argent à la banque	5
3	Faire des sandwichs aux œufs	7
4	Se rendre dans la forêt	1
5	Choisir la forêt	Aucun
6	Faire le plein d’essence	2
7	Faire cuire les œufs (pour les sandwichs)	5

Créer le diagramme de réseau

Maintenant que vous avez vos antécédents immédiats en tête, vous pouvez dessiner le diagramme de réseau de votre projet à partir des informations du tableau 7-3. Pour ce faire, procédez comme suit :

Commencez votre projet par un jalon appelé début.
Trouvez sur le tableau toutes les activités n’ayant pas d’antécédents immédiats. Elles peuvent débuter dès le démarrage du projet.
Dans notre exemple, seule l’activité 5 n’a pas d’antécédent immédiat.
Commencez votre diagramme en dessinant le lien entre le début de votre projet et le début de l’activité 5 (voir la figure 7-4).
Mettez l’activité 5 dans une case et dessinez une flèche qui part de la case début et va vers elle.

Figure 7-4 : Démarrez le diagramme de réseau de votre projet de pique-nique au lac.
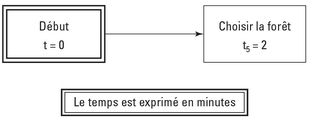
Trouvez toutes les activités ayant comme antécédent immédiat votre première activité.
Dans notre exemple, le tableau 7-3 montre que les activités 2 et 7 ont comme antécédent immédiat l’activité 5. Dessinez des cases représentant ces deux activités et tracez des flèches partant de l’activité 5 et pointant vers les activités 2 et 7 (voir la figure 7-5).
Faites de même avec les activités restantes.
Vous remarquerez sur le tableau 7-3 que seule l’activité 6 a comme antécédent immédiat l’activité 2. Dessinez donc une case pour représenter l’activité 6 et tracez une flèche partant de l’activité 2 et pointant vers l’activité 6.

Le tableau 7-3 montre également que seule l’activité 3 a comme antécédent immédiat l’activité 7. Dessinez donc une case pour représenter l’activité 3 et tracez une flèche partant de l’activité 7 et pointant vers l’activité 3. La figure 7-5 montre l’état de votre diagramme à ce stade.

Figure 7-5 : Continuez le diagramme de réseau de votre projet de pique-nique en forêt.

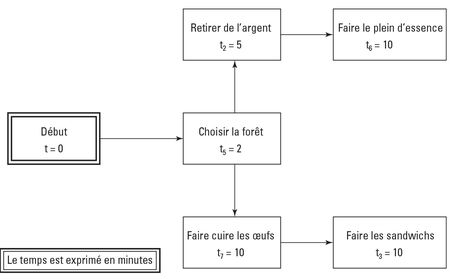
Vous noterez que l’activité 1 a à la fois les activités 3 et 6 comme antécédents immédiats. Dessinez donc une case pour représenter l’activité 1 et tracez des flèches partant des activités 3 et 6 et pointant vers l’activité 1.

Le reste est très simple. Dans la mesure où seule l’activité 4 a comme antécédent immédiat l’activité 1, dessinez une case pour représenter l’activité 4 et tracez une flèche partant de l’activité 1 et pointant vers l’activité 4.
Après avoir placé toutes les activités sur le diagramme, dessinez une case pour représenter la fin et tracez une flèche partant de l’activité 4 (la dernière activité à mener à bien) et pointant vers la case fin (la figure 7-6 vous montre le diagramme de réseau terminé).

Figure 7-6 : Le diagramme de réseau terminé de votre projet de pique-nique au lac.

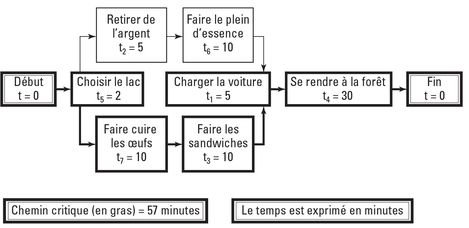
Passons maintenant aux questions de durée. Premièrement, combien de temps vous faudra-t-il pour arriver à la forêt ? Le chemin supérieur (début, activités 5, 2, 6, 1, 4 et fin) s’effectue en 52 minutes, tandis qu’il faut 57 minutes pour l’itinéraire inférieur (début, activités 5, 7, 3, 1, 4 et fin). Il s’écoulera donc 57 minutes entre le moment où vous débutez votre projet et celui où vous arrivez au parc. L’itinéraire inférieur est le chemin critique.

La seconde question de durée à laquelle vous devez répondre est la suivante : pouvez-vous retarder des activités tout en arrivant à votre forêt en 57 minutes ? Si la réponse est oui, de quelles activités s’agit-il et quel est le retard que vous pouvez prendre ? Pour répondre à ces questions, tenez compte des éléments suivants :

Le diagramme de réseau révèle que les activités 5, 7, 3, 1 et 4 sont toutes sur le chemin critique. Vous ne pouvez donc retarder aucune d’entre elles si vous voulez rejoindre la forêt en 57 minutes ;
Les activités 2 et 6 ne sont pas sur le chemin critique et peuvent être effectuées en même temps que les activités 7 et 3. Il faut 20 minutes pour réaliser les activités 7 et 3, contre 15 minutes pour les activités 2 et 6. Vous disposez donc d’une marge de 5 minutes pour les activités 2 et 6 réunies.

Le calendrier de son projet

Le développement du calendrier de votre projet est une combinaison d’activités, de ressources et de séquences d’activités qui vous offre la meilleure chance de répondre aux attentes de votre client tout en prenant un minimum de risques.

Développer le calendrier de son projet

Cette section vous aide à entamer la création du calendrier de votre projet. Il traite également des pièges et solutions potentiels pour respecter les délais.

Prendre les premières mesures

Une fois spécifiées les activités de votre projet (voir la discussion sur la création d’un organigramme technique de projet, au chapitre 6, prenez les mesures suivantes pour développer un calendrier initial :

Identifiez les antécédents immédiats de toutes les activités.
Ce sont les antécédents immédiats qui déterminent la structure de votre diagramme de réseau.
Déterminez les ressources humaines et non humaines nécessaires pour toutes les activités.
Le type, la quantité et la disponibilité des ressources influent sur le temps nécessaire pour mener chaque activité à son terme.
Évaluez la durée de toutes les activités.
Pour savoir comment vous y prendre, reportez-vous à la section « Estimer la durée des activités », plus loin dans ce chapitre.
Identifiez toutes les dates intermédiaires et finales à respecter.
Ces dates constituent les critères que devra respecter votre calendrier.
Identifiez toutes les activités ou jalons hors projet influant sur les activités de votre projet.
Une fois ces activités et jalons identifiés, vous pouvez définir leurs dépendances avec ceux de votre projet.
Dessinez votre diagramme de réseau.
Utilisez le diagramme de réseau pour fixer le calendrier de votre projet.
Analysez le diagramme de réseau de votre projet afin de repérer tous les chemins critiques, ainsi que leur longueur, et de mettre au jour les marges dont vous disposez au sein des chemins non critiques.
Ces informations vous aident à choisir les activités à surveiller et à définir la fréquence de ces contrôles. Elles suggèrent également les stratégies à adopter pour se remettre sur les bons rails en cas de retards imprévus. (Pour en savoir plus sur les chemins critiques et non critiques, voir la section « Interpréter un diagramme de réseau », plus haut dans ce chapitre.)

Si la date d’achèvement convient à votre client, vous en avez fini avec la phase d’établissement du calendrier. Cependant, si votre client veut une fin plus précoce que celle stipulée par votre calendrier initial, il va vous falloir effectuer quelques analyses.

Éviter le piège de la programmation à rebours

L’établissement d’un calendrier à rebours (à savoir commencer par la fin puis remonter jusqu’au début du projet, dans un processus d’identification des activités et durées estimées, afin de respecter la date de fin souhaitée par le client) est à prendre avec la plus grande prudence. L’utilisation de cette approche diminue les chances de respecter les délais pour les raisons suivantes :

Il se peut que vous oubliiez des activités car vous serez focalisé sur la contrainte de date et non sur l’identification de tous les travaux à exécuter ;
Vous fondez vos estimations sur la durée que vous jugez pouvoir consacrer aux activités et non sur le temps nécessaire pour les mener à bien ;
L’ordre choisi ne sera peut-être pas le plus efficace.

Il y a quelque temps, en révisant le plan de projet d’une collègue, nous avons remarqué qu’elle avait prévu de consacrer une semaine à la vérification et à l’approbation de son rapport final. Quand nous lui avons demandé si elle jugeait cette estimation réaliste, elle nous a répondu que ce n’était absolument pas réaliste mais qu’elle devait tabler sur cette durée pour que le plan fonctionne. Autrement dit, elle fondait ses délais sur ses souhaits et non sur ses capacités à les respecter.

Respecter une contrainte de temps établie

Supposons que, selon votre calendrier initial, vous deviez boucler votre projet en l’espace de trois mois, mais que votre client veuille que tout soit terminé au bout de deux mois. Voici les options qui s’offrent à vous pour réduire la longueur des chemins critiques :

Revoyez les durées originales.
- • Assurez-vous d’avoir clairement décrit le contenu de l’activité ;
- • Si vous vous êtes appuyé sur un projet passé pour évaluer les durées, vérifiez bien que la situation présente les mêmes caractéristiques ;
- • Demandez à d’autres experts de contrôler et valider vos estimations ;
- • Demandez aux personnes chargées de l’exécution des travaux de contrôler et valider vos estimations.
Envisagez d’employer des personnes plus expérimentées. Il arrive qu’elles puissent exécuter les tâches en un temps plus court. Bien entendu, cela vous coûtera peut-être plus cher. En outre, vous n’êtes pas le seul individu de l’entreprise à les solliciter. Elles ne seront peut-être pas disponibles !
Envisagez de recourir à d’autres stratégies pour mener à bien les activités. Par exemple, si vous estimez à trois semaines le délai nécessaire pour accomplir une tâche en interne, voyez si vous pouvez la sous-traiter à un prestataire extérieur capable de l’exécuter en deux semaines.
Pensez à l’exécution accélérée par chevauchement, qui vous amène à conduire en même temps des tâches normalement prévues pour s’enchaîner. Si l’exécution accélérée par chevauchement peut raccourcir le temps nécessaire pour venir à bout de toutes les tâches, elle accroît aussi le risque de devoir refaire certaines parties des travaux. Soyez donc paré à cette éventualité.

Lorsque vous diminuez la longueur des chemins critiques, surveillez ceux qui ne l’étaient pas au départ au cas où ils le seraient devenus. Si un ou plusieurs chemins sont devenus critiques, employez les mêmes méthodes pour diminuer leur longueur.

Appliquer différentes stratégies pour parvenir plus vite en forêt

Prenons l’exemple des préparatifs pour le pique-nique (présenté dans la section « Utiliser un diagramme de réseau pour analyser un exemple simple ») pour voir comment pourraient s’appliquer ces approches de réduction de la durée à votre projet.

La figure 7-6 illustre votre plan initial de 57 minutes. Si cette durée vous convient, votre analyse est terminée. Mais, supposons que vous et votre ami décidiez qu’il est impératif d’atteindre la forêt en moins de 45 minutes. Quels changements pouvez-vous apporter pour grignoter 12 minutes ?

Vous pouvez être tenté de ramener la durée du trajet à 18 minutes au lieu des 30 prévues, en vous imaginant qu’il suffira de rouler plus vite. Malheureusement, ça ne marchera pas s’il faut bien 30 minutes pour rejoindre la forêt. N’oubliez pas que votre plan doit illustrer une approche dont vous estimez qu’elle fonctionnera (sans pour autant être garantie). Si, pour faire le trajet en 18 minutes, vous devez rouler à 140 sur de mauvaises routes, votre correctif a peu de chance d’être efficace et vous expose surtout à écoper d’une amende pour excès de vitesse.

Pour bâtir un plan plus réaliste afin de raccourcir le calendrier de votre projet, procédez comme suit :

Commencez par diminuer la durée de votre projet en trouvant le chemin critique, puis en réduisant sa durée de sorte qu’un second chemin devienne critique ;
Pour réduire encore plus la durée de votre projet, ramenez les deux chemins critiques à la même durée, plus courte, de sorte qu’un troisième chemin devienne critique ;
Pour raccourcir encore plus la durée, ramenez les trois chemins critiques à la même durée, plus courte, de sorte qu’un quatrième chemin devienne critique, et ainsi de suite.

Effectuer simultanément plusieurs activités

Une façon de raccourcir la durée nécessaire pour exécuter un groupe d’activités consiste à sortir une ou plusieurs activités du chemin critique et de les mener à bien parallèlement aux autres. Il faut cependant faire preuve de créativité pour parvenir à réaliser simultanément plusieurs activités.

Prenez le chemin de 57 minutes de la figure 7-6. Imaginons qu’un distributeur automatique se trouve près de la station-service dans laquelle vous faites le plein. Si vous tombez sur un employé très sympa, il vous fera le plein pendant que vous retirez de l’argent (et non l’inverse !). Cette stratégie vous permettra d’effectuer en même temps les activités 2 et 6, en 10 minutes au lieu des 15 prévues dans le diagramme de réseau initial. À première vue, vous pouvez ainsi ramener la durée totale à 52 minutes. Mais, regardez bien, ces deux activités ne figurent pas sur le chemin critique. Les terminer plus rapidement n’aura pas d’influence sur le calendrier global du projet. (Avant de songer à gagner 5 minutes supplémentaires en aidant votre ami à faire les sandwichs, n’oubliez pas que vous avez convenu de ne pas modifier l’affectation des personnes aux différentes activités.)

Vous devez donc essayer autre chose. Cette fois-ci, n’oubliez pas que, pour gagner du temps, vous devez réduire la longueur du chemin critique. Voici une autre idée : quand vous faites route pour la forêt, vous et votre ami êtes tous deux dans la voiture, mais un seul est au volant, l’autre étant un passager passif. Si c’est vous qui conduisez, votre ami peut faire les sandwichs dans la voiture (en faisant attention aux miettes, hein !). Cette modification semble raccourcir le chemin critique de 10 minutes. Mais est-ce vraiment le cas ?

Le diagramme de la figure 7-6 révèle que le chemin supérieur (activités 2 et 6) demande 15 minutes et le chemin inférieur (activités 7 et 3) 20 minutes. Le chemin inférieur étant le chemin critique, raccourcir sa longueur de 5 minutes peut diminuer le temps total nécessaire pour achever le projet. Toutefois, ce faisant, la longueur du chemin inférieur devient identique à celle du chemin supérieur (15 minutes). Résultat, ils sont maintenant tous deux critiques.

Gagner 5 minutes supplémentaires sur le chemin inférieur (car la préparation des sandwichs demande 10 minutes) ne fait pas gagner plus de temps sur l’ensemble du projet, car il faut toujours 15 minutes pour parcourir le chemin supérieur. En revanche, ôter ces 5 minutes du chemin inférieur offre bien une marge de 5 minutes.

La figure 7-7 illustre ce changement sur votre diagramme de réseau. Vous pouvez maintenant reconsidérer votre idée première de retirer de l’argent pendant que le pompiste fait le plein de votre voiture. Cette fois-ci, cette modification peut vous permettre de gagner 5 minutes car le chemin supérieur est maintenant critique.

Figure 7-7 : Préparer les sandwichs en chemin.

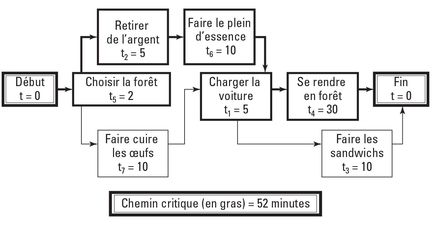
Enfin, vous pouvez choisir la forêt où vous allez pique-niquer tout en chargeant la voiture, ce qui vous fera gagner 2 minutes supplémentaires. La figure 7-8 illustre la solution finale à 45 minutes.

Figure 7-8 : Rallier la forêt en 45 minutes.

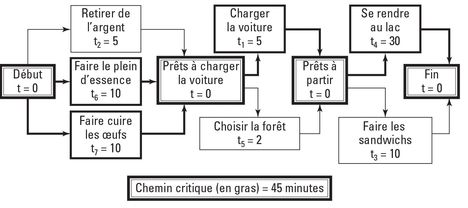
Prenez une situation dans laquelle vous devez mener plusieurs activités à bien avant de pouvoir vous attaquer à plusieurs autres. Montrez cette relation dans votre diagramme en définissant un jalon représentant l’achèvement de ces activités, en traçant des flèches qui partent des activités et pointent vers ce jalon, puis en traçant des flèches qui partent de ce jalon et pointent vers les nouvelles activités (voir la figure 7-8).

Dans notre exemple du pique-nique, vous terminez d’abord les activités retirer de l’argent, faire le plein d’essence et faire cuire les œufs, puis vous pouvez effectuer les activités charger la voiture et choisir la forêt. Vous représentez cette relation en traçant une flèche partant de chacune des trois premières activités et pointant vers le nouveau jalon prêts à charger la voiture, puis en traçant des flèches partant de ce jalon et pointant vers les activités charger la voiture et choisir la forêt.

Si vous jugez que cette analyse se complique, vous avez raison. C’est le prix à payer pour effectuer plus vite un groupe d’activités. Ce prix comprend :

Une planification qui prend plus de temps : vous devez détailler précisément toutes les activités et les relations qu’elles entretiennent car vous ne pouvez vous permettre de faire des erreurs ;
Des risques accrus : la liste des suppositions s’allonge, augmentant ainsi la probabilité qu’une ou plusieurs s’avèrent fausses.

Dans l’exemple du pique-nique, pour parvenir à une durée totale de 45 minutes, vous faites les suppositions suivantes :

Vous êtes à la station-service un peu après 8 heures ;
Un pompiste est disponible pour faire le plein dès que vous arrivez ;
Le distributeur automatique est libre et en état de marche quand vous arrivez ;
Vous et votre ami parvenez à charger la voiture et à vous décider sur le choix de la forêt sans que cela se transforme en une dispute qui dure une heure ;
Votre ami est capable de préparer les sandwichs pendant le trajet sans en mettre partout à l’intérieur de la voiture.

Si faire ces suppositions accroît les risques d’erreur, les identifier peut augmenter la probabilité qu’elles s’avèrent exactes ou tout du moins vous convaincre de penser à un plan de secours si ce n’est pas le cas.

Prenez l’hypothèse que vous puissiez arriver à la station-service peu après 8 heures un samedi matin. Vous pouvez appeler le gérant de la station et demander si votre hypothèse est sensée. S’il vous répond qu’il ignore le temps que vous devrez attendre pour qu’un employé vous fasse le plein, vous pouvez toujours lui demander s’il en serait de même si vous sortiez un joli billet de 200 euros. Quand il ajoute immédiatement qu’il privatisera sa station à votre intention entre 7 h 55 et 8 h 20 et mettra deux employés à votre service (un pour faire le plein et un autre pour encaisser la transaction), de façon que cela ne dure pas plus de 10 minutes, vous vous apercevez qu’il est des incertitudes qui disparaissent à condition d’y mettre le prix ! Votre mission est de déterminer à quel point vous pouvez diminuer l’incertitude et combien vous devez mettre sur la table pour y parvenir.

Échafauder une toute nouvelle stratégie

Vous avez donc un plan pour vous rendre en forêt en 45 minutes. Vous ne pouvez être certain que ce plan fonctionnera mais, au moins, c’est du domaine du faisable. Néanmoins, supposons que votre ami vous dise qu’il doit absolument rallier la forêt en 10 minutes et non 45 ! Votre réaction première sera sans doute de lui dire : « Impossible ! » Se montrer créatif est une chose, mais comment tout boucler en 10 minutes quand il faut déjà 30 minutes pour rejoindre la forêt ?

En clamant qu’il est absolument impossible d’atteindre la forêt en 10 minutes quand le trajet à lui seul dure 30 minutes, vous avez oublié que la réussite de votre projet repose sur le fait d’arriver en forêt pour pique-niquer et non de mener à bien un groupe d’activités prédéterminées. Vos sept activités initiales étaient parfaites, tant qu’elles ne vous empêchaient pas de rallier la forêt en respectant votre lot de contraintes. Mais, si les activités ne vous permettent pas de connaître le succès comme vous le définissez maintenant (arriver à la forêt en 10 minutes), prévoyez alors de modifier les activités.

Supposons que vous décidiez de vous rendre en forêt autrement qu’en voiture. Après quelques recherches, vous découvrez que vous pouvez louer un hélicoptère pour 500 euros la journée qui vous déposera en lisière de forêt en 10 minutes. Vous réalisez cependant que vous aviez tous deux pensé dépenser 10 euros pour votre pique-nique (frais d’autoroute). Vous concluez qu’il est absurde de dépenser 500 euros pour un pique-nique budgété à 10 euros. Vous ne parlerez donc même pas à votre ami de la possibilité de louer un hélicoptère. Vous réaffirmez donc qu’il est impossible de rallier la forêt en 10 minutes. Malheureusement, quand vous avez décidé de ne pas faire part à votre ami de la solution aérienne, vous ne saviez pas que votre ami pouvait gagner 10 000 euros sur une affaire s’il mettait 10 minutes pour se rendre à votre forêt. Cela vaut-il la peine de dépenser 500 euros pour en empocher 10 000 ? Et comment ! Mais vous ne saviez pas pour les 10 000 euros quand vous avez abandonné l’idée de rejoindre la forêt en 10 minutes.

Quand vous préparez un calendrier, vous n’avez pas à anticiper la décision d’une autre personne. Présentez plutôt toutes les options, ainsi que les coûts et avantages associés au décideur, afin qu’il puisse trancher en toute connaissance de cause. Dans notre exemple, vous auriez dû parler à votre ami de la solution de l’hélicoptère. Il aurait ainsi pu en tenir compte au moment de prendre la décision finale.

Subdiviser les activités

Souvent, vous pouvez diminuer le temps nécessaire pour dérouler une séquence d’activités en en subdivisant une ou plusieurs, afin de pouvoir exécuter plusieurs parties en même temps. Pour revenir à notre exemple du pique-nique, votre ami peut faire cuire les œufs et préparer les sandwichs en 7 minutes de moins que prévu grâce à l’approche illustrée par la figure 7-9. Voici ce qu’il doit faire :

Diviser la cuisson des œufs en deux parties :
- • Préparer la cuisson des œufs : sortir la casserole du placard, les œufs du réfrigérateur, remplir la casserole d’eau et y mettre les œufs, placer la casserole sur la gazinière et allumer le feu. Durée estimée à 3 minutes ;
- • Faire cuire les œufs : faire cuire les œufs jusqu’à ce qu’ils soient durs. Durée estimée à 7 minutes.
Diviser la préparation des sandwichs en deux parties :
- • Suivre les étapes initiales de la préparation des sandwichs : sortir le pain, la mayonnaise, la laitue et les tomates du réfrigérateur, le papier aluminium du tiroir. Couper deux morceaux de pain, puis les ouvrir et mettre la mayonnaise, la laitue et les tomates dans le pain. Durée estimée à 7 minutes ;
- • Finir de préparer les sandwichs : sortir les œufs de la casserole, les éplucher, les couper en tranches et les mettre dans le pain. Emballer les sandwichs dans le papier aluminium. Durée estimée à 3 minutes.
Préparer d’abord les œufs pour la cuisson. Ensuite, les faire cuire et réalisez en même temps les étapes initiales de la préparation des sandwichs. Enfin, terminer l’opération.

Figure 7-9 : Diminuer la durée de préparation des sandwichs en subdivisant les tâches.

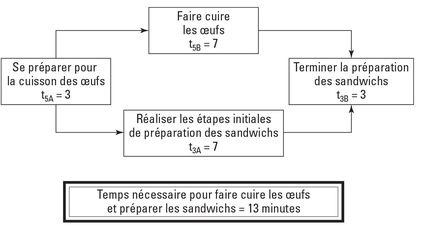
Comme le montre la figure 7-9, le temps nécessaire pour faire cuire les œufs et préparer les sandwichs est de : 3 minutes + 7 minutes + 3 minutes = 13 minutes.

Remarque : à l’origine, le temps total nécessaire pour faire cuire les œufs est de 10 minutes (3 minutes de préparation et 7 minutes de cuisson) et le temps total nécessaire pour préparer les sandwichs est également de 10 minutes (7 minutes pour les étapes initiales et 3 minutes pour terminer la préparation). Mais, en subdivisant les activités et en les programmant plus en détail, vous pouvez réaliser le tout en 13 minutes et non plus en 20.

Estimer la durée des activités

Une estimation de durée correspond au temps que vous estimez nécessaire pour réaliser une activité. L’estimation ne correspond pas à vos souhaits ou à la durée fournie et considérée par quelqu’un comme obligatoire. Il s’agit de votre évaluation.

Les estimations de durée trop optimistes ou irréalistes peuvent entraîner l’allongement d’une activité pour les deux raisons suivantes :

Dans la mesure où les estimations irréalistes semblent satisfaire vos objectifs de calendrier, vous ne recherchez pas d’alternatives réalistes qui augmenteraient les chances de mener à bien les activités selon le temps imparti ;
Si les gens jugent les estimations de durée complètement irréalistes, ils vont arrêter d’essayer de les respecter et considérer le retard comme inévitable au lieu de tenter d’y remédier.

Cette section approfondit les éléments nécessaires pour estimer avec précision la durée d’une activité, notamment en comprenant ses composants et processus, ainsi que les ressources mises en œuvre pour exécuter ces processus.

Déterminer les facteurs associés

La structure d’une activité conditionne sa durée. En conséquence, pour estimer avec précision la durée d’une activité, vous devez décrire ses différents aspects et déterminer l’effet de chacun de ces aspects sur la longueur de l’activité.

Pour estimer la durée d’une activité, fondez-vous sur vos expériences passées, l’avis d’experts et les autres sources d’information disponibles afin de clarifier les composants suivants de l’activité :

Travaux réalisés par des personnes : activités physiques et mentales menées par des personnes : rédiger un rapport, assembler un matériel, réfléchir à des idées pour une campagne publicitaire ;
Travaux réalisés par des ressources non humaines : activités réalisées par des ordinateurs et d’autres machines : test d’un logiciel sur un ordinateur, impression d’un rapport sur une imprimante ultrarapide ;
Processus physiques : réactions physiques ou chimiques : séchage d’un ciment, d’une peinture et réactions chimiques en laboratoire ;
Délais : temps pendant lesquels rien ne se passe : nécessité de réserver une salle de conférence deux semaines avant la tenue d’une réunion (les délais sont généralement imputables à l’indisponibilité de ressources).

Prendre en compte les caractéristiques des ressources

Connaître les types de ressource nécessaires pour une activité peut vous aider à mieux préciser sa durée estimative. Par exemple, toutes les photocopieuses ne présentent pas la même vitesse de traitement.

En précisant les caractéristiques de la machine qui sera utilisée, vous pouvez affiner votre estimation.

Les travaux de votre projet peuvent nécessiter les types de ressource suivants : personnel, équipement, installations, matières premières, informations et fonds. Pour chaque ressource nécessaire, vous devez déterminer sa :

Capacité : productivité pendant une durée prédéterminée ;
Disponibilité : quand une ressource sera utilisable.

Par exemple, une photocopieuse ayant une vitesse de 1 000 copies à la minute peut effectuer le travail en deux fois moins de temps qu’il n’en faut à une machine capable de faire 500 copies à la minute. De même, un travail d’impression volumineux peut prendre deux fois moins de temps si vous avez accès à une photocopieuse quatre heures et non deux heures par jour. (Pour en savoir plus sur l’évaluation des exigences d’un projet en termes de ressources non humaines, filez au chapitre 8.)

Trouver des sources d’information utiles

Pour améliorer la précision de votre estimation de durée, il faut avant tout vous appuyer sur les bonnes informations, par exemple le temps qu’ont duré des activités similaires par le passé et non les évaluations qu’avaient faites les gens à l’époque. Cependant, la précision de votre estimation dépend aussi de l’exactitude des informations exploitées.

Souvent, vous pouvez trouver en divers endroits les informations dont vous avez besoin. Faites donc une comparaison auprès des diverses sources suivantes :

Sources historiques indiquant le temps qu’ont nécessité des activités similaires par le passé ;
Personnes ayant réalisé des activités similaires par le passé ;
Personnes qui vont être chargées de ces activités ;
Experts qui connaissent ce type d’activité, même s’ils n’en ont pas réalisé d’identique.

Améliorer l’estimation de durée des activités

Outre l’exploitation de données précises et complètes, faites ceci pour améliorer la qualité de vos estimations de durée :

Définissez clairement vos activités. Employez le moins de jargon technique possible et décrivez en détail les processus ;
Subdivisez vos activités jusqu’à ce que l’estimation de durée de vos activités de dernier niveau soit de deux semaines, voire moins ;
Définissez clairement le début et la fin ; Impliquez dans le processus d’estimation de la durée les personnes qui vont réaliser une activité ;
Minimisez l’utilisation de la réserve de temps. Une réserve de temps correspond au temps que vous ajoutez à votre meilleure estimation afin d’« assurer ». Il s’agit par exemple de rajouter automatiquement 50 % du temps à votre estimation finale. La réserve de temps compromet la planification de votre projet pour les raisons suivantes :
- • Les travaux ont tendance à se prolonger pour respecter le temps alloué. Si vous êtes capable de mener à son terme en deux semaines une activité mais vous prenez en compte la réserve de temps de 50 %, il n’y a pratiquement aucune chance que vous boucliez votre activité en moins de trois semaines ;
- • Les gens exploitent la réserve de temps afin d’éviter de devoir étudier les activités en profondeur. Résultat, leur stratégie d’exécution des travaux n’est pas viable ;
- • Les membres de l’équipe et les autres parties prenantes du projet ne croient plus en la fiabilité et la faisabilité de votre plan car ils savent que vous jouez sur les chiffres au lieu d’étudier minutieusement les activités.

Malgré la plus grande volonté du monde, il est parfois pratiquement impossible d’estimer avec précision la durée de certaines activités. Par exemple, vous pouvez rencontrer d’énormes difficultés à y parvenir avec des activités que vous découvrez, des activités que vous allez mener à bien dans le futur et des activités connues pour être imprévisibles. Dans ce cas :

Estimez la durée du mieux que vous pouvez en suivant les approches et directives présentées dans cette section ;
Surveillez de près les activités au fur et à mesure afin d’identifier des détails susceptibles d’influer sur votre estimation initiale ;
Transposez aussitôt sur votre calendrier le moindre changement.

Si jamais vous avez effectué une activité à de nombreuses reprises et disposez de données historiques sur le temps qu’elle a chaque fois demandé, vous pourrez peut-être en évaluer la durée avec une assez bonne précision pour la prochaine fois. Dans des situations moins prévisibles, il se peut que vous soyez amené à considérer la durée de l’activité comme une variable aléatoire aux probabilités et valeurs multiples.

La méthode PERT (Program Evaluation and Review Technique, ou méthode du chemin critique) est une méthode de planification qui considère la durée d’une activité comme une variable aléatoire, aux valeurs différentes, décrites par une distribution bêta. Selon les caractéristiques d’une distribution bêta, vous déterminez la valeur moyenne (également appelée valeur attendue) de la durée de l’activité à partir des trois estimations suivantes :

Estimation optimiste (to) : si vous réalisez 100 fois l’activité, sa durée sera supérieure ou égale à ce chiffre à 99 reprises ;
Estimation plus probable (t_pp) : si vous réalisez 100 fois l’activité, sa durée sera le plus souvent celle-ci ;
Estimation pessimiste (t_p) : si vous réalisez 100 fois l’activité, sa durée sera inférieure ou égale à ce chiffre à 99 reprises.

La valeur attendue de la durée (t_a) s’obtient alors avec la formule suivante :

Valeur attendue = (t_a) = (t_o) + 4(t_pp) + (t_p) / 6

Si seules quelques activités sont incertaines, vous pouvez estimer que leur durée sera égale à leur valeur attendue, déterminer le chemin critique, les dates de début et de fin au plus tôt et au plus tard, ainsi que les marges comme les fois précédentes. Cependant, si toutes les activités de votre diagramme de réseau sont incertaines, vous pouvez choisir de faire trois estimations pour chaque activité. Dans ce cas, vous pouvez utiliser les propriétés de la distribution bêta pour déterminer que la longueur du chemin critique correspond aux fourchettes spécifiées de chaque côté de la valeur attendue.

Présenter le calendrier de son projet

À moins que toutes vos activités ne figurent sur un chemin critique, votre diagramme de réseau ne révèle pas exactement votre calendrier mais vous donne des informations utiles pour bâtir ce dernier. Une fois les dates réelles sélectionnées, choisissez l’un des formats suivants pour présenter votre calendrier :

Liste de jalons : tableau répertoriant les jalons et les dates auxquelles vous envisagez de les atteindre ;
Liste d’activités : tableau répertoriant les activités et les dates auxquelles vous envisagez de les débuter et de les terminer ;
Liste combinée jalons/activités : tableau qui inclut les dates des jalons et activités ;
Diagramme de Gantt : tableau chronologique illustrant la date de début de chaque activité, sa durée et sa date de fin ;
Combiné diagramme de Gantt et liste de jalons : tableau chronologique illustrant la date de début de chaque activité, sa durée et sa date de fin, ainsi que la date à laquelle doivent être atteints les différents jalons.

Quel que soit le choix que vous fassiez dans les éléments que nous vous présentons ci-dessus, et une fois que vous serez sûr de la qualité du contenu, votre présentation devra absolument respecter deux règles d’esthétique :

Règle nº 1 : une présentation visuelle
Toute présentation doit rester attractive et, pour cela, elle devra rester visuelle. Évitez de présenter tout document de travail qui, pour celui qui sera assis au fond de la salle, paraîtra être un gros amas sombre d’informations illisibles. Optez donc pour une présentation visuelle et qui fera sens pour tous. Si vous choisissez d’introduire votre projet avec un diaporama, ne choisissez que quelques mots clés par diapositive, puis dans la diapositive suivante, le schéma de la figure 7-10.
Règle nº 2 : une vision globale en une seule page !
Le message clé de votre présentation sera le schéma de la figure 7-10. Ne le décomposez pas en plusieurs diapositives. Dans la mesure où il reste synthétique et présente les grandes étapes du projet, veillez à le présenter en une seule page. L’information synthétique a beaucoup de pouvoir sur un projet. Nombre de gens, en phase de démarrage et préparation, se sont déjà perdus dans les détails, or si vous arrivez avec une vision globale de ce qui les attend, vous les épaterez. Il faudra bien sûr par la suite faire du détail, mais n’oubliez jamais de prendre du recul en leur faisant faire un bond en arrière et en présentant l’information de manière synthétique, ce sera votre force !

La figure 7-10 présente le calendrier de votre pique-nique en forêt (durée de 45 minutes) (tiré de la figure 7-8), sous forme de liste combinée jalons/ activités.

Figure 7-10 : Représentez le calendrier de votre pique-nique en forêt sous forme de liste jalons/activités.

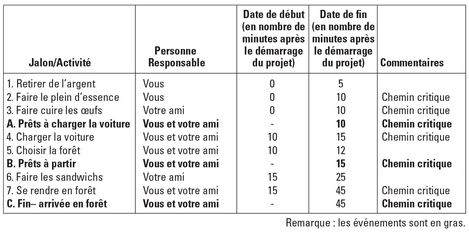
Vous pouvez associer plusieurs formats dans une présentation. La figure 7-11 montre notre exemple du pique-nique avec un OTP combiné, une matrice d’affectation des responsabilités (voir le chapitre 6) et un diagramme de Gantt (dans lequel les triangles représentent les jalons). Outre l’avantage de nécessiter moins de préparatifs et d’être plus facile à actualiser que les documents séparés, une présentation combinée donne un meilleur aperçu du plan et révèle plusieurs aspects qui facilitent une comparaison.

Figure 7-11 : Représentez le calendrier de votre pique-nique en forêt sous forme d’OTP combiné, de matrice d’affectation des responsabilités et de diagramme de Gantt.

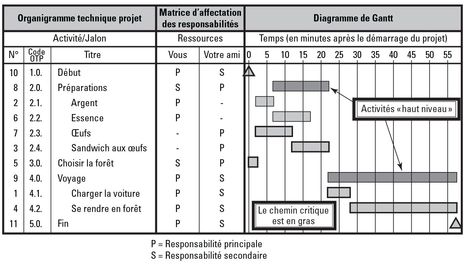
Chaque format a son efficacité en fonction de la situation. Voici quelques conseils pour faire votre choix :

Les listes de jalons et les listes d’activités sont plus efficaces quand il s’agit d’indiquer des dates précises ;
Le diagramme de Gantt offre une vision plus claire de la durée des différentes activités et des chevauchements ;
Le diagramme de Gantt offre une meilleure vue d’ensemble du projet.