Austrian Economics Re-Examined

Microanalysis of money

The modern macroeconomic revolution is associated with Keynes’ General Theory. We refer here to the division of economics into two major areas or fields: micro- and macrotheory. At least until the mid-1970s, the two areas evolved semi-autonomously. This theoretical isolation diminished somewhat with the quest for the microeconomic foundations of macrotheory.

Subjectivists always felt uneasy about this bifurcation. In particular, Mises and Hayek consciously sought to integrate monetary economics and microtheory. They viewed the marginal revolution basically as a microeconomic upheaval, a triumph of micro- over macroanalysis. They saw monetary theory as a backwater in which macroeconomic reasoning dominated (O’Driscoll, 1977, pp. 135–42). In other words, monetary theory was macroeconomic in its orientation before the Keynesian episode. Hayek and Mises specifically criticized the quantity-theory tradition for being mechanistic and aggregative, a holdover from the macroeconomic approach of classical (Ricardian) political economy. Along with other pre-Keynesians, they recast monetary theory in light of modern microeconomics. Thus, Hicks’ “Suggestion for Simplifying the Theory of Money” (1935) met with great professional acclaim precisely because it encapsulated the unifying theme or goal of these contributions. The fruits of all these efforts were swept aside by the Keynesian tide, which was a macroeconomic inundation.1

Hayek criticized Keynesian macroeconomics for lacking microfoundations – indeed, for being inconsistent with microtheory on key issues. In particular, he questioned the validity of analyzing the determination of aggregate demand and national income as distinct theoretical problems. He argued that the process of moving toward equilibrium in individual markets is identical with that of achieving full employment of resources. What is called “unemployment” equilibrium is a manifestation of microeconomic discoordination. Macroeconomic phenomena can be analyzed properly only by microeconomic analysis. There are macroeconomic effects of economic disequilibrium, but there is no distinct macroeconomic theory. That is, there is no consistent theory of macroaggregates that can be couched solely in terms of these aggregates or that consistently relates aggregates to each other (see Lachmann, 1973).

In terms of the literature on both microfoundations and rational expectations, Hayek and Mises anticipated some modern theoretical arguments. Moreover, their specific theories pointed in the direction toward which important contemporary theories are evolving. For this reason, we devote some time to presenting their position and relating it to modern theoretical developments.

Hayek’s monetary theory of economic fluctuations is couched in terms of changing relative prices and costs. Monetary shocks produce particular types of discoordination in markets. The process of adjusting to these shocks produces effects on aggregative variables. It is not possible, however, to analyze these effects in terms of a standard macrotheory. The level of aggregation necessarily obscures the economic phenomena being studied. If one were, for instance, to aggregate heterogeneous capital goods into “capital,” the complex relationships among capital goods would be lost. The concept of “aggregate demand” is problematical because, among other things, it obscures the potentially inverse relationship between consumption and investment. An increase in consumption expeditures does not simply increase aggregate demand and national income: it may also decrease investment. Investment alone leads to capital formation, which provides for a future supply of output. As a result, a given quantitative increase in consumption, compared with the same increase in investment, can have qualitatively different effects on employment and real income.

Hayek’s approach is ultimately as inconsistent with monetarist as it is with Keynesian macroeconomics. The precise points of contention change, but not the ultimate theoretical questions. Monetarists focus on the determination of the price level. The determination of the equilibrium price level is analyzed separately from that of relative prices. Monetarists thereby implicitly invoke a limited neutrality assumption. Unanticipated monetary shocks may cause the growth rate of output to deviate from its trend rate, but these shocks change neither relative prices nor the composition of output. Monetary shocks and concomitant price level effects are superimposed on a given structure of production and set of relative prices (O’Driscoll and Shenoy, 1976, pp. 192–3). In contrast, Hayek integrated the analysis of the value of money with that of the determination of relative prices.

Modern neutrality assumptions virtually rule out the possibility of relative-price effects of monetary shocks. By integrating monetary analysis and the theory of prices, economists make it feasible to analyze relative-price effects that may exist. The former approach closes off theoretical avenues of inquiry while the latter opens them up.

Menger’s theory of money similarly integrates micro- and monetary analysis. It analyzes the evolution of money and the effects of monetary development on economic activity. There is no distinction in the theory between micro- and macroanalysis. Menger does distinguish, however, between the intended and unintended consequences of human actions. This distinction is central to his analysis of monetary evolution. In his theory of monetary evolution, he treated theoretical and institutional analysis as complementary endeavors. Indeed, his approach is a model of the theoretical-institutional approach sought by the New Institutional economists (Langlois, 1982a, pp. 11–17).

Menger and Hayek each adopted a microeconomic approach to traditional macroeconomic questions. Each thereby evidenced his aversion to macroeconomic reasoning. In what follows, we both explicate the theoretical basis of this attitude and develop the respective theories. We begin with Menger’s seminal analysis of money and monetary institutions.

The origin of money

The central issue with which Menger dealt was the question of “how … certain commodities come to be exalted into general media of exchange?” (Jones, 1976, p. 758).2 In distinguishing between money and nonmoney goods, analysts have traditionally highlighted intrinsic physical characteristics, such as portability and divisibility. Money and banking textbooks still repeat these explanations. Menger’s contribution was to focus not on physical but on market characteristics of goods. In taking this path, Menger was being more modern than are most contemporary monetary theorists. As Robert Jones observed in his study, “analysis suggests that the rationale for using a medium of exchange in the first place might be found in the differing market characteristics of goods and the decentralized nature of exchange” (Jones, 1976, p. 775).

The evolution of money is a paradigm case of the development of an organic social institution. In his Principles, Menger summarized the evolutionary process in the following way:

As each economizing individual becomes increasingly more aware of his economic interest, he is led by this interest, without any agreement, without legislative compulsion, and even without regard to the public interest, to give his commodities in exchange for other, more saleable, commodities, even if he does not need them for any immediate consumption purpose. With economic progress, therefore, we can everywhere observe the phenomenon of a certain number of goods, especially those that are most easily saleable at a given time and place, becoming, under the influence of custom, acceptable to everyone in trade, and thus capable of being given in exchange for any other commodity. These goods were called “Geld” by our ancestors, a term derived from “gelten” which means to compensate or pay. Hence the term “Geld” in our language designates the means of payment as such.

(Menger, 1981, p. 260)

Menger’s theory is reminiscent of Adam Smith’s invisible hand reasoning. He based his theory of money on his analysis of commodity-stock holdings. Economies progress from economic self-sufficiency, to production on order, to speculative production for the market. In the course of this evolutionary process, transactors increasingly hold inventories of unfinished and finished goods. They do so in order to enhance their ability to consummate future trades and to further their own consumption plans.

In committing themselves to holding commodity stocks, traders are concerned, among other things, with the marketability (absatzfahigkeit) or saleability of the goods held in their inventories. Traders discover that some commodities are especially marketable and widely acceptable, while other commodities are less so. Menger was almost exhaustive in discussing the factors impeding and facilitating marketability (Menger, 1981, pp. 248–53). For the purpose of our discussion, it is sufficient to observe that such factors exist and lead to differences in the saleability of various commodities.

Over time, entrepreneur-traders will prefer holding their wealth in more marketable commodities. This preference accentuates the differences in marketability among commodities. Those commodities perceived to be more saleable will tend to become even more so as individuals act on their perceptions. In building inventories of preferred commodities, wealth-owners create a wider and more active market for the commodity. Subjective factors thus play a crucial role in this market process, far more than is captured in arguments focusing on physical characteristics of commodities. Because the free choices of traders and the sequence of events affect the ultimate outcome, it is partly an accident of history which goods become the most marketable. This indeterminism is typical of evolutionary processes.

If a good is sufficiently marketable, particular individuals (mainly professional traders) would be willing to hold inventories of it even if they have no final demand for it. The good becomes a store of value. If the process continues, the store of value becomes a medium through which other transactions are conducted. In other words, we are describing the economic rationale for indirect exchange. Again, however, we are analyzing the productivity of indirect exchange on microeconomic grounds and in terms of a general theory of inventory holdings. Moreover, the focus is on subjective perceptions and market characteristics of goods, not on their physical attributes.

Menger initially developed this theory by observing that goods do not have a unique price, but have different buying and selling prices. Not only is there a bid-asked spread, but this spread varies for different commodities. This phenomenon was not explicable in terms of standard demand and supply theory. Menger’s explanation of bid-asked spreads is essentially a transactions-cost explanation. The bid-asked spread helps compensate wealth-owners for the costs of disposing of goods, costs that vary among goods. Since money is the most liquid commodity, it alone has a unique price, there being no bid-asked spread.

Sir John Hicks has succinctly characterized liquidity preference as a desire for flexibility: “Liquidity is not a property of a single choice; it is a matter of a sequence of choices, a related sequence. It is concerned with the passage from the known to the unknown – with the knowledge that if we wait we can have more knowledge” (Hicks, 1974, pp. 38–9; see Shackle, 1967, p. 6). In contrast, “by holding the imperfectly liquid asset the holder has narrowed the trend of opportunities which may be open to him … He has ‘locked himself in’ ” (Hicks, 1974, pp. 43–4). Liquidity provides economic agents with flexibility, flexibility that lowers the cost of specialized production.

So large are the cost savings that the development of a complex economic order depends crucially on monetary evolution. Without the evolution of a highly liquid commodity with general acceptability, economic development would be impossible. Specialized production depends on the ability of transactors to calculate efficiently, and money alone makes this calculation possible. In our schematic analysis, we linked the progress of economic development with that of monetary evolution. Monetary evolution must be far advanced before a complex market system can evolve. In other words, a non-monetary economy must logically be a primitive one. This implication is corroborated by the notable absence of highly developed market economies utilizing barter.3

Modern monetary theory characterizes money as though it were in some sense invented, despite the fact that over 100 years ago Menger realized that “money is not the product of an agreement on the part of economizing man nor the product of legislative acts. No one invented it” (Menger, 1981, p. 262). Of the modern literature on the evolution of money, Jones has commented that “although these works illuminate how money might overcome logistical difficulties of reaching an efficient allocation with decentralized exchange, they offer no suggestions of how a monetary pattern of trade could evolve without a centralized decision” (Jones, 1976, p. 759). Jones himself avoided this pitfall, but did not solve the problem of simultaneously determining the money good and its market value. Menger had, however, accomplished this in the Principles and in “Geld.” There, Menger noted that, since money is simply the most marketable good, it has always had an exchange value. As it evolves into the medium of exchange, demand for the good increases. This process increases the relative price of the commodity money over time.

There is, of course, no unique point at which a good becomes money, no logical or historical break in economic history. One day’s price builds upon yesterday’s. At some point, we recognize that a commodity has become money in the modern sense, but any arbitrariness derives from our perception, not from the historical events themselves. In very recent times, economic historians have tended to look to the enactment of legal tender laws as marking the monetization of a good. Aside from perpetuating the myth that money is the invention of the state, this approach overlooks the fact that governments have done no more than sanction the existence of what has evolved on the market. The approach embodies the error dubbed “constructivism” by Hayek.

Consider the issue of monetary reform as an application of the evolutionary principle being discussed. Monetary reform proposals are often long on lists of advantages of adopting a new standard or monetary constitution, but short on transitional details. Hall has stated that “[e]xperience in countless nations shows that the simple announcement of the definition of a national monetary unit, without any compulsion for its use, is sufficient to bring about almost unanimous use” (Hall, 1982, p. 2). This casual empiricism is not compelling. Consider the example of a government’s introducing a new monetary unit, the “ecru.” To be a clear test of the thesis, the ecru cannot be linked to another currency. If, for instance, the ecru were declared to be worth one British pound, then the country would be effectively going on a sterling standard rather than introducing a new standard: the ecru would simply be the name for a pound sterling in the hypothetical country. There are many practical legal, political and economic problems inherent in such a change; but these are not the problems that concern us here.

Introducing the pure ecru standard raises the following analytical problem, which is Menger’s central problem in another guise. No economic agent would have an incentive to accept ecrus, because no one would have any grounds for forming expectations about the ecru’s future expected value. By assumption, the ecru has never existed before. Accordingly, it has no established value. Even if the government were to declare the ecru legal tender, no one would have a clue as to its market value: no one, for instance, would know the ecru-price of a pair of shoes. Until that question can be resolved, ecrus will not circulate as a medium of exchange.4

We are simply restating the fact that the marginal utility of money depends on its exchange value, the reverse of the ordinary relationship for goods. In general equilibrium analysis, the equilibrium values of all economic variables are simultaneously determined. Actual market prices are not established, however, by everyone sitting down and jointly solving a system of equations that describes the economy. The mutual determination of prices is a characteristic of general equilibrium, not a method of attaining that equilibrium. No market mechanism exists that could provide information to transactors as to what prices would be if all of them were to accept ecrus as the means of payment. The assumption to the contrary is an implicit denial that we are analyzing a decentralized system.

In the nineteenth century, Hall’s “simple announcement” of a new monetary unit consisted of a country’s adopting either the gold or silver standard. In the twentieth century, “new” monetary units have typically come about in one of the following two ways. First, a government may link its national currency to another major currency, such as the pound or dollar. In this case, the government has effectively adopted a sterling or dollar standard. Second, a government may institute currency reform, substituting five, ten or 100 units of the old currency for a unit of the new currency. If the government couples this conversion with newly found monetary stringency, then the action can have value in speeding adjustment to anti-inflationary policies.

To some extent, of course, it is a purely verbal issue whether this change is characterized as introducing a new monetary standard. Verbal issues aside, however, the success of the change depends crucially on the new standard’s being defined in terms of the old standard. If it were not, the policy action would be equivalent to trying to adopt the ecru standard. With respect to the second type of currency reform, the cases of Germany in the 1920s and France in the 1950s come to mind. In each case, a new currency was defined in terms of the old. Both were successful reforms.

Following Menger, Hayek has suggested that money is an evolved social institution in the same sense that language is. The analogy in fact can help illuminate the issue at hand. Modern linguists do not suppose that recognized languages are invented.

To suppose that they could be invented would be to involve oneself in absurdities. To convince a whole population to switch its language, one would have to assure each individual that everyone else would use the language if he did. To introduce successfully the new language, one must thus find a population already conversant with the language. The richer one makes the example, the more overwhelming the informational and organizational problems become. (What motivates anyone to play this game? In what language do they negotiate, the new or the old?)

The problems with designed linguistic innovation derive from the complexity of undesigned orders. Money and monetary institutions are largely undesigned or evolved social institutions. Policy actions do, of course, affect the evolution of institutions. Policy actions cannot precisely determine the eventual outcome, however, as is illustrated by the failure of attempts in French-speaking countries to maintain the “purity” of the language, and by the failure of the Irish government to maintain Gaelic as a living language.

We are not arguing against monetary reform or against the idea of permitting a new monetary standard to evolve. We are suggesting, however, that reform proposals ought to take account of the complexity of evolved social institutions, as well as the exigencies of decentralized social systems. Actual historical examples of monetary reform do not illustrate governmental power to implement change so much as they illuminate the constraints on reformers. Reforms have consisted of precisely those types that we have treated as being feasible. Governments can no more alter the monetary system by mere announcement than they can change their citizens’ language by fiat.

Constructivist monetary reform proposals attempt to predetermine outcomes, rather than permit these to be determined by market forces. Market-determined outcomes reflect all relevant factors, not just the comparatively small number that can be included in economic models. Constructivist reform proposals overlook the fact that markets embody more information than will ever be available to a single mind or even to a group of experts (Hayek, 1945). The proposals treat these institutions and practices as being susceptible to centralized planning. In reality, monetary institutions – indeed, money itself – are shaped by the same kind of forces affecting ordinary business practices and market institutions.

Indeed, in monetary matters generally, economists adopt procedures and theorize in ways rejected in other areas. Few economists would accept the validity of trying to reason a priori about the optimal qualities that should be possessed by a cup of coffee or a glass of wine. These are recognized to be things that can be determined only by market test, and which, moreover, typically show great variation across brands or trademarks. Yet most monetary economists believe that rational economic theory ought to be capable of prescribing the optimal qualities, if not the optimum quantity, of money. In part, these attitudes reflect the belief that money is “different,” different in a way possessing normative significance. This belief, though long incorporated into theoretical assumptions, is yet to be convincingly substantiated. At the very least, there is an heuristic value to carrying the analysis of money as an ordinary good, generated by market forces, as far as it can be carried. This would better determine the limits of policy-making than would continued applications of a priori reasoning about desirable properties of money.

Economic theory can perhaps specify the likely limits of monetary reform or the range of possible institutional outcomes. The range is not, however, open-ended; monetary systems that are postulated to be the product of market processes must be the probable outcome of such processes. They must also be consistent with incentives facing individuals in the situations postulated (see O’Driscoll, 1983, p. 331).

Business cycles

Cyclical variations generate profit opportunities, a fact that is most apparent in the case of unemployed resources. Unemployed resources represent a mismatching of inputs to outputs. As long as final output is scarce, versatile resources ought not to be persistently unemployed. Entrepreneurs who can reallocate resources to superior uses will earn profits. There are also profit opportunities in speculating against markets in cyclical expansions. For instance, the housing and construction boom of the 1970s should have provided as many potential arbitrage possibilities as any eighteenth-century “bubble.”

We are characterizing the phases of an economic cycle as periods in which plans are persistently discoordinated. Any attempt to analyze such movements, however, presents insuperable problems for models based on general equilibrium theory. The logic of static general equilibrium theory cannot generate processes in which decentralized systems move away from equilibrium. It cannot do so even if it postulates exogenous disturbances. Even then, general equilibrium theory “can do no more than demonstrate that … the economic system always reacts to such changes by its well-known method of adaptation, i.e. by the formation of a new equilibrium” (Hayek, 1966, pp. 42–3).

In essence, rational expectations theorists have renewed Hayek’s critique of business cycle analysis. In his own work, Lucas (1977) has explicitly referred to that critique. Rational expectations theorists have generally focused their criticism on the expectational assumptions of traditional macroeconomic models. In their own positive theory, they treat the business cycle as an “equilibrium” phenomenon, utilizing static models to analyze cyclical activity. This is one way to resolve the theoretical dilemma in question, but one that we suggest does violence to the phenomenon. In our analysis, we adopt Hayek’s view of the cycle as a disequilibrium phenomenon. We restate his analysis, however, in terms of our own formulation of process theory. In particular, we argue that the distinction between typical and unique aspects of phenomena is especially useful in analyzing economic fluctuations.

Analyzing expectational equilibrium is one aspect of the more general problem of modeling error in economics. Ex ante error has been all but eliminated from neoclassical economics. Models can accommodate ex post forecast errors, so long as these do not cause agents to revise their forecasting function. In other words, there is error without regret or revision. Such errors must be uncorrelated with information available at the time decisions were implemented. In models of stochastic equilibrium, agents are correct on average. “Error” observations result from serially uncorrelated, random disturbances. Business cycles, however, represent a jarring element in this weltanschauung. Maddock and Carter concisely stated the issue:

If expectations are rational, then expectation errors should be randomly distributed over time. A straightforward implication of that for this model is that the level of output (or unemployment) is uncorrelated over time. Yet everybody knows that the GNP and the unemployment series have a high degree of serial correlation. We tend to go through a series of years in which unemployment is below the “natural rate” and then a series of years in which it is above the “natural rate.” It doesn’t seem to be distributed very randomly.

(Maddock and Carter, 1982, p. 44)

Any consistent theory of cyclical fluctuations must incorporate time and expectational error in the analysis. It must also explain the important sources of expectational error. As we argued in the previous chapter, it is insufficient merely to invoke uncertainty, even radical uncertainty, to explain the cycle of economic expansion and contraction. Individual firms are continuously making errors, which show up as profits and losses. Some entrepreneurs underestimate demand, resulting in an excess demand for their goods. Others overestimate demand, resulting in an excess supply of their goods. These errors tend to be negatively correlated, not because of the law of large numbers but because of the Law of Markets. If excess demand exists in some markets, there must be a corresponding excess supply somewhere else. Over a cycle, however, there tends to be not only serial correlation in error terms within given time series, but an observed correlation in errors across markets. In simplified terms, periods of general excess demand for commodities (accelerations in the inflation rate) alternate with periods of general excess supply of commodities (disinflation). This is the problem of the “clustering of errors” referred to in Chapter 8. While the stylized facts require more precise statement, they do point up the problem of using received theory to analyze the business cycle.

In general equilibrium theory, markets always equilibrate because of the adjustment process triggered by matched purchases and sales: every sale constitutes a demand for other goods. It is in this sense that theory embodies Say’s Law of Markets (Hayek, 1966, p. 42n.). Money alone can break the mechanical linkage of matched purchases and sales, because only money constitutes a source of demand for real goods with no corresponding supply of real goods. In the Mengerian or Hicksian sense, a demand for money expresses a preference for liquidity or generalized purchasing power, with no implied commitment to purchase any particular commodity. Similarly, variations in individuals’ money stocks, whether caused by a demand or a supply shift, can cause the demand for some produced goods to increase (decrease) with no corresponding diminution in demand for other produced goods (see Hayek, 1966, p. 45).

The difference between a money and a barter economy is the essential ingredient in any analysis of economic fluctuations. This insight does not itself constitute a cycle theory, nor does it commit one to a monetary theory of the cycle, except in the broadest sense of the term. Though the formulation of the problem may strike one as “Keynesian,” in no sense can Keynes be credited with this particular insight. If we have paraphrased anyone, it is Hayek. Hayek, however, was merely restating here a position well established in classical political economy. The existence of a variable money supply, i.e., one at least partially composed of fiduciary media, changes the “black letter” statement of the theory of value. It can be readily established that classical economists were aware of the point. For instance, after articulating what would now be called a caricature of the quantity theory, including a strong neutrality proposition, John Stuart Mill observed that

[t]he proposition which we have laid down, respecting the dependence of general prices upon the quantity of money in circulation, must be understood as applying only to a state of things in which money, that is gold or silver, is the exclusive instrument of exchange, and actually passes from hand to hand at every purchase, credit in any of its shapes being unknown. When credit comes into play as a means of purchasing, distinct from money in hand, we shall hereafter find that the connection between prices and the amount of money in circulation is much less distinct and intimate, and that such connection as does exist no longer admits of so simple a mode of expression.

(Mill, 1973, p. 495)

We have insisted on viewing formal economic theory as incorporating Say’s Law, thereby implicitly denying the frequently repeated distinction between Say’s Law and Walras’ Law. There simply is no distinction, at least not at the level of generality specified here. Say’s Law is a statement of the interdependency of all markets, a statement formalized but not fundamentally changed by Walras. Economists relying on Say’s Law recognized that monetary factors introduced complications, as is indicated by the previous quotation from Mill. Similarly, business cycles fascinated economists, from the South Sea Bubble down through the end of the nineteenth and into the early twentieth centuries. What was missing was a consistent monetary analysis in which existing insights were woven into a story that shed light on economic cycles.

The use of money in a decentralized economy reflects the scarcity of information available to transactors, a scarcity that generates pervasive uncertainty. If money had not evolved, individuals could neither cope with this uncertainty nor solve the allocational problem confronting them. Money itself, however, can produce informational problems, causing particular types of disequilibrium. It can do so by interfering with market forces tending to produce consistency of plans. Monetary shocks can, then, discoordinate plans and economic activity. In the next section we develop these points.

A subjectivist theory of economic fluctuations

The existence of business cycles evidences coordination failure. The price system fails to accomplish the task assigned to it by static economic theory. In a modern economy, any serious coordination failure disrupts entrepreneurial planning. In analyzing economic fluctuations, then, we focus on entrepreneurial expectations, particularly those embodied in decisions to utilize or abandon concrete capital goods. Expectations, coordination and capital allocation are the analytical building blocks of a subjectivist theory of economic fluctuations.

Our analysis fits within the Thornton-Wicksell monetary tradition, a tradition focusing on the interest rate mechanism for coordinating saving and investment decisions. We follow the Austrian development of that tradition, a variant originally enunciated by Mises and Hayek. O’Driscoll (1977) restated the theory; Garrison (1978) clarified the static capital theory underlying it; and Wainhouse (1982) confronted the theory with postwar evidence.

In presenting our version or approach, we recognize that other schools have developed the Wicksellian theme differently: the Stockholm School (Lindahl, Ohlin, Myrdal) and the early Cambridge School (Hawtrey, Robertson, Keynes), presented alternative formulations of savings-investment disequilibrium (Leijonhufvud, 1981a). Though the differences among these variants are important, where appropriate we draw on insights from the broad Thornton-Wicksell tradition.

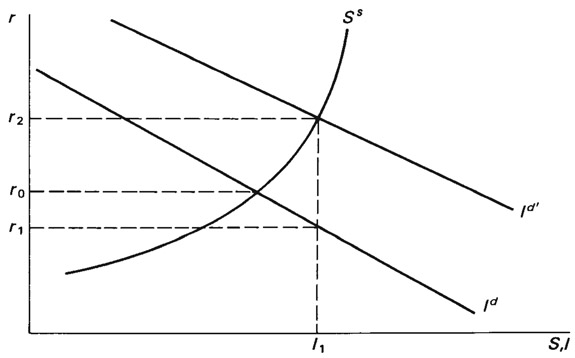
We begin with the familiar loanable funds approach to the determination of market interest rates (Figure III.5). At an interest rate r₀, the plans of savers and investors are consistent in the aggregate. Planned saving equals planned investment at this rate, which is Wicksell’s “natural rate.” At an interest rate below r₀, such as r₁, planned investment exceeds planned saving (by I₁ – S₁). Only if the banking system creates additional liabilities in the course of extending credit will r₁ persist, and will I₁ be the actual or ex post level of investment. In this case, the supply of loanable funds is increasing by more than the supply of savings. The difference is made up by the creation of bank money or bank credit.

Figure III.5 Determination of interest rates

An interest rate of r₀ represents neutral bank policy. Bank policy is neutral if it does no more than intermediate between savers and investors. If policy is neutral, changes in the supply of credit are governed by changes in the supply of planned saving (see Leijonhufvud, 1981a, p. 153). If policy is non-neutral, then some plans must be frustrated or go unfulfilled. The form that this frustration takes depends crucially upon the assumed sequence of events. In what follows, we specify a sequence of events.

Assume that the bank policy is adhered to for several periods, and does not merely represent a once-and-for-all shock. So long as the policy is effective, the market or loan rate will be less than the equilibrium rate. Each period, entrepreneurs plan to invest more income than recipients plan to save. As explained in Chapter 8, entrepreneurs will implement projects geared to produce greater consumption output in the more distant future, but relatively less in the near term. Consumers’ plans, however, entail greater consumption in the near term, and relatively less in the more distant future (compared with producers’ plans).

Something must adjust as the result of the implied intertemporal plan discoordination. In the aggregate, income recipients will be unable to acquire the consumer goods that they would wish to purchase at that income level. Consumption plans cannot all be fulfilled, since, by assumption, a smaller proportion of consumption goods is being produced at the very time that incomes are being bid up. The complete allocational and distributional stories await development of the relative-price story. What is being described here, however, corresponds to the concept of “forced saving” in nineteenth-century British monetary economics (Hayek, 1932; O’Driscoll, 1977, pp. 51–6). In real terms, consumers are compelled to consume less than planned for each period.

The assumed sequence of events is as follows.

(1) In period 1, bank money is created in the form of business credits.
(2) In period 2, entrepreneurs spend the money on factor services, bidding up incomes.
(3) In period 3, income recipients bid up the prices of consumer goods.

The transmission mechanism goes from money, to incomes, to prices, and then to output. At this point, we have linked the Thornton-Wicksell tradition with that of Richard Cantillon. As Hayek (1967a, pp. 8–9) pointed out, it is a logical connection. Cantillon argued that, because the inflation process is sequential, i.e., takes place in real time, there will be gainers and losers. Some incomes rise before others: early recipients of increased income do not confront higher prices. In the case that Cantillon adduced, owners of gold mines and those supplying them with goods clearly gained from an inflow of bullion. Their incomes rose before prices increased. In the third and fourth rounds, incomes still rose more quickly than did prices. At some point in the sequence, however, we discover consumers who face higher prices but whose incomes have not risen proportionately. They are the losers in the inflation process. So long as the inflow of bullion continues, the distribution effects will be operative. These distribution effects generate, mutatis mutandis, allocational effects. In Cantillon’s analysis, there is no sharp distinction between the allocational and distributional effects, because there is no sharp distinction between real and monetary shocks.

For Cantillon’s comparatively simple case, it was relatively easy to outline the sequence in some depth. The greater complexity of our case requires somewhat more analysis, which we develop in the following subsection.

Prices and production

A fall in interest rates, generated by monetary expansion, will not increase uniformly the value of all investment projects. The value of investment projects yielding consumption output in the more distant future rises relative to projects with more immediate payoffs. We call these projects and capital goods type 1 and type 2, respectively. Here, a “project” is defined as a set of interrelated, heterogeneous capital goods. The full impact of the fall in interest rates comprises (1) a discount rate effect, (2) derived-demand effects and (3) cost effects.

Ceteris paribus, the decline in interest rates will increase the value of all long-lived assets. This effect reflects the negative elasticity of present value with respect to the interest rate. It is, however, a partial effect, as can be seen by considering the full effect on individual capital goods. The demand for type 2 capital goods is affected more immediately by the demand for current consumption output than by current interest rates (the derived-demand effect). Consumption demand has declined, at least in relative terms. In other words, the increased demand for type 1 capital goods is equivalent to a decline in demand for type 2 goods. In terms of a standard present value (PV) formula for a capital good yielding services over n periods,

there are derived-demand effects for different capital goods, effects that show up in the numerator. The interest rate disturbance causes the expected stream of quasi-rents (S) accruing to capital goods to change. For type 1 goods the stream tends to rise; for type 2 goods the stream tends to fall. For some goods, therefore, the quasi-rent and interest rate effects reinforce each other; for other goods, these are offsetting effects. To calculate the full impact of the kind of disturbance being analyzed, we must also take account of cost effects.

The prices of complementary factors, which we designate “labor” and “raw materials,” will be affected in this process. Entrepreneurs undertaking type 1 projects will be able to bid factors away from type 2 projects. Moreover, this occurs as the derived demand for the latter is declining. Owners of type 2 goods are thus caught in a price-cost squeeze. Of course, none of this implies that already completed type 2 projects will be abandoned. So long as depreciation is sufficient to pay the increased variable costs, these projects can be continued. The quasi-rents accruing to these projects will, however, decline. More importantly, new investment funds will tend to flow to type 1, not type 2, projects.

In any period, net investment is small relative to the value of the existing capital stock. Nonetheless, investment is a large component of each period’s GNP. Moreover, shifts in investment expenditures can have substantial impact on production and employment in the affected industries. We are interested primarily in changes in the pattern of investment flows, not in the demand for “capital.”

In analyzing the effects of changes in capital value on users of capital goods, it may be useful to assume the short-run fixity of capital. It is misleading to do so, however, for producers of capital goods. Monetary disturbances affect credit markets, which in turn cause demand for new capital goods to change. Adjustments in the capital goods industries begin as soon as the change is perceived to be permanent, or at least long-lived enough to warrant a commitment of resources.

Our analysis involves expectational assumptions at each stage, and we now make some of these more explicit. First, we assume that all information possessed by entrepreneurs is embodied in the I^d function. This includes not only future expected returns, but also information on current economic policy. Changes in entrepreneurial knowledge or beliefs show up as shifts in I^d. The investment demand function might, then, be specified as follows:

where

r = relevant interest rate
s = profit (quasi-rent) expectations
i = a portmanteau information variable.

We have thus packed a great deal into i. We by no means wish to argue that information will remain fixed during the cumulative process: indeed, the contrary is almost surely the case. Certain factors change, mutatis mutandis, as the cumulative process proceeds. One could attempt to incorporate all these into the elasticity measure. We argue below, however, that at least one factor will show up as a shift effect. Moreover, as indicated above, we are not trying to present the analysis in terms of aggregate investment. So we do not pursue the analysis in each of n periods in terms of stable aggregate saving and investment functions. If the reader is more comfortable in doing so, he may do so to get a “first approximation” of the theory. This would be a rough approximation at best, and one that ultimately does violence to the microeconomic approach being employed. We are not, strictly speaking, presenting an over-investment model, but one of mal- or misdirected investment (see Rothbard, 1963, pp. 34–5).

Second, we assume that entrepreneurs are ex ante profit-maximizers, making use of the best information that they have. Entrepreneurs will devote resources to acquiring relevant information, so long as they expect it to be cost-effective. To the degree that they are successful, they may modify their actions compared with what they would have done in the absence of that information. This assumption does not, however, warrant any inference that monetary policy will be ineffective. In a decentralized economy, the kind of information acquired by agents is not sufficient to insulate them completely from the effects of monetary shocks. We can outline the reasons here; we elaborate on some of these points in dealing with rational expectations.

Agents know prices and other endogenous variables, but not the structure of the system. They may have acquired information in the past about demand and supply conditions in the neighborhood of a prior, temporary equilibrium point. This information is subject to obsolescence, a process speeded up by the kind of shocks that we are analyzing here. Agents may have theories about how the system works, but, as recently clarified by Frydman (1982), theory conflict ensures that entrepreneurial error will not be eliminated. Information characteristics of decentralized economies ensure that agents will disagree on the effects of policy and on the future course of events generally.

We return now to the dynamics of the expansion. Reallocation of capital and other factors is occurring, but in a manner inconsistent with preferences and opportunities (revealed, for instance, in the planned savings (S) and investment (I) functions).5 As the output of current consumption goods declines, investment in this sector declines. Future-period consumption is being provided for at an ever increasing rate. Investment is being committed to multi-period projects, and their future output cannot be used now to satisfy consumption demand. (People cannot consume half completed steel plants and hydroelectric dams.) Rising incomes make the satisfaction of consumption demand more urgent, but interest rate and relative-price signals continue to make the satisfaction of future-period consumption demand seem even more profitable. At some point, ex post returns in consumer goods industries will begin rising. In theory, this might ameliorate or slow the process (Hayek, 1969). If it did, however, it could do so only by leading entrepreneurs in consumer goods industries (type 2 investment projects) to enter into a bidding war with the capital goods (type 1) industries. To the degree the former succeeded, some of the new projects would be rendered unprofitable.

Both practical and theoretical considerations argue against this happening, especially in earlier stages of an expansion. First, policy-makers normally view with alarm any slowdown in the recovery of business investment. One Keynesian legacy is to define economic recovery virtually in terms of the profitability of producers of capital goods (i.e., “smokestack industries”). Excessive attention to capital goods industries leads monetary authorities to respond by accelerating the rate of growth of money. Consequently, they are induced to step on the accelerator until signs of recovery in investment occur. If the past is any guide, they will kick the accelerator again at least once in any recovery, in order to maintain the strength of the recovery and, thereby, the growth in the capital goods sectors.

A theoretical consideration also argues against an endogenous end to a malinvestment cycle. This consideration depends on the complementarity of capital goods. The more resources that have already been sunk in the capital-intensive production methods, the greater will be the demand for additional resources that can be used to complete the projects. If a project is nearly complete, then the incremental resources needed to complete it will have a far greater value than would have been the case ex ante. In the limit, entrepreneurs would be willing to pay up to the discounted value of the future quasi-rents accruing to the entire project in order to obtain a comparatively small additional sum needed to complete the project.

Indeed, it was precisely this consideration that led Hayek (1937b) to one of his most important analytical contributions to business cycle theory. The capital complementarity effect helps explain the pro-cyclical behavior of interest rates, apart from any Fisher effects. A prolonged cycle of capital investment is likely to increase the expected returns from additional borrowing and investment. Past investment raises the demand for current investable funds, driving up real market interest rates. Toward the end of a cycle, the real short-run interest rate, which would clear the market, will be higher – perhaps significantly higher – than the long-run equilibrium rate.

Figure III.6 Interest rate dynamics

Consider the stylized analysis in Figure III.6. If the savings-investment equilibrium had been maintained throughout at an interest rate r₀, then investment expenditures would have remained at the correct level “in the aggregate,” and would have been “efficiently allocated.”⁶ As a consequence of an expansionary policy, rates are driven to r₁. Toward the end of the cycle, therefore, the investment demand schedule will have increased to I^d ′. Presumably, price inflation has accelerated by then, particularly for consumer goods. Assume that monetary authorities now wish to engage in a “tight” monetary policy. Merely to hold investment expenditures to I^d ′, monetary policy would have to increase real rates to r₂. This is higher than the long-run equilibrium rate. If the inflation expectation effects are operative, nominal interest rates would have to rise by that much more.

In fact, we believe that Hayek’s analysis is consistent with the basic facts of cycles. In the next section, we present evidence to support this contention. For the moment, we take it as an assumption. We suggest, further, that investment cycles typically end in a credit crunch, with a comparatively sudden and simultaneous financial “crisis” for numerous firms. At r₂ the interest rate is too high for long-run equilibrium. Many projects, newly undertaken, will have to be abandoned. Entrepreneurs simply will not be able to command the complementary factors to complete these projects. In particular, labor and raw materials will be prohibitively expensive for entrepreneurs to purchase at an interest rate of r₂. The initial round of unemployment and cyclical decline begins as these factors are released from type 1 projects.

How will the rest of the decline look? It will appear to be “Keynesian.” Entrepreneurs will decrease their demand for investment funds, particularly for type 1 projects. The resulting unemployment will, however, eventually spill over to type 2 industries. Unemployment spreads because of income-constrained processes. Investment demand collapses: entrepreneurial expectations turn pessimistic in response to realizations of lower sales and profits. Indeed, investment demand could fall below I. If monetary policy does not respond quickly, a Wicksellian cumulative contraction may develop. Market interest rates are now too high; even an interest rate of r₀ could be temporarily too high during such a downward-adjustment phase.

Notice, however, that a Hayekian analysis (or a similar story) is needed to rationalize a quasi-Keynesian ending. Keynesian analysis begins in the middle of a cyclical story: the marginal efficiency of capital declines. This decline is either exogenous, or is predicated on a view of capital goods as all gross substitutes. Analysis predicated purely on exogenous shifts in expectations is objectionable on a number of grounds. If it is an accepted mode of analysis, then any story can be told with no a priori grounds for distinguishing among them. Further, the Keynesian story depends on waves of optimism or pessimism striking large numbers of entrepreneurs simultaneously. This latter assumption appears to be the conclusion of dubious amateur psychological reasoning.

Some analysts (e.g., Leijonhufvud, 1968) attribute a kind of Schumpeterian hypothesis to Keynes. After a long period of high investment, expected returns decline. For the reasons indicated in the previous chapter, we are not sanguine about analysis of economic cycles based on technological innovations. Such innovations surely help explain the direction that investment takes in a cycle, but are dubious as an explanation of the cyclic character of investment.

D. H. Robertson (1940) was virtually the only one to have perceived the connection between Hayek’s theory of expansion and crises and Keynes’ theory of contraction. By the time Robertson pointed this connection out, however, neither party to the Keynes-Hayek controversies wanted to listen to Robertson’s resolution. In essence, Robertson pointed out that each had offered part of a complete Wicksellian theory: Hayek and Keynes wrote about different problems. In our judgment, Hayek’s theory was more complete on a number of grounds, especially in his far greater attention to capital and interest theory. We do not wish, however, to press this doctrinal point here.7

Evidence

As a result of the Keynesian revolution, economists basically lost interest in monetary analysis and monetary problems (see O’Driscoll, 1977, pp. 35–7). Interest in the Quantity Theory revived first, a process beginning with Milton Friedman’s 1956 restatement of that tradition. The Austro-Wicksellian tradition languished in the shadow of Keynes for another decade. The Austrian revival began with Hicks’ (1967) recounting of “the Hayek Story,” an analysis to which Hayek (1969) responded. Buchanan (1969) restated the Austrian-subjectivist theory of cost. With Dolan (1976), a modest amount of new work in that area began to appear. While Havek’s theory of economic fluctuations received a great deal of attention, no one went back to check the consistency of the data with the predictions of the theory. Earlier works on the Great Depression by Robbins (1934) and Rothbard (1963) did not use modern statistical and econometric techniques. In addition, Robbins had repudiated his earlier views; and Rothbard’s thesis won him opposition from monetarists as well as Keynesians. Part of Rothbard’s thesis has since been justified by Gallaway and Vedder (1987). In a still more comprehensive study, Wainhouse (1982) systematically confronted Hayek’s monetary theory of the cycle with postwar data.

Wainhouse formulated six operational propositions derived from Hayek’s original statement of his theory (1967a); these consisted of three propositions about causality and three propositions about relative-price movements. Wainhouse applied causality tests to the first three propositions. He also compared actual with expected relative-price movements. He used monthly data from January 1959 to June 1981 (January 1959 being the first month that all series were available as monthly data).

His six propositions were as follows:

(1) Changes in the supply of savings are independent of changes in the supply of bank credit.
(2) Changes in the supply of credit lead to changes in rates of interest. Furthermore, changes in credit and interest rates are inversely related.
(3) Changes in the rate of change of credit lead to changes in the output of producers’ goods.
(4) The ratio of producers’ goods’ prices to consumers’ goods’ prices tends to rise after the initiation of a credit expansion.
(5) Prices of producers’ goods closest to final consumption tend to decline relative to the prices of producers’ goods located further away from the consumers’ goods in the production scheme (in the expansion phase of a cycle).
(6) The prices of consumers’ goods rise relative to the prices of producers’ goods, reversing the initial shift in relative prices.

With respect to the first three propositions, Wainhouse tested for Granger “causality.” He first estimated state-space models for the variables, and then employed the equivalent Auto-Regressive Moving Average (ARMA) representation of each state-space form. Proposition 1 asserts the strict independence of changes in savings and changes in credit; this is a particularly strong interpretation of Hayek’s thesis. It also implies that bank policy is not neutral. Proposition 2 establishes that monetary policy initiates cyclical activity, rather than responding to real shocks. Again, a more general formulation of Hayek’s theory would allow real shocks to initiate the process. Proposition 3 is an explicit statement of non-neutrality. Wainhouse found that the empirical evidence produces significant support for the three causality propositions.

Wainhouse next identified credit cycles corresponding to Hayekian cycles (though not necessarily National Bureau of Economic Research (NBER) Reference Cycles). He examined relative-price movements after the initiation of each cycle, comparing them with price averages 24 months before the onset of the cycle. In proposition 4, Wainhouse presents Hayek’s prediction of the broad pattern of relative-price movements after the initiation of the cycle. Over two-thirds of the observations are consistent with the prediction. Most of the anomalous findings are concentrated in one particular credit cycle. Again, over two-thirds of the observations confirm the broad prediction of proposition 5. Proposition 6 contains one of the most controversial aspects of Hayek’s theory: the reversal of relative-price movements in the contraction. It is a precise statement of the proposition that the seeds of recessions are sown in the prior expansion, suggesting the inevitability of recessions after an expansionary period. Wainhouse found evidence in the majority of cases to be consistent with this sixth proposition.

Wainhouse’s results are robust, not varying significantly with alternative formulations. In his study, Wainhouse utilized state-of-the-art time series analysis. Moreover, he applied Hayek’s theory to recent periods, in which the economy had changed fundamentally from the nineteenth-century institutions that Hayek (1969, p. 282) had in mind. Wainhouse’s evidence not only corroborates key elements of Hayek’s theory, but also suggests that further empirical research would be rewarded.

Rational expectations

In this section, we do not claim to present a comprehensive treatment of the rational expectations revolution. That revolution is in progress, currently doing intellectual battle with a counter-revolution. No clear resolution has yet emerged. Our concern here is to relate our theory to this controversy, and to forestall misunderstandings about what we are and are not saying.

The first problem is to define carefully what rational expectations means or implies. Definitions are often either so broad as to be almost vacuous, or so stringent as to seem like a virtual caricature of themselves. Consider the variety of formulations offered by one author, David K. H. Begg (1982), in a recent survey:

(1) The Rational Expectations Hypothesis asserts that individuals do not make systematic mistakes in forecasting the future (p. xi).

(2) These expectations are rational in the following sense: when these expectations are fed back into the model the actual evolution of the economy will imply that there are no systematic forecasting errors which could have been discovered by individuals using information available at the date they had to form expectations (pp. 12–13).

(3) The hypothesis of Rational Expectations … is concerned with incentives to acquire information and exploit profitable opportunities for revising behavior. It admits the notion of an equilibrium set of expectations, even when the economy is not in a static equilibrium (p. 28).

(4) The recent work on the hypothesis of Rational Expectations has commanded considerable attention because it seems to rely on a good optimizing principle: individuals should not make systematic mistakes in forecasting the future. It is not appealing to assume that individuals make predictable errors yet take no action to revise their rule for forming expectations, but ad hoc expectations assumptions typically possess this property; only under Rational Expectations is the contradiction avoided (p. 71).

Begg’s first definition sometimes appears as the contention that “rational forecasting requires that forecast errors be serially uncorrelated” (Poole, 1976, p. 465). Each formulation has been disputed. Consider the following rebuttal by Milton Friedman:

For about five years, the future price of the Mexican peso was decidedly below the current price. And every year, while the Mexican government maintained the price of the peso at 8¢ a peso, the people operating in the futures market made an error in the same direction. Anybody who sold the peso short was bound to lose money. Did that mean that expectations were not rational? Not at all. What it meant was that every single year there was one chance in four that the peso was going to go down 50 percent; and that meant that it was appropriate for the future price to be 12½ percent below the current price. And that continued for 4 or 5 years.

(Friedman, 1977, p. 14)

We agree with Professor Friedman that the peso story points to the need for precision in defining rational expectations. One general implication of Friedman’s parable should be noted. It will not generally be possible to infer the rationality of expectations by observing patterns of forecast error. But, conversely, data on forecasts that were correct, ex post, tell us little about the optimality or rationality of these forecasts. Agents may have been ignoring information that would have generated forecasts that, in retrospect, turned out to be incorrect. In Friedman’s case, speculators were “wrong for the right reason”: in the latter case, they may be “right for the wrong reason.”

Begg’s second definition is more precise, and, in this case, admits of a wider range of phenomena. Friedman’s peso example meets the criterion of this definition: the experience of the same error year after year gave transactors no reason to revise what were optimal forecasts. This definition also points to the importance of specifying what kind of information transactors possess. We come back to this point shortly.

The third statement purports to characterize rational expectations. It is, however, precisely what the rational expectations hypothesis is not concerned with. Rational expectations models typically begin with the assumptions that all profit opportunities have been exploited and all necessary information has already been acquired. Critics (e.g., O’Driscoll, 1979) have long pointed to this deficiency. There is no analysis of the adjustment process in the rational expectations hypothesis, no theory of discovery.

The fourth statement is outrageous but useful for being so clear a statement of a view that we suspect is more often believed than articulated. The rational expectations hypothesis is neither the “only” alternative to ad hoc theorizing about expectations, nor the only expectational hypothesis involving optimizing behavior. While it may not be appealing to assume that individuals make errors that they themselves could have predicted (ex ante error), it is not obviously wrong to suppose that others could have predicted the errors of the first group. Any act of entrepreneurship or speculation involves trying to outguess the market, to do better than the crowd or the median asset-holder. Entrepreneurs and speculators are constantly taking actions that assume that most people make “predictable” errors (predictable by entrepreneurs).

In market economies, information is localized and specialized, implying the existence of differential returns. Because of changing circumstances and the fleeting value of information, this situation is always characteristic – indeed, is an essential characteristic – of markets. And decentralization of information is certainly an essential ingredient of any subjectivist economic theory. Any theory that begins with the elimination of profit and informational differences has assumed that the market process has come to an end.

There is another, important information difference sloughed over in the rational expectations hypothesis. That hypothesis takes it as axiomatic that there is no difference in the information possessed by the theorist, who is an ideal observer, and the human agents in the model. This assumption is thoroughly anti-subjectivist, making it difficult ultimately to reconcile rational expectations and subjectivist theories. To reiterate, we are not interested in refuting rational expectations per se. It may be that our objections are only to “the simplicity of the models in which rational expectations have so far been embedded” (Begg, 1982, p. 255). It does appear at this juncture, however, that rational expectations theorists are leading the profession down a garden path. From what we have seen of the trail thus far, it is a route that we are unwilling to follow.

There certainly are features or implications of rational expectations with which we agree or are in sympathy. Rational expectations theorists have correctly focused attention of the importance of expectational assumptions in macroeconomic analysis and policy-making. Though the Keynesian revolution began as an attempt to incorporate expectations more fully into economic reasoning, it paradoxically ended by suppressing expectational issues. In the General Theory, Keynes emphasized the exogenous aspects of entrepreneurial expectations. As a modeling technique, he assumed that they were completely exogenous in the short run. Short-run exogeneity became the static expectations of Keynesian macromodels, an assumption inhibiting further analysis (see Begg, 1982, pp. 19–22; Leijonhufvud, 1983a, pp. 6–11).

Extravagant claims to revolutionary character notwithstanding, the commonsense core of the rational expectations hypothesis represents a return to inherited wisdom. This core hypothesis has been referred to as “Lincoln’s Law,” as in the following passage:

You can’t fool all of the people all of the time. Eventually the masses come to understand the schemes of their rulers. Then the cleverly concocted plans of inflation collapse … Inflation is not a monetary policy that can be considered as an alternative to a sound-money policy. It is at best a temporary makeshift. The main problem of an inflationary policy is how to stop it before the masses have seen through their rulers’ artifices. It is a display of considerable naivety to recommend openly a monetary system that can work only if its essential features are ignored by the public.

(Mises, 1953, p. 419)

Mises developed the thesis that inflationary expectations emerge with a lag. Once expectations of inflation become embedded in the system, however, the effects of inflationary finance become more far-reaching and serious (Mises, 1953, pp. 418–19). Wicksell articulated even more concisely this commonsense core of any sound expectational theory:

Those people who prefer a continually upward moving to a stationary price level forcibly remind one of those who purposely keep their watches a little fast so as to be more certain of catching their trains. But to achieve their purpose they must not be conscious or remain conscious of the fact that their watches are fast; otherwise they become accustomed to take the extra few minutes into account and so, after all, in spite of their artfulness, arrive too late …

(Wicksell, 1965, pp. 3–4)

Rational expectations theorists have taught us that, in game-theoretic terminology, agents play games with policy-makers. Agents’ strategy can offset the intended effects of policy actions. These will not, however, always be the games supposed in the rational expectations literature. Consider the following situation.

(1) Agents are very good predictors of policy-makers’ actions.
(2) One or more endogenous variables are exclusively controlled by a policy-maker.
(3) The payoff of an action to a policy-maker depends on whether his policy will be anticipated.

In this situation, Frydman et al. (1982) have shown rigorously that policy-makers may have no uniquely rational course of action to follow. Different theories suggest different optimal behavior. If no rational course of action exists for the policy-maker, agents cannot then form a rational expectation. This follows because a rational course of action must incorporate a theory of the policy-makers’ behavior, and there is a conflict of theories. The situation is further complicated if, in order to forestall prediction by the public, the policy-maker engages in nonsystematic behavior. This dilemma, known as “Newcomb’s Problem,” depends on all parties attempting to behave rationally. In a game-theoretic setting, then, fully rational behavior may be inconsistent with the formation of rational expectations.

Frydman et al. (1982) highlight the problem of conflict among theories. Rational expectations theorists assume this problem away by postulating that agents’ expectations are “essentially the same as the predictions of the relevant economic theory” (Muth, 1961, p. 316). In macroeconomics, however, there is an embarassingly large number of theories claiming relevance. Applications of these theories to the same data often produce results that, from the perspective of the different theories, can be taken as corroborating rather than being inconsistent. In this case, theorists have no incentive to revise their views and converge to a single “correct” theory. Agents who interpret the world with these conflicting theories, or who purchase forecasts based on conflicting theories, may also fail to converge on a unique theory. In fact, Frydman (1982) investigated the possibility of convergence to an expectational equilibrium in some detail. His analysis led him to conclude that

the possibility of convergence to the rational expectations equilibrium appears to be remote in the context of models of decentralized competitive markets in which agents are assumed to be making individual decisions on the basis of market prices and their private information (p. 664).

Economists have basic disagreements about macroeconomics, particularly concerning causal relationships between monetary changes and income, prices and output. Expectational theories cannot ignore this disagreement or conflict. As Leijonhufvud (1983b, p. 5) put it, “When theorists are not sure they understand, or cannot agree, it is doubtful that they are entitled to the assumption that private sector agents understand and agree.”

Frydman (1982) has offered a criterion for incorporating information into economic models that is consistent with both optimization and information decentralization.8 In specifying the information available to individual actors, the economic modeler should include “only information they can acquire according to the model in the process of making individual decisions and observing market outcomes.” This postulate “requires that the REH [rational expectations hypothesis] be internally consistent with other informational assumptions of the model” (Frydman and Phelps, 1983, p. 15). Frydman finds this criterion violated in the rational expectations models that he considers. This violation is theoretically equivalent to postulating that agents can perform actions violating the resource constraints in the model. In other words, agents are acting in ways that are strictly infeasible in terms of the model’s other assumptions.

One recent development in monetary economics is both encouraging and consistent with the spirit of the Hayek–Frydman criterion. This is the new economics of monetary regimes, or what used to be called the monetary standard. Leijonhufvud has described a monetary regime as

a system of expectations that governs the behavior of the public and that is sustained by the consistent behavior of the policy-making authorities … The present definition assumes that people understand the systematic components of the authorities’ behavior in a general sort of way but avoids a linkage so tight as to build, for example, short-run neutrality or policy ineffectiveness assertions into the concept itself. Nonetheless, it is in effect an equilibrium concept.

(Leijonhufvud, 1983b, p. 2)

This literature explicitly links institutions and expectations formation. Specifically, it postulates that the amount and quality of information possessed by individuals depends on the institutional environment (the “regime”) within which they operate. A monetary regime or institutional environment generates patterns or regularized features among economic variables. On the basis of this pattern, agents can form reasonably firm expectations. In the course of gaining experience under a given regime, individuals learn the typical features of the monetary environment. Different regimes produce different features or relationships, possibly requiring a different theory. Changes in regimes render obsolete knowledge about typical features.

Leijonhufvud examines two regimes: one embodying a “quantity principle” (e.g., a modern fiat standard) and the other, a “convertibility principle” (e.g., a commodity standard). Macroeconomists frequently mismatch theory and regime. Further, today’s regime is not merely a hybrid, but, according to Leijonhufvud, is really no standard at all (Leijonhufvud, 1983b, p. 27).

Klein (1975) is an example of empirical work informed by analysis in terms of alternative regimes. Among other things, Klein found that public recognition of a change in monetary regime occurs slowly and over a long period of time. Consequently, in a transition from a regime of stable prices to one of high and variable inflation, the public may be caught unaware or else may anticipate a return to the old regime. During a transition phase, inflation may be largely unanticipated. Once there is public recognition of the change in regime, however, inflation will tend to be anticipated. If there is a great deal of unpredictability in prices, however, expectations formation will be difficult and costly. Thus, a regime in which inflation is higher on average but more predictable might, ceteris paribus, be preferred to a highly unpredictable but lower average inflation rate (if such a choice is possible).

The monetary regime approach may also explain why, under the gold standard, monetary growth was frequently comparatively large over periods of months and even years with no acceleration in price inflation. What would be an alarming rate of monetary growth under a pure fiduciary standard is not worrisome under a commodity standard, so as long as people believe in the government’s commitment to the standard. A standard is an investment in creating public trust that rules and goals will be adhered to (see Klein, 1975, pp. 482–3). The investment may take the tangible form of real resources held as reserves, or it may involve legal limits on policy-makers that can be relaxed only at great cost (e.g., constitutional rules). The trust cannot, however, be obtained costlessly.

These theoretical insights cannot be incorporated into models by assuming the availability of information to all agents at low cost and independent of the character of monetary institutions. The Hayekian criterion for information, recently restated by Frydman, together with an institutional approach to monetary analysis, represents a promising avenue of analytical inquiry (see O’Driscoll, 1984a).

We have focused on expectational issues because they are important for any theory of economic fluctuations. The main conclusions of our theory do not depend, however, on expectational errors – at least not in the conventional sense. Most theories of economic fluctuations attribute deviations from trend rates of growth of economic variables to expectational error. If, for instance, there is a monetary innovation, then prices accelerate, output increases and unemployment declines. There are real effects only because transactors misperceive purely nominal changes as real changes. Workers, for example, supply more labor as wage rates rise, in the mistaken belief that real wage rates have risen. The process is reversed once expectations are revised.

Expectational errors may be sufficient, but they are surely not necessary for the existence of fluctuations in economic activity. Monetary shocks – changes in the rate of monetary growth – have real effects quite apart from those generated by expectational error. These shocks have distributional and allocational effects, which we have labeled “Cantillon effects.” In the model presented in this chapter, these consequences depend on capital-theoretic considerations first adduced in the previous chapter (and simplified greatly in our type 1 and type 2 capital goods model). The profitability of alternative investment projects is affected by monetary policy. Entrepreneurs are not making errors in responding to these changes, though, of course, it may take time to discover the new opportunities. Indeed, entrepreneurs would be committing mistakes if they ignored the profitable opportunities just because they had not resulted from what economists choose to call “real factors.”

Inflation-induced economic growth is not sustainable. Nonetheless, there are profits to be made from exploiting temporary situations. US postwar expansions average three to four years in length, time enough for entrepreneurs to reap profits. It is true, of course, that expansionary monetary policy tends to increase the profitability of projects having longer periods of investment. In the last chapter, we already noted that entrepreneurs in earlier stages of a production process can make profits selling to later stages, even if the latter eventually experience losses. And owners of nonspecific resources (e.g., raw materials) can still profit from a fully anticipated cyclical episode (i.e., expansionary and recessionary phases of a cycle). Such a situation might reflect, however, one set of entrepreneurs benefiting at the expense of another set. Can a Hayekian cycle occur if fully anticipated by all?

To answer this question, we must distinguish between “micro-” and “macro-” prediction. Entrepreneurs may understand the macroaspects of a cycle, which correspond roughly to the typical features of cycles. They understand that investment, the profitability of which depends on continued inflation of the money stock, cannot be sustained once the inflation ceases. Though entrepreneurs understand this at an abstract (or macro) level, they cannot predict the exact features of the next cyclical expansion and contraction. That is, they do not know how the unique aspects of one cyclical episode will differ from the last such episode or from the “average” cycle. They lack the ability to make micropredictions, even though they can predict the general sequence of events that will occur. These entrepreneurs have no reason to foreswear the temporary profits to be garnered in an inflationary episode. In the end, of course, all profits are purely temporary. And each individual investment opportunity carries with it a risk. For one thing, other entrepreneurs may be quicker. Or so many may have perceived an opportunity that there is a temporary excess supply at some point in the future.

From an individual perspective, then, an entrepreneur fully informed of the Austrian theory of economic cycles will face essentially the same uncertain world he always faced. Not theoretical or abstract knowledge of economic relationships, but knowledge of the circumstances of time and place is the source of profits. In any case, real effects of monetary expansion will be a compound of the distributional impact of the expansion and errors of prediction about inflation’s impact. This case probably corresponds best to the real-world situation.

What if entrepreneurs could predict the exact sequence of redistribution, relative-price changes and output responses resulting from a given monetary expansion? To hypothesize this case quickly gets us into the general paradoxes (including Morgenstern’s and Richardson’s) resulting from assuming perfect foresight. Nonetheless, this case presents no additional problems of logic or theory. Fully anticipated monetary shocks should have the same general implications as a fully anticipated change in tastes or a fully anticipated (exogenous) redistribution of income. The complexity of the case derives from the assumption of the self-reversing character of the allocational changes. And, as in other instances of perfect foresight models, one cannot begin to specify what one entrepreneur will do without also specifying what all others will do. “Perfect foresight” here, as elsewhere, implies perfect prediction of the actions of all other relevant parties. It really is the Holmes-Moriarty example multiplied to an n-player case. If the players were not paralyzed by their dilemma, then they presumably would make investment commitments that have a positive present value over the cycle or relevant planning horizon. They would not get caught unaware by the downturn, though they might experience accounting losses in some periods.

Let us put the case starkly, and shorn of some of the capital-theoretic issues emphasized heretofore. Assume that the Federal Open Market Committee (FOMC) decides to engage in an aggressive monetary expansion over the next two years. It breaks with tradition by immediately announcing its intentions in great detail. Included in this announcement is the statement that it is simply going to give all the newly created money to Roger Garrison. Over the next two years, the money supply will increase by 50 percent. Assume further that no one doubts the Fed’s intentions, etc. (The 12 district banks post a bond equal to the proposed increase in the money supply.) Once all adjustments are made, prices will have risen approximately 50 percent.

Will the fact that the subsequent price inflation is fully anticipated make Mr. Garrison other than a rich man? Surely not. (Those who do doubt this conclusion should not be willing to pay a positive price to take Garrison’s place.) In fact, the openness of the procedure clarifies the way in which Garrison benefits. It also clarifies that, except for thought experiments à la Hume or Friedman, the process of expanding the money supply involves redistribution of wealth. Though the redistribution may or may not be random and unpredictable, it is redistribution nonetheless. (The non-randomness of the redistribution constitutes the empirical content of our hypothesis.)

“Surely,” says the neoclassical economist, “the anticipation of the event will offset the effects.” The answer is “no,” if we adhere consistently to the assumptions of economic decentralization and competition. Garrison, we assume, is either a canny Scotsman or closely related to one. He will not pay more for his purchases just because he is wealthier. Given his greater wealth, he may, of course, purchase higher quality products. His wealth elasticity of demand is not equal to one for every good. To pursue this line of reasoning would call into question even the long-run neutrality of money (see Mises, 1953), a point that we are not interested in pursuing here.

If the rest of us could get together and, as it were, gang up on Garrison, we could nullify his wealth gain. That is, every potential supplier could agree to charge Garrison – and only Garrison – prices that are 50 percent higher than before. We would however, no longer be describing a competitive environment. If some of us were parties to such an agreement, good neoclassical theory would remind us that the canny Scotsmen among us would cheat on the agreement. Garrison would retain his wealth gain, not because printing pieces of paper creates wealth, but because monetary expansion can transfer wealth.

The problem of anticipating monetary shocks and their effects surely exacerbates the costs of inflation (see below). Neither entrepreneurs nor the monetary authority can predict the microdetails of a given policy change. Expectational errors probably account for a significant portion of the real effects of inflation. At the theoretical level, however, it is important to distinguish between these real effects and those arising from the distributional consequences of inflation and deflation of the money stock. For one thing, the distinction helps one avoid arid debates on whether fully anticipated monetary policy matters.

In a sense, we are having our cake and eating it too. In emphasizing the importance of Cantillon effects, we can also recognize the role of the unexpected component of policy changes. Thus, we agree that, as an inflationary policy comes to be anticipated, its effects diminish. We do not follow the rational expectations theorist or even the monetarist in concluding that real effects of monetary expansion and contraction can be eliminated once agents understand the structure of the economy or the causal nexus among economic variables. This strikes us as analogous to suggesting that the horrors of war would be eliminated once citizens understood the causes of war.

We are not, of course, suggesting that the FOMC meets every six weeks and decides whom to enrich the following period. To the extent that wealth and income redistributions accompany monetary accelerations and decelerations, these effects are undoubtedly no part of the intention of the members of that committee. Resulting redistributions and misallocations may be offset by other factors or benefits. Nonetheless, it is important that all the significant effects of inflation be understood before deciding to engage in some of it. Further, if we are correct, then the conventional wisdom on the “costs” of fighting inflations is fundamentally wrong.

Unsustainable monetary expansions generate resource misallocation. The pattern of investment in such expansions is self-reversing; once the growth of money ceases or even decelerates, the pattern will begin to be reversed. The “costs” have been incurred in the expansionary phase. That misallocations occur during the expansionary phase of a business cycle is one thesis of rational expectations models with which we are in complete agreement. The recession phase constitutes the recognition of costs already incurred and errors already made. Ending an inflation does not generate costs but reveals those already incurred. This is true unless an actual monetary contraction is imposed on the previous expansion. Of course, without specifying a regime, it is impossible to say exactly what would constitute a contractionary policy. With an endogenous component of the money supply, a fall in the stock of money may merely reflect the decreased demand for credit in a contractionary phase of the cycle. If authorities attempt to offset any decline, they may perpetuate what they are attempting to remedy.

Three basic policies have been derived from the Austrian development of Wicksell’s theory. Hayek (1967a) argued for maintaining the amount of spending (M x V) constant. He suggested that this would entail a rough constancy in factor prices, and, in a growing economy, a falling price level of final output. Rothbard (1963) argued for constancy in the money supply, all but ensuring secular deflation. More recently, however, White (1984) has criticized any inflexible monetary rule derived from a priori theorizing. He argues for a system of free banking, in which the quantity of money is market-determined by the interaction of competitive suppliers (unregulated banks) and demanders (the nonbank public). From our perspective, the question is not yet settled. We do expect the renewed interest in monetary regimes to help provide a resolution, if not to offer new alternatives.

Notes

1 We are not suggesting that Hicks (1935) represents a consistent subjectivist analysis. This article is, however, a pioneering effort in the microeconomic analysis of money. It thus belongs to a literature of which the subjectivist work of Mises, Hayek and others is one part.

4 The government might try circumventing this problem by promulgating the price of one commodity, e.g., a representative pair of shoes. For this promulgation to be effective, however, transactors would have to perceive informational value in the decreed price. The price certainly would not have the same informational content as a market price, which conveys information about the exchange rate at which shoes are bought and sold on a regular basis. For this and other reasons, we suspect that this strategy would not work. We are aware that this line of reasoning calls into question the ability of the government to introduce a truly fiat currency, a doubt also expressed by Mises (1953).

5 As Hayek (1939) pointed out, equality between savings and investment is an imprecise and ultimately unsatisfactory way of describing intertemporal equilibrium. In his words, the “starting point” of a Wicksellian theory should be “(a) the intentions of all the consumers with respect to the way in which they wish to distribute at all the relevant dates all their resources (not merely their ‘income’) between current consumption and provision for future consumption, and (b) the separate and independent decisions of the entrepreneurs with respect to the amounts of consumers’ goods which they plan to provide at these various dates. Correspondence between these two groups of decisions would be characteristic of the kind of equilibrium which we now usually describe as a state where savings are equal to investment and with which the idea of an equilibrium rate of interest is connected.” Hayek’s microeconomic approach takes account of the complexities of the multi-period case sloughed over in the macroeconomic formulation that S = I. It also makes clear that “the” rate of interest is a shorthand for the whole set of relative prices involved in the intertemporal coordination process (and certainly not merely some loan rate of interest).

6 We do not mean to imply that, but for money, the economy would be in general equilibrium. Following the distinction made in the previous chapter, we are distinguishing between an economy characterized by normal entrepreneurial error and one subjected to persistent monetary shocks. In the latter case, we argue that systematic errors are being made; and economic activity will be discoordinated in a systematic and predictable manner.

7 Any comparison between Hayek and Keynes depends on one’s interpretation of Keynes. Leijonhufvud (1983a) offers an interpretation that makes Keynes seem more Wicksellian, and hence more attractive, than the “textbook” Keynes.

8 As Frydman and Phelps (1983, p. 15) make clear, this criterion is the very one first offered by Hayek (1937a).

Prices and production

Evidence

9
The microanalytics of money

Introduction

Microanalysis of money

The origin of money

Business cycles

A subjectivist theory of economic fluctuations

Rational expectations

Conclusion

Notes

9The microanalytics of money

Introduction

Microanalysis of money

The origin of money

Business cycles

A subjectivist theory of economic fluctuations

Prices and production

Evidence

Rational expectations

Conclusion

Notes

9
The microanalytics of money