
HOW TO WRITE GOOD PROGRAMS
12.1 Procedural Programming – Word Processing
12.2 Object Oriented Programming – Breakout
12.3 Describing the Problem as a Process
12.4 Rules for Programmers
12.5 Summary

In this chapter
There is no general agreement on how best to put together a good program. Good, by the way, means functionally correct, readable, modifiable, reasonably efficient, and that solves a problem that someone needs solved. This chapter will be distinct from the others in this book: we’ll move into second person narrative, partly because of the more personal nature of the subject material. Writing code for some people is like telling a story or making a painting: it’s not that it is art, but that it is personal. If you wish to insult a programmer, say that their code is poorly structured, or naïve, or in some way less than adequate.
There are many processes that have been described for programming, and the truth is that not only is there not one best one, but it is rarely certain than any of them is better than any of the others. When someone writes a program, they are trying to solve a problem. What they are doing is translating a loose collection of ideas into a form that can be represented on a computer, which is to say as
numbers. The ideas are associated with algorithms, things that can be shown to work for at least a range of situations. Then that needs to be converted into a sequence of steps that leads to a solution to the original problem.
This is in part a problem in synthesis, the combining of separate components, elements, and ideas into a coherent whole. There is something called synthesis programming, but that’s not what is being discussed. The parts of a program include decision constructs (IF statements), looping (FOR and WHILE), expressions, assignment statements, and data structures (tuples, dictionaries, strings, etc.). There is a degree of skill involved in using these units to build a sensible larger program. This skill is somewhat individual. No two programmers will create exactly the same program for a non-trivial problem.
What we’re going to do in this chapter is show the development of an entire computer program, with all of the intermediate steps, flaws, errors, and flashes of genius (if any). Why? The answer is “because that is rarely done in lectures or in a book.” When teaching mathematics the professor often shows the proof of a theorem on the blackboard (or as PowerPoint slides) and explains the steps. What they never do is show how the theorem was actually proved when the original person proved it—dead ends, days of no progress, good ideas, bad ideas: the whole messy process.
This is crucial. No theorem and no computer program flows fully formed and correct from someone’s head. Observing the full process may be a valuable stage in the education of a programmer. They will see that the process is prone to error, even for good programmers. They’ll see that not all ideas that seem good are actually good; that the process is not a linear one, but that it appears in some sense to spiral, gaining functionality at each loop. And they will see that there can be a simple and obvious method that could be agreed upon by many different programmers and yet adapted for each new situation. The method that we’ll use is called iterative refinement, and it is nearly independent of language or philosophy. Of course, not everyone will agree.
One example program will be a computer game, and one that can’t be played without a computer. It will be a breakout style game that uses circles instead of rectangles. The other will be a system that formats typed text.
12.1 PROCEDURAL PROGRAMMING – WORD PROCESSING
In the early days of desktop publishing, the programs that writers used did not display the results on the screen in “what-you-see-is-what-you-get” form. Formatting commands were embedded within the text and were implemented by the program, which would create a printable version that was properly formatted. Programs like roff, nroff, tex, and variations thereof are still used, but most writing tools now look like Word or PageMaker with commands being given through a graphical user interface.
There is a limit to what kind of text processing can be done using simple text files, but when you think about it that’s really what a typewriter produces—simple text on paper with fixed size fonts. That worked for a very long time. It was good enough for Ernest Hemingway and Raymond Chandler.
The program that will be developed here will accept text from a file and format it according to a set of commands that have a specific format and are predefined by the system. The input will resemble that accepted by nroff, an old Unix utility, but will be a subset for simplicity. Since it uses standard text input and output any measurements will be made in characters, not inches or points. Commands will begin on a new line with a “.” character and will be alphabetic. A line beginning with “.br”, for instance, results in a forced line break. Some commands take a parameter: the command “.ll 55” sets the line length to 55 characters.
Here is a list of all of the commands that the system will recognize:
The program will read a text file and identify the words and the commands. The words will be written to an output file formatted as described by the commands. The default will be to right justify the text, and to use empty lines as paragraph breaks. The questions to be answered here are:
1. How does one begin creating such a program?
2. Can the process of program creation be described?
a. Is the process systematic or casual?
b. Is there only one process?
Beginning with the last question first, there is no single process. What is presented here is only one, but it should be understood that there are others, and that some processes probably work better than others for some kinds of program. The program to be created here will not use classes, and will involve a classical or traditional methodology generally referred to as top-down. Some people only use object-oriented code, but a problem with teaching that way is that a class contains traditional, procedure-oriented code. To make a class, one must first know how to write a program.
12.1.1 Top-Down
The idea behind top-down programming is that the higher levels of abstraction are described first. A description of what the entire program is to do is written in a kind-of English/computer hybrid language (pseudocode), and this description involves making calls to functions that have not yet been written but whose function is known. When the highest level description is acceptable, then the functions used are described. In this way the high-level decisions are described in terms of the lower level, whose implementation is postponed until the details are appropriate. The process repeats until all parts have been described, at which time the translation of the pseudocode into a real programming language can proceed, and should be straightforward. This can result in many distinct programs, but all should do basically the same thing, simply in somewhat different ways.
For the task at hand, the first step is to sketch the actions of the program as a whole. The program begins by opening the text file and opening an output file. The basic action is to copy from input to output, with certain additions to the output text. The data file is read in as characters or words, but output as lines and pages. So perhaps the following:
Open input file inf
Open output file outf
Read a word w from inf
While there is more text on inf:
If w is a command:
Process the command w
Else:
The next word is w. Process it
Read a word from inf
Close inf
Close outf
This represents the entire program, although lacking a degree of detail. As Python this would look almost the same:
filename = input ("PYROFF: Enter the name if the input
file: ")
inf = open (filename, "r")
outf = open ("pyroff.txt. "w")
w = getword (inf)
while w != "":
if iscommand(w):
process_command (w)
else:
process_word (w)
w = getword(inf)
inf.close()
outf.close()
In order for the program to compile the functions, they must exist. They should initially be stubs, relatively non-functional but resulting in output:
from random import *
def getword (f):
print ("Getword ")
def iscommand(w):
print ("ISCOMMAND given ", w)
if random()< 0.5:
return False
return True
def process_command (w):
print ("Processing command ", w)
def process_word (w):
print ("Processing the word ", w)
This program will run, but never ends because it never reads the file. Still, we have a structure.
Now the functions need to be defined, and in the process further design decisions are made. Consider getword(): what comprises a word and how does it differ from a command? A command starts at the beginning of a line with a “.” character. It is followed by two alphabetic characters that are defined by the system. If the two characters do not match any combinations in the list of commands, then it is not a command. A word, on the other hand, begins or ends with a white space (blank, tab, or end of line) and contains all of the characters between those white spaces. It may not be a word in the traditional sense, in that it may not be an English word; it could be a number or other sequence of characters. Those may cause problems, but it will be left up to the user to figure it out. Example: a long URL may extend over a line. The program has to do something, and so will probably put an end of line when the count of characters exceeds a maximum and leave the problem to the user to fix.
So, let’s figure out the getword() function. It will construct a word as a character string from individual characters that have been read from the input file. A first try could be:
def getword(f):
w = ""
while whitespace(ch(f)):
nextch(f)
while not whitespace(ch(f)):
w = w + ch(f)
nextch(f)
print ("Getword is ", w)
return w
The function whitespace() returns True if its parameter is a white space character. The function nextch() reads the next character from the specified file, and the function ch() returns the value of the current character. To effectively test getword(), we need to implement these three functions. Here’s a first attempt:
def whitespace (c):
if c == " ": return True
if c == "\t": return True
if c == "\n": return True
return False
def ch(f):
global c
return (c)
def nextch(f):
global c
c = f.read(1)
This way of handling input is a bit unusual, but there is a reason for it. We are anticipating a need to buffer characters or to place them back on the input stream. It is similar to the input scheme used in Pascal, or the system found in early forms of UNIX which used getchar – putchar - ungetc. The necessity of extracting commands from the input stream, and that commands must begin a new line, might make this particular scheme useful. The initial implementation of nextch() simply reads a new character from the file, but it could easily be modified to extract a character from a buffer, and refile the buffer if it is empty. Both would look the same to the programmer using them.
The program runs, but has a problem: it never terminates. After the text file has been read, the program seems to call nextch() repeatedly. After some thought the reason is clear—when the input request results in an empty string (“”) the current character is not a white space, and the loop in getword() that is building a word runs forever. This is a traditional end-of-file problem and can be solved in a few different ways: a special character can be used for EOF, a flag can be set, or the empty string can be tested for in the loop explicitly. The latter solution was chosen, and fixes the infinite loop. The word construction loop in getword() becomes:
while not whitespace(ch(f)) and ch(f) !="":
A possible next step is to distinguish between commands and words. Because a command starts a line and begins with a “.” there are two things to do: mark the beginning of a new line, and look up the input string in a table of commands. The command could be searched first, then if it matches a command name we could back up the input to see if it was preceded by a newline character (“\n”). A newline counts as a white space, and another option would be to set a flag when a newline character is seen, clearing it when another character is read in. Now a string is a command if the flag set before it was read in and it matches one of the commands. Timing is everything in this method, but white space separates words, so it could work by simply remembering (saving) the last white space character seen before any word. That sounds like a good idea.
Oops. When implemented, none of the commands are recognized. A table of names was implemented as a tuple:
table = (".pl",".bp",".br",".fi",".nf",".na",".ce", ".ls",".ll",".in",".ti",".nh",".hy",".sp")
The nextch() function was modified so:
def nextch(f):
global c, lastws
c = f.read(1)
if whitespace(c):
lastws = c
and the function iscommand() is implemented by checking for the newline and the match of the string in the table:
def iscommand(w):
global table, lastws
if lastws == "\n":
if w in table:
return True
return False
To discover the problem some print statements were inserted that show the previous white space character and the match in the table for all calls to iscommand(). The problem, which should have been obvious, is that when the command is read in, the last white space seen will be the one that terminated it, not the one in front of it.
A solution: keeping the same theme of remembering white space characters, how about save the previous two white space characters seen. The most recent white space will be the one that terminated the word string, and the second most recent will always be the one before it. All of the others, if any, would have been skipped within getword(). The solution, as coded in the nextch() function, would be:
def nextch(f):
global c, clast, c2last
c = f.read(1)
if whitespace(c):
c2last = clast
clast = c
There are two variables needed, clast being the previous white space and c2last being the one encountered before clast. Now iscommand() is modified slightly to look for c2last:
def iscommand(w):
global table, c2last
if c2last == "\n":
if w in table:
return True
return False
Yes, this now identifies the commands in the source file, even the text that looks like a command but is not: “.xx.”
Notice that the development of the program consists of an initial sketch and then filling in the code as stubs and coding the stubs to be functional code, one at a time. Sometimes a stub requires further undefined functions to be used, and those could be coded as stubs too, or completed if they are small so as to allow testing to proceed. It’s a judgment call as to whether to complete the stubs down the chain for one part of the program or to proceed to the next one at the current level. For example, should we have completed the nextch() and ch() functions before trying to design process_command()? It does depend on how testing can proceed and what “level” we’re at. The nextch() function looks like it won’t call other functions that have not been implemented, and it is tough to test getword() without finishing nextch().
This discussion speaks to what the next step will be from here, and the answer is “there could be many.” Let’s look at commands next, because they will dictate the output, and then deal with formatting last. It is known that a string represents a command, and the function called as a consequence is process_command(). This function must determine which command string was seen and what to do about it. The way commands are handled and the way the output document is specified has to be sorted out before this function can be finished, but a set of stubs can hold the place of future decisions as before.
The string that was seen to be a command is stored in a tuple. The index of the string within the tuple tells us which command was seen, although a string match could be done directly. Using a tuple is better because new commands can always be added to the end of the tuple during future modifications and it is easier to modify command names. The function, which used to be a stub, is now:
def process_command (w):
global table, inf, page_length, fill, center, center_
count, global spacing, line_length, adjust, hyphenate
k = table.index(w)
if k == 0: # .PL
s = getword(inf)
page_length = int(s)
elif k == 1: # .BP
genpage()
elif k == 2: # .BR
genline()
elif k == 3: # .FI
fill = True
elif k == 4: # .NF
fill == False
elif k == 5: # .NA
adjust = False
elif k == 6: # .CE
center = True
s = getword(inf)
center_count = int(s)
elif k == 7: # .LS
s = getword(inf)
spacing = int(s)
elif k == 8: # .LL
s = getword(inf)
line_length = int(s)
print ("Line length ", line_length, "characters")
elif k == 9: # .IN
s = getword(inf)
indent (int(s))
elif k == 10: # .TI
s = getword(inf)
temp_indent (int(s))
elif k == 11: # .NF
hyphenate = False
elif k == 12: # .HY
hyphenate = True
elif k == 13: # .TL
dotl ()
elif k == 14: # .SP
s = getword(inf)
space (int(k))
This completes iteration 5 of the system and generates quite a few new stubs and defines how some of the output functions will operate. There are some flags (hyphenate, center, fill, adjust) and some parameters for the output process (line_length, spacing, etc.) that are set, and so will be used in sending output text to the file. These parameters being known, it is time to define the output process, which will be implemented starting with the function process_word().
As was mentioned earlier, the program reads data one character at a time and emits it as words. There is a specified line length, and words can be read and stored until that length is neared or exceeded. Words could be stored in a string. When the line length is reached, the string could be written to the file. If right justification is being done, spaces could be added to some other spaces in the string until the line length was met exactly, or the final word could be hyphenated to meet the line length. If right justification is not being done, then the line length only has to be approached, but not exceeded.
For text centering input lines are padded with equal numbers of spaces on both sides. The page size is met by counting lines, and then by creating a new page when the page size is met, possibly by entering a form feed or perhaps by printing empty lines until a specified count is reached. Indenting is simple: the in command results in a fixed number of spaces being placed at the beginning of each output line; the ti command results in a specified number of spaces being placed at the beginning of the current line. Hyphenation is done by table lookup. Certain suffixes and prefixes and letter combinations are possible locations for a hyphen. The final word on a line can be hyphenated if a location within it is subject to a hyphen as indicated by the table.
The process is to read and build words and copy them to a string, the next output line. No action is taken until the string nears the line length, at which point insertion of spaces, hyphenation, or other actions may be taken to make the string fit the line, either closely or precisely. After a line meets the size needed it is written, perhaps followed by others if the line spacing is larger than one. So, the basic action of the process_word() function will be to copy the word to a string, the output buffer, under the control of a set of variables that are defined by the user through commands:
| page_length | 55 | Number of lines of text on a single page |
| fill | True | Controls whether the text is being formatted |
| adjust | True | Controls whether the text is right justified |
| center | False | Controls whether text is being centered |
| center_count | 0 | Number of lines still to be centered |
| spacing | 1 | Number of lines output per line of text |
| nindent | 0 | Number of spaces on the left |
| line_length | 66 | Number of characters on one line |
| hyphenate | True | Are words hyphenated by the system? |
The simplest version of process_word() would copy words to the buffer until the line was full and then simply write that line to the output file.
def process_word (w):
global buffer, line_length
if len(buffer) + len(w) + 1 <= line_length:
buffer = buffer + " " + w
else:
emit(buffer)
buffer = w
The code above adds the given word plus a space to the buffer if there is room. Otherwise it calls the emit() function to write the buffer to the output file and places the word at the beginning of a new line. This is nearly correct. Some of the output for the sample source is:
This is sample text for testing Pyroff. The default is to right
adjust continuously, but embedded commands can change this.
Now the line width should be
30 characters, and so the left
margin will pulled back. This
line is centered .xx not a
command. Indented 4
Note that the command “.ll 30” was correctly handled, but that there is an extra space at the beginning of the first line. That’s due to the fact that process_word() adds a space between words, and if the buffer is empty that space gets placed at the beginning. The solution is to check for an empty buffer:
if len(buffer) + len(w) + 1 <= line_length:
if len(buffer) > 0:
buffer = buffer + " " + w
else:
buffer = w
This was a successful fix, and completes iteration 6 of the system, which is now 150 lines long.
Within process_word() there are multiple options for how words will be written to the output. What has been done so far amounts to filling but no right justification. Other options are: no filling, centering, and justification. When the filling is turned off, an input line becomes an output line. This is true for centering as well. When justification is taking place the program will make the output lines exactly line_length characters long by inserting spaces in the line to extend it and by hyphenation, where permitted, to shorten it. The rule is that the line must be the correct length and must not begin or end with a space. The implementation of this part of the program is at the heart of the overall system, but would not be possible without a sensible design up to this point.
12.1.2 Centering
First, a centered line is to be written to output when an end of line is seen on input. This means that the clast variable will be used to identify the end of line and to emit the text. Next, the line will have spaces added to the beginning and end to center it. The buffer holds the line to be written and has len(buffer) characters. The number of spaces to be added totals line_length – len(buffer), and half will be added to the beginning of the line and half to the end. A function that centers a given string would be:
def do_center (s):
global line_length
k = len(s) # How long is the string?
b1 = line_length - k # How much shorter than the line?
b2 = b1//2 # Split that amount in two
b1 = line_length - k - b2
s = " "*b1 + s + " "*b2 # Add spaces to center the text
emit(s) # Write to file
In the process_word() function some code must be added to handle centering. This code has to detect the end of line and pass the buffer to do_center(). It also counts the lines, because the “.ce” command specifies a number of lines to be centered.
if center: # Text is being centered, no fill
if len(buffer) > 0: # Add this word to the line
buffer = buffer + " " + w
else:
buffer = w
if clast == "\n": # An input line = an output line
do_center(buffer) # Emit the text
center_count = center_count - 1 # Count lines
if center_count <= 0: # Done?
center = False # Yes. Stop centering.
This code is not quite enough. There are two problems observed. One problem is that the buffer could be partly full when the “.ce” command is seen, and must be emptied. This problem is serious, because filling may be taking place and the line might have to be justified. For the moment a call to emit() will happen when the “.ce” command is seen, but this will have to be expanded.
The other problem is simpler: the do_center() function does not empty the buffer so the line being centered occurs twice in the output. For example:
margin will pulled back.
This line is centered ← This is correct
This line is centered .xx not ← This is wrong. Text is repeated.
a command. Indented 4
The solution is to clear the buffer after do_center() is called:
do_center(buffer) # Emit the text
buffer = "" # Clear the buffer
12.1.3 Right Justification
Centering text is a first step to understanding how to justify it. Right justified text has the sentences arranged so that the right margin is aligned to the line. When centering, spaces are added to the left and right ends of the string so as to place any text in the middle of the line. When justifying, any space in the line can be made into multiple spaces, thus extending the text until it reaches the right margin. Naturally it would not be acceptable to place all of the needed spaces in one spot. It looks best if they are distributed as evenly as possible. However, no matter what is done there will be some situations that cause ugly spacing. We’ll have to live with that.
The number of spaces needed to fill up a line is line_length – len(buffer), just as it was when centering. As words are added to the line this value becomes smaller, and when it is smaller than the length of the next word to be added, then the extra spaces must be added and a new line started. That is, when
k = line_length - len(buffer)
if k < len(word):
then adjusting is performed. First, count the spaces in the buffer and call this nspaces. If k>nspaces then change each single space into k//nspaces space characters and set k = k%nspaces. This will rarely happen. Now we need to change some of the spaces in the buffer into double spaces. Which ones? In an attempt to spread them around, set xk = k + k//2. This will be used as an increment to find consecutive spots to put spaces. So for example, let k = 5, in which case xk = 7. The first space could be placed in the middle, or at space number 2. Now count xk positions from 2, starting over at zero when you hit the end. This will give 4 as the next position, followed by 1, then 3, and then 0. This process seems to spread them out. Now the buffer is written out and the new word is placed in an empty buffer.
This sounds tricky, so let’s walk through it. Never enter code that is not likely to work! Inside of the process_word() function, check to see if adjusting is going on. If so, check to see if the current word fits in the current line. If so, put it there and move on.
elif adjust:
k = line_length - len(buffer) # Number of spaces
# remaining
if k > len(w): # Does the word w fit?
if len(buffer) == 0: # Yes. Empty buffer?
buffer = w # Yes. Buffer = word.
else: # No. Add word to the
# buffer
buffer = buffer + " " + w
print ("Buffer now ", buffer, k, len(w))
else: # Not enough space remains
print (buffer, k, w, len(w))
nspaces = buffer.count(" ") # How many spaces in
# buffer?
xk = k + k//2 +1 # Space insert increment
while k > 0:
i = nth_space (buffer, xk)
buffer = buffer[0:i] + " " + buffer[i:]
k = k - 1
xk = xk + 1
emit(buffer)
buffer = w
The function nth_space (buffer, xk) locates the nth space character in the string s modulo the string length. The spaces were not well distributed with this code in some cases. There was a suspicion that it depended on whether the number of remaining spaces was even or odd, so the code was modified to read:
. . .
xk = k + (k+1)//2 # Space insert increment
if k%2 == 0:
xk = xk + 1
. . .
which worked better. The output for the first part of the test data was:
This is sample text for testing Pyroff. The default is to right adjust continuously, but embedded commands can change this.
Now the line width should be
30 characters, and so the left
margin will pulled back.
This line is centered
.xx not a command. Indented 4
characters. The idea behind
top-down programming is that
the higher levels of
abstraction are described
. . .
The short lines are right justified, but the distribution of the spaces could still be better.
The function nth_space() is important, and looks like this:
def nth_space (s, n):
global nindent
nn = 0 # nn is a count of spaces seen so far
i = 0 # i is the index of the character being examined
while True:
if s[i] == " ": # Is character i a space?
nn = nn + 1 # Yes. Count it
if nn >= n: # Is this enough spaces?
return i # Yes, return the location
i = (i + 1)%len(s) # Next i, wrapping around the end
12.1.4 Other Commands
The rest of the commands have to do with hyphenation, pagination, and indentation, except for the “.br” command. Dealing with indentation first, the command “.in” specifies a number of characters to indent, as does “.ti.” The “.in” command begins indenting lines from the current point on, whereas “.ti” only indents the next line. Since the “.ti” command only indents the next line of text, perhaps initializing the buffer to the correct number of spaces will do the trick. The rest of the text for the line will be concatenated to the spaces, resulting in an indented line.
The “.in” command currently results in the setting of a variable named nindent to the number of spaces to be indented. Following the suggestion for a temporary indent, why not replace all initializations of the buffer with indented ones? There are multiple locations within the process_word() function where the
buffer is set to the next word:
buffer = w
These could be changed to:
buffer = " "*nindent +w
This sounds clean and simple, but it fails miserably. Here is what it looks like. For the input text:
Indented 4 characters.
.in 2
The idea behind top-down programming is that the higher levels of abstraction are described first. A description of what he entire program is to do is written in a kind-of English/computer hybrid language (pseudocode), and this description involves making calls to functions that have not yet been written but whose function is known.
We get:
Indented 4 characters. The
idea behind top-down
programming is that the
higher levels of abstraction
are described first. A
description of what he
entire program is to do is
written in a kind-of
English/computer hybrid
language (pseudocode), and
this description involves
making calls to functions
that have not yet been
Can you figure out where the problem is by looking at the output? This is a skill that develops as you read more code, write more code, and design more code. There is a place in the program that will add spaces to the text, and clearly that has been done here. It is, in fact, how the text is right adjusted. The spaces are counted and sometimes replaced with double spaces. This happened here to some of the spaces used to implement the indent.
Possible solutions include the use of special characters instead of leading blanks, to be replaced when printed; finding another way to implement indenting; modifying the way right adjusting is done. Because the number of spaces at the beginning of the line is known, the latter should be possible: when counting spaces in the adjustment process, skip the nspaces characters at the beginning of the line. This is a modification to the function nth_character() to position the count after the indent:
def nth_space (s, n):
global nindent
nn = 0
i = 0
while True:
print ("nn=", nn)
if s[i] == " ":
nn = nn + 1
print (ꞌ" "ꞌ)
if nn >= n:
return i
i = (i + 1)%len(s)
if i < nindent+tempindent: ←
i = nindent+tempindent ←
A second problem in the indentation code is that there should be a line break when the command is seen. This is a matter of writing the buffer and then clearing it. This should also occur when a temporary indent occurs, but before it inserts the spaces. Say, the temporary indent will have the same problem as indent with respect to right adjustment, and we have not dealt with that.
The line break can be handled with a new function:
def lbreak ():
global buffer, tempindent, nindent
if len(buffer) > 0:
emit(buffer)
buffer = " "*(nindent+tempindent)
tempindent = 0
The break involves writing the buffer and clearing it. Clearing it also means setting the indentation. Because this sequence of operations happens elsewhere in the program, those sequences can be replaced by a call to lbreak(). Note that a new variable tempindent has been added; it holds the number of spaces for a temporary indentation, and is added to the regular nindent value everywhere that variable is used to obtain the total indentation for a line. Now right adjustment of a temporarily indented line should work.
The lbreak() function is used directly to implement the “.br” command. A stub previously named genline() can be removed and replaced by a call to lbreak().
Line spacing can be handled in emit(), which is where lines are written to the output file. After the current buffer is written, a number of newline characters are written to equal the correct line spacing. The new emit() function is:
def emit (s):
global outf, lines, tempindent, spacing, page_length
outf.write(s+"\n")
lines = (lines + 1)%page_length
for i in range (1, spacing):
outf.write ("\n")
lines = (lines + 1)%page_length
tempindent = 0
What about pages? There is a command that deals with pages directly, and that is “.bp,” which starts a new page. The page length is known in terms of the number of lines, and emit counts the lines as it writes them. Implementing the “.bp” command should be a matter of emitting the number of lines needed to complete the current page. Something like this:
def genpage():
global page_length, lines
lbreak()
for i in range (lines, page_length):
emit ("")
At this point all that is missing is the ability to hyphenate, which will be left as one of the exercises. The system appears to do what is needed using the
small test file, so the time has come to construct more thorough tests. A file “preface.txt” holds the text for the preface of a book named “Practical Computer Vision Using C.” This book was written using Nroff, and the commands not available in pyroff were removed from the source text so that it could be used as test data. It consists of over 500 lines of text. The result of the first try was interesting.
Pyroff appeared to run using this input file but never terminated. No output file was created. The first step was to try to see where it was having trouble, so a print statement was added to show what word had been processed last. That word was “spectrograms,” and it appears in the first paragraph of text, after
headings and such. Now the data that caused the problem is known. What is the program doing? There must be an unterminated loop someplace. Putting prints in likely spots identifies the culprit as the loop in the nth_space() function. Tracing through that loop finds an odd thing: the value of nindent becomes negative, and that causes the loop never to terminate. The test data contained a situation that caused the program to fail, and that situation resulted from a difference between Nroff and pyroff: in Nroff the command “.in -4” subtracts 4 from the current indentation, whereas in pyroff it sets the current indent to -4.
This kind of error is very common. All values entered by a user must be tested against the legal bounds for that variable. This was not done here, and the fix is simple. However, it reminds us to do that for all other user input values. These are processed in the function process_command(), so locating those values is easy. Once this was done things worked pretty well. There was one problem observed, and that was an indentation error. Consider the input text:
.nf
1. Introduction
.in 3
1.1 Images as digital objects
1.2 Image storage and display
1.3 Image acquisition
1.4 Image types and applications
The program formats this as:
1. Introduction
1.1 Images as digital objects
1.2 Image storage and display
1.3 Image acquisition
1.4 Image types and applications
There is an extra space in the first line after the indent. This seems like it should be easy to find where the problem is, but the function that implements the command, indent(), looks pretty clean. However, on careful examination (and printing some buffer values) it can be seen that it should not call lbreak() because that function sets the buffer to the properly indented number of space characters. This means that when the later tests for an empty buffer occur, the buffer is not empty and text is appended to it rather than being simply assigned to it. That is, for an empty buffer the first word is placed into it:
buffer = word
Whereas if text is present the word is appended after adding a space:
buffer = buffer + " " + word
The indent function now looks like this:
def indent (n):
global nindent, buffer
nindent = n
emit(buffer)
buffer = ""
The preface now formats pretty well, if not up to Word standards. Other problems may well exist, and should be reported to the author and publisher when discovered. The book’s wiki is the place for such discussions.
12.2 OBJECT ORIENTED PROGRAMMING – BREAKOUT
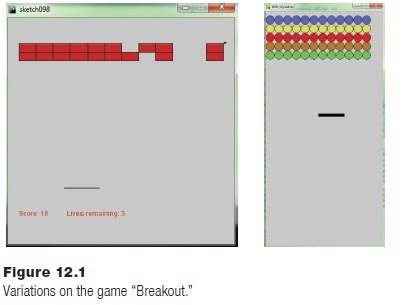
The original game named Breakout was built in 1976, conceived by Nolan Bushnell and Steve Bristow and built by Steve Wozniak (some say aided by Steve Jobs). In this game there are layers of colored rectangles in the upper part of the screen. A simulated ball moves around the game window, and if it hits a rectangle it accumulates points and bounces. The ball also bounces off of the top and sides of the window, but will pass through the bottom and be lost unless the player moves a paddle into its path. If so the ball will bounce back up and perhaps score more points; if not the ball moves out of play. After a fixed number of balls are lost the game is over.
The game being developed here will use circles, that we’ll call tiles, rather than rectangles. There will be 5 rows of tiles, each of a different color and point value: 5, 10, 15, 10, and 5 points for each row respectively. That way the most concealed row has the most points. The player will get three balls to try to clear all of the tiles away. The paddle will move left when the left arrow key is pressed and right when the right arrow key is pressed. The speed of the ball and of the paddle will be determined when the game is tested. A sound will play when a tile is removed, when the ball hits the side or top of the window, when the ball hits the paddle, and when the ball is lost. The current score and the number of balls remaining will be displayed on the screen someplace at all times.
Figure 12.1 shows an example of a breakout game clone on the left, with rectangular bricks. On the right is a possible example of how the game that we’re developing here might look.
12.3 DESCRIBING THE PROBLEM AS A PROCESS
The first step is to write down a step-by-step description of how the program might operate. This may be changed as it is expanded, but we have to start someplace. A problem occurs almost immediately: is the program to be a class? Functions? Does it use Glib?
This decision can be postponed a little while, but in most cases a program is not a class. It is more likely to be a collection of classes operated by a mail program. However, if object orientation is a logical structure, and it often is, it should evolve naturally from the way the problem is organized and not impose itself on the solution.
The game consists of multiple things that interact. Play is a consequence of the behavior of those things. For example, the ball will collide with a tile resulting in some points, the tile disappearing, and a bounce. The next event may be that the ball collides with a wall, or bounces off of the paddle. The game is a set of managed events and consequences. This makes it appear as if an object oriented design and implementation would be suitable. The ball, each time, and the paddle could be objects (class instances) and could interact with each other under the supervision of a main program which kept track of all objects, time, scores, and other details.
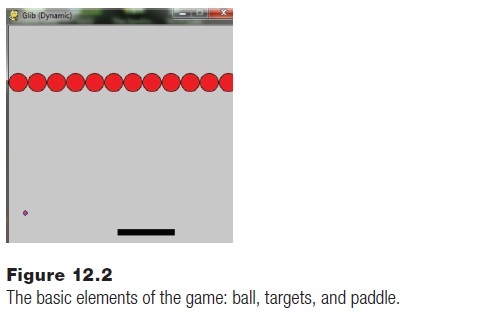
Let’s just focus on the gameplay part of the game, and ignore introductory windows and high score lists and other parts of a real game. The game will start with an initial set up of the objects. Tiles will be placed in their start locations, the paddle will be placed, the locations of the walls defined; then it will be drawn. The initial setup was originally drawn on paper and then a sample rendering was made, shown in Figure 12.1. The code that draws this is:
# Ver 0 - Render initial play area
import Glib
Glib.startdraw(400, 800)
Glib.fill (100, 100, 240)
for i in range (0, 12):
Glib.ellipse(i*30+15, 30, 30, 30)
Glib.fill (220, 220, 90)
for i in range (0, 12):
Glib.ellipse(i*30+15, 60, 30, 30)
Glib.fill (220, 0, 0)
for i in range (0, 12):
Glib.ellipse(i*30+15, 90, 30, 30)
Glib.fill (180, 120, 30)
for i in range (0, 12):
Glib.ellipse(i*30+15, 120, 30, 30)
Glib.fill (90, 220, 80)
for i in range (0, 12):
Glib.ellipse(i*30+15, 150, 30, 30)
Glib.fill (0)
Glib.rect (180, 350, 90, 10)
Glib.enddraw()
This code is just for a visual examination of the potential play area. The first one is always wrong, and this one is too, but it allows us to see why it is wrong and to define a more reasonable set of parameters. In this case the tiles don’t fully occupy the horizontal region, the tile groups are too close to the top, because we want to allow a ball to bounce between the top row and the top of the play area, and the play area is too large vertically. Fixing these problems is a simple matter of modifying the coordinates of some of the objects. This code will not be a part of the final result. It’s common, especially in programs involving a lot of graphics, to test the visual results periodically, and to write some testing programs to help with this.
This program already has some obvious objects: a tile will be an object. So will the paddle, and so will the ball. These objects have some obvious properties too: a tile will have a position in x,y coordinates, and it will have a color and a size. It will have a method to draw it on the screen, and a way to tell if it has been removed or if it still active. The paddle has a position and size, and so does the ball, although the ball has not been seen yet.
What will the main program look like if these are the principal objects in the design? The first sketch is very abstract and depends on many functions that have not been written. This fleshes out the way the classes and the remainder of the code will interact and partly defines the methods they will implement. The initialization step will involve creating rows of tiles that will appear much like those in the initial rendering above but actually consist of five rows of tile objects. This will be done from a function initialize(), but each row would be created in a for loop:
for i in range (0, 12):
tiles = tiles + tile(i*30+15, y, thiscolor, npoints)
where the tile will be created and is passed its x,y position, color, and number of points. The entire collection of tiles is placed into a tuple named tiles. The ball will be created at a random location and with a random speed within the space between the paddle and the tiles, and the paddle will be created so that is initially is drawn in the horizontal center near the bottom of the window.
def initialize ():
score = 0
nballs = 2
b = ball () # Create the ball
p = paddle () # create the paddle
thiscolor = (100,100,240) # Blue
npoints = 5 # Top row is 5 points each
for i in range (0, 12):
tiles = tiles + tile(i*30+15, y, thiscolor, npoints)
# and so on for 4 more rows
The main draw() function will call the draw() methods of each of the class instances, and they will draw themselves:
def draw():
background (200)
b.move() # Move the ball
b.draw() # Draw the ball
p.draw() # Draw the paddle
for k in tiles:
k.draw() # Draw each tile
text ("Score is:"+score, scorex, scorey)
text ("Balls remaining: "+nballs, remainx, remainy)
When this function is called (many times each second) the ball is placed in its new position, possibly following a bounce, and then is drawn. The paddle is drawn, and if it is to be moved it will be done through the user pressing a key. Then the active tiles are drawn, and the messages are drawn on the screen. The structure of the main part of the program is defined by the organization of the classes.
12.3.1 Initial Coding for a Tile
A tile has a graphical representation on the screen, but it is more complex than that. It can collide with a ball and has a color and a point value. All of these aspects of the tile have to be coded as a part of its class. In addition, a tile can be active, meaning that it appears on the screen and can collide with the ball, or inactive, meaning that the ball has hit it and it is out of play for all intents and purposes. Here’s an initial version:
class tile:
def __init__(self, x, y, color, points):
self.x = x
self.y = y
self.color = color
self.points = points
self.active = True
self.size = 30
def draw(self):
if self.active:
Glib.fill (self.color)
Glib.ellipse (self.x, self.y, self.size, self.size)
At the beginning of the game every tile must be created and initialized with its proper position, color, and point value. Then the draw() function for the main program will call the draw() method of every tile during every small time interval, or frame. According to the code above if the tile is not active, then it will not be drawn. Let’s test this.
Rule: Never write more than 20-30 lines of code without testing at least part of it. That way you have a clearer idea where any problems you introduce may be.
A suitable test program to start with could be:
def draw():
global tiles
for k in tiles:
k.draw()
Glib.startdraw(360, 350)
red = (250, 0, 0)
print (red)
tiles = ()
for i in range (0, 12):
tiles = tiles + (tile(i*30, 90, red, 15),)
Glib.enddraw()
which simply places some tiles on the screen in a row, passing a color and point value. This almost works, but the first tile is cut in half by the left boundary. If the initialization becomes:
tiles = tiles + (tile(i*30+15, 90, red, 15),)
then a proper row of 12 red circles is drawn. Modifications will be made to this class once we see more clearly how it will be used.
12.3.2 Initial Coding for the Paddle
The paddle is represented as a rectangle on the screen, but its role in the game is much more profound: it is the only way the player has to participate in the game. The player will type keys to control the position of the paddle so as to keep the ball from falling out of the area. So the ball has to be drawn, as the tiles do, but also must be moved (i.e., change the X position) in accordance with the player’s wishes. The paddle class initially has a few basic operations:
def __init__(self, x, y):
self.x = x
self.y = y
self.speed = 3
self.width = 90
self.height = 10
def draw(self):
Glib.fill (0)
Glib.rect (self.x, self.y, self.width, self.height)
def moveleft(self):
if self.x <= self.speed:
self.x = 0
else:
self.x = self.x – self.speed
def moveright (self):
if self.x > width-self.width-self.speed:
self.x = width-self.width
else:
self.x = self.x + self.speed
When the right arrow key is pressed a flag is set to True, and the paddle moves to the right (i.e., its x coordinate increases) each time interval, or frame. When the key is released the flag is set to False and the movement stops as a result. Movement is accomplished by calling moveleft() and moveright(), and these functions enforce a limit on motion: the paddle cannot leave the play area. This is done within the class so that the outside code does not need to know anything about how the paddle is implemented. It is important to isolate details of the class implementation to the class only, so that modifications and debugging can be limited to the class itself.
The paddle is simply a rectangle, as far as the geometry is concerned, and presents a horizontal surface from which the ball will bounce. It is the only means by which the player can manipulate the game, so it is important to get the paddle operations and motion correct. Fortunately, moving a rectangle left and right is an easy thing to do.
Testing this initial paddle class used a draw() function that randomly moved the paddle left and right, and a main program, that creates the paddle:
def draw():
global p,f
Glib.background(200)
p.draw()
if f:
p.moveright()
else:
p.moveleft()
if random()< .01:
f = not f
Glib.startdraw(360, 350)
f = True
p = paddle (130)
Glib.enddraw()
This code works, and sums up the functionality of the paddle.
12.3.3 Initial Coding for the Ball
The ball really does much of the actual work in the game. Yes, the bounces are controlled by the user through the paddle, but once the ball bounces off of the paddle it has to behave properly and do the works of the game: destroying tiles. According to the standard class model of this program, the ball should have a draw() method that places it into its proper position on the screen. But the ball is moving, so its position has to be updated each frame. It also has to bounce off of the sides and top of the playing area, and the draw() method can make this happen. The essential code for doing this is:
class ball():
def __init__ (self, x, y):
self.x = x
self.y = y
self.dx = 3
self.dy = -4
self.active = True
self.color = (230, 0, 230)
self.size = 9
def draw(self):
if not self.active:
return
Glib.fill (self.color[0], self.color[1],
self.color[2])
Glib.ellipse (self.x, self.y, self.size, self.size)
self.x = self.x + self.dx
self.y = self.y + self.dy
if (self.x <= self.size/2) or \
(self.x >= Glib.width-self.size/4):
self.dx = -self.dx
if self.y <= self.size/2:
self.dy = -self.dy
elif self.dy >= Glib.height:
self.active = False
This version only bounces off of the sides and top, and passes through the bottom. Testing it requires a main program that creates the ball and a draw() function that simply calls the ball’s draw() method:
global b
Glib.background(200)
b.draw()
Glib.startdraw(360, 350)
b = ball (300, 300)
Glib.enddraw()
The ball is created at coordinates (300,300) and does three bounces, disappearing through the bottom after that. A bouncing ball has been coded before, so there is nothing new here yet.
12.3.4 Collecting the Classes
A next step is to test all three classes running together. This will ensure that there are no problems with variable, method, and function names and that interactions between the classes are in fact isolated. All three should work together, creating the correct visual impression on the screen. The code for the three classes
was copied to one file for this test. The main program simply creates instances of each class as appropriate, really doing what the original test program did in each case:
Glib.startdraw(360, 350)
red = (250, 0, 0)
print (red)
tiles = ()
for i in range (0, 12):
tiles = tiles + (tile(i*30+15, 90, red, 15),)
f = True
p = paddle (130)
b = ball (300, 300)
Glib.enddraw()
The draw() function calls the draw() methods for each class instance and moves the paddle randomly as before:
def draw():
global tiles,p,f,b
Glib.background(200)
for k in tiles:
k.draw()
p.draw()
if f:
p.moveright()
else:
p.moveleft()
if random()< .01:
f = not f
b.draw()
The result was that all three classes functioned together the first time it was attempted. The game itself depends on collision, which will be implemented next, but at the very least the classes need to cooperate, or at least not interfere with each other. That’s true at this point in the development.
12.3.5 Developing the Paddle
Placing the paddle under control of the user is the next step. When a key is pressed then the paddle state will change, from still to moving, and vice versa when released. This is accomplished using the keypressed() and keyreleased() functions. They will set or clear a flag, respectively, that causes the paddle to move by calling the moveleft() and moveright() methods. The flag movingleft will result in a decrease in the paddle’s x coordinate each time draw() is called; movingright does the same for the +x direction:
def keyPressed (k):
global movingleft, movingright
if k == Glib.K_LEFT:
movingleft = True
elif k == Glib.K_RIGHT:
movingright = True
def keyReleased (k):
global movingleft, movingright
if k == Glib.K_LEFT:
movingleft = False
elif k == Glib.K_RIGHT:
movingright = False
From the user perspective the paddle moves as long as the key is depressed. Inside of the global draw() function, the flags are tested at each iteration and the paddle is moved if necessary:
def draw(): # 07-classes-01-20.py
global … movingleft,movingright
. . .
if movingleft:
p.moveleft()
elif movingright:
p.moveright()
p.draw()
. . .
The other thing the paddle has to do is serve as a bounce platform for the ball. A question surrounds the location of collision detection; is this the job of the ball or the paddle? It does make sense to perform most of this task in the ball class, because the ball is always in motion and is the thing that bounces. However, the paddle class can assist by providing necessary information. Of course, the paddle class can allow other classes to examine and modify its position and velocity and thus perform collision testing, but if those data are to be hidden, the option is to have a method that tests whether a moving object might have collided with the paddle. The y position of the paddle is fixed and is stored in a global variable paddle, so that is not an issue. A method in paddle that returns True if the x
coordinate passed to it lies between the start and end of the paddle is:
def inpaddle(self, x):
if x < self.x:
return False
if x > self.x + self.width:
return False
return True
The ball class can now determine whether it collides with the paddle by checking its own y coordinate against the paddle and by calling inpaddle() to see if the ball’s x position lies within the paddle. If so, it should bounce. The method hitspaddle() in the ball class returns True if the ball hits the paddle:
def hitspaddle (self): # 08classes-01-21.py
if self.y<=paddleY+2 and self.y>=paddleY-2:
if p.inpaddle(self.x):
return True
return False
The most basic reaction to hitting the paddle is to change the direction of dy from down to up (dy = -dy).
12.3.6 Ball and Tile Collisions
The collision between a ball and a tile is more difficult to do correctly than any of the other collisions. Yes, determining whether a collision occurs is a similar process, and then points are collected and the tile is deactivated. It is the bounce of the ball that is hard to figure out. The ball may strike the tile at nearly any angle and at nearly any location on the circumference. This is not a problem in the original game, where the tiles were rectangular, because the ball was always bouncing off of a horizontal or vertical surface. Now there’s some thinking to do.
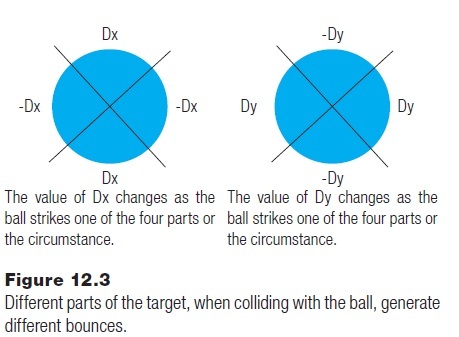
The correct collision could be calculated, but would involve a certain amount of math. The specification of the problem does not say that mathematically correct bounces are required. This is a game design choice, perhaps not a programming choice. What does the game look like if a simple bounce is implemented? That could involve simply changing dy to –dy.
This version of the game turns out to be playable, even fun; but the ball always keeps the same x direction when it bounces. What would it look like if it bounced in roughly the right direction, and how difficult would that be? The direction of the bounce would be dictated by the impact location on the tile, as seen in Figure12.3. This was figured out after a few minutes with a pencil and paper, and is intuitive rather than precise.
We’ll have to figure out where the ball hits the tile, determine which of the four parts of the tile this lies in, and then create the new dx and dy values for the ball. A key aspect of the solution being developed is to avoid too much math that has to be done by the program. Is this possible?
The first step is to find the impact point. We could use a little bit of analytic geometry, or we could approximate. The fact is that the ball is not moving very fast, and the exact coordinates of the impact point are not required. At the beginning of the current frame the ball was at (x,y) and at the beginning of the next is will be at (x+dx, y+dy). A good estimate of the point of impact would be the mean value of these two points, or (x+dx/2, y+dy/2). Close enough for a computer game.
Now the question is: within which of the four regions defined in Figure 12.3 is the impact point? The regions are defined by lines at 45 degrees and -45 degrees. The atan() function will, when using screen coordinates, have the –dx points between -45 and +45 degrees. The –dy points, where the direction of Y motion changes, involve the remaining collisions. What needs to be done is to find the angle of the line from the center of the tile to the ball and then compare that to -45 … +45.
Here is an example method named bounce() that does exactly this.
# Return the distance squared between the two points
def distance2 (self, x0,y0, x1, y1):
return (x0-x1)*(x0-x1) + (y0-y1)*(y0-y1)
def bounce (self, t):
dd = t.size/2 + self.size/2 # Bounce occurs when the
# distance
dd = dd * dd # Between ball and tile <
# radii squared
collide = False
if self.distance2 (self.x, self.y, t.x, t.y) >= dd and \
self.distance2 (self.x+self.dx, self.y+self.dy, t.x,
t.y) < dd:
self.x = self.x + self.dx/2 # Estimated impact
# point on circle
self.y = self.y + self.dy/2
collide = True
elif self.distance2 (self.x, self.y, t.x, t.y) < dd:
collide = True # Ball is completely inside
# the time
if not collide:
return
# If the ball is inside the tile, back it out.
while self.distance2 (self.x, self.y, t.x, t.y) < dd:
self.x = self.x - self.dx*0.5
self.y = self.y - self.dy*0.5
if self.x != t.x: # Compute the ball-tile angle
a = atan ((self.y-t.x)/(self.x-t.y))
a = a * 180./3.1415
else: # If dx = 0 the tangent is infinite
a = 90.0
if a >= -45.0 and a<=45.0: # The x speed change
self.dx = -self.dx
else:
self.dy = -self.dy # The y speed changes
After some testing the code:
# If the ball is inside the tile, back it out.
while self.distance2 (self.x, self.y, t.x, t.y) < dd:
self.x = self.x - self.dx*0.5
self.y = self.y - self.dy*0.5
was added. It was found that if the ball was too far inside the tile then its motion was very odd; as it moved through the tile it constantly changed direction because the program determined that it was always colliding.
12.3.7 Ball and Paddle Collisions
Now we return to examine the collision between the ball and the paddle. The paddle seems to be flat, and colliding with any location on the paddle should have the same result. Perhaps. What if the ball hits the paddle very near to one end? There is a corner, and maybe hitting too near to the corner should yield a different bounce. This was the case in the original games. If the ball struck the near edge of the paddle on the corner it could actually bounce back in the original direction to a greater or lesser degree. This gives the player a greater degree of control, once they understand the situation. Otherwise the game is really predetermined if the player merely places the paddle in the way of the ball. It will always bounce in exactly the same manner.
The proposed idea is to bounce at a different angle depending on where the ball strikes the paddle. We need to decide how near and how intense the effect will be. If the ball hits the paddle near the center, then it will bounce so that the incoming angle is the same as the outgoing angle. When it hits the near end of the paddle it will bounce somewhat back in the incoming direction, and when it strikes the far end the bounce angle will be shallower a bounce from the center.
Let’s say that if the ball hits the first pixel on the paddle it will bounce back in the original direction, meaning that dx = -dx and dy = -dy. A bounce from the center does not change dx but does set dy = -dy. If the relationship is linear across the paddle, the implication would be that striking the final pixel would set dx = 2*dx and dy = -dy. Striking any pixel in between would divide the change in dx by the number of pixels in the paddle, initially 90. If the ball hits pixel n the result will be:
delta = 2*dx/90.0
dx = -dx + n*delta
A problem here is that the dx value will decrease continuously until the ball is bouncing up and down. Perhaps the incoming angle should not be considered. The bounce angle of the ball could be completely dependent on where it hits the paddle and nothing else. If dx is -5 on the near end of the paddle and +5 on the far end, then:
dx = -5 + n*10.0/90.0
The code in the draw() method of the ball class is modified to read:
if self.hitspaddle():
self.dy = -self.dy
self.dx = -5 + (1./9.)*(self.x-p.x)
The user now has a lot more control. The game does appear slow, though. And there is only one ball. Once that is lost, the game is over.
12.3.8 Finishing the Game
What remains to be done is to implement multiple balls. Multiple balls are tricky because there are timing issues. When the ball disappears through the bottom of the play area it should reappear someplace, and at a random place. It should not appear immediately, though, because the player needs some time to respond; let’s say three seconds. Meanwhile the screen must continue to be
displayed. It’s time to introduce states.
A state is a situation that can be described by a characteristic set of parameters. A state can be labeled with a simple number but represents something complex. In this instance specifically there will be a play state, in which the paddle can be moved and the ball can score points, and a pause state, which happens after a ball is lost. The draw() function is the place where each step of the program is performed at a high level, and so will be responsible for the management of states.
The current stage of the implementation has only the play state, and all of the code that manages that is in the draw() function already. Change the name of draw() to state0() and create a state variable state that can have values 0 or 1: play is 0, pause is 1. The new draw() function is now created:
def draw ():
global playstate, pausestate
if state == playstate:
state0()
elif state == pausestate:
state1()
where:
playstate = 0
pausestate = 1
The program should still be playable as it was before as long as state == playstate. What happens in the pause state? The controls of the paddle should be disabled, and no ball is drawn. The goal of the pause state is to allow some time for the user to get ready for the next ball, so some time is allowed to pass. Perhaps the player should be permitted to start the game again with a new ball when a key is pressed. This eliminates the need for a timer, which are generally to be avoided. So, the pause state is entered when the ball departs the field of play. The game remains in the pause state until the player presses a key, at which point a new ball is created and the game enters the play state.
Entering the pause state means modifying the code in the ball class a little. There is a line of code at the end of the draw() method of the ball class that looks like this:
elif self.dy >= Glib.height:
self.active = False
This is where the class detects the ball leaving the play area. We need to add to this:
elif self.dy >= Glib.height:
self.active = False
while, of course, making certain that the variables needed are listed as global. This did not do as was expected until it was noted that the condition should have been if self.y >= Glib.height. The comparison with dy was an error in the initial coding that had not been noticed. Also, it seems like the active variable in the ball class was not useful, so it was removed.
Now in the keyPressed() function allow a key press to change from the pause to the play state. Any key will do:
if state = pausestate:
resume()
The resume() function must do two things. First, it must change state back to play. Next it must reposition the ball to a new location. Easy:
def resume():
global state, playstate
b.x = randrange (30, Glib.width-30)
b.y = 250
state = playstate
This works fine. The game is to only have a specified number of balls, though, and this number was to be displayed on the screen. So, when in the play state and a ball is lost, the count of remaining balls (balls_remaining) will be decreased by one. If there are any balls remaining, then the pause state is entered. Otherwise the game is over. Perhaps that should be a third state: game over? Yes, probably.
The game over state is entered when the ball leaves the play area and no balls are left (in the ball class draw() method. In the global draw() function the third state determines if the game is won or lost and renders an appropriate screen:
. . .
Glib.text ("Score: "+str(score), 10, 30)
if score >= maxscore:
Glib.background (0,230, 0)
Glib.text ("You Win", 200, 200)
else:
Glib.background (100, 10, 10);
Glib.text ("You Lose", 200, 200)
Glib.text ("Score: "+str(score), 10, 30)
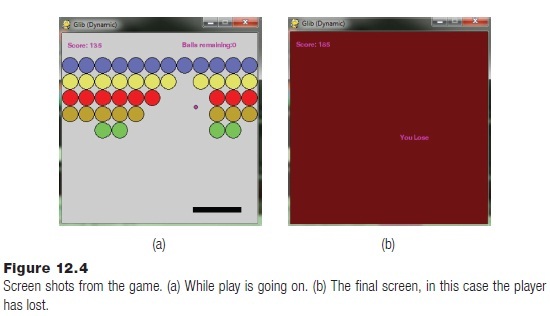
And that’s it! Screen shots from the game in various states are shown in
Figure 12.4. (14playble3.py)
12.4 RULES FOR PROGRAMMERS
The author of this book has collected a set of rules and laws that apply to writing code, and on tens of thousands of lines written and 45 years as a programmer (he started very young). There are over 250 of them, but not all apply to Python. For example, Python enforces indenting and has no begin-end symbols. The ones that do apply are as follows:
2. Use four-space indents and not tabs.
5. Place a comment in lieu of a declaration for all variables in languages where declarations are not permitted.
6. Declare numeric constants and provide a comment explaining them.
7. Rarely use a numeric constant in an expression; name and declare them.
8. Use variable names that refer to the use or meaning of the variable.
9. Make your code clean from the beginning, not after it works.
10. A non-working program is useless, no matter how well structured.
11. Write code that is as general as possible, even if that makes it longer.
12. If the code you write is general, then keep it and reuse it when appropriate.
13. Functions longer than 12 (not including declarations) lines are suspect.
15. Avoid recursion wherever possible.
16. Every procedure and function must have comments explaining function and use.
17. Write external documentation as you code—every procedure and function must have a description in that document.
18. Some documentation is for programmers, and some is for users. Distinguish.
19. Documentation for users must never be in the code.
20. Avoid using operating system calls.
21. Avoid using machine dependent techniques.
22. Do use the programming language library functions.
23. Documentation for a procedure includes what other procedures are called.
24. Documentation for a procedure includes what procedures might call it.
26. When doing input: assume that the input file is wrong.
27. Your program should accept ANY input without crashing. Feed it an executable as a test.
28. Side effects are very bad. A proper function should return a value that depends only on its parameters. Exceptions do exist and should be documented.
29. Everything not defined is undefined.
33. Buffers and strings have fixed sizes. Know what they are and be constrained by them.
34. A handle is a pointer to a structure for an object; make certain that handles used are still valid.
35. Strings and buffers should not overlap in storage.
36. Contents of strings and buffers are undefined until written to.
40. Every variable that is declared is to be given a value before it is used.
41. Put some blank lines between method definitions.
42. Explain each declared variable in a comment.
44. Solve the problem requested, not the general case or subsets.
45. White space is one of the most effective comments.
48. Avoid global symbols where possible; use them properly where useful.
49. Avoid casts (type casting).
50. Round explicitly when rounding is needed.
51. Always check the error return codes.
52. Leave spaces around operators such as =, ==, !=, and so on.
53. A method should have a clear, single, identifiable task.
54. A class should represent a clear, single, identifiable concept.
57. Do the comments first.
58. A function should have only one exit point.
59. Read code.
60. Comments should be sentences.
61. A comment shouldn’t restate the obvious.
62. Comments should align, somehow.
65. Don’t confuse familiarity with readability.
67. A function should be called more than once.
68. Code used more than once should be put into a function.
69. All code should be printable.
70. Don’t write very long lines. 80 Characters.
71. The function name must agree with what the function does.
72. Format programs in a consistent manner.
75. Have a log.
76. Document all the principal data structures.
77. Don’t print a message for a recoverable error—log it.
78. Don’t use system-dependent functions for error messages.
79. You must always correctly attribute all code in the module header.
80. Provide cross references in the code to any documents relevant to the understanding of the code.
81. All errors should be listed together with an English description of what they mean.
82. An error message should tell the user the correct way to do it.
83. Comments should be clear and concise and avoid unnecessary wordiness.
84. Spelling counts.
85. Run your code through a spelling checker.
87. Function documentation includes the domain of valid inputs to the function.
88. Function documentation includes the range of valid outputs from the function.
91. Each file must start with a short description of the module contained in the file and a brief description of all exported functions.
92. Do not comment out old code—remove it.
93. Use a source code control system.
95. Comments should never be used to explain the language.
96. Don’t put more than one statement on a line.
97. Never blindly make changes to code trying to remove an error.
98. Printing variable values in key places can help you find the location of a bug.
99. One compilation error can hide scores of others.
100. If you can’t seem to solve a problem, then do something else.
101. Explain it to the duck. Get an inanimate object and explain your problem to it. This often solves it. (Wyvill)
102. Don’t confuse ease of learning with ease of use.
103. A program should be written at least twice—throw away the first one.
104. Haste is not speed.
105. You can’t measure productivity by volume.
106. Expect to spend more time in design and less in development
107. You can’t program in isolation.
108. If an if ends in return, don’t use else.
109. Avoid operator overloading.
110. Scores of compilation errors can sometimes be fixed with one character—start at the first one.
111. Programs that compile mostly still do not work.
112. Incrementally refine your code. Start with BEGIN-SOLVE-END, then refine SOLVE.
113. Draw diagrams of data and algorithms.
114. Use a symbolic debugger wherever possible.
115. Make certain that files have the correct name (and suffix!) when opening.
116. Never assign a value in a conditional expression.
117. If you can’t say it in English, you can’t say it in any programming language.
118. Don’t move language idioms from one language to another.
119. First, do no harm.
120. If object oriented, design the objects first.
121. Don’t write deeply nested code.
122. Multiple inheritance is evil. Avoid sin.
123. Productivity can be measured in the number of keystrokes (sometimes).
125. Your code is not perfect. Not even close. Have no ego about it.
126. Variables are to be declared with the smallest possible scope.
127. The names of variables and functions are to begin with a lowercase letter.
133. Collect your best working modules into a code library.
134. Isolate dirty code (e.g., code that accesses machine dependencies) into distinct and carefully annotated modules.
135. Anything you assume about the user will eventually be wrong.
136. Every time a rule is broken, this must be clearly documented.
137. Write code for the next programmer, not for the computer.
138. Your program should always degrade gracefully.
139. Don’t surprise your user.
140. Involve users in the development process.
142. Most programs should run the same way and give the same results each time they are executed.
143. Most of your code will be checking for errors and potential errors.
144. Normal code and error handling code should be distinct.
145. Don’t write very large modules.
146. Put the shortest clause of an if/else on top.
149. Have a library of error-reporting code and use it (be consistent).
150. Report errors in a way that they make sense.
151. Report errors in a way that allows them to be corrected.
152. Only fools think they can optimize code better than a good compiler.
153. Change the algorithm, not the code, to make things faster. Polynomial is polynomial.
154. Copy and paste is only for prototypes.
155. It’s always your fault.
156. Know what the problem is before you start coding.
157. Don’t re-invent the wheel.
158. Keep things as simple as possible.
159. Data structures, not algorithms, are central to programming. (Pike)
160. Learn from your mistakes.
161. Learn from the mistakes of others.
162. First make it work; THEN make it work faster.
163. We almost never need to make it faster.
164. First make it work; then make it work better.
165. Programmers don’t get to make big design decisions—do what is asked, effectively.
166. Learn new languages and techniques when you can.
167. Never start a new project in a language you don’t already know.
168. You can learn a new language effectively by coding something significant in it, just don’t expect to sell the result.
169. You will always know only a subset of any given language.
170. The subset you know will not be the same as the subset your coworkers know.
171. Object orientation is not the only way to do things.
172. Object orientation is not always the best way to do things.
173. To create a decent object, one first needs to be a programmer.
174. You may be smarter than the previous programmer, but leave their code alone unless it is broken.
175. You probably are not smarter than the previous programmer, so leave their code alone unless it is broken.
176. Your program will never actually be complete. Live with it.
177. All functions have preconditions for their correct use.
178. Sometimes a function cannot tell whether its preconditions are true.
180. Computers have gigabytes of memory, mostly. Optimizing it is the last thing to do.
181. Compute important values in two different ways and compare them.
182. 0.1 * 10 is not equal to 1.
183. Adding manpower to a late software project makes it later.
184. It always takes longer than you expect.
185. If it can be null, it will be null.
186. Do not use catch and throw unless you know exactly what you are doing.
187. Be clear about your intention. i=1-i is not the same as if(i==0) then i=1 else i=0.
188. Fancy algorithms are buggier than simple ones, and they’re much harder to implement. (Pike)
189. The first 90% of the code takes 10% of the time. The remaining 10% takes the other 90% of the time.
190. All messages should be tagged.
191. Do not use FOR loops as time delays.
192. A user interface should not look like a computer program.
193. Decompose complex problems into smaller tasks.
194. Use the appropriate language for the job, when given a choice.
195. Know the size of the standard data types.
198. If you simultaneously hit two keys on the keyboard, the one that you do not want will appear on the screen.
199. Patterns are for the weak—it assumes you don’t know what you are doing.
200. Don’t assume precedence rules, especially when debugging—parenthesize.
202. ++ and -- are evil. What’s wrong with i = i + 1??
204. It’s hard to see where a program spends most of its time.
205. Fancy algorithms are slow when n is small, and n is usually small. (Pike)
206. Assume that things will go wrong.
207. Computers don’t know any math.
208. Expect the impossible.
209. Test everything. Test often.
210. Do the simple bits first.
211. Don’t fix what is not broken.
212. If it is not broken, then try to break it.
213. Don’t draw conclusions based on names.
214. A carelessly planned project takes three times longer to complete than expected; a carefully planned project takes only twice as long.
215. Any system which depends on human reliability is unreliable.
216. The effort required to correct course increases geometrically with time.
217. Complex problems have simple, easy to understand, and wrong answers.
218. An expert is that person most surprised by the latest evidence to the contrary.
219. One man’s error is another man’s data.
220. Noise is something in data that you don’t want. Someone does want it.
12.5 SUMMARY
There is no general agreement on how best to put together a good program. A good program is one that is functionally correct, readable, modifiable, reasonably efficient, and that solves a problem that someone needs solved. No two programmers will create the same program for a non-trivial problem. The program development strategy discussed in this chapter is called iterative refinement, and is nearly independent of language or philosophy.
There is no single process that is best for writing programs. Some people only use object-oriented code, but a problem with teaching that way is that a class contains traditional, procedure-oriented code. To make a class, one must first know how to write a program.
The idea behind top-down programming is that the higher levels of abstraction are described first. A description of what he entire program is to do is written in a kind-of English/computer hybrid language (pseudocode), and this description involves making calls to functions that have not yet been written but whose function is known—these functions are called stubs. The first step is to sketch the actions of the program as a whole, then to expand each step that is not well-defined into a detailed method that has no ambiguity. Compile and test the program as frequently as possible so that errors can be identified while it is still easy to see where they are.
The key to object-oriented design is identifying the best objects to be implemented. The rest of the program will take a logical shape depending on the classes that it uses. Try to isolate the details of the class from the outside. Always be willing to rethink a choice and rewrite code as a consequence.
Exercises
1. Add sound to the game. When the ball collides with an object a sound effect should play.
2. Consider how hyphenation might be added to Pyroff. How would it be decided to hyphenate a word, and where would the new code be placed? In other words, sketch a solution.
3. In some versions of Breakout-style games, certain of the tiles or targets have special properties. For example, sometimes hitting a special target will result in the ball speeding up or slowing down, will have an extra point value, or will change the size of the paddle. Modify the game so that some of the targets speed up the ball and some others slow it down.
4. The Pyroff system can turn right adjusting off, but not on. This seems like a flaw. Add a new command, “.ra,” that will turn right adjusting on.
5. Most word processors allow for a header and a footer, some space and possibly some text at the beginning and end, respectively, of every page. Design a command “.he” that at the least allows for empty space at the beginning of a page, and a corresponding command “.fo” that allows for some lines at the end of a page.
6. Which three of the Rules for Programmers do you think make the greatest difference in the code? Which three affect code the least? Are there any that you don’t understand?
Notes and Other Resources
Bouncing a ball off of a wall: https://sinepost.wordpress.com/2012/08/19/bouncing-off-the-walls/
1. Jon Bentley. (1999). Programming Pearls, 2nd ed., Addison-Wesley Professional, ISBN-13: 978-0201657883.
2. Adrian Bowyer and John Woodwark. (1983). A Programmer’s Geometry, Butterworth-Heinemann Ltd., ISBN-13: 978-0408012423.
3. Frederick Brooks. (1995). The Mythical Man-Month: Essays on Software Engineering, Anniversary Edition, Addison-Wesley Professional.
4. Jim Parker. (2015). 100 Cool Processing Sketches, eBook, https://leanpub.com/100coolprocessingsketches
5. Jim Parker. (2015). Game Development Using Processing, Mercury Learning and Publishing.
6. R. Rhoad, G. Milauskas, and R. Whipple. (1984). Geometry for Enjoyment and Challenge, rev. ed., Evanston, IL, McDougal, Littell & Company.
7. Gerald M. Weinberg. (1998). The Psychology of Computer Programming, Anl Sub ed., Dorset House, ISBN-13: 978-0932633422.