3 NEWTON’S LAWS

MICHAEL A. STRAUSS

Copernicus made the great breakthrough of explaining planetary motions in terms of the heliocentric universe, by placing the Sun at the center of what we now call the solar system. The various planets, including Earth, are all moving in orbits around the Sun. We are sitting on a moving platform. To figure out how fast Earth is going, we need to determine how far it goes in a specific interval of time; its speed is then that distance divided by that time.

As we saw in chapter 2, Kepler showed that Earth’s orbit is an ellipse. In fact, the orbits of most of the planets in our solar system are close to circles, so we will take the approximation, for the time being, that Earth is moving in a circle, around which it travels in a year. The radius of that circle, the distance from the Sun to Earth, is a quantity that we find ourselves using constantly in astronomy. As described in the last chapter, it is officially named the Astronomical Unit, or AU, for short. One AU is approximately 150 million kilometers, or 1.5 × 10⁸ km.

We thus go around the circumference of a circle 150 million km in radius in one year. The circumference of a circle is 2π times its radius. Everyone knows that π is approximately 3. That’s the kind of approximation astronomers like to use when making rough estimates. We need to divide the circumference by the time, which is 1 year.

We would like to express that year in seconds, which will be useful for present purposes. The number of seconds in a year is 60 (seconds in a minute), times 60 (minutes in an hour), times 24 (hours in a day), times 365 (days in a year). You could multiply that out on a calculator, but recall that, in chapter 1, Neil said that he drank champagne on his billionth second when he was about 31 years old. Thus, a year is about 1/30 of a billion, which is about 30 million seconds. We will write this as approximately 3.0 × 10⁷ seconds in a year.

Putting this all together, we find that the speed at which Earth is orbiting the Sun is 2πr/(1 year) = 2 × 3 × (1.5 × 10⁸ km)/(3 × 10⁷ sec) = 30 km/sec. That’s how fast we are going around the Sun right now. We are trucking! We think of ourselves as sitting still, which may explain why it was so natural for the ancients to imagine that they were at the center of the universe. It seemed so obvious. But in fact there is a great deal of motion going on. Earth is rotating on its axis once a day. It is going around the Sun once a year, traveling at 30 km/sec. We’ll see in Part II of this book that the Sun is moving as well (carrying Earth and the other planets with it) in a variety of additional motions.

Copernicus told us that the various planets are orbiting the Sun. Kepler used Tycho Brahe’s data to determine the orbits of the various planets and learn about their properties. As mentioned in chapter 2, he abstracted three laws from these orbits. Isaac Newton, one of the greatest heroes of our story, was able to deduce from Kepler’s third law that gravity was a radial force between pairs of objects, proportional to one over the square of the distance between them.

Newton was perhaps the greatest physicist, maybe the greatest scientist of any type, who ever lived. He made an amazing number of fundamental discoveries. He wanted to understand how everything moved: not just the planets orbiting the Sun, but a ball tossed in the air or a rock rolling down a hill.

In science, one takes a large number of observations and tries to abstract from them a small number of laws that encompass and explain these observations. Newton came up with his own three laws of motion. The first is the law of inertia. What does inertia mean? In everyday usage, if you say “I have a lot of inertia today,” it means you really don’t want to get going; you are sitting still, and you want to continue to be a couch potato and not budge. It takes something else to get you going. An object at rest (like a couch potato) will remain at rest unless acted on by a force.

Let’s talk about what the force is. Newton’s law of inertia comes in two parts. The first part states that an object that is at rest will remain at rest, unless acted on by an external force. That makes sense. Consider an apple sitting on the table. It has no net force acting on it, and it remains at rest.

The second part of Newton’s law of inertia is less intuitive: an object with uniform velocity will remain at that uniform velocity, unless acted on by an external force. Uniform velocity means that it goes at a certain speed and in a certain direction, neither of which change. If I roll a ball along the floor, it doesn’t continue at a constant speed and in a constant direction forever, but rather slows down and stops, because a force is acting on it: friction between the ball and the floor. Friction is ubiquitous in everyday circumstances. Consider throwing a piece of paper through the air: it slows and then flutters to the floor. Actually, two forces are acting on it: (1) gravity, about which we will have a great deal to say in a moment, and (2) the force due to the resistance of the air itself. The paper has a large surface area for the air to strike, making air resistance important.

The idea that an object in motion will continue to move with constant velocity unless acted on by a force is not intuitive, because friction is all around us. It’s hard to find everyday situations in which there’s no friction, and therefore no force. A figure skater has little friction between the ice and her skates, and thus she can effortlessly glide for a long time across the ice. In the limit of no friction at all, an object given a push would retain a constant velocity. Galileo figured this out. Outer space offers the most dramatic examples of being away from all frictional forces. In space, you really can send something off with uniform velocity and know that it will keep on going, because there is nothing in its path to stop it. Newton formulated this all into a basic law.

Newton’s second law of motion tells us about what happens when an object is being acted on by a force. An object can be acted on by a variety of forces, but whatever those forces are, it is the sum of all the forces that causes a deviation from this uniform velocity. We use the term acceleration to quantify this deviation: acceleration is the change in velocity per unit of time. The second law, then, relates the acceleration of an object to a force acting on it. When you push an object with some force, the object will accelerate. If the object has a small mass, the acceleration will be large, whereas if it is very massive, the acceleration will be smaller for the same amount of force. This relationship gives us Newton’s most famous equation, F = ma; force equals mass times acceleration.

Newton’s third law of motion can be phrased colloquially as, “I push you, you push me.” That is, if one body exerts a force on another, that second body pushes back on the first with an equal and opposite force. If you push down on a tabletop with your hand, you feel a pressure back on your hand; the table is pushing back on you. Every force is paired with an equal and opposite force.

Consider an apple sitting in your hand. It is clearly sitting still. Does it have any forces acting on it? Yes, gravity from Earth. It should be accelerating downward, but clearly it’s not. The reason is that your hand is holding the apple, pushing upward on it (using your arm muscles). In response, by Newton’s third law, the apple is pushing down on your hand; that’s what we refer to as the apple’s weight. The gravitational force from Earth pulling downward on the apple and the force of your hand pushing back up on the apple balance each other out; the sum of these two forces is zero. Zero force means zero acceleration by Newton’s second law, so the apple, which starts at rest, is not going anywhere.

Actually, the story is a bit more interesting than that. Earlier we calculated that Earth is going around the Sun in a circle, at 30 km/sec, and thus the apple is moving at that same speed. To think about this, we need to take a detour to talk about the nature of circular motion.

Motion at constant speed of 30 km/sec in a circle is not uniform velocity, because the direction of Earth’s motion is constantly changing as it circles the Sun. If it didn’t change direction, Earth would just go off on a straight line, not a circle. The acceleration that arises from going around in a circle is familiar from everyday life. Various rides in amusement parks send you around in a circle, and you can feel the acceleration viscerally.

Newton used the tools of differential calculus, which he had just invented, to determine the acceleration of an object moving in a circle of radius r at a constant speed v. That acceleration is v²/r, directed toward the center of the circle. The apple in your hand, which we considered to be standing still, is in fact moving at 30 km/sec in an enormous circle; it’s being accelerated. From Newton’s second law, we know that there must be a force acting on it. That force is the gravitational attraction of the Sun. The Sun is pulling Earth around in an orbit, and it’s pulling our apple around as well. The apple is subject to the force of the Sun’s gravity just as you and I are.

We’re moving at 30 km/sec around the Sun. Given that enormous speed, you might expect the resulting acceleration to be large, but the acceleration is actually quite small, because the radius of the circle is so enormous. Let’s calculate just how small. The velocity of Earth is 30 km/sec, or 30,000 meters/sec, and the radius of Earth’s orbit is 150,000,000,000 meters. Using our formula v²/r, the acceleration a equals (30,000 meters/sec)²/150,000,000,000 meters = 0.006 meters/sec ², or 0.006 meters per second per second. That means that every second, the velocity changes by 6 millimeters per second. That is tiny. Galileo found that the acceleration of an object falling to the ground under the influence of Earth’s gravity is about 9.8 meters per second per second, a much larger value. Therefore, although we’re moving around the Sun at very high speed, Earth is being accelerated by only a small amount. On an amusement ride, in contrast, we’re not going anywhere near 30 km/sec, but the radius r of the circle we’re moving around is tiny; when we divide by that small value of r in the formula v²/r, the resulting acceleration gets quite large, and we are immediately aware of the pull of this acceleration. (For example, a ride moving you at 10 meters per second with a radius of 10 meters, would give an acceleration of 10 meters per second per second.)

When we try to observe the acceleration due to the Sun, our situation is more subtle. The Sun is gravitationally accelerating everything on Earth—you, the book you’re holding, the apple in your hand—all at the same rate. We are all in a free-fall orbit around the Sun. We don’t detect any motion relative to the objects around us. It seems to us that we are stationary; we don’t notice that we are moving, nor do we notice that we’re being accelerated.

But the fact remains, Earth is being accelerated toward the Sun by an amount v²/r. Newton then used Kepler’s third law to figure out how the acceleration produced by the Sun varies with radius. The orbital period P of the planet is

P = (2πr/v);

that is, the orbital period, P, is the distance the planet travels in completing one orbit (2πr) divided by its velocity (v). Thus,

P is proportional to r/v, and
P² is proportional to r²/v².

Kepler told us that P² is proportional to a³, where a is the semi-major axis of the planet’s orbit. In this case, Earth’s orbit is nearly circular, so we can say approximately that r = a, and therefore, substituting r for a, we find:

P² is proportional to r³.

Since P² is also proportional to r²/v²,

r²/v² is proportional to r³.

Dividing by r, we get:

r/v² is proportional to r².

Inverting, we find,

v²/r (the acceleration) is proportional to 1/r².

With these few steps of reasoning, Kepler’s third law, and a little algebra, we’ve shown that the gravitational acceleration, and thus the force, exerted by the Sun on a body at distance r away is proportional to one over the square of that distance: Newton’s “inverse-square” law of gravity. We have it in Newton’s own words:

‘I was in the prime of my age for invention & minded Mathematicks & Philosophy more than any time since’ [my] ensuing deduction ‘from Kepler’s rule of the periodical times of the Planets being in a sesquialterate proportion of their distances from the centers of their Orbs’ that ‘the forces which keep the Planets in their Orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve.’1

Newton applied this understanding of gravity to Earth and the Moon. Consider the famous falling apple that inspired Newton. It lies one Earth radius from the center of Earth and falls toward Earth with an acceleration of 9.8 meters per second per second. The Moon lies at a distance of 60 Earth radii. If the gravitational attraction of Earth falls off like 1/r² (as is true for the Sun), then at the orbit of the Moon, Earth’s gravitational attraction should cause an acceleration (60)² times smaller than the 9.8 meters per second per second at Earth’s surface, or about 0.00272 meters per second per second.

Just as we did for the motion of Earth around the Sun, we can calculate the acceleration of the Moon as it undergoes circular motion around Earth, using its period (27.3 days) and the radius of its orbit (384,000 kilometers). Plugging in the numbers to v²/r gives an acceleration of 0.00272 meters per second per second. Eureka! It agrees beautifully with the prediction from the apple. As Newton himself said, he found the two results to “answer pretty nearly.” The same force that pulls the apple toward Earth also pulls the Moon toward Earth, curving its path away from a straight-line trajectory to keep the Moon in an approximately circular orbit around Earth. The gravity exerted by Earth that causes the apple to fall to Earth extends to the orbit of the Moon. Newton discovered this while staying at his grandmother’s house when Cambridge University was closed during the plague years. But he didn’t publish his results. Perhaps he was upset that the agreement between the prediction and the observation was not perfect, a slight discrepancy caused by the fact that Newton did not have a really accurate measurement of the radius of Earth to work with. In any case, it was only many years later that he would be prodded by Edmund Halley (of comet fame) into publication.

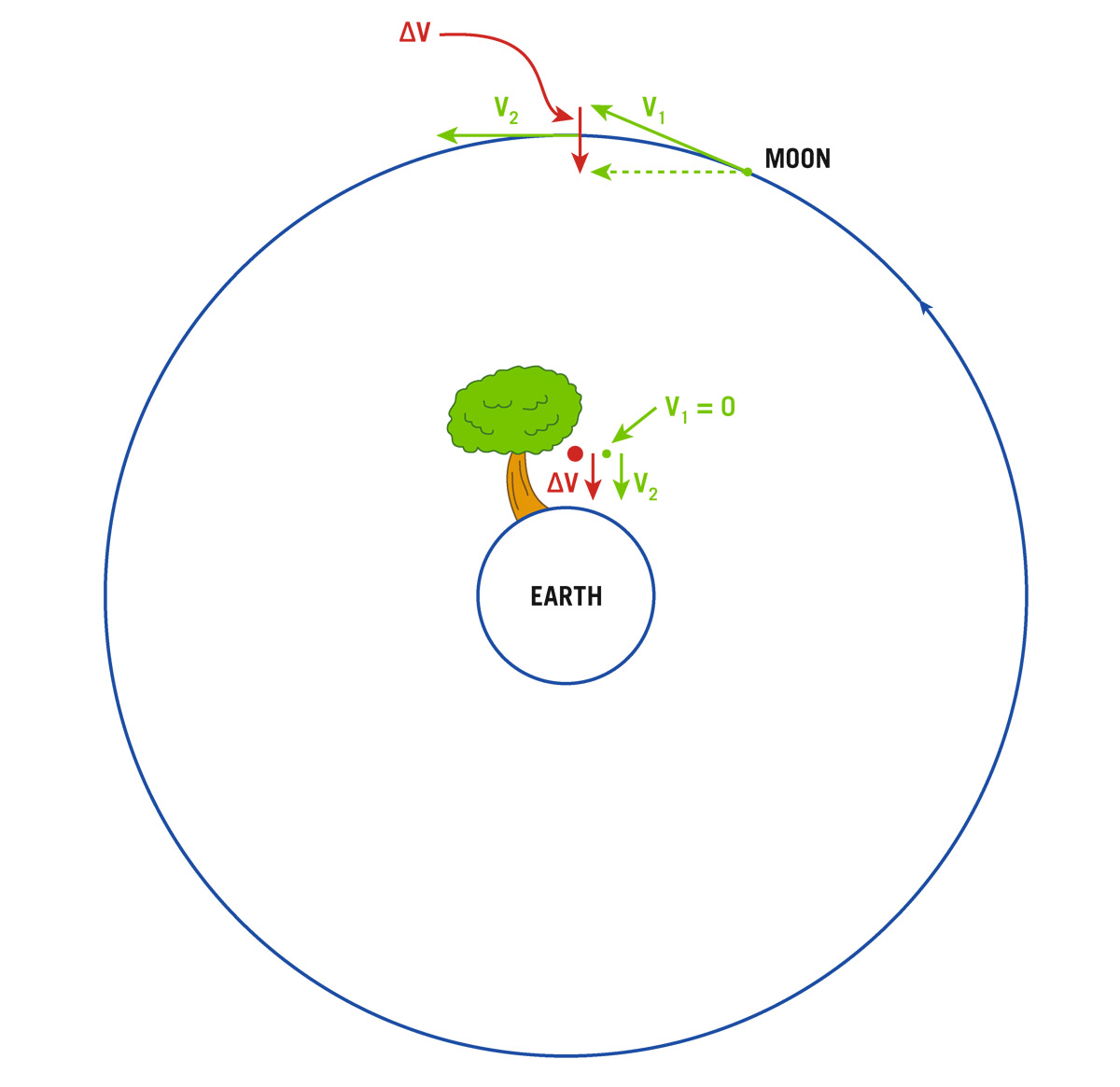
Acceleration of the Moon and Newton’s apple, falling from its tree. Note that in each case, the acceleration (change of velocity) is directed toward the center of Earth. J. Richard Gott

FIGURE 3.1. Acceleration of the Moon and Newton’s apple, falling from its tree. Note that in each case, the acceleration (change of velocity) is directed toward the center of Earth. Credit: J. Richard Gott

Newton worked out what is sometimes rather grandly called the universal law of gravitation, introduced in chapter 2. Consider two objects, say, Earth and the Sun. The distance between them (1 AU, or 1.5 × 10⁸ km) is about 100 times the diameter of the Sun itself (1.4 × 10⁶ km). They have masses M_Earth and M_Sun, respectively.

Newton found that the force of gravity between the two bodies is proportional to each of their masses, and to the inverse square of the distance r between them (using the reasoning from Kepler’s third law, as just described). “Proportional” here means that the force will involve a constant of proportionality, which we call G, or Newton’s constant, in Sir Isaac’s honor. Here’s Newton’s formula for the force between the Sun and Earth:

F = GM_SunM_Earth/r² .

The force is attractive: the two bodies attract each other, and thus the force is directed from each object toward the other.

By Newton’s third law of motion, this formula covers both the gravitational force of the Sun on Earth and the force of Earth on the Sun. But the Sun’s mass is much, much larger than Earth’s mass. Newton’s second law tells us that the acceleration is the force divided by the mass. As a consequence, the acceleration of Earth is much, much larger than that of the Sun, and therefore, the motion of the Sun due to this force is tiny compared with that of Earth. (They both orbit their mutual center of mass, but this is inside the surface of the Sun. The Sun executes a tiny circular motion about this center of mass, while Earth makes a grand circuit around the Sun.)

Here is another fascinating consequence of Newton’s formula. By Newton’s second law, the force of gravity, which we have just written down, is equal to the mass of Earth (M_Earth) times its acceleration, and for circular motion, the acceleration is equal to v²/r. So in this case, F = ma can be rewritten as:

GM_SunM_Earth/r² = M_Earthv²/r .

Note that the mass of Earth appears on both sides of this equation, and thus we can divide it out, leaving:

GM_Sun/r² = v²/r .

What this means is that the acceleration of Earth (GM_Sun/r² = v²/r) does not depend on Earth’s mass. That’s a remarkable fact. The acceleration of gravity does not depend on the mass of the object being accelerated, either for orbits around the Sun or for objects falling in Earth’s gravitational field, because the mass of the object appears on both sides of the F = ma equation and thus factors out. If I drop both a book and a piece of paper, they will feel the same acceleration, and should fall at the same rate, even though the book is much more massive. That’s what Galileo said would occur in the vacuum. Does it work in practice? No, a book and a piece of paper fall at different rates, because of air resistance. Air resistance exerts a force on both the book and the paper, but since the book is much more massive than the piece of paper, the acceleration of the book due to the air resistance is small—essentially negligible. However, if I put the piece of paper on top of a big book, so that the book blocks the air resistance to the paper, and drop them again, the paper will stay sitting on the book as they fall together at the same rate. Try the experiment yourself!

When the Apollo 15 astronauts went to the Moon, they brought along a hammer and a feather to do an experiment to test this principle. The Moon has effectively no atmosphere: a very good vacuum exists above its surface, and hence there is no appreciable air resistance. When the astronauts dropped the feather and the hammer simultaneously, they fell at exactly the same rate, just as Newton (and Galileo) had predicted. You can see the video record of their lunar experiment online.

You may know that Aristotle got this wrong. Aristotle said that more massive objects would be subject to a greater acceleration and fall faster. He said that because it seemed logical to him, but in fact he never did an experiment to see whether his idea was correct. He could have taken big rocks and little rocks (neither of which is much affected by air resistance) and dropped them to discover that they would fall at the same rate. The bottom line here is that in science, it is crucial to check your intuitions with experiment!

But an apple falling (straight down) surely doesn’t seem to be the same as the orbital motion of the Moon. Why does the Moon go in circles, whereas the apple simply hits the ground? To put the apple into orbit, I’d have to throw it hard horizontally, so hard that it could go all the way around Earth. Consider the case of the Hubble Space Telescope, just a few hundred kilometers above Earth’s surface. It travels completely around Earth, a circumference of 25,000 miles, in about 90 minutes. If we convert this to a speed, it turns out to be about 5 miles per second. So, to get an apple into orbit, I’d have to throw it horizontally at about 5 miles per second.

Imagine standing on top of a high mountain (above the frictional effects of the atmosphere) and throwing objects horizontally at ever greater speeds. Throw that apple as hard as you can; it quickly falls to the ground. Get a major league pitcher to toss it; it will go somewhat farther, but it will still fall down. Now let’s get Superman to throw it. As he throws harder and harder, the apple will go farther and farther before its downward-curving trajectory hits the surface of Earth. But Earth’s surface is not flat; it also curves downward in the distance. Superman can indeed throw an object at 5 miles per second. The object will also fall under the influence of gravity, but its curved trajectory now matches the curvature of Earth such that it never hits the surface and will end up in a circular orbit. The object in orbit is falling the entire time, albeit with plenty of sideways motion. When you drop an apple, it falls down due to the acceleration of Earth’s gravity. That same gravity is causing both the Hubble Space Telescope to orbit Earth and the Moon to go around Earth (in a much higher orbit, therefore moving more slowly). In low-Earth orbit, you are falling at the same rate that Earth curves around, and you never hit the ground. Newton understood this, and proposed the idea of an artificial satellite in orbit around Earth—270 years ahead of its actually being done!

If you’ve ever been in an elevator that suddenly jerks down quickly, for a very brief period you’re falling, and everything around you is falling with you. When you drop an apple, you yourself don’t fall with it, because the force of the ground on the soles of your feet keeps you up. You are standing at rest relative to your surroundings, but the apple feels the acceleration and it falls. If you were knocked off your feet and fell with the apple, I would see the apple falling with you (at least until you and the apple both hit the floor).

You have probably seen images of astronauts in the International Space Station in orbit around Earth. Earth’s gravity is acting on the astronauts and the International Space Station alike. But everything in the space station is falling at the same rate—recall our calculation that the acceleration of gravity does not depend on the mass of the object in orbit. With everything falling at the same rate, the astronauts feel weightless. “Weight” means what a bathroom scale registers when you stand on it (or equivalently, how much the bathroom scale pushes back on you, by Newton’s third law). But if the scale is falling just as you are, you are not pushing down on the scale, and it registers your weight as zero. You are weightless.

This doesn’t mean that your mass is zero, however. Mass and weight are not the same thing! Mass, according to Newton, is the quantity that goes into his second law of motion (relating forces, masses, and acceleration); it’s also the quantity that gives rise to gravity. When people talk about losing “weight” what they really want to do is lose mass. Fat has mass, and they wish to get rid of some of that. Then, with the same amount of force, they can accelerate faster, and get around more easily.

Let’s now take stock of what Newton accomplished. From observations of the motions of the planets known at the time, Kepler had abstracted three laws to describe their orbits. Then Newton came along and thought about this in a whole different way; with his three laws of motion, he attempted to understand how everything moves, not just the six planets known at the time to orbit the Sun. In addition, he developed a physical understanding of the force of gravity, the most important force in astronomy. Using Kepler’s third law, he showed that the force of gravity must fall off like 1/r². He found that the gravitational force between two bodies was attractive: the gravitational force of the Sun on a planet was F = GM_SunM_Planet/r². Putting these together, we saw that we could understand Kepler’s third law in terms of Newton’s laws of motion and law of gravity. Newton came up with a much broader understanding of the physics behind Kepler’s third law than Kepler had done.

In a final triumph, Newton showed that his law of gravitation predicted that a planet would trace out a perfect elliptical orbit with the Sun at one focus, and that a line connecting the planet to the Sun would sweep out equal areas in equal times. All three of Kepler’s laws can now be seen as a direct consequence of Newton’s one law of gravitational attraction, together with his three laws of motion.

Newton’s laws of gravity were the first laws of physics we understood. Importantly, they could be used to make predictions that could be tested. Halley used Newton’s laws to discover that several comet appearances over the centuries (including one in 1066 recorded in the Bayeux Tapestry) were actually all the same comet on a highly elliptical orbit. It returned approximately once every 76 years. It was perturbed by Jupiter and Saturn as it crossed their orbits, and its somewhat variable time of arrival could be predicted with Newton’s laws—whereas with Kepler’s laws, it would have been exactly periodic. Halley predicted the comet would return again in 1758. Halley died in 1742 and didn’t live to see the event, but when it did reappear in 1758 as he had predicted, they named it after him the next year: Halley’s comet. Its closest approach to the Sun was predicted by Alexis Clairaut, Jérôme LaLande, and Nicole-Reine Lepaute, using Newton’s laws, with an accuracy of 1 month. This was a remarkable confirmation of Newton’s laws of gravity.

Newton’s laws had another great success. The planet Uranus was not following Newton’s laws exactly; its orbit seemed to be perturbed. Urbain Le Verrier found that this could be explained if Uranus was being pulled by the gravity of another unseen planet farther out from the Sun. He predicted where this planet could be found, and in 1846, Johann Gottfried Galle and Heinrich Louis d’Arrest, using Le Verrier’s calculations, found it only 1° in the sky away from where Le Verrier had predicted it would be. Newton’s laws had been used to discover a new planet: Neptune. Newton’s reputation soared.

We’ll find ourselves using these basic notions of forces and gravity again and again throughout this book for understanding the universe.