2
FROM THE DAY AND NIGHT SKY
TO PLANETARY ORBITS
NEIL DEGRASSE TYSON
In this chapter, we will cover 3,000 years of astronomy. Everything that happened from antiquity, the time of the Babylonians, up until the 1600s. This is not going to be a history lesson, because I’m not going to cover all the details of who thought and who discovered what first. I just want to give you a sense of what was learned during all that time. It begins with people’s attempts to understand the night sky.
Here’s the Sun (figure 2.1). Let’s draw Earth next to it; it’s not drawn to scale in either size or distance, but is simply meant to illustrate certain features of the Sun–Earth system. Way out, of course, are the stars in the sky. I’m going to pretend that the sky is just stars, dots of light on the inside of a big sphere, which will make some other things easier to describe.
Earth, as you probably know, spins on an axis, and that axis is tilted relative to our orbit around the Sun. That angle of tilt is 23.5°. How long does it take for us to spin once? A day. How long to go around the Sun once? A year. Thirty percent of the general public in America who were asked that second question got the wrong answer.
A spinning object in space is actually quite stable, so that, as it orbits, its orientation in space remains constant. If we move the Earth around the Sun, from June 21 to December 21, as it comes around the other side of the Sun (to the right in figure 2.1), Earth will still preserve that spin orientation in space—its axis points in that same direction for the entire journey around the Sun. This makes for some interesting features. For example, on June 21, a vertical line perpendicular to the plane of the Earth’s orbit divides the Earth into day and night. What can you say about the part of the Earth to the left of that line, away from the Sun? That’s nighttime. But on December 21, when Earth is on the opposite side of its orbit, nighttime is now on the opposite side—to the right in the illustration. All the people on Earth who look up in the nighttime can see only that part of the sky opposite the Sun. The nighttime sky on June 21 is different—the stars on the far left—from the nighttime sky you see on December 21—the stars on the far right. During the summer nights, we see the “summer” constellations, such as the Northern Cross and Lyra, whereas during the winter nights, we see the “winter” constellations, such as Orion and Taurus.
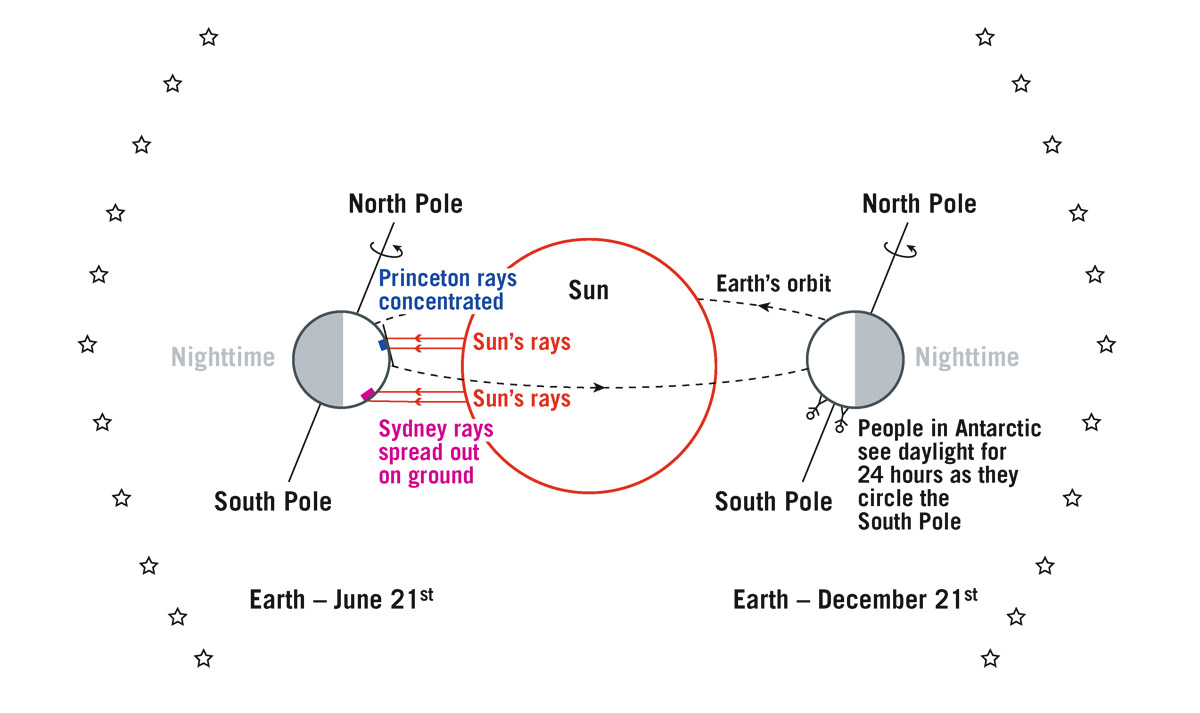
FIGURE 2.1. Earth circles the Sun, providing different nighttime views as the seasons change. Because of the tilt of Earth’s axis relative to its orbit, on June 21, the Northern Hemisphere receives the Sun’s rays more directly, while Australia and the entire Southern Hemisphere receive them obliquely. On December 21, people south of the Antarctic Circle see daylight for 24 hours as they circle around the South Pole as Earth rotates. Credit: J. Richard Gott
Let’s look at something else. On December 21, if it’s nighttime to the right of the vertical line and Earth turns on its axis, what about the upside-down people standing in Antarctica, south of the Antarctic circle? They go around the South Pole. Does a person there see darkness? Nope. On December 21, a person there sees 24 hours without dark—24 hours of sunlight—as Earth rotates. There is no nighttime for anybody within the entire South Polar cap of Earth on that day. That’s true for anyone between the Antarctic Circle and the South Pole. Following this argument, if I come up to the North Pole and I watch people North of the Arctic circle revolve around the North Pole—Santa Claus and his friends—they never rotate into the daytime side of Earth. For them, on December 21, there are 24 hours of darkness. As you might suspect, on June 21, the reverse happens: it’s the people south of the Antarctic Circle who have no day at this time of the year and the people in the Arctic who have no night.
Let’s observe from Princeton, New Jersey—it’s close to New York City, but with no skyscrapers or bright city lights to interfere with the view. The town’s latitude on Earth is about 40° North. At dawn on June 21, the Northern Hemisphere rotates New Jersey into daytime, receiving quite direct sunlight, whereas the sunlight hitting the Southern Hemisphere is rather oblique to Earth’s surface.
Noon is when the Sun reaches its highest point in the sky. Did you know that nowhere in continental United States is the Sun ever directly overhead at any time of day, on any day of the year? Odd because if you grab people in the street and ask, “Where is the Sun at 12 noon?” most will answer, “It’s directly overhead.” In this case and in many others, people simply repeat the stuff they think is true, revealing that they’ve never looked. They’ve never noticed. They’ve never conducted the experiment. The world is full of stuff like that. For example, what do we say happens to the length of daylight in winter? “The days get shorter in the winter, and longer in the summer.” Let’s think about that. What’s the shortest day of the year? December 21, which is the solstice and also the first day of winter in the Northern Hemisphere. If the first day of winter is the shortest day of the year, what must be true for every other day of winter? They must get longer. So days get longer in the winter, not shorter. You don’t need a PhD or a grant from the National Science Foundation to figure that out. Hours of daylight get longer during the winter and shorter during the summer.
What’s the brightest star in the nighttime sky? People say the North Star. Have you ever looked? Most haven’t. The North Star (also known as Polaris) is not in the top 10. It’s not in the top 20. It’s not in the top 30. It’s not even in the top 40. Australia sits too far to the south for anybody there to see the North Star. They don’t even have a South Pole star to look at. And while we’re talking celestial hemispheres, don’t ever be jealous of the constellations in the southern sky. Take the Southern Cross; you may have heard about it. People write songs about it. But did you know that the Southern Cross is the smallest constellation out of all 88 of them? A fist at arm’s length covers the entire constellation completely. Meanwhile, the four brightest stars of the Southern Cross make a crooked box. There is no star in the middle to indicate the center of the cross. It’s more accurately thought of as the Southern Rhombus. In contrast, the Northern Cross covers about 10 times the area in the sky and has six prominent stars—it looks like a cross, with one star in the middle. In the North we’ve got some great constellations.
The North Star is actually the 45th brightest star in the nighttime sky. So do me a favor and grab people in the street, ask them that question, and then set them straight. If you must know, the brightest star in the nighttime sky is Sirius, the Dog Star.
Now let’s compare what happens to the sunlight at two locations on Earth. Look at the ground at noon in Princeton on June 21—sunlight hits it from a very high angle (see figure 2.1). The two parallel rays traveling from the Sun hit Princeton only a short distance apart on the ground. The ground at Sydney, Australia, at noon takes in a similar pair of rays, except that the rays are coming in at a much lower angle and are spread much farther apart on the ground. What’s going on here? Which place is getting its ground heated more efficiently? Princeton, of course. The energy impinging on Princeton’s ground is more concentrated, because of how directly the rays intersect Earth’s surface, making Princeton’s ground hotter. It’s summertime in Princeton on June 21. At this same time of year, it’s winter in Sydney, Australia. The reverse will apply 6 months later on December 21.
The Sun heats the ground; the ground heats the air. The Sun does not appreciably heat the air itself, which is transparent to most of the energy that comes from the Sun. The Sun’s energy peaks in the visible part of the spectrum, and you already know that you can see the Sun through the atmosphere. From this we conclude the obvious fact that the Sun’s visible light is not being absorbed by the air, otherwise, you wouldn’t see the Sun at all. If you are indoors in a room with no windows, you can’t see the Sun, because the roof of your building is absorbing the visible light from the Sun. You must either look out a transparent window or go outside to see the Sun. So, in sequence, light from the Sun passes through the transparent air and hits the ground. The ground absorbs the light from the Sun, and then reradiates that energy as invisible infrared light, which the atmosphere can and does absorb—we’ll talk more about these other parts of the spectrum in chapter 4.
The ground absorbs visible light from the Sun, gets hotter, and then the ground heats the air through the infrared energy it emits. This doesn’t happen instantaneously. It takes time. But how much time? What’s the hottest time of day? It’s not 12 noon—the time of peak ground heating. The hottest time of day is never 12 noon. It’s always a few hours later because of this effect: 2 pm, 3 pm. Even as late as 4 pm in some places.
So that’s summertime in the Northern Hemisphere. In summer the North Pole of Earth’s axis tilts toward the Sun, and of course this is winter for those in the Southern Hemisphere. For the same reason that the hottest time of day is after 12 noon, the hottest time of year in the Northern Hemisphere is after June 21. That’s why the season of summer starts on June 21, and it gets hotter after that. Similarly, December 21 is the start of winter in the Northern Hemisphere, and it gets colder after that.
Three months later, on March 21, spring starts. Every part of Earth rotates both into sunlight and out of sunlight on the first day of Northern Hemisphere spring (March 21) and on the first day of Northern Hemisphere fall (September 21). So everybody on Earth gets equal amounts of darkness and lightness on those two days—the equinoxes.
Earth’s North Pole points toward Polaris, the North Star. A cosmic coincidence? Not really, because we don’t point exactly there. You can fit 1.3 full-moon widths between the actual spot in the sky where our axis points (the North Celestial Pole) and the position of Polaris.
Let’s go back to Princeton, as shown in figure 2.2. Standing there at night, you’ll see any star on one side of the sky at that instant. In the figure, these stars are marked “Stars visible above Princeton’s horizon.” Princeton’s horizon is drawn—this line is tangent to the surface of Earth where you’re standing. When you look up, you’ll see stars making circles around Polaris, as Earth turns (shown on the right in figure 2.2). (Polaris is so close to the North Celestial Pole that it barely moves.) So there’s a cap in the sky where these stars make circles around Polaris but never actually set below your horizon. These are called circumpolar stars.
Suppose you look at a star farther away from Polaris. That star sets, then comes around and rises again. That’s what the sky looks like, the view from Earth. One of the more familiar asterisms (star patterns) of the night sky is the Big Dipper, well-known because its stars are bright and it goes around Polaris (see figure 2.2). It dips down, just skimming the horizon (as seen from Princeton), and then comes back up again. Anything much farther from Polaris than the Big Dipper actually sets. How high is Polaris, in angle, as seen from Princeton? We can figure this out. First, let’s say we have gone to visit Santa Claus at the North Pole. Where is Polaris in the sky? If you’re visiting Santa Claus, Polaris will be (almost directly) straight overhead. It’s always straight overhead there. A star halfway up in the sky as seen from the North Pole circles Polaris as Earth turns, always staying above the horizon. A star right on the horizon circles along the horizon, so every star you can see stays above the horizon. No star rises, no star sets; they all circle Polaris overhead, and you see the entire Northern Hemisphere of the sky. That’s Santa’s view.
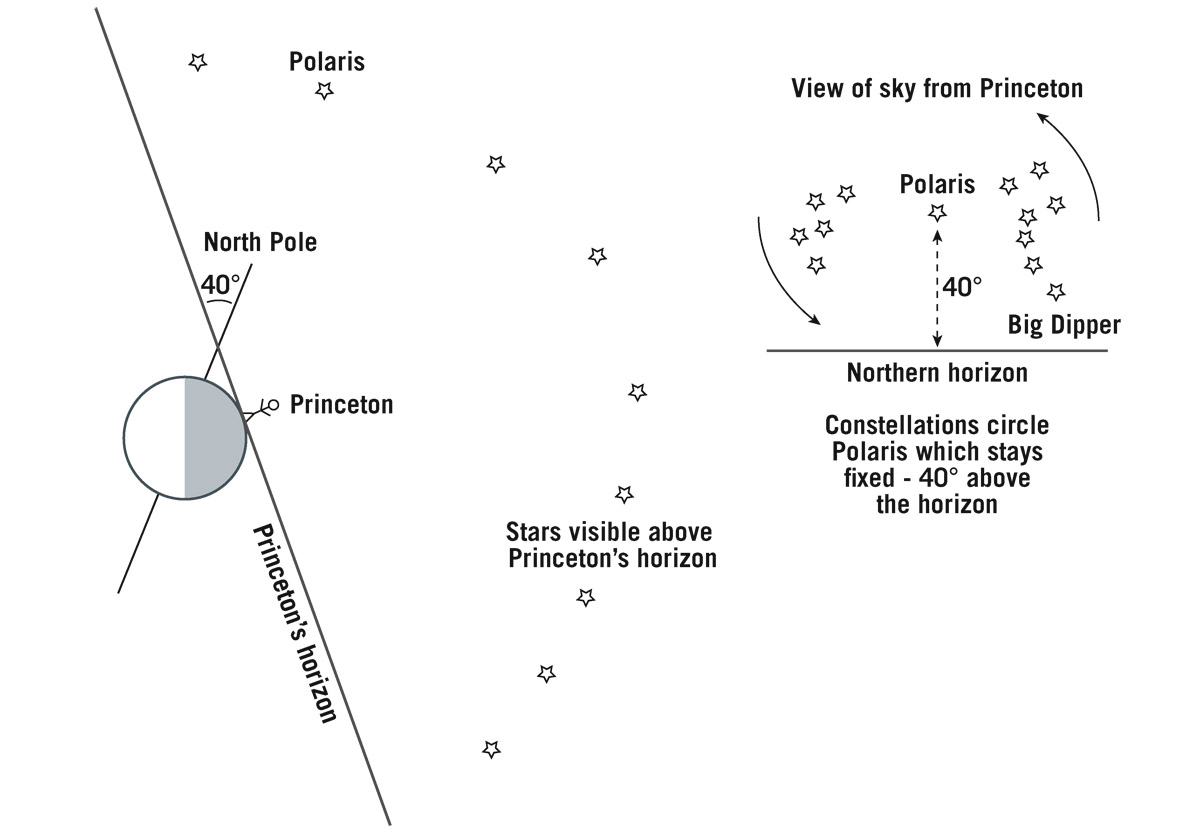
FIGURE 2.2. Nighttime view of the sky from Princeton (at 40° North latitude). Polaris stays stationary, 40° above the northern horizon. The Big Dipper revolves counterclockwise around it. Credit: J. Richard Gott
What’s the latitude of the North Pole? Ninety degrees. What’s the altitude of Polaris from the horizon as seen from the North Pole? It’s 90°—the same number. That’s not a coincidence. Polaris is 90° up, and you’re at 90° latitude. Let’s go down to the equator. What’s the latitude of the equator? Zero degrees. Polaris is now on the horizon, 0° up. What’s my latitude in Princeton? Forty degrees. So, from Princeton, the altitude of Polaris is 40° above the horizon.
People who navigate by the stars know that the altitude of Polaris you observe is equal to your latitude on Earth. Christopher Columbus set sail at a fixed latitude that he maintained for his entire journey across the Atlantic Ocean. Go back and look at his maps. That’s how they navigated; they kept at that latitude by keeping Polaris at the same altitude above the horizon during the trip.
Did you ever play with a top when you were a kid, and watch the top wobble? Earth wobbles. We are a spinning top, under the influence of the gravitational tug from the Sun and Moon. We wobble. The time it takes to make one complete wobble is 26,000 years. We rotate once in a day and wobble once in 26,000 years. That has an interesting consequence. First, consider the sphere of stars that I drew around the solar system. As Earth moves around the Sun, the Sun occupies a different place against the background of stars. On June 21, in our earlier figure 2.1, the Sun sits between us and the stars on the far right, which means that the Sun passes in front of those stars as seen by us on June 21. But on December 21, the Sun is between us and the stars to the far left. In between times, the Sun occupies a place in front of different sets of stars throughout the year, as it circles the sky. Long ago, when most of the world was illiterate, when there was no evening television, no books or internet, people put their culture onto the sky. Things that mattered in their lives. The human mind is very good at making patterns where none really exist. You can easily pick patterns out of random assortments of dots. Your brain says, “I see a pattern.” You can try this experiment: if you’re good at programming a computer, take dots and place them randomly on a page. Take about a thousand dots, look at them, and you may think, “Hey, I see . . . Abraham Lincoln!” You’ll see stuff. In a similar way, these ancient people put their culture on the sky when they had no other idea what was going on. They didn’t know what the planets were doing; they didn’t understand laws of physics. They said, “Hmm! The sky is bigger than I am—it must influence my behavior.” So they supposed, “There’s a crustacean-looking constellation of stars over here, and it’s got some personality traits; the Sun was in that part of the sky when you were born. That must have something to do with why you’re so weird. And then over here we’ve got some fishes, and over there we’ve got some twins. Because we don’t have HBO, let’s weave our own storylines and pass these stories on from person to person.” In so doing, ancient peoples laid out the zodiac, the constellations in front of which the Sun appears to move throughout the year.
There were twelve of these zodiac constellations; you know them all—Libra, Scorpio, Aries, and so on. And you know them because they’re in nearly every daily news feed. Some person you’ve never met makes money telling you about your love life. Let’s try to understand that. First of all, it’s not really twelve constellations that the Sun moves through, it’s thirteen. They don’t tell you that, because they couldn’t make money off of you if they did. Do you know what the thirteenth constellation of the zodiac is? Ophiuchus. It sounds like a disease, as in: “Do you have Ophiuchus today?” I know you know what your sign is, so don’t lie and say, “I never read my horoscope.” Most Scorpios are actually Ophiuchans, but we don’t find Ophiuchus in the astrology charts.
Well, let’s keep this up for a minute. When did they lay out the zodiac? It was encoded 2,000 years ago. Claudius Ptolemy published maps of it. Two thousand years is 1/13 of 26,000 years. Almost 1/12. Do you realize that because of Earth’s wobble (we call it precession, the official term), the month of the year in which the Sun is seen against a particular constellation in the zodiac shifts? Every single zodiacal constellation that has been assigned to the dates identified in the newspapers is off by an entire month. So, Scorpios and Ophiuchans are currently Librans.
Therein lies the greatest value of education. You gain an independent knowledge of how the universe works. If you don’t know enough to evaluate whether or not others know what they’re talking about, there goes your money. Social anthropologists say that state lotteries are a tax on the poor. Not really. It’s a tax on all those people who didn’t learn about mathematics, because if they did, they would understand that the probabilities are against them, and they wouldn’t spend a dime of their hard-earned money buying lottery tickets.
Education is what this book is all about. Plus a dose of cosmic enlightenment.
Let’s discuss the Moon, and then get straight to Johannes Kepler and then to my man, Isaac Newton, whose home I visited when filming Cosmos: A Spacetime Odyssey.
But first, we’ve got Earth going around the Sun, and of course we have the Moon going around Earth, so let’s show that in figure 2.3. We put the Sun way off in the distance to the right and Earth in the center of the diagram, and we show the Moon at different positions as it circles Earth. We are looking down on the north pole of the Moon’s orbit, as sunlight comes in from the right.
Both Earth and the Moon are always—at all times—half illuminated by the Sun. If you’re standing on Earth, looking at the Moon when it is opposite the Sun, what do you see? What phase is the Moon? Full. The big pictures in figure 2.3 show the appearance of the Moon as seen from Earth at each point in its orbit.

FIGURE 2.3. The Moon’s phases as it circles Earth. The Sun, at right, always illuminates half of Earth and half of the Moon. The diagram shows the sequence (counterclockwise) of positions the Moon occupies as it orbits Earth. We are looking down on the orbit from the north. The Moon always keeps the same face toward Earth. Notice that at new moon, its back side, never seen from Earth, is illuminated. The large photographs show the appearance of the Moon at each position as seen from Earth. Photo credit: Robert J. Vanderbei
Why don’t we have a lunar eclipse every month, when Earth is between the Sun and Moon like this? It is because the Moon’s orbit is tipped at about 5° relative to Earth’s orbit around the Sun. So, in most months, the Moon passes north or south of Earth’s shadow in space, preserving our normal view of the full Moon. Once in a while, when the Moon is full as it crosses the plane of Earth’s orbit, it will pass into Earth’s shadow, and we have lunar eclipse.
Now let the Moon continue 90° counterclockwise in its orbit. The Moon is now in third-quarter phase. Colloquially known as half-Moon—you see the moon half illuminated. Bring the Moon 90° further along, counterclockwise in its orbit, and the Moon passes between Earth and the Sun. Only the side of the Moon facing the Sun is lit up and you can’t see that, so when standing on Earth, you can’t see the Moon at all. We call it new Moon. The Moon usually passes north or south of the Sun, during this phase. Occasionally, when it passes directly in front of the Sun, we get a solar eclipse.
So far, we have full Moon, third-quarter Moon, and new Moon. Come around another 90°, and we get first-quarter Moon, when it is half illuminated again. We also have in-between phases. Crossing from new Moon to first-quarter Moon, what do you see? Only a little smidgen. A crescent. It’s called a waxing crescent Moon, because it grows thicker every day. And just before new Moon, we get a waning crescent. These crescents face opposite directions as the Moon shrinks and then grows again.
Between first-quarter and full Moon we have something called waxing gibbous. It’s a pretty awkward looking phase, and is almost never drawn by artists, even though half the time we ever see the Moon it’s in a gibbous phase—not quite full, not quite a quarter Moon. If artists were drawing the sky randomly throughout the year, we might expect to see a gibbous Moon half the time in their work, yet they typically choose to draw either a crescent Moon or a full Moon. They are not capturing the full reality that lay in front of them.
Of course, this entire cycle takes a month, formerly known as a “moonth.” If the full Moon is opposite the Sun, what time of day does it rise? If it is opposite the Sun and the Sun is setting, then we conclude the full Moon is rising, at sunset. And if the Sun is rising, the full Moon is setting.
The situation is different at other times of the month. When the third-quarter Moon is high in the sky, the Sun is rising. Notice in the diagram, where Earth is rotating counterclockwise, you are getting rotated into sunlight when the third-quarter Moon is high in the sky. Imagine taking your brain and your eyes into that picture, looking around, and then stepping back in the real world, to check your result.
I have an app on my computer, such that every time I bring up the desktop, the Moon is there, showing its phase, day by day. That’s my lunar clock. It connects me to the universe even when I’m staring at my computer screen.
Let’s get back to the solar system—mid-to-late 1500s. In Denmark, there lived a wealthy astronomer named Tycho Brahe. The crater Tycho on the Moon is named after him.
I spent an hour once with someone who was native to Denmark, learning how to pronounce this astronomer’s name correctly: tī’kō brä. I worked hard on that. But of course in America, we pronounce it however it looks to us.
Tycho Brahe cared a lot about the planets, enough to keep track of them. He built the best naked-eye instrument of the day, maintaining the most accurate measurements of planetary positions ever. Telescopes were not invented until 1608, so Tycho used sighting instruments, while writing down the positions of stars on the sky and of planets as a function of time. Tycho had an enormous database, and a brilliant assistant, the German mathematician Johannes Kepler.
Kepler took the data, and he figured stuff out. Kepler said to himself, “I understand what the planets are doing. In fact I can create laws that describe exactly what the planets are doing.” Before Kepler, the organization of the universe was plain and obvious: “Look, the stars revolve around us. The Sun rises and sets. The Moon rises and sets. We must be at the center of the universe.” This not only felt good to believe, it also looked that way. It stoked the human ego, and the evidence supported it, so no one doubted it—until the Polish astronomer Nicolaus Copernicus came along. If Earth were in the middle, what are the planets doing? You look up, and from day to day you watch Mars move against the background stars. Hmm. Right now it’s slowing down now. Oh wait, it stopped. Now it’s going backward (that’s called retrograde motion), then it’s going forward again. Why should it do that?
Copernicus wondered—if the Sun were in the middle, and Earth went around the Sun, what then? Well, these forward and backward motions get explained in a snap. The Sun is in the middle, Earth goes around the Sun in an orbit, like a racecar going around a racetrack. Mars, the next planet out from the Sun, orbits more slowly, like a slower racecar in an outer lane. When Earth passes Mars on the inside track, Mars seems to be going backward in the sky for a while. If you are in the fast lane on the highway and pass a slower car in the next lane, that car appears to drift backward relative to you. If you put the Sun in the middle, and made Earth and Mars go around the Sun in simple circular orbits, it explained the retrograde motion; it explained what was going on in the nighttime sky. Planets farther from the Sun orbited more slowly. Copernicus published all this in a tome called De Revolutionibus orbium coelestium. If you try to buy the first edition of that book at auction, it will cost you over two million dollars, as it is one of the most important books ever written in human history.
It was published in 1543, and it got people thinking. Copernicus had been afraid to publish the book at first, and had been showing his manuscript to colleagues privately. You couldn’t just start saying to everyone that Earth was no longer in the center of universe. The powerful Catholic Church had other ideas about things, asserting that Earth was in the center.
Aristotle had said so. In ancient Greece, Aristarchus had correctly deduced that Earth orbited the Sun—but Aristotle’s view won out, and the church still subscribed to it, since it was consistent with Scripture. So, when did Copernicus publish his book? When he lay on his deathbed. You can’t be persecuted when you’re dead. He reintroduced the Sun-centered universe, called the heliocentric model.
“Helio-” means Sun. Before then, we had geocentric models. That came from Aristotle, Ptolemy, and later, by decree, the church.
And then came Kepler. Kepler, who agreed with Copernicus, up to a point. Copernicus invoked orbits that were perfect circles. But because these didn’t quite match the observed motions of the planets, Copernicus had adjusted them by adding smaller epicyclic circles (as Ptolemy had done as well). Still, they didn’t exactly match the positions of the planets in the sky. Kepler figured that the Copernican model needed fixing. And from the data—planetary position measurements over time—left to him by Tycho Brahe, he deduced three laws of planetary motion. We call them Kepler’s laws.
The first one says: Planets orbit in ellipses, not circles (see figure 2.4). What’s an ellipse? Mathematically, a circle has one center, and an ellipse sort of has two centers: we call them foci. In a circle, all points are equidistant from the center, whereas in an ellipse, all points have the same sum of distances to the two foci. In fact, a circle is the limiting case of an ellipse, in which the two foci occupy the same spot. An elongated ellipse has foci that are far apart. As I bring the foci together, I get something that more closely resembles a perfect circle.
According to Kepler, planets orbit in ellipses with the Sun at one focus. This is already revolutionary. The Greeks said, if the universe is divine, it must be perfect, and they had a philosophical sense of what being perfect meant. A circle is a perfect shape: every point on a circle is the same distance from its center; that’s perfection. Any movement in the divine universe must trace perfect circles. Stars move in circles, they thought. This philosophy had endured for thousands of years. Then here comes Kepler saying, no, people, they are not circles. I’ve got the data, left to me by Tycho, to show they’re ellipses.
He further showed that as planets orbit, the speed of a planet varies with its distance from the Sun. Imagine an orbit that is a perfect circle. There’s no reason for the speed to be any different on one part of the circle than another; the planet should just keep the same speed. But not so with the ellipse. Where would the planet have the most speed? As you might suspect, when the planet is closest to the Sun. Kepler found that a planet travels fast when it is close to the Sun and more slowly when it is farther away.
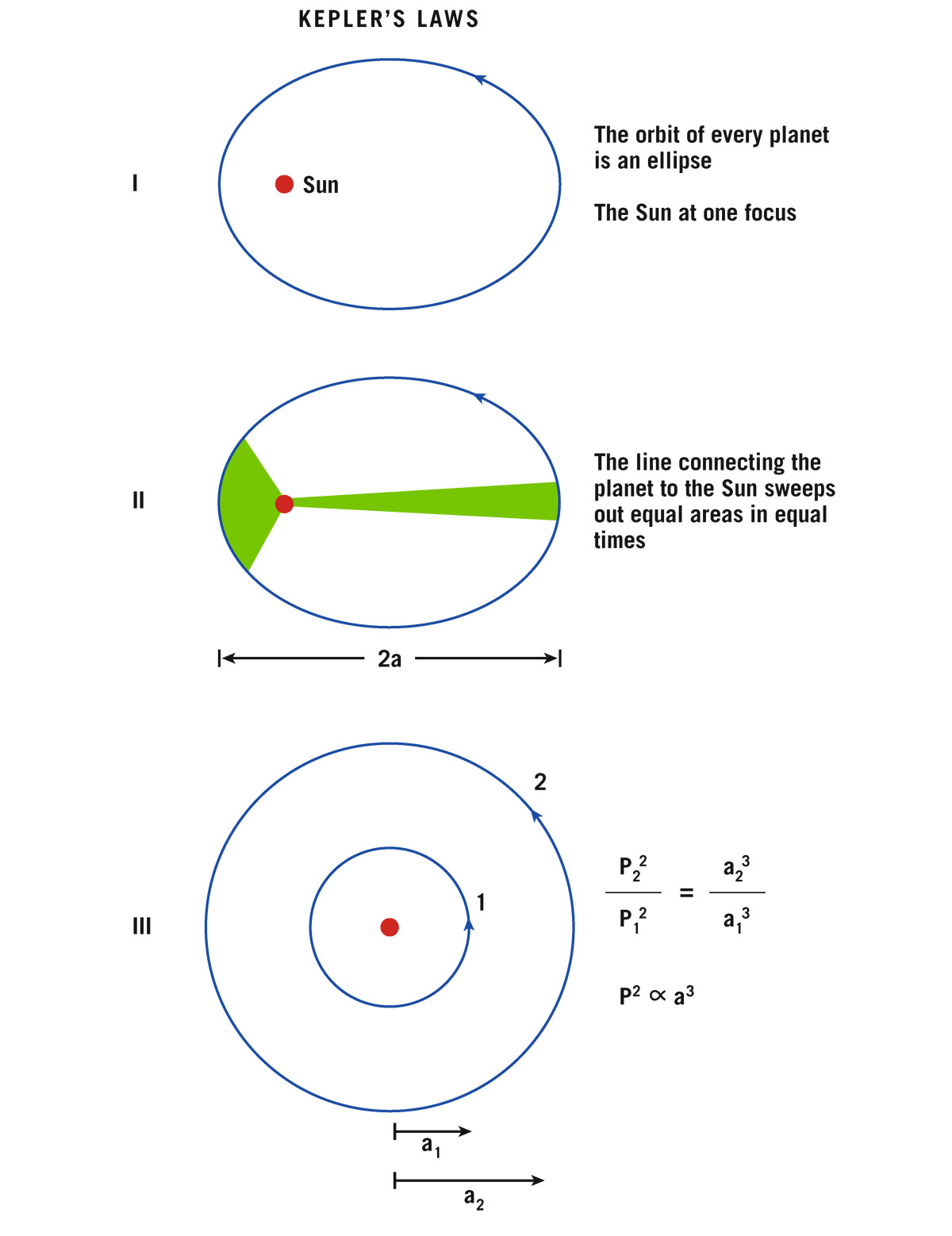
FIGURE 2.4. Kepler’s Laws. The quantity a is the semi-major axis, half the long diameter of the elliptical orbit. For a circular orbit, with zero eccentricity, the semi-major axis is the same as the radius. Credit: J. Richard Gott
Thinking about the problem geometrically, Kepler said, “let’s measure how far the planet goes, for example, in a month.” When it is close to the Sun and moving fast, in a month it will sweep out a certain area of its orbit, in a stubby, fat fan (see figure 2.4). Call this area A1. Let’s do that same experiment in another part of the orbit, when it is farther away from the Sun. Kepler observed that it is moving more slowly when it is farther away, and therefore it’s not going to travel as far in the same amount of time. As it travels a shorter distance, it will trace out a long, thin, fan-shaped area, A2, in the same 1-month period. Kepler was clever enough to notice that the area it swept out in a month was the same whether it was close or far from the Sun: A1 = A2. He therefore made a second law: Planets sweep out equal areas in equal times.
This has a fundamental derivation, which comes about from the conservation of angular momentum. If you’ve never seen that term before, you can understand it intuitively.
Ice skaters use it. Notice how spinning figure skaters start with their arms out. What do they do? They pull their arms in, shortening the distance between their arms and their axis of rotation, and their rotation speeds up in response. As the planet on an elliptical orbit moves closer to the Sun, shortening its distance to the Sun, it speeds up.
We call it conservation of angular momentum. Kepler didn’t have this vocabulary available to him at the time. But that is, in fact, what he had found.
Kepler’s third law was brilliant, just brilliant (see figure 2.4 again). It took him a long time. The first two laws he just banged right out, practically overnight. The third law took him 10 years, and he struggled with it. He was trying to figure out a correspondence between the distance of a planet from the Sun and the time it takes to go around the Sun, its orbital period. The outer planets take longer to make a complete orbit than the inner planets do.
How many planets were then known? Mercury; Venus; Earth; Mars; Jupiter; and everybody’s favorite planet, Saturn.
Third graders used to name Pluto as their favorite planet—which put me on their bad list when, at the Rose Center for Earth and Space, we downgraded Pluto’s planetary status to that of an ice ball in the outer solar system.
The Greek word planetos meant “wanderer.” To the ancient Greeks, Earth was not considered a planet, because we were at the center of the universe. And the Greeks recognized two other planets I haven’t listed; what would they be? They were also moving against the background stars: the Sun and the Moon. By the definition from ancient Greece, these were the seven planets. And the seven days of the week owe their names to the seven planets or the gods related to them. Some are obvious, like Sunday and Monday. Saturday is Saturn-day. You have to go to other languages to get the rest; we have Frigga for Friday, for example. Frigga (or sometimes Freyja) was the Norse goddess associated with Venus.
At last, Kepler figured out an equation. It’s the first equation of the cosmos.
Kepler started by measuring all distances in Earth–Sun units.
We call these Astronomical Units, or AU. The distance of a planet from the Sun varies with time. An ellipse is a flattened circle; it has a long axis and a short axis, which are called the major and minor axes, respectively. Kepler (brilliantly) figured out that he should take half the major axis of its orbit as his measure of a planet’s distance from the Sun. We call this the semi-major axis; it’s the average of the planet’s maximum and minimum distances from the Sun.
And if we measure time in Earth-years, we have an equation that was the dawn of our power to understand the cosmos. If we use the symbols P, a planet’s orbital period in Earth-years, and a, the average of the planet’s minimum and maximum distances from the Sun in AU, we get:
P2 = a3,
Kepler’s third law. Let’s see if that works for Earth. Let’s try out the equation. Earth has period 1. And its average min-max distance is 1. So the equation gives 12 = 13. Or 1 = 1. It works. That’s good.
If this is a Solar-System-wide law, it should work for any planet (or other object orbiting the Sun) that was known then, or would later be discovered. How about Pluto? Kepler didn’t know about Pluto. Let’s do Pluto. Pluto’s average min-max distance from the Sun is 39.264 AU. So the law says P2 = 39.2643. What’s 39.264 cubed? It’s 60,531.8. You can check that on a calculator. The orbital period P has to equal the square root of 60,531.8, which is 246.0, rounded to four digits. What is the actual period for Pluto in its orbit? 246.0 years.
Kepler was badass.
When Isaac Newton invented the universal law of gravitation, he invoked P2 = a3 to figure out how gravitational attraction fell off with distance. It fell off like one over the square of the distance. To arrive at his answer, he used calculus—which, conveniently, he had just invented. Newton generalized Kepler’s law to find a law that no longer applied to just the Sun and planets. It applied to any two bodies in the universe, based on a newly revealed gravitational force attracting them toward each other given by:
F = Gmam b/r2
G is a constant, ma and m b are the masses of the two bodies, and r is the distance between their two centers.
From that equation, you can derive Kepler’s third law, P2 = a3, as a special case. You can also derive Kepler’s first and second laws: that the general orbit of a planet around the Sun is an ellipse with the Sun at one focus, and that a planet sweeps out equal areas in equal times! That’s how powerful Newton’s law of gravitation is, and it’s even bigger than this. It is the entire description of the force of gravity between any two objects any place in the universe, no matter what kinds of orbit they have. Newton expanded our understanding of the cosmos and came out with a description of the planets that went far beyond anything Kepler imagined. Newton derived this formula before he turned 26. Newton discovered the laws of optics, labeled the colors of the spectrum, and he determined that amazingly, the colors of the rainbow, when combined, gave you white light. He invented the reflecting telescope. He invented calculus. He did all this.
The next chapter is all about him.