6
STELLAR SPECTRA
NEIL DEGRASSE TYSON
What’s actually happening inside a star? A star is not just a flashlight that you switch on and light emerges from its surface. Thermonuclear processes are going on deep in its core, making energy, and that energy slowly makes its way out to the surface of the star, where it is then liberated and moves at the speed of light to reach us here on Earth or anywhere else in the universe. It’s time to analyze what goes on when this bath of photons moves through matter, which doesn’t happen without a fight.
We first must learn what the photons are fighting on their way out of the Sun. Our star, and most stars, are made mostly of hydrogen, which is the number one element in the universe: 90% of all atomic nuclei are hydrogen, about 8% are helium, and the remaining 2% comprise all the other elements in the periodic table. All the hydrogen and most of the helium are traceable to the Big Bang, along with a smidgen of lithium. The rest of the elements were later forged in stars. If you are a big fan of the argument that somehow life on Earth is special, then you must contend with an important fact: if I rank the top five elements in the universe—hydrogen, helium, oxygen, carbon, and nitrogen—they look a lot like the ingredients of the human body. What is the number one molecule in your body? It’s water—80% of you is H2O. Break apart the H2O, and you get hydrogen as the number one element in the human body. There’s no helium in you, except for when you inhale helium from balloons, and temporarily sound like Mickey Mouse. But helium is chemically inert. It’s in the right-hand column of the periodic table: with an outer electron shell that’s closed—all filled up, with no open parking spaces to share electrons with other atoms—and therefore, helium doesn’t bond with anything. Even if helium were available to you, there’s nothing you could do with it.
Next in the human body, we have oxygen, prevalent once again from the water molecule H2O. After oxygen comes carbon—the entire foundation of our chemistry. Next we have nitrogen. Leaving out helium, which does not bond with anything, we are a one-to-one map of the most abundant cosmic elements into human life on Earth. If we were made of some rare element, such as an isotope of bismuth, you would have an argument that something special happened here. But, given the cosmically common elements in our bodies, it’s humbling to see that we are not chemically special, but at the same time, it’s quite enlightening, even empowering, to realize that we are truly stardust. As we’ll discuss in the next few chapters, oxygen, carbon, and nitrogen are all forged in stars, over the billions of years that followed the Big Bang. We are born of this universe, we live in this universe, and the universe is in us.
Consider a gas cloud—something with the cosmic mixture of hydrogen, helium, and the rest—and let’s watch what happens. Atoms have a nucleus in the center composed of protons and neutrons, with electrons orbiting them. It’s constructive, if pictorially misleading, to imagine a simple, classical-quantum atom like Neils Bohr proposed about a hundred years ago. It has a ground state, the tightest orbit an electron could have: let’s call this ground state energy level 1. The next possible orbit out would be an excited state, and this would be energy level 2. Let’s draw a two-level atom just to keeps things simple (see figure 6.1). An atom has a nucleus and a cloud of electrons, which we say are “in orbit” around the nucleus, but these are not the classical orbits that we know from gravity and planets and Newton; in fact, rather than use the word “orbits,” we introduce a new word derived from it: orbitals. We call them orbitals, because they are like orbits, but they can take a variety of different shapes. Actually they are “probability clouds” where we are likely to find the electrons. Electron clouds. Some are spherically shaped, some are elongated. There are families of them, and some have higher energies than others. We are going to abstract that and simply talk about energy levels, when we are actually representing orbitals, places occupied by electrons surrounding nuclei of atoms.
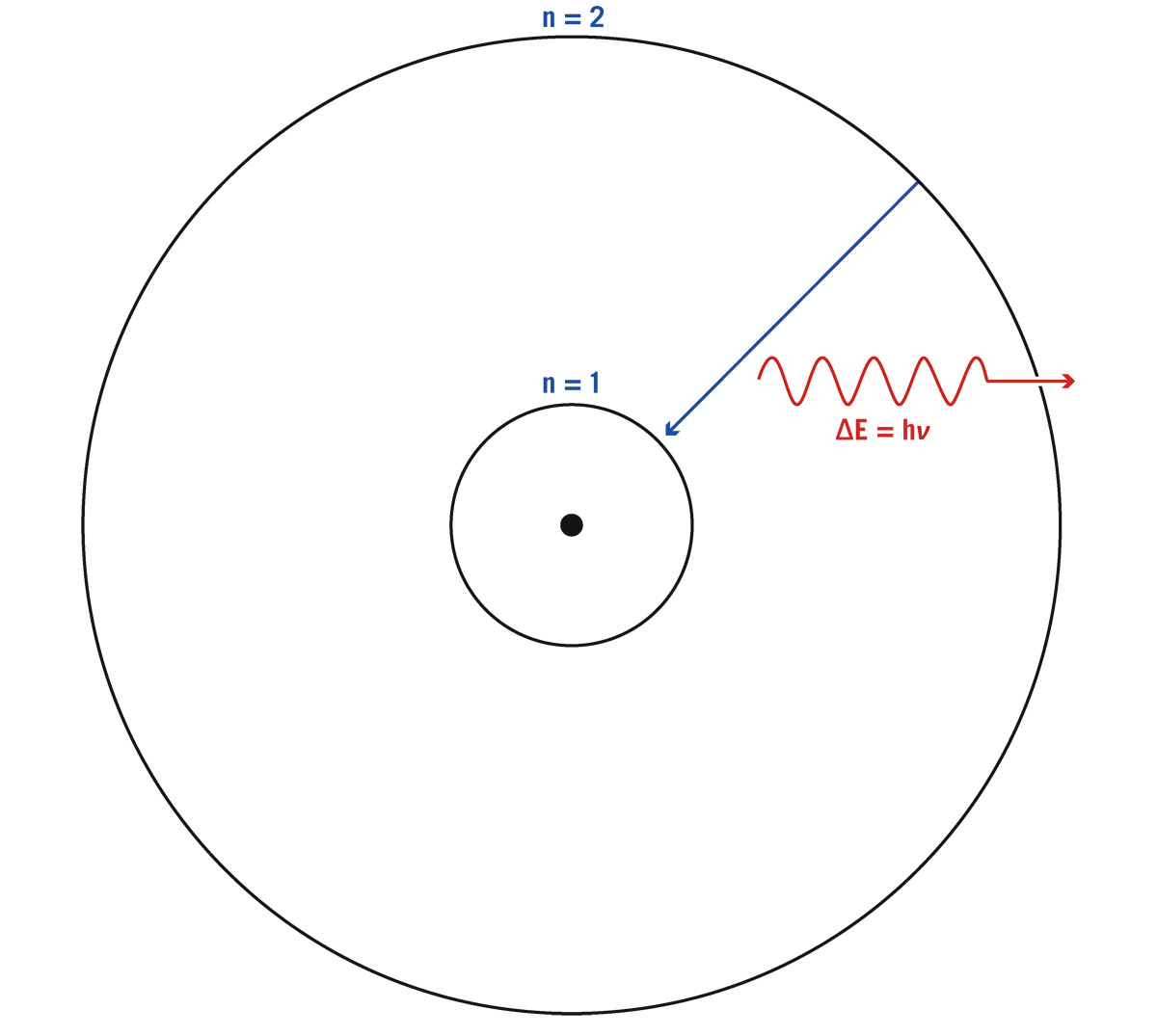
FIGURE 6.1. Atomic energy levels. A simple atom is shown with two electron orbitals, n = 1 and n = 2. If the electron starts further out in energy level 2, and drops down to the lower energy level 1, it emits a photon with an energy ΔE = hν, where ΔE = E2–E1 is the difference in energy between level 2 and level 1. After the electron is in energy level 1, it can absorb a photon with energy ΔE = hν and jump back up to energy level 2. Credit: Michael A. Strauss
The nucleus is the dot in the center. Energy level n = 1 corresponds to an electron in a spherical orbital closest to the nucleus. Energy level n = 2 is a spherical orbital farther away from the nucleus. Energy level n = 2 corresponds to an electron that is less tightly bound to the nucleus. Electrons and protons attract: it takes energy to move the electron away from the nucleus to a more distant orbital. Energy level 2 is higher in energy than energy level 1.
Suppose there is an electron sitting in the ground state, energy level 1. This electron cannot hang out anywhere between energy level 1 and 2. There is no place for it to sit. This is the world of the quantum. Things do not change continuously. For the electron to jump up to the next level, you have to give it energy. It must absorb energy somehow, and for the moment, a nice source of energy is a photon. A photon comes in, but it is not going to be just any photon. It would only be a photon having energy equal to the difference in energy between the two levels. If the electron sees it, it eats the photon and jumps up to energy level 2. If the photon has slightly more energy or slightly less energy, it goes right on by, unconsumed. Now, unlike humans, atoms have no interest in staying excited—this electron in energy level 2, if given enough time, will spontaneously drop down to the lower energy level 1 (as shown by the blue arrow in figure 6.1).
In some cases, enough time means a hundred millionth of a second. Electrons don’t spend much time at all staying excited in an atom. So, when they drop back down, what must happen? They must spit out a photon—a new photon, of exactly the same energy that entered the first time. Jumping up involves absorption of a photon. Falling back down involves emission of a photon, as shown in red in figure 6.1. The energy E of this photon, by Einstein’s famous equation, equals hν, where h is Planck’s constant and ν is the frequency of the photon. The energy of the emitted photon exactly equals the energy difference between the two energy levels, ΔE. (A capital Greek letter delta, Δ, commonly symbolizes a difference or change in a quantity.) This gives the equation ΔE = hν, which allows us to calculate the frequency of the photon emitted when the electron drops from level 2 to level 1.
Ever play with one of those glow-in-the-dark Frisbees? To make it glow in the dark, you must expose it to some light first. You stick it in front of a light bulb. What’s going on? The electrons embedded in the toy’s atoms and molecules are rising to higher energy levels (these larger atoms have many energy levels) as they absorb photons of light. The designers chose material that takes some time for these electrons to cascade back down, and as they do, they emit visible light, but not forever. It stops glowing after the electrons have descended back to their original states. Glow-in-the-dark Frisbees, and those glow-in-the-dark skeleton costumes you had as a kid, all operate on the same principle.
The energy an electron absorbs can come from a photon, but there are other possible sources of that energy. The electron could be kicked by another atom by bumping into it, and when it’s kicked, the electron can be sent up to a higher energy level. In this case, kinetic energy is doing the job. How does that work in a cloud of hydrogen gas? First, we have to ask, what is the temperature of this hydrogen cloud? The temperature in kelvins is proportional to the average kinetic energy of the molecules or atoms in the cloud. The bulk motion of the cloud is not contributing to this measurement. Kinetic energy, of course, is energy of motion, so the higher the temperature, the faster these particles are jostling back and forth. If I’m an electron in the ground state, and I’m getting kicked in the pants, I can ask what the energy is of that kick. If that kick, that energy, would only get me part way up to energy level 2, I stay put. But, if that kick is exactly the right amount of energy to reach the second level, I’ll take that energy, absorb it, and jump up to level 2.
Depending on the temperature, you can sustain an entire population of atoms with some fraction of their electrons in a higher state. You can keep it in equilibrium by arranging conditions so that every time an electron drops, you kick it back up. It’s like the juggler who is keeping all the balls in air. And it’s all a function of the temperature. At low temperatures, the great majority of electrons hang out in energy level n = 1 with only very few electrons in energy level n = 2. As the temperature gets hotter, more electrons get kicked up into energy level n = 2.
Let’s put all this together. Consider an interstellar gas cloud being illuminated by the light from a 10,000 K star. Most atoms will have multiple energy levels with great complexity; that’s the natural order of things—by comparison, hydrogen’s energy levels are simple. It is the mixture of all these that wreaks havoc on the pure thermal spectrum that is emitted by the 10,000 K star. So let’s take a look at what havoc is wrought.
First, I give you the full-blown hydrogen atom. It has an infinite number of energy levels corresponding to concentric orbitals that go farther and farther out: n = 1 (the ground level—innermost orbital), n = 2 (the first excited level), n = 3, n = 4, n = 5, n = 6, . . . , n = ∞. The energy level diagram looks like a ladder, so we call it a ladder diagram. The lower energy levels, which are more tightly bound to the nucleus, are lower down in the diagram (figure 6.2).
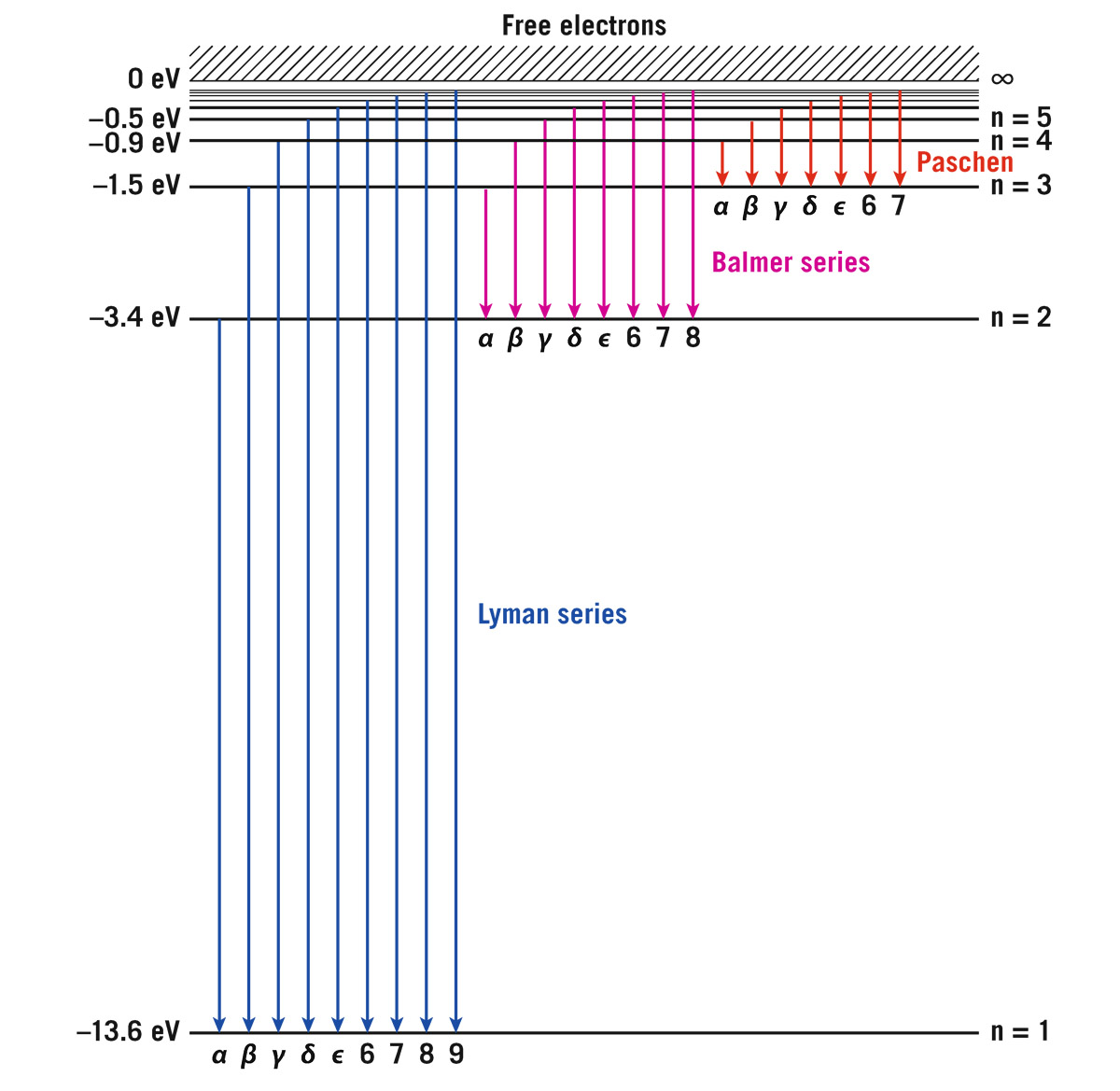
FIGURE 6.2. Energy level diagram for hydrogen. Horizontal lines indicate different energy levels for the electron in a hydrogen atom, in electron volts (eV). Arrows indicate transitions an electron can make from one energy level to another, emitting a photon of energy equal to the difference in energy. Transitions are shown to the first energy level (the Lyman series, which gives photons in the ultraviolet part of the spectrum), to the second energy level (the Balmer series, which gives visible light photons), and to the third energy level (the Paschen series, in the near infrared). The diagram shows electrons dropping down and emitting photons. If an electron is in level n = 3 and drops to level n = 2, as indicated by the red arrow, it will emit an Hα (Balmer series) photon with an energy of 1.9 eV. Credit: Michael A. Strauss
For hydrogen, the first excited state n = 2 is three-quarters of the way up, followed by n = 3, then n = 4, then n = 5, and so on. The energy tops out at zero. An electron with a high n occupies a very large orbital that is only weakly bound to the proton. In atoms, we measure energy in electron volts, eV. That’s the energy it takes to move an electron across a voltage difference of 1 volt. Let’s say you have a flashlight that operates using a 9 volt battery. Each electron generates 9 eV of energy in the form of light and heat as it passes through the wires of the flashlight. This flashlight might be passing 6.24 × 1018 electrons per second through its wires, generating 9 × (6.24 × 1018) eV per second (or 9 watts) of light and heat energy. One electron volt is thus a very small amount of energy; it is just a convenient unit for talking about the small amounts of energy associated with electronic transitions. For example, –13.6 eV in the figure is the energy of level n = 1. This is shown as a negative energy. You have to add 13.6 eV to that electron in energy level n = 1 to remove it from the atom. We say 13.6 eV is the binding energy of the ground state n = 1. What happens if an electron in the ground state sees a photon with energy greater than 13.6 eV? Can it absorb that photon? Here comes a photon with that much energy—what will the electron do with it? If the electron absorbs this photon, it will have enough energy to jump up above n = ∞. What is above n = ∞? That would be freedom. If an electron pops up there to an energy above zero, the electron escapes from the atom and leaves the proton by itself. We say we have ionized the atom—stripped it of an electron. (The atom now has a net charge, making it an ion.) The departed electron has an energy above zero; that “excess” energy above zero becomes its kinetic energy of motion as it escapes the atom. As you might suspect, an atom can also get ionized by being slammed by another atom.
With this knowledge of energy levels, we can now understand how the light comes out of a 10,000 K star. At a temperature of 10,000 K, it is hot enough that a small but significant fraction of the hydrogen atoms have electrons in the first excited state n = 2. That’s why I chose this star, because a temperature of 10,000 K maximizes the situation we are about to describe. Deep inside the star there is this thermal radiation spectrum, a beautiful Planck curve. It is trying to emerge from the outer layer of the star; that smooth, 10,000 K thermal spectrum hits those hydrogen atoms in the outer layer with some electrons in the first excited state, and those electrons are hungry. I can ask the question, in that thermal spectrum, how much energy do the individual photons have? The energies of many of those photons are found in the visible part of the spectrum, it just so happens, and the 10,000 K hydrogen gas has some hungry hydrogen atoms with electrons in the n = 2 level, and they are absorbing appropriate photons like mad and getting kicked up to higher energy levels for having done so.
But not all photons are being absorbed—only those whose wavelengths would kick an electron exactly up to a particular higher energy level. For example, an electron in level n = 2 (at an energy of –3.4 eV) can absorb a photon with just enough energy to make it jump up to level n = 3 (at an energy of –1.5 eV; see figure 6.2). The energy difference between those two levels is 1.9 eV. That’s how much energy the electron must get to jump up. Such an electron will absorb a photon with energy 1.9 eV. This photon is called an H-alpha, or Hα, photon. It has a wavelength of 6,563 Ångstroms, or 656.3 nanometers—its color is Burgundy red. That photon gets taken out, kicking an electron up from level 2 to level 3; that photon is now gone from the spectrum. Many electrons doing this causes a dip in the Planck spectrum at a wavelength of 6,563 Ångstroms, called an H-alpha (Hα) absorption line. Photons with a wavelength of 4,861 Ångstroms can boost an electron from level 2 to level 4; that causes another dip in the spectrum called the H-beta (Hβ) absorption line. There are more lines: H-gamma (Hγ) at 4,340 Ångstroms, H-delta (Hδ) at 4,102 Ångstroms, and so on, where photons are being taken out, sending electrons from n = 2 to levels n = 5, n = 6, . . . . In comes a continuous spectrum, out goes what we call an absorption spectrum, with narrow lines knocked out where those photons are getting eaten, making deep narrow valleys in the spectrum that are called absorption lines. The entire group of them is called the Balmer series: Hα, Hβ, Hγ, Hδ, Hε, followed by H6, H7, H8, and so on (nobody is expected to remember that many Greek letters). The spacing of these lines relates to those differences in energy on the ladder diagram. Figure 6.3 shows the spectrum of an actual 10,000 K star. The inset shows a close-up of the shorter-wavelength portion.
If we look at a star whose surface is a bit hotter, say, 15,000 K, the story changes dramatically: the electrons have so much energy from getting kicked in the pants that they leave the hydrogen atoms altogether: the electrons and the protons are running around separately—the atoms have become ionized. Ionized hydrogen no longer possesses discrete energy levels, and will no longer absorb Balmer photons. This is why the Balmer series is seen strongly in 10,000 K stars but not in hotter stars.
So far, we have only been considering what happens to hydrogen. Throw in calcium, and carbon, and oxygen, and everybody is getting a piece of the action. I will give you my favorite analogy—a tree. You can think of the outermost layer of the star as a tree. Do you know what is coming toward the tree (from inside the star)? Mixed nuts. We have a mixed-nut cannon (the interior of the star) firing mixed nuts (photons of different frequencies) into the tree, and in the tree we have squirrels. My squirrels like acorns (Hα photons)—these are acorn squirrels. They see all these mixed nuts coming through, but they are only grabbing the nuts they like, the acorns; on the other side (outside the star), out come mixed nuts minus the acorns (the thermal radiation minus the Hα photons). Now let’s bring in another species: let’s get some macadamia chipmunks. What comes out the other side? Mixed nuts minus acorns and minus macadamia nuts. For every species of rodent we stick in that tree, each preferring to eat a different kind of nut, you can infer who is hanging out in the tree based on what is missing on the other side, if you know what they eat.
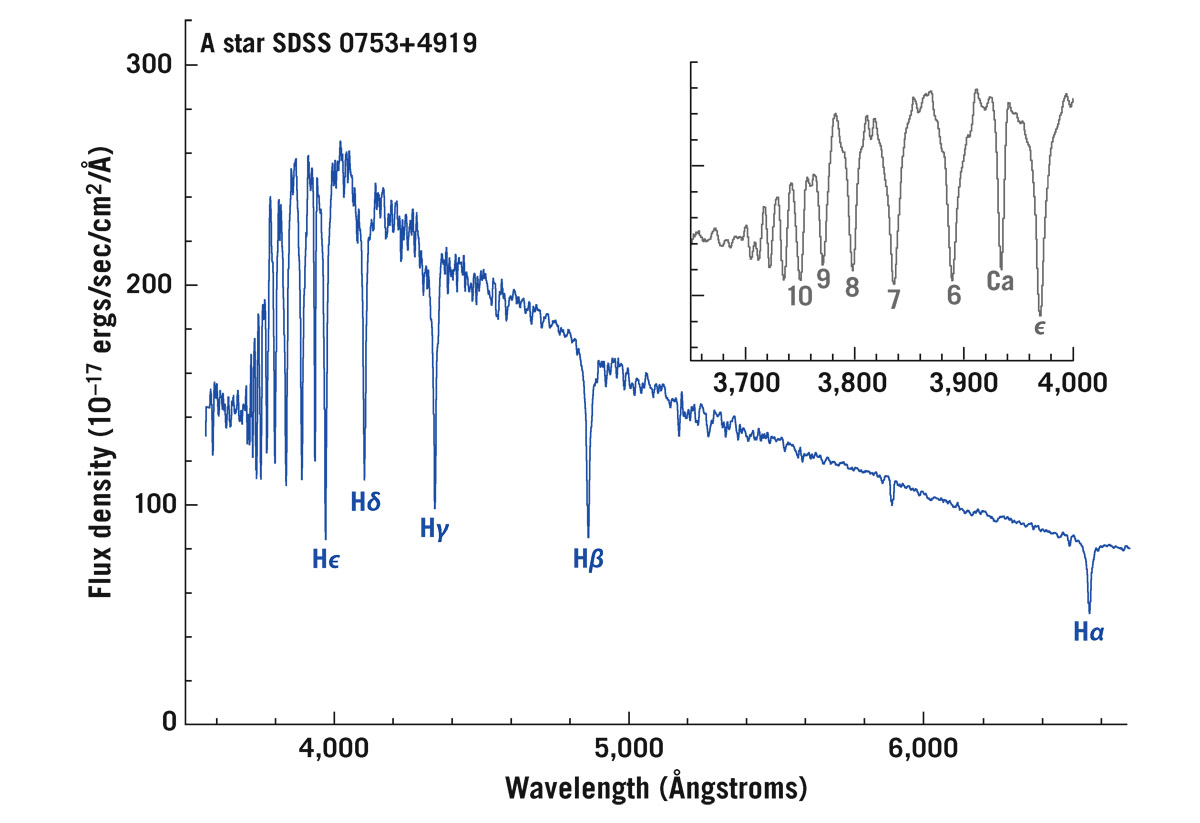
FIGURE 6.3. Stellar spectrum showing Balmer absorption lines. Spectrum of an A star from the Sloan Digital Sky Survey, showing the Balmer series of absorption lines of hydrogen; they are called Hα, Hβ, Hγ, and so forth. The lines pile up at the shortest wavelengths; the inset shows an expanded view, labeling the lines up to H10 (by convention, numbers are used rather than Greek letters beyond Hε). There is also one line due to singly ionized calcium, marked “Ca.” Credit: Sloan Digital Sky Survey and Michael A. Strauss
This is precisely the problem we face in astrophysics. Because we can’t go in the star (you wouldn’t want to go in there anyway; it’s too hot), we analyze it from afar, observing the light to see what gets taken out of the continuous thermal spectrum. We look at its spectrum and ask, does it match the lines of hydrogen? Mostly, but it has other elements too. Go to the lab, check out calcium, and the other elements, to see what frequencies they absorb in a laboratory setting. Then check each element to see whether it matches this star’s pattern, because each element leaves a unique fingerprint. These energy levels, these ladder diagrams, are unique to each element and molecule. (For example, figure 6.3 shows an absorption line due to calcium, labeled Ca, in addition to the lines from hydrogen.)
For the general case, let’s not even think of a star, but a cloud of gas in interstellar space, a hydrogen cloud with a continuous spectrum of energy coming in from a bright nearby star. Light from the star enters the cloud and comes out on the other side, so there is an absorption spectrum with lines missing. We must now account for the energy somehow; light at those wavelengths got absorbed, with electrons rising to higher energy levels. These electrons will fall back down, emitting photons as they fall. Thus, it’s a temporary affair between the electron and the photon. As the electron returns to its original energy level, a photon just like the one the electron absorbed gets sent out in a random direction. It’s as if the squirrels and chipmunks had indigestion and spit out the nuts they had just eaten in random directions. If the gas cloud is in equilibrium, with the average number of electrons in level 2 unchanging in time, then the number of nuts eaten and spit back out must be equal. If you are in the line of fire of the cannon (looking along the line of sight to the star), you will see an intense beam of mixed nuts from the cannon coming at you, minus acorns and macadamia nuts. However, if you stand at a random place looking at the tree but not in the line of fire of the cannon (not along the line of sight to the star), you will not see mixed nuts from the cannon, but looking just at the tree (the gas cloud), you will see acorns and macadamia nuts flying out of the tree. These will be bright emission lines at just those wavelengths that were absorbed before. From the acorns and macadamia nuts you see, you can deduce that there are squirrels and chipmunks in the tree. By analogy, the emission lines you see emanating from the gas cloud can enable you to identify some of the elements it contains. The picture of the Rosette Nebula in figure 6.4 shows that the nebula is red. The gas is emitting light in the emission line of hydrogen-alpha (Hα) at a wavelength of 6,563 Ångstroms. So this cloud contains hydrogen. Astronomers can take excellent pictures of emission nebulae like the Rosette Nebula using a filter that only lets in the Hα wavelength. That way, almost all the light from the rest of Earth’s atmosphere—the light pollution—is blocked out. The light from the young bright blue stars in the center of the Rosette Nebula (which you can see in the figure) bump its hydrogen atoms up to level n = 3, and when they drop back down to n = 2, they emit Hα photons in all directions, making the nebula glow in red Hα light, in the same way a neon sign glows orange.
We have been discussing the family of transitions for hydrogen, Hα, Hβ, Hγ, Hδ, and so on, called the Balmer series. This series of transitions was discovered in 1885 and is named after Johann Jakob Balmer, who figured them out. It doesn’t matter which way you draw the arrowhead in the energy level diagram—it’s the same photon coming in or going out. It can be absorbed (up) or emitted (down), but all the transitions in the Balmer series have the first excited state, n = 2, as the base, and the relevant photons find themselves in the visible part of the spectrum (see figure 6.2, which shows the emission of photons as electrons fall down). That’s why the Balmer series was discovered first, because the Balmer photons are in the visible region of the spectrum. But there are two other common series we can refer to. One of them, the Paschen series, is based at the n = 3 state. These are shorter jumps on the energy scale, so all the participating photons will have lower energy than visible light (see figure 6.2). This lands the Paschen series entirely in the infrared. Once we invented good detectors to reliably measure infrared light, the Paschen series showed up. You should know that these families continue, but I’m only going to mention three: Paschen, Balmer, and one more, the Lyman series (as before, our Greek letter nomenclature gives Lyman-alpha, Lyman-beta, etc.). The ground state, n = 1, forms its base, and all its transitions are in the ultraviolet. The lowest energy transition of the Lyman series has a higher energy than the highest energy transition of the Balmer series (see figure 6.2 again).

FIGURE 6.4. Rosette Nebula, a star-forming gas cloud. The red color is due to emission from hydrogen, specifically the n = 3 to n = 2 transition (Hα). Photo credit: Robert J. Vanderbei
This means that when you look for those transitions in the spectrum, the Balmer series is sitting there distinct from the other series, the Lyman series is distinct, and the Paschen series is also distinct, which made them easy to isolate and understand. I could draw an atom for which that is not the case. I can make up an atom—we’ve got some strange atoms out there—for which the energy jumps in its Lyman and Balmer and Paschen series might be similar, such that these three families would overlap in a spectrum. When thinking about these lines and how we decode them for yet-to-identified elements, we must account for this possibility.
For thousands of years, all we could do was measure the brightness of a star, its position on the sky, and maybe note its color. This was classical astronomy. It became modern astrophysics when we started obtaining spectra, because spectra allowed us to understand chemical composition, and our accurate interpretation of spectra came from quantum mechanics. I want to impress on you the importance of this. We had no understanding of spectra until quantum mechanics was developed. Planck introduced his constant in 1900, and in 1913 Bohr made his model of the hydrogen atom, with electrons in orbitals based on quantum mechanics, which explained the Balmer series. Modern astrophysics really didn’t get under way until after that, in the 1920s. Think about how recent this is. The oldest people alive today were born when astrophysics was starting. For thousands of years, we were essentially clueless about stars, yet in one human lifetime we have come to know them well. I have an astronomy book from 1900, and all it talks about is “here is a constellation,” “there is a pretty star,” “there are a lot of stars over here,” and “fewer stars here.” It has an entire chapter on Moon phases, another whole chapter on eclipses—that’s all they could talk about. Textbooks written after the 1920s, however, talk about the chemical composition of the Sun, the sources of nuclear energy, the fate of the universe. In 1926, Edwin Hubble discovered that the universe is bigger than anybody had thought, because he revealed that galaxies live far beyond the stars of our own Milky Way. And in 1929, he discovered that the universe is expanding. These leaps of understanding happened in the lifetime of people alive today. Extraordinary. I often ask myself, what revolutions await us in the next several decades? What cosmic discoveries will you witness that you can tell your descendants about?
With these lessons of history, you might just avoid making bonehead predictions like that of the French philosopher Auguste Comte, who, in his 1842 book, The Positive Philosophy, declared of the stars: “We can never learn their internal constitution, nor, in regard to some of them, how heat is absorbed by their atmosphere.”