1
WHY LOGIC?
THE WORLD IS A VAST and complicated place. If we want to understand it we need to simplify it. There are two ways to make something simpler–we can forget parts of it, or we can become cleverer so that things that used to seem incomprehensible become clear to us. This book is about the role that logic can and should play in this process of understanding. It is about how logic can help us see and understand the world more clearly. It is about the light that logic shines.
Logic involves both aspects of making something simpler. Forgetting details is the process of abstraction, where we find the essence of a situation and concentrate on it for a while. Importantly, we must not forget critical details–that would be simplistic rather than illuminating. And we only do it temporarily, so that we are not claiming to have understood everything, but rather, a central core on which all further understanding can be rooted.
We will begin, in this chapter, by discussing why logic is a good foundation for all understanding, and what role logic can possibly have in a world of illogical human beings.
ACCESSING TRUTH
All areas of research and study are concerned with uncovering truths about the world. It might be the earth, the weather, the outer reaches of the universe, birds, electricity, brains, blood, people thousands of years ago, numbers, or something else. Depending on what you’re studying, you’ll need different ways of determining what is true, and of convincing other people that you’re right. Anyone can make claims about what they think is true, but unless they back up their claims in some way, maybe nobody will believe them, and rightly so.
So different subjects have different ways of accessing truth.
Scientific truth is determined using the scientific method, which is a clearly defined framework for deciding how likely something is to be correct. It usually involves forming a theory, gathering evidence, and rigorously testing the theory against the evidence.
Mathematical truth is accessed by logic. We can still use emotions to feel it, understand it, and be convinced of it, but we use only logic to verify it. This distinction is important and subtle. In a way, we do access mathematical truth using emotions, but it doesn’t count as true until we have verified it using logic.
The word “logic” is sometimes thrown around in disagreements to try and give an argument weight. “Logically this has to be true”, or “Logically that can’t be right”, or “You’re just not being logical!” The word “mathematically” also gets thrown around in this way. “Mathematically, they just can’t win the election.” Unfortunately these uses are often meaningless, more of a last-ditch way to try and shore up a weak argument. While the abuse of these words devalues them and so makes me sad, I am an optimist and so I choose to find something heartening in this as well: I am heartened to think that at some level people know that logic and mathematics are irrefutable and so should conclusively end an argument. If their names are being taken in vain to vanquish an opponent, at least this means there is some sense in which their power is being acknowledged.
Instead of simply lamenting the misunderstanding of logic and mathematics, I choose to address it, in the hope that their power might actually be used to good purpose. That is why I’ve written this book.
ADVANTAGES OF USING LOGIC
One of the main reasons to have a clear framework for accessing truth is to be able to agree about things. This seems very radical in a world in which people seem to revel in disagreeing with other people as much as possible. And it even happens in sport, when fans get angry with a decision that a referee has made, although the referee is supposed to be simply applying the agreed rules.
I remember watching the Oxford–Cambridge boat race one year when the boats clashed dangerously, and Cambridge was penalized. As a Cambridge person I was outraged because it looked to me that Oxford had obviously veered into them deliberately, so it looked like Oxford’s fault. I thought the referee was in a conspiracy with Oxford and was being biased. However, instead of railing against this assumed conspiracy I looked up some expert commentary to try and understand what had happened. I learned that during the race up the river Thames, an imaginary line is drawn along the middle of the river, and each boat has priority on their side of the river. This means one boat can leave a lot of space, perhaps when taking a bend, and “lure” the other boat across the line. Then the boat with priority can deliberately veer into the boat that crossed the line, knowing they won’t get the penalty. Is it morally right? Who’s fault is that, really? We’ll unravel questions of blame and responsibility in Chapter 5.
This idea of a clear framework for reaching consensus is also a bit like how medical diagnosis works. The medical profession tries to make a clear checklist so that a diagnosis is unambiguous, and so that diagnoses are made consistently by different people across the profession.
The idea of logic is to have clear rules so that conclusions can be drawn unambiguously and consistently by different people. This is wonderful in theory, and perhaps here “in theory” means in the abstract world of mathematics. Mathematics has a remarkable ability to make progress. Philosopher Michael Dummett writes in The Philosophy of Mathematics:
Mathematics makes a steady advance, while philosophy continues to flounder in unending bafflement at the problems it confronted at the outset.
Why are mathematicians able to reach agreements about what is true? And why do those things remain true thousands of years later, where other subjects appear to be continually refining and updating their theories? I believe the answer lies in the robustness of logic. That is its great advantage.
There are also some disadvantages of the logical world. One is that you can’t win arguments just by yelling loudly. Of course, this is only a disadvantage if you like winning arguments by yelling loudly, which I actually don’t. But unfortunately plenty of people do, so they don’t like the logical world. And they don’t like the fact that in the logical world they can’t get the better of a small, soft-spoken, uncool person like me. Because in the logical world strength doesn’t come from big muscles, large amounts of money, or sporting prowess. It comes from sheer logical intellect.
Another disadvantage of the logical world is that you don’t really have your feet on the ground any more, because we’re no longer in the concrete world. It can sometimes feel like you’re floating around in mid-nowhere, but I find that this is quite a pleasant sensation once you get used to it. The key, as with putting the first human in space, is to be able to come back again. In this book we are not just going to float around in the abstract world for fun. We are going to come back to earth and use powerful logical techniques to disentangle real, relevant, urgent arguments about the state of society. We are going to show that accessing the logical abstract world enables us to get further in the real world, just as flying through the sky enables us to travel further and faster in real life. In essence, this is the whole point of mathematics.
WHAT MATH IS AND ISN’T
There are many misconceptions about mathematics. These probably come from the way math is presented at school, as a set of rules you have to follow to get the right answer. The right answer in school math is usually a number. When proof finally comes into it it’s often in the form of geometry, where “logical proofs” are constructed using peculiar facts to prove other pointless results such as that if you have some configuration of lines crossing each other in a bunch of different places then one angle over here turns out to be related to another one over there.
Warning/reassurance: this example is a spoof and can’t be solved.
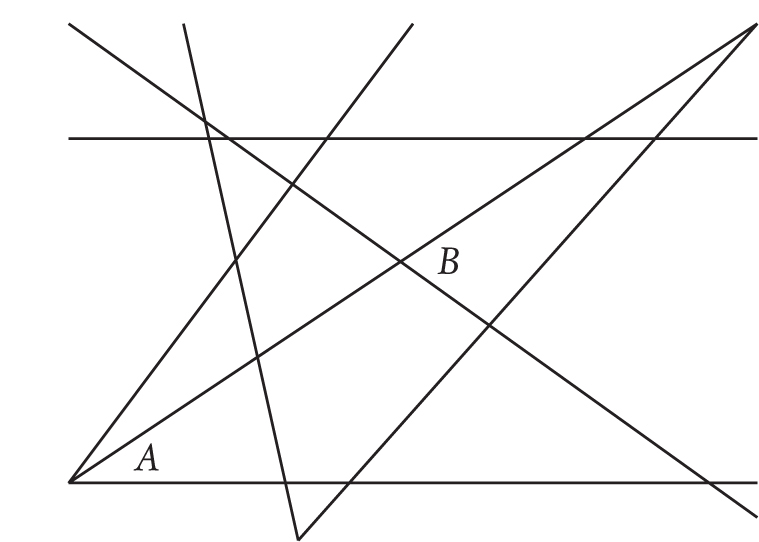
“Show that angle A is half of angle B.”
You then have a series of tests and exams thrown at you, where you’re asked to do a whole series of these pointless exercises under an arbitrary time pressure. If you make it through all that and somehow still believe you like math, you might go to university to do math, where the whole thing is likely to happen all over again except harder. If you make it through that and still think you like math, you might do a PhD and start doing research. Here, finally, mathematics starts to resemble what I think mathematics really is. Not a series of hoops to jump through, not an attempt to get the “right answer”, but a world to explore, discover and understand: the logical world.
At this point some people realize that the thing they liked about “math” up until then was jumping through hoops and getting the right answer. They liked being able to get the right answer easily, and once they get to this exploratory world of math they run away.
Other people held on to a love of math throughout unfortunate school experiences because they somehow knew that math was going to be better and more exciting than that in the end, when they got to do research. Educator Daniel Finkel calls this being “inoculated” against school math classes. I was inoculated against them by my mother, who showed me that math was more than what we did at school. Some people are inoculated by an excellent math teacher–it sometimes only takes one teacher, for one class, to effect the inoculation and convince students that no matter what happened to them before and what happens to them after that class, math will be open-ended and fascinating if they pursue it long enough.
So what is this “real math” that we usually only meet when we start research? What is mathematics? Many people think it is “the study of numbers”, but it is so much more than that. I gave a talk about symmetry to an elementary school in Chicago, and one little boy complained afterwards “Where are the numbers?” I explained that math is not just about numbers, and he wailed “But I want it to be about numbers!”
The rules of scientific discovery involve experiments, evidence and replicability. The rules of mathematical discovery do not involve any of those things: they involve logical proof. Mathematical truth is established by constructing logical arguments, and that is all.
My favorite way to think about math is: it is the study of how things work. But it’s not the study of how any old things work: it’s the study of how logical things work. And it’s not any old study of how logical things work: it’s the logical study of how logical things work.
Any research discipline has two aspects:
1. what it studies, and
2. how it studies it.
The two are linked, but in mathematics they are particularly cyclically linked. Usually the objects we’re studying determine how we’re going to study them, but in math the way we’re studying them also determines what we can study. The method we’re using is logic, and so we can study any objects that behave according to the rules of logic. But what are those? That is the subject of the first part of this book.
RULES
Different games and sports have different rules for deciding who is best in an unambiguous way. Personally, I am more comfortable with the ones that are very clear cut, like: who passed the finish line first, or who jumped over the highest bar without knocking it down. Other sports like gymnastics or diving seem more complicated, confusing and ambiguous if they require a panel of judges to make decisions according to certain criteria. The criteria are supposed to be set up to be unambiguous and to remove human judgement from the situation. But if they were truly unambiguous the judges would never disagree, and we wouldn’t need a whole panel of them.
But even the apparently clear-cut sports have plenty of rules. If we look more closely at the 100m sprint or the high jump, we see that there are rules about false starts, drug use, who is allowed to participate as a woman, who is allowed to participate as able-bodied, and more.
One problem with logic, as with sport, is that the rules can be baffling if you’re not very used to them. I am pretty baffled by the rules of American football. Americans often assume that this is because I’m British and so used to “soccer” football, but in fact I’m baffled by that kind of football too. Although it does at least involve moving a ball around with your feet, so I understand that much.
We need to be clear what the rules of a sport are before we can really start playing it, and we need to be clear what the rules of logic are before we can really start using it. As with sport, the more advanced we get, the more deeply we’ll have to understand the rules and all their subtleties. It’s an effort, but the more we understand about the underlying principles of logic, the better and more productive arguments we’ll be able to have.
A THEORY FOR ARGUING
The internet is a rich and endless source of flawed arguments. There has been an alarming gradual increase in non-experts dismissing expert consensus as elite conspiracy, as with climate science and vaccinations. Just because a lot of people agree about something doesn’t mean there is a conspiracy. Many people agree that Roger Federer won Wimbledon in 2017. In fact, probably everyone who is aware of it agrees. This doesn’t mean it’s a conspiracy: it means there are very clear rules for how to win Wimbledon, and many, many people could all watch him do it and verify that he did in fact win, according to the rules.
The trouble with science and mathematics in this regard is that the rules are harder to understand, so it is more difficult for non-experts to verify that the rules have been followed. But this lack of understanding goes back to a much more basic level: different uses of the word “theory”. In some uses, a “theory” is just a proposed explanation for something. In science, a “theory” is an explanation that is rigorously tested according to a clear framework, and deemed to be statistically highly likely to be correct. (More accurately, it is deemed statistically unlikely that the outcome would occur without the explanation being correct.)
In mathematics, though, a “theory” is a set of results that has been proved to be true according to logic. There is no probability involved, no evidence required, and no doubt. The doubt and questions come in when we ask how this theory models the world around us, but the results that are true inside this theory must logically be true, and mathematicians can all agree on it. If they doubt it, they have to find an error in the proof; it is not acceptable just to shout about it.
It is a noticeable feature of mathematics that mathematicians are surprisingly good at agreeing about what is and isn’t true. We have open questions, where we don’t know the answer yet, but mathematics from 2000 years ago is still considered true and indeed is still taught. This is different from science, which is continually being refined and updated. I’m not sure that much science from 2000 years ago is still taught, except in a history of science class. The basic reason is that the framework for showing that something is true in mathematics is logical proof, and the framework is clear enough for mathematicians to agree on it. It doesn’t mean a conspiracy is afoot.
Mathematics is, of course, not life, and logical proofs don’t quite work in real life. This is because real life has much more nuance and uncertainty than the mathematical world. The mathematical world has been set up specifically to eliminate that uncertainty, but we can’t just ignore that aspect of real life. Or rather, it’s there whether we ignore it or not.
Thus arguments to back something up in real life aren’t as clean as mathematical proofs, and that is one obvious source of disagreements. However, logical arguments should have a lot in common with proofs, even if they’re not quite as clear cut. Some of the disagreement around arguments in real life is unavoidable, as it stems from genuine uncertainty about the world. But some of the disagreement is avoidable, and we can avoid it by using logic. That is the part we are going to focus on.
Mathematical proofs are usually much longer and more complex than typical arguments in normal life. One of the problems with arguments in normal life is that they often happen rather quickly and there is no time to build up a complex argument. Even if there were time, attention spans have become notoriously short. If you don’t get to the point in one momentous revelation, it is likely that many people won’t follow.
By contrast a single proof in math might take ten pages to write out, and a year to construct. In fact, the one I’m working on while writing this book has been eleven years in the planning, and has surpassed 200 pages in my notes. As a mathematician I am very well practiced at planning long and complex proofs.
A 200-page argument is almost certainly too long for arguments in daily life (although it’s probably not that unusual for legal rulings). However, 280 characters is rather too short. Solving problems in daily life is not simple, and we shouldn’t expect to be able to do so in arguments of one or two sentences, or by straightforward use of intuition. I will argue that the ability to build up, communicate and follow complex logical arguments is an important skill of an intelligently rational human. Doing mathematical proofs is like when athletes train at very high altitude, so that when they come back to normal air pressure things feel much easier. But instead of training our bodies physically, we are training our minds logically, and that happens in the abstract world.
THE ABSTRACT WORLD
Most real objects do not behave according to logic. I don’t. You don’t. My computer certainly doesn’t. If you give a child a cookie and another cookie, how many cookies will they have? Possibly none, as they will have eaten them.
This is why in mathematics we forget some details about the situation in order to get into a place where logic does work perfectly. So instead of thinking about one cookie and another cookie, we think about one plus one, forgetting the “cookie” aspect. The result of one plus one is then applicable to cookies, as long as we are careful about the ways in which cookies do and don’t behave according to logic.
Logic is a process of constructing arguments by careful deduction. We can try to do this in normal life with varying results, because things in normal life are logical to different extents. I would argue that nothing in normal life is truly entirely logical. Later we will explore how things fail to be logical: because of emotions, or because there is too much data for us to process, or because too much data is missing, or because there is an element of randomness.
So in order to study anything logically we have to forget the pesky details that prevent things from behaving logically. In the case of the child and the cookies, if they are allowed to eat the cookies, then the situation will not behave entirely logically. So we impose the condition that they are not allowed to eat the cookies, in which case those objects might as well not be cookies, but anything inedible as long as it is separated into discrete chunks. These are just “things”, with no distinguishable characteristics. This is what the number 1 is: it is the idea of a clearly distinguishable “thing”.
This move has taken us from the real world of objects to the abstract world of ideas. What does this gain us?
ADVANTAGES OF THE ABSTRACT WORLD
The advantage of making the move into the abstract world is that we are now in a place where everything behaves logically. If I add one and one under exactly the same conditions in the abstract world repeatedly, I will always get 2. (I can change the conditions and get the answer as something else instead, but then I’ll always get the same answer with those new conditions too.)
They say that insanity is doing the same thing over and over again and expecting something different to happen. I say that logic (or at least part of it) is doing the same thing over and over again and expecting the same thing to happen. Where my computer is concerned, it is this that causes me some insanity. I do the same thing every day and then periodically my computer refuses to connect to the wifi. My computer is not logical.
A powerful aspect of abstraction is that many different situations become the same when you forget some details. I could consider one apple and another apple, or one bear and another bear, or one opera singer and another opera singer, and all of those situations would become “1 + 1” in the abstract world. Once we discover that different things are somehow the same, we can study them at the same time, which is much more efficient. That is, we can study the parts they have in common, and then look at the ways in which they’re different separately.
We get to find many relationships between different situations, possibly unexpectedly. For example, I have found a relationship between a Bach prelude for the piano and the way we might braid our hair. Finding relationships between different situations helps us understand them from different points of view, but it is also fundamentally a unifying act. We can emphasize differences, or we can emphasize similarities. I am drawn to finding similarities between things, both in mathematics and in life. Mathematics is a framework for finding similarities between different parts of science, and my research field, category theory, is a framework for finding similarities between different parts of math. We will show the efficacy of thinking in terms of relationships in Chapter 6.
When we look for similarities between things we often have to discard more and more layers of outer details, until we get to the deep structures that are holding things together. This is just like the fact that we humans don’t look extremely alike on the surface, but if we strip ourselves all the way down to our skeletons we are all pretty much the same. Shedding outer layers, or boiling an argument down to its essence, can help us understand what we think and in particular can help us understand why we disagree with other people.
A particularly helpful feature of the abstract world is that everything exists as soon as you think of it. If you have an idea and you want to play with it, you can play with it immediately. You don’t have to go and buy it (or beg your parents to buy it for you, or beg your grant-awarding agency to give you the money to buy it). I wish my dinner would exist as soon as I think of it. But my dinner isn’t abstract, so it doesn’t. More seriously, this means that we can do thought experiments with our ideas about the world, following the logical implications through to see what will happen, without having to do real and possibly impractical experiments to get those ideas.
HOW DO WE GET TO THE ABSTRACT WORLD?
Getting to the abstract, logical world is the first step towards thinking logically. Granted, in normal life we might not need to go there quite so explicitly in order to think logically about the world around us, but the process is still there when we are trying to find the logic in a situation.
A new system was recently introduced on the London Underground, where green markings were painted onto the platforms indicating where the doors would open. Passengers waiting for the train were instructed to stand outside the green areas, so that those disembarking the arriving train would have space to do so, instead of being faced with a wall of people trying to get on. The aim was to try and improve the flow of people and reduce the terrible congestion, especially during the rush hour.
This sounds like a good idea to me, but it was met with outcry from some regular commuters. Apparently some people were upset that these markings spoilt the “competitive edge” they had gained through years of commuting and studying train doors to learn where they would open. They were upset that random tourists who had never been to London before would now have just as much chance of boarding the train first.
This complaint was met with ridicule in return, but I thought it gave an interesting insight into one of the thorny aspects of affirmative action: if we give particular help to some previously disadvantaged people, then some of the people who don’t get this help are likely to feel hard done by. They think it’s unfair that only those other people get help. Like the absurdly outraged commuters, they might well feel miffed that they are losing their “competitive edge” that they feel they have earned, and they think that everyone else should have to earn it as well.
This is not an explicitly mathematical example but this way of making analogies is the essence of mathematical thinking, where we focus on important features of a situation to clarify it, and to make connections with other situations. In fact, mathematics as a whole can be thought of as the theory of analogies. We will use analogies to pivot between apparently unrelated situations throughout this book, and will provide a detailed analysis of the role of analogies in Chapter 13. Finding analogies involves stripping away some details that we deem irrelevant for present considerations, and finding the ideas that are at the very heart making it tick. This is a process of abstraction, and is how we get to the abstract world where we can more easily and effectively apply logic and examine the logic in a situation.
To perform this abstraction well, we need to separate out the things that are inherent from the things that are coincidental. Logical explanations come from the deep and unchanging meanings of things, rather than from sequences of events or personal decisions and tastes. The inherentness means that we should not have to rely on context to understand something. We will see that our normal use of language depends on context all the time, as the same words can mean different things in different contexts, just as “quite” can mean “very” or “not much”. In normal language people judge things not only by context but also relative to their own experiences; logical explanations need to be independent of personal experiences.
Understanding what is inherent in a situation involves understanding why things are happening, in a very fundamental sense. It is very related to asking “why?”, repeatedly, like a small child, and not being satisfied with immediate and superficial answers. We have to be very clear what we are talking about in the first place. As we will see, logical arguments mostly come down to unpacking what things really mean, and in order to do that you have to understand what things mean very deeply. This can often seem like making an argument all about definitions. If you try having an argument about whether or not you exist, you’ll probably find that the argument will quickly degenerate into an argument about what it means to “exist”. I usually find that I might as well pick a definition that means I do exist, as that’s a more useful answer than saying “Nope, I don’t exist.”
LOGIC AND LIFE
I have already asserted the fact that nothing in the world actually behaves according to logic. So how can we use logic in the world around us? Mathematical arguments and justifications are unambiguous and robust, but we can’t use them to draw completely unambiguous conclusions about the world of humans. We can try to use logic to construct arguments about the real world, but no matter how unambiguously we build the argument, if we start with concepts that are ambiguous, there will be ambiguity in the result. We can use extremely secure building techniques, but if we use bricks made of polystyrene we’ll never get a very strong building.
However, understanding mathematical logic helps us understand ambiguity and disagreement. It helps us understand where the disagreement is coming from. It helps us understand whether it comes from different use of logic, or different building blocks. If two people are disagreeing about healthcare they might be disagreeing about whether or not everyone should have healthcare, or they might be disagreeing about the best way to provide everyone with healthcare. Those are two quite different types of disagreement.
If they are disagreeing about the latter, they could be using different criteria to evaluate the healthcare systems, for example cost to the government, cost to the individuals, coverage, or outcomes. Perhaps in one system average premiums have gone up but more people have access to insurance. Or it could be that they are using the same criteria but judging the systems differently against those same criteria: one way to evaluate cost to individuals is to look at premiums, but another way is to look at the amount they actually have to pay out of their own pockets for any treatment. And even focusing on premiums there are different ways to evaluate those: means, medians, or looking at the cost to the poorest portion of society.
If two people disagree about how to solve a problem, they might be disagreeing about what counts as a solution, or they might agree on what counts as a solution but disagree about how to reach it. I believe that understanding logic helps us understand how to clear up disagreements, by first helping us understand where the root of the disagreement is.
In the first part of this book we are examining what logic is as a discipline for building arguments, and as a piece of mathematics. In the second part we’ll see what the limitations of logic are. And in the third part we’ll see how important it is, given those limitations, to take our emotions seriously.
LOGIC AS ILLUMINATION
Our aim throughout all of this is to shed light on the world. If we push our use of logic too far we risk overstepping that aim, and we will open ourselves to accusations of pedantry. Unfortunately mathematicians and extremely logical types of people are often accused of being pedantic by non-mathematicians or less logical people. Here, at the risk of sounding pedantic myself (and becoming very self-referential), I’m trying to shed light on the difference between pedantry and precision. I think the difference is illumination. I would characterize pedantry as precision that has gone further than necessary to shed light on a situation. There is plenty of precision that is there to clear things up, just like getting definitions right before trying to construct arguments with them. However, when extra precision does not help, I would call that pedantry.
Thus, self-referentially, I think that my distinction between pedantry and precision is itself a case of precision, not pedantry, because I think it sheds light on the situation.
Of course, people may disagree on where the lines are. One person’s precision may well be another person’s pedantry. It depends how much someone is seeking precision, and how much tolerance they have for ambiguity.
One of the difficulties that children have in learning about the world is dealing with the ambiguities of language. They are liable to take things rather literally because they haven’t yet learned to use context to interpret the ambiguities. They haven’t yet developed a tolerance for (or understanding of) subtle shades of nuance. A friend of mine recounted an incident when her small son was eating a bag of crisps and said he’d had enough. “You can just leave them on the table,” she said, whereupon he obediently tipped them out onto the table.
As adults we develop the ability to become more relaxed about figurative language, and more relaxed about how precise we need things to be in order to get on with our lives. This is a bit like how accurately you need to measure things. When I’m weighing sugar to make a cake, I know it doesn’t matter all that much if I’m off by 10g or so. However, when I’m weighing sugar to make macarons I know it matters an awful lot so I’ll try to weigh to the nearest gram according to my digital scales. If someone is measuring the amount of anaesthetic to use to put someone under general anaesthetic I rather hope they’ll measure extremely accurately. Indeed I was rather put out the one time I did go under general anaesthetic, for a knee operation, when the anaesthetist discovered I was a mathematician and said in that cheerful way people do, “Oh, I’m terrible at math!” I did not feel heartened.
I admit that I often find myself seeking more precision than some other people, and I do get accused of pedantry. But I’m convinced that I’m honestly just trying to shed light on situations. Actually, I tend to like more light in situations physically as well. I have bright lights on my desk, and I love bright sunshine because I like seeing everything more clearly. I like this in my thought processes as well. Achieving the illuminating precision sometimes takes longer–more thought, more words of explanation, more groundwork–and this is often unacceptable in today’s world of soundbites, memes, and so-called mic-drops. It turns out that saying something with impact is often more important than saying something true. But there should be a way to show truth without sacrificing impact, and of having an impact without sacrificing truth. That is the best way to use logic in this complex world of unpredictable, emotional, beautiful humans.
I imagine shining a bright light to illuminate the things we are trying to understand. If we hold it close, the light will be bright but will illuminate only a small spot. If we move it further up, we illuminate a wider area but the light will be less bright. Eventually if we hold it too far out the light will become so diffuse that we won’t see anything at all. But if we put it right on top of the things we’re studying, we also won’t see much.
Logic and abstraction are like shining a light at things. As we get more abstract, it’s like raising the light off the ground. We see a broader context, but with less fierce detail; however, understanding the broad context helps us understand the detail later. In all cases the aim should be illumination of some kind. First we need some light, and then we can decide where, and how, to shine it.