13
ANALOGIES
WE HAVE SEEN THAT abstraction is how we get to the world where logic works. The abstract world is a world of ideas and concepts, removed from our concrete, messy world of objects, humans and feelings. But how then does that logical world interact with the world we actually live in? Understanding logical situations is all very well but one of its limits comes from the fact that the abstract world sheds light on our “real” world, but is not actually our real world, and so something is bound to be lost or distorted when we move back to the real world.
In this chapter we’ll talk about how abstract ideas interact with real world situations in the form of analogies, how analogies can help us understand both good and bad arguments about our world, and what some of the pitfalls are when we invoke analogies.
ABSTRACTION
At the beginning of this book we discussed the fact that nothing in the real world actually behaves according to logic. So in order to study anything using logic we have to perform some abstraction, that is, ignore some of the details of the situation so that we move to the abstract world of ideas, where things do work according to logic. This is sometimes like modelling a situation with a simplified version, or like focusing on just certain aspects of a situation. Doing this abstraction enables us to use logic, but the process of abstraction is not itself logical–we have to choose what to focus on and how to simplify. In the previous chapter we saw that there can be many different ways of finding an abstract version of the same situation. This doesn’t mean that some are right and some are wrong, it means that different abstractions show us different things, and we should be aware of what we have lost and gained by doing it.
When we forget details about situations, many different situations start looking the same. Abstraction is a way of finding what different situations have in common, just like we did with the cubes and cuboids of privilege in Chapter 6: we discovered aspects of various different situations that could be understood in cuboid-shaped interactions.
This is why abstraction is linked to analogies: an analogy is a similarity between two different situations, and abstraction takes that similarity very seriously and treats it as a situation in its own right. One of the most basic analogies is between objects like two apples, two bananas, and two chairs. The thing that those situations have in common is the concept of “two”, which comes from taking what is analogous between those situations and regarding it as a concept in its own right. Arguably all of mathematics comes from finding similarities between different situations in this way, and when we study them as concepts in their own right we have moved one level more abstract than before.
Following what we learned in Chapter 6 about the efficacy of highlighting relationships between things, we could draw these relationships like this:
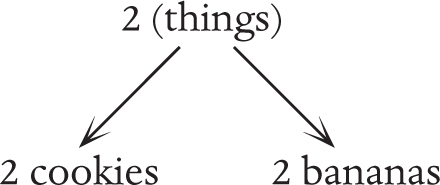
Here the arrows represent the process of going from something general or abstract to an instance of it. Abstraction is a way to pivot between different situations that have something in common. In fact, I’ve drawn the diagram of abstraction to look a bit like a pivot. The number two enables us to pivot from a situation involving two cookies (perhaps one and then another one) to a situation involving two of something else.
Moving to the abstract level is one way to find the logic in a situation, but making an analogy is a way to do it without explicitly going through the abstract world. Usually in normal life we make the analogy without being explicit about what the abstract version is. This can be helpful in real-world situations where exhibiting abstract logic would be rather pedantic–precise, without illuminating the situation unless you’re talking to others trained in abstract logic. In fact, the way we teach small children numbers usually involves showing them sets of two things over and over again and encouraging them to find what is analogous between them themselves.
By contrast in math great power comes from making the abstract version explicit, as we did for the cuboid of privilege. It means we can make analogies that are more complicated or subtle, or enable us to encompass examples that are much further from where we started. We’re really just like monkeys jumping from tree to tree and discovering that we can get further if we swing from a branch rather than just jumping. In fact, this is an analogy about analogies, so we will now look at the abstract principle behind analogies themselves.
FRAMEWORK FOR ANALOGIES
Whenever mathematicians feel like they’re doing the same thing over and over again, they look for an abstract version that represents the situation. I find myself making analogies repeatedly, so what about the abstract version of an analogy? The general situation is that we are making an analogy between concepts A and B, via an abstract principle X that is often implicit rather than explicit. The diagram looks like this:
As with monkeys swinging from branches, we should think about what level of abstraction we choose to pivot from. The more details we ignore about a situation, the more things become the same. Math tends to get more and more abstract as it goes on, gradually losing people at each stage as they become uncomfortable with the level of abstraction. People often tell me that they lost it when “numbers became letters”. This abstract pivot could be shown like this:

Here a and b represent the numbers 1, 2, 3, or something else. But there’s a level even more abstract than that, where we draw an analogy between addition and multiplication themselves, and think about “binary operations”, which include addition and multiplication but also many other things. Here is the further level of abstraction, with the symbol  representing a binary operation that could be +, × or something else:
representing a binary operation that could be +, × or something else:
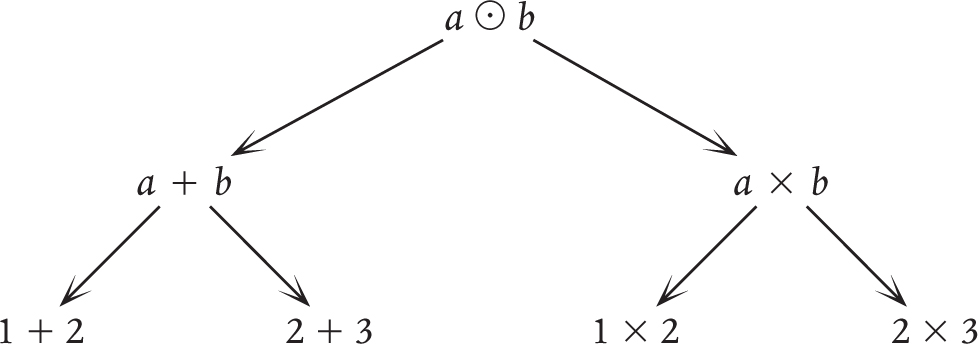
At the first level, 1 + 2 is analogous to 2 + 3 but not to 1 × 2. At the second level addition itself is analogous to multiplication, so everything on the bottom row can now be treated analogously. For some purposes the top level is a good level, but for other purposes we should only go as far as the middle level.1
One of the important lessons my PhD supervisor Martin Hyland taught me was the importance of finding the right level of abstraction for the situation. This is like shining a light at an appropriate distance so that you can see enough detail but also enough context around the thing you’re looking at. In a way, for abstraction, this consists of forgetting as many details as possible while still retaining the truth of what you are trying to study. If we forget details that are relevant, we might forget something that is critical to the situation. After all, if we forget enough details eventually everything becomes the same, and that is arguably not a productive way to look at the world. (Although I do think we gain something from remembering that all humans are at root the same.)
However, if we don’t go abstract enough, we might miss the chance to draw some links between more things. This happens with numbers in this diagram:
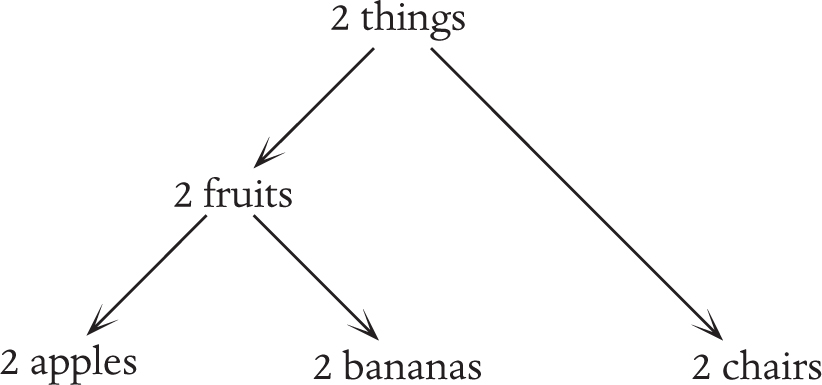
If we only go up to the level of “2 fruits” we will get an analogy between 2 apples and 2 bananas, but will omit 2 chairs. In order to include “2 chairs” we need to go up further, to the level of “2 things”. This is what happened when we found the cube of privilege in Chapter 6. We started with the cube for factors of 30, and the one for factors of 42, and we found that they had the same shape because both numbers are a product a×b×c of three different prime numbers. The analogy is expressed in this diagram:
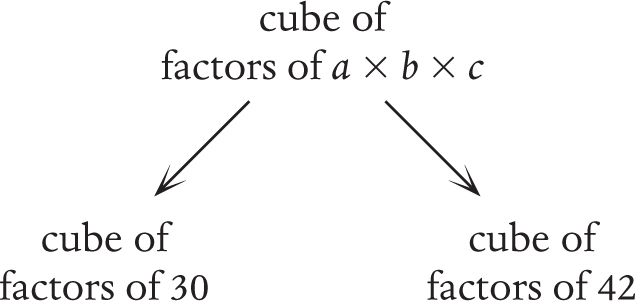
But then we realized that if we go one level more abstract and think of it as a cube of subsets of {a, b, c} then the analogy applies to many more things, including any three types of privilege. We have gone up a level of abstraction as here:
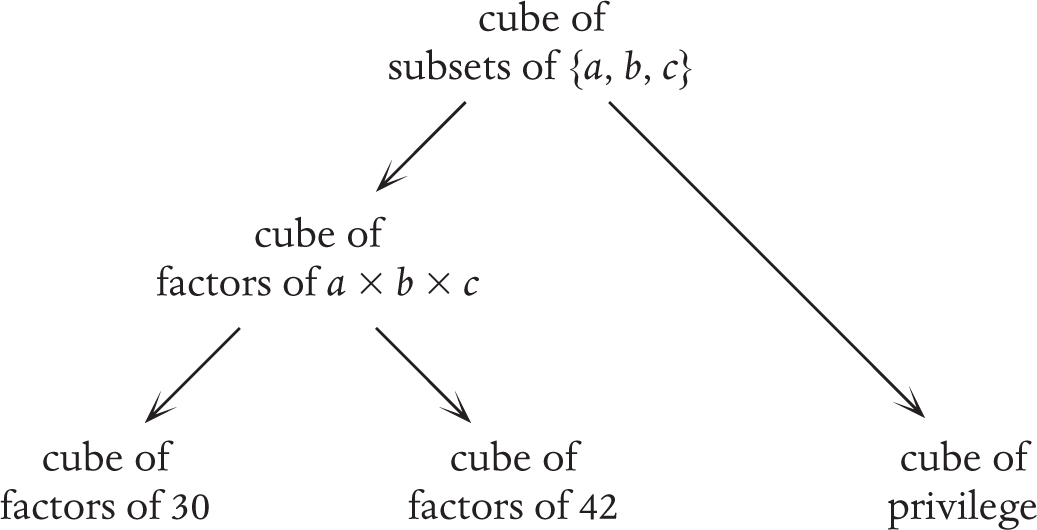
This gives us a way of expressing the possibly surprising fact that although thinking about something more abstractly appears to take us further away from concrete ideas (vertically in the picture), it enables us to pivot further away from where we started (horizontally), and thus encompass more ideas, including more concrete ones. Much of my argument about math comes from my view that math is a little removed from normal life, so if we pick low pivots we will not get very far out of math, perhaps only as far as physics. But if we get more abstract we can pivot far from math and apply our analogies to very real situations in life. Here is an example that is very real in life:
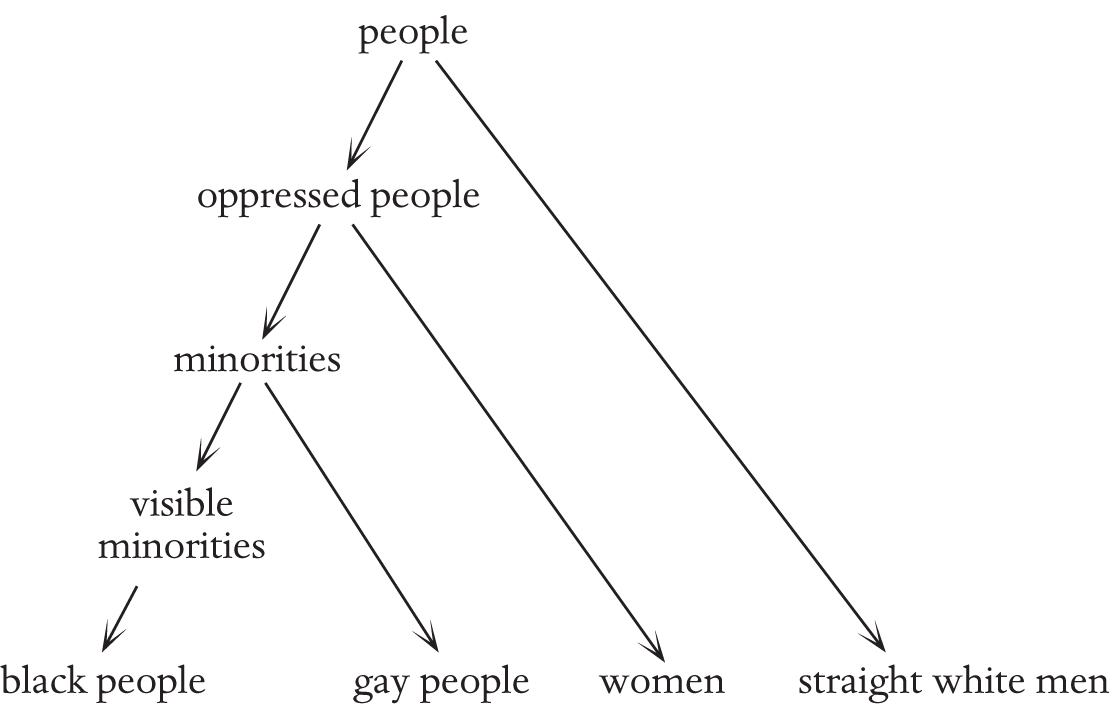
The question is whether the experience of the people along the bottom row is analogous. A nuanced answer is: it depends how far up the levels of abstraction you go. Unfortunately, divisive arguments often arise because everyone picks the level of abstraction that best suits their argument and refuses to consider the possibility that other levels could in any way be valid.
We’ve already discussed many abstractions and analogies–in fact, perhaps the whole book is about how carefully chosen abstractions and analogies can generally shed light on all our arguments in the world. But here are some specific ways in which analogies can help us.
FINDING AXIOMS
In Chapter 11 we talked about finding axioms for our personal belief systems, that is, the fundamental beliefs from which all our beliefs stem. Thinking about analogies can help us understand what our personal axioms are, or what someone else’s personal beliefs are.
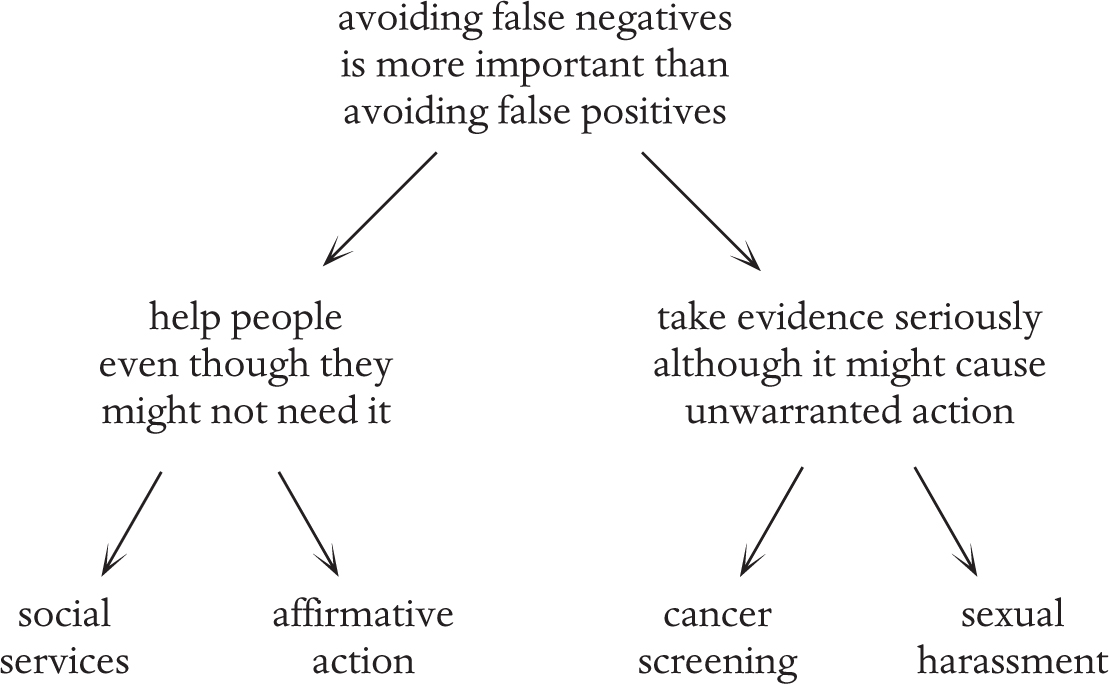
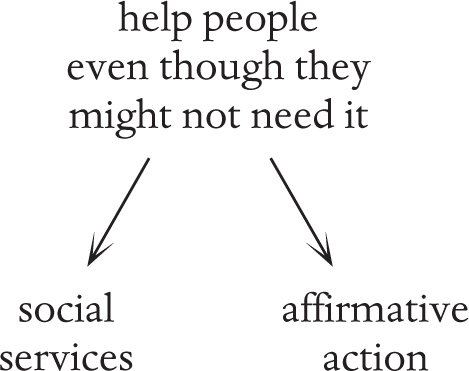
In Chapter 2, I discussed discovering my own axiom that I care more about false negatives than false positives. It came from thinking about believing in social services, and the sense in which that is analogous to the following wide variety of situations.
When arguing about affirmative action on grounds of race, some people are opposed to it on the grounds that there are people of color who come from well-off backgrounds who need help much less than some disadvantaged white people. Or, when arguing about school backgrounds and university entrance, some people argue that there are state schools (say, famous grammar schools in the UK) that give people just as much advantage as some private schools, if not more. Should we help those people? I still believe we should try to help all people of color, and all people from less privileged schools, even if some of them don’t “need” it.
When arguing about screening for cancer, some people are concerned that the tests are not entirely accurate and result in some positive results even when people don’t have cancer. This causes them unnecessary trauma and sometimes unnecessary treatment. This is a serious concern, but I still think this is better than people having cancer that is undiagnosed for too long, making treatment difficult or impossible.
When arguing about sexual harassment, some people are concerned that if we take all accusations seriously we will end up with people (usually men) suffering from the stigma of accusations even if they’re innocent. However, up until now we have a huge problem of too many people getting away with sexual harassment, sexual assault and indeed rape, and thus widespread sexual misconduct being pervasive across society. Being falsely accused of sexual misconduct is indeed a trauma that nobody should have to go through, but I believe we need to be more concerned with the quantity of sexual misconduct going unstopped.
There is something analogous between all these situations although they range across many different aspects of life. The analogy may be implicit but I have found it helpful to isolate it and express it explicitly. At first sight it might appear that only the first two scenarios have something in common:
The second two might appear analogous separately, because of a different principle:
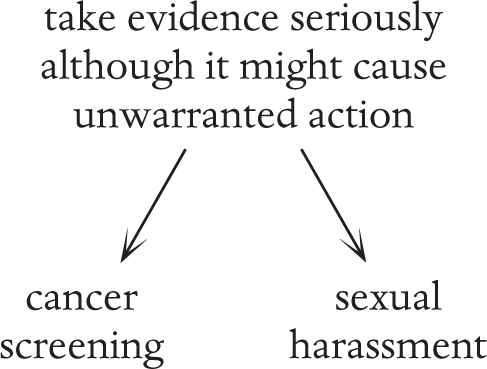
but at a further level of abstraction I can encapsulate all the scenarios in the fact that I seem to believe that false negatives are more important than false positives. Opposite is the diagram of the different levels of abstraction producing different analogies:
Going all the way to the top enables me to clarify my thinking about complex issues, by distilling the thought process behind my beliefs. I can then apply it to more situations, explain it succinctly to others, and hold it in my brain more easily and thus reason with it better.
Indeed after going up to that level of abstraction I realized I could encompass another situation: the idea of compulsory voting in general elections, as in Australia. I used to disagree with this principle, as I think democracy means that everyone should have the right to vote, not the obligation. However, I then read an article explaining that it’s not about forcing people to vote, it’s about forcing the government to make it possible for everyone to vote, to reduce voter suppression and disenfranchisement. I had not thought of that and immediately changed my mind. I now see that it is another example of false positives vs false negatives. Without compulsory voting, you risk false negatives, that is, people who are unable to vote for logistical or more nefarious reasons (such as voter suppression). With compulsory voting you risk false positives, that is, forcing people to vote who don’t want to–but they can still leave their ballot blank or spoil it. It is yet another situation where I care about preventing false negatives the most; I just hadn’t realized that was the issue until someone pointed it out to me. I will later discuss the fact that I think the ability to change your mind in the light of new information is an important sign of rationality.
TESTING PRINCIPLES
Analogies also enable us to test our principles. We may think that we are doing something because of some fundamental principle of ours, but if that is really true we should be able to move to an analogous situation and apply the same principle. If that doesn’t hold it is a sign that our principle wasn’t a true one, or that we picked the wrong level of abstraction. Unfortunately people often do this wilfully to try and convince themselves or others they are working to strong fundamental principles rather than prejudice.
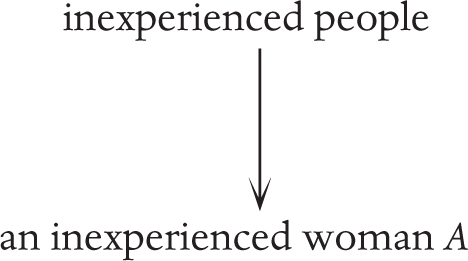
For example, perhaps a woman is not picked for a job and the hiring panel is accused of sexism. They may claim that it was not sexism, it was simply that the woman did not have enough experience. However, if they then hire a man who has even less experience, it shows that this principle was not a true logical principle at work. It is often more tricky than this as the analogous situation might not be real, and we are then pushed to imagine what would happen in an analogous situation. This question arose in relation to Hillary Clinton and Barack Obama in their respective elections. People who didn’t support Clinton were accused of sexism. They fought back and said they didn’t support her because “she was a liar” (for example). And yet, many (perhaps all) male politicians lie about things, and are still supported. Similarly people who didn’t support Obama were accused of racism. Those who were accused fought back and said they didn’t support him because “he was inexperienced”, for example. And yet white men with far less experience might win their support.
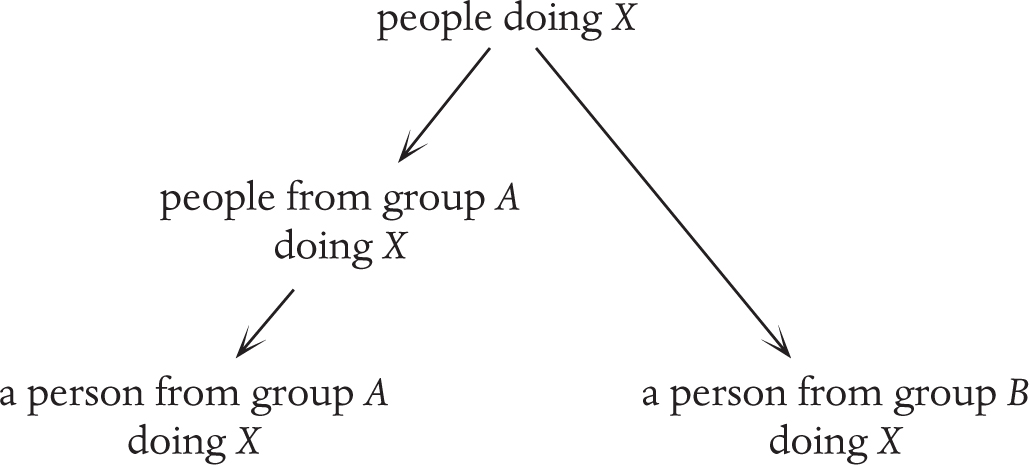
We can clarify this using diagrams. Someone might think they’re applying a principle about inexperienced people in general, regardless of the fact that person A is a woman:
However, if that is really the case we should be able to pivot, using the abstract principle, to an analogous situation with an inexperienced man:
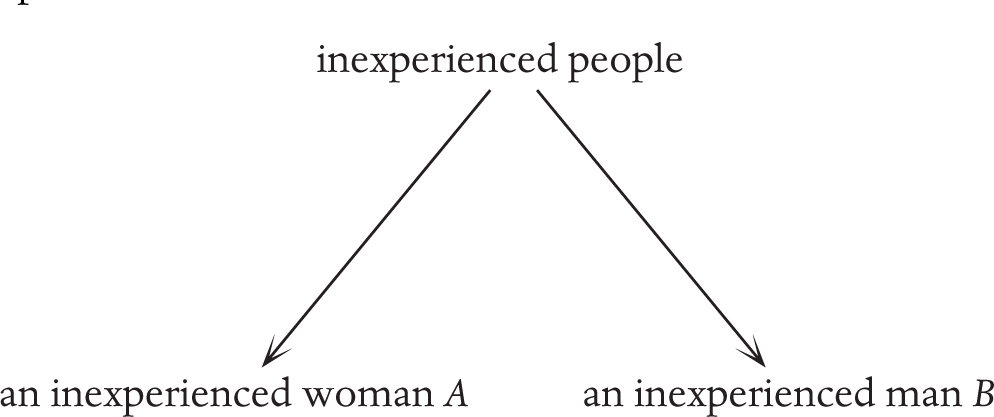
If the inexperienced man gets more credit or more support, then the two are not being treated analogously according to this particular principle, and we should consider whether there is another principle lurking:
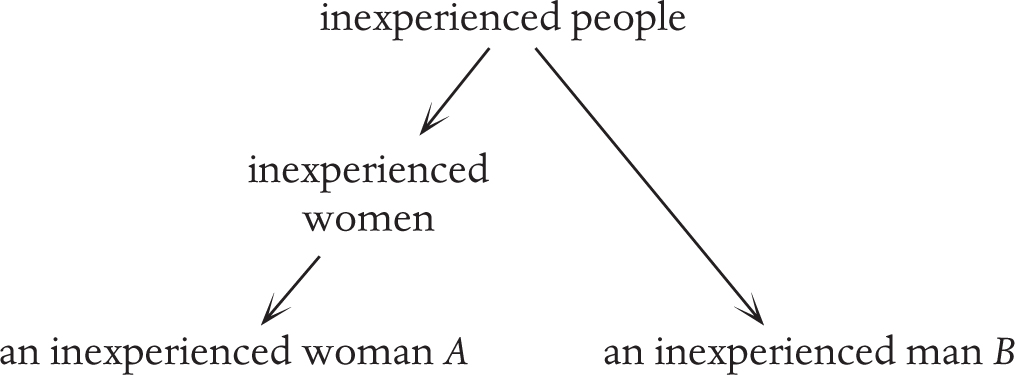
According to the intermediate level of “inexperienced women”, the bottom two items are no longer analogous. The abstract version is this:
If the person from group A is treated differently from the person in group B, it’s a sign that the intermediate principle is at work, not the general one. As discussed in Chapter 3, this applies every time a black person is shot by police in the US, when the same argument repeats about whether it was racism or not. We can ask ourselves whether a white person in the same situation would be treated the same way. If not, then it’s a sign that the intermediate principle (the person was black) is at play, not the general one of just the fact that they were doing X.
We should use these principles to test our own arguments as well as those of other people. In arguments about science vs religion there is an analogy that I think scientists should feel uncomfortable about. Many scientists are disparaging about religion because it consists of people believing things without scientific evidence, because of something written in a book or told to them by a religious leader. However, science is asking people to believe in it in a somewhat similar way: there may well be evidence to back up scientific findings, but non-scientists are not expected to read all the research data and check all the research for themselves. Scientists seem to be asking nonscientists to believe them, or believe what is written in books and journals, in an analogous way to religious leaders asking people to believe what they preach, or what is written in the Bible or another holy book. There may well be something crucially different about those situations, but if so we should admit that at this level of abstraction the two appear somewhat similar, and thus, the argument that you “shouldn’t just believe what someone says” is not a very convincing argument in favor of science. Using our diagrams again, we have a proposed argument:

But if this is really a general principle, it is applicable to science as well:
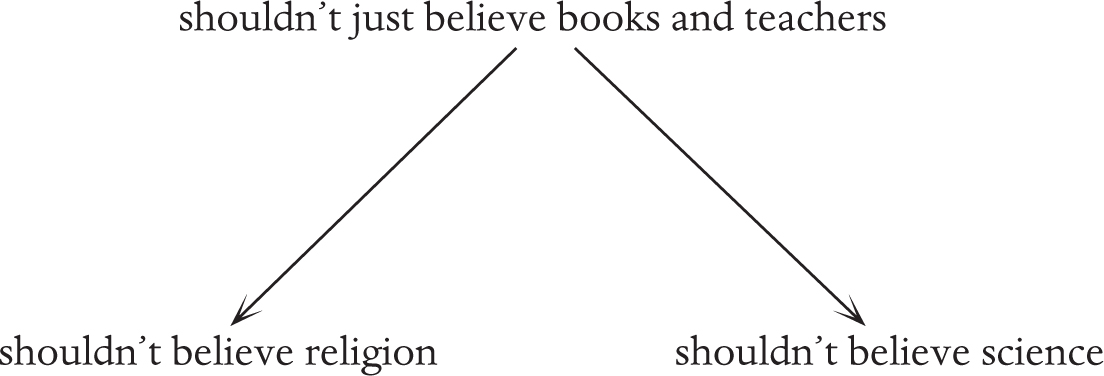
If scientists want to argue that science is more reliable than religion, they need to find a more nuanced intermediate principle that distinguishes the two, and then only go up to the level of that nuanced principle so that science and religion are not analogous:
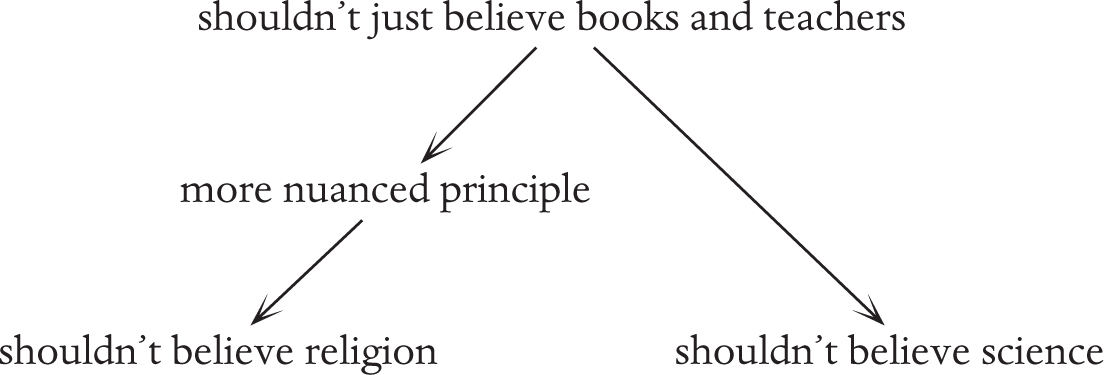
That nuanced principle might be that we shouldn’t just believe books and teachers unless they are backed up by reproducible evidence, but that still leaves the question of how we can tell if the evidence is reproducible. One might say that religious scripture is eyewitness testimony from people we can’t ask, but we might also say that some science is based on eyewitness testimony from people we can’t ask, scientists who ventured into the jungle and observed creatures now extinct, or who landed on the moon and reported what they saw. The situation is more subtle than most arguments about it betray, and I think this is a more productive way to see why so many people believe in religion rather than (as some scientists do) declaring that all those people are stupid.
ENGAGING EMOTIONS
Analogies can help us to engage our emotions, if we can find an analogous situation that resonates more closely with us. This is an important way that we can find an emotional connection to back up a logical argument, if the logic by itself has not convinced us or someone else. This can help us understand other people’s points of view, or help us explain our points of view to other people.
For example, sometimes men get exasperated about sweeping statements made about men, calling them privileged, aggressive, insensitive, or if we say that there is a “pervasive culture of sexual harassment by men against women”. My initial instinct is to argue that we are not actually saying that every man is like that, and also, that when it is the oppressed group (women) calling out the dominant group (men) it is more excusable.
However, I see this with more empathy if I think of an analogous situation in which I am privileged. For example, some people generally regard graduates of Oxford and Cambridge as snobs who were just born to posh families and who are handed success on a plate without having to work hard. I take issue with that, personally, as I think I have worked very hard to achieve what success I have achieved, but I have to be circumspect and realize that I am privileged to have studied at Cambridge and that those who did not have such an opportunity may have reason to feel hard done by in general, by comparison.
The analogy between the situations both helps me understand why men are frustrated, and also helps me understand why people feel animosity towards Oxbridge graduates. This analogy uses the abstract concept of a power relationship, which I will depict with this symbol  as follows:
as follows:
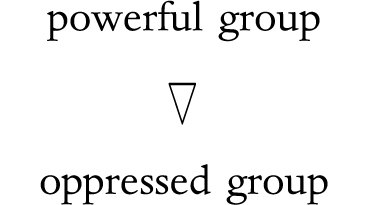
I can then use this to pivot between a situation in which I am in the top group and a situation in which I am in the bottom group (shown in bold in each case), and thus understand both better.

Similarly as an Asian person I can pivot between being in the oppressed group (see over):
and being in a privileged group in the context of non-white people (as Asian people are arguably more privileged than others among non-white people)

I can use this analogy to perform a pivot:
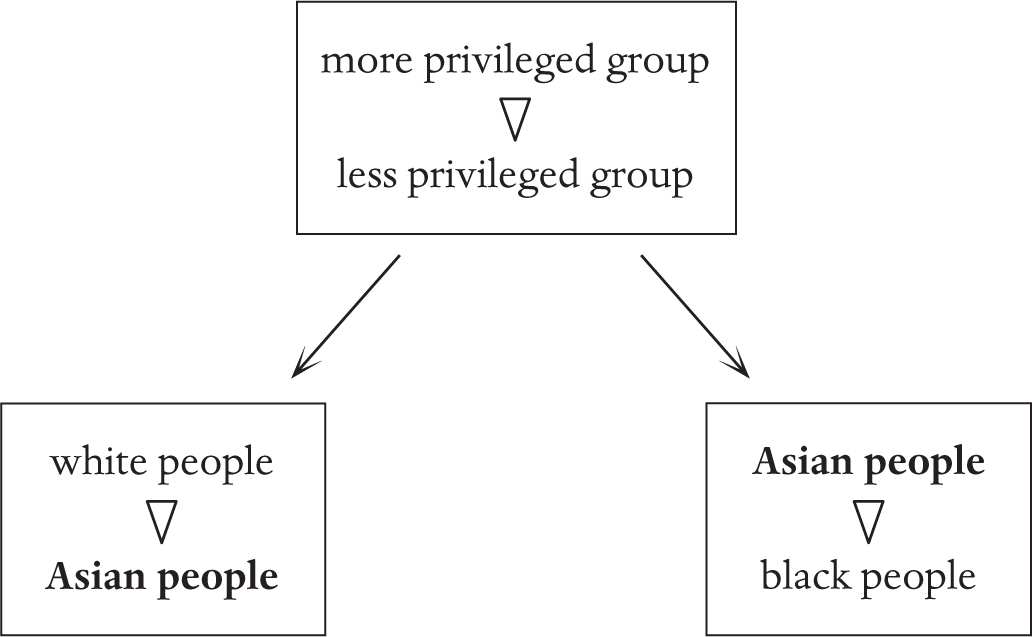
and understand racial discrimination from opposite points of view. To abstract from this further, it comes down to the fact that everyone is less privileged than someone, and more privileged than someone else:
group A: more privileged than you
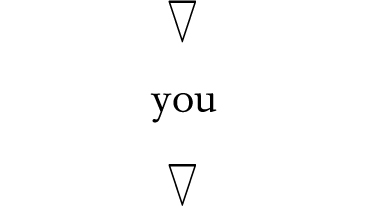
So everyone could perform a pivot to see things from both ways:

As discussed in Chapter 6, sometimes people are liable to see themselves only in the less privileged situation, and see other people in the more privileged. It is offputtingly hypocritical when someone complains about their treatment at the hands of their group A while simultaneously inflicting analogous treatment on group Z. This happens when white women complain about sexism but exclude or neglect women of color, or when white gay men complain about homophobia but exclude gay men of color.
It is understandable to be more aware of people more privileged than you as they are the ones most likely to be a threat to you or prevent your progress, but we need to learn to perform more of the above pivots and become more aware of those less privileged than us without feeling that it contradicts or invalidates whatever lack of privilege we also experience.
WAKING US UP WITH AN EXTREME
Analogies can also engage our emotions not by finding a situation closer to our own lives, but by pushing a principle to an extreme to shock us into seeing that a principle is not so fundamental after all. For example, some people say that universal healthcare is bad because everyone should take responsibility for themselves and not expect someone else to, say, help fund their healthcare.
But in that case does that mean everyone should also take responsibility for protecting themselves and thus we should have no police? No military? No public transport? Should we have no team sports? No families? No basic infrastructure like roads?
Here is the diagram of the supposed principle:

Here is an extreme that is “analogous” according to the supposed principle:

If they do in fact believe in roads, then a more nuanced argument is needed to explain why they oppose universal healthcare.
Sometimes someone will counterargue that pushing it to that extreme makes it different. This may well be true, but then the general principle is not really a general principle–it only works within some limits and then, typically, we can discover that disagreements are about where those limits are, rather than about the principle itself. And there is probably a gray area in which the principle gradually stops working. The question about healthcare should really be one about the extent to which we believe people should look after themselves and the extent to which society and government should look after people. Political disagreements often come down to a fundamental difference in basic axioms, concerning just how much responsibility someone thinks a government should take, compared with individuals. Other times it is about what counts as a necessity and what counts as an optional extra. We might then get this diagram:
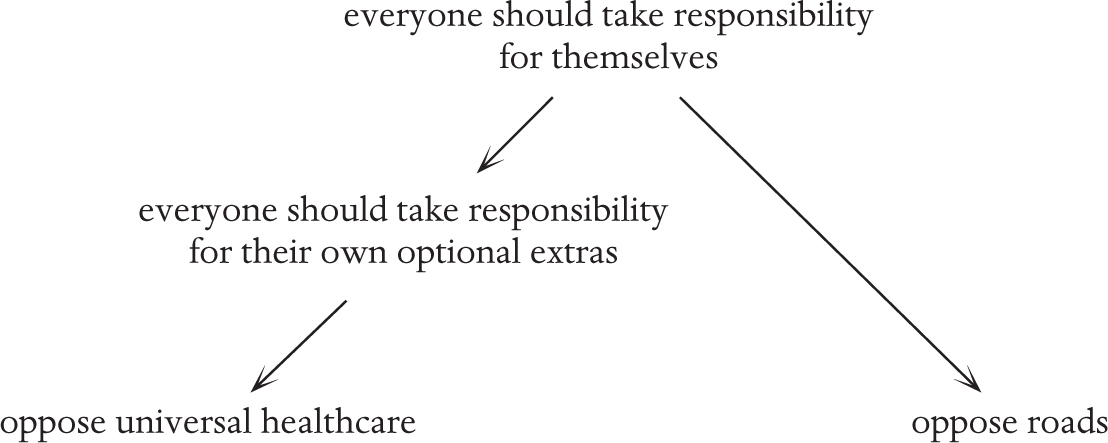
This actually explains the sense in which the healthcare denier thinks healthcare and roads are different. Then we can argue about whether healthcare is an optional extra or not–another gray area. There are arguments within that about which aspects of healthcare count as essential and which count as extra, with contentious issues including cosmetic surgery, gender reassignment surgery, expensive cancer treatment, IVF, and even basic maternity care.
The purpose of pushing something to extremes is to show that many (or even most or all) general principles have limits to their scope, and the difficult part is not in establishing the principle but in establishing the scope. It is a key to understanding disagreements, as the source of the disagreement is often exactly where to draw the line, rather than the principle itself. It’s a way we can use gray areas, to show that the difference between opposing positions might not be black and white, but in shades of gray. If we can show that a difference in positions is quantitative rather than qualitative, we have started bridging the gap between opposing ideas.
PICKING THE RIGHT LEVEL OF ANALOGY
My wise friend Gregory Peebles says analogies are like bridges that can take us anywhere–so we’d better be careful what bridge we choose. Indeed, if we pick a high level of abstraction we’ll encompass practically everything as analogous, which could include things we didn’t want at all. This is how using analogies can sometimes go wrong and cause worse arguments rather than better ones.
Using an analogy in a discussion usually goes like this. You’re trying to argue or explain a statement A. You draw an analogy to a statement B that is more engaging, accessible, or clear cut. Implicitly there is a principle X at work. The claim is:
A is analogous to B.
B is true.
Therefore A is true.
This is much less watertight than using an actual logical equivalence:
A is logically equivalent to B.
B is true.
Therefore A is true.
The reason is that the analogy must go via some implicit principle X. The unspoken part of what is going on is:
A is true because of principle X.
B is also true because of principle X.
B is true.
Therefore A is true.
There is now a logical flaw in the argument, which is that just because B is true it doesn’t mean that principle X is true. In a sense we are trying to move backwards up the right-hand arrow.
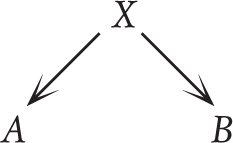
This is made worse by the fact that in normal arguments in life we often don’t state what principle X is at all: we just leave people to infer it from statement B. This is very flawed because there are many possible principles that could play the role of X and they could give us very different results. We gave an example earlier with different types of minorities and whether or not their experiences are analogous. This can become a more concrete argument if it is to do with what should count as acceptable or morally allowed behavior.
For example, supporters of same-sex marriage say that a same-sex relationship is no different from a heterosexual one so same-sex couples should be allowed to get married. They are using this general principle:
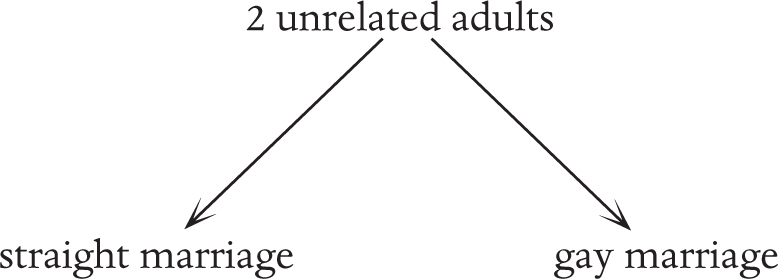
Those opposed sometimes claim that if we allow same-sex marriage, then “the next thing we know we’ll be allowing incest”. They are erroneously (or wilfully) supposing this level of abstraction is at play (see over):

The disagreement in this argument is in the principle X that is being assumed to be the cause of A and B. Those opposed to same-sex marriage want the principle only to go as far as “unrelated man and woman” so that straight marriage is not analogous to gay marriage:
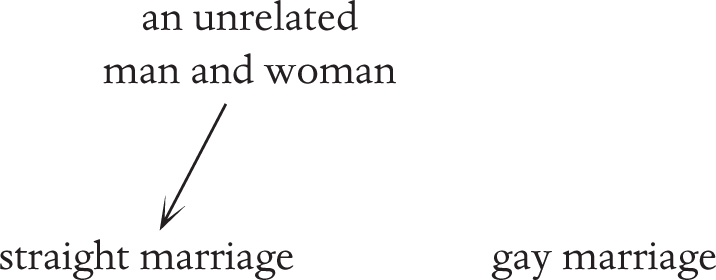
In seeing someone adopt a higher level of abstraction their imagination or fear sends them escalating much further than the other person has really gone:
In fact, there’s a big hierarchy of increasingly wild arguments. Some people think allowing gay marriage will encompass paedophilia or bestiality. If we make explicit the abstract principles behind these different concepts, we get a diagram like the one below. Each arrow represents the process of going from a principle to an instance of the principle:
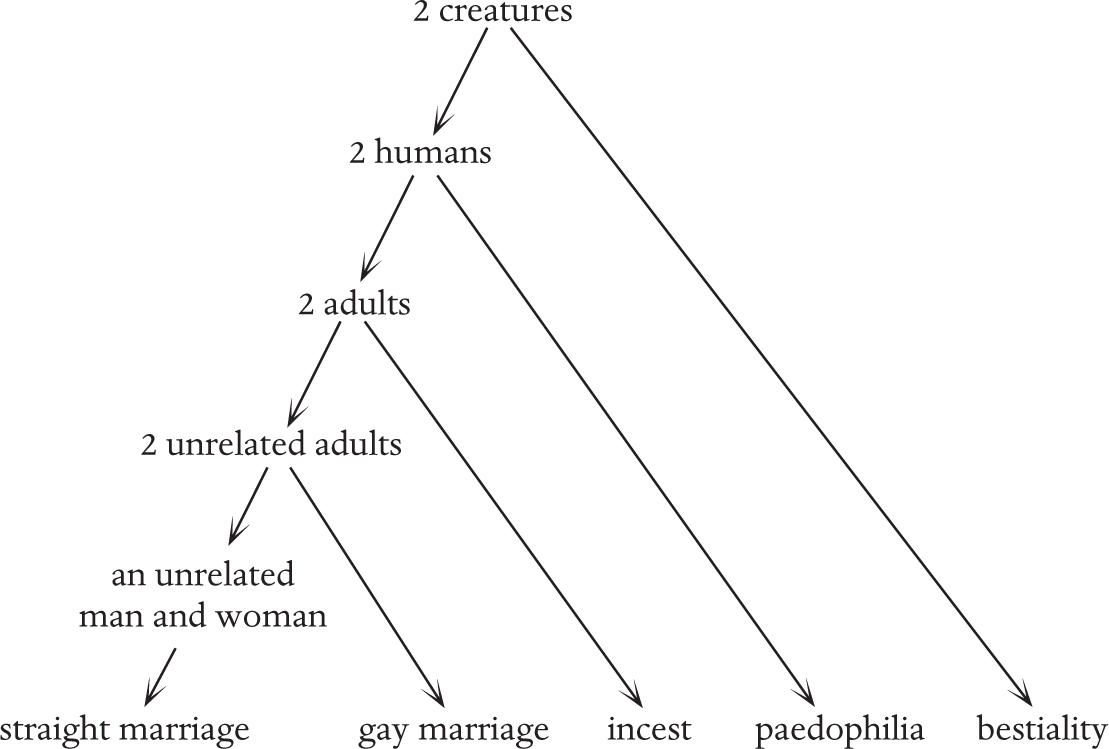
We see that as we get more and more abstract, more and more extreme examples get included. The fact that someone is pro–gay marriage does not mean they have necessarily accepted the principles all the way up to the top.
It is worth remembering that there used to be further levels below “an unrelated man and woman”, when marriage was not allowed between white people and non-white people. A more nuanced argument than “the same” vs “not the same” would be to think about where on that left-hand edge is a justifiable place to stop. Claiming that going up one level necessarily involves going up more than one is an erroneous argument.
IMPLICIT LEVELS
Many of these problems arise because in life, unlike in math, we do not explicitly state what abstract principles we are referring to, leaving it to be inferred from the analogy. But the people who hear the analogy can infer the abstract principle in different ways, and are especially likely to do so if they disagree with us.
In a way the most reasonable abstract principle to infer from an analogy is the minimal one, like the lowest common multiple, or the first meeting place of the arrows in the diagram. In the above example, the higher meeting places were much too high–they weren’t minimal and it was not reasonable to assume that the pro-gay marriage person believed in the generality any further than the lowest meeting point of “2 unrelated adults”.
One of the reasons analogies are ambiguous in normal life is that we rarely make explicit what abstract principle we are invoking. After all, one of the main points of the exercise is to appeal to people intuitively and not have to exert their abstraction abilities. However, everyone then has to guess what principle is being invoked. Whereas in math, making the abstract principle explicit is practically the entire point. We look at analogous situations A and B, and make a precise statement of what principle X we are going to study that causes them. There can therefore be no ambiguity: if A and B are both examples of X, and X is true, then A and B must both be true.
Disagreements over analogies basically take two forms, as in the argument about gay marriage. It starts by someone invoking an analogy of this form:
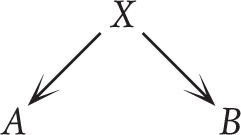
However, typically X is not explicitly stated. Now someone objects, either because they see a more specific principle W at work that is really the reason behind A, so they do not consider A and B to be analogous:
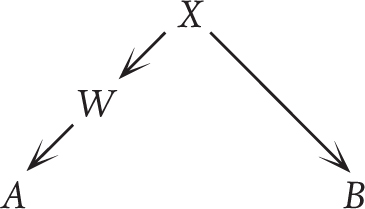
Or, they see a more general principle Y that they think the first person is invoking. This makes some other thing C analogous, and they object to that:
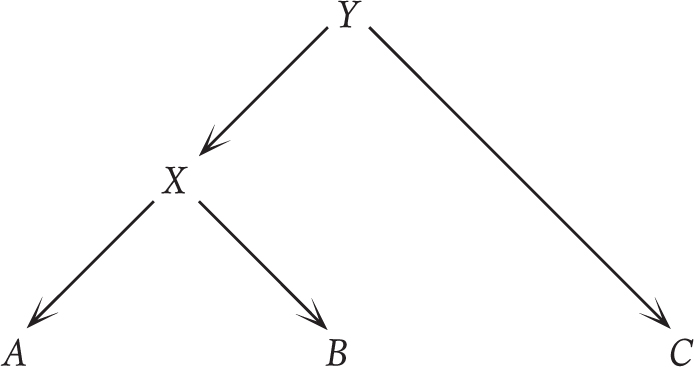
In both cases it would be more helpful to be clearer about what the principles at work really are, to explore the sense in which the different cases are and aren’t analogous, rather than just declaring that something is or is not analogous.
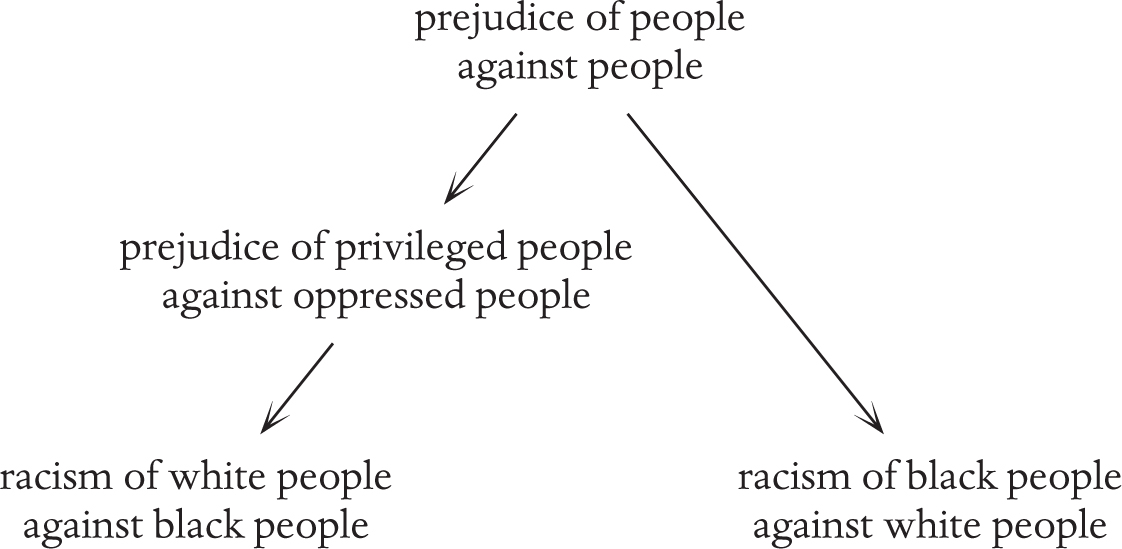
For example, is racism by white people against black people the same as racism by black people against white people? Here is a diagram that shows the sense in which it is and isn’t the same:
The argument is really about which level of principle we should go up to.
There is no right answer to what a good level of abstraction is for understanding a situation. All analogies break down somewhere. That is the whole point of an analogy: it is not the same as the original thing; it is similar in some way but therefore it is also different in some way. Pointing out that an analogy breaks down does not mean the analogy is bad. But if the analogy breaks down in some way that is relevant to what we’re discussing, that could be more important.
I think the best we can do is explore different levels and find out what levels cause analogies to appear and to break. This shows us what abstract principle is at work. In the end the whole aim is to reach greater understanding of in what way situations are equivalent and in what way they are not. This is the subject of the next chapter.
1 One way in which addition and multiplication are not analogous is if we consider inverses. Adding a number can always be inverted (undone) by subtraction. But multiplication by a number can’t always be undone–we can’t undo multiplication by 0, because we “can’t divide by 0”. What that really comes down to is that multiplication by 0 results in 0 wherever we start, so if we try to reverse that process we have no way of knowing where to go back to, whereas with addition we always know.