8
TRUTH AND HUMANS
HOW TRUTH IS ACCESSED, CONVEYED AND RECEIVED
WE HAVE SEEN THE power of logic in producing rigorous unambiguous justifications. Now we are going to address the limits of that power. It is important to acknowledge those limits and not pretend that logic is the ultimate answer to everything: it certainly isn’t.
When you discover your bicycle can’t fly, should you throw it away? No. A bicycle is a wonderful device, as long as you don’t try to use it beyond its limits, or beyond your limits with it. Cycling on the motorway or up Mount Everest might not go very well. Cycling in traffic would be a terrible idea for me but is a great way for better cyclists than me to get around. Sometimes in the rush hour you can even go faster than the cars. It does take more effort, but you might regard that as a good thing if you like being fit, or like burning up your own body fat as fuel rather than petrol.
Logic also has limits, especially in this messy, human, beautiful real world of ours. That doesn’t mean it has failed, and it doesn’t mean we should give up on it in some situations. But it does mean we shouldn’t push it further than its limits. Rather, we should understand those limits and understand what we can do when we are beyond the reaches of pure logic. Understanding how and why logic has limits is the subject of this second part of the book.
I’m going to start by discussing something a little uncomfortable: the extent to which even mathematical proof is, in fact, a social construct, and so logical justifications in life are doomed to be as well. This might seem to fly in the face of everything I’ve said about mathematics being completely rooted in logic, but the situation is more subtle than that.
In Chapter 2 we started discussing the fact that logic has no beginning–it has to start somewhere, and the starting point has to be some truths we assume, without justification. These are called axioms, and they are one aspect of the limits of logic. In Chapter 11 we will discuss how we come up with those axioms, as it must be by some means other than logic.
But another limit to logic is the end–when do we stop justifying things? Mathematical proofs are entirely rooted in logic, and they certainly don’t go against logic. It’s just that strictly logical proofs are impossible to write down for two reasons. One is that the logic they use depends on the rules of logic, and where did those come from? We have to assume some rules of logic even to use logic in the first place. We will come back to this paradox in the next chapter.
The other problem with writing strictly logical proofs, even once we’ve agreed to accept the basic rules of logic, is that they are utterly impractical to write down in full rigor, beyond a certain (rather low) level of complexity. And they would also not be illuminating even if we could do it. So what do we do instead? I think we can look at what mathematicians do to convince each other of their arguments, and extend those ideas to learn about how we can and should justify ourselves to other human beings in the wider world. Logic by itself is not enough. We do something a bit like trial by jury.
TRIAL BY JURY
Logic reaches its limits when it isn’t powerful enough. One way in which that happens is when we simply don’t have enough information or time, and then we have to resort to something other than logic to reach a conclusion. This is the subject of Chapter 10. But another way in which logic isn’t powerful enough is when we need to convince someone else of our argument. Logic turns out to be a good way to verify truth, but this is not the same as convincing others of truth. Verifying truth and conveying truth are two different things.
Mathematicians set out to convince each other that a strictly logical proof is possible. A long proof is difficult to think up in very small steps, and so we usually sketch it out in broad brush strokes first, to see if the overall idea of the argument is likely to work. This isn’t necessary if the argument is very short. If you’re writing a quick email to someone you are very unlikely to plan it first–you just sit down, start writing it, say all the things you needed to say, and then sign off. But if you’re writing a whole book, it would be quite extraordinary to simply start at the beginning and keep writing until you get to the end. In writing this one I started with broad ideas for the three parts, then ideas for chapter topics, and then ideas for the sections within chapters, and then a list of the main points in each section. It’s sort of a fractal approach.
A fractal is a mathematical object that resembles itself at all scales, so that if you zoom in on a small part of it, that small part looks like the whole thing. In order for that to work, there has to be an infinite amount of detail, otherwise at some point you’ll zoom in and there will be nothing more going on. This is a type of symmetry called “self-similarity”.
Here is a picture of a fractal tree. At each level, each branch splits into two. And then at the next level, each branch splits into two again. This keeps going “forever”. If you zoom in on any particular branching point, the part above it will look like a copy of the entire tree.
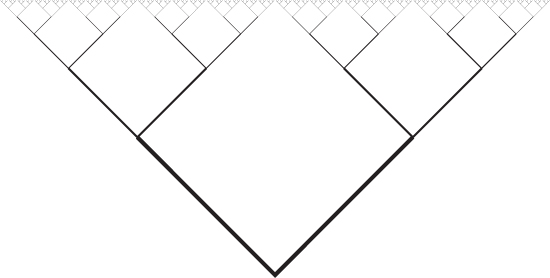
This tree represents how finding a proof works, in my head. The base is the thing you’re trying to show is true, a bit like in our diagrams of causation in Chapter 5. The two branches going into it are the main factors that logically imply it. (Of course, there might be more than two main factors, and we can indeed have a fractal tree with more than two branchings at each point, but it becomes very difficult to draw so I’ll just stick with two here.)
Next, you think about each of those main factors, and think about what are the main factors causing those to be true. So we get the next level of branches:

Note that there is still quite a large gap in between them.
So we think of each of those four factors, and what is causing them to be true, and if we keep going a few more times we get this:
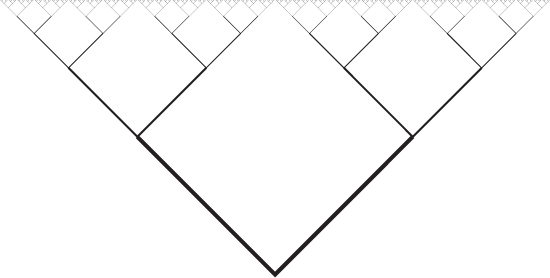
At this point the branches have become close enough together that there aren’t really any gaps, and also, they are so small at the top that they are barely visible. Branching any further would hardly be distinguishable, so even though it’s not a genuinely infinite fractal, we might as well stop from the point of view of showing another human what the fractal looks like.
This is somewhat how proofs work–at some point you just decide to stop filling in gaps any more, because you think that justifying things any further would not help. In arguments in real life, we should keep going until the other person is convinced, or until we realize that our fundamental starting points are so different that we will never be able to convince them unless we can change their fundamental beliefs.
In practice mathematical proof is a bit like trial by jury. In experimental science, peer review means that some scientific peers decide whether they think they could reproduce the experiment you did. The peer scientists don’t actually have to try to reproduce it, they just decide if they are convinced that they could. In mathematics, peer review means that some mathematical peers decide whether they think that the proof could be made entirely logical. They are unlikely to try turning it into a strictly formal logical proof, but they are quite likely to try filling in some of the gaps between branches, to see if they can. Disagreements can arise when a mathematician doesn’t see how to fill a gap in, but in that case they ask the person who wrote the proof, and the onus is then on the original author to fill at least some of the gap in until the skeptical mathematician becomes convinced.
The point about trial by jury is that unless someone confesses to a crime (and even if they do), it is highly unlikely that definitive proof can be found that someone did it. So the burden of proof becomes not logical proof, but a sociological standard–you have to be able to convince a jury of peers, that is, randomly selected people. It is a flawed system but it is a clever one in unideal circumstances. It is flawed because the people on the jury are in fact people, so they are susceptible to emotions and confusion, and so the art of the trial lawyer might focus more on how to sway the emotions of those people more than presenting the logic of the situation.
Peer review is flawed in similar if different ways. The peers who are reviewing the proof are humans so they too can be swayed by emotions, such as their feeling about the author’s reputation. You might think that papers should then be reviewed anonymously, but in practice this is impossible. It’s a bit like marking exams anonymously if your class has only three students and you’ve been working with them closely all year–whether or not they write their names on the exam paper, you will know exactly which student is which. The same is true for research in very high-level mathematics–there aren’t that many people working in each rarefied field, and good researchers are likely to present versions of their work at conferences first, to road test it a bit. In life as well, there are people we decide to trust, and we listen to what they say with a predisposition to believe them, whereas with other people we have a strong urge to be skeptical. This may or may not be justified, and we’ll discuss this more later.
Mathematicians are sometimes reluctant to admit to these sociological and human aspects of math outside of mathematical circles, because they don’t want to cast doubt on the truth of their work. We might not want to admit that our framework of rigorous proofs and peer review is anything less than completely, totally and utterly rock solid. But I believe that overstating the remit and achievement of a system is dangerous because it gives people an opportunity to doubt one part of what you say, and thus doubt all of it. I am dismayed when people dismiss mathematics as irrelevant or boring, but I am also dismayed when people place it on a pedestal of universal power and irreproachability. I would rather we appreciated mathematics for what it is: something in between. Something that helps us sort out our messy human world, but is necessarily still a little bit messy in places. Something powerful and relevant, but with limits.
The interaction between the logical and the human parts of the mathematical process can teach us about those interactions in all human discourse. We’ll discuss this more in Chapter 15 on emotions.
Research papers also deliberately include material that is not strictly logical, to help mathematicians trying to understand the logical proofs. The help comes in the form of analogies, ideas, informal explanations, pictures, background discussion, small test-case examples, and more. None of this is part of the formal proof, but is part of the process of helping mathematicians get their intuition to match the logic of the proof. We know that if the logic is sound but the outcome doesn’t match someone’s intuition, they will still be skeptical. Dealing with skepticism is an important part of the mathematical process: we aim to iron out all possibilities for reasonable skepticism. This is like the idea of “reasonable doubt” in trials.
However, it is worth noting that there is a fine line here between reasonable and unreasonable objections on grounds of intuition. This is a bit like the difference between peer review and audience vote.
REASONABLE OBJECTIONS
Competitions decided by an audience vote are often somewhat derided, and “experts” might poke fun at non-expert audience members who, the experts say, don’t know what they’re talking about. This happens when audiences love crossover singers who sing a famous and heart-rending excerpt from an opera (say, Nessun Dorma), but without “proper opera singing technique”. However, according to the rules of an audience vote, that stirring singer can win fairly and squarely. Unlike peer review it’s just a vote, and nobody has to justify their vote. In the process of peer review, objections need to be justified too, not just stated.
In normal life, outside some specialized situations, there isn’t a clearly defined panel acting as peer review on our logical arguments. In a court of law it’s the jury, and their decisions might be based less in the logic of the arguments and more in their emotional response to witness testimony. Either way, jury is not generally required to justify its decision. For politicians, the “peer review” is the election–it doesn’t matter if they’re right or not, and it doesn’t matter if their arguments are sound or not, it just matters if people vote for them or not. Voters do not have to justify their vote either. You might hope that the votes will depend on the soundness of the politicians’ arguments, but probably not if you’ve ever experienced an election. For corporations, the “peer review” is the money: they just need to persuade people to buy their product, and it doesn’t necessarily matter if their methods are sound or logical (although if they’re outright fraudulent they might get into legal trouble).
Politicians, corporations, and anyone seeking to sway people’s opinions can be seen to be using non-logical methods to influence and manipulate them via their emotions. It is easy to be swept along by this, but if you don’t want to be so easily manipulated it is important to remain skeptical. This doesn’t mean outright denying everything everyone says, but requiring at least some level of justification, and having a framework so that you are prepared to believe someone if they achieve that level, and not if they don’t. This is the difference between reasonable and unreasonable skepticism, and we will come back to it when discussing how to be rational in Chapter 16.
Reasonable skepticism about a mathematical proof can arise in two ways:
1. Someone might think there’s a gap or error in your logic.
2. Your conclusion might contradict someone’s intuition.
The first is a simple logical objection, and is dealt with in a simple logical way, by filling in more of the logic to make clear that the gap can be filled in or that the supposed error isn’t one.
The second type of objection is more slippery. It has happened to me several times in my research and happens all the time in politics. It happens every time someone doesn’t believe some scientific research because it contradicts their own experience or strongly held belief. It’s why some people still believe that vaccinations cause autism although there is no scientific evidence for it. It’s why some people still believe the universe is only a few thousand years old or that the earth is flat or that human life did not originate in Africa or that Barack Obama was not born in Hawaii, despite evidence.
An intuitive objection is much harder to deal with than a logical objection, because you have to change someone’s intuition in order to convince them, and there is not a clearly defined way of doing that. It should be clear that restating the evidence is not going to help, and telling people they are stupid definitely doesn’t help. We will talk more about this in Chapter 15. In theory, this type of objection has no place in rigorous mathematics, because if someone can’t find a fault in your proof then they do not have a valid objection. However, mathematical research is still about convincing humans of things, and so in practice this very human type of objection is a problem, not least because if humans aren’t convinced of your result then they won’t use it, build on it, or value it.
When this sort of objection happens to me I do console myself with the fact that logic contradicting intuition is one of the reasons we use logic at all–if logic always matched intuition it would be somewhat redundant to use it. Crucially, I don’t just dismiss the intuitive objection, but rather, I try to find the root of it so that I can resolve it. Often something seems intuitive from one point of view but counter-intuitive from another, and so resolving the conflict involves persuading someone to acknowledge the other point of view. But it is also important to acknowledge the validity of their point of view. To do this, we have to start by understanding what their point of view is, to see where their intuition is coming from.
Whether we’re writing mathematical papers and talks, or developing arguments to back up our own views, being able to imagine a skeptical person is an important discipline, so that we can pre-empt these situations and perhaps remove people’s reasonable skepticism in advance.
I often imagine a skeptical person arguing with me. We are allowed to imagine that they are as intelligent as us, which is why it is called peer review and not idiot review, but I imagine that they are highly skeptical of everything I’m saying, or that they are actively trying to find a mistake in my proof, so that I can find any possible mistakes myself.
Imagining someone very skeptical arguing with you is a good way to test your logic in life as well. It does require you to be able to think like someone else, but this in itself is an important skill and a crucial aspect of having discussions that build bridges with other people rather than widening divides. It can also genuinely open your eyes to new ways of thinking about something. I find that I understand things much more by teaching them, because I have to think about how to explain them to skeptical students. Even while writing this book I keep having new revelations about the interaction between logic and the world.
If you only imagine talking to people who already agree with you then you never have to test your arguments. Worse, many people only talk to people who agree with them, both in reality and in their imagination. The online version of this is the much-discussed “echo chamber” that we are apparently being kept inside by search engines and social media algorithms. To avoid this, I think it’s important to seek out different viewpoints to try and understand where they are coming from. I sometimes test out my powers by reading what I think is a reasonable article and then trying to guess what the main objections will be in the online comments section. Often the disagreements come from differences in fundamental beliefs, as we’ll discuss in Chapter 11. But sometimes the comments are knee-jerk reactions that may well be true but have nothing much to do with the argument in the article. Whenever there is an article about dogs there is bound to be a thread of comments declaring, apropos of nothing in particular, that “they eat dogs in China”. This brings us to the difference between truth and illumination.
TRUTH VS ILLUMINATION
They may well eat dog meat somewhere in China, but this doesn’t make that statement relevant to an article about, say, a dog-walking app matching busy dog owners with freelance dog walkers in Chicago. Not all truth is relevant or helpful. Things that are true are not necessarily illuminating. This is another sense in which logic reaches its limits: truth can be assessed using logic, but illumination can’t really. Truth and illumination should not be mistaken for each other but the way in which they interact is important. Again we can start looking at this through the lens of mathematical truth, and the surprising fact that equations are all lies.
Did you react to that assertion? I’m afraid I said it largely just to get a reaction. It was like clickbait, although there was nothing to click on. Admittedly the statement “Equations are all lies” is not true, but I said it to make a point. (Indeed, later we’ll discuss the fact that truth and attention grabbing are largely independent.)
Here is an equation that is not a lie: 1 = 1. However, that equation is true but not at all illuminating, so I don’t really want to count it as an equation. So, as we learned in the first part of this book, I should really refine my statement. I could say “Most equations are lies” but that might not be true: there are after all infinitely many true equations of the form x = x because there is one for every number at least:
1 = 1
2 = 2
3 = 3
4 = 4

and so on. What I really mean is that the only equations that aren’t lies are trivial, in which case they’re pointless. So:
What do I really mean by this? As we mentioned right at the start, one of the enduring myths about mathematics is that it is all about numbers and equations. While this is not exactly true, numbers and equations certainly play a central role. So how can I say that all those equations are lies? Admittedly I’m still playing to emotions a bit by using the word “lie”. What I really mean is that all equations are hiding something that is not an equality, so they are not really, logically, totally and utterly an equation. For example let’s think about this equation:
10 + 1 = 1 + 10.
You might remember this as the commutative law for addition, or you might just know instinctively that if you take ten things and one thing you will have the same number of things as if you took one thing first and ten things afterwards. However, this is something that children have to get used to. I have helped children with math at school for years, and when they first learn to add up by “counting on”, the commutativity of addition is not at all obvious. If you ask them ten plus one they will happily put ten in their head, count on one with their fingers, and get to eleven. But if you ask them one plus ten they will put one in their head and arduously count on ten with their fingers. Depending on how adept they are at it, they may or may not arrive at the correct number after all that laborious counting. To them, ten plus one is not the same process as one plus ten.
In fact, in high-level mathematics, 1 + 10 is not defined to be the same thing as 10 + 1. That is why the commutative law for addition is a law and not a definition. Also, that is why the equation above is useful and illuminating. It tells us that although ten plus one is a different process from one plus ten, they will produce the same answer, and so we can pick whichever one is easier for us. Once children work this out, they can use it to help them add up by counting on, knowing that it will always be easier to start with the larger number in their head and count on by the smaller number. So this equation is not a true equation: the left-hand side and the right-hand side are not exactly the same. Its power is in the fact that in one sense (the process) they are different but in another sense (the answer) they are the same.
All equations that we study in mathematics are like this. They show us two things that can be regarded as the same in some way even though they are different in other ways. This is how equations help us. If there was really nothing different about the two sides, the equation would be true but unilluminating. The equations that really have nothing different about the two sides are the ones of the form
x = x
and these ones are never useful.
HOW WE CONVINCE PEOPLE
We have seen that the logical truth is not always illuminating, and in practice it often isn’t logic that actually convinces us of something. This is related to the fact that logic is not usually helpful for thinking up a proof in the first place. When we’re thinking up a proof we often use gut instinct, vague suspicions, hunches, inklings, we look for things that slightly remind us of other things, we wait for flashes of inspiration. We then try to fill in all those things using logic, but only after we’ve used many not-entirely-logical processes to get our first ideas in place. This is perhaps the origin of the myth of math “geniuses”–there is often a mysterious element of inspiration at the start of mathematical work, but let’s not forget the sheer hard work that goes into constructing the logic afterwards.
We don’t entirely use logic to understand logical proofs either. Often in a research paper a logical proof will be accompanied by a description of what “the idea is”, which is something more informal, not rigorous, but invokes ideas and imagery that might help us to understand the logic. It might be a picture, like the fractal tree picture I used to talk about filling in the gaps in a proof. It might be some sort of schematic diagram showing how things fit together, like my diagrams of causation in Chapter 5. It might be an analogy, or a small example. These things are not exactly logical themselves but they help us understand the logic. Often once we’ve understood the idea like this we can fill in the logical steps ourselves with much less help. Feeling why something is true helps us understand why it’s true logically, even in an area as abstract as mathematics. If we don’t get the idea of why it’s true we might follow every step of the logic but still feel disconcerted that we don’t feel like we really understand what is going on.
The experience of knowing something logically but not emotionally happens in proofs, and it happens in grief, when you know intellectually that something terrible has happened but some emotional part of you can’t yet believe or accept it. I think this is the difference between knowing something intellectually and knowing something emotionally. Our intellect and our emotions don’t necessarily take us to different conclusions all the time, it’s just that sometimes there’s a lag between them.
This comes into play when we are learning things. If we engage our emotions or personal experiences while learning something it is quite likely to get embedded more deeply in our consciousness. People say that the best way to learn things is by experience, and I think this is because if we learn something by experience we really feel what it’s like, and then the thing we’ve learned sits somewhere deeper inside us than if we’ve just read about it in books.
This is related to the contentious argument about the role of memorization in learning math. Some people take it entirely for granted that some rote memorization is necessary if you’re going to be good at math. But other people, often professional research mathematicians themselves (including me), are convinced that they have never really memorized anything in math. In fact, one of the main reasons I always loved math was exactly the fact that it didn’t require memorization, only understanding. And yet, many people tell me the whole reason they were put off math was having to memorize things. I sympathize, as I am also put off by having to memorize facts, I just don’t agree that math requires that. Usually when I say this someone will challenge me and say “But surely you learned your times tables.” Somehow times tables always come up as the essential thing that surely nobody could avoid memorizing.
Now, I am certainly not an amazing whizz at arithmetic, not one of those human calculator types who enjoy rapidly multiplying five-digit numbers in their head. However, I am perfectly fine at basic arithmetic and certainly above average compared with the general population, and yet I have never memorized my times tables. I know my times tables by some other, more subtle route that does not involve memorizing. I think this is like the fact that I know my name, but I have not memorized my name. I have internalized it.
Logic, math and science can be difficult to internalize if they appear to be devoid of emotional content. We should be clear that it is only the methods of justification that should be devoid of emotional content, not the methods of communication and understanding. Emotional engagement is a much more powerful way to make logical truth convincing. In fact, it can make anything convincing, logical or otherwise, true or otherwise, as can be seen from the success of so-called internet “memes”.
MEMES
Things can be true without being illuminating, but things can also be illuminating without being true. Internet memes are a rich source of this latter type of situation.
I saw one this week on the subject of the scientific method. The text said this:
On the whole I think the point it’s trying to make is that the interaction between science and politics has become unideal, with politicians overstepping their remit and encroaching on tasks that should be dealt with by scientists. However, I disagree with the summary of “How it should be”, because I think scientists should actually say something more like “We are 99 percent sure there’s a problem” and then scientists should investigate what the solutions are. Politicians should then debate whether or not the solutions should be funded, which should come down to weighing up the dangers involved with not solving the problem, the level of certainty of the scientists, and the cost and likelihood of success in solving the problem. However, this is much less catchy and probably too much text to fit in a meme.
Another example I saw recently said:
Again, I agree with the overall point which is, I believe, to support universal healthcare. However, I’m not sure if the meme is true–arguably some people have been trying to destroy and privatize the National Health Service in the UK.
However, details, nuance and well-structured arguments do not help memes go viral. Rather, catchy phrases and pithy one-liners help memes go viral (together with amusing graphics).
This sometimes makes rational people throw up their arms in despair. But I think we can do something better than that: we can learn from it. Explaining something to someone who doesn’t already understand it always involves making it digestible in some way. With some advanced mathematical or scientific topics that means simplifying it for people who haven’t gone through the years of training necessary to understand it fully. Some people think this compromises the subject so much that it’s not worth it, and so they don’t bother with any attempts at “popularization” of science.
However, I disagree with that. I think that we can find ways of simplifying arguments that still capture their essence, and also attempt to engage emotions and amusement in the way that memes do. When I saw the above meme about science, I wanted to edit it. I wanted to find a trade-off between the full nuanced description, which is probably too long, and something which is still punchy but more accurate, perhaps this:
In summary, we should look at engaging people’s emotions to convince them of logical arguments, rather than using logical argument alone. In the rest of this book we are going to look at various ways in which logic has limits, and how emotions can help us get beyond those limits. We should particularly not pit emotions against logic. They are not opposites, but can work together to make things that are both defensible and believable.