10 WHERE LOGIC CAN’T HELP US

EMERGENCIES, IGNORANCE AND TRUST

CARDIAC SURGEON STEPHEN WESTABY writes in Fragile Lives about the fact that if the heart stops, the brain and nervous system will be damaged in less than five minutes. So he often had five minutes or less to decide how to perform surgery. This might not be long enough to do a full logical analysis–only the simplest of logical arguments could be constructed in that time. And there would be no point doing a longer logical analysis if the patient was brain dead when you came to your logical conclusion.

In this chapter I’ll start talking about situations in which logic can’t entirely help us. We have already seen that logic has to start with something, and that the starting point cannot itself come from logic. But also, we will see that logic also might end somewhere, like a machine running out of fuel. Where logic is concerned, the fuel is usually information. If we don’t have enough information to feed into our logic machine, we won’t be able to get any further. This can be because of lack of resources, or lack of time, or simply because we are dealing with other human beings and we can’t know how they will respond and react.

This doesn’t mean we should directly go against logic, but it does mean there is a limit to how much we can rely on logic within the given constraints. We will have to invoke something not entirely logical to help us beyond that.

Emotions, gut feeling or intuition can help us make a crucial final leap; that will be the subject of the third part of this book. It’s important to understand how far logic gets us and where emotions have to help, rather than pretend that logic can get us all the way there. But we’ll start by thinking about where logic can start to kick in, which is only after some help with finding starting points. We’ll begin with something that’s a very natural part of our everyday lives: language.

LANGUAGE

Language has a certain quantity of more or less logical rules. One source of frustration when learning new languages is that there seem to be huge quantities of rules to remember, and also huge quantities of exceptions. It’s a tricky combination of logic and non-logic. Some languages are more logical than others. I always enjoyed the logical structure of Latin, but there are still certain things you simply have to remember, such as how the verbs conjugate. At least in English there is little to remember on that front, and no genders to remember for nouns, but there’s the awfully confounding question of pronunciation, which is not logical at all. Spanish pronunciation is much more logical (that is, consistent) but still has plenty of exceptions to grammar rules.

We can trace back the etymology of the language we speak now, to see how it came to be the way it is over time, through gradual morphing, borrowing from other languages, and sometimes misunderstanding. But as with logic, at a certain point we get back to a starting point that we can’t explain. Many English words come from old German or Latin, but where did those words come from? An etymology dictionary tells me that “cat” comes from Latin but might ultimately go back to an Afro-Asiatic language. Why, at some point in history, did people decide that “cat” was a good way to refer to a small, sleek furry four-legged creature? Some words are more obvious than others, like “cuckoo” which sounds more or less like the sound the bird makes. “Cat” in Cantonese is a high-pitched “mow” (rhyming with cow), which does sound quite like the sound a cat makes. More than “cat” does, anyway. These are the starting points of language and they must once have come from some sort of free or random association. After, all not all concepts make sounds that we can imitate in our naming of them.

One of the difficult aspects of learning a new language is the sheer quantity of vocabulary you have to learn to get yourself started. A certain amount of memorization is hard to avoid. However, as with learning times tables, I have found that memorization doesn’t help with actually using the language, because when you’re speaking you don’t have time to run through your verb conjugation to pick the right one. You have to be able to access it faster than that, from some non-logical, deep-rooted place in your consciousness. We don’t learn to speak our native language logically, we do it by immersion, by copying, by emotional connections, and by desire. Children first learn to say things they have a strong desire to say, like “Mama”, “Dada”, “cat”, “ball”, “more” or “mine”. They often try to proceed logically with language and have to learn that English, alas, doesn’t work like that. They might start to notice a pattern with how the past tense is formed, but then they’ll say things like “Mummy gived me ice cream”.

In any case, children often learn words by adults saying them repeatedly when pointing to something or giving that thing to them. They hear “milk” repeatedly when being given milk, and eventually make a connection. There is no explanation for why that sound goes with that concept: it’s a starting point.

FLASHES OF INSPIRATION

Starting points in a creative process might be thought of as flashes of inspiration. You might argue about whether they really exist or not, but I have definitely had moments that I would describe like that. Perhaps it would be less melodramatic to call them an “idea”. Where do ideas come from?

Art and music are perhaps the most obvious places where this might happen. I am neither a prolific composer nor a prolific artist, but I have written various pieces of music in my life (some of which I quite like) and made some art of which I’m genuinely proud. In each case, some ideas have just sort of occurred to me. I have no idea where they came from. Some of the music is in the form of songs that I wrote after I read a poem and music just floated into my brain with the poem. That is not logical. There are “logical” ways to develop music, and great composers have many of these techniques at their fingertips. It can be to do with thematic development, harmonic structure, polyphony where different “voices” are introduced with themes wrapping around one another. Some composers, famously Bach and Schoenberg, used symmetry to transform parts of their composition into new but related music. Unfortunately as a composer I am adept at none of these techniques, so I can only wait for music to float into my brain. This probably explains why I am not very prolific, and why all the pieces I write are rather short.

The rules Bach followed when he was writing harmony were very strict, but that still left him plenty of artistic choices to make within the constraints of those rules. Similarly the rules in sport still leave infinitely many possible outcomes within the rules. The structural rules for Shakespeare’s sonnets are quite restrictive but there is still a huge amount of scope for choices and expression while following those rules. The rules narrow down what is allowed, but the rules alone do not determine how the sonnet will go.

Math is another area where flashes of inspiration often start us off. As we mentioned in Chapter 8 on truth and humans, it is an aspect of the non-logical processes involved with thinking up a mathematical proof. Once we have had the ideas we proceed using logic, but that part comes afterwards, when we test and exhibit the robustness of our idea. In the next part of this book we will see that this is a valid way to find logical arguments in life as well–start with our instinctive feeling or opinion about a situation, and then try to uncover the logic inside it. It is certainly much more robust than simply declaring all opinions to be “facts”.

WHERE LOGIC ENDS

So much for where logic begins. What about where logic ends? Even when we have understood or decided on our logical starting points, or axioms, there might be situations where they don’t fully determine what decisions we should make. Imagine choosing from the following menu at a restaurant.

Perhaps you’ve decided that you can’t spend more than $20, and also you don’t like fish. This logically narrows down your options to the chicken and the vegetable tart, but beyond that, logic can’t tell you anything. It would be actively illogical to choose the ostrich at this point, but would it be fully logical to choose the chicken? I would call it logically plausible rather than fully logical.

One of the reasons that making decisions is hard is that in most cases logic narrows down the possibilities for us, but several plausibly logical choices still remain. Life is very complicated and much of it is unknowable, with the result that we often end up in situations that logic can’t completely decide for us, and it’s easy to get stuck in indecision.

To make the decision we can do several things. We can try to add more axioms to the system so that the logical choices are narrowed down to one. For example, we could decide at the last minute that in the absence of any other preference you’d like to try something you’ve never had, and that means carmelized pineapple. Or you might decide to have the cheapest thing that fits your needs, which would be the vegetable tart. Or you might decide to somehow think about which one sounds the most appealing, by seeing which one makes your mouth water when you think about it. Or you could toss a coin.

Sometimes I’m unable to decide until the very last second, when the server has taken everyone else’s order and if I wait any longer I’ll just be causing an obstruction. A time pressure is one of the things that helps or requires us to override logic, because logic is too slow.

EMERGENCIES

In an emergency we have to make a rapid decision one way or another. There will be no point making a more logical one if we are flattened by an oncoming truck before we can finish doing the logical deductions. This doesn’t mean you should do something that goes against logic.

If there is a fire you will, I hope, have an instinctive reaction “I must get out!” If this is an instantaneous instinctive reaction, it probably wasn’t exactly processed logically. But it isn’t illogical either. We could at a stretch express this as a series of logical deductions from

A: There is a fire.

X: I must get out.

It might go like this:

A is true (there is a fire).

A implies X (If there is a fire I must get out)

Therefore X (I must get out) by modus ponens.

Unfortunate stereotypes about mathematicians aside, I can’t really imagine anyone being pedantic enough to run from a fire shouting “Modus Ponens!”

I can, however, imagine explaining to a child why it is important to escape from a fire. Maybe the child doesn’t understand fire yet, so you might have to insert another level of explanation:

Let A = There is a fire.

Let B = I stay here.

Let C = I burn.

Then we have:

A is true.

A and B implies C.

C implies bad.

Therefore I must make sure B is false, i.e. I must get out.

Expressing that in logical terms is a bit over the top but it does show in what way escaping a fire is logical deep down, even if you don’t go through those logical steps each time to come to the conclusion, because you have internalized them.

On the other hand I think we can all agree that this would not be a logical deduction:

There is a fire.

I will stay here.

Sometimes something starts logical and then by repetition we embed it somewhere deeper in our consciousness so that we can access it more quickly than by logical thought processes. (This is a bit like embedding foreign language verbs into our consciousness by using them, rather than just learning to conjugate them using the rules.) I would say that the conclusion is logical even though we haven’t accessed it by entirely logical means.

There seems to be a process by which something logical gets embedded so deeply in our feelings that we then access it by feelings rather than by logic, but if we really needed to explain the logic of it we should be able to turn it back into a logical explanation. Accessing things by feelings is often faster than accessing them by logic, which is why I think one way to become powerfully logical is to convert logic into feelings, just like when you can find your way around a city just by feelings or instinct, without necessarily being able to draw a map or give someone else directions.

INSUFFICIENT INFORMATION

With the menu and with emergencies, logic can run out because there is not enough information around. With menus I often decide I’d like to eat the dish with the least calories, but I can only do that logically if the information is available. Otherwise I have to guess the information and then apply my logic.

In emergencies there might be insufficient time to make all the necessary logical deductions or to gather all the necessary information. This can happen in an emergency but it can also happen in sport, where the trajectory of a ball is in principle entirely governed by physics, but we can’t take all the necessary measurements in time to do the calculation before needing to hit the ball. It can also be because of lack of resources or physical feasibility. Chess is in principle a very logical game but it is massively complicated by the sheer number of different possible combinations of moves. As a result it is physically impossible to work through all the logical possibilities.

The weather forecast is also, in principle, entirely governed by some laws of physics. But we simply can’t gather all of that data. Also there might be so much data and so many tiny variables interacting that the system has in some places become “chaotic”. This is a mathematical term that means a system is entirely determined by all the data in theory, but in practice it is so sensitive to tiny fluctuations that in terms of forecasts it might as well be random, as we will never be able to collect data accurately enough to avoid those fluctuations. We should not blame the weather forecasters too much when the forecast is wrong, as the system is somewhat beyond the reaches of logic in practice.

Another example where we are hindered by complexity and insufficient data is in economics. Economic theories can be hampered by the fact that we don’t exactly know how humans are going to respond to certain situations. For example, some people say with certainty that raising the highest level of income tax will not bring in any more income, because the wealthiest people will simply leave the country. This might be true, but we can’t know for sure what people would actually do in a hypothetical situation. Anyone who claims to know has, at best, unreasonable certainty about their guesses.

It is possible that we could understand the world entirely logically in principle, but that is never going to happen in practice because we will almost certainly never have enough information. Any consequences involving human reactions to things are almost certain to be guesses about human behavior, rather than logical conclusions.

This is one of the reasons that voting is so complicated in a “first-past-the-post” voting system. This is where the person with the most votes wins, and no second and third choices are taken into account, as in general elections in the UK and presidential elections in the US.¹ If your main aim is to prevent a certain person being elected, you have to guess how everyone else is going to vote, in order to know who is the most likely candidate to beat the one you really object to. The trouble is that if many other people are also trying to guess, the situation becomes rather confused. Deciding in advance who to vote for as a group, in order to mount a robust opposition to a particular candidate, is also tricky. How do you know everyone will act as agreed? Issues of trust cannot be settled by logic alone.

TRUST AND THE PRISONER’S DILEMMA

As we can’t have full information about how another human being is going to act, we often have to guess. This is often a question of trust. Do we guess thinking the best of someone or the worst?

You can decide based on past experience, or evidence of their past behavior, but at some level trusting someone else is a leap of faith. Someone who has appeared trustworthy before can always fail later. Sometimes you just have to decide instinctively whether you trust someone or not.

The prisoner’s dilemma is a conundrum that examines issues of logic and trust. We imagine two prisoners who have been arrested for committing a crime together, but are locked up separately so that they can be manipulated, and can’t confer with each other.

Let’s call them Alex and Sam again. The prosecutor offers them each a plea bargain. The prosecutor admits that they don’t have enough evidence to convict them of the main charge, so in the absence of more evidence they can only convict them of a lesser charge and they’ll get a year each. However, if Alex testifies against Sam, they can convict Sam of the worse charge and Sam will get ten years, and in return Alex will be let off. If Sam testifies against Alex, then Alex will get ten years and Sam will be let off. If they both testify against each other then they’ll each get five years. If one of them testifies and the other doesn’t, they can’t suddenly change their mind and decide to take the plea bargain after all.

This is a bit confusing so here is a grid showing the possible actions and resulting outcomes. Sam’s outcomes are in the bottom left half of each square and Alex’s outcomes in the top right:

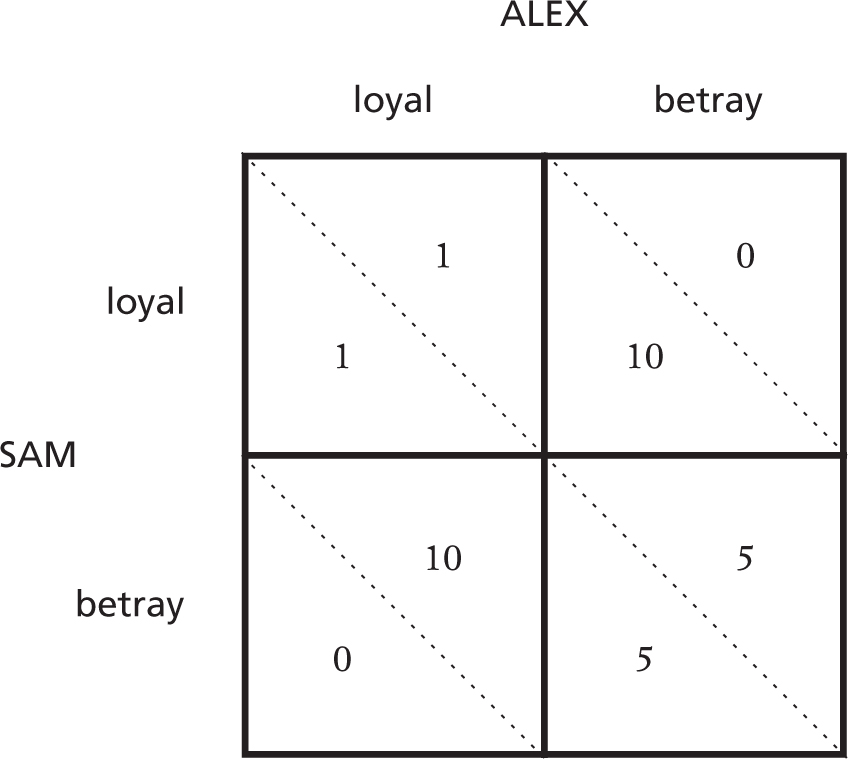
Now, if they both stay loyal they’ll both just get one year. But imagine you’re Alex thinking about that possibility. If you stay quiet you have to trust that Sam will also stay quiet. What if Sam actually lands you in it and goes free? Then it would be safer for you to testify as well, to protect against that possibility. Meanwhile Sam is thinking the same thing: it is safer to testify, in case Alex can’t be trusted to stay quiet. So they both testify, and they both get five years. Whereas if they had both stayed quiet, they would both have got one year. But that option requires trust. You have to trust that the other person is perfectly logical, and also that they trust that you are perfectly logical, and that you trust that they are perfectly logical, and so on. No wonder it’s a bit much to expect of real humans.

It can sometimes help clarify our thinking if we consider more extreme versions of the same basic situation. Imagine that some evil opponent is asking a group of people to betray the group. If you denounce the group you will be rewarded $1000 and everyone else will be fined $1000. If someone else denounces the group you will be fined $1000, but if you also denounced the group this just means your reward will be cancelled out to 0. But if nobody denounces anyone at all, everyone will get a reward of $500.

Here the grid for your rewards looks like this:

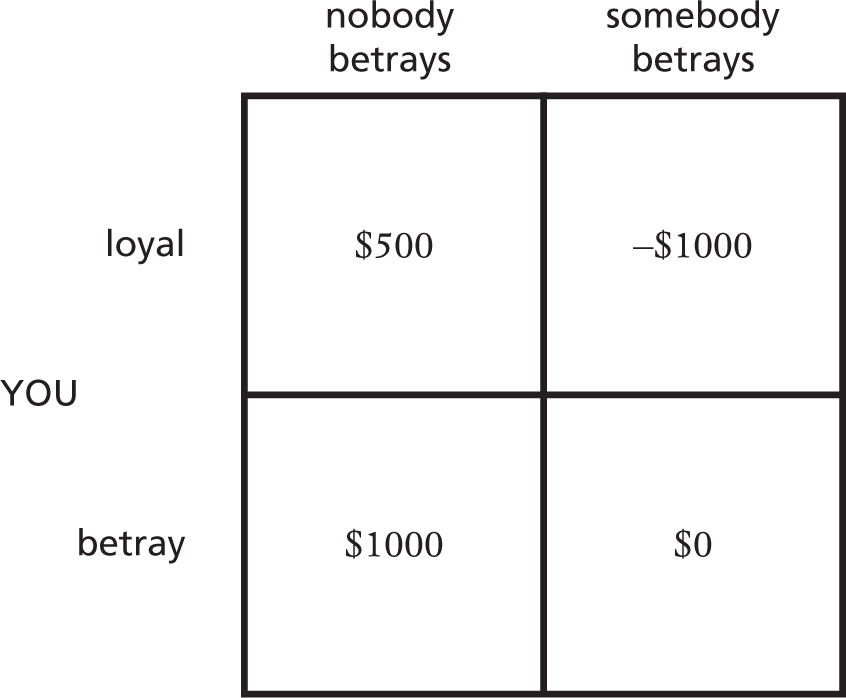
What would you do? If the only other person involved is your best friend then hopefully you know and trust each other enough to know that you won’t denounce each other and you’ll go home with $500 each. However, imagine doing this with a group of 100 strangers. How likely do you think it is that nobody will denounce the group? I would imagine it rather unlikely, and so I am rather likely to do some denouncing myself, in order not to be out of pocket.

In fact, the logic of game theory says that betrayal is logically the best strategy in a precise sense. This is gauged by examining what the possible outcomes are if you betray. We don’t know in advance what the other person (or people) will do, so we have to consider each possibility and ask whether it would be better to betray or stay quiet. Looking at the table above, we consider each column in turn and see which of our two possible actions produced the better outcome. We see that in both cases betraying produces a better outcome for us. In the case where nobody betrays, we do better by betraying and getting $1000. In the case where somebody betrays, we do better by betraying and getting $0 rather than a fine.

This shows us that in all scenarios for other people’s behavior, you get a better outcome if you betray. In game theory this is called a dominant strategy and the logic says that this is the strategy that you should take for the best outcome in either scenario. And yet everyone gets a better outcome if everyone can somehow collaborate and do the opposite of the dominant strategy.

Another example where trust and collaboration come into play with rather variable results is the question of climate change. The idea with climate agreements is that all countries cooperate. There is some cost involved with cooperating, but the benefit is global. If nobody cooperates then the effect on the world could be drastic. However, if one country defects and refuses to cooperate, then that country benefits the most–not only do they not incur the costs of cooperating on emissions, but they reap the global benefits of the fact that the entire rest of the world is improving the climate situation. Now, according to the logic of the prisoner’s dilemma, we should expect everyone to defect. It is perhaps heartening that this isn’t universally the case.

One difference between this situation and the prisoner’s dilemma, unfortunately, is the extent to which the different parties actually believe the reward exists. In the case of climate change, some people don’t believe there is anything to be gained by cutting emissions, because they don’t believe the huge quantity of evidence pointing to the fact that humans are contributing to dangerous climate change. Even if they do believe in it, they might correctly discern that since all the other countries on earth have announced their intention to cut emissions, it might not make that much difference, on a global scale, if the last country does or not. Thus they can save money by not having to make those changes to infrastructure, but still reap the full reward that comes from everyone else having made those changes. This is related to the “commons dilemma”, in which a common resource can be used in moderation by a group, but if one person acts selfishly and overuses it they can deplete it, causing an eventual detriment to the whole group including themselves. The commons dilemma focuses more on ongoing situations and different timescales of benefit, whereas the prisoner’s dilemma focuses on the curious combination of logic and suspicion causing a system to collapse.

Perhaps the level of trust inside a relationship or a community can be gauged by the extent to which they would be able to cooperate when faced with a prisoner’s dilemma. It is interesting that a community’s trust and cohesion appears to mean that they can go against the logic of game theory. But the larger the group is, the more fragile that trust is. The cohesion and fragility can happen, at least in principle, at the level of personal relationships, families, communities, countries and the world. I think what this is actually saying is that if a community is infused with enough trust to act as a coherent whole rather than as a collection of selfish individuals, then the logic of the situation changes, and becomes one that can benefit everyone rather than everyone suffering as a result of a few selfish individuals. It shows that there is a sense in which behaving illogically can result in better outcomes than behaving logically. There are situations in which trusting logic alone is not enough, and we would benefit as both individuals and as a group if we trusted in more human aspects of thought as well.

In the last part of this book we will examine what rational humans should do when we are beyond the reaches of logic. We have seen that logic cannot explain and decide everything in the world, so we are going to have to do something when it runs out. We should not pretend that those non-logical things are logical, but we should also not assume that those non-logical things are bad.

¹ In US presidential elections first-past-the-post is currently used to appoint electors of the Electoral College in most but not all states.