9
PARADOXES
WHEN LOGIC CAUSES CONTRADICTIONS
I AM AN AVID writer of to do lists. I find it an excellent way to procrastinate in a mildly useful way. Sometimes if I’m feeling particularly tired or stressed I will put some very easy things on my to do list so that I can easily declare that I’ve achieved something. This might be something like “eat breakfast” or “check email”. I went through a phase of putting “get up” on my to do list, so that I could immediately cross that off. It suddenly occurred to me to put “Do something on this list” on my list. Could I then immediately cross that off? I got quite confused wondering about that.
I often get intrigued by looped-up thoughts like this. For example, I really want to go round telling everyone not to give unsolicited advice, but I fear that this would constitute unsolicited advice. Then there’s the fact that I can’t keep ice cream in the house because if there is any, I will immediately eat all of it, and then there won’t be any. A more serious contradiction happened to me when I was filling in a form online for a visa application. It sternly told me that I had to fill in my full name and it had to match my name in my passport. However, my middle name in my passport has a hyphen, and the online form would not allow me to input a hyphen. “Invalid name: only alphabetic characters are allowed.” So I found myself stuck–I had to fill in my name exactly as it appeared in my passport, but was not allowed to. I am surely not the only person with a hyphenated name ever to have applied for a visa, not to mention those with apostrophes or accents.
I think of these loops and contradictions as paradoxes of life. Paradoxes occur when logic contradicts itself or when logic contradicts intuition. Both cases show us some of the limitations of strictly logical thinking. In the first case we see how we may need to take more care over how we set up our logic, our definitions, or the scope of our thinking. In the second case we see that we shouldn’t necessarily trust our intuition, or that we should take some time to understand quite where that intuition is coming from. The first type illuminates our treatment of logic and the second illuminates our view of the world.
In this chapter we’ll explore some of my favorite mind-bending paradoxes, some of which are famous mathematical paradoxes, and some of which are weird things I’ve noticed about life. Historically, paradoxes have sometimes been so illuminating that they have led to huge developments of entire fields of mathematics. They are a very interesting place to study the limits of logic. They are curious situations where pursuing logic too hard appears to cause contradictions.
THE LIAR PARADOX
It is remarkably easy to get yourself into a logical paradox: just declare “I’m lying!” I have seen logically inclined children do this and then collapse into giggles. They have created a paradox–if they’re telling the truth, then they’re lying. But if they’re lying, they’re telling the truth. This is a classical paradox known as the liar paradox. It also happens if I say “Don’t take my advice.” Should you then take that advice? If you take it, that means you shouldn’t take it. And if you don’t take it, that means you’ve taken it.
We can make a pair of statements into similarly loopy paradoxes like this:
1. The following statement is true.
2. The previous statement is false.
There is also the curious sentence discussed by Douglas Hofstadter in Metamagical Themas:
Cette phrase en français est difficile à traduire en anglais.
which can be translated literally as
This sentence in French is difficult to translate into English.
but it no longer makes sense.
At this point I should apologize to the French translator of this book, if there is one. Except of course, that sentence has just made it worse because it is somewhat difficult to translate into French.
CARROLL’S PARADOX
Lewis Carroll is probably best known for being the author of Alice’s Adventures in Wonderland but he was in fact a mathematician called Charles Lutwidge Dodgson who worked at the University of Oxford. He wrote about a logical paradox in an article entitled “What the Tortoise Said to Achilles” for the philsophical journal Mind. The article is written in the form of a dialogue, in which a tortoise argues Achilles into a corner, or rather, an infinite abyss. His use of the tortoise and Achilles characters is a nod to Zeno’s paradoxes, which we’ll look at shortly.
In Carroll’s paradox, he explores how logical arguments are built up by logical implications. We discussed in the previous chapter the fact that logic reaches a limit because in order to use it we have to start by assuming some rules of logic. Carroll’s paradox is about what happens if we don’t do that–we just never get there, endlessly filling in more logical steps and never reaching a conclusion. It’s like trying to draw a genuinely infinite fractal tree, rather than one that just looks filled in enough–you can never finish in a lifetime.
Carroll’s tortoise asks Achilles to compare two sides of a triangle to see if they are the same length. You might pick up a ruler and measure both sides and discover they are both 5 cm and so they’re the same as each other.
This involves the statements:
A: Both sides of the triangle equal the length of 5 cm.
Z: Both sides of the triangle equal each other.
The tortoise asks Achilles if Z follows from A, and Achilles says yes of course. Perhaps you agree. But the tortoise says this is only true if we know that A implies Z. So we have another statement mediating between them:
A: Both sides of the triangle equal the length of 5cm.
B: A implies Z.
Z: Both sides of the triangle equal each other.
Now the tortoise asks Achilles if A and B together imply Z. But that is itself a new statement:
A: Both sides of the triangle equal the length of 5 cm.
B: A implies Z.
C: A and B imply Z.
Z: Both sides of the triangle equal each other.
Now the tortoise asks if A, B and C imply Z. But that is a new statement:
A: Both sides of the triangle equal the length of 5 cm.
B: A implies Z.
C: A and B imply Z.
D: A, B and C together imply Z.
Z: Both sides of the triangle equal each other.
The story ends with the tortoise still sitting there torturing Achilles by making him write down all these intermediate statements; it becomes clear that this will go on forever.
So how do we ever deduce anything from anything else? Or have we in fact never correctly deduced anything from anything else? The answer is that we have to use the rule of inference, modus ponens (mentioned in Chapter 4), which we must assume to be valid in order to get anywhere at all. This paradox warns us that there is always a level of meta-logic controlling our logic, and we can only understand this by keeping those levels separate.
This is somewhat like attempts to find all the factors that caused something to happen, as we discussed in Chapter 5:
A: I dropped the glass.
B: A implies Z because the glass was too fragile.
C: A and B imply Z because the floor was too hard.
D: A, B and C together imply Z because gravity intervened.
E: A, B, C, and D together imply Z because I didn’t catch the glass.
F: A, B, C, D and E together imply Z because nobody else caught the glass.
G: A, B, C, D, E and F together imply Z because …

Z: The glass broke.
If we don’t decide enough is enough, we will never be able to conclude anything.
ZENO’S PARADOXES
Lewis Carroll’s use of the tortoise and Achilles is a tribute going a couple of thousand years back to Zeno, who used these characters in a different, more concrete paradox. He imagines a tortoise in a foot race against the extremely fast Achilles, in which the tortoise gets a head start. But then Zeno argues like this: by the time Achilles gets to the place where the tortoise started, the tortoise will have moved forwards a bit, say to point B. By the time Achilles gets to point B, the tortoise will have moved forward a bit, say to point C. By the time Achilles gets to point C, the tortoise will have moved forward a bit, say to point D. This will go on forever and so Achilles will never overtake the tortoise. And yet, in reality, we know that Achilles will definitely win the race.
Zeno was a Greek philosopher who lived in the fifth century BC, and several famous paradoxes are attributed to him. Like many paradoxes over history, these ones are arrived at through thought experiments, with the aim of trying to understand some fundamental aspect of how to study the world. This is different from trying to understand the world.
The three most famous of Zeno’s paradoxes are to do with motion, distances and infinitely small things. The first is the one about the tortoise and Achilles. The next one involves travelling from A to B all by yourself. Zeno argues that first you must cover half the distance, then half the remaining distance, then half the remaining distance, and so on. This will go on forever, so you will never get there. And yet, in reality, we do succeed in travelling to places every day.
The third paradox involves an arrow flying through the air. Zeno argues that if you only saw it for one instant, you would not see it moving. This is true at any instant at all. Therefore how can it be moving? And yet we do know that things move although, indeed, at any given instant nothing can be seen to be moving. This is why photos are stationary images, unlike videos.
Paradoxes fall broadly into two types. The first is veridical paradoxes, in which there is nothing wrong with the logic, but the logic pushes us into a situation that is at odds with our view of the world. The second is falsidical paradoxes, where a fault of logic has been hidden in the argument, and that is what causes the strange result.
Zeno’s paradoxes are falsidical paradoxes: the error is in the logic, not in our intuition about the world. The error is very subtle though, and it took mathematicians a couple of thousand years to work out how to correct it. It all comes down to how you interpret “forever”, and how you think about sticking instantaneous moments together to make longer periods of time. In fact, it all comes down to how we deal with the question of sticking together infinitely many infinitesimally small things. If you do it without nuance, or assume it works the same way as adding together finitely many finite things, you produce these strange paradoxes. What this warns us is not that our view of the world is wrong, but that we need to be more careful about both infinitely large and infinitely small things.
Taking care over infinitely small things leads to questions about sliding scales and gray areas, which we mentioned in Chapter 4 and will come back to in more depth in Chapter 12 on gray areas. Taking care over infinitely large things includes questions about when it is valid to add up an infinitely long string of numbers. A popular Numberphile video claimed that adding up all the numbers 1, 2, 3, and so on forever “equals”  They argued using what they call “mathematical hocus pocus” which actually consisted of some leaps of logic that were perhaps intuitively meaningful but logically flawed–they made unfounded assumptions about how infinitely long strings of numbers behave.
They argued using what they call “mathematical hocus pocus” which actually consisted of some leaps of logic that were perhaps intuitively meaningful but logically flawed–they made unfounded assumptions about how infinitely long strings of numbers behave.
I hope you feel that the end result is absurd, not least because all the numbers we’re adding get bigger and bigger to infinity. Indeed this is why the infinite sum
1 + 2 + 3…
cannot be said to have a sensible answer without substantial qualification. There is some very profound mathematics that gives a sense in which this “equation” has a meaning, but it is definitely not by adding up this infinite quantity of numbers.
Unfortunately the video fooled millions of people, partly because of the good reputation of Numberphile videos in general. It is perhaps a case in point about memes being popular and believable even if they contradict both logic and intuition. It is perhaps also an example of a general belief that math is a bit ridiculous, which is very unfortunate. What the “equation” should be is a starting point for thinking about how infinitely large things cause strange situations, as in the next example.
HILBERT’S PARADOX
The paradox of Hilbert’s Hotel is a thought experiment about infinitely large things causing peculiar situations.
David Hilbert was a mathematician who lived almost two thousand years after Zeno, but mathematicians were still (and are still) trying to understand infinity. Hilbert’s thought experiment involves an infinite hotel, with rooms numbered 1, 2, 3, 4, and so on forever. Imagine that the hotel is full, so you also need to imagine an infinite number of people. Neither the infinite hotel nor the infinite people are possible in real life, but this is a thought experiment. Now imagine that a new guest arrives. The hotel is full, so no room is available for the new guest. However, we could move everyone up a room, so that the person in room 1 moves to room 2, the person in room 2 moves to room 3, and so on. Because there are an infinite number of rooms, everyone has a room they can move to, at the slight expense of kicking the occupant out. But after being kicked out, that occupant can in turn move to a new room. All this leaves room 1 empty and the new guest can move in.
The paradox here is not in the logic but in our intuition. In normal life, if a hotel has no empty rooms you can’t just move people around and miraculously make an empty room appear, without getting people to share rooms. The difference is that in normal life all hotels are finite. This is a veridical paradox that challenges our intuition around infinity. It warns us that we can’t just extend our intuition about finite numbers to infinite numbers, because strange things start happening. Those things aren’t wrong, they’re just different.
Hilbert’s Hotel paradox can be extended to thinking about more new guests arriving, and even infinite new guests arriving. It leads to the study of infinity as a new type of number that does not obey the same rules as ordinary numbers.
This might seem rather removed from real life as we do not have infinitely many of anything in real life. Or do we? One way we consider having infinitely many things in life goes back to Zeno’s paradox, and in the fact that any distance can be divided into infinitely many increasingly small distances. This might seem like a technicality, but remarkably this technicality enables us to understand motion and is therefore critical to everything that is automated in our modern world.
But another way we have effectively infinitely many things is by thinking about unlimited supply. Hilbert’s hotel has an unlimited supply of hotel rooms, and another vacant room can always be produced with essentially no incremental cost. This is somewhat like the situation with digital media now, as extra copies of files can be made at will, with no incremental cost. Although we do not actually have infinitely many copies of a file, it makes some sense to model the situation as having an infinite supply, which goes some way to explaining why the value of digital media has plummeted to zero, or very close to it. This is of course related to the issue of piracy, and some people argue that the supply is only infinite because of pirates, and thus that preventing people from stealing digital content will cause the supply to go back to being finite. Another point of view says that copying digital content is not really the same as “stealing”, because you’re not removing the object from someone. Indeed, the theory of infinity developed following Hilbert’s paradox tells us that subtracting one from infinity still leaves infinity. The math can’t tell us what to do about these moral issues, but it can give us clearer terms in which to discuss them.
GÖDEL’S PARADOX
All of these paradoxes are related to, and historically lead up to, Gödel’s incompleteness theorems. Kurt Gödel was a logician who lived from 1906 to 1978. In 1931 he proved a theorem about the limitations of mathematics which proved quite shocking to mathematicians of the time. The theorem basically says that any consistent logical system is doomed to have statements that can neither be proved nor disproved, unless the logical system is rather small and boring. “Consistent” and “logical” have formal meanings here: logical means it has been built up from axioms in a precise way, and consistent means that it does not contain any contradictions, so that if something is true it can’t also be false.
Of course, “small” and “boring” are very informal words, and sound like subjective descriptions. But, for example, any logical system that is merely large and interesting enough to express the arithmetic of the whole numbers is already doomed to have this property of incompleteness. First-order logic, without quantifiers, doesn’t fall into this category. In fact, first-order logic can be proved to be complete, in that everything is provably true or false. Second-order logic cannot.
A bit like Russell’s paradox (see the next section), it comes down to questions of self-reference. As soon as a statement is allowed to reference itself, strange loops can be caused. Sometimes these loops produce beautiful structures like fractals or infinite loops in computer programs. But logical loops can cause us problems, as referenced in Douglas Hofstadter’s book title I Am a Strange Loop.
Gödel’s incompleteness theorem is discussed extensively in Hofstadter’s exquisite earlier book Gödel, Escher, Bach. In it Hofstadter elucidates not only the incompleteness theorem but all sorts of fascinating links between logical structures and abstract structures in the music of Bach and the prints of Escher, both of whose works are deeply mathematical while also being immensely artistically satisfying.
The proof of the incompleteness theorem involves constructing a statement that creates a paradox through self-reference. The ingenuity and shock of it comes from being able to do this entirely formally in a mathematical system, essentially using numbers. It is easy enough to utter a sentence in normal English that is unprovable, such as “I am happy”, but that is just because “happy” is not a logical enough concept to prove or disprove using logic.
Before Gödel’s theorem, many mathematicians believed that, unlike the real world, the mathematical world was a perfectly logical world in which everything was provable. Gödel threw cold water all over that. He basically formally encoded the sentence.
This statement is unprovable.
First of all we can determine that this statement is true: if it were false then this would mean it is provable, but that would make it true and would give a contradiction. However, the fact that it is true means that it is unprovable, because that is what the statement says. (If you’re anything like me, you might get dizzy thinking about that.)
Gödel showed that it is possible to make this statement using the language of arithmetic, thus showing that any mathematical system that includes arithmetic must be incomplete. There certainly are smaller mathematical systems than that which are complete, but they don’t include arithmetic so can hardly claim to be all of mathematics.
Gödel’s paradox is a veridical paradox–there is nothing wrong with the logic, although some mathematicians were so outraged by its conclusion that they refused to believe it. This is an example of the fact that even in the logical world of mathematics if a conclusion feels wrong there are mathematicians who refuse to believe it although they can’t find anything logically wrong with the proof. What the paradox warns us is that we should limit our expectations of what mathematics can do. Mathematicians have by and large recovered from that shock now.
In fact, even before this shock there was an earlier threat to the very foundations of mathematics, coming from Bertrand Russell.
RUSSELL’S PARADOX
When I meet people and say I’m a mathematician I often get slightly strange responses. The usual ones are “Ooh, I’m no good at math” or, more recently, “I wish I understood more about math”. It’s funny how some people immediately boast about how bad they are at math, but other people immediately try to show off how knowledgeable they are. I once met a guy at a wedding who immediately said “Doesn’t Russell’s paradox show that math is a failure?” This was a particularly curious approach because someone who knows enough about math to know this thing called Russell’s paradox would usually know enough to understand why this doesn’t mean math is a failure. But of course he was the kind of guy who wanted to belittle me, probably because he felt inadequate.
Bertrand Russell (1872–1970) was a philosopher and mathematician (among other things). His paradox dates from 1901 and is also related to questions about keeping levels separate. It can be stated in informal terms like this.
Imagine a male barber in a town. The barber shaves all the men in the town who do not shave themselves, and nobody else. Who shaves the barber?
Now, the barber is supposed to shave all the men who do not shave themselves. So if the barber does not shave himself, then the barber is supposed to shave himself, and if he doesn’t shave himself, then he does. This is very tangled up. Let’s consider any man A in the town:
• If person A shaves person A, then the barber doesn’t shave person A.
• If person A does not shave person A, the barber shaves person A.
This results in a problem if person A is the barber, which is allowed because A represented any person in the town. In this case the two statements become:
• If the barber shaves the barber, then the barber doesn’t shave the barber.
• If the barber doesn’t shave the barber, then the barber shaves the barber.
Each of these statements produces a contradiction. This is Russell’s paradox. Formally, the paradox is stated in terms of sets instead. It says: consider the set S of all sets that are not members of themselves. Is this set a member of itself? If it is, then it isn’t. And if it isn’t, then it is. It’s a paradox.
The problem in this situation is not the logic per se but the very statement we started with. With the barber, we simply conclude that no such barber can exist. We have to do the same for the sets as well: no such set S can exist, which is to say that this is not a valid way of defining a set.
Russell’s paradox did not break the entirety of mathematics, contrary to what that guy I met at the wedding tried to claim. Rather, it highlights an important nuance that needs to be taken into account when we’re defining mathematical sets, which is that some descriptions allow sets that will result in a contradiction, so we have to be careful to rule that possibility out. This led to the very careful axiomatization of set theory so that a set is not just “a collection of things” but is “a collection of things that can be defined by a particular list of constructions, and no others”. The technical goal of the axioms is basically to avoid Russell’s paradox. The idea is to say that we have different “levels” of sets, a bit like how we have different “levels” of logic. Russell’s paradox is caused by statements involving sets that loop back on themselves. As long as we have different levels, we can declare that a set of all sets is on a different level, and this prevents us making statements that loop back on themselves.1
This paradox, like many studied by mathematicians, might seem rather technical and abstract. However, it has helped me understand some crucial questions about tolerance in society.
TOLERANCE
I sometimes see people getting very looped up thinking about tolerance and open-mindedness. You might aspire to be a tolerant and open-minded human being, and I would argue that this is a good thing. But does that mean you have to tolerate hateful and intolerant views? Does that mean you have to be open-minded towards closed-minded behavior? I would argue that you do not. I think this is a subtle form of Russell’s paradox, and that we can resolve it by narrowing the scope of our quantifier. We might think that tolerant means “tolerant of all things”, but I think instead we should say something like “tolerant of all things that do not hurt other people” or some other qualification.
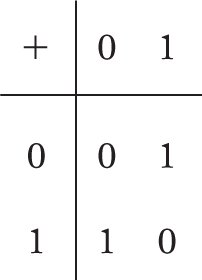
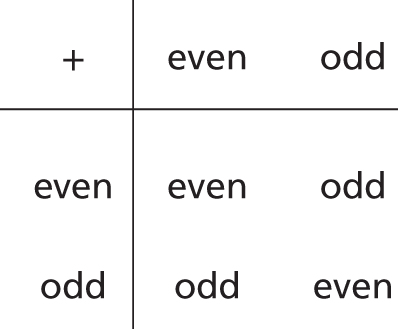
I think that there is a structure here similar to the fact that two negatives make a positive. If I am “not not hungry” then I am hungry. If we add up the “nots” we find that 1 “not” plus another 1 “not” makes zero “nots”.
This is what I call a Battenberg cake structure, as it resembles a Battenberg cake:2

This is a mathematical structure that pops up all over the place. It happens if we think about addition of odd and even numbers:
or multiplication of positive and negative numbers:

I think it also comes up if we think about tolerance and intolerance:
• if you’re tolerant of tolerance then that is tolerance
• if you’re intolerant of tolerance that is intolerance
• if you’re tolerant of intolerance that is intolerance
• if you’re intolerant of intolerance that is tolerance.
This fits in a Battenberg grid like this:

For me this means that I feel no pressure to be tolerant of hateful, prejudiced, bigoted or downright harmful people, and moreover, I feel an imperative to stand up to them and let them know that such behavior is unacceptable.
A further way to resolve this paradox comes from mimicking the way that mathematicians resolve Russell’s paradox using different levels. There, the levels consist of:
1. Collections of objects, carefully defined. These are called sets.
2. Collections of sets; these are sometimes called large sets.
3. Collections of large sets, which we might call super-large sets.
4. Collections of super-large sets, which we might call supersuper-large sets.
5. … and so on.
We could do this with tolerance as well. We could set up levels like this:
2. Ideas about things.
3. Ideas about ideas about things; we might call these meta-ideas.
4. Ideas about meta-ideas, which we might call meta-metaideas.
5. … and so on.
In this case we could decide that we are going to be tolerant of people’s ideas, but not necessarily of their meta-ideas. Their intolerance of other people’s ideas would then count as a meta-idea, and we wouldn’t feel required to tolerate it.
It is important to be aware that separating concepts into levels can also be used against us, for example in the case of shared knowledge. We could set up levels like this:
1. Things.
2. Knowledge about things.
3. Knowledge about knowledge about things; we might call this meta-knowledge.
4. Knowledge about meta-knowledge, which we might call meta-meta-knowledge
5. … and so on.
This arises when allegations of sexual harassment emerge, especially against a well-known figure. Unfortunately it sometimes happens that people in the relevant industry declare that “everyone knew” about this for years. But did everyone know that everyone knew? This would be at the level of meta-knowledge. Sometimes it takes meta-meta-knowledge before victims can unite enough to bring down the perpetrator. This is one of the reasons the aggressors try to prevent communication between victims, with threats and abuses of power, or even a settlement and non-disclosure clause, or other forms of payment. Shared knowledge and meta-knowledge at all levels is an important tool against this sort of manipulation.
It may come as a surprise that thinking about logic and mathematical paradoxes can take us to a discussion of things so apparently distant from mathematics as tolerance and open-mindedness. But to me this is just part of the fact that logical thinking helps us in all aspects of life, even in our personal interactions with illogical humans.
1 In Russell’s paradox, what results is that the supposed “set S of all sets that are not members of themselves” is not an ordinary set, but what we might call a meta-set. Then our two statements:
• If A is a member of the set A, then A is not a member of the set S.
• If A is not a member of set A, then A is a member of the set S.
only apply to normal sets A, not meta-sets. Since S is a meta-set, we now can’t just see what happens if A is S, because S is not a valid example of a set A. This avoids the logical collapse.
2 Readers of my previous books will recognize this image. I do love Battenberg.