4
OPPOSITES AND FALSEHOODS
HOW WE ARGUE AGAINST THINGS
THERE ARE ONLY TWO DEBATES I remember from the debating club at school. One was “This house believes that Margaret Thatcher should go”, which was particularly memorable because she actually resigned the morning of the debate. The other one was “This house believes that strawberries are better than raspberries”, a classic pointless and contentless debating topic. It is easy to think that both sides of this debate have an equally impossible task, because how could you ever argue that one kind of berry is better than another? What does “better” mean? However, the key with this type of debate is that the house only decides whether they will support the motion or not. So the proposers have to argue that strawberries are better than raspberries, but the other side only has to argue that the proposers are wrong. There are many ways they could be wrong. One way would be if, in fact, raspberries are better. But they could also be wrong if strawberries and raspberries are equally good. Or if “better” is impossible to define. Or if the entire idea is idiotic.
Most arguments are not like debates, but still consist of someone claiming that something is true, and the other person saying they’re wrong. If they are attempting to be logical, the first person will try to justify what they’re saying by constructing a logical argument to back it up. The second person should then either try to find a flaw in their logical argument, or try to construct their own logical argument to back up their assertion that the person is wrong.
Logic, mathematics and science are all ways of finding out what is true. But they are also ways of finding out what is not true. Admitting the possibility of being wrong and having ways to detect it is an important part of being a rational human being, I am sure. (But I could be wrong.)
Negation is how we argue against things. Unfortunately in normal life we often do it very badly. Arguments degenerate into insults, intimidation or yelling all too quickly, especially in online comments sections. I optimistically think that this is out of frustration at one’s own failure to get a point across, rather than because everyone enjoys insulting, intimidating or yelling at people. My optimism leads me to do things like write books about logic, because I think most people can do better than that, and I even think that most people might want to. Or failing that, could be persuaded to want to.
One reason that arguing against things in normal life doesn’t go very smoothly is that we don’t always properly understand which things are equivalent to each other and therefore which things are true refutations. Once we understand negation, we can start to build logical power; one of the first steps is to understand many different points of view on the same idea, and how they agree or oppose each other.
NEGATION VS OPPOSITE
Imagine a debate about education systems in which someone claims, as someone periodically does, that the Asian education system is better than the British or American one. There are two ways to oppose this view:
1. Measured and calm: I don’t think the Asian education system is better.
2. Extreme and excited: No way! The British education system is better!
Emotional tone aside, these are logically two different ways of opposing the original view. The second (extreme) way is what we think of as being the “opposite” in normal language. But it is not the logical opposite. In logic, to make the negation we take the original statement and simply declare that it is not true. This is the first (calm) opposition above: the negation of “the Asian education system is better than the British one” is “It is not true that the Asian education system is better than the British one”. Or, to put it in more natural wording, “The Asian education system is not better than the British one.” Just like the question of strawberries and raspberries, there are many ways in which the Asian education system could be “not better”. What does “better” mean, in any case? What are the systems aiming to do? How are we measuring what they achieve? What do we want an education system to achieve? Some people seem to measure everything in terms of math and science achievement, or other standardized test results, whereas other people want to measure in terms of readiness for the workplace. Is that all we want education to do–train people to score highly in standardized tests and be a good employee?
Here are some more examples showing the difference between logical negation and “opposites” in normal language:
• Original statement: I think the EU is fantastic.
Opposite: I think the EU is terrible.
Negation: I do not think the EU is fantastic. This is not the same as thinking it’s terrible. It is possible to be “not fantastic” without being “terrible”. For example, it could be mostly very good but with some flaws. However there is a tricky issue of language here because with a particular tone of delivery it could sound like a wry understated way of saying it’s terrible. However, this is a quirk of language rather than a logical negation.
• Original statement: Margaret Thatcher was the greatest Prime Minister.
Opposite: Margaret Thatcher was the worst Prime Minister.
Negation: Margaret Thatcher was not the greatest Prime Minister. But perhaps she was not the worst either–she could have been the second worst, or the tenth worst, or something.
• Original statement: Climate change is definitely real.
Opposite: Climate change is definitely fake.
Negation: Climate change is not definitely real. Is anything definite about anything? However, that doesn’t mean it’s definitely fake–it’s highly likely to be real because of a huge quantity of evidence pointing towards it, where here “real” means a scientifically sound theory according to the strict framework of science.
• Original statement: Sugar is good for you.
Opposite: Sugar is bad for you.
Negation: Sugar is not good for you. But it’s also not directly bad for you as a small amount every day probably won’t do you any harm, it’s just that in large quantities it’s probably bad for you.
• Original statement: I am male.
Opposite: I am female.
Negation: I am not male. I still might not be female as I could be one of the estimated 1.7 percent of the population born intersex.
In general the negation is a broader statement than the opposite. The opposite is the exact opposite extreme, or, as we might say for emphasis, the “polar opposite”. The polar opposite of the North Pole is the South Pole, but there’s an awful lot of world in between those poles.
• Original statement: Barack Obama is black.
Opposite: Barack Obama is white.
Negation: Barack Obama is not black. In fact, his father was black and his mother white, so he is arguably as much black as he is white, or perhaps neither.
Thinking about opposites instead of negations is an extreme and very black-and-white way of looking at things, figuratively or otherwise. In the case of Barack Obama, most people would feel strange calling him white, and he is generally called black although he is in some sense equally both. So why does it seem to make more sense to call him black than white? Does it in fact make any sense? This is part of a question about gray areas.
GRAY AREAS
People are often not very good at dealing with gray areas. There are many arguments in real life that turn into arguments about opposite extremes. If two people go to a concert together one might enthuse “That was great!” and the other refutes with “How can you think that? I thought it was terrible.” Political decisions usually result in some people saying it’s a great decision and everyone else saying it’s terrible.
People argue about whether a certain leader was good or bad, with people on one side mentioning all the good things they did, and people on the other mentioning all the bad things they did. In reality, most people do some good things and some bad things. In fact, most things are themselves partly good and partly bad. A more logical negation would be if someone was arguing that a leader did some good, and the other side argued that the leader did not do some good, i.e., did no good at all (which is very extreme). Or if one side argued that a leader was utterly evil, and someone else pointed out that they were evil overall but also did some good at some point. Unfortunately, if you don’t condemn every single thing a person did then it can sound to some (less logical) people that you are supporting them. This is the trouble with black and white thinking.
People are not very good at dealing with gray areas, and in fact nor is logic. We’ll come back to this later (in Chapter 12) but for now it’s important to note that the gray area should be included somewhere, otherwise we’re just ignoring part of reality.
In a formal debate situation it is clearly set out where the gray area is: it is included in the opposition. So with the strawberries and raspberries debate, the motion is that strawberries are “definitely” better than raspberries. All the gray areas are in the opposition: the two types of berry could be rougly equal, they could be sometimes better and sometimes worse, and so on.
If we’re thinking about the concept of “good”, then the gray (mediocre) is included in “not good”, so it gets lumped in with “bad”. If we’re thinking about whether or not the EU is terrible, then the gray (so-so) is included with “not terrible”, so it gets lumped in with “fantastic”.
If we’re looking at the (already flawed) notion of race and thinking about white people, then all shades of gray are included with black in “not white”. This idea was enacted in some parts of the US in the twentieth century when anyone with just one drop of “black blood” was considered to be black. At other times the arbitrary cut-off point was picked to be one eighth or one quarter ancestry.
If we only talk about black people and white people then we have either picked an arbitrary cut-off point as above, or actually erased everyone else from our discussion, including mixed-race people, Asians, Native Americans, and anyone else who is neither black nor white.
In logic this is called the Law of the Excluded Middle. It says that “true” and “not true” are the only two options we are going to deal with at the moment. So all types of “not true” have to be included. It also means that if something is not not true then it has to be true. It doesn’t mean we’ve excluded the middle in the sense of throwing it away or ignoring it, it just means we’ve included it with one side or the other so that there is effectively no middle any more.
Here is a picture of a sliding scale from white to black:

Where should we draw the line between white and black? One strictly logical approach is to consider black and not black:

But another way that is just as logical is to consider white and not white, in which case the line is towards the opposite end:

There is much that is unsatisfactory about these approaches as in both cases the line has been pushed to one extreme. When considering racial issues it can be productive to talk about white people and non-white people as the privilege of white people does not seem to extend to mixed-race people unless they can “pass” as white. However, on the other hand, calling everyone who is non-white some sort of “other” can be a symptom of white supremacy and the reluctance of white people to let others into their part of society.
Pushing the lines to the extremes is at least more logically sound than considering only the extremes and ignoring the whole gray area–after all, if we act as if the middle doesn’t exist then what we are saying is simply untrue.

Another less extreme but less logical approach that happens a lot in real life is that we place the line abitrarily in the middle somewhere:

Yet another alternative is to designate an area in the middle and call it something like “gray”:

Of course, this still means we have to pick a place to put the lines between white and gray, and between gray and black. This is to some degree what happens with the terminology of “heterosexual”, “homosexual” and “bisexual”. One extreme consists of people who are sexually attracted exclusively to those of the opposite sex, and the other extreme those who are sexually attracted exclusively to those of the same sex. The middle is then those who are sexually attracted to both. However, where do we draw the lines? If someone is attracted to those of the opposite sex but also to one person of the same sex, is that enough to call them bisexual? What if someone is attracted to those of the same sex but also to one person of the opposite sex–are they in that case not gay? The simple answer, to me, is that everyone is entitled to call themselves what they choose, but, as with considerations of race, there is an undercurrent of power imbalance pulling these considerations in one direction: the scale is not symmetrical. After a long history of oppression, black people and gay people have a lot more at stake in these classification systems, whether it’s the need to assert one’s identity or hide it, the need to protect one’s community or the need to be allowed to integrate into the power-holding community as everyone deserves. While logic can helpfully simplify situations by ignoring irrelevant details, we should be careful not to oversimplify by ignoring important aspects of context.
In Chapter 12 we will come back to this issue and see that although the approach of placing lines somewhere in the middle is less extreme, and at least doesn’t ignore the entire gray area, it causes other contradictions instead. We will discuss more nuanced ways of dealing with gray areas with the aim of simultaneously avoiding extremes, ignorance and contradictions. Where gray areas are concerned this is easier said than done.
Absorbing the gray area into one side or the other is a simplification, but at least not incorrect or contradictory. Whereas denying its existence altogether is where black and white thinking usually goes wrong.
VENN DIAGRAMS
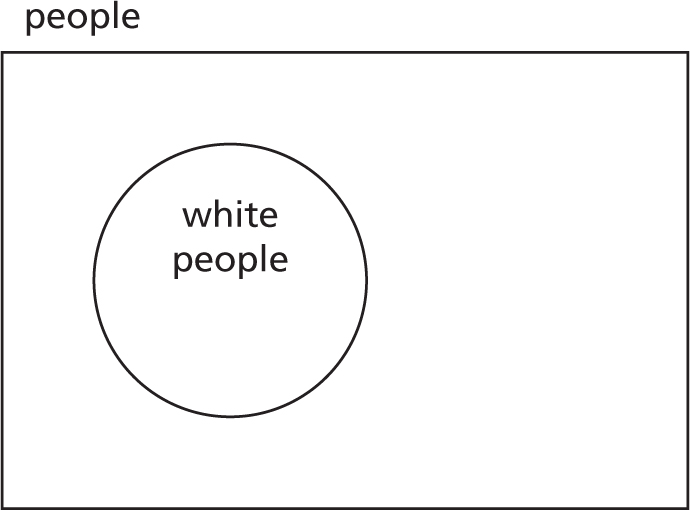
To think about how to consider negation, consider white people and non-white people. We could have a Venn diagram of people, with a region for white people like this:
The outside part is then where we have all the people who are not white, shaded in here:
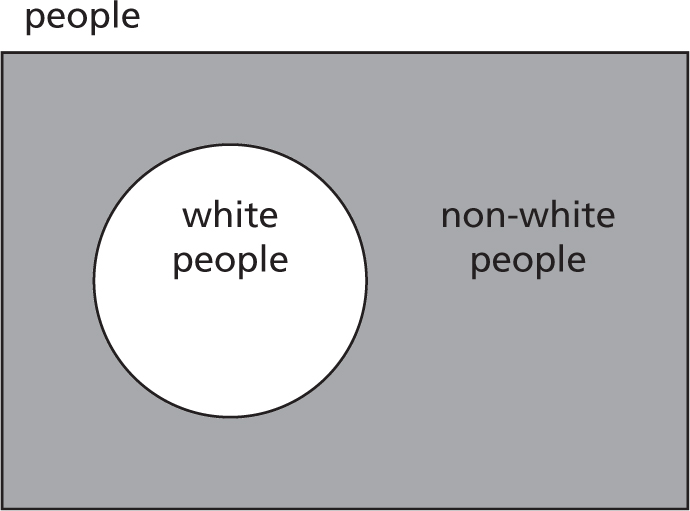
The non-white part then includes black people, Asian people, Latin people, Native American people, and anyone else who isn’t white.
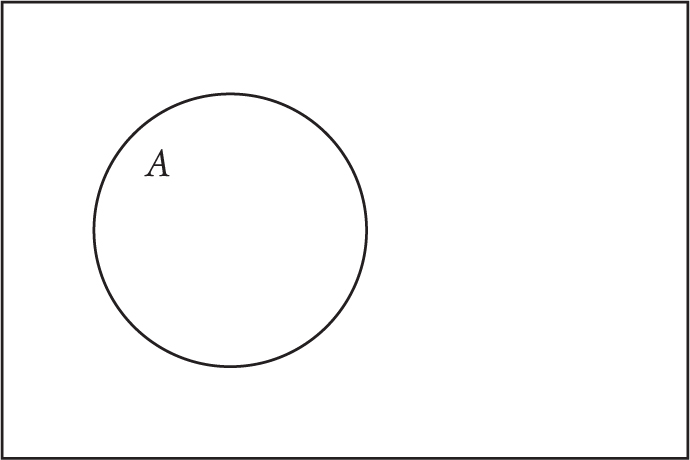
In general we could think about a statement “A is true” and draw a Venn diagram like this:
In that case the region where “A is not true” is the outside of the A circle.

Here we come up against the problem of gray areas again, and the fact that we’re using the law of the excluded middle: the negation takes up all the space outside the circle, and there is nothing in between that space and the circle itself. In the language of sets and Venn diagrams this is called the complement–the part that fits together with A perfectly. If we had a gray area it might look like this:
Now, if the concepts we are thinking about are “white” and “not white”, the dividing circle is in the middle:

Whereas if we are thinking about “black” and “not black” the dividing circle is at the outside, just where the deep black starts.1
We will see Venn diagrams with more sets in the next chapter when we think about how logical statements are connnected.
TRUTH VALUES
Mathematicians might seem like they’re trying to make things more complicated all the time, but really they’re trying to make things simpler so that we can try to understand them better. There’s an important difference between simple and simplistic though, and I think it’s to do with illumination. If you make things simplistic you are probably ignoring crucial details that actually are illuminating. Whereas the key to a good simplification is to keep some pertinent illuminating details and forget everything else–at least for now. Another key is to be aware of what you’re forgetting all the time, rather like deliberately leaving your umbrella at home if the weather forecast is fine, rather than accidentally forgetting it and also forgetting to look at the forecast. If you’re aware of what you’re forgetting then you can also be aware of the limitations of what you’re doing, and the situations you shouldn’t get yourself into.
In a way the law of the excluded middle is a simplification. We will later see that this means there are certain situations we really can’t deal with without modifying our logic. Another way of viewing this law is that we are viewing truth as binary, just “yes” or “no”. Mathematicians push this further and give truth a value: 0 if something is false, and 1 if it is true. You might think mathematicians just love turning things into numbers, but remember: math isn’t just about numbers, it’s about many other things too. However, numbers are so familiar and easy to reason with that if we can turn a situation into some numbers it can be very helpful.
The law of the excluded middle says that there is no truth value in between 0 and 1. You might cry foul at this point and say doesn’t this mean we have thrown away the middle? There are, after all, a lot of decimal numbers between 0 and 1. These might try to encapsulate partial truth. Perhaps if something has truth value 0.5 that means it is half true? There is a form of logic that takes this approach, called “fuzzy logic”, and we’ll come back to it in Chapter 12 when we discuss more ways to deal with gray areas.
Using 0 and 1 as the only possible truth values is like allowing only the answers “Yes” and “No” in court, a favorite tool of lawyers when they’re pressuring someone to say something that casts them in a bad light (at least, this is what fictional lawyers do). In logic, and in court, things are simply true or not true, 1 or 0. This can sound draconian, which is why it’s important to remember that “not true” does include all possible shades of gray.
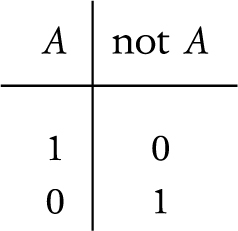
If a statement is true then its negation must be false. Also, if something is false then its negation must be true. We can sum this up in this little truth table. Here A is any statement, and “not A” is its negation:
Truth tables, like Venn diagrams, are another useful way to encapsulate logic. They get a little bit further away from intuition, but sometimes when you move away from intuition two things happen. One is that you are better able to engage your logical brain. The other is that you actually develop new intuition, intuition about logic rather than anything else. If logical intuition sounds like a contradiction then I apologize. (And that’s a promise rather than a logical implication.)
Finally I should note that there is one other possibility for truth values: it is possible that the truth value for something cannot be determined. We’ll come back to this in Chapter 9 on paradoxes. Some paradoxes are caused by a statement that is so self-contradictory that it can’t be given any truth value–true or false–without causing a contradiction. That means it can’t have any truth value at all. It doesn’t mean it’s false, it means that it is unknowable.
Here are some statements whose truth value is currently unknown, but only as a result of the limitations of current human knowledge, not because of internal logical problems:
1. The universe is finite.
2. One day we will be able to cure all cancer.
3. A meteor caused the extinction of the dinosaurs.
NEGATING IMPLICATION
Now that we understand more about negation we can try applying it to a more complicated statement: a statement of implication.
We have seen the implication “If you are white then you have privilege”. We have seen that the converse “If you have privilege then you are white” isn’t true because you could be non-white but have other forms of privilege, for example by being male, rich, straight, cisgendered,2 able-bodied, tall, thin, educated. Since it isn’t true, we should be able to negate the statement.
It is tricky to negate implication. There isn’t a simple way to negate it by just sticking a “not” into the sentence, although it is tempting. We can try to say “If you have privilege then you are not white” which isn’t true. If you have privilege you might be white, but you might not.
We might try to say something like “There are other types of privilege besides white privilege”. This is a good step towards a logical negation, but we haven’t talked about “There are…” and what this means yet. (We will in Chapter 7.)
Until then, really the only logical way to negate “implies” is by saying “does not imply”, as in “Having privilege does not imply that you are white”. Or we can just tack “It is not true that…” onto the beginning of the statement. This is a foolproof way of negating a statement, it just tends to result in an unnatural sounding sentence. “It is not true that if you have privilege then you are white”.
In symbols we just sort of cross out the implication arrow and write
A 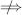 B.
B.
Implications that are not true are often at the root of disagreements.
FAULTY IMPLICATIONS
Here is a faulty argument that some white people use to try and argue that white privilege doesn’t exist:
“Some black people are better off than me, therefore I don’t have white privilege.”
Now, it is true that some black people are better off than you, even if you are white; for example, unless you’re very unusual Barack Obama and Oprah Winfrey are probably better off than you. However, this does not mean you don’t have white privilege.
Here is how that faulty argument tries to proceed, in more detail:
1. Some black people are better off than me even though I am white.
2. If some black people are better off than you then you don’t have white privilege.
3. Therefore I do not have white privilege.
The process of concluding something from a logical implication is called inference. This rule of inference is very fundamental to the use of logic, and has a fancy name: modus ponens, which is Latin for “way of affirming”. It is essentially the only way we can progress from one known truth to another one. (In Chapter 9 we will look at Carroll’s paradox which explores the impossible state we would get into if we were not allowed to use this rule of inference.) Modus ponens says that if we know “A implies B” then we can infer B from A as follows:
1. A is true.
2. A implies B.
3. Therefore B is true.
In the above example the conclusion is “I do not have white privilege.” There are now two ways the conclusion could be false: either (1) is false, which would mean that you are better off than all black people (or you are not white) or (2), the implication itself, is false. For our example some people think (2) is true, but this is a misunderstanding of what white privilege means. It is a straw man fallacy, that is, when an argument is replaced by one that is not the same but is much easier to knock down (a straw man) and is then duly knocked down. (We will come back to straw man arguments in Chapter 14 on equivalence.) White privilege doesn’t mean that every white person is better off than every non-white person; it means that if any given non-white person were in exactly the same circumstances but white, they would be better placed in society and life.
The key is to remember that it is both statements “A” and “A implies B” that together allow us to infer statement B. So if statement B is not true it is either because A isn’t true or because “A implies B” isn’t true. The possibility of the implication being untrue is often overlooked. In the next chapter we will look more closely at how factors combine to produce results, and how some factors are often overlooked so that blame is unfairly focused on one particular person or circumstance.
CONTRAPOSITIVE
I believe that a great deal of logical power comes from flexibility, and this comes from being able to see things from different but equivalent points of view. Understanding how negation interacts with implication gives us a way of doing that. In the above argument, believing that
“If some black people are better off than a white person then that person does not have white privilege.”
is equivalent to believing this:
“If you have white privilege then you are better off than all black people.”
The second statement is logically equivalent to the first. This means that the second one follows from the first, but also the first one follows from the second, so they are logically interchangeable (but they might still give slightly different emphasis to us non-logical humans.) For example, suppose I tell you:
If you travel abroad you must have a passport.
This is logically equivalent to saying:
If you don’t have a passport you can’t travel abroad.
However, they are perhaps emotionally a bit different–the first version is more about what you need to do in order to travel whereas the second is more about what you can’t do without a passport. These are two slightly different points in human terms although they’re logically equivalent.
These pairs of equivalent implications are called “contrapositives”. Formally, the contrapositive is a new statement that you can make, starting from an implication
A  B
B
The contrapositive statement is then
B is false  A is false
A is false
and is logically equivalent to the original statement. This means that whenever the original is true, the contrapositive is true. And whenever the original is false, the contrapositive is false. This is not to be confused with the converse, which is
B  A
A
and is logically independent of the original. It is also not to be confused with what you get if you just negate A and B individually:
A is false  B is false
B is false
which is the contrapositive of the converse, and so equivalent to the converse.
Negating A and B individually is the mistake people are making when they look at the statement
If you are a US citizen then you can legally live in the US. and turn it into
If you are not a US citizen then you can’t legally live in the US.
Finally, the contrapositive is not to be confused with the negation:
A  B
B
which does not fit into the above picture anywhere. If an implication is false you can’t deduce anything from anything else, except that the argument is broken.
EVIDENCE
A logical implication is much more powerful than a piece of evidence. A logical implication means that something is definitely true. A piece of evidence only contributes to the probability that something is true. This is an important difference. Evidence can’t contribute to the logic of something being true; only a logical justification can do that.
For example, suppose you think all Chinese people are good at math. Perhaps every time you see a Chinese-looking math person (like me) you think this adds to your theory. You are thinking of the implication
Being of Chinese origin implies being good at math.
Every time you meet a Chinese-looking mathematician you store this up as evidence. One issue is that you might be succumbing to confirmation bias, where you only notice evidence that backs up your theory. However, another issue is simply that evidence doesn’t contribute to logic. With our new power in dealing with contrapositive statements, we can perhaps see this more clearly. The contrapositive of the statement is
Working by the idea that “evidence contributes to logic”, this means that every time you see a non-Chinese non-mathematician this should also add to your theory. For example, every time you see a Canadian goose, or a French macaron, this should add to your theory that all Chinese people are good at math. You might object that we’re only thinking about people here, not animals or food. But that still means that if you meet an American singer or a British football player, that should add to your theory that all Chinese people are good at math.
Intuitively this might seem much more bizarre than adding to your theory every time you meet a Chinese mathematician, but logically speaking both cases make equally little sense.
NEGATION IN SCIENCE
While we’re thinking about evidence, it is just as well to think about what evidence does do for us in scientific experiments, and how it interacts with negation. After all science, like mathematics and all fields, has a framework for showing that things are not true as well as for showing that they are true.
Scientific experiments usually proceed by starting with a hypothesis, that is, a statement that a scientist thinks might be true, but whose truth value is currently unknown. In school science experiments it usually has to be something rather simple that scientists have in reality known for a very long time. This always made me feel that science experiments at school were contrived. Because of my lack of motivation for doing the experiments, I was not very good at them. I wish they had been presented more as a way of exploring the scientific method and learning how to verify things that have been told to us as facts.
One experiment that I remember actually going well was the one about Hooke’s law. The hypothesis is: the extension of a spring is proportional to the load that is hanging from it.
Scientists (or school pupils) will then look for evidence to support the hypothesis. In this case, an experiment would involve selecting various different springs and measuring them with various different loads hanging from them, and then analysing the data. The field of statistics deals with what sort of data you need to back up various types of hypotheses. If you find you have the right kind of data then you make a logical conclusion of this form:
There is sufficient evidence to suggest that this hypothesis is true, to within 95 percent certainty (for example).
If you find you do not have the right data then your logical conclusion should be the negation of this statement, which is:
There is not sufficient evidence to suggest that this hypothesis is true, to within 95 percent certainty.
It is important to note that this is logically different from concluding that the hypothesis is false, which would be the opposite rather than the negation. If you have insufficient evidence to support a hypothesis, it means that the truth value is still unknown. Maybe you need more data. Maybe you need a better experiment. In the example above what we really need is a refined hypothesis:
The extension of a spring is proportional to the load hanging from it, within a maximum load limit.
This is Hooke’s law of springs. Once the truth of a hypothesis has been scientifically established it typically gets “promoted” to the status of a law. A scientific law is something that has been determined to be probably true, to within levels of certainty accepted by science. This is different from logical truth. However, logical truth interacts with scientific truth: we proceed logically from the scientific law by saying if the law is true then various things can be deduced from it logically.
Sometimes people point to the percentage certainty involved with scientific experiments and declare that this shows it’s “only a theory” and therefore we’re entitled not to believe it. This is misunderstanding the scientific method, statistics and probability. If something is found to be true with 50 percent certainty then indeed the jury is out and it could go either way, and we’d probably be wise not to act based on either its truth or its falsehood, but to await further input. However, if something is found to be true with 95 percent certainty then it is very likely to be true, although there is still a small chance it is not true. Scientists pick their percentage boundaries based on the seriousness of the situation–again it’s a question of false positives and false negatives. Would it be worse to say it’s true when it isn’t, or say it’s false when it’s true? For life-threatening situations like drug side effects, a higher level of certainty is used, but because absolute certainty is never possible outside of logic, there will never be 100 percent certainty. But if we only acted based on things we knew with 100 percent certainty, we would rarely do anything at all.
On the other hand if something is deemed to be true with 1 percent certainty then it is indeed quite certain to be false, but even then it could still be true. My excellent math teacher, Mr. Muddle, taught us that when you work as a professional statistician, if you do not have the right data to support your hypothesis the correct negation is “There is insufficient evidence to support this hypothesis and therefore we need more funding in order to pursue the matter further.”
1 You might be able to see an optical illusion at work in the first diagram (without the inner black circle). There seems to be a white glowing circle outside the A, with the central part looking more gray. This is an illusion: the whole centre really is white, but somehow our eyes interpret the outer ring as more white, probably because of its proximity to the gray. I feel like there might be a metaphorical interpretation here, that we also think of there being a demarcation between white and non-white in our heads even when it’s a sliding scale, especially if we’re too used to being in the middle of the white. We’ll come back to this question as it pertains to racial prejudice later.
2 Cisgendered: your personal gender identity matches the sex you were assigned at birth.