14

EQUIVALENCE

WHEN THINGS ARE AND AREN’T THE SAME

ONE LONG-STANDING MYTH about mathematics is that it is all about “getting the right answer”. That everything is simply right or wrong. Another pervasive myth is that it’s all about equations.

These myths both have some truth in them, but are very far from being completely true. Equations do arise a lot in school math, but as the objects we study become more interesting than numbers, the issues become more interesting than equations too.

But there is an important idea at the heart of equations, which is that they are about finding things that are the same as each other. However, nothing is actually the same as anything except itself. As we saw in Chapter 8, equations are all lies apart from those of the form x = x, which is not at all illuminating. Other equations have some truth in them, so, there is a sense in which the two sides are the same, but, crucially there is a sense in which they are not. We saw that in this equation: 10 + 1 = 1 + 10 the two sides are the same in that they produce the same answer, but they are not the same in the sense that technically they describe a different process.

The point of equations in math, where they do arise, is to find two things that aren’t the same in one sense and that are the same in another sense. We can then use the sense in which they are the same to pivot between the ways in which they aren’t the same, and thus gain some understanding, as we described in the previous chapter. This idea continues into research-level math, where the senses of “sameness” become more and more subtle, and increasing amounts of technical effort have to be put into finding and describing appropriate notions of sameness.

We saw in the previous chapter that analogies involve finding situations that aren’t exactly the same, but that are the same in some sense–and necessarily different in another. We can then pivot using the sense in which they’re the same, and perhaps land in a place that is logically similar but more emotionally engaging, or more extreme and thus easier to judge morally.

But there are different levels of abstraction that produce different analogies with different quantities of sameness. Which one should we pick? This is another place where gray areas arise all the time. There are different ways in which things can be equivalent and not equivalent. A better question than “Are these the same or not?” is “In what sense are these the same and in what sense are they different?”

EQUIVALENCE IN MATHEMATICS

When we first learn math it is all about numbers. And numbers don’t really have ways of being the same as each other except by being equal, so math is mostly about equations as well. However, as math progresses it starts involving things that are much more interesting and subtle than numbers, like shapes and curves and surfaces and spaces and patterns. These have many more ways in which they can be the same as each other, depending on how stringent you want to be. As humans we are quite used to different levels of sameness in different situations. For example, if two different people write the letter “a”, it won’t come out exactly the same, but we’ll recognize both as being “the same letter”. However, we might be able to tell they’re written by different people. If I write the letter “a” several times they’ll all look slightly different, but a handwriting expert should be able to tell that they’re all written by the same person:

One of the problems with “handwriting” fonts on computers is that if you look closely you can see that every letter “a” is exactly, precisely the same, so while the text might look handwritten at first glance, on close inspection you can quickly tell it isn’t.

In math too we may want different levels of equivalence for different contexts. You might remember that two triangles are called congruent if they are exactly the same shape and size, that is, they have the same angles as each other and the same length of sides. They are, in some sense, exactly the same. If they have the same angles as each other but possibly different lengths of sides then one is a scaled version of the other and they are called similar:

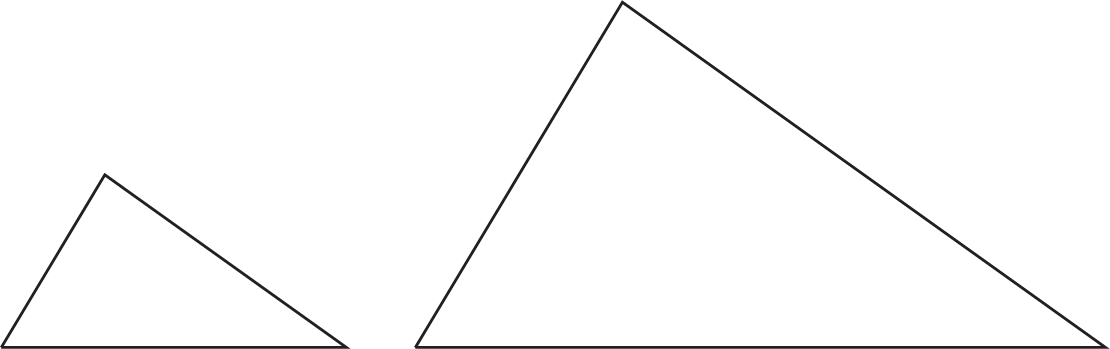
They are not exactly the same, but there is a sense in which they are the same. In a way the second one is what the first one would look like if we held it closer to our eyes. And what about this one?

It’s just the first triangle but flipped over sideways. Does flipping a triange over make it a different shape? It depends what you’re using it for. When children learn how to write letters they sometimes have trouble getting them the right way round. I sympathize, because we are expecting them to understand that these are not the same:

although in some very strong sense they are the same shape.

In fact, all equivalence and sameness depends on what you take into account and what you ignore–except strict equalities like x = x. There is no way to make that not equal. So as math becomes more advanced it becomes more and more about finding the sense in which things are the same and the sense in which they are different. The more dimensions something has, the more different ways there are in which it could count as the same, and the more subtle it becomes.

One of the most famous recently solved mathematical problems was the Poincaré conjecture, which was essentially about this subtlety. It involves looking at higher-dimensional spaces (of a certain special kind) and asking what happens if we count them as the same if they’re “the same shape” where we don’t care about size but we also don’t care about curvature and pointiness. This can be thought of as taking a playdough shape and squashing it around without breaking it or sticking parts together, and counting that as the same, with the famous example that in this case a (ring) doughnut is “the same” as a coffee cup with a handle–the hole in the doughnut corresponds to the handle in the coffee cup. Of course, it’s a bit hard to understand what playdough would be in higher dimensions, but that’s why math doesn’t actually refer to it as playdough. Anyway, the Poincaré conjecture is about which spaces count as the same and which ones count as different under this condition. It doesn’t mean that those spaces are the same; it just means that viewed in this particular light they can be seen as the same.

Under this type of sameness (which is technically called “homotopy equivalence”) a square is the same as a circle. But a square is certainly not the same as a circle if, say, you are making a wheel. A square might be as good as a circle if you are making a cake–except that a square cake tin is harder to wash than a circular one because of the corners. (And also the corners are likely to get more cooked than the rest of the cake.)

In life there are even more ways in which two things could be considered the same and not the same, because the things we think about in life are much more subtle than the things we think about in math. So really, we should be even more careful about the ways in which things are the same and different, rather than just declaring they are the same, or not the same. In fact, it’s another example where we tend to see in black and white instead of comprehending the whole gray area in between.

We have seen the most obvious sense in which things are the same: if they are actually equal. But this is not helpful. At the other extreme we can see the most extreme sense in which things are not the same–false equivalence. We will discuss that next, before thinking about the gray area.

FALSE EQUIVALENCE

Periodically an argument breaks out about the “gendering” of children’s clothes and toys. On one side, people point out that boys and girls can play with the same toys if they want, and there’s no reason that a T-shirt with dinosaurs on it should be called a boys’ T-shirt, and one with flowers a girls’ T-shirt. Usually people on the other side will complain about political correctness and declare that we should just “let boys be boys and girls be girls”.

It seems to me that they are equating the argument “boys and girls can play with the same toys” with a desire to turn boys into girls and girls into boys. This is a false equivalence.

Erroneously equating one statement with another one is a devious tactic, and is not logical. It is often invoked to twist someone’s words and turn their reasonable position into a much worse one, and then attack them for it. It often drives arguments into further and further extremes. It involves an incorrect piece of logic, claiming two things are logically equivalent when they are not, so is a form of logical fallacy.

In Chapter 12 we talked about good logical ways of dealing with gray areas. One way that false equivalence arises is when we don’t deal with gray areas well–we often end up lumping things in with extremes. “If you’re not with us you’re against us.” Well, you might be neither totally with them nor totally against them. You might support some things someone does but not others. Some of these are versions of false equivalence, and some can find their root in false negations, when a statement is negated incorrectly to produce a more polarized opposite. Sometimes it’s a flawed analogy as described in the previous chapter, where someone goes to too high an abstract level and claims your statement is analogous to something absurd. In all cases this creates divisions instead of finding common ground.

In fact, I have somewhat pushed the argument about boys’ and girls’ clothes to extremes myself: in order to show the counterargument in the worst possible light, I have picked the most harmless manifestation of the “politically correct” argument that I can think of. Really there is a more complex argument going on underneath, about gender stereotypes and gender pressures. When people get very upset about someone else’s point of view it is worth trying to work out what the underlying issue really is, which might not be logical at all. It might be very personal.

PERSONAL TASTE

When someone expresses personal taste, it sometimes happens that other people get offended. I might say “I hate toast” (which I do), and someone else will take offence because they really like toast.

This might sound silly with the toast example, but perhaps it’s more believable that when I say “I find Mozart boring” people who like Mozart take it as an insult, or if I say “I don’t like jazz” people who like jazz think I’m criticizing them. Or if I say “I don’t want to be fat” and people think I’m fat-shaming.

I think a false equivalence is at work. Someone hears

“I don’t like toast.”

and thinks it is equivalent to

“I don’t like people who like toast.”

This is a false equivalence: the two statements are not logically equivalent. I am perfectly happy for you to like toast, I just happen not to like it myself. This is different from

“I don’t like stealing.”

because in fact I also don’t like people who like stealing. There is also a false equivalence between

I don’t want to be fat.

and

I think people who are fat are bad.

This is not a logical equivalence. We could make an abstract version of this:

I don’t want to be X.

and

I think people who are X are bad.

If X is “a doctor” then it’s obviously a false equivalence: I don’t want to be a doctor, but I don’t think doctors are bad, I just happen not to want to be one. On the other hand if X is “a horrible person” then the second statement actually explains the first one: I think horrible people are bad, so I don’t want to be one. This shows that the error is a form of converse error. We have these statements:

A: I don’t want to be X.

B: I think people who are X are bad.

This implication is not very contentious:

B A

but the people getting upset with me are mistakenly thinking this converse is true:

A B

If the converse were true it would make A and B logically equivalent, but the false converse causes the false equivalence.

A similar form of false equivalence is when I say “I like weighing myself every day” and someone thinks it is equivalent to “I think everyone should weigh themselves every day”, thus they get offended if they don’t do that. Again we can look at

I like doing X every day.

and

I think everyone should do X every day.

For example, what if X is “playing the piano”? I certainly like playing the piano every day but that doesn’t mean I think everyone should do it. On the other hand if X is “brushing my teeth”, I like doing that every day and think everyone should do it every day if they can.

So much for the logic of the situation. It is an example of how I can always be right, by restricting my statement to my own personal taste or aspirations about myself.

However, people do often get upset when I say I don’t want to be fat, and they are rarely placated by my explanation of the logic. In the next chapter we are going to talk more about attempting to override emotional responses, but I think it’s worth noting here that uncovering the false equivalence gives us the logic behind their feeling of offence: they are equating me not wanting to be fat with me criticizing people who are fat. A more compassionate thing to do with this piece of logic is to admit that human language is not the same as logic, because it can carry connotations in a way that logic doesn’t. If I am genuinely not criticizing fat people, I should perhaps find a different way to express myself. Or I should examine myself carefully to see if a tiny part of myself is criticizing them but hiding behind the logical security of making it a statement about myself, like when people express an inflammatory view and claim they are playing devil’s advocate.

DAMNING ACCUSATIONS

We have just seen how false equivalence causes people to think I am accusing them of something when I’m not. Another case is when false equivalence causes people to make damning accusations of me. This quickly spirals into an antagonistic argument, the kind where instead of trying to see eye to eye, two people try to cast each other in worse and worse lights and thus drive the disagreement further and further apart.

For example, I might say that I don’t want to be fat so I am careful what I eat. Someone might then say to me “You’re fat-shaming and that is misogynistic”. I get criticized for not wanting to be fat in many ways, but this is one of the common ones. Apparently not wanting to be fat makes me misogynistic. Suddenly it turns into an argument about misogyny.

A sign that someone is about to make a false equivalence is when they launch in with “You’re basically saying…‘’ which is a sign they’re about to twist your words into something they’re not. You might say “I think it’s unfair that some people just inherit tons of money so never have to worry about anything, whereas other people are born with nothing.” Someone might argue “So you’re basically saying that everyone’s money should be confiscated when they die so that they can’t pass it on.” That’s not what I’m saying at all. There are a lot of possibilities in between simply allowing inequality to be handed down from generation to generation and forcibly confiscating all money at death. But the arguments in between are complicated. They involve things like trying to even out inequality at all stages of life, trying to help those who are born with nothing so that they can rise out of that situation and then maybe they too can have something to pass on to their children. The arguments in between are usually too complex for a fast-paced shouting match or an online exchange.

In general, an antagonistic argument driven by a false equivalence might go like this:

You are saying A.

A is equivalent to B.

B is bad.

Therefore you are a terrible person.

The logic of this can fail in two places: maybe B isn’t really bad, or maybe A isn’t really equivalent to B. Of course, it could also fail in both places. Arguing against logic that fails in multiple places can be strangely confusing, like you’re giving too many excuses or protesting too much. An example of this is if you support reproductive education at school, and someone declares that’s equivalent to condoning sex outside marriage, so is evil. I don’t think it is equivalent to condoning sex outside marriage, but I also don’t think sex outside marriage is evil.

FALSE DICHOTOMY

There is another aspect to the argument about boys’ and girls’ toys: in fact it is a false dichotomy. The arguer thinks there are only two options:

A: Label some toys “for boys” and others “for girls”.

B: Force boys to be girls and girls to be boys.

A dichotomy is when the options are cleanly split between some option A and option B, with those being the only two possibilities. A false dichotomy is when you think the options are perfectly cleanly split between A and B, but in reality they are not. As a result you mistakenly think that A is equivalent to “not B” and B is equivalent to “not A”, which is why it’s an example of a false equivalence.

In the above argument, the person thinks that B is the negation of A, but it isn’t. Not doing A could involve simply removing the labels on toys that declare them to be for one gender or the other; boys can still be boys and girls can still be girls and everyone can play with whatever toys they want. I suspect the people who believe in the false negation are acting out of some deep fear of gray areas, but it’s hard to pin down exactly what it is. A simpler case is if you say to someone “I wouldn’t call you skinny” and they burst into tears wailing “You think I’m fat!” They are jumping to this false dichotomy:

A: I am skinny.

B: I am fat.

possibly out of fears that come from society’s pressure on women to be thin. It’s a false dichotomy because it’s possible for neither A nor B to be true.

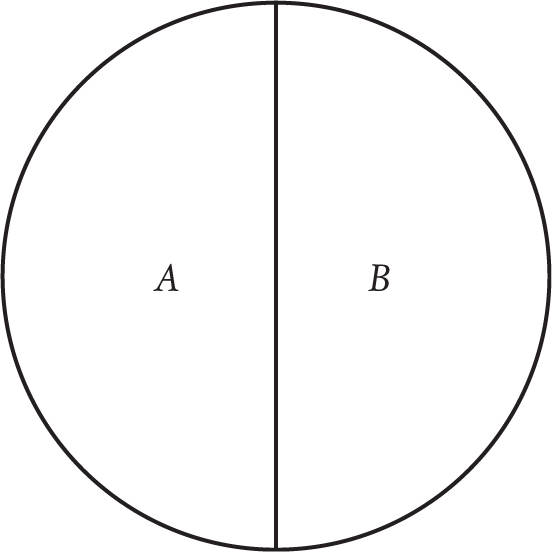
We can express this in the pictures shown on the next page, showing the relationships between the different statements involved. Here is a true dichotomy, where the circle is perfectly split between A and B:

False dichotomies can then occur in two ways. Sometimes it’s a false dichotomy because it’s possible for neither thing to be true, as in the case of being skinny vs being fat:

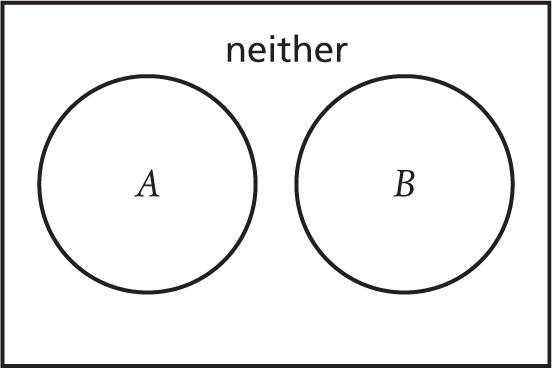
Sometimes it’s a false dichotomy because it’s possible for both things to be true at the same time:

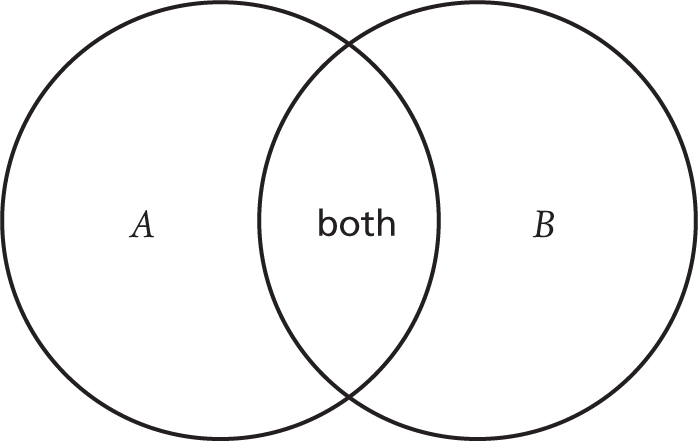
Of course, it’s possible to fail in both of those ways at the same time. We’ll see an example of the second type of false dichotomy now.

DIETING

A false dichotomy that often gets me into trouble with people is:

A: Some people should watch what they eat (because it helps them stay healthy).

B: Some people should not watch what they eat (because it hinders them).

It is certainly helpful for me to watch what I eat, but I acknowledge that for other people it causes problems. We should all pick whatever’s best for us. Unfortunately when I say A, people think I’m negating B, and then they get angry and say that it is better for them not to “go on a diet”. But this is not a disagreement: it is perfectly possible for both A and B to be true (and I’m sure they are both true).

The true negation of B would be the much more extreme statement “Everyone should watch what they eat”, so perhaps the error is a false equivalence between this and my rather mild original statement.

We saw in Chapter 6 how helpful it can be to draw diagrams of relationships between concepts, so I will now draw some for false dichotomies. In the following diagram, my point is the top left one, and the typical refutation is the bottom right argument, when in fact these do not disagree:

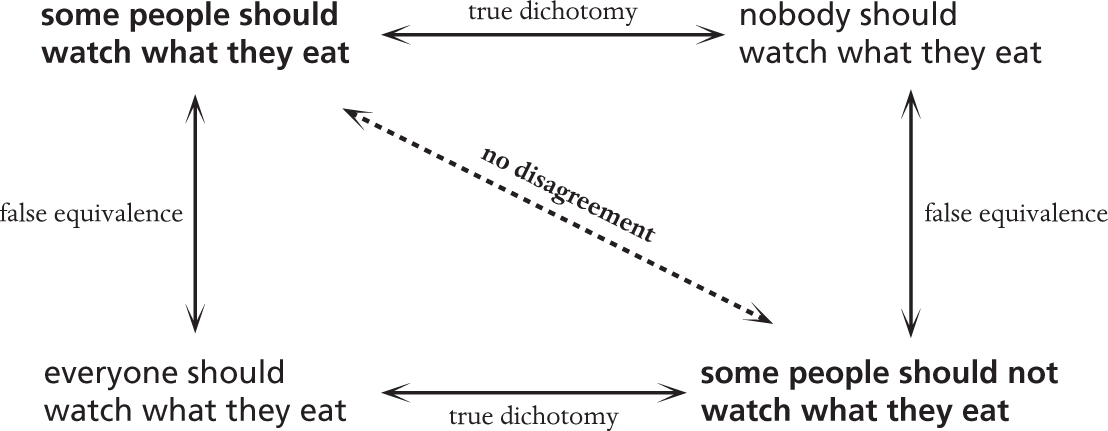
The really funny thing about this argument is that it usually turns into a meta-argument about whether or not we’re disagreeing. I try to point out that we’re both making the same point, and the arguer usually insists that we’re not. I think they really feel that I am criticizing them for not being careful about what they eat. The result is that we go from these two compatible reasonable points:

A: Some people should watch what they eat.

B: Some people should not watch what they eat.

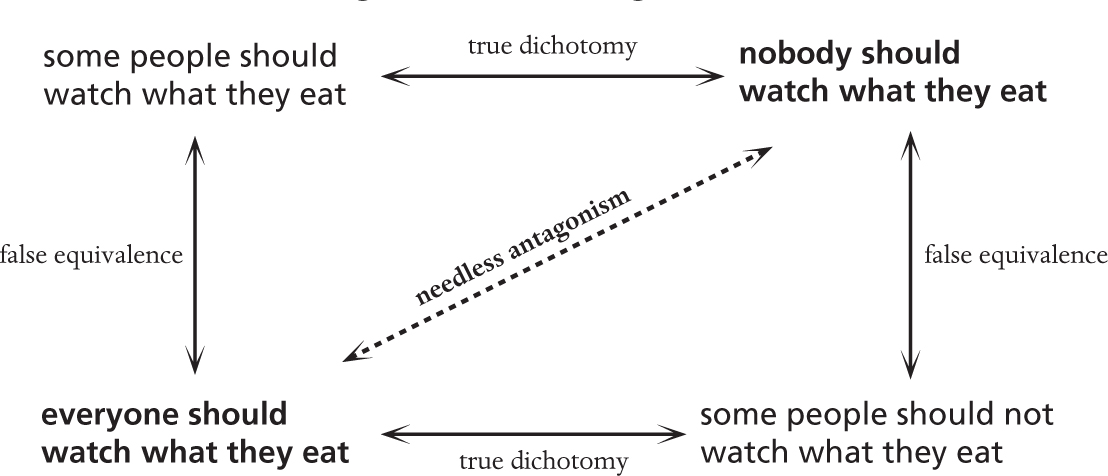
To these two absurd and antagonistic ones:

A: Everyone should watch what they eat.

B: Nobody should watch what they eat.

This is the other diagonal of the diagram:

I think this is another example of the general false equivalence between making a choice A, and thinking that no other choice is valid. Just because I choose A, it doesn’t mean I think everyone should choose A. And yet when I choose something that someone else didn’t choose (like watching what I eat) people too often assume I am criticizing their choice. I suppose in many cases people are criticizing different choices, but it doesn’t have to be that way, if we don’t let false dichotomies push us to extremes.

STRAW MAN ARGUMENT

False equivalences are a source of straw man arguments, where an argument is replaced by one that is much easier to knock down (a straw man) and is then duly knocked down. However, if the new argument is not equivalent to the original one, all you have done is knocked down an argument that nobody was making.

The emphasis on “STEM” subjects (Science, Technology, Engineering and Mathematics) is sometimes criticized on the grounds that creativity is important too. This is making a false dichotomy between science and creativity, possibly stemming from a more fundamental one between

A: Being creative.

B: Being logical.

Sometimes this causes creative people to justify being illogical, or to refuse to be logical. There’s also a false equivalence between creativity and art, and another between logic and science. There is logic and creativity in both art and science:

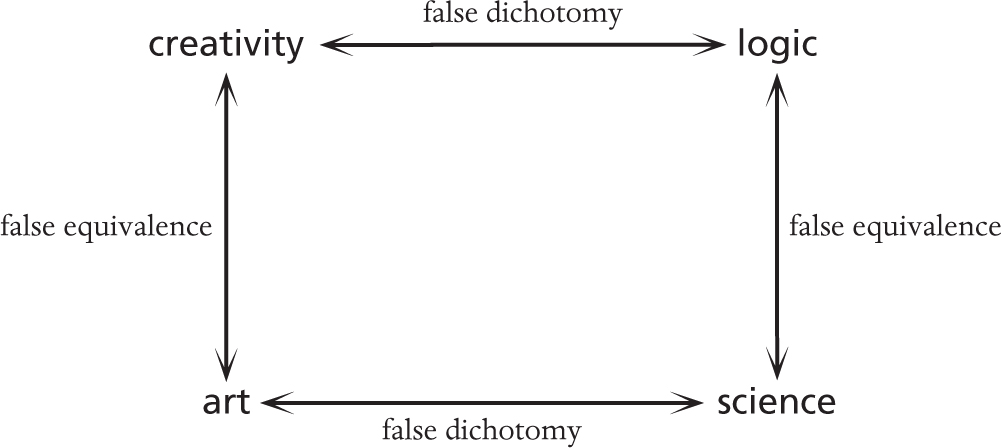
Thus to use creativity as an argument against emphasizing STEM education is a straw man. There are plenty of valid ways to advocate for arts education without denigrating science.

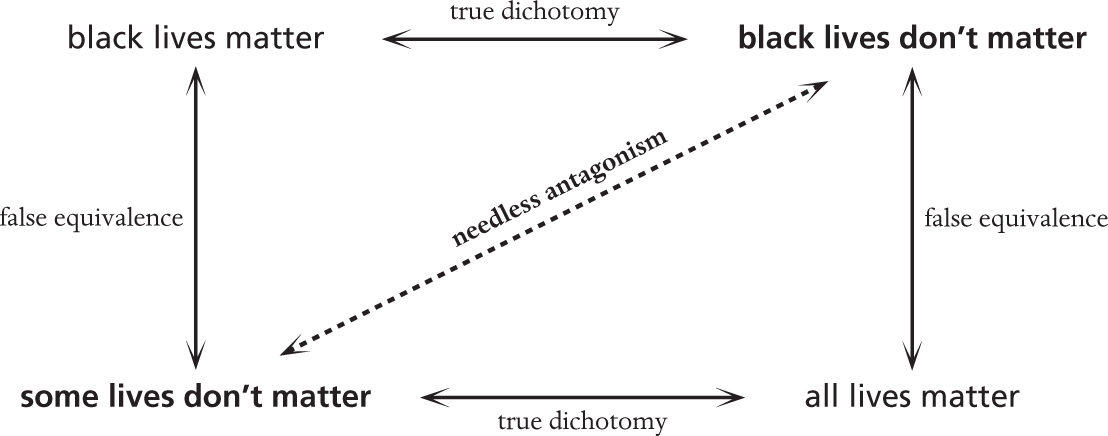
The most pernicious straw man argument I see regularly is “All lives matter” as a response to “Black lives matter”. The straw man as I see it is this. What the slogan “Black lives matter” really means is “Black lives matter just as much as other lives, but are currently being treated as if they do not matter as much, and we need to do something to correct this injustice.” Of course, that is not as catchy a slogan.

The straw man argument wilfully misinterprets “Black lives matter” to mean “Black lives matter and other lives don’t” which is easily refuted by saying “All lives matter”. The frustrating thing about this argument, apart from the fallacy of it refuting something that nobody was trying to argue, is that it is almost impossible to argue against it. To do so we would have to argue “Some lives don’t matter”, and apart from some reprehensible extremists, we do not think that. As in the rather more trivial example of watching what we eat, we can represent this push to extremes in diagrams. Strictly logically, there is no disagreement between the statements “black lives matter” and “all lives matter”. However, if we replace “black lives matter” with the inequivalent straw man argument “some lives don’t matter” then the diagonal with no disagreement in the first diagram (below) gets pushed to the extreme and antagonistic diagonal of the second diagram (opposite):

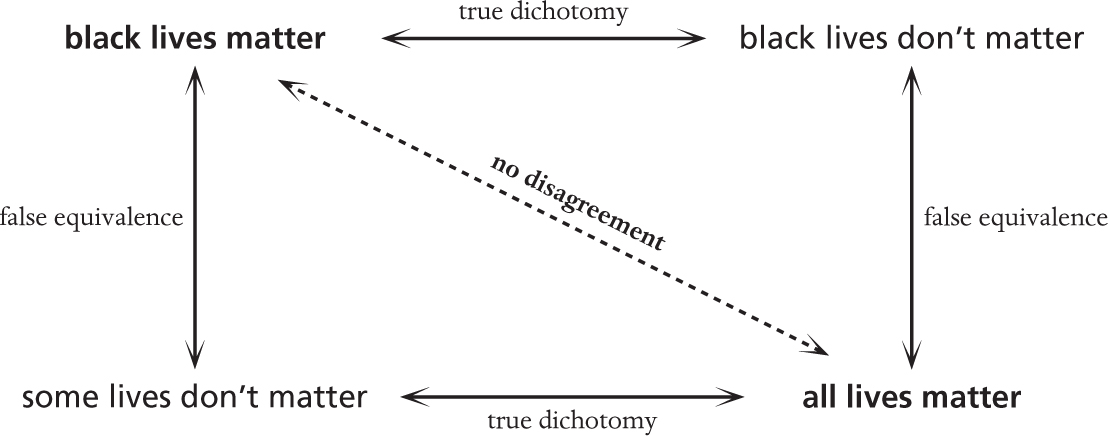
In order to have a logical argument, we need to persuade the person who opposes “black lives matter” to refute the true argument “Black lives matter just as much as other lives, but are currently being treated as if they do not matter as much, and we need to do something to correct this injustice.”

This has three parts, connected by “and”:

A: Black lives matter just as much as other lives.

B: Black lives are currently being treated as if they do not matter as much.

C: We need to do something to correct this injustice.

The argument being made is:

A and B and C.

To refute this, you just need to refute one of those. If the refuter is persuaded to admit which one (or more) they disagree with, we can get closer to understanding what the argument is.

If the refuter does not agree with A then we can conclude that they are an out-and-out explicit racist. If the refuter does not agree with B then I would conclude that they are ignorant about the state of the world, or deluding themselves. If they do not agree with C then they might not think they are actively racist because they might not be engaging in active oppression, but if you do not try to take steps to defeat oppression then you are arguably complicit with the oppressors. At least if we gain this clarity we can have a more productive investigation into why the person disagrees with B and C. Is it because they think that black people are bringing it on themselves? Is it because they do not think it is anyone’s responsibility to help other people, in general? In the first case I would try to persuade them to understand how systems work, that people do not operate independently of a system that has put them there, and in this case it is a whole historical system of abuse, mistreatment and oppression.

In the second case we are more likely to reach an impasse. If someone doesn’t believe in helping other people, that is a basic difference in axioms from mine.

There is also a non-logical but emotionally valid possibility for what the opposer is really trying to say, which is they oppose the “Black Lives Matter” movement on the grounds that they associate it with anger and aggression which they think is counterproductive. In Chapter 15 we will discuss the importance of uncovering the emotional reasons for arguments that don’t seem to make logical sense. In this particular case we should then have a discussion about

1. whether or not the Black Lives Matter movement is really synonymous with anger and aggression, and

2. when anger and aggression are reasonable.

We could perform an abstraction pivot to build a gray area bridge and agree that there are some situations in which aggression is not reasonable (for example if you go to buy something in a shop but they’ve sold out) and some situations in which aggression is reasonable (for example, if someone is trying to kill you then you could be forgiven for fighting them aggressively). The question is then one of gray areas and the possibility that the treatment of black people in the US is similar enough to someone trying to kill them that they can be forgiven for fighting back aggressively.

Of course, this analysis is far too complex for interactions on social media, but unfortunately this is where so many of these arguments take place. It is also too complex for people who are riled up by anger or fear. Complex arguments require a certain level of calm. This is true in mathematics as well–if I get overexcited about a result I’m about to prove, I won’t be able to prove it. Or if I panic that my time is running out, perhaps because of a looming deadline or a talk I’m supposed to give, I also won’t be able to prove it.

If you want to avoid someone making a straw man argument at you, it helps to state your position precisely. We have seen from Chapter 5 that we should look at all factors that cause a situation, and really if we express ourselves imprecisely and leave ourselves open to an easy straw man argument we are a little bit complicit in it, even if the straw man has involved some wilful misinterpretation by someone determined to disagree with us. It takes longer to make an argument precise than to use a catchy slogan, which is problematic in a world of memes and 280-character messages. In Chapter 16 we will come back to our need for slower arguments despite our fast-paced world.

ANALOGIES

In the last chapter we saw that complex false equivalence situations can arise when you try and argue a point by making an analogy. This is usually a bit fraught because analogies don’t always play a strictly logical role in an argument, but rather, an emotional role in persuading people of things. These false equivalences are not exactly logical fallacies any more, but something more subtle in the gray area.

A false equivalence logical fallacy often comes into an attempted logical argument like this:

A is (falsely) equivalent to B.

B is true.

Therefore A is true

Someone might well successfully argue statement B, but if B is not actually equivalent to A then they have not argued A at all. Often in life this takes the form:

A is (falsely) logically equivalent to B.

B is good/terrible.

Therefore A is good/terrible.

This general situation also happens in a straw man argument, as we discussed earlier, for example:

Saying we should remove gender labels from children’s clothes (A)

is logically equivalent to

saying we don’t want to just let girls be girls and let boys be boys (B).

B is terrible.

Therefore A is terrible.

Using analogies is a more nuanced way of using equivalence as a pivot. Instead of claiming a logical equivalence between A and B, we invoke an analogy involving a certain principle X, which we represented in this type of diagram in the previous chapter:

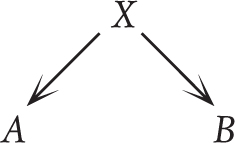
We can then try to convince someone of the principle by applying it to situation B that makes a more emotional connection. The idea is that A and B are equivalent at the level of the abstract principle X. The example doesn’t justify the principle, but is supposed to help us feel the principle.

As we discussed, the question is about the level of abstraction and thus the extent to which A and B really are similar because, after all, everything is the same if we go up to a high enough level of abstraction, but that would not illuminate the argument at all. So the question should not be “Are these things equivalent?” but rather “in what sense are these things equivalent?”

In the diagram below, A and B are analogous according to principle X, but not according to principle Y. If someone says A and B are analogous we can’t simply say it’s a false equivalence or not: we should discuss which principle is appropriate.

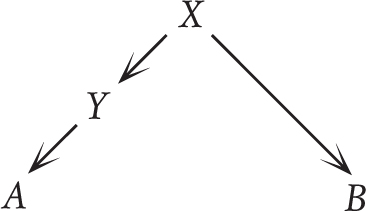
An example of this situation is in arguments about “mansplaining”. I have found that using the term “mansplain” is likely to cause at least one person (usually a male person) to get rather wound up, but I usually think that is more evidence that we need to continue using it.

Mansplanation is not just when men explain things to women in a patronizing way. This is a false equivalence. Mansplanation is in fact when a man explains something to a woman despite the fact that there is strong evidence that the woman already knows it, and a man is ignoring this evidence as part of the systemic societal assumption that men know more things than women, whether or not he is consciously applying that bias in this particular case. This happens to me a lot, for example, if a man explains something very basic about infinity to me despite the fact that I have written a book about infinity. Rebecca Solnit coined the term after a guy explained her own book to her, after she mentioned having written a book on the subject. He did it to show that this book was much more important than hers, apparently without ever considering that it might be hers.

Sometimes it happens that someone explains your own area of expertise to you, so the evidence that you don’t need the explanation is in the fact that you are an expert. But sometimes the evidence that you don’t need the explanation is that you already said that very thing yourself. The assumption of the woman’s ignorance isn’t just generally patronizing, it is specifically part of a broad pattern in society of men undervaluing or neglecting the contributions of women. Because this contextual aspect is built into the word “mansplain”, it is by definition not something that women can do. The frequent straw man argument is that “women mansplain things too”. I would say the straw man in this case is misrepresenting the argument as claiming that only men explain unnecessary things in a patronizing way. While in my experience it is almost always men who do that, that is not the point. The point is that when men do it, it is part of a society-wide assumption about women, and that is why it is so aggravating.

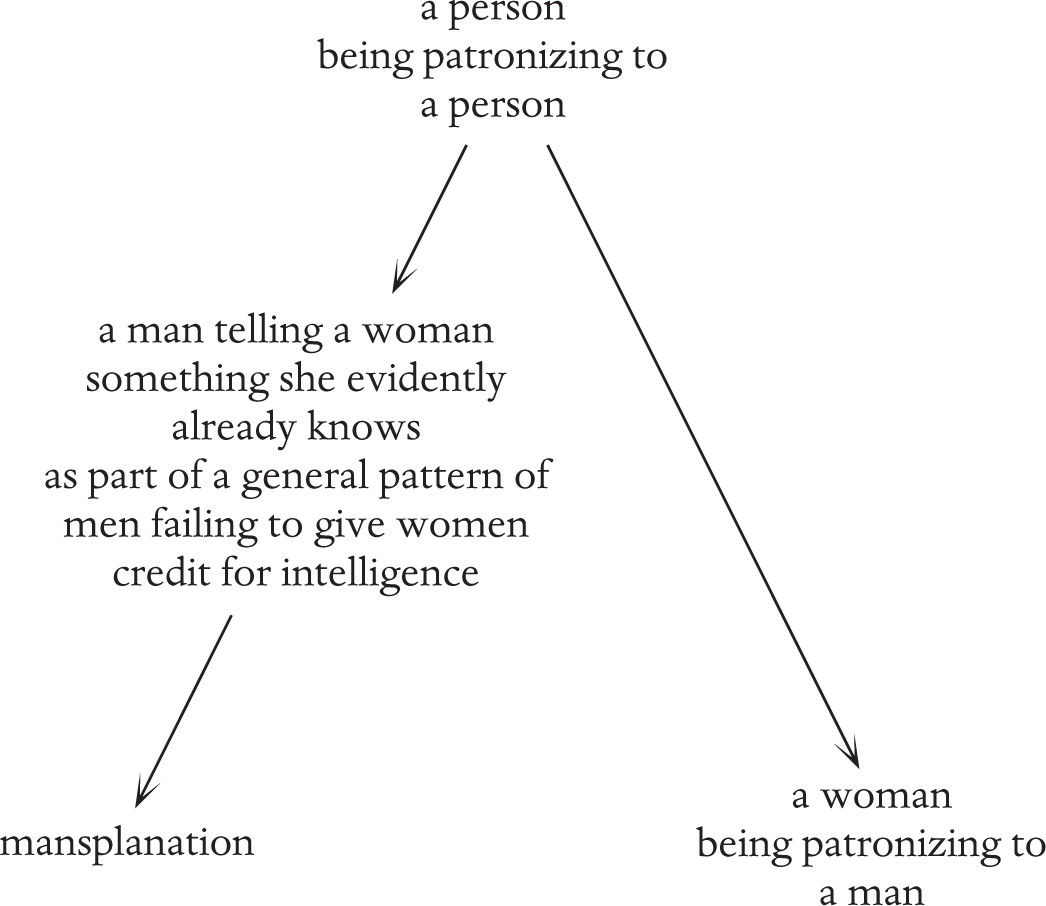
Those who think “women mansplain things too” seem to think that mansplanation was coined just to describe men being patronizing to women. If we go all the way up to the top level of this diagram then this is indeed analogous to women being patronizing to men, but this is a level of abstraction too high.

FALSE FALSE EQUIVALENCE

We’ve seen with mansplaining that, if we’re not careful, false equivalences can be used to shut down valid arguments. But so can false accusations of false equivalence.

Imagine an argument about whether higher education should be paid for by the government. One person objects on the grounds that higher education is optional and everyone gets to decide for themselves whether they go or not, so if it’s paid for by the state then individuals get to decide how to spend the government’s money.

Someone else might argue that this is true of healthcare as well–when healthcare is paid for by the state, individuals get to decide whether to go to the doctor or not, so they too are essentially deciding how to spend the government’s money. Of course this argument won’t work with someone who doesn’t believe healthcare should be paid for either, but what if the person objects to government-funded higher education but supports government-funded healthcare? Is that inconsistent?

At this point if you accuse someone of inconsistency in this way they’re likely to exclaim “That’s not the same”, which is the usual battle cry when someone is trying to argue against another person’s analogy. But of course the analogy isn’t the same–it’s an analogy. The question is whether the analogy breaks down on a crucial rather than an irrelevant point.

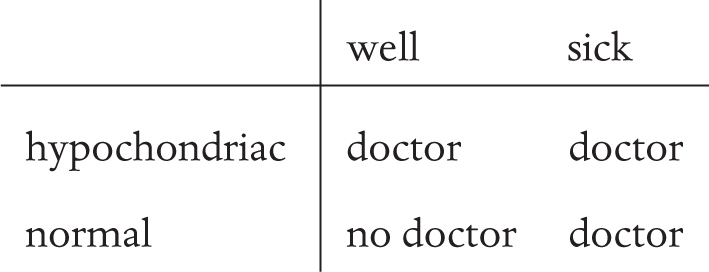
You could argue that people don’t “decide” to go to the doctor, they just go when they’re sick. Whereas in fact I think an arguably analogous level of decision goes into going to see the doctor and going on to higher education. Different people decide to go at different points for different reasons. I don’t think it’s as clear cut as “hypochondriacs vs normal people”, and “sick people vs well people”. Some people seem to think it is a black and white logic system:

whereas I think it’s more like a fuzzy logic system:

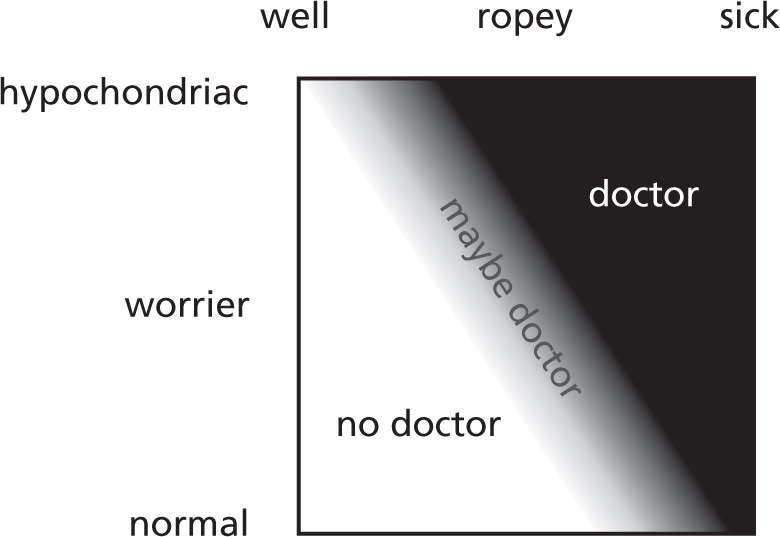
Some people refuse ever to go to the doctor. Will Boast’s haunting memoir Epilogue talks of his father dying in his car by the side of the road rather than hitting the emergency button, so averse was he to the idea of getting medical help.

Aside from that, there are situations in which most people would seek medical attention, such as if they’ve broken all their limbs, or got third-degree burns, and others in which some people would go to the doctor and others would decide not to. Notoriously, many people go to the doctor when they have a bad cold, and want antibiotics although antibiotics do nothing for viruses, whereas I just go to bed and drink whisky. All this is to say that we do make choices about using healthcare.

Compare this with higher education. It is not exactly a free choice whether to go or not, as so many professions are inaccessible nowadays if you do not have a degree. This is very different from, say, fifty years ago when it was more of an indulgence to go, unless you wanted to be a doctor or a research scientist (or perhaps a few other things). You could still be a banker, a civil servant, a teacher without a degree. Today you can choose not to go but then you’ll probably either be restricted to a low-paid unskilled job, or you’ll have to rely on being a rare entrepreneur. Even artists are mostly expected to have degrees now although vocational apprenticeships fortunately still exist in some fields.

The two different points of view can be represented like this. One person thinks education and health care are not analogous, because they are using these principles:

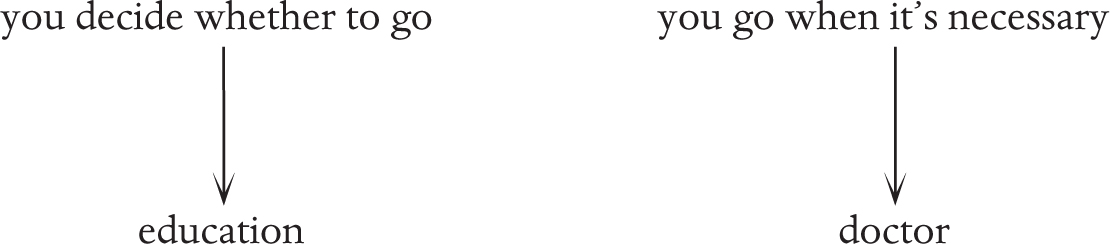
Someone else thinks they are analogous, by using this principle:

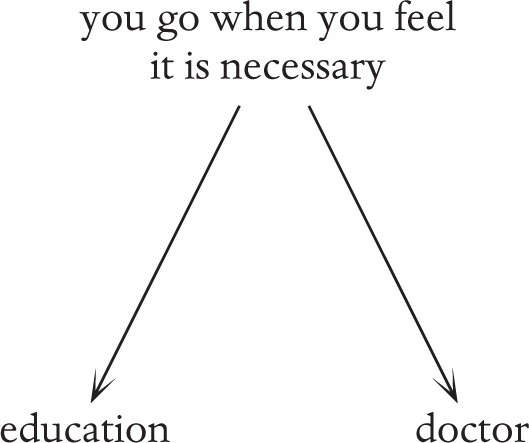
I think with both college and the doctor, most people go because they perceive it to be crucial to their future life. However, that level of perception is subjective, and what looks like an involuntary, critical matter to one person can look like an indulgent choice to another. I will concede that there might be some exceptions–rich people who go to university just for the sheer fun of it, as they will never need to depend on their education in their lives. Perhaps this is analogous to hypochondriacs who go to the doctor for no particular reason?

So, are the situations equivalent or not? A claim of “false equivalence” itself needs to be justified. Just saying that something isn’t the same does not mean that it isn’t equivalent in some crucial way.

MANIPULATION

False equivalence and false dichotomies in general lead to false arguments and fabricated division between people who might not really be disagreeing. This can be exploited by politicians, the media, or just people who have more to gain from discord than from unity.

This can be a particular problem in partisan politics, where one party makes opposition their entire purpose. Then if the party on the left moves to the centre to win more votes, the opposition has to move much further to the right in order to oppose them robustly.

Individuals can also cast people, opinions or policies in a much worse light by making a persuasive false equivalence to something considered to be bad. They might declare a position to be “unpatriotic”, thereby invoking strong emotions from those people who care about patriotism. For example, some people proclaim that voting to remain in the EU was “unpatriotic”, or that kneeling during the national anthem is “unpatriotic”.

A nuanced argument would then look into what exactly “patriotic” means. Perhaps it means something like loving and supporting your country. We could then have a discussion about whether believing in the EU means that you don’t love and support your country. What if, in fact, you want the best for the UK and you believe that the best means staying in the EU? It then comes back to an argument about what is best for the UK, which is what the argument should be about, rather than simple name-calling.

Similarly for the national anthem, some people argue that kneeling during the national anthem shows that you don’t love and support your country. What if, in fact, you want the best for your country and you believe that the best means eliminating racism, and that kneeling during the national anthem is a way of raising awareness and showing solidarity for this cause?

False equivalence arguments can be obstructive, but in worse cases they can actually be destructive. Some homophobic people erroneously perpetuate the myth of an association or even equivalence between homosexuality and paedophilia. Transphobic people make an association between transgender people and perverts. These are abhorrent, demonstrably false equivalences, that can be demonstrated to be false with extensive statistics, but the false equivalences are still perpetuated by people who want to drum up hatred.

These are some of the most destructive ways in which people can be manipulated by emotional means. Such methods of manipulation rely on us not being able to think logically enough to see through them. Unfortunately, because of the power of emotions over logic, there are many people who are either unable to think logically enough, or prevented from doing so once their emotions are stirred up. In the next chapter we will explore what a better interaction between emotions and logic could be.