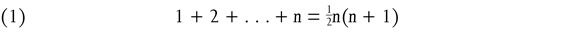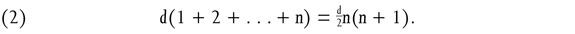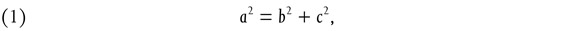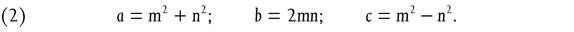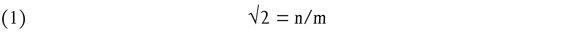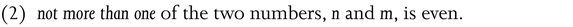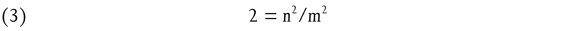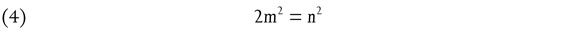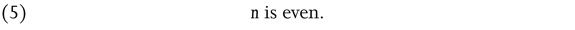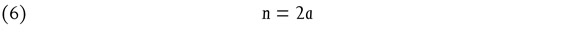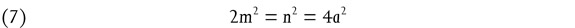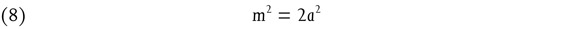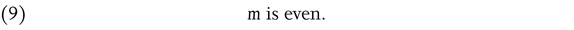I
It was after some hesitation that I decided to take as my point of departure the present position of English philosophy. For I believe that the function of a scientist or of a philosopher is to solve scientific or philosophical problems, rather than to talk about what he or other philosophers are doing or might do. Any unsuccessful attempt to solve a scientific or philosophical problem, if it is an honest and devoted attempt, appears to me more significant than a discussion of such a question as ‘What is science?’ or ‘What is philosophy?’ And even if we put this latter question, as we should, in the slightly better form, ‘What is the character of philosophical problems?’, I for one should not bother much about it; I should feel that it had little weight, even compared with such a minor problem of philosophy as the question whether every discussion or every criticism must always proceed from ‘assumptions’ or ‘suppositions’ which themselves are beyond argument.1
When describing ‘What is the character of philosophical problems?’ as a slightly better form of ‘What is philosophy?’ I wished to hint at one of the reasons for the futility of the current controversy concerning the nature of philosophy: the naïve belief that there is an entity such as ‘philosophy’, or perhaps ‘philosophical activity’, and that it has a certain character or essence or ‘nature’. The belief that there is such a thing as physics, or biology, or archaeology, and that these ‘studies’ or ‘disciplines’ are distinguishable by the subject matter which they investigate, appears to me to be a residue from the time when one believed that a theory had to proceed from a definition of its own subject matter.2 But subject matter, or kinds of things, do not, I hold, constitute a basis for distinguishing disciplines. Disciplines are distinguished partly for historical reasons and reasons of administrative convenience (such as the organization of teaching and of appointments), and partly because the theories which we construct to solve our problems have a tendency3 to grow into unified systems. But all this classification and distinction is a comparatively unimportant and superficial affair. We are not students of some subject matter but students of problems. And problems may cut right across the borders of any subject matter or discipline.
Obvious as this fact may appear to some people, it is so important for our present discussion that it is worth while illustrating it by an example. I need hardly mention that a geologist’s problem such as assessing the chances of finding deposits of oil or uranium in a certain district has to be solved with the help of theories and techniques usually classified as mathematical, physical and chemical. It is however less obvious that even a more ‘basic’ science such as atomic physics may have to make use of a geological survey, and of geological theories and techniques, to solve a problem in one of its most abstract and fundamental theories; for example the problem of testing predictions about the relative stability or instability of atoms of an even or odd atomic number.
I am quite ready to admit that many problems, even if their solution involves the most diverse disciplines, nevertheless ‘belong’ in some sense to one or another of the traditional disciplines; the two problems just mentioned clearly ‘belong’ to geology and physics respectively. This is because each of them arises out of a discussion characteristic of the tradition of the discipline in question. Each arises out of the discussion of some theory, or out of empirical tests bearing upon a theory; and theories, as opposed to subject matter, may constitute a discipline (which might be described as a somewhat loose cluster of theories undergoing challenge, change, and growth). But this does not affect my point that the classification into disciplines is comparatively unimportant, and that we are students not of disciplines but of problems.
But are there philosophical problems? The present position of English philosophy—my point of departure—originates, I believe, in the late Professor Ludwig Wittgenstein’s doctrine that there are none; that all genuine problems are scientific problems; that the alleged problems of philosophy are pseudo-problems; that the alleged propositions or theories of philosophy are pseudo-propositions or pseudo-theories; that they are not false (if they were false, their negations would be true propositions or theories) but strictly meaningless combinations of words,4 no more meaningful than the incoherent babbling of a child who has not yet learned to speak properly.5
As a consequence, philosophy cannot contain any theories. Its true nature, according to Wittgenstein, is not that of a theory, but that of an activity. The task of all genuine philosophy is to unmask philosophical nonsense, and to teach people to talk sense.
My plan is to take this doctrine6 of Wittgenstein’s as my starting point. I shall try to explain it (in section ii); to defend it, to some extent; and to criticize it (in section iii). And I shall illustrate all this (in sections iv to xi) by some examples from the history of scientific ideas.
But before proceeding to carry out this plan I wish to reaffirm my conviction that a philosopher should philosophize: he should try to solve philosophical problems, rather than talk about philosophy. If Wittgenstein’s doctrine is true, then nobody can philosophize, in my sense. Were this my opinion I would give up philosophy. But it so happens that I am not only deeply interested in certain philosophical problems (I do not much care whether they are ‘rightly’ called ‘philosophical problems’), but inspired by the hope that I may contribute—if only a little, and only by hard work—to their solution. My only excuse for talking here about philosophy—instead of philosophizing— is my hope that in carrying out my programme for this address an opportunity may turn up to do a little philosophizing after all.
II
Ever since the rise of Hegelianism there has existed a dangerous gulf between science and philosophy. Philosophers were accused—rightly, I believe—of ‘philosophizing without knowledge of fact’, and their philosophies were described as ‘mere fancies, even imbecile fancies’.7 Although Hegelianism was the leading influence in England and on the Continent, opposition to it, and contempt of its pretentiousness, never died out completely. Its downfall was brought about by a philosopher who like Leibniz, Berkeley, and Kant before him had a sound knowledge of science, and especially of mathematics. I am speaking of Bertrand Russell.
Russell is also the author of the classification, closely related to his famous theory of types, which is the basis of Wittgenstein’s view of philosophy: the classification (criticized below on p. 309) of the expressions of a language into
- (1) True statements
- (2) False statements
- (3) Meaningless expressions, among which there are statement-like sequences of words, the so-called ‘pseudo-statements’.
Russell used this distinction to solve the problem of the logical paradoxes which he discovered. For his solution it was essential to distinguish more especially between (2) and (3). We might say, in ordinary speech, that a false statement like, ‘3 times 4 equals 173,’ or, ‘All cats are cows’, is meaningless. Russell, however, reserved the term ‘meaningless’ for expressions such as, ‘3 times 4 are cows,’ or ‘All cats equal 173’, that is for expressions of a sort which it is better not to describe as false statements. They are better not described as false because the negation of a meaningful but false statement will always be true. But the prima facie negation of the pseudo-statement, ‘All cats equal 173’, is, ‘Some cats do not equal 173’, and this is just as unsatisfactory a pseudo-statement as the original statement. Negations of pseudo-statements are again pseudo-statements, just as negations of proper statements (true or false) are proper statements (false or true, respectively).
This distinction allowed Russell to eliminate the paradoxes (which, he said, were meaningless pseudo-statements). Wittgenstein went further. Led perhaps by the feeling that what philosophers, especially Hegelian philosophers, were saying was somewhat similar to the paradoxes of logic, he used Russell’s distinction in order to denounce all philosophy as strictly meaningless.
As a result there could be no genuine philosophical problems. All alleged philosophical problems could be classified under four heads:8 (1) those which are purely logical or mathematical, to be answered by logical or mathematical propositions, and therefore not philosophical; (2) those which are factual, to be answered by some statement belonging to empirical science, and therefore again not philosophical; (3) those which are combinations of (1) and (2), and therefore again not philosophical; and (4) meaningless pseudo-problems such as, ‘Do all cats equal 173?’ or, ‘Is Socrates identical?’ or, ‘Does an invisible, untouchable, and apparently altogether unknowable Socrates exist?’.
Wittgenstein’s idea of eradicating philosophy (and theology) with the help of an adaptation of Russell’s theory of types was ingenious and original (and more radical even than Comte’s positivism, which it resembles closely).9 This idea became the inspiration of a powerful modern school of language analysts who have inherited his belief that there are no genuine philosophical problems, and that all a philosopher can do is to unmask and dissolve the linguistic puzzles which have been proposed by traditional philosophy.
My own view of the matter is that only as long as I have genuine philosophical problems to solve shall I continue to take an interest in philosophy. I fail to understand the attraction of a philosophy without problems. I know, of course, that many people talk nonsense; and it is conceivable that it should become one’s task (an unpleasant one) to unmask somebody’s nonsense, for it may be dangerous nonsense. But I believe that some people have said things which were not very good sense, and certainly not very good grammar, but which were all the same highly interesting and exciting, and perhaps more worth listening to than the good sense of others. I may mention the differential and integral calculus which, especially in its early forms, was no doubt completely paradoxical and nonsensical by Wittgenstein’s (and other) standards; which became, however, reasonably well founded as the result of some hundred years of great mathematical efforts; but whose foundations even at this very moment are still in need, and in the process, of clarification.10 We might remember in this context that it was the contrast between the apparent absolute precision of mathematics and the vagueness and imprecision of philosophical language which deeply impressed the earlier followers of Wittgenstein. But had there been a Wittgenstein to use his weapons against the pioneers of the calculus, and had he succeeded in eliminating their nonsense where their contemporary critics (such as Berkeley, who was fundamentally right) failed, he would have strangled one of the most fascinating and philosophically important developments in the history of thought. Wittgenstein once wrote: ‘Whereof one cannot speak, thereof one must be silent.’ It was, if I remember rightly, Erwin Schrödinger who replied: ‘But it is only here that speaking becomes worth while.’10a The history of the calculus—and perhaps of Schrödinger’s own theory11— bears him out.
No doubt we should all train ourselves to speak as clearly, as precisely, as simply, and as directly, as we can. Yet I believe that there is not a classic of science, or of mathematics, or indeed a book worth reading that could not be shown, by a skilful application of the technique of language analysis, to contain many meaningless pseudo-propositions and what some people might call ‘tautologies’.
Moreover, I believe that even Wittgenstein’s original adaptation of Russell’s theory rests upon a logical mistake. From the point of view of modern logic there no longer appears to be any justification for speaking of pseudo-statements or type mistakes or category-mistakes within ordinary, naturally grown languages (as opposed to artificial calculi) so long as the conventional rules of custom and grammar are observed. One may even say that the positivist who tells us with the air of the initiated that we are using meaningless words, or that we are talking nonsense, literally does not know what he is talking about—he simply repeats what he has heard from others who also did not know. But this raises a technical question which I cannot deal with here. (It is dealt with, however, in chapters 11 to 14, below.)
III
I have promised to say something in defence of Wittgenstein’s views. What I wish to say is, first, that there is much philosophical writing (especially in the Hegelian school) which may justly be criticized as meaningless verbiage; secondly, that this kind of irresponsible writing was checked, for a time at least, by the influence of Wittgenstein and the language analysts (although it is likely that the most wholesome influence in this respect was the example of Russell who, by the incomparable charm and clarity of his writings, established the fact that subtlety of content is compatible with lucidity and unpretentiousness of style).
But I am prepared to admit more. In partial defence of Wittgenstein’s views, I am prepared to adopt the following two theses.
My first thesis is that every philosophy, and especially every philosophical ‘school’, is liable to degenerate in such a way that its problems become practically indistinguishable from pseudo-problems, and its cant, accordingly, practically indistinguishable from meaningless babble. This, I shall try to show, is a consequence of philosophical inbreeding. The degeneration of philosophical schools in its turn is the consequence of the mistaken belief that one can philosophize without having been compelled to philosophize by problems which arise outside philosophy—in mathematics, for example, or in cosmology, or in politics, or in religion, or in social life. In other words my first thesis is this. Genuine philosophical problems are always rooted in urgent problems outside philosophy, and they die if these roots decay. In their efforts to solve them, philosophers are liable to pursue what looks like a philosophical method or technique or an unfailing key to philosophical success.12 But no such methods or techniques exist; in philosophy methods are unimportant; any method is legitimate if it leads to results capable of being rationally discussed. What matters is not methods or techniques but a sensitivity to problems, and a consuming passion for them; or, as the Greeks said, the gift of wonder.
There are those who feel the urge to solve a problem, those for whom a problem becomes real, like a disorder which they have to get out of their system.13 They may make a contribution even if they bind themselves to a particular method or a technique. But there are others who do not feel this urge, who have no serious and pressing problem but who nevertheless produce exercises in fashionable methods, and for whom philosophy is application (of whatever insight or technique you like) rather than search. They are luring philosophy into the bog of pseudo-problems and verbal puzzles; either by offering us pseudo-problems for real ones (the danger which Wittgenstein saw), or by persuading us to concentrate upon the endless and pointless task of unmasking what they rightly or wrongly take for pseudo-problems or ‘puzzles’ (the trap into which Wittgenstein fell).
My second thesis is that what appears to be the prima facie method of teaching philosophy is liable to produce a philosophy which answers Wittgenstein’s description. What I mean by ‘prima facie method of teaching philosophy’, and what would seem to be the only method, is that of giving the beginner (whom we take to be unaware of the history of mathematical, cosmological, and other ideas of science as well as of politics) the works of the great philosophers to read; the works, say, of Plato and Aristotle, Descartes and Leibniz, Locke, Berkeley, Hume, Kant and Mill. What is the effect of such a course of reading? A new world of astonishingly subtle and vast abstractions opens itself before the reader; abstractions on an extremely high and difficult level. Thoughts and arguments are put before his mind which sometimes are not only hard to understand, but which seem to him irrelevant because he cannot find out what they may be relevant to. Yet the student knows that these are the great philosophers, that this is the way of philosophy. Thus he will make an effort to adjust his mind to what he believes (mistakenly, as we shall see) to be their way of thinking. He will attempt to speak their queer language, to match the tortuous spirals of their argumentation, and perhaps even tie himself up in their curious knots. Some may learn these tricks in a superficial way, others may begin to become genuinely fascinated addicts. Yet I feel that we ought to respect the man who having made his effort comes ultimately to what may be described as Wittgenstein’s conclusion: ‘I have learned the jargon as well as anybody. It is very clever and captivating. In fact, it is dangerously captivating; for the simple truth about the matter is that it is much ado about nothing—just a lot of nonsense.’
Now I believe such a conclusion to be grossly mistaken; yet it is the almost inescapable outcome, I contend, of the prima facie method of teaching philosophy here described. (I do not deny, of course, that some particularly gifted students may find very much more in the works of the great philosophers than this story indicates—and without self-deception.) For the student’s chance of discovering the extra-philosophical problems (mathematical, scientific, moral, and political problems) which inspired these great philosophers is very small indeed. As a rule, these problems can be discovered only by studying the history of, for example, scientific ideas, and especially the problem-situation in mathematics and the sciences during the period in question; and this in turn presupposes a considerable acquaintance with mathematics and science. Only if he understands the contemporary problem-situation in the sciences can the student of the great philosophers understand that they tried to solve urgent and concrete problems; problems which they found could not be dismissed. And only after understanding this can the student attain a different picture of the great philosophies—one which makes sense of the apparent nonsense.
I shall try to establish my two theses with the help of examples; but before turning to these examples, I wish to summarize my theses, and to balance my account with Wittgenstein.
My two theses amount to the contention that as philosophy is deeply rooted in non-philosophical problems, Wittgenstein’s negative judgment is correct, by and large, so far as philosophies are concerned which have forgotten their extra-philosophical roots; and that these roots are easily forgotten by philosophers who ‘study’ philosophy, instead of being forced into philosophy by the pressure of non-philosophical problems.
My view of Wittgenstein’s doctrine may be summed up as follows. It is perhaps true, by and large, that ‘pure’ philosophical problems do not exist; for indeed the purer a philosophical problem becomes the more is lost of its original significance, and the more liable is its discussion to degenerate into empty verbalism. On the other hand there exist not only genuine scientific problems, but genuine philosophical problems. Even if, upon analysis, these problems turn out to have factual components, they need not be classified as belonging to science. And even if they should be soluble by, say, purely logical means they need not be classified as purely logical or tautological. Analogous situations arise in physics. For example, the problem of explaining series of spectral lines (with the help of a hypothesis concerning the structure of atoms) may turn out to be soluble by purely mathematical calculations. But this again does not imply that the problem belonged to pure mathematics rather than to physics. We are perfectly justified in calling a problem ‘physical’ if it is connected with problems and theories which have been traditionally discussed by physicists (such as the problem of the constitution of matter) even if the means used for its solution turn out to be purely mathematical. As we have seen, the solution of problems may cut through the boundary of many sciences. Similarly, a problem may rightly be called ‘philosophical’ if we find that although originally it arose in connection with, say, atomic theory it is more closely connected with the problems and theories which have been discussed by philosophers than with theories nowadays treated by physicists. And again, it does not matter in the least what kind of methods we use in solving such a problem. Cosmology, for example, will always be of great philosophical interest even though in some of its methods it has become closely allied with what is perhaps better called ‘physics’. To say that since it deals with factual issues it must belong to science rather than to philosophy is not only pedantic but clearly the result of an epistemological, and thus of a philosophical, dogma. Similarly, there is no reason why a problem soluble by logical means should be denied the attribute ‘philosophical’. It may well be typically philosophical, or physical, or biological. Logical analysis played a considerable part in Einstein’s special theory of relativity; and it was partly this fact which made the theory philosophically interesting, and which gave rise to a wide range of philosophical problems connected with it.
Wittgenstein’s doctrine turns out to be the result of the thesis that all genuine statements (and therefore all genuine problems) can be classified into one of two exclusive classes: factual statements (synthetic a posteriori), which belong to the empirical sciences, and logical statements (analytic a priori), which belong to pure formal logic or pure mathematics. This simple dichotomy, although extremely valuable for a rough survey, turns out to be for many purposes too simple.14 But although it is specially designed, as it were, to exclude the existence of philosophical problems, it falls considerably short of this aim; for even if we accept the dichotomy we can still claim that factual or logical or mixed problems may turn out, in certain circumstances, to be philosophical.
IV
I now turn to my first example: Plato and the Crisis in Early Greek Atomism.
My thesis here is that Plato’s central philosophical doctrine, the so-called Theory of Forms or Ideas, cannot be properly understood except in an extra-philosophical context;15 more especially in the context of the critical problem situation in Greek science16 (mainly in the theory of matter) which developed as a result of the discovery of the irrationality of the square root of two. If my thesis is correct, Plato’s theory has not so far been fully understood. (Whether a ‘full’ understanding can ever be achieved is, of course, most questionable.) But a more important consequence would be that it can never be understood by philosophers trained in accordance with the prima facie method described in the foregoing section—unless, of course, they are specially and ad hoc informed of the relevant facts. (These they may have to accept on authority—which means abandoning the prima facie method of teaching philosophy described above.)
It seems likely17 that Plato’s Theory of Forms is both in origin and in content closely connected with the Pythagorean theory that all things are in essence numbers. The details of this connection and the connection between Atomism and Pythagoreanism are perhaps not so well known. I will therefore briefly tell the story here, as I see it at present.
It appears that the founder of the Pythagorean order or sect was deeply impressed by two discoveries. The first was that a prima facie purely qualitative phenomenon such as musical harmony was, in essence, based upon the purely numerical ratios 1 : 2; 2 : 3; 3 : 4. The second was that the ‘right’ or ‘straight’ angle (obtainable for example by folding a leaf twice so that the two folds form a cross) was connected with the purely numerical ratios 3 : 4 : 5, or 5 : 12 : 13 (the sides of rectangular triangles). These two discoveries, it appears, led Pythagoras to the somewhat fantastic generalization that all things are, in essence, numbers or ratios of numbers; or that number is the ratio (logos = reason), the rational essence, of things, or their real nature.
Fantastic as this idea was, it proved fruitful in many ways. One of its most successful applications was to simple geometrical figures such as squares, rectangular and isosceles triangles, and also to certain simple solids such as pyramids. The treatment of some of these geometrical problems was based upon the so-called gnōmōn.
This can be explained as follows. If we indicate a square by four dots,
we may interpret this as the result of adding three dots to the one dot on the upper left corner. These three dots are the first gnōmōn; we may indicate it thus:
By adding a second gnōmōn, consisting of five more dots, we obtain
One sees at once that every number of the sequence of odd numbers, 1, 3, 5, 7 …, forms the gnōmōn of a square, and that the sums 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, … are the square numbers, and that if n is the (number of dots in the) side of a square, its area (total number of dots = n2) will be equal to the sum of the first n odd numbers.
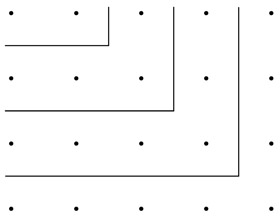
As with the treatment of squares, so with the treatment of equilateral triangles. The following figure may be regarded as representing a growing triangle—growing downwards through the addition of ever new horizontal lines of dots.
Here each gnōmōn is a last horizontal line of dots and each element of the sequence 1, 2, 3, 4, … is a gnōmōn. The ‘triangular numbers’ are the sums 1 + 2; 1 + 2 + 3; 1 + 2 + 3 + 4, etc., that is, the sums of the first n natural numbers. By putting two such triangles side by side
we obtain the parallelogram with the horizontal side n + 1 and the other side n, containing n(n + 1) dots. Since it consists of two isosceles triangles its number is 2(1 + 2 + … + n), so that we obtain the equation
and thus
From this it is easy to obtain the general formula for the sum of an arithmetical series.
We also obtain ‘oblong numbers’, that is the numbers of oblong rectangular figures of which the simplest is
with the oblong numbers 2 + 4 + 6 …; the gnōmōn of an oblong is an even number, and the oblong numbers are the sums of the even numbers.
These considerations were extended to solids; for example, by summing the first triangular numbers, pyramid numbers were obtained. But the main application was to plane figures, or shapes, or ‘Forms’. These were believed to be characterized by the appropriate sequence of numbers, and thus by the numerical ratios of the consecutive numbers of the sequence. In other words, ‘Forms’ are numbers or ratios of numbers. On the other hand, not only shapes of things, but also abstract properties, such as harmony and ‘straightness’ are numbers. In this way the general theory that numbers are the rational essences of all things is arrived at.
It seems probable that the development of this view was influenced by the similarity of the dot-diagrams with the diagram of a constellation such as the Lion, or the Scorpion, or the Virgo. If a Lion is an arrangement of dots it must have a number. In this way Pythagoreanism seems to be connected with the belief that the numbers, or ‘Forms’, are heavenly shapes of things.
V
One of the main elements of this early theory was the so-called ‘Table of Opposites’, based upon the fundamental distinction between odd and even numbers. It contains such things as

In reading through this strange table one gets some idea of the working of the Pythagorean mind, and why not only the ‘Forms’ or shapes of geometrical figures were considered to be numbers, in essence, but also abstract ideas, such as Justice and, of course, Harmony and Health, Beauty and Knowledge. The table is interesting also because it was taken over, with very little alteration, by Plato. The earliest version of Plato’s famous theory of ‘Forms’ or ‘Ideas’ may indeed be described, somewhat roughly, as the doctrine that the ‘Good’ side of the Table of Opposites constitutes an (invisible) Universe, a Universe of Higher Reality, of the Unchanging and Determinate ‘Forms’ of all things; and that True and Certain Knowledge (epistēmē = scientia = science) can be of this Unchanging and Real Universe only, while the visible world of change and flux in which we live and die, the world of generation and destruction, the world of experience, is only a kind of reflection or copy of that Real World. It is only a world of appearance of which no True and Certain Knowledge can be obtained. All that can be obtained in the place of Knowledge (epistēmē) are the plausible but uncertain and prejudiced opinions (doxa) of fallible mortals.18 In his interpretation of the Table of Opposites Plato was influenced by Parmenides, the man whose challenge led to the development of Democritus’ atomic theory.
VI
The Pythagorean theory, with its dot-diagrams, contains no doubt the suggestion of a very primitive atomism. How far the atomic theory of Democritus was influenced by Pythagoreanism is difficult to assess. Its main influences came, so much seems certain, from the Eleatic School: from Parmenides and from Zeno. The basic problem of this school, and of Democritus, was that of the rational understanding of change. (I differ here from the interpretations of Cornford and others.) I think that this problem derives from Heraclitus, and thus from Ionian rather than from Pythagorean thought,19 and that it still remains the fundamental problem of Natural Philosophy.
Although Parmenides was perhaps not a physicist (unlike his great Ionian predecessors), he may be described, I believe, as having fathered theoretical physics. He produced an anti-physical20 (rather than a-physical, as Aristotle said) theory which, however, was the first hypothetico-deductive system. And it was the beginning of a long series of such systems of physical theories, each of which was an improvement on its predecessor. As a rule the improvement was found necessary because it was realized that the earlier system was falsified by certain facts of experience. Such an empirical refutation of the consequences of a deductive system leads to efforts at its reconstruction, and thus to a new and improved theory which as a rule clearly bears the marks of its ancestry, of the older theory as well as of the refuting experience.
These experiences or observations were, we shall see, very crude at first, but they became more and more subtle as the theories became more and more capable of accounting for the cruder observations. In the case of Parmenides’ theory the clash with observation was so obvious that it would seem perhaps fanciful to describe the theory as the first hypothetico-deductive system of physics. We may, therefore, describe it as the last pre-physical deductive system, whose refutation or falsification gave rise to the first physical theory of matter, the atomistic theory of Democritus.
Parmenides’ theory is simple. He finds it impossible to understand change or movement rationally, and concludes that there is really no change—or that change is only apparent. But before we indulge in feelings of superiority in the face of such a hopelessly unrealistic theory we should first realize that there is a serious problem here. If a thing X changes, then clearly it is no longer the same thing X. On the other hand, we cannot say that X changes without implying that X persists during the change; that it is the same thing X, at the beginning and at the end of the change. Thus it appears that we arrive at a contradiction, and that the idea of a thing that changes, and therefore the idea of change, is impossible.
All this sounds very philosophical and abstract, and so it is. But it is a fact that the difficulty here indicated has never ceased to make itself felt in the development of physics.21 And a deterministic system such as the field theory of Einstein might even be described as a four-dimensional version of Parmenides’ unchanging three-dimensional universe. For in a sense no change occurs in Einstein’s four-dimensional block-universe. Everything is there just as it is, in its four-dimensional locus; change becomes a kind of ‘apparent’ change; it is ‘only’ the observer who as it were glides along his world-line and becomes successively conscious of the different loci along this world-line; that is, of his spatiotemporal surroundings …
To return from this new Parmenides to the older father of theoretical physics, we may paraphrase his deductive theory roughly as follows.
- (1) Only what is, is.
- (2) What is not does not exist.
- (3) Non-being, that is, the void, does not exist.
- (4) The world is full.
- (5) The world has no parts; it is one huge block (because it is full).
- (6) Motion is impossible (since there is no empty space within which anything could move).
The conclusions (5) and (6) were obviously contradicted by facts. Thus Democritus argued from the falsity of the conclusion to that of the premises:
- (6’) There is motion (thus motion is possible).
- (5’) The world has parts; it is not one, but many.
- (4’) Thus the world cannot be full.22
- (3’) The void (or non-being) exists.
So far the theory had to be altered. With regard to being, or to the many existing things (as opposed to the void), Democritus adopted Parmenides’ theory that they had no parts. They were indivisible (atoms), because they were full, because they had no void inside.
The main point about this theory is that it gives a rational account of change. The world consists of empty space (the void) with atoms in it. The atoms do not change; they are Parmenidean indivisible block universes in miniature.23 All change is due to rearrangement of atoms in space. Accordingly all change is movement. Since the only kind of novelty which can arise on this view is novelty of arrangement,24 it will be possible, in principle, to predict all future changes in the world, provided we manage to predict the motion of all atoms (or, in modern parlance, all mass-points).
Democritus’ theory of change was of tremendous importance for the development of physical science. It was partly accepted by Plato, who retained much of atomism, explaining change, however, not only by unchanging yet moving atoms but also by other ‘Forms’ which were subject neither to change nor to motion. But it was condemned by Aristotle who taught in its stead25 that all change was the unfolding of the inherent potentialities of essentially unchanging substances. Aristotle’s theory of substances as the subjects of change became dominant; but it proved barren;26 and Democritus’ metaphysical theory that all change must be explained by movement became the tacitly accepted programme of work in physics down to our own day. It is still part of the philosophy of physics, in spite of the fact that physics itself has outgrown it (to say nothing of the biological and social sciences). For with Newton, in addition to moving mass-points, forces of changing intensity (and direction) enter the scene. True, the changes of the Newtonian forces can be explained as due to, or dependent upon, motion; that is, upon the changing position of particles. But they are nevertheless not identical with changes in the position of particles; owing to the inverse square law the dependence is not even a linear one. And with Faraday and Maxwell, changing fields of forces become as important as material atomic particles. That our modern atoms turn out to be composite is a minor matter; from Democritus’ point of view not our atoms but rather our elementary particles would be the real atoms—except that these too turn out to be liable to change. Thus we have a most interesting situation. A philosophy of change, designed to meet the difficulty of understanding change rationally, serves science for thousands of years, but is ultimately superseded by the development of science itself; and this fact passes practically unnoticed by philosophers who are busily denying the existence of philosophical problems.
Democritus’ theory was a marvellous achievement. It provided a theoretical framework for the explanation of most of the empirically known properties of matter (discussed already by the Ionians), such as compressibility, degrees of hardness and resilience, rarefaction and condensation, coherence, disintegration, combustion, and many others. But the theory was important not only as an explanation of the phenomena of experience. First, it established the methodological principle that a deductive theory or explanation must ‘save the phenomena’;27 that is, be in agreement with experience. Secondly, it showed that a theory may be speculative, and based upon the fundamental (Parmenidean) principle that the world as it must be understood by argumentative thought turns out to be different from the world of prima facie experience, from the world as seen, heard, smelled, tasted, touched;28 and that such a speculative theory may nevertheless accept the empiricist ‘criterion’ that it is the visible that decides the acceptance or rejection of a theory of the invisible29 (such as the atoms). This philosophy has remained fundamental to the whole development of physics, and has continued to conflict with all ‘relativistic’ and ‘positivistic’30 philosophical tendencies.
Furthermore, Democritus’ theory led to the first successes of the method of exhaustion (the forerunner of the calculus of integration), since Archimedes himself acknowledged that Democritus was the first to formulate the theory of the volumes of cones and pyramids.31 But perhaps the most fascinating element in Democritus’ theory is his doctrine of the quantization of space and time. I have in mind the doctrine, now extensively discussed,32 that there is a shortest distance and a smallest time interval; that is to say, that there are distances in space and time (elements of length and time, Democritus’ amerēs33 in contradistinction to his atoms) such that no smaller ones are possible.
VII
Democritus’ atomism was developed and expounded as a point for point reply34 to the detailed arguments of his Eleatic predecessors, of Parmenides and his pupil Zeno. Especially Democritus’ theory of atomic distances and time intervals is the direct result of Zeno’s arguments, or more precisely, of the rejection of Zeno’s conclusions. But nowhere in what we know of Zeno is there an allusion to the discovery of irrationals which is of decisive importance for our story.
We do not know the date of the proof of the irrationality of the square root of two, or the date when the discovery became publicly known. Although there existed a tradition ascribing it to Pythagoras (sixth century B.C.), and although some authors35 call it the ‘theorem of Pythagoras’, there can be little doubt that the discovery was not made, and certainly not publicly known, before 450 B.C., and probably not before 420. Whether Democritus knew about it is uncertain. I now feel inclined to believe that he did not; and that the title of Democritus’ two lost books, Peri alogōn grammōn kai nastōn, should be translated ‘On Illogical Lines and Full Bodies (Atoms)’,36 and that these two books do not contain any reference to the discovery of irrationality.37
My belief that Democritus was unaware of the problem of irrationals is based on the fact that there are no traces of a defence of his theory against the blow which it received from this discovery. Yet the blow was as fatal to Atomism as it was to Pythagoreanism. Both theories were based on the doctrine that all measurement is, ultimately, counting of natural units, so that every measurement must be reducible to pure numbers. The distance between any two atomic points must, therefore, consist of a certain number of atomic distances; thus all distances must be commensurable. But this turns out to be impossible even in the simple case of the distances between the corners of a square, because of the incommensurability of its diagonal d with its side a.
The English term ‘incommensurable’ is somewhat unfortunate. What is meant is, rather, the non-existence of a ratio of natural numbers; for example, what can be proved in the case of the diagonal of the unit square is that there do not exist two natural numbers, n and m, whose ratio, n/m, is equal to the diagonal of the unit square. ‘Incommensurability’ thus does not mean incomparability by geometrical methods, or by measurement, but incomparability by arithmetical methods of counting, or by natural numbers, including the characteristic Pythagorean method of comparing ratios of natural numbers and including, of course, the counting of units of length (or of ‘measures’).
Let us look back, for a moment, at the characteristics of this method of natural numbers and their ratios. Pythagoras’ emphasis upon Number was fruitful from the point of view of the development of scientific ideas. This is often but somewhat loosely expressed by saying that the Pythagoreans initiated numerical scientific measurement. Now what I want to emphasize is that for the Pythagoreans all this was counting rather than measuring. It was the counting of numbers, of invisible essences or ‘Natures’ which were Numbers of little dots. They knew that we cannot count these little dots directly, since they are invisible, and that we actually do not count the Numbers or Natural Units, but measure, i.e. count arbitrary visible units. But they interpreted the significance of measurements as revealing, indirectly, the true Ratios of the Natural Units or of the Natural Numbers.
Thus Euclid’s methods of proving the so-called ‘Theorem of Pythagoras’ (Euclid, 1, 47) according to which, if a is the side of a triangle opposite to its right angle between b and c,
was foreign to the spirit of Pythagorean mathematics. It seems now accepted that the theorem was known to the Babylonians and geometrically proved by them. Yet neither Pythagoras nor Plato appear to have known Euclid’s geometrical proof (which uses different triangles with common base and height); for the problem for which they offered solutions, the arithmetical one of finding the integral solutions for the sides of rectangular triangles, can, if (1) is known, be easily solved by the formula (m and n are natural numbers, and m > n)
But formula (2) was apparently unknown to Pythagoras and even to Plato. This emerges from the tradition38 according to which Pythagoras proposed the formula (obtained from (2) by putting m = n + 1)
which can be read offthe gnōmōn of the square numbers, but which is less general than (2), since it fails, for example, for 17: 8: 15. To Plato, who is reported39 to have improved Pythagoras’ formula (3), is attributed another formula which still falls short of the general solution (2).
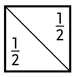
In order to show the difference between the Pythagorean or arithmetical method and the geometrical method, Plato’s proof that the square over the diagonal of the unit square (that is, the square with the side 1 and an area of measure 1) has an area of twice the unit square (that is, an area of measure 2) may be mentioned. It consists in drawing a square with the diagonal
and then showing that we may extend the drawing thus
from which we obtain the result by counting. But the transition from the first to the second of these figures cannot possibly be shown to be valid by the arithmetic of dots, and not even by the methods of ratios.
That this is, indeed, impossible, is established by the famous proof of the irrationality of the diagonal, that is, of the square root of 2, assumed as well-known by Plato and Aristotle. It consists in showing that the assumption
that is, that √2 is equal to a ratio of any two natural numbers, n and m, leads to an absurdity.
We first note that we can assume that
For if both were even, then we could always cancel out the factor 2 so as to obtain two other natural numbers, n′ and m′, such that n/m = n′/m′, and such that at most one of the two numbers, n′ and m′, would be even. Now by squaring (1) we get
and from this
and thus
Thus there must exist a natural number a so that
and we get from (3) and (6)
and thus
But this means
It is clear that (5) and (9) contradict (2). Thus the assumption that there are two natural numbers, n and m, whose ratio equals √2, leads to an absurd conclusion. Therefore Ö2 is not a ratio, it is ‘irrational’.
This proof uses only the arithmetic of natural numbers. It therefore uses purely Pythagorean methods, and the tradition that it was discovered within the Pythagorean school need not be questioned. But it is improbable that the discovery was made by Pythagoras, or that it was made very early: Zeno does not seem to know it, nor does Democritus. Moreover, as it destroys the basis of Pythagoreanism, it is reasonable to assume that it was not made long before the order reached the height of its influence; at least not before it was well established; for it seems to have contributed to its decline. The tradition that it was made within the order but kept secret seems to me very plausible. It may be supported by considering that the old term for ‘irrational’—‘arrhētos’, ‘unutterable’, or ‘unmentionable’—may well have hinted at an unmentionable secret. Tradition has it that the member of the school who gave away the secret was killed for his treachery.40 However this may be, there is little doubt that the realization that irrational magnitudes (they were, of course, not recognized as numbers) existed, and that their existence could be proved, undermined the faith of the Pythagorean order; it destroyed the hope of deriving cosmology, or even geometry, from the arithmetic of natural numbers.
VIII
It was Plato who realized this fact, and who in the Laws stressed its importance in the strongest possible terms, denouncing his compatriots for their failure to gauge its implications. I believe that his whole philosophy, and especially his theory of ‘Forms’ or ‘Ideas’, was influenced by it.
Plato was very close to the Pythagorean as well as to the Eleatic School; and although he appears to have felt antipathetic to Democritus he was himself a kind of atomist. (Atomist teaching remained as one of the school traditions of the Academy.41) This is not surprising in view of the close relation between Pythagorean and atomistic ideas. But all this was threatened by the discovery of the irrationals. I suggest that Plato’s main contribution to science sprang from his realization of the problem of the irrational, and from the modification of Pythagoreanism and atomism which he undertook in order to rescue science from a catastrophic situation.
He realized that the purely arithmetical theory of nature was defeated, and that a new mathematical method for the description and explanation of the world was needed. Thus he encouraged the development of an autonomous geometrical method. It found its fulfilment in the ‘Elements’ of the Platonist Euclid.
What are the facts? I shall try briefly to put them all together.
(1) Pythagoreanism and atomism in Democritus’ form were both fundamentally based on arithmetic; that is to say on counting.
(2) Plato emphasized the catastrophic character of the discovery of the irrationals.
(3) He inscribed over the gates of the Academy: ‘Nobody Untrained in Geometry May Enter My House’. But geometry, according to Plato’s immediate pupil Aristotle42 as well as Euclid, typically treats of incommensurables or irrationals, in contradistinction to arithmetic which treats of ‘the odd and the even’ (i.e. of integers and their relations).
(4) Within a short time after Plato’s death his school produced, in Euclid’s Elements, a work one of whose main points was that it freed mathematics from the ‘arithmetical’ assumption of commensurability or rationality.
(5) Plato himself contributed to this development, and especially to the development of solid geometry.
(6) More especially, he gave in the Timaeus a specifically geometrical version of the formerly purely arithmetical atomic theory; a version which constructed the elementary particles (the famous Platonic bodies) out of triangles which incorporated the irrational square roots of two and of three. (See below.) In nearly all other respects he preserved Pythagorean ideas as well as some of the most important ideas of Democritus.43 At the same time he tried to eliminate Democritus’ void; for he realized44 that motion remains possible even in a ‘full’ world, provided motion is conceived as of the character of vortices in a liquid. Thus he retained some of the most fundamental ideas of Parmenides.45
(7) Plato encouraged the construction of geometrical models of the world, and especially models explaining the planetary movements. And I believe that Euclid’s geometry was not intended as an exercise in pure geometry (as is now usually assumed), but as an organon of a theory of the world. According to this view the ‘Elements’ is not a ‘textbook of geometry’ but an attempt to solve systematically the main problems of Plato’s cosmology. This was done with such success that the problems, having been solved, disappeared and were almost forgotten; though a trace remains in Proclus who writes, ‘Some have thought that the subject matter of the various books [of Euclid] pertains to the cosmos, and that they are intended to help us in our contemplation of, and theorizing about, the universe’ (op. cit., note 38 above, Prologus, II, p. 71, 2–5). Yet even Proclus does not mention in this context the main problem—that of the irrationals (of course he does mention it elsewhere); though he points out, rightly, that the ‘Elements’ culminate with the construction of the ‘cosmic’ or ‘Platonic’ regular polyhedra. Ever since46 Plato and Euclid, but not before, geometry (rather than arithmetic) appears as the fundamental instrument of all physical explanations and descriptions, in the theory of matter as well as in cosmology.47
IX
These are the historical facts. They go a long way, I believe, towards establishing my main thesis: that what I have called the prima facie method of teaching philosophy cannot lead to an understanding of the problems that inspired Plato. Nor can it lead to an appreciation of what may be justly claimed to be his greatest philosophical achievement, the geometrical theory of the world. The great physicists of the Renaissance—Copernicus, Galileo, Kepler, Gilbert—who turned from Aristotle to Plato intended by this move to replace the Aristotelian qualitative substances or potentialities by a geometrical method of cosmology. Indeed, that is what the Renaissance (in science) largely meant: a renaissance of the geometrical method, which was the basis of the works of Euclid, Aristarchus, Archimedes, Copernicus, Kepler, Galileo, Descartes, and became the basis of the works of Newton, Maxwell, and Einstein.
But is this achievement properly described as philosophical? Does it not rather belong to physics—a factual science; and to pure mathematics—a branch, as Wittgenstein’s school would contend, of tautological logic?
I believe that we can at this stage see fairly clearly why Plato’s achievement (although it has no doubt its physical, its logical, its mixed, and its nonsensical components) was a philosophical achievement; why at least part of his philosophy of nature and of physics has lasted and, I believe, will last.
What we find in Plato and his predecessors is the conscious construction and invention of a new approach towards the world and towards knowledge of the world. This approach transforms an originally theological idea, the idea of explaining the visible world by a postulated invisible world,48 into the fundamental instrument of theoretical science. The idea was explicitly formulated by Anaxagoras and Democritus49 as the principle of investigation into the nature of matter or body; visible matter was to be explained by hypotheses about invisibles, about an invisible structure which is too small to be seen. With Plato this idea is consciously accepted and generalized; the visible world of change is ultimately to be explained by an invisible world of unchanging ‘Forms’ (or substances, or essences, or ‘natures’; that is, as I shall try to show in more detail, geometrical shapes or figures).
Is this idea about the invisible structure of matter a physical or a philosophical idea? If a physicist merely acts upon this theory, if he accepts it, perhaps unconsciously, by accepting the traditional problems of his subject as furnished by the problem-situation with which he is confronted; and if he, so acting, produces a new specific theory of the structure of matter, then I should not call him a philosopher. But if he reflects upon it, and, for example, rejects it (like Berkeley or Mach), preferring a phenomenological or positivistic physics to the theoretical and somewhat theological approach, then he may be called a philosopher. Similarly, those who consciously sought the theoretical approach, who constructed it, and who explicitly formulated it, and thus transferred the hypothetical and deductive method from theology to physics, were philosophers, even though they were physicists in so far as they acted upon their own precepts and tried to produce actual theories of the invisible structure of matter.
But I shall not pursue the question of the proper application of the label ‘philosophy’ any further; for this problem, which is Wittgenstein’s problem, clearly turns out to be one of linguistic usage; it is indeed a pseudo-problem, and one which by now must be rapidly degenerating into a bore to my audience. Yet I wish to add a few words on Plato’s theory of Forms or Ideas, or, to be more precise, on point (6) in the list of historical facts given above.
Plato’s theory of the structure of matter can be found in the Timaeus. It has at least a superficial similarity to the modern theory of solids which interprets them as crystals. His physical bodies are composed of invisible elementary particles of various shapes, the shapes being responsible for the macroscopic properties of visible matter. The shapes of the elementary particles are determined in their turn by the shapes of the plane figures which form their sides. And these plane figures, in their turn, are ultimately all composed of two elementary triangles: the half-square (or isosceles rectangular) triangle which incorporates the square root of two, and the half-equilateral rectangular triangle which incorporates the square root of three, both of them irrationals.
These triangles, in their turn, are described as the copies50 of unchanging ‘Forms’ or ‘Ideas’, which means that specifically geometrical ‘Forms’ are admitted into the heaven of the Pythagorean arithmetical Form-Numbers.
There is little doubt that the motive of this construction is the attempt to solve the crisis of atomism by incorporating irrationals into the last elements of which the world is built. Once this has been done the difficulty arising from the existence of irrational distances is overcome.
But why did Plato choose just these two triangles? I have elsewhere51 expressed the view, as a conjecture, that Plato believed that all other irrationals might be obtained by adding to the rationals multiples of the square roots of two and three.52 I now feel more confident that the crucial passage in the Timaeus does imply this doctrine (which was mistaken, as Euclid later showed). For in the passage in question Plato says quite clearly, ‘All triangles originate from two, each having a right angle’, going on to specify these two as the half-square and half-equilateral. But in the context this can only mean that all triangles originate somehow from these two. This seems to be a hint at the mistaken theory of the relative commensurability of all irrationals with sums of rationals and the square roots of two and three.53
But Plato does not pretend that he has a proof of the theory in question. On the contrary, he says that he assumes the two triangles as principles, ‘in accordance with an account which combines likely conjecture with necessity’. And a little later, after explaining that he takes the half-equilateral triangle as the second of his principles, he says, ‘The reason is too long a story; but if anybody should probe into this matter, and prove that it has this property’ (I suppose the property that all other triangles can be composed of these two) ‘then the prize is his, with all our good will’.54 The language is somewhat obscure, and the likely reason is that Plato was conscious that he lacked a proof of his (mistaken) conjecture concerning these two triangles, and felt it should be supplied by somebody.
The obscurity of the passage had, it appears, the strange effect that Plato’s quite clearly stated choice of triangles which introduce irrationals into his world of Forms escaped the notice of most of his readers and commentators in spite of Plato’s emphasis upon the problem of irrationality in other places. And this in turn may perhaps explain why Plato’s Theory of Forms could appear to Aristotle to be fundamentally the same as the Pythagorean theory of form-numbers,55 and why Plato’s atomism appeared to Aristotle merely as a comparatively minor variation on that of Democritus.56 Aristotle, in spite of taking for granted both the association of arithmetic with the odd and even, and of geometry with the irrational, does not appear to have taken the problem of the irrationals seriously. Proceeding as he did from an interpretation of the Timaeus which identified Plato’s Space with matter, he seems to have taken Plato’s reform programme for geometry for granted; it had been partly carried out by Eudoxus before Aristotle entered the Academy, and Aristotle was only superficially interested in mathematics. He never alludes to the inscription over the Academy gates.
To sum up,56a it seems probable that Plato’s theory of Forms and also his theory of matter were both restatements of the theories of his predecessors, the Pythagoreans and Democritus respectively, in the light of his realization that the irrationals demanded that geometry should come before arithmetic. By encouraging this emancipation of geometry Plato contributed to the development of Euclid’s system, the most important and influential deductive theory ever constructed. By his adoption of geometry as the theory of the world he provided Aristarchus, Newton, and Einstein with their intellectual toolbox. The calamity of Greek atomism was thus transformed into a momentous achievement. But Plato’s scientific interests are partly forgotten. The problem-situation in science which gave rise to his philosophical problems is little understood. And his greatest achievement, the geometrical theory of the world, has influenced our world-picture to such an extent that we unreflectingly take it for granted.
X
One example never suffices. As my second example, out of a great many interesting possibilities, I choose Kant. His Critique of Pure Reason is one of the most difficult books ever written. Kant wrote in great haste,57 and about a problem which, I shall try to show, was not only insoluble but also misconceived. Nevertheless it was not a pseudo-problem, but an inescapable problem which arose out of the contemporary situation in science.
His book was written for people who knew something about Newton’s stellar dynamics and who had at least some idea of his forerunners—of Copernicus, Tycho Brahe, Kepler and Galileo.
It is perhaps hard for intellectuals of our own day, spoilt and blasé as we are by the spectacle of scientific success, to realize what Newton’s theory meant, not just for Kant but for any eighteenth-century thinker. After the unmatched daring with which the Ancients had tackled the riddle of the Universe there had come long periods of decay and recovery, and then a staggering success. Newton had discovered the long sought secret. His geometrical theory, based on and modelled after Euclid, had been received at first with great misgivings, even by its own originator.58 The reason was that the gravitational force of attraction was felt to be ‘occult’, or at least something which needed an explanation. But although no plausible explanation was found (and Newton scorned recourse to ad hoc hypotheses) all misgivings had disappeared long before Kant made his own important contribution to Newtonian theory, 68 years after the Principia.59 No qualified judge60 of the situation could doubt any longer that Newton’s theory was true. It had been tested by the most precise measurements, and it had always been right. It had led to the prediction of minute deviations from Kepler’s laws, and to new discoveries. In a time like ours, when theories come and go like the buses in Piccadilly, and when every schoolboy has heard that Newton has long been superseded by Einstein, it is hard to recapture the sense of conviction which Newton’s theory inspired, or the sense of elation, and of liberation. A unique event had happened in the history of thought, one which could never be repeated: the first and final discovery of the absolute truth about the universe. An age-old dream had come true. Mankind had obtained knowledge, real, certain, indubitable, and demonstrable knowledge—divine scientia or epistēmē, and not merely doxa, human opinion. This sense of conviction became—through Voltaire—the origin of the Enlightenment.60a
Thus for Kant Newton’s theory was simply true, and the belief in its truth remained unshaken for a century after Kant’s death. Kant to the end accepted what he and everybody else took for a fact, the attainment of scientia or epistēmē. At first he accepted it without question. This state he called his ‘dogmatic slumber’. He was roused from it by Hume.
Hume had taught that there could be no such thing as certain knowledge of universal laws, or epistēmē; that all we knew was obtained with the help of observation which could be only of singular (or particular) instances, so that all theoretical knowledge was uncertain. His arguments were convincing (and he was, of course, right). Yet there was a fact, or what appeared as a fact—Newton’s attainment of epistēmē.
Hume roused Kant to the realization of the near absurdity of what he never doubted to be a fact. Here was a problem which could not be dismissed. How could a man have got hold of such knowledge? Knowledge which was general, precise, mathematical, demonstrable, and indubitable, like Euclidean geometry, and yet capable of giving a causal explanation of observed facts?
Thus arose the central problem of the Critique: ‘How is pure natural science possible?’ By ‘pure natural science’—scientia, epistēmē—Kant simply meant Newton’s theory. (This he does not say, unfortunately; and I do not see how a student reading the first Critique, 1781 and 1787, could possibly find out. But that Kant has Newton’s theory in mind is clear from the Metaphysical Foundations of Natural Science, 1786, where he gives an a priori deduction of Newton’s theory, see especially the eight theorems of the Second Main Part, with its Additions, especially Addition 2, Note 1, paragraph 2. Kant relates Newton’s theory, in the fifth paragraph of the final ‘General Note on Phenomenology’, to the ‘starry heavens’. It is also clear from the ‘Conclusion’ of the Critique of Practical Reason, 1788, where the appeal to the ‘starry heavens’ is explained, at the end of the second paragraph, by a reference to the a priori character of the new astronomy.61)
Although the Critique is badly written, and although bad grammar abounds in it, Kant’s central problem was not a linguistic puzzle. Here was knowledge. How could Newton ever attain it? The question was inescapable.62
But it was also insoluble. For the apparent fact of the attainment of epistēmē was no fact. As we now know, or believe we know, Newton’s theory is no more than a marvellous conjecture, an astonishingly good approximation; unique indeed, but not as divine truth, only as a unique invention of a human genius: not epistēmē, but belonging to the realm of doxa. With this Kant’s problem, ‘How is pure natural science possible’, collapses, and the most disturbing of his perplexities disappears.
Kant’s proposed solution of his insoluble problem consisted of what he proudly called his ‘Copernican Revolution’ of the problem of knowledge. Knowledge—epistēmē—was possible because we are not passive receptors of sense data, but their active digestors. By digesting and assimilating them we form and organize them into a Cosmos, the Universe of Nature. In this process we impose upon the material presented to our senses the mathematical laws which are part of our digestive and organizing mechanism. Thus our intellect does not discover universal laws in nature, but it prescribes its own laws and imposes them upon nature.
This theory is a strange mixture of absurdity and truth. It is as absurd as the mistaken problem it attempts to solve; for it proves too much, being designed to prove too much. According to Kant’s theory, ‘pure natural science’ is not only possible; although he does not always realize this, it becomes, contrary to his intention, the necessary result of our mental outfit. For if the fact of our attainment of epistēmē can be explained at all by the fact that our intellect legislates for nature, and imposes its own laws upon it, then the first of these two facts cannot be contingent any more than the second.63 Thus the problem is no longer how Newton could make his discovery but how everybody else could have failed to make it. How is it that our digestive mechanism did not work much earlier?
This is a patently absurd consequence of Kant’s idea. But to dismiss it offhand, and to dismiss his problem as a pseudo-problem, is not good enough. For we can find an element of truth in his idea (and a much needed correction of some Humean views) after reducing his problem to its proper dimensions. His question, we now know, or believe we know, should have been: ‘How are successful conjectures possible?’ And our answer, in the spirit of his Copernican Revolution, might, I suggest, be something like this: Because, as you said, we are not passive receptors of sense data, but active organisms. Because we react to our environment not always merely instinctively, but sometimes consciously and freely. Because we can invent myths, stories, theories; because we have a thirst for explanation, an insatiable curiosity, a wish to know. Because we not only invent stories and theories, but try them out and see whether they work and how they work. Because by a great effort, by trying hard and making many mistakes, we may sometimes, if we are lucky, succeed in hitting upon a story, an explanation, which ‘saves the phenomena’; perhaps by making up a myth about ‘invisibles’, such as atoms or gravitational forces, which explain the visible. Because knowledge is an adventure of ideas. These ideas, it is true, are produced by us, and not by the world around us; they are not merely the traces of repeated sensations or stimuli or what not; here you were right. But we are more active and free than even you believed; for similar observations or similar environmental situations do not, as your theory implied, produce similar explanations in different men. Nor is the fact that we create our theories, and that we attempt to impose them upon the world, an explanation of their success,64 as you believed. For the overwhelming majority of our theories, of our freely invented ideas, are unsuccessful; they do not stand up to searching tests, and are discarded as falsified by experience. Only a very few of them succeed, for a time, in the competitive struggle for survival.65
XI
Few of Kant’s successors appear ever to have understood clearly the precise problem-situation which gave rise to his work. There were two such problems for him: Newton’s dynamics of the heavens, and the absolute standards of human brotherhood and justice to which the French revolutionaries appealed; or, as Kant puts it, ‘the starry heavens above me, and the moral law within me’. But Kant’s ‘starry heavens’ are seldom recognized for what they were: an allusion to Newton.66 From Fichte onward,67 many have copied Kant’s ‘method’ and the difficult style of parts of his Critique. But most of these imitators, unaware of Kant’s original interests and problems, busily tried either to tighten, or else to explain away, the Gordian knot in which Kant, through no fault of his own, had tied himself up.
We must beware of mistaking the well-nigh senseless and pointless subtleties of the imitators for the pressing and genuine problems of the pioneer. We should remember that his problem, although not an empirical one in the ordinary sense, nevertheless turned out, unexpectedly, to be in some sense factual (Kant called such facts ‘transcendental’), since it arose from an apparent, but non-existent, instance of scientia or epistēmē. And we should, I submit, seriously consider the suggestion that Kant’s answer, in spite of its partial absurdity, contained the nucleus of a true philosophy of science.
Notes