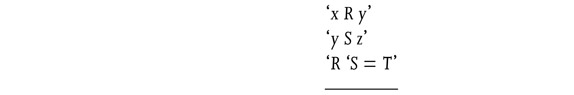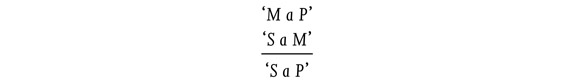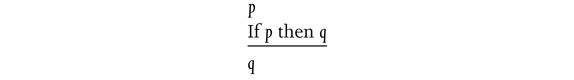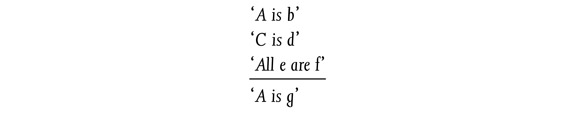Professor Ryle has confined his contribution1 to the applicability of the rules of logic, or more precisely, to the logical rules of inference. I intend to follow him in this, and only later to extend the discussion to the applicability of logical and arithmetical calculi. The distinction I have just made between the logical rules of inference and the so-called logical calculi (such as the propositional calculus or the class calculus or the calculus of relations) needs, however, some clarification, and I shall discuss the distinction, as well as the connection between the rules of inference and the calculi, in section i, before taking up the two main problems before us: that of the applicability of the rules of inference (in section ii), and that of the applicability of the logical calculi (in section viii).
I shall allude to, and make use of, some ideas from Professor Ryle’s paper, and also from his Presidential Address to the Aristotelian Society, Knowing How and Knowing That (1945).2
I
Let us consider a simple example of an argument or of reasoning, formulated in some language, say in ordinary English. The argument will consist of a series of statements. We may assume, perhaps, that somebody argues: ‘Rachel is the mother of Richard. Richard is the father of Robert. The mother of the father is the paternal grandmother. Thus, Rachel is the paternal grandmother of Robert.’
The word ‘thus’ in the last sentence may be taken as an indication that the speaker claims that his argument is conclusive, or valid; or in other words, that the last statement (the conclusion) has been validly drawn from the three foregoing statements (the premises). In this claim, he may be right or wrong. If he is usually right in claims of this kind, then we can say that he knows how to argue. And he may know how to argue without being able to explain to us in words the rules of the procedure which he observes (in common with others who know how to argue); just as a pianist may know how to play well without being able to explain the rules of procedure that underlie a good performance. If a man knows how to argue without always being aware of the rules of procedure, then we usually say that he argues or reasons ‘intuitively’. And if we now read through the above argument, then we may be able to say, intuitively, that the argument is valid. There is little doubt that most of us reason, as a rule, intuitively, in the sense indicated. The formulation and discussion of the rules of procedure that underlie ordinary intuitive arguments is a rather specialized and sophisticated sort of inquiry; it is a business peculiar to the logician. While every reasonably intelligent man knows how to argue— provided the arguments do not become too complicated—there are few who can formulate the rules which underlie these performances and which we may call ‘rules of inference’; there are few who know that (and fewer perhaps who know why) a certain rule of inference is valid.
The particular rule of inference which underlies the argument stated above can be formulated, making use of variables and a few other artificial symbols, by a scheme like this:3
From three premises of the form:
a conclusion may be drawn of the form: ‘x T z’
Here, for ‘x’, ‘y’, and ‘z’, any proper name of individuals may be substituted, and for ‘R’, ‘S’, and ‘T’ any names of relations between individuals; for ‘x R y’, etc., any statement asserting that R holds between x and y, etc.; for ‘R ‘S’ any name of a relation holding between x and z if, and only if, there exists a y such that x R y and y S z; and ‘=’ expresses here equality of extension between relations.
It should be noted that this rule of inference makes assertions about statements of a certain kind or form. This fact distinguishes it clearly from a formula of a calculus (in this case, the calculus of relations) such as:
‘For all R, S, and T; and for all x, y, and z: if x R y and y S z and R ‘S = T, then x T z.’
This formula, undoubtedly, has some similarity to our rule of inference; in fact, it is that statement (in the calculus of relations) which corresponds to our rule of inference. But it is not the same: it asserts something conditionally about all relations and individuals of a certain kind, while the rule of inference asserts something, unconditionally, about all statements of a certain kind—namely that every statement of a certain form is deducible, unconditionally, from a set of statements of another form.
In a similar way, we should distinguish, for instance, between the rule of inference (called ‘Barbara’) of traditional logic:
and the formula of the calculus of classes ‘If M a P and S a M, then S a P’, (or in slightly more modern writing: ‘If c⊂ b and a ⊂ c, then a ⊂ b’); or between the rule of inference—which is called the ‘principle of inference of propositional logic’, or the modus ponendo ponens:
and the formula of the calculus of propositions: ‘If p, and if p then q, then q’.
The fact that, to every well-known rule of inference, there corresponds a logically true hypothetical or conditional formula of some well-known calculus—a ‘logician’s hypothetical’, as Professor Ryle calls these formulae—has led to confusion between rules of inference and the corresponding conditional formulae. But there are important differences. (1) Rules of inference are always statements about statements, or about classes of statements (they are ‘meta-linguistic’); but the formulae of the calculi are not. (2) The rules of inference are unconditional statements about deducibility; but the corresponding formulae of the calculi are conditional or hypothetical ‘If … then …’ statements, which do not mention deducibility or inference, or premises or conclusions. (3) A rule of inference, after substitution of constants for the variables, asserts something about a certain argument—an ‘observance’ of the rule—namely, that this argument is valid; but the corresponding formula, after substitution, yields a logical truism, i.e. a statement such as ‘All tables are tables’, although in hypothetical form, as for example, ‘If it is a table, then it is a table’ or ‘If all men are mortal, and all Greeks are men, then all Greeks are mortal’. (4) The rules of inference are never used as premises in those arguments which are formulated in accordance with them; but the corresponding formulae are used in this way. In fact, one of the main motives in constructing logical calculi is this: by using the ‘logician’s hypotheticals’ (i.e. those hypothetical truisms which correspond to a certain rule of inference) as a premise, we can dispense with the corresponding rule of inference. By this method we can eliminate all the different rules of inference—except one, the above-mentioned ‘principle of inference’ (or two, if we make use of the ‘principle of substitution’, which, however, can be avoided). In other words, the method of building up a logical calculus is a method of systematically reducing a vast number of rules of inference to one (or two). The place of all the others is taken by formulae of the calculus; which has the advantage that all these formulae—an infinite number, in fact—can be, in turn, systematically inferred (using the ‘principle of inference’) from a very few formulae.
We have indicated that for each of the well-known rules of inference there exists an asserted (or demonstrable) formula in a well-known logical calculus. The converse is not true in general (though it is true for hypothetical formulae). For example, to the formula ‘p or non-p’; or to ‘non-(p and non-p)’; and to many others which are not hypothetical, there exists no corresponding rule of inference.
Thus rules of inference and formulae of logical calculi have to be carefully distinguished. This need not, however, prevent us from interpreting a certain sub-set of these formulae—the ‘logician’s hypotheticals’—as rules of inference. In fact, our assertion that to every such hypothetical formula there corresponds a rule of inference justifies such an interpretation.
II
After these somewhat technical preliminaries, we now turn to Professor Ryle’s treatment of the question: ‘Why are rules of inference applicable to reality?’ This question forms an important part of our original problem, for we have just seen that a certain sub-set of the formulae of the logical calculi (viz., those which Professor Ryle calls ‘the logician’s hypotheticals’) can be interpreted as rules of inference.
Professor Ryle’s central thesis, if I understand him rightly, is this. The rules of logic, or more precisely, the rules of inference, are rules of procedure. This means that they apply to certain procedures, rather than to things or facts. They do not apply to reality, if by ‘reality’ we mean the things and facts described, for example, by scientists and historians. They do not ‘apply’ in the sense in which a description, say of a man, may apply to—or fit—either the man described or some other man; or in the sense in which a descriptive theory, for example of nuclear resonance absorption, may apply to—or fit—the atoms of uranium. Logical rules, rather, apply to the procedure of drawing inferences, comparable to the way in which the rules of the highway code apply to the procedure of riding a bicycle or driving a car. Logical rules can be observed or contravened, and to apply them does not mean to make them fit, but means to observe them, to act in accordance with them. If the question ‘Why are the rules of logic applicable to reality?’ is mistakenly intended to mean ‘Why do the rules of logic fit the things and the facts of our world?’ then the answer would be that the question assumes that they can, and do, fit the facts, whereas it is not possible to predicate of the rules of logic that they are ‘fitting the facts of the world’ or ‘not fitting the facts of the world’. This is not possible any more than it is possible to predicate such a thing of the highway code or of the rules of chess.
Thus it seems that our problem disappears. Those who wonder why the rules of inference apply to the world, vainly trying to imagine what an illogical world would be like, are the victims of an ambiguity. Rules of inference are procedural rules or rules of performance, so that they cannot ‘apply’ in the sense of ‘fit’ but only in the sense of being observed. Thus a world in which they do not apply would not be an illogical world, but a world peopled by illogical men.
This analysis (which is Professor Ryle’s) seems to me true and important, and it may well indicate the direction in which a solution of our problem can be found. But I do not feel satisfied that in itself it offers a solution.
The position appears to me in this way. Professor Ryle’s analysis shows that one way of interpreting the problem reduces it to nonsense, or to a pseudo-problem. Now I have for many years made it a personal rule of procedure not to be easily satisfied with the reduction of problems to pseudo-problems. Whenever somebody succeeds in reducing a problem to a pseudo-problem, I always ask myself whether one could not find another interpretation of the original problem—an interpretation which shows, if possible, that apart from the pseudo-problem there is also a real problem behind the original problem. I have found in many cases that this rule of procedure was fruitful and successful. I fully admit that an analysis which attempts to reduce the original problem to a pseudo-problem may often be extremely valuable; it may show that there was a danger of muddled thinking, and it may often help us to find the real problem. But it does not settle it. All this is the case here too, I believe.
III
I accept Professor Ryle’s view that the rules of logic (or of inference) are rules of procedure, and, as he himself indicates, that they may be considered as good or useful or helpful rules of procedure. And now I suggest that the problem ‘Why are the rules of logic applicable to reality?’ might be interpreted to mean ‘Why are the rules of logic good, or useful, or helpful rules of procedure?’
That this interpretation is justifiable can hardly be denied. The man who applies the rules of logic, in the sense that he acts according to them, or, as Professor Ryle says, observes them, does so probably because he finds them useful in practice. But this means, ultimately, that he finds them useful in dealing with real situations, i.e. with reality. If we ask, ‘Why are these rules useful?’, we ask something very similar to the question ‘Why are they applicable?’ and the similarity is sufficient, I believe, for claiming that this may very well be what the original questioner had in mind. On the other hand, there is no doubt any longer that our question ceases to be a pseudo-problem.
IV
I believe that our question can be answered comparatively easily. The man who finds observance of the rules of logic useful is, we have seen, a man who draws inferences. That is to say, he obtains from some statements or descriptions of facts, called ‘premises’, other statements or descriptions of facts, called ‘conclusions’. And he finds the procedure useful because he finds that, whenever he observes the rules of logic, whether consciously or intuitively, the conclusion will be true, provided the premises were true. In other words, he will be able to obtain reliable (and possibly valuable) indirect information, provided his original information was reliable and valuable.
If this is correct, then we must substitute for our question ‘Why are the rules of logic good rules of procedure?’ another question, namely, ‘What is the explanation of the fact that the logical rules of inference always lead to true conclusions, provided the premises are true?’
V
I believe this question, too, can be answered comparatively easily. Having learned to speak, and to use our language for the purpose of describing facts, we soon become more or less conversant with the procedure called ‘reasoning’ or ‘arguing’, that is to say, with the intuitive procedure of obtaining some kind of secondary information which was not explicitly stated in our original information. Part of this intuitive procedure can be analysed in terms of rules of inference. The formulation of these rules is the principal task of logic.
Accordingly we may lay it down that a logician’s rule of inference is, by definition, a good or ‘valid’ rule of inference if, and only if, its observance ensures that we obtain true conclusions, provided our premises are true. And if we succeed in finding an observance of a suggested rule which allows us to obtain a false conclusion from true premises—I call this a ‘counter example’—then we are satisfied that this rule was invalid. In other words, we call a rule of inference ‘valid’ if, and only if, no counter example to this rule exists; and we may be able to establish that none exists. Similarly, we call an observance of a rule of inference—that is to say an inference—‘valid’, if, and only if, no counter example exists to the observed rule.
Thus a ‘good’ or ‘valid’ rule of inference is useful because no counter example can be found, i.e. because we can rely on it as a rule of procedure that leads from true descriptions of facts to true descriptions of facts. But since we can say of a true description that it fits the facts, ‘applying’ in the sense of ‘fitting’ does enter into our analysis in some indirect way, after all. For we can say that rules of inference apply to facts in so far as every observance of them which starts with a fitting description of facts can be relied on to lead to a description which likewise fits the facts.
It is perhaps not without interest that the fundamental importance of the principle that a valid inference from true premises invariably leads to true conclusions has been discussed at some length by Aristotle (Anal. Prior., II, 1–4).
VI
In order to see whether this result is of any use I shall try to apply it to a criticism of the three main views of the nature of logic. The views I have in mind are
(A) The rules of logic are laws of thought.
(A1) They are natural laws of thought—they describe how we actually do think; and we cannot think otherwise.
(A2) They are normative laws—they tell us how we ought to think.
(B) The rules of logic are the most general laws of nature—they are descriptive laws holding for any object whatsoever.
(C) The rules of logic are laws of certain descriptive languages—of the use of words and especially of sentences.
The reason why (A1) has been so widely held is, I believe, the fact that there is something compelling and inescapable about logical rules—at least about the simple ones. They are said to hold good because we are compelled to think in accordance with them—because a state of affairs for which they do not hold good is inconceivable. But an argument that proceeds from inconceivability, is, like other appeals to self-evidence, always suspect. The fact that a rule, or a proposition, appears to be true, convincing, compelling, self-evident, or what not, is obviously no sufficient reason why it should be true, although the opposite may well be the case—its truth may be the reason why it appears to us to be true, or convincing. In other words, if the laws of logic hold for all objects, i.e. if (B) is correct, then their compelling character would be clear and reasonable; otherwise we may perhaps feel compelled to think in this way merely because we have a neurotic compulsion. In this way, our criticism of (A1) leads to (B).
But another criticism of (A1) leads to (A2); namely, the observation that we do not always reason in accordance with the laws of logic, but that we sometimes commit what is usually called a ‘fallacy’. (A2) asserts that we ought to avoid such breaches of the rules of logic. But why? Is it immoral? Certainly not. ‘Alice in Wonderland’ is not immoral. Is it stupid? Hardly. Obviously, we ought to avoid breaches of the rules of logic if, and only if, we are interested in formulating or deriving statements which are true, that is to say, which are true descriptions of facts. This consideration, again, leads us to (B).
But (B)—a position which has been held by men like Bertrand Russell, Morris Cohen, and Ferdinand Gonseth—seems to me not altogether satisfactory. First, because the rules of inference, as we have emphasized with Professor Ryle, are rules of procedure rather than descriptive statements; secondly, because an important class of logically true formulae (viz., precisely those which Professor Ryle would call the logician’s hypotheticals) can be interpreted as, or correspond to, rules of inference, and because these, as we have shown, following Professor Ryle, do not apply to facts in the sense in which a fitting description does. Thirdly, because any theory which does not allow for the radical difference between the status of a physical truism (such as ‘All rocks are heavy’) and a logical truism (such as ‘All rocks are rocks’ or perhaps ‘Either all rocks are heavy or some rocks are not heavy’) must be unsatisfactory. We feel that such a logically true proposition is true not because it describes the behaviour of all possible facts but simply because it does not take the risk of being falsified by any fact; it does not exclude any possible fact, and it therefore does not assert anything whatsoever of any fact at all. But we need not go here into the problem of the status of these logical truisms. For whatever their status may be, logic is not primarily the doctrine of logical truisms; it is, primarily, the doctrine of valid inference.
The position (C) has been criticized—rightly, I think—as unsatisfactory so long as it was bound up with the view that by a language we can, for the purpose of logic, understand a ‘mere symbolism’, i.e. a symbolism apart from any ‘meaning’ (whatever this may mean). I do not think that this view can be upheld. And our definition of a valid inference would most certainly not be applicable to such a mere symbolism since this definition makes use of the term ‘truth’; for we could not say of a ‘mere symbolism’ (which is void of meaning) that it contains true or false statements. We should therefore have no inference in our sense, and no rules of inference; and as a consequence, we should have no answer to our question why the rules of logic are valid or good or useful.
But if we mean by a language a symbolism that allows us to make true statements (and in respect of which we can explain, as was first done by Tarski, what we mean when we say of a certain statement that it is true) then, I believe, the objections which so far have been raised against (C) lose most of their force. A valid rule of inference with regard to such a semantic language system would be a rule to which, in the language in question, no counter example can be found, because no counter example exists.
It may be said in passing that these rules of inference need not necessarily have that ‘formal’ character which we know from our logical studies; their character will depend, rather, on the character of the semantic language system under investigation. (Examples of semantic language systems have been analysed by Tarski and Carnap.) Yet for languages similar to those usually considered by logicians, the rules of inference will be of that ‘formal’ character to which we are accustomed.
VII
As indicated by my last remarks, the rules of procedure which we are discussing, i.e. the rules of inference, are, to a certain extent, always relative to a language system. But they all have this in common: their observance leads from true premises to true conclusions. Thus there cannot be alternative logics in the sense that their rules of inference lead from true premises to conclusions which are not true, simply because we have defined the term ‘rule of inference’ in such a way that this is impossible. (This does not exclude the possibility of considering the rules of inference as special cases of more general rules, for example, of rules which allow us to attach to certain quasi-conclusions a certain ‘probability’, provided that certain quasi-premises are true.) Yet there can be alternative logics in the sense that they formulate alternative systems of rules of inference with respect to more or less widely different languages—languages which differ in what we call their ‘logical structure’.
We may take, for example, the language of categorical propositions (subject-predicate statements), for which the traditional system of categorical syllogisms formulates the rules of inference. The logical structure of this language is characterized by the fact that it contains only a small number of logical signs—signs for the copula and its negation, for universality and particularity, and perhaps for the complementation (or negation) of its so-called ‘terms’. If we now consider the argument formulated in section I, third paragraph, then we see that all three premises as well as the conclusion can be formulated in the language of categorical propositions. Nevertheless, if so formulated, it is impossible to formulate a valid rule of inference which exhibits the general form of this argument; and accordingly, it is no longer possible to defend the validity of this argument, once it has been couched in the language of categorical propositions. Once we have fused the words ‘mother of Richard’ into one term—the predicate of our first premise—we cannot separate them again. The logical structure of this language is too poor to exhibit the fact that this predicate contains, in some way or other, the subject of the second premise, and part of the subject of the third premise. Similar remarks hold for the other two premises and for the conclusion. Accordingly, if we try to formulate the rule of inference, we get something like
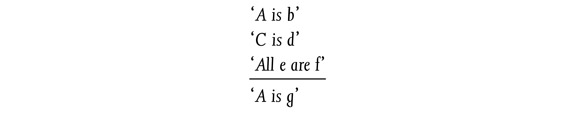
(Here ‘A’ and ‘C’ stand for ‘Rachel’ and ‘Richard’, ‘b’ for ‘mother of Richard’, ‘d’ for ‘father of Robert’, ‘e’ for ‘mothers of fathers’, ‘f’ for ‘paternal grandmothers’, and ‘g’ for ‘paternal grandmother of Robert’.) This rule, of course, is invalid since we can produce in the language of categorical propositions as many counter examples as we like. Thus a language, even though it may be rich enough for describing all the facts we wish to describe, may not permit the formulation of the rules of inference needed to cover all the cases in which we can safely pass from true premises to true conclusions.
VIII
These last considerations may be used for extending our analysis to the problem of the applicability of the calculi of logic and arithmetic; for we must not forget that so far (following Professor Ryle) we have discussed only the applicability of rules of inference.
I believe that the construction of so-called ‘logical calculi’ can be said to be due, mainly, to the desire to build up languages with regard to which all those inferences which we intuitively know how to draw can be ‘formalized’, that is to say, shown to be drawn in accordance with a very few explicit, and valid, rules of inference. (These rules of inference, as rules of procedure, speak about the language or calculus we are investigating. They are, therefore, not to be stated in the calculus under investigation, but in the so-called ‘meta-language’ of this calculus, i.e. in the language which we use when discussing this calculus.) Syllogistic logic, for example, can be said to have been an attempt to construct such a language, and many of its adherents still believe that it was successful and that all inferences which are really valid are formalized in its figures and moods. (We have seen that this is not the case.) Other systems have been built up, with similar aims (for example Principia Mathematica), and have succeeded in formalizing practically all valid rules of inference as observed not only in ordinary discourse but also in mathematical arguments. One is tempted to describe the task of constructing a language or calculus such that we can formalize all valid rules of inference (partly with the help of the logical formulae of the calculus itself, and partly with the help of a few rules of inference pertaining to this calculus) as the prima facie fundamental problem of logic. Now there is good reason to believe that this problem is insoluble, at least if we do not admit, for the purpose of formalizing relatively simple intuitive inferences, procedures of an entirely different character (such as inferences drawn from an infinite class of premises). The position appears to be this: although it is possible, for any given valid intuitive inference, to construct some language permitting the formalization of this inference, it is not possible to construct one language permitting the formalization of all valid intuitive inferences. This interesting situation which was first discussed, to my knowledge, by Tarski, with reference to investigations by Gödel, bears on our problem in so far as it shows that the applicability of every calculus (in the sense of its suitability as a language with regard to which every valid intuitive inference can be formulated) breaks down at some stage or other.
I shall now turn to our problem of applicability, this time, however, confined to the logical calculi, or more precisely, to the asserted formulae (the axioms and theorems) of the logical calculi, rather than to the rules of inference. Why are these calculi—which may contain arithmetic—applicable to reality?
I shall try to answer this question in the form of three statements.
(a) These calculi as a rule are semantical systems,4 that is to say, languages designed with the intention of being used for the description of certain facts. If it turns out that they serve this purpose then we need not be surprised.
(b) They may be so designed that they do not serve the purpose; this can be seen from the fact that certain calculi—for example, the arithmetic of natural numbers, or that of real numbers—are helpful in describing certain kinds of fact, but not other kinds.
(c) In so far as a calculus is applied to reality, it loses the character of a logical calculus and becomes a descriptive theory which may be empirically refutable; and in so far as it is treated as irrefutable, i.e. as a system of logically true formulae, rather than a descriptive scientific theory, it is not applied to reality.
A remark that bears on (a) will be found in section ix. In the present section, only (b) and (c) will be briefly discussed.
As to (b), we may note that the calculus of natural numbers is used in order to count billiard balls, or pennies, or crocodiles, while the calculus of real numbers provides a framework for the measurement or the calculation of continuous magnitudes such as geometrical distances or velocities. (This is especially clear in Brouwer’s theory of the real numbers.) We should not say that we have, for instance, 3.6, or perhaps π, crocodiles in our zoo. In order to count crocodiles, we make use of the calculus of natural numbers. But in order to determine the latitude of our zoo, or its distance from Greenwich, we may have to make use of π. The belief that any one of the calculi of arithmetic is applicable to any reality (a belief that seems to underlie the problem which was set to our symposium) is therefore hardly tenable.
As to (c), if we consider a proposition such as ‘2 + 2 = 4’, then it may be applied—for example to apples—in different senses, of which I shall discuss only two. In the first of these senses, the statement ‘2 apples + 2 apples = 4 apples’ is taken to be irrefutable and logically true. But it does not describe any fact involving apples—any more than the statement ‘All apples are apples’ does. Like this latter statement, it is a logical truism; and the only difference is that it is based, not on the definition of the signs ‘All’ and ‘are’, but on certain definitions of the signs ‘2’, ‘4’, ‘+’, and ‘=’. (These definitions may be either explicit or implicit.) We might say in this case that the application is not real but only apparent; that we do not here describe any reality, but only assert that a certain way of describing reality is equivalent to another way.
More important is the application in the second sense. In this sense, ‘2 + 2 = 4’ may be taken to mean that, if somebody has put two apples in a certain basket, and then again two, and has not taken any apples out of the basket, there will be four in it. In this interpretation the statement ‘2 + 2 = 4’ helps us to calculate, i.e. to describe certain physical facts, and the symbol ‘+’ stands for a physical manipulation—for physically adding certain things to other things. (We see here that it is sometimes possible to interpret an apparently logical symbol descriptively.5) But in this interpretation the statement ‘2 + 2 = 4’ becomes a physical theory, rather than a logical one; and as a consequence, we cannot be sure whether it remains universally true. As a matter of fact, it does not. It may hold for apples, but it hardly holds for rabbits. If you put 2 + 2 rabbits in a basket, you may soon find 7 or 8 in it. Nor is it applicable to such things as drops. If you put 2 + 2 drops into a dry flask, you will never get four out of it. In other words, if you wonder what a world would look like in which ‘2 + 2 = 4’ is not applicable, it is easy to satisfy your curiosity. A couple of rabbits of different sexes or a few drops of water may serve as a model for such a world. If you answer that these examples are not fair because something has happened to the rabbits and to the drops, and because the equation ‘2 + 2 = 4’ only applies to objects to which nothing happens, then my answer is that, if you interpret it in this way, then it does not hold for ‘reality’ (for in ‘reality’ something happens all the time) but only for an abstract world of distinct objects in which nothing happens. To the extent, it is clear, to which our real world resembles such an abstract world, for example, to the extent to which our apples do not rot, or rot only very slowly, or to which our rabbits or crocodiles do not happen to breed; to the extent, in other words, to which physical conditions resemble the pure logical or arithmetical operation of addition, to the same extent, of course, does arithmetic remain applicable. But this statement is trivial.
An analogous statement may be made about the addition of measurements. That any two straight sticks which, if placed side by side, are each of the length a, will, if placed end to end, be together of the length 2a, is by no means logically necessary. We can easily imagine a world in which sticks do behave according to the rules of perspective, i.e. exactly as they appear to behave in the visual field and on photographic plates—a world in which they shrink if moved away from a certain centre (e.g. that of the lens). In fact, for the purpose of the addition of certain measurable quantities—velocities—we do seem to live in such a world. According to special relativity, the ordinary calculus of addition is inapplicable to the measurement of velocities6 (i.e. it leads to false results); it has to be replaced by a different one. Of course, it is possible to reject the claim that the ordinary calculus of addition of velocities is inapplicable, and to resist, on principle, any demand that it should be changed. Such a principle would be tantamount to saying that velocities must necessarily be added in the ordinary way, or in other words, to claiming, implicitly, that they are to be defined as obeying the ordinary laws of addition. But in this case, of course, velocities can no longer be defined by empirical measurements (for we cannot define the same concept in two different ways) and our calculus no longer applies to empirical reality.
Professor Ryle has helped us to approach the problem from the angle of an analysis of the word ‘applicable’. My last remarks may be taken as a complementary attempt to tackle the problem by analysing the word ‘reality’ (and also the problem of the distinction between the logical and the descriptive use of symbols). For I believe that whenever we are doubtful whether or not our statements deal with the real world, we can decide it by asking ourselves whether or not we are ready to accept an empirical refutation. If we are determined, on principle, to defend our statements in the face of refutations (such as are provided by rabbits or drops or velocities), we are not speaking about reality. Only if we are ready to accept refutations are we speaking about reality. In Professor Ryle’s language, we should have to say: Only if we know how to abide by a refutation do we know how to speak about reality. If we wish to formulate this readiness or ‘knowledge how’, then we have to do it again with the help of a rule of procedure. It is clear that only a performance rule can help us here, for speaking about reality is a performance.7
IX
My last remarks—on (c)—indicate the direction in which, perhaps, an answer may be found to what I hold to be the most important aspect of our many-sided problem. Yet I do not wish to conclude this paper without making it quite clear that I believe that the problem can be taken further. Why, we could ask, are we at all successful in speaking about reality? Is it not true that reality must have a definite structure in order that we can speak about it? Could we not conceive of a reality which would be like a thick fog—and nothing else, no solids, no movement? Or perhaps like a fog with certain changes in it—rather indefinite changes of light, for example? Of course, by my very attempt to describe this world I have shown that it can be described in our language, but this is not to say that any such world could be so described.
I do not think that, in this form, the question is a very serious one, but I also do not think that it should be too quickly dismissed. In fact, I believe that we are all most intimately acquainted with a world that cannot be properly described by our language which has developed mainly as an instrument for describing and dealing with our physical environment—more precisely, with physical bodies of medium size in moderately slow motion. The indescribable world I have in mind is, of course, the world I have ‘in my mind’—the world which most psychologists (except the behaviourists) attempt to describe, somewhat unsuccessfully, with the help of what is nothing but a host of metaphors taken from the languages of physics, of biology, and of social life.
But whatever the world to be described may be like, and whatever may be the languages we use, and their logical structure, there is one thing we can be sure of: as long as our interest in describing the world does not change, we shall be interested in true descriptions, and in inferences—that is to say, in operations which lead from true premises to true conclusions: in the application of logic to reality. On the other hand, there is certainly no reason to believe that our ordinary languages are the best means for the description of any world. On the contrary, they are probably not even the best possible means for a finer description of our own physical world. The development of mathematics, which is a somewhat artificial development of certain parts of our ordinary languages, shows that with new linguistic means new kinds of facts can be described. In a language possessing, say, five numerals and the word ‘many’, even the simple fact that in field A there are 6 more sheep than in field B cannot be stated. The use of an arithmetical calculus permits us to describe relations which simply could not be described without it.
There are, however, further and possibly deeper problems concerning the relations between the means of description and the described facts. These relations are rarely seen in the right way. The same philosophers who oppose a naïve realism with regard to things are often naïve realists with regard to facts. While perhaps believing that things are logical constructs (which, I am satisfied, is a mistaken view) they believe that facts are part of the world in a sense similar to that in which processes or things may be said to be parts of the world; that the world consists of facts in a sense in which it may be said to consist of (four dimensional) processes or of (three dimensional) things. They believe that, just as certain nouns are names of things, sentences are names of facts. And they sometimes even believe that sentences are something like pictures of facts, or that they are projections of facts.8 But all this is mistaken. The fact that there is no elephant in this room is not one of the processes or parts of the world; nor is the fact that a hailstorm in Newfoundland occurred exactly 111 years after a tree collapsed in the New Zealand bush. Facts are something like a common product of language and reality; they are reality pinned down by descriptive statements. They are like abstracts from a book, made in a language which is different from that of the original, and determined not only by the original book but nearly as much by the principles of selection and by other methods of abstracting, and by the means of which the new language disposes. New linguistic means not only help us to describe new kinds of facts. In a way, they even help us to create these new kinds of (perfectly objective) facts, new kinds of states of affairs. In a certain sense, these facts obviously existed before the new means were created which were indispensable for their description; I say, ‘obviously’ because a calculation, for example, of the movements of the planet Mercury of 100 years ago, carried out today with the help of the calculus of the theory of relativity, may certainly be a true description of the facts concerned, even though the theory was not yet invented when these facts occurred. But in another sense we might say that these facts do not exist as facts before they are singled out from the continuum of events and pinned down by statements—the theories which describe them. These questions, however, although closely connected with our problem, must be left for another discussion. I have mentioned them only in order to make clear that even should the solutions I have proposed be more or less correct, there would still be open problems left in this field.
Notes