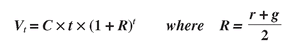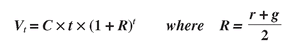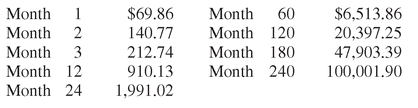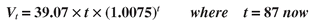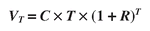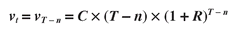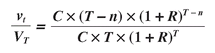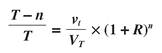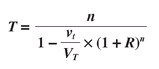5
Establishing the Value Path
Chapter 4 covered plans and techniques for achieving your investment value goal with
dollar cost averaging. Occasional readjustments to the plan were needed to eventually target in on the final investment goal. With
value averaging, the situation is easier. By its very nature, the value averaging strategy involves a portfolio “readjustment” at every investment period, as you buy or sell shares to make your value equal the target value path.
1
VALUE AVERAGING VALUE PATHS
There are a lot of ways to set up the value path for value averaging—that is, the schedule of what you want the value of your holdings to be at every point in time. Not all value paths make sense, though. Suppose you wanted to build up value monthly, resulting in $100,000 after 20 years. As presented in the “pure” linear form of value averaging, you could establish a linear value path that goes up by the same amount (1/240 of $100,000) each month. That would be an increase of $416.67 in value every month, and would require a $416.67 initial investment for the first month. As we discussed in Chapter 3, that would be an ineffective and unnatural approach that excessively front-loads the investment, while requiring no investment, or even disinvestment—later in the plan. After 19 years, the value would be $95,000. The expected monthly return on that amount (1.0%), is +$950, more than double the planned, or “allowable,” increase calculated above. You would actually be expected to be a net seller of stock during the last 12 years of the plan.
The Value Path Formula
Value averaging requires a target value for you to achieve at each point in time. What we really need is a “compounding” value path that is similar to the value achieved with the growth-adjusted dollar cost averaging strategies. That is, we want our value averaging plan to account for: growth from expected return on our portfolio value, from monthly investment contributions, and from growth in these monthly investments. Formula
(15) from Chapter 4 accomplishes all those things and is repeated here as formula
(19):
Using this simple formula for your value path, you can construct a complete schedule of target values for every period in your investment time frame. This would take only a few quick steps with a spreadsheet. You can relate this value path to your investment goals and capabilities by setting your final value goal (such as the V240 = $100,000 used earlier), your desired initial or average net investment contribution ($C), and how much you are willing to increase your net investment contribution over time (g). Even though you will not have a consistent monthly investment amount with value averaging, you still want to set the plan up so that after accounting for an investment return on your existing shares, you still expect to put in some investment contribution (like $C) to meet your value path. Depending on the market’s actual performance, you will end up investing more or less than that each month—but if the market performs roughly as expected, then you should be able to handle the average net amount that you need to invest, just as with dollar cost averaging.
For example, suppose you wanted to build a fund worth $100,000 over 20 years, were willing to increase your average monthly investment contribution by 0.5% per month, and expected a 1.0% monthly return on your investment. Averaging
r and
g, you get
R = 0.75%, or 0.0075. Putting all those figures into formula
(19), solve for
C = $69.34, just as you did with dollar cost averaging. Therefore:
$100,000 = $C × 240 × (1.0075)240 = 1,442.2 × $C
$C = $69.34
Putting this value into the equation for
C, this gives the target value for each month
t from month 1 to month 240:
Sample Value Path Formula
This is the
growth-adjusted value path formula. Putting in some representative values for
t, sample points on the value path are as follows:
These are the target values you strive to match each month by buying or perhaps selling shares. At this rate, you make steady progress toward your final goal while smoothing out your investment exposure over time.
Flexible Variations on the Value Path Formula
What if you are not starting from scratch? Some investors may wish to start value averaging with existing shares that already have value. In that case, the best and most flexible method is probably for you to use a computer spreadsheet, as discussed later in this chapter. But if you are willing to calculate another formula, you can set up a value path that accounts for your investment progress to date, instead of starting from scratch. What you will do is set up a value path that is “in progress,” and still has the proper length of time remaining before achieving your goal.
For example, suppose you have 17 years to develop a portfolio of $100,000, and you are happy with the r = 1.0% and g = 0.5% market return and investment growth parameters established in earlier examples. But you also have $6,500 in a fund that you want to bring into the value averaging plan as seed money. We can now figure out a value path that includes: those growth factors; has a value of $6,500 somewhere in the middle; and then, 17 years (204 months) later, has a value of $100,000. You see, by bringing seed money into the program, you effectively put yourself many months away from impoverished month zero. In this case, it works out that you are already effectively 87 months into a 291-month VA strategy that ends in a value of $100,000. The difference between month 87 and month 291 is 204 months, or 17 years, which is the time you have remaining to achieve your goal. The artificial 87 months that came before your starting point are nothing more than a convenient placeholder, in that your accumulated $6,500 corresponds to what you would have now had you started from scratch 87 months ago. You simply “skipped” those 87 months by bringing that amount ($6,500) with you to the starting point.
Now we’ll construct the formula you can use to begin value averaging with a head start. We’ll let
n be the number of periods you have available from the present in which to achieve your investment goal (
n = 204 here). The variable
t (an unknown) will designate the period number in the value path formula that corresponds to
today (where we will have $6,500). The variable
T, which we must solve for, designates the period number at the end of the value path formula (where we will have $100,000). Of course, we need to find a
t (now) and a
T (later) that are
n periods apart:
t =
T −
n. Two variables for value, current and future, are required and should be known:
vt is our current value ($6,500), and
VT is our required future value ($100,000). The factor
R remains an average of
r and
g. You can solve for
T, the ending period number to use in establishing your value path, using this formula:
Head-Start VA Readjustment Formula to calculate T
The derivation is shown in endnotes.
2 Solving this formula for the
T that applies in this example involves putting in
vt = 6,500 and
VT = 100,000;
n = 204 months; and
R = 0.0075 monthly. The solution is 290.8, which we round up
3 to 291; the current time parameter
t must be 87, since there must be 17 years (204 months) in between:
t =
T −
n = 291 − 204 = 87. This means that instead of starting at
t = 0 (with no initial value) and finishing at
T = 204, we are artificially indexing the current month as
t = 87 so as to account for the “past history” of our $6,500 initial value. This allows for the value path formula showing a required value of $6,500 (which we have now) at month 87 (which we will thus call
now). Using
T = 291 and
equation (19), we can solve for the specific value path formula that applies in this example by solving for $
C (as shown earlier). By placing
VT = 100,000 and
R = 0.0075 along with
T = 291 in the formula, we can calculate that
C = $39.07. The specific value path formula for us to follow, then, is:
(22)
Using t = 87 (today’s period number) in that formula gives us Vnow = $6,511, pretty close to the $6,500 we really have. We’ll set next month’s target at Vt = $6,636 using t = 88. In 17 years, when t = 291, our target value will be $100,000—go ahead and plug in the number t = 291 and check.
NOTE: If you calculate T to be negative, it simply means that your final target, VT, is too small for your head-start current value of vt. That is, at rate R, your current investment value will grow (with no help from you) to more than your target value. In such a case, either reduce R, increase your final target VT, or both, and try the calculation again.
Readjusting the VA Plan
The beauty of this addition to your bag of tools is that it allows you to
readjust your plan and your value path to account for unforeseen changes. Suppose, for instance, you are at month 24 in the value averaging example at the beginning of this chapter, having accumulated a value of $1,991.02 with a 20-year goal of $100,000 (see
equation (20)). What happens if your investment goal then changes to $120,000, or if much higher government bond rates cause you to revise your expectation of stock market returns upward (increasing
R)? You can’t just start over at
t = 0 of a new value path, nor can you ignore the nearly $2,000 you’ve already accumulated. You can, however, simply use the process accompanying
equation (21) above to put yourself “in progress” with a new value path
4 that will get you from
vt = $1,991.02 now to
VT =
Vt + 216 = $120, 000 over the next 216 months, the remaining 18 years. (This problem is solved in endnote 4). This same situation works if your investment time frame changes or if you must take existing capital out of your investment plan to meet some unforeseen expense. The process described here gives you total flexibility in readjusting your value averaging accumulation plan for whatever changes may occur over time. And this readjustment process appears to be easier than the two-pot reverse solution method required in similar DCA cases. See the Appendix at the end of this chapter for ideas on how to use a spreadsheet to take the work out of using this important and effective investment management tool.
A Cautionary Note
The big problems occur with value averaging (or most other strategies) when you have a really bad market performance after you’ve already built up a sizable portfolio toward your goal. Investors approaching their final goal in December 1987 were certainly shocked and disappointed by the crash in October of 1987 and certainly would have missed their end-of-year December goal, which had been almost achieved. In some sense, the risk of bad performance hurts more as you get closer to your investment goal, because there’s really no time to recoup losses.
To this end, it may make sense to be a bit conservative in your initial expectations. This will cause you to put a little more money in up front, but it will leave you with the welcome “problem” of exceeding your value goal more often than possibly not meeting it. There are a few ways to use the value path formula while being conservative. You could plan on less time, meeting your value goal for your child’s college education a year early or so. You could set your final value goal at a pessimistically high level—if a range of expected public college costs in the year 2010 is given at $90,000 to $130,000, for example, you might pick the higher number (people seldom cry about having money left over). You can alternatively use lower figures for the parameters r or g, resulting in a higher initial investment, $C, and a quicker wealth buildup in the early years.
An Alternate Method
For the computer literate, perhaps a better way to track the value path is with a spreadsheet rather than a formula. If the time indexing in formula
(21) bothered you, this direct approach using a computer might appeal to you. Pick any number you want for the initial investment $
C, and a starting value (which is 0 unless you have a “head start”). Pick your growth factors
r and
g. Then calculate the value path by applying the growth factors directly to the investment quantities that are growing. By setting the target value for month
t equal to: the target value for the previous month times (1 +
r), plus the additional investment
C(1 +
g)
t, you can create the target value for every month as a function of the prior month.
5 By playing with the parameter
C (and perhaps
g), you can set up a value path that achieves a final value of the investment goal you have in mind. Note that formula
(21) is
not used with this alternative method. This method has the advantage of being totally flexible, because you can change parameters in mid-program and still calculate the value path over any remaining months.
SUMMARY
However you establish your value path, remember that you do not have to go to extremes to slavishly conform to it. Several variations of the strategies are discussed in this book so that you can tailor an approach to your needs using whatever variations and actions that make sense to you. It’s your investment plan—the numbers can only be your guide.
Some tips on how to apply these techniques in real life are provided in Chapter 10. A full case-study example that deals with many of the complexities of a value averaging strategy is included in Chapter 11.
ENDNOTES
1 Note that value averaging involves much more radical readjustments than occasional changes to $
C or
g that we undertook in dollar cost averaging. If we were over our “target value path” in dollar cost averaging, we stayed there and simply lowered our trajectory over the entire remainder of the investment period by reducing the level of, or the growth in, the monthly investment amount. The process of “getting back on track” was totally smoothed out over time. With value averaging, though, if we ever find ourselves above or below the target value path, we
immediately get back on track by selling or buying the required number of shares.
2 Using the value path formula
(19) at the final investment period (
T) gives the final value goal:
(1)
We can write the same formula for the value at the intermediate point in time, vt, realizing that t = T − n:
(2)
Dividing the second equation by the first, we get:
(3)
Canceling the
C and (1 +
R)
T terms and multiplying through by (1 +
R)
n, we get:
(4)
Solving this equation for
T gives the formula in the text:
(5)
3 There’s really no need to round it at all, but most people prefer to work with integers.
4 For anyone playing along at home, the readjustment due to the goal increase from $100,000 to $120,000 at the 24-month point is given here. The new time parameters would be
T = 236 and
t = 20, and the new value path formula would be:
Vt = 87.18 × t × (1.0075)t
where
t is currently 20. Next month, which is now month 21, our value path goal is $2,142. We will now have to “grow” our funds more quickly to get from $1,991.02 now to $120,000 in 18 years.
5 That is, the alternate formula for the value path for each time period
t is:
Vt = (1 + r) × Vt - 1 + (1 + g)t × C
Appendix to Chapter 5
Constructing a VA Readjustment Spreadsheet
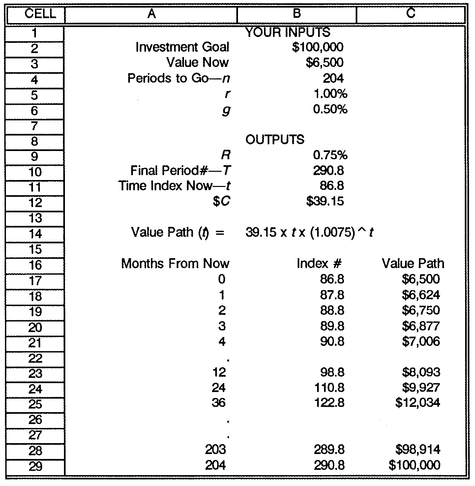
The following spreadsheet shows the solution to the value averaging readjustment problem from Chapter 5, page 90. Start with $6,500, with 17 years (204 months) to attain a $100,000 goal, and add other inputs as shown. What would the value path look like for monthly value averaging?
Put in the 5 inputs you know, and the spreadsheet does all the rest. The outputs are calculated in cells B9-B12, with the value path formula in cell B14. The solution involves an artificial time index as described in the text. This is shown at the bottom of the spreadsheet, where each month is indexed by the solution t = 86.8. The value path is shown for current and selected future months; your spreadsheet could show the value path for all months. The spreadsheet and the formulas needed to construct the spreadsheet are shown on pages 98 and 99.
Of course, if you start with a “Value Now” of $0, this spreadsheet will calculate a standard value averaging value path, as discussed on pages 88-89.
Lotus 1-2-3 Spreadsheet, VA Readjustment Program
Formulas for Lotus 1-2-3 VA Readjustment Program
| A2: | W18] “Investment Goal |
| A3: | ”Value Now |
| A4: | “Periods to Go—n |
| A5: | ”r |
| A6: | “g |
| A9: | ”R |
| A10: | “Final Period #—T |
| A11: | ”Time Index Now—t |
| A12: | “$C |
| A14: | ’Value Path (t) = |
| A16: | ’Months from Now |
| A17: | 0 |
| A18: | 1 |
| A19: | 2 |
| A20: | 3 |
| A21: | 4 |
| A22: | ”. |
| A23: | 12 |
| A24: | 24 |
| A25: | 36 |
| A26: | ”. |
| A27: | ”. |
| A28: | 203 |
| A29: | 204 |
| B1: | ’YOUR INPUTS |
| B2: | (C0) 100000 |
| B3: | (C0) 6500 |
| B4: | 204 |
| B5: | (P2) 0.01 |
| B6: | (P2) 0.005 |
| B8: | ’OUTPUTS |
| B9: | (P2) @AVG(B6..B5) |
| B10: | (F1) +B4/(1-(1+B9) ^ B4*B3/B2) |
| B11: | (F1) +B10-B4 |
| B12: | (C2) +B2/(B10*(1+B9) ^ B10) |
| B14: | @STRING(B12,2)&”x t x (“&@STRING(1+B9,4)&”) ^ t” |
| B16: | “Index # |
| B17: | (F1) +A17+$B$11 |
| B18: | (F1) +A18+$B$11 |
| B19: | (F1) +A19+$B$11 |
| B20: | (F1) +A20+$B$11 |
| B21: | (F1) +A21+$B$11 |
| B23: | (F1) +A23+$B$11 |
| B24: | (F1) +A24+$B$11 |
| B25: | (F1) +A25+$B$11 |
| B28: | (F1) +A28+$B$11 |
| B29: | (F1) +A29+$B$11 |
| C16: | ”Value Path |
| C17: | (C0) +$B$12*B17*(1+$B$9) ^ B17 |
| C18: | (C0) +$B$12*B18*(1+$B$9) ^ B18 |
| C19: | (C0) +$B$12*B19*(1+$B$9) ^ B19 |
| C20: | (C0) +$B$12*B20*(1 +$B$9) ^ B20 |
| C21: | (C0) +$B$12*B21 *(1 +$B$9) ^ B21 |
| C23: | (C0) +$B$12*B23*(1 +$B$9) ^ B23 |
| C24: | (C0) +$B$12*B24*(1 +$B$9) ^ B24 |
| C25: | (C0) +$B$12*B25*(1 +$B$9) ^ B25 |
| C28: | (C0) +$B$12*B28*(1 +$B$9) ^ B28 |
| C29: | (C0) +$B$12*B29*(1 +$B$9) ^ B29 |