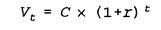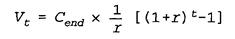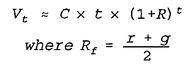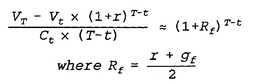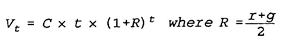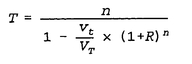11
Examples: Strategies at Work
The previous chapter discussed several of the details and strategy twists you might want to consider in tailoring and using your own investment strategy for accumulating wealth. To really apply the seemingly basic accumulation strategies, you must determine your goal, choose an investment, estimate market return and investment growth figures, establish a value path (for VA), and then implement your plan to achieve your goal. Throughout the process, you must deal with the changes and realities of the marketplace—you should reevaluate your goal (as inflation changes), your progress toward that goal (as your investment returns vary), and the risk you are willing to bear (as you get closer to your goal). This chapter shows you how to put all this together and how to keep it together over time.
While I hope each of many previous hints and tips made sense in isolation, I suspect they are easier to digest if actually seen in action. How would a real investor put the DCA or VA strategies to work in real life, facing the real taxes, uncertainties, and other complications that we invariably must deal with over time?
We’ll look at thorough examples of putting the DCA and VA strategies to work. We’ll follow a mutual fund investor through a 10-year period (ending in 1991) of accumulation in a real investment, the Vanguard Index Trust 500 mutual fund. We’ll see how to deal with realities like inflation, taxes, and market variability, and how to keep our investment target in our sights by monitoring and readjusting our position as needed. The chapter is very detail-oriented, and very reality-oriented, so you can hopefully see how to apply the lessons learned in prior chapters.
THE GOAL AND INVESTMENT ENVIRONMENT
The time is December 31, 1981. Larry wants some land to build a vacation cabin. Nothing fancy, just a spot in the hills near a lake in a nearby state. Larry doesn’t yet have anything saved up for his dream, but would like to be able to buy the land outright in ten years (and would then be able to finance the cabin). His typical dream lot costs just under $58,000 right now, and he expects these land prices to stay even with inflation over time.
Choosing an Investment
Larry could choose to meet his goal by investing in fixed income securities (bonds, CDs, etc.) that would exactly meet his goal in ten years (December 1991) with very little risk—if he had the money now to invest. Even in that case, such a plan would not work out very well, for at least two reasons. First of all, the future price of the lot will vary with future inflation, which is uncertain, and makes fixed income investments a poor fit. Second, the return on fixed income is quite low.
Equity investments help with both of these problems to some extent. Since he has no money saved yet, Larry will need to accumulate wealth toward that goal over the next ten years. Larry wants a no-load, low-expense, well-diversified equity investment, and chooses the
Vanguard Index Trust 500 mutual fund (which is described following
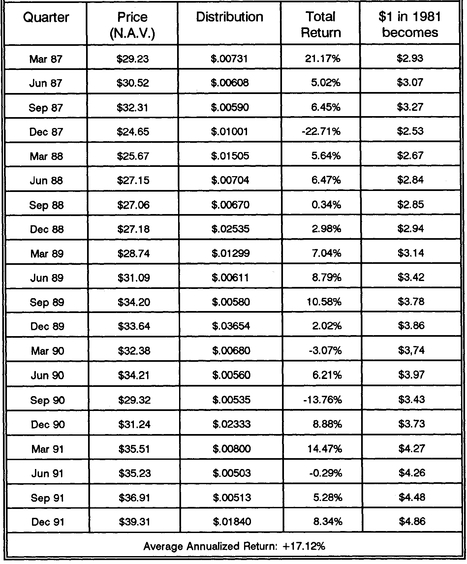
Table 10-1 in Chapter 10). We will use actual price and dividend data provided by that fund for the period December 31, 1981-December 31, 1991. This will turn out to be a very good investment for Larry (the fund averages over 17% annually over the coming 10 years); of course, he can’t possibly know this back in 1981.
TABLE 11-1: Quarterly Price and Return Data for Vanguard Index Trust 500 Mutual Fund
Setting the Goal (Dealing with Inflation)
How much money will Larry need for his goal? $58,000? Only if he can make time (or the price level) stand still. If the 1981 price is about $58,000, then inflation will drive the future (1991) price well above that figure. At a 7% inflation rate, prices almost double in 10 years.
What expected inflation rate should Larry use? No one knows for sure. Inflation was pretty high back in 1981; high interest rates reflected people’s expectations that high inflation would continue (we know
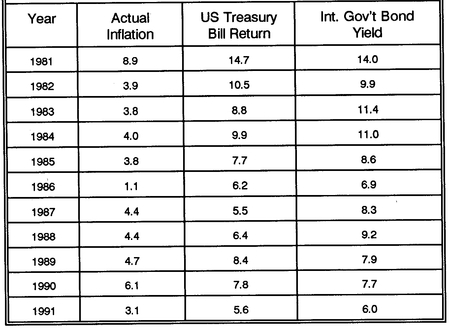
now that it didn’t, but that’s with a decade of hindsight). Some of the relevant economic information from 1981 is shown in the top row of
Table 11-2. The inflation rate had been 8.9% during 1981, and Treasury bills returned 14.7% that year. For 1982, Treasury bills promised (as of the end of 1981) to return 10.5%. Market yields on intermediate Treasury bond yields at the end of 1981 were 14.0%.
With this information, one can roughly approximate a reasonable estimate of the inflation rate to be expected in the future. It will seldom be very accurate, but on average, it is better than a good guess. One way to think about inflation in the future is that recent inflation rates give a good guide; by this approach, 8.9% would be the expected inflation rate. This approach ignores the important fact that the future is seldom like, or even expected to be like, the past. We can turn to Treasury bill and bond yields to get some idea of what the financial markets expect inflation to be in the future.
Yields on bills and bonds generally provide investors with an expected return over and above inflation. Long-term investments (bonds) historically provide, on average, almost a 1% higher excess return than do short-term investments like bills. In modern times, as a long-run average, bonds seem to provide about a 3% “bonus” over expected rates of inflation; short-term bills give about 2% above-inflation returns. Since Treasury bonds were yielding 14.0% at the end of 1981, a reasonable expectation of long-term future inflation rates would be 3% lower, or 11.0%. One-year Treasury bills were promising to return 10.5% over the next year (and did so); thus, based on these yields, an expected inflation rate over the next year would be 2% lower, or 8.5%.
Consolidating the various educated guesses about future inflation would give Larry about a 10% inflation estimate to use in the future. The old inflation rate (8.9%) and the expected next-year inflation rate (8.5%) may be fine for the immediate future, but they are flimsy indicators for our 10-year time frame. A better figure is the intermediate term (7-10 year) expected inflation estimate of 11.0%. Averaging the estimates, but giving more weight to the more relevant figure, gives us a 10% inflation estimate.
At a 10% annual inflation rate, $1 grows to $2.59 in price over 10 years. Thus, Larry’s land, priced at nearly $58,000 currently, will cost him about $150,000 (= 58,000 × 2.59) in 1991. This is merely an estimate; if inflation settles below 10%, the land will cost less. But for now, Larry’s investment goal, accounting for expected inflation, is $150,000.
How Much Should He Invest?
Accumulating $150,000 from a standing start in 10 years is quite a task. Ignoring interest, that’s $1,250 per month, or $3,750 per quarter. The task is much less daunting, however, since Larry can expect a positive return on money he can invest.
Larry figures he can save about $400-$500 monthly at this time; although, he has no idea whether that will be enough (or too much) to meet his goal. A very simple approach is to use the annuity formula #4-4 (Chapter 4, formula 4) to see what a series of $400 regular monthly investments would grow to over 10 years. (For ease of reference, I’ve repeated the most important formulas in a box at the end of this chapter.) If we assume an average compound monthly return of 1% (12.68% annually), the account would grow to only $92,000.
1 A $500 monthly investment would accrue to $115,000 over 10 years.
2To keep his bookkeeping simpler, Larry decides he will invest quarterly, for 40 quarters. He can afford about $1,200 to $1,500 per quarter. Assuming an average compound quarterly return of 3% (12.55% annually), he could accumulate anywhere between $90,500 ($1,200 at the end of each quarter) and $116,500 ($1,500 at the start of each quarter). Using a financial calculator to compute the required investment as shown in Chapter 4, we find that Larry needs to set aside about $1,990/quarter for 40 quarters, and earn a compound average annual return of 12.55%
after taxes, in order to meet his goal.
3 This is about $660 per month; is the goal beyond his reach? To answer this, let’s examine the expected return on investment more closely, along with taxes, and then look at Larry’s options.
INVESTMENT RETURN & TAXES
What return on investment should Larry project into the future? The higher the assumed return, the easier it will appear for him to achieve his goal. But if he is overly ambitious in his assumptions, he will end up investing too little money toward his goal. The penalty for this unfulfilled optimism could be as bad as never meeting his investment goal; or, more likely, he will need to invest painfully high sums as his goal approaches (to make up for the planned-for investment returns that never materialized).
Expected Return
Here is where the discussion of market returns in Chapters 1 and 10 come into play. Larry has chosen an investment that tracks the market (has a beta of 1.0), so he can expect roughly market returns. Intermediate government bonds are promising a yield of 14%, so investors must be expecting (demanding!) much more for a risky stock market investment. Based on
Table 10-2, when bond rates are 14%, an investment with a beta of 1.0 could be expected to return a compound average quarterly rate of approximately 4.5%.
4If we can expect a 4.5% compound quarterly return, then the quarterly investment required is only $1,401 ($467 monthly). It appears that, based on current inflation and expected investment rates, Larry can set enough aside to meet his goal.
Taxes
But what about taxes? We’ve assumed a 4.5% quarterly return on investment (before taxes), but then went ahead and used the figure as if taxes had already been taken care of. Unfortunately, we will have to make some provision for taxes—this will obviously make it more difficult to achieve the final investment goal of $150,000 spendable dollars. Suppose Larry is in the 28% tax bracket.
5 There are three basic ways that these taxes might be accounted for, depending on how Larry “shelters” his investment, if at all.
If the investment is made with pre-tax dollars—such as an IRA, 401k, Keogh plan, etc.—all taxes are deferred until withdrawal, on every dollar invested or accumulated. For example, in the plan above, we invested $1,401 and earned 4.5% quarterly, resulting in $150,000 in ten years. But after paying 28% taxes on this, we would only have $108,000 to spend, falling well short of our goal. Thus, to clear $150,000 after taxes, we would need to accumulate a fund of $208,333; paying 28% taxes would cost $58,333, leaving us with our goal. This would require a quarterly investment of $1,946. This seems like too much, but recall that Larry could set aside $400-$500 per month, presumably after taxes. He would need to have $555-$694 available monthly before taxes (at 28%) to accomplish this; thus the goal is within his sights.
A second approach would be if investments are made after taxes (unlike above), but that all investment earnings are tax-deferred (as above). Let’s see how this would affect our plan above, investing $1,401 to achieve $150,000 in ten years. We would only pay taxes on our $94,000 in profits (having already been taxed on the 40 × $1,401 = $56,000 invested), costing us $26,300 in taxes, and leaving us that much short of our goal. To clear $150,000 as desired, we would need to accumulate $1,700 quarterly toward a $181,900 ten-year goal.
6 Taxable profits on the $68,000 invested total would be $113,900; at a 28% tax rate, we would owe $31,900 in taxes, leaving $150,000 to spend. This $1,700 quarterly requirement is quite a bit over our funds available.
The final approach is “pay as you go.” As we earn our 4.5% quarterly return, we would pay a 28% tax on it. Thus, our after-tax earnings would only be 72% of 4.5%, or 3.24%. At this lower rate, it would be much harder to accumulate $150,000. Quarterly investments of $1,883 would be needed to achieve our goal;
7 this is well above Larry’s limited budget.
What will Larry’s tax situation be? This problem is unlikely to fit the first scenario, as it is not a retirement goal. If we assume that his investments take place outside of a tax-sheltered account, then it seems like the last scenario applies: Pay taxes as you go. Thus, we will use the 3.24% quarterly rate of return for planning purposes (4.5%, less 28% of that for taxes, as above). In reality, though, our stock index fund investment will provide some tax deferral benefit. You only pay taxes on mutual fund distributions, and on gains when you sell. Much of our ongoing return from the fund will be unrealized or paper gains, which will be deferred and taxed as in the second scenario above (and at the capital gains rate, as well). Thus, the reality will lie between the last two, “tax-deferred” and “pay-as-you-go” scenarios described above. We’ll use the latter approach, reducing our planned rate of return to 3.24% quarterly, as it is the most conservative approach. To achieve the broadest possible coverage, we’ll go back and look at the first approach (tax-sheltered retirement fund) later, when we use the value averaging strategy.
IMPLEMENTING DOLLAR COST AVERAGING
After considering taxes, Larry’s investment problem seems difficult; recall that $1,883 would be needed each quarter, if a level investment approach (pure-DCA) is used. At this point, we need to specify a particular investment approach. First, we will plan and implement Larry’s accumulation plan using dollar cost averaging. After working through ten years of the DCA approach, we will examine the use of value averaging to conclude the chapter.
1981: Setting Up DCA
Armed with the information estimated above, we are prepared to set up a dollar cost averaging plan to achieve our goal. Let’s review the important figures at our disposal, December 31, 1981:
| $ 57,830 | Current cost of land |
| $150,000 | Expected cost of land in 10 years (goal) |
| $ 1,500 | Limit on funds available for quarterly investment |
| 10% | Expected annual inflation rate |
| 4.50% | Expected pre-tax quarterly return on fund investment |
| 3.24% | Expected after-tax quarterly return |
| 40 | Number of quarters to accumulate goal |
We’ve already investigated setting up a level-DCA approach, but we found out that it required $1,883/quarter, which was too much current income to set aside. We failed to account for the fact that Larry may be able to increase his investment contributions over time. Thus, we can begin with a lower, more reasonable initial DCA contribution, and then increase it regularly over the ten years to keep up with inflation. This “growth-adjusted” DCA strategy has been discussed often in earlier chapters.
How much would Larry need to start investing if he decided to increase his investment contributions at the inflation rate? For that, we turn to formula #4-15, the “Approximate Growth-Adjusted DCA Formula.” The variable we will want to solve for is C, the initial quarter’s DCA amount or investment contribution. We have already estimated Vt to be $150,000, and know t to be 40 quarters.
The other input,
R, is the average rate;
R = (
r +
g) ÷ 2, is calculated by averaging the quarterly expected rate of investment return, and the quarterly rate at which you plan to increase the DCA amount. Here, if we average the
r = 3.24% after-tax return with the
g = 2.50% planned growth in DCA amount,
8 we get
R = 2.87%. This calculates to a growth factor of 124.05; that is, if our initial DCA amount,
C, is $1, our expected accumulated total after 40 quarters is $124.05. Since we plan to accumulate $150,000, we must divide that by the growth factor, arriving at an initial quarterly DCA amount of
C = $1,209.
9This falls in the low end of our available investment range of $400-$500 per month, so Larry could invest more, to be conservative. He could also reduce some of the assumed inputs, to allow less chance of falling short of expectations. For example, Larry could reduce his expected after-tax return on the fund to r = 3.00%, and reduce his required increase in future contributions to g = 2.00%, and still get a reasonable required investment of C = $1,397. Larry feels that we have been quite conservative already in our various assumptions, and decides to stick with C = $1,209.
Larry should begin by investing $1,209 for the initial quarter, and then should increase this amount each quarter by 2.5% (to $1,239, $1,270, $1,302, etc., subsequently). To keep things simpler, Larry would prefer to only adjust his investment amount each year. If he increases his investment by 10% at the end of the year, that leaves all his quarterly contributions lower than they should be. Thus, he decides to start with an amount 5% higher than his initial “requirement” and stay with it; this would be $1,270. At the beginning of the year, he is investing 5% over his goal; but as his goal increases over the course of the year, he is investing 5% under his goal by the end of the year, as he left the investment amount unchanged. At that time, he would increase the investment amount by 10% (to $1,397), leaving it there for the entire second year. So, Larry puts $1,270 into the mutual fund on the last day of 1981, and hopes for the best. He also sends off for some drawings and floor plans for several cabin designs that struck his fancy.
1982-1983 Investment Results
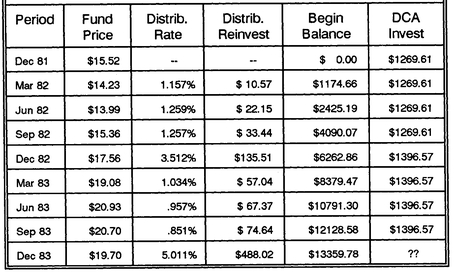
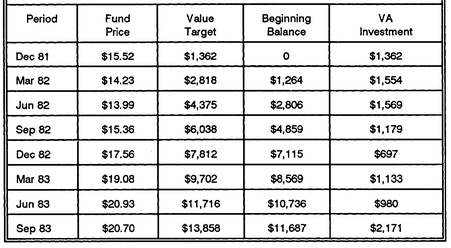
The DCA investment results for the first eight quarters are recorded in
Table 11-3. The first entry shows that there was no investment balance in 1981, until the first investment of $1,269.61 at a price of $15.52 per share at the end of December.
The March 1982 entry shows the investment performance over the first quarter. The fund price fell by −8.3% from $15.52 to $14.23; combined with a distribution (income dividends and realized capital gains) of 1.157%, the total return on investment for the period was −7.2%. The distribution of $14.68, taxable at 28%, results in a tax of $4.11, leaving $10.57 available for reinvestment. All of this results in an investment balance of $1,174.66 just prior to the March 31, 1982, investment of $1,269.61.
Continuing like this through the remaining seven quarters, Larry’s investment fund grows to $13,359.78 by December 31, 1983. His eight quarterly investments totalled $10,664.72, but his tax basis would be higher due to the $888.74 of total reinvested distributions. The tax basis is $11,553.46, so the “paper gains” yet to be taxed are $1,806.32 (taxes on these gains are deferred until they are realized, when the fund shares are sold).
1983: Reassessment and Readjustment
There were many changes and surprises over the first two years of Larry’s investment plan. First of all, his index fund did considerably better than he had expected—after eight quarters, Larry had expected a fund balance of only $12,130.
10 Instead, he has $13,360 of value built up, a nice surprise of $1,230 extra.
Also, inflation has been kind to him; prices only increased by 3.87% and 3.80% in 1982 and 1983, as opposed to the 10% expected inflation rate. Thus, in current dollars, the plot of land costing $57,830 in 1981 cost $60,070 in 1982, and $62,350 at the end of 1983.
Expected inflation over the next eight years has abated as well. Using last year’s inflation, we could expect 3.8% inflation again in 1984. Based on promised T-bill rates for 1984 (less 2%), we could project a 7.85% inflation rate. Using the longer term T-bond yields (less 3%), an 8.41% inflation prediction would result. Weighting the latter prediction most heavily, these indicators average out to an estimated expected inflation rate of 7%. Applying this 7% estimate to the current land price of $62,350 and compounding for eight years, our investment goal for 1991 is only $107,130.
Most of the news is good. Our investment goal has been revised downward considerably due to reduced inflation, and we are further along toward our investment goal than expected due to a spate of good market returns. But not all the news is good. In this lower rate environment, expected or required rates of return on both stocks and bonds are lower as well. Based on the 11.41% intermediate government bond rate, the average return that we can expect on our index fund investment can be estimated from
Table 10-2 to be about 3.9% quarterly (down from 4.5% before). Thus, while our destination is much closer than we expected, the speed limit on the road to that destination has been substantially reduced.
Given all these major changes and their obvious impact on the original investment plan, the time has come to readjust the plan in order to re-target our goal. This process of regular readjustment was discussed in detail in Chapter 4. Larry planned to readjust his figures every two years, based on new information and unexpected changes in his goals, his investment success, and his expected future returns.
Given these new estimates to work with, we can recalculate the investment amounts required to meet our new goal. We should account for the expected growth in our existing “pot” of money already accumulated, and then calculate the future investments required to get us the rest of the way to the final goal. This procedure is described in Chapter 4.
Our $13,360 worth of funds already accumulated should grow at an expected rate of return of 3.9% quarterly (before taxes). Adjusted for 28% taxes, this leaves a 2.81% quarterly return. Over the 32 quarters remaining, our “1st pot” of money here would grow to about $32,430 by 1991.
This analysis leaves out one seemingly minor point on taxes that must be considered. In the section above, we note that Larry has already accumulated, but not yet paid taxes on, $1,806.32 of “paper gains” that have not yet been realized. The taxes on that amount are about $506 and must be accounted for at some point. I see at least a couple of ways to deduct these tax liabilities from our investment results. At one extreme, it is possible to defer taxation of these gains until sale in 1991. This would result in a 1991 tax bill of $506, reducing our final investment amount of $32,430 to $31,924. At the other extreme, we could “charge ourselves” for the taxes now, since all of our other tax calculations are “pay-as-you-go.” Thus, of the $13,360 we currently have, we could treat $506 of it as really belonging to the I.R.S., leaving us with $12,854 now, after taxes. Over the time remaining, this would be expected to grow to about $31,201, even lower than above. This is a more conservative approach, and I will use it for all of Larry’s calculations. Admittedly, this unrealized tax obligation does not make a huge difference, but if we consistently ignore such tax liabilities, we will consistently find ourselves short of our goals when the tax bill finally arrives.
So after a conservative adjustment for taxes, we expect the current investments to grow to about $31,200, leaving us $75,930 short of our final goal. We now have 32 quarters to build up an investment of that size. We will want to solve DCA Formula #4-15 for C, the initial investment amount that we will increase by g each quarter. With inflation expected to be 7.0%, we will use 1.75% for g, as Larry will increase his investment over time at the expected inflation rate. We have already determined the expected quarterly after-tax rate of return on investment to be r = 2.81%. Averaging the two, we get R = 2.28%. We know that the target value for this “second pot” of future investments is V = $75,930, and that there are t = 32 quarters remaining. The calculation, with these numbers, simplifies to: 75,930 = C × 65.8, or C = $1,154.
So now, after readjusting for the many surprises and changes in 1983, we find that a quarterly investment of $1,154 is all that is required to meet the investment goal. Note that we had been investing $1,397 per quarter throughout 1983; Larry is prepared to (and expected to) invest over $1,400 per quarter and would prefer to invest more than the $1,154 needed.
There are several approaches to dealing with this very good news. One obvious choice is to simply keep setting aside larger amounts (say, $1,454), applying $1,154 to the DCA plan for the land, and having $300 available to start investing toward a separate goal, perhaps a fishing boat. A second approach, as discussed in Chapter 4, is to trade up to a higher investment amount (C⇑) for now, but growing it slower (g⇓) in the future. If we held the investment amount the same as last year ($1,397), the quantity (1 + Rf)32 would have to equal 1.70 (see formula #4-16). This would mean that R would have to be 1.67% in the future; we could only get this with r = 2.81% by averaging it with a projected growth of g = 0.53%. That is, if we invest $1,397 now, we would only have to grow our investment contributions by about .53%/quarter, or 2% per year, instead of the 7% inflation rate as planned above. A third approach, even more conservative, would be to reduce our projected return on investment (r), and recalculate the required investment. A final alternative is to “downshift risk” by transferring some of our “excess funds” over to a safer investment.
This final alternative is the approach that Larry chooses to use during each biannual readjustment process. His logic is that he wants to be fairly sure that he will achieve his investment goal in 1991. This is obviously quite difficult to assure when using a risky equity investment. As 1991 draws near, Larry should be more and more nervous about having his entire stash sitting in a fund with potentially high price swings. If he can afford to, he will occasionally shift some of his investment into low-risk vehicles, such as a money-market fund.
11 By downshifting risk, he trades away some of the expected high returns (of equity) for less risk and less chance of disappointment. In addition, moving money from equity funds to money market funds involves a sale of the equity funds, which results in a tax realization (more on this later).
Larry decides to tailor such an approach to his needs. He is willing to have his quarterly investment increase at the inflation rate, so if C is calculated to be lower than expected (as it was here), he is willing to shift accumulated money over to a money market fund, which would require a higher investment amount (C) to make up for the lower expected return. He decides, however, to never shift more than half of his equity fund over to the money market fund at one time.
How would this work at the 1983 readjustment? Recall that Larry’s 1983 quarterly contribution was $1,397; given the 7% expected inflation rate, he would be willing for that amount to go up to $1,495 for 1984. As we saw above, though, good fortune has had the result of lowering the required quarterly contribution to $1,154, if we keep all of the money sitting where it is, in the high-risk, high-return equity fund. Suppose that we move 50% of our available money to the money market fund, which is yielding only 1.64% per quarter after taxes (or, 2.28% pre-tax) right now. Out of our account balance of $13,360, we move $6,680 to a money market fund.
Taxes will complicate this. Recall our $1,806 of accumulated paper gains? If we sell half our investment, we will realize half of these gains, and must pay taxes of 28% of the $903 realized profit—a $253 tax bill. Thus, we will have $6,427 moved to the money market fund after accounting for these taxes.
The “1st pot” of money now consists of a $6,427 money market fund, with an expected quarterly return of 1.64%; and, a $6,680 index fund (conservatively “worth” only $6,427 after accounting for taxes due on unrealized gains, as discussed above), with an expected quarterly return of 2.81%. All of this is after taxes. At these rates, the funds should grow to $10,820 and $15,600, respectively, for a total 1991 value of $26,420. Note that this is considerably lower than the $31,200 expected future value arrived at above, where we kept all money in the equity fund. To achieve our 1991 goal of $107,130, we will need to accumulate about $80,700 over the next 32 quarters. This requires a growing quarterly investment with an initial value of C = $1,226. This is more than $1,154, but still considerably less than Larry can afford.
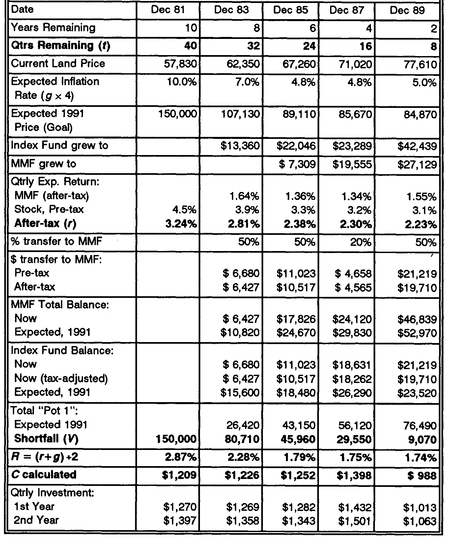
As we are only increasing the investment amount annually, we will adjust the beginning amount upwards by half the inflation rate, and then wait a year before increasing the amount for inflation. Thus, we will begin with a $1,269 investment each quarter until December 1984, at which time we will increase the amount by 7% to $1,358 per quarter until December 1985. At that time, we will again readjust the investment plan. The above discussion on the 1983 plan readjustment in summarized in the numbers in
Table 11-4 below.
The 1985 Readjustment
After our leisurely and detailed stroll through the initial set-up and the 1983 readjustment, we can quickly move through the high points of the next readjustment in 1985. The key points for each readjustment are summarized in logical order in
Table 11-4 below.
By the end of 1985, inflation had continued at well below its expected pace, bringing the current price of the land up to $67,260. A rough estimate of future expected inflation is 4.8% at this time, giving an expected goal of only $89,110 in 1991 dollars. The accumulated investment in the index fund has grown to $22,046 (including paper profits of $3,615), while the 1983 investment in the money market fund has grown gradually to $7,309.
These already accumulated investments will grow over the 24 quarters remaining until 1991. The money market fund is currently yielding 1.36% after taxes; it is expected to amount to $10,110 by 1991. As for the equity investment, accounting for potential taxes of $1,012 on the paper profits, there is $21,034 really available in the index fund after taxes. The expected quarterly investment return should be 3.3%, or almost 2.38% after taxes. At this rate, the money in the index fund should grow to $36,970 by 1991. Combined with the money market fund, we can expect roughly $47,080 by 1991 from our current investments (assuming no additional transfer to the money market fund to “downshift risk”). This would leave a shortfall of $42,030 to be accrued with additional investments over the next 24 quarters.
To solve for the required investment amount, we need to determine the expected value for R. By averaging the quarterly inflation rate of 1.2% with the after-tax r of 2.376%, we get a value of R = 1.788%. By solving for C using t = 24, we get a required investment of only C = $1,145 per quarter.
This value is quite a bit lower than we expected, due again to our good fortune in terms of low inflation and high investment returns. Larry can again take an opportunity to reduce risk by shifting some investment funds over into the money market fund, while still maintaining enough upside to achieve his goal.
We shift 50% of his index fund money over to the money market fund, adding $10,517 to his balance after paying gains taxes. This transaction results in $17,826 in the money market fund, and leaves $11,023 in the index fund (“worth” $10,517 after a provision for taxing paper profits). At the expected investment rates on the two funds, they should yield respective balances of $24,670 and 18,480, or a total of $43,150, by 1991.
We still need to fund the shortfall of $45,960 with future investments. Using R = 1.788% and t = 24 as above, the required investment is calculated to be C = $1,252. Using this as the base, Larry invests $1,282 each quarter in 1986, and plans to increase this by inflation to $1,343 for 1987.
And So On and So On . . .
The last couple of readjustments, in December 1987 and 1989, are also shown in detail in
Table 11-4. Low inflation continues to temper our investment goal, keeping it down in the $85,000 range in 1991 dollars. The stock market crash of 1987 puts a damper on Larry’s investment success, but the plan still performs well enough to allow a transfer of 20% of the index fund into the money market at the end of 1987, while still keeping the required investment amount down to
C = $1398, the same as his investment way back in 1983. At this point, he has moved well over half of his investment funds over to the money market, and is thus not exposed to much risk of falling short of his investment goal.
TABLE 11-4: Summary of DCA Plan Set-up and Readjustment
The final readjustment in 1989 reflects substantial success in the index fund over 1988 and 1989. By accumulating a total of almost $70,000 already by 1989, Larry can essentially “coast” for the remaining two years. Even when he transfers half of his risky investment over to the money market fund, and accounts for taxes, he is still so close to the final goal that he only requires quarterly investments of C = $988. With two years left, Larry is positioned well with about $47,000 in the money market fund and about $20,000 after taxes in the index fund. In reality, it would probably make sense to readjust the plan one more time as we come down to the last year, just to make sure that the final goal stays in sight. But Larry’s approach at this point is so conservative, and his financial slack (in terms of being able to increase his investment contribution over the $988 required) so great, that there is really little room for concern.
Wrapping It Up: 1991 Results
By 1991, the price of the land which was Larry’s brass ring had risen to
$84,870; no real surprises in the last four years or so. His money market fund investment rose in value to $51,970, and his index fund investment rose to $36,250, giving a total investment fund of $88,220. But since much of the index fund value represented paper profits (capital gains) of $8,446, there were taxes due in the amount of $3,102 on these gains. This reduces the investment fund to a spendable, after-tax amount of
$85,120, just more than enough to cover the cost of his goal.
12 Larry’s gone fishin’.
This concludes the detailed example of the actual planning and implementation of a DCA strategy. I hope this has provided you with a thorough exposition of the problems, judgments, pitfalls, and techniques required to achieve your own investment goal. Larry’s experience brings to light the importance of planning, making reasoned estimates, being flexible, dealing up front with taxes, and readjusting the plan on a regular basis.
Now we will turn to the same investment problem, using the alternate strategy of value averaging.
IMPLEMENTING VALUE AVERAGING
We’ll now follow Larry’s journey through this same investment scenario to observe the issues and techniques involved in planning and implementing with value averaging. Much of the discussion above, on setting up a DCA plan, will also apply here. The basic 1981 information is the same: the land price of $57,800 is still expected to cost $150,000 in 1991 at a 10% expected inflation rate; the pre-tax and after-tax quarterly expected returns on the index fund are 4.5% and 3.24%, respectively; Larry still has a rough idea that his available after-tax investment funds are in the $1,200-$1,500 range (quarterly) now, although he would expect that contribution to grow with inflation over time. The main difference is that here, Larry chooses to use value averaging in formulating his investment plan. One other difference here is that we will use Larry’s tax-sheltered retirement account—such as his 401k plan, which uses pre-tax investment money and postpones all taxes until withdrawal.
Establishing the Value Path
The simple formula that takes account of expected market returns and the (on average) increasing investment contributions is the value path. As described in Chapter 5, its role is to set up a target value for every point in time between now and your final goal, resulting in reaching that goal in the time available. The VA Formula, #5-19, is reproduced in the box at the end of this chapter.
We’ve already discussed all the inputs above; there are some changes here, in consideration of the different tax status. There are t = 40 quarters. Since the 401k investment is made with pre-tax dollars, all taxes are deferred until withdrawal, on every dollar invested or accumulated. Our goal is $150,000; but since we must pay taxes on our entire withdrawal at a 28% rate, we really need to accrue $208,333, to clear $150,000 after paying $58,333 in taxes—thus, V40 = 208,333 is our investment goal. Also, due to the use of pre-tax dollars, Larry’s ability to save $1200-$1500 quarterly after taxes translates into about $1550-2100 of pre-tax money made available for investment contributions.
Our quarterly expected return on investment, pre-tax, is r = 4.5%. We’ll call C the initial contribution; while we cannot determine (as in DCA) future contributions in VA, C is the amount that we will expect to put in, on average, to meet our value goal, after accounting for an investment return on existing shares. To allow this expected investment contribution to increase with inflation over time, we set g = 2.5%, our estimate of the quarterly inflation rate. R, which is simply the average of r and g, is 3.5% here.
Solving the formula to meet our 1991 goal, we get an initial contribution figure of
C = $1,315.48. This gives a value path formula of:
Vt = 1,315.48 × t × (1.035)t
This value path solves for the target value we should achieve at every point in time. Starting with t = 1, we must invest to achieve a target value of $1,362. Next quarter, we will invest whatever is required to bring our fund value up to $2,818. At t = 40, we would invest enough to reach our final pre-tax target goal of $208,333.
The timing of this plan is actually a bit conservative, as we are beginning our investment right away (t = 1 now, instead of t = 0). This means that t = 40, our final investment, occurs at September 1991, a quarter before our need. This is good, though, since in neither plan (VA nor DCA) did we want to need an investment in December 1991. By making our last investment in the quarter before our goal, we can “coast in” at money market rates with no risk of missing our goal. A much less conservative approach would be to recompute C, letting t = 41; this would require an unknown and potentially huge cash investment in December 1991, which is probably not what Larry wants.
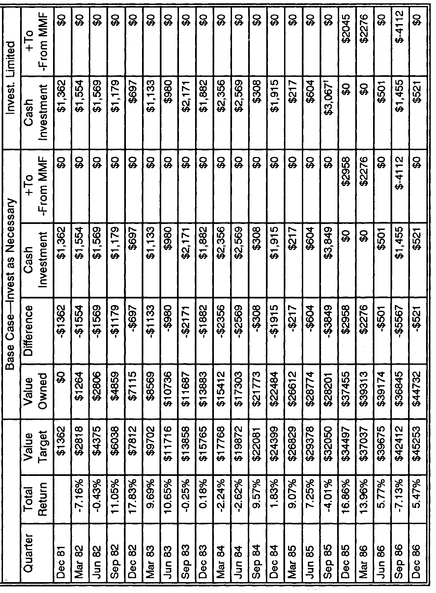
The plan implementation begins with a $1,362 investment on the last day of 1981. The first eight quarters of the VA plan are shown in
Table 11-5. Any dividends or fund distributions are reinvested; the “Beginning Balance” for March 82 reflects the actual value (which was set to equal the value target) in December 81, less the decrease in price, plus fund distributions. Due to losses in the fund, the March and June investments are slightly larger than expected; the opposite is true over the next year, as the fund is providing above-expected gains that contribute toward the value target (making our investment lower than “planned”). After two years we “rest” and reevaluate our inputs and assumptions, and check to see if our plan needs to be readjusted.
1983: Readjusting the VA Plan
As in the previous (DCA) example, much can change over a few years. The two major changes that will affect the value averaging trajectory toward the goal are changes in the goal itself and changes in the expected rate of return. Inflation and interest rates dropped considerably over the 1982-3 period, creating a new investment landscape for us to traverse.
Based on our discussion of inflation from the DCA section, our new expected 1991 after-tax goal is $107,132. Allowing for 28% taxes, our pre-tax goal is now V = $148,800, down about $60,000 from before. We should now be “further along” our value path than we had expected.
But the expected return on our investments, as well as our inflation or growth adjustment, has dropped as well. The new quarterly figures of r = 3.9% and g = 1.75% give an average rate of R = 2.825%.
Due to the new goal and the new expected return, we are effectively on a new value path (which we have yet to calculate). It’s a value path that, at R = 2.825%, will grow to V = $107,132 over the next 32 quarters. Treating December 1983 as our 1st quarter, we can go back and use our September 1983 value of $13,858 as our “0th quarter,” or starting point. Now we simply have to adjust for the fact that, on this new value path, we have a $13,858 “head-start.”
That’s where the VA Readjustment Formula (#5-21) is useful. If we set T = 32 as our goal, with t = 1 now and t = 0 as our starting point, the standard value path formula would give our starting value as $0; we had $13,858 to “start with” last quarter. The readjustment formula simply comes up with a new “time index” for our goal and our starting point (but still keeps them 32 quarters apart). Solving for T with the inputs just discussed, the formula yields T = 41.4 as our new time index for our goal. Our starting point is 32 quarters earlier, so last quarter is indexed t = 9.4, and right now it is nominally t = 10.4. This has little intrinsic meaning, other than that we are effectively already 9.4 periods along the way of a 41.4-period value path, with 32 to go. This is “better” than being only 8 periods into a 40-period value path; more progress, so to speak.
The new time index is used to recalculate our figure for C, so that we can calculate our new value path, giving us new targets for each quarter that will achieve our new goal. We know that at our 1991 goal, T = 41.4 and VT = 148,800. Using R = 2.825% and these inputs in the value path formula #5-19, we get C = $1,134. This is the C we will use to create the value path formula. But what does it mean? Recall the C simply designates the average expected investment contribution at t = 0; this contribution grows each quarter by rate g. Thus, by quarter 10.4 (December 1983, which is now), this expected contribution is now (1 + g)10.4 times as large, or, $1,358—and still growing. Note that this figure is roughly as large as our initial quarterly value from back in 1981. The fact that the readjusted figure has not increased for inflation is a positive sign of Larry’s better-than-expected progress toward his goal.
We use the
C = $1,134 figure, the new time index, and the value path formula, to compute a new value path that gets us to our goal in time. We can first put in
t = 9.4 to check that the required value for last quarter was $13,858, which was in fact the value.
13 Our current target for December 1983 (
t = 10.4) is $15,765, increasing up to $32,050 in September 1985, and on to $148,800 in eight years when we reach our goal.
Future VA Readjustments
We will readjust again in December 1985; and 1987; and 1989. The mechanics and the impact of these readjustments are shown in
Table 11-6. The increasing values of
T and decreasing values of
C indicate that reduced inflation is moving Larry along toward his goal a bit quicker than expected.
TABLE 11-6 Summary of VA Plan Set-up and Readjustment
VA Investments
Having set up and occasionally readjusted the value paths, we have yet to look at the actual investment cash flows and performance. The value averaging approach ensures that you will reach your goal, but doesn’t tell you anything about what you will need (to invest) to get there. We’ll look at two versions of implementing the VA plan: a base case with highly variable investment flows and no controls, and a “smoother” version that simply controls the out-of-pocket investment contributions.
The fund’s total return performance and the value path are detailed on the left-hand side of
Table 11-7. The center section shows the base case, where you apply value averaging with no controls on your out-of-pocket investment—you invest whatever necessary to achieve your value target. Recall that the average expected quarterly investment at a given point in time is
C, adjusted upward for inflation; we’ll call this
Ct below, where
Ct =
C × (1 +
g)
t.We expect to invest that much each quarter; the money market fund (MMF) will be used to help out where necessary.
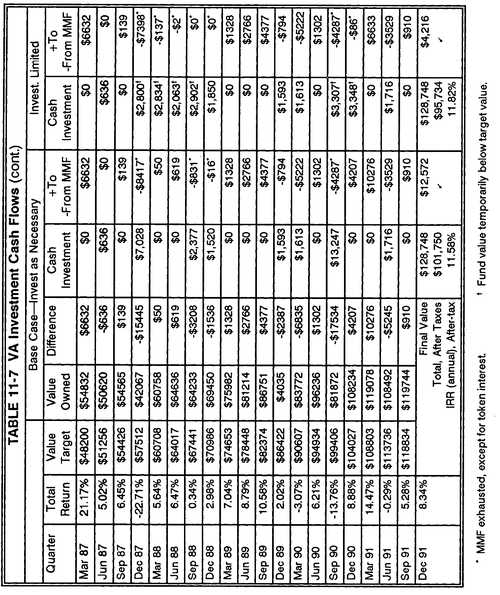
Here’s the procedure Larry used for moving money around to meet his value target. If there is no money in the MMF, Larry comes up with the entire investment from cash (see Dec81- Sep85). If there are excess funds (as in Dec85-Mar86), they are moved to the MMF. If the funds required are less than expected (<Ct), they will be newly invested out of cash (e.g., Jun86, Dec86). Any funds needed over Ct will be taken from the MMF (e.g., Sep86). Finally, if the need is so great that it exhausts the MMF, then any additional requirement to meet the value target will come from cash (as in Dec87 and Sep90).
The final result of the base case was that we ended up with too much money. Even after paying taxes, we still have $16,000 of extra money over and above our $85,600 goal. Some of this is due to a sizable unexpected pot of money in the MMF (discussed below). Another reason is that we set up our value path to reach its goal in Sep91, and then let the funds stay invested, letting the account wander up and down in value (mostly up!) with the market for the rest of the year. It would have made more sense to reduce our risk by shifting our money out of the risky investment (and into the MMF) once we had come close to achieving our goal. It makes even more sense to have done this gradually, “downshifting risk” over at least the last two years of the plan. This philosophy was described and implemented in detail in the DCA section of this chapter.
Note one serious problem with this “uncontrolled” approach—the cash investment requirements are too variable and sometimes unreasonably high. Ignoring the flows that are simply moving back and forth between the index fund and the MMF, we focus on the column headed Cash Investment. On three occasions (Sep85, Dec87, and Sep90), the cash investment required seems too high, due to steep market downturns. As the market rebounds, much of this invested cash ends up parked in the MMF. This is one reason why the base case “overshoots” the value target, as over $12,000 of “extra money” is parked in the MMF by our Dec91 goal.
Larry decided to take a more controlled approach to investing cash into the plan, as he desired more investment stability; this approach is detailed in the last two columns of
Table 11-7. He decided to limit his out-of-pocket investment to 2 ×
Ct (double the expected amount).
14 The first example of this is in Sep85, where the value target called for $3,849 to be invested, and there was as yet no MMF built up. Adjusted for inflation, the expected investment that quarter was about $1,534—double that was $3,067, the limit of Larry’s investment. Notice (in the second-last column of
Table 11-7) that this is what he invested, leaving him temporarily short of his value target. This shortage is made up during the next investment period. By looking at the “problem areas” of Dec87 and Sep90, you can see how this restriction smooths out the sizable investment requirements after exhausting the MMF. Not only does this spread the investment requirement over a few periods, but it also gives later market recoveries a chance to “kick in some of the needed dollars,” as in Dec90-Mar91.
The results of this plan are not only smoother and lower cash investments, but also less excess money parked in the MMF as we reach our final goal. Here, Larry ends up with only onethird as much extra MMF money in Dec91; he only overshoots his goal by about $10,000, most of which is due to an unexpectedly high market return in the quarter after we had achieved our goal (this risk can be removed, as discussed above). The annualized return on investment was 11.82% after taxes with this version of the strategy, slightly higher than the uncontrolled version with its more volatile cash flows.
There are obviously many other possible approaches Larry could have taken to planning, readjusting, controlling, and implementing his VA strategy. We’ve only looked at two methods of controlling cash flows; create methods of readjusting and controlling the plan that you can be comfortable with.
SUMMARY
With these detailed DCA and VA examples, I hope I’ve given you plenty of real-world issues to think about, and maybe even answered a few of your questions about implementation. There are as many ways to achieve your investment goals as there are investors. With whatever method you choose, I hope you have as much success as Larry did.
What broad lessons can we learn from Larry’s experience? Being flexible is good, but being flexible with a plan is better. It may not be fun to think about taxes, but you’ll either work them into your plan or else have an incredibly nasty surprise lurking between you and your goal. Ditto with inflation. Don’t be scared to make educated guesses (we’ve called them “estimates” and “expectations”), but be prepared to reevaluate them on a regular basis.
KEY FORMULAS
Lump-Sum Investment
(4-3)
Periodic Investments
(4-4)
Approximate Growth-Adjusted DCA Formula
(4-15)
DCA Readjustment Formula
(4-16)
VA Value Path Formula
(5-19)
VA Readjustment Formula
(5-21)
ENDNOTES
1 The annuity formula assumes end-of-period investments. If we account for the investment being made at the beginning of the month, we get an extra 1%, or one month’s compounding (see formula #4-5); the result is then about $93,000.
2 Accounting for beginning-of-month investment, the result would be over $116,000.
3 Or about $1930/quarter, based on beginning-of-quarter investment timing. For simplicity of calculations, we will compute required investment amounts based on end-of-period investments. This will result in a conservative approach, because required investments will be calculated to be slightly higher than necessary.
4 The 14% bond rate is off the chart; the quarterly figure calculated as 4.5% could be approximated by extrapolating the numbers in
Table 10-2. I know this (roughly 20% annually) expected return seems huge by today’s standards, but remember how likely today’s 3% money market rates seemed back in 1981!
5 Actually, tax “brackets” changed several times over this 10-year period. The “readjustment” process followed later in the chapter deals with changing tax rates quite well, but, for simplicity, we will keep Larry in the 28% bracket throughout the decade.
6 How did we get this figure of $181,900? Trial-and-error will get you there, but so will a little algebra. Let
G be our unknown pre-tax investment goal. Our “profits” will be the difference between
G and our investment, which will be $
C for
n periods; taxes at 28% of profits will amount to: Tax = .28 × (
G-nC). We also want to have $150,000 after reducing
G by taxes, so:
150000 = G − .28 × (G-nC); rearranging,
150000 = .72G + .28nC
If we knew C, the required periodic investment, we would be done, but C depends on our unknown goal, G. Recall that C is related to G by the annuity factor, A = [(1 + r)t − 1]/r (see formula 4-40): C = G/A
Substituting for C, 150000 = .72G + .28nG/A
Grouping G’s, 150000 ÷ (.72 + .28n/A) = G
Here, since r = 4.5%, the annuity factor is A = 107.03, and n = 40. Substituting, G = 150000/.82464 = $181,897
7 Note the difference in these last two methods of $183 (= $1883 − $1700). This is the value of the tax deferral, as opposed to having to pay taxes on income as you earn it.
8 This is based on the 10% annual inflation rate. The 2.50% quarterly rate ignores compounding to keep things simple. Minor approximations like these are inconsequential, given the number of other approximations and estimations required by this, or any other investment planning process.
9 Using the “exact” DCA formula #4-9 gives a slightly higher result of
C = $1,240.
10 Simply set
t = 8 in the DCA Formula #4-15, yielding
V8 = $12,130.
11 Of course, he could choose to invest in a truly “fixed-income” investment, such as an 8-year zero-coupon bond that would mature in 1991. This would avoid any “investment risk,” but would leave him totally exposed to “inflation risk.” Recall that unexpected bad news about investment returns is only one reason why he could fail to meet his final goal. The other (just as important) reason is a potential unexpected increase in inflation. An investment locking in a fixed-dollar amount would do nothing to address inflation risk. Since money-market funds, or other short-term investments, carry “floating” interest rates that tend to move with inflation, they may actually be better suited for situations where you’re “trying to hit a moving target.”
12 The total cash invested into the plan was $51,712 over the 10 years. The internal rate of return, after all taxes, was 2.25% per quarter. That is, on his cash invested in the two funds, Larry earned an average annualized rate of return of 9.32% after taxes.
13 Don’t fret if you get a number a few dollars off. None of my calculations were rounded off, even though I’m reporting rounded figures for inputs and outputs in the text.
14 There is actually some logic behind this (2 times the expected amount) restriction. Supposedly,
Ct is the cash investment you would expect in a typical quarter. But some quarters you will invest less, perhaps even as low as 0. Other quarters you will invest more—as much as you limit yourself to. By limiting that multiple (of
Ct) to 2, you are, in a loose sense, keeping your expected amount in the middle, varying your actual investments around it in a somewhat symmetrical way.