This chapter reviews basic math terminology and definitions including the number line, positive and negative numbers, digits, rounding off, multiplying and dividing, using the order of operations, fractions, decimals, and percents.
The arithmetic on the Mathematical Reasoning test is not necessarily the arithmetic you learned in school. The folks who write the test are striving to make GED® math more relevant to real life. Consequently, you won’t find any questions on the more theoretical aspects of arithmetic—properties of integers, for example. Nor will there be any questions about prime numbers, imaginary numbers, or any of the other terms that generally go under the name “axioms and fundamentals.” Instead, the test focuses on practical math. Several of the questions will be word problems that try to evoke situations you might find in everyday life.
In this chapter, we’re going to show you all the basic arithmetic topics that come up on the Mathematical Reasoning test. With each topic, we’ll first show you the concept behind the topic, then illustrate it with typical examples, and finally give you a small drill so you can practice the concept on your own. At the end of the entire chapter, there will be a big drill in GED® test format, including all the concepts we’ve shown you. The purpose of this is to give you some practice recognizing the different types of questions when they are all mixed together—as they are on the real GED® test. In the next chapter, we’ll cover applied arithmetic topics in just the same way.
Here are the basic arithmetic concepts that appear on the GED® test:
The number line
Rounding off
Operations with positive and negative numbers
Order of operations
Commutative and distributive properties
Fractions
Decimals
Percents
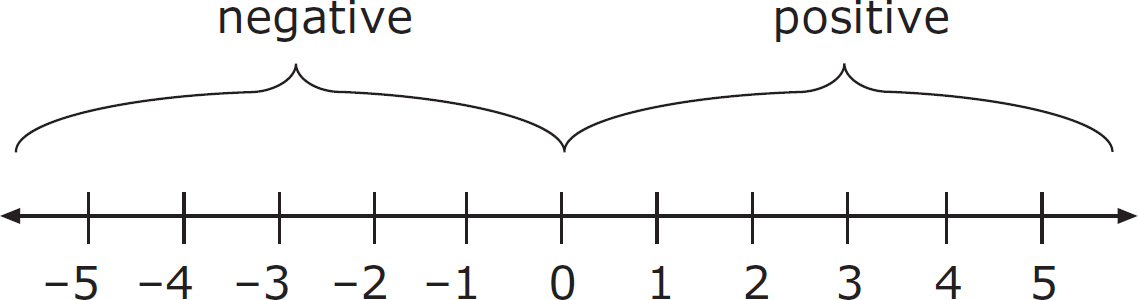
The number line is a visual way of understanding positive and negative numbers in relation to one another.
Positive numbers are to the right of zero on the number line above. Negative numbers are to the left of zero on the number line above. Zero itself is neither negative nor positive.
Note that positive numbers get bigger as they move away from zero. Negative numbers get smaller. For example, –3 is smaller than –1. A number line can extend infinitely to the left or right, but the number lines on the GED® test generally look like the example on the previous page, with a fairly small number of position points. Let’s try identifying some points on the number line.
Find point X on the number line. What number does point X represent? If you said 4, you were absolutely right. How about points Y and Z? If you said –3 and 1, you were right again. Here’s how a number line problem would look on the GED® test:
Question 1 refers to the following number line.
1. Which point represents the number –3?
Click on the number line to plot a point.
Here’s How to Crack It
Generally, the only thing that’s difficult in a number line problem is orienting yourself. The best place to begin is to find 0. Did you find it? Now, determine the scale. Count the number of spaces between 0 and 5. There are five. Therefore, each space is represents 1. Now, in which direction do you move for negative numbers? To the left. And how many places to the left do you count from 0? Three. Mark your point there (or click the cursor on the real GED® Mathematical Reasoning test) and you’re done!
Here’s a slightly more difficult number line problem:
Question 2 refers to the following diagram.
2. On the number line above, AB = BC = CD. If AD = 12, then what is the length of AB?
A. 3
B. 4
C. 5
D. 8
Here’s How to Crack It
In this problem, there is no way to orient yourself because neither the diagram nor the problem identifies a specific point on the number line. Instead, this problem is concerned with the lengths of segments on the line. On the GED® test, lengths are always positive, never negative. In this case, the only actual length you are given is AD, which equals 12. Let’s look at the other information in the problem. If AB = BC = CD, then these segments break up AD into three equal parts. Because the whole is 12, what is the length of a single part? Divide the total length 12 by the 3 equal segments to find that the length of AB is 4, and the answer is (B).
The absolute value of a number is the distance from the number to zero on a number line. Since absolute value measures distance (or length), it is always a nonnegative number. To write the absolute value of a number, you place the number in between two vertical lines. For example, you would write the absolute value of –5 as |–5|. How far from zero is –5 on the number line? –5 is five steps from 0, so |–5| = 5. The absolute value of a number will always be positive (or zero).
Sometimes number line problems will ask you about the midpoint of a line segment. A midpoint is simply the place halfway between either end of the line segment. A GED® problem might look like this:
Question 3 refers to the following diagram.
3. If point X on the line above represents –2 and point Y on the line represents 3, then the midpoint of segment XY would be between which two numbers?
A. –2 and –1
B. –1 and 0
C. 0 and 1
D. 1 and 2
Here’s How to Crack It
This time, there are concrete numbers marked on the number line, so take a second to get oriented. Now, the midpoint of XY is the point exactly halfway between point X and point Y. Count how many spaces there are between X and Y. Did you get 5? Good. What is half of 5? Half of 5 is 2 
. So all you have to do is count over 2 to the right of point X or 2 to the left of point Y. In either case, the midpoint is between 0 and 1, and the correct answer is (C).
You can check your answers in Part VIII: Answer Key to Drills.
Questions 1 through 3 refer to the diagram below.
1. On the number line above, point A is 
point B.
2. On the number line above, what is the distance from point A to point B?
A. –4
B. –3
C. 3
D. 4
3. If a new point E was to be added to the number line exactly halfway between points A and D, where would it be located?
A. between points –3 and –2
B. at point 0
C. between points 0 and 1
D. at point 2
All numbers are made up of digits. The number 6,342 has four digits: 6, 3, 4, and 2. In this case, the 2 is in the ones place. The 4 is in the tens place, the 3 is in the hundreds place, and the 6 is in the thousands place.
The number 0.57 has two non-zero digits: 5 and 7. In this case, the 5 is in the tenths place. The 7 is in the hundredths place.
The GED® test writers sometimes ask you to round off a number. The problem might read, “To the nearest thousand, how many…” or “What number to the nearest tenth….”
Whether you round to the nearest thousand or the nearest tenth, the process is exactly the same. Let’s begin by rounding to the nearest dollar. If you have up to $1.49, then to the nearest dollar you have $1. If you have $1.50 or more, then to the nearest dollar you have $2.
Exactly the same principles hold true when you round any type of number.
1. Identify the place you are rounding to.
• For example, let’s round 6,342.57 to the nearest ten.
• Which digit is in the tens place? The 4 is in the tens place.
Since we are rounding to the tens place, draw a number line that counts by tens:
2. Look at the digit that comes after the place you are rounding to.
In our example, what is the digit after 4? The next digit is 2.
• If that digit is 0, 1, 2, 3, or 4, you will round the tens place down. (Keep the 4.)
• If that digit is 5, 6, 7, 8, or 9, you will round the tens place up. (Change the 4 to a 5.)
Let’s look at this on the number line. Make a mark where the original number lies.
Is it closer to 6,340 or to 6,350? In this case, it is closer to the smaller amount, 6,340.
3. Replace any digits after the rounding place with zeros.
• Which digits will we replace with zeros? The 2, 5, and 7 all get replaced.
• So our number now looks like 6,340.00.
Do we need the zeros after the decimal point? Nope. Go ahead and drop those off to get the final answer: 6,340.
Here’s how this might look on the GED® test.
1. You buy a loaf of bread for $2.99, deli meat for $3.65, and sliced cheese for $4.49. To the nearest dollar, how much will you owe at checkout?
Here’s How to Crack It
There are two steps to the problem. The first step is to add up the items you will be purchasing. $2.99 + $3.65 + $4.49 = $11.13. Great—now don’t forget about Step 2! The problem asks for the total “to the nearest dollar.” So Step 2 is to round. Which is the dollars place? If you aren’t sure, try saying the number out loud: “Eleven dollars and thirteen cents.” So we have 11 dollars plus 13 cents more. Now look at the first digit after the dollars place, which is 1. Since this is less than 5, round down. The correct answer is $11.
You can check your answers in Part VIII: Answer Key to Drills.
1. To the nearest thousand, what is 3,400?
2. To the nearest tenth, what is 3.46?
3. To the nearest hundred, what is 565?
4. What is $432.70 to the nearest dollar?
5. What is 4.80 to the nearest hundredth?
Let’s look at that number line one more time.
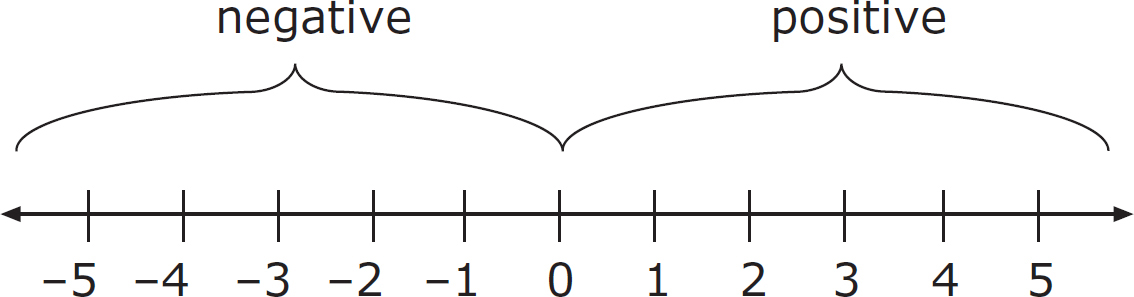
Many people have trouble adding and subtracting negative numbers. The number line helps us perform these operations effectively. First, lets look at adding. For example, (–2) + 6.
To add any two numbers, begin by locating the first number on the number line.
The absolute value of the second number tells us how many steps we’ll move. |6| = 6, so we’ll move six steps.
If that second number is positive, we’ll move that many steps to the right. If it’s negative, we’ll move that many steps to the left. The number 6 is positive, so we’ll move six steps to the right from (–2).
So, we see that (–2) + 6 = 4.
This method works whether you are adding two positives, a positive and a negative, or two negative numbers!
Using the same method, we can see that 7 + (–5) = 2, and (–3) + (–5) = (–8).
Subtracting positive and negative numbers is also pretty straightforward, if we consider one thing: subtracting is the same as adding the opposite. Did you notice, in our example above, that 7 + (–5) is the same as 7 – 5? That’s an illustration of this very idea.
Whenever you have a subtraction question, you can change it to an addition (of the opposite) question, and solve it like we did above. This is very helpful when you are subtracting with negative numbers. Here’s how it works:
4 – 7 =
Let’s rewrite this, so instead of subtracting, we’re adding the opposite.
4 – 7 is the same as 4 + (–7). Now we’ve got an addition question, so we’ll use our addition method, and see that 4 + (–7) = (–3).
This method works on all subtraction questions, even the kind that most people find the trickiest: subtracting a negative. Consider this example:
(–11) – (–7) =
This is perplexing at first. So many minuses! But let’s rewrite it so we’re adding the opposite. Instead of subtracting –7, we’ll add the opposite of –7, which is positive seven. So, (–11) – (–7) = (–11) + 7.
Use your addition steps above, and count 7 steps to the right of –11. Where do you land? On –4.
(–11) – (–7) = (–11) + 7 = (–4)
It might take a little time and practice to perfect these adding and subtracting processes, but that time and energy is worth it. These processes work no matter what the numbers are.
Multiplication is actually just the process of adding a number several times. For example, to multiply 4 by 3, you are actually just adding 4 three separate times
4 × 3 = 4 + 4 + 4 = 12
or adding 3 four separate times
3 × 4 = 3 + 3 + 3 + 3 = 12
To multiply 5 by 2, you are actually just adding 5 two separate times
5 × 2 = 5 + 5 = 10
or adding 2 five separate times
2 × 5 = 2 + 2 + 2 + 2 + 2 = 10
Of course, it’s a lot quicker to use the multiplication (times) tables. We just wanted to remind you of the theory behind multiplication. If your times tables are a little rusty, don’t worry. You’re going to get lots of opportunity to practice over the next three chapters.
There are four rules regarding the multiplication of positive and negative numbers.
positive × positive = positive: 2 × 3 = 6
positive × negative = negative: 2 × –3 = –6
negative × positive = negative: –2 × 3 = –6
negative × negative = positive: –2 × –3 = 6
We have provided the following multiplication table for you to fill in to refresh your memory.
Division is actually the opposite of multiplication. If we multiply 2 by 3, we get 6. If we divide 6 by 2, we are actually asking what number times 2 equals 6?
6 ÷ 2 = 3. You can also write this as
or
.
The same four rules of multiplication apply to the division of positive and negative numbers.
positive ÷ positive = positive: 6 ÷ 2 = 3
positive ÷ negative = negative: 6 ÷ –2 = –3
negative ÷ positive = negative: –6 ÷ 2 = –3
negative ÷ negative = positive: –6 ÷ –2 = 3
Do these problems first on your own. Then, on a separate piece of paper, do them again using your calculator.
You can check your answers in Part VIII: Answer Key to Drills.
1. 5 + (–3) =
2. (–4) + (–7) =
3. (6 × 3) =
4. (–2)(6) =
5. (–3) – (2) + (6) =
6. 10 ÷ 2 =
7. (–5)(–2) =
8. –21 ÷ –7 =
9. 12 ÷ –3 =
10. –12 ÷ 3 =
Remember the number line from earlier in the chapter.
Let’s look at the numbers 5 and –5. What do they have in common? Remember that positive and negative numbers are defined based on their relationship to 0. Positive numbers are to the right of 0, and negative numbers are to the left of 0. In particular, the number 5 is five units to the right of 0, and the number –5 is five units to the left of 0. Even though they are in different positions on the number line, both are the same distance from the number 0. In math, this is said to mean that they have the same absolute value. Since both 5 and –5 are five away from 0, both have an absolute value of 5. In an equation or an expression, the absolute value is represented by two vertical lines: | |. Therefore, it can be written that |5| = |–5| = 5.
Although, by definition, the absolute value refers to distance from 0, it can be used to express the distance from any other number. Consider |4 – 1| and |–2 – 1|. One way of thinking about this is by taking the difference and then taking the absolute value of the result like below.
|4 – 1| = |3| = 3
|–2 – 1| = |–3| = 3
Another way of thinking about this is by considering the distance on the number line to both 4 and –2 from 1. Both quantities above are equal to 3 because both 4 and –2 are three units from 1 on the number line: –2 is three units to the left and 4 is three units to the right.
You can check your answers in Part VIII: Answer Key to Drills.
In a problem that involves several different operations, the operations must be performed in a particular order. There’s an easy way to remember the order of operations:
Please Excuse My Dear Aunt Sally
First, you do operations enclosed in Parentheses; then you take care of Exponents; then you Multiply and Divide; finally you Add and Subtract. We’re going to save exponents for the next chapter, but let’s try out PEMDAS with a couple of problems.
How about this one?
If you did these in the correct order, you should have gotten the same answer both times: 0.
During Part 2 of the Math test, you will be provided with an on-screen Texas Instruments TI-30XS calculator, which automatically knows the order of operations. As long as you enter the equation correctly, it will give you the correct answer every time. But entering the equation correctly can be painstaking work. For example, in the operation above, you would enter 3, hit the “plus” key, then the “left parentheses” key, then 8, then the “division” key followed by the 2, then the “right parentheses” key, then the “multiplication” key, then the “left parentheses” key, then the 4 followed by the “minus” key, then the 5, then the “right parentheses” key, then the “plus” key, then the 1 key, and finally the “enter” key.
Many students find that they can do this faster on paper.
The Commutative Property: When you add a string of numbers, you can add them in any order you like. The same thing is true when you are multiplying a string of numbers.
4 + 5 + 8 is the same as 8 + 5 + 4.
6 × 7 × 9 is the same as 9 × 7 × 6.
The Commutative Property applies ONLY to addition and multiplication. It does NOT pertain to subtraction or division.
The Distributive Property: The GED® test writers will sometimes use an equation that can be written in two different ways. They do this to see if you know about this equation and if you can spot when it is in your interest to change the equation into its other form.
The distributive property states that
a(b + c) = ab + ac and a(b – c) = ab – ac
Example: 3(4 + 2) = 3(4) + 3(2) = 18
Example: 3(4 – 2) = 3(4) – 3(2) = 6
If a problem gives you information in “factored” format—a(b + c)—you should distribute it immediately. If the information is given in distributed form—ab + ab—you should factor it. Take the following example:
Finding of 5 and of 3 is a bit troublesome because the answers do not work out to be whole numbers. It isn’t that you can’t find half of an odd number if you have to (or at least you will be able to, after our review of fractions later in this chapter), but why do more work than necessary?
Look at what would happen if we changed this distributed equation into its factored form instead:
Isn’t that a lot easier? One half of 8 equals 4. Always be on the lookout for chances to do less work on the GED® test. It’s a long, tiring test, and you need to conserve your strength. Now, try this one.
1. If 3X + 3Y = 21, then what is the value of X + Y?
A. 3
B. 6
C. 7
D. Not enough information is given.
Here’s How to Crack It
Everyone’s first impulse on a problem like this is to pick (D), not enough information is given. After all, there are two different variables (X and Y), so unless we know what both variables are, how can we figure out the problem?
The answer is the distributive property. You may not have noticed that the equation in the problem above was in one of the formats we were just looking at: ab + ac, otherwise known as the distributive form. Therefore, before we give up hope, let’s try putting the equation into its mirror-image format: a(b + c), otherwise known as its factored form.
3X + 3Y = 3(X + Y) = 21
Hmm. You want to know what (X + Y) equals. Well, three times (X + Y) equals 21. Three times what number equals 21? That’s right, 7, and the correct answer to this question is (C).
Do these problems first on your own. Then on a separate piece of paper, do them again using your calculator.
You can check your answers in Part VIII: Answer Key to Drills.
Absolute value is a number’s distance from zero—in other words, on the number line, how many steps away from 0 is the number. This is very simple to calculate, as long as you keep in mind that an absolute value is never negative (because it is a distance, and distance cannot be negative). The symbol for absolute value is bars on either side of the number (or numbers), like this: |9|
Since 9 is nine steps from zero, |9| = 9.
Likewise, |–9| = 9, because –9 is also nine steps from zero. That it’s nine steps in the opposite direction does not affect the absolute value. So, another way to think of absolute value is you can calculate it just by dropping the negative sign, if there is one, from the number inside the bars.
So, absolute value is pretty simple when there is just one number inside the bars. On the other hand, if there are multiple numbers and one or more operations inside the bars, you need to do the indicated operations (according to PEMDAS) until you have just one number as a result, and then take the absolute value of that one resulting number. For example,
|–3 + 2| =
We add the numbers together, keeping the absolute value bars around them,
|–3 + 2| = |–1|
And then find the absolute value of that resulting number,
|–1| = 1
And that’s our answer. If you have other numbers and operations outside the absolute value bars, then find the absolute value you need before combining that absolute value with the rest of the question.
10 + |4 × (–2)| = 10 + |–8| = 10 + 8 = 18
In this way, absolute value works kind of like parentheses, since you need to calculate what’s inside and find the absolute value of that before moving on to the rest of the question.
Factors are numbers that divide evenly into a given number. For example, what would be the factors of 6?
6 ÷ 1 = 6, 6 ÷ 2 = 3, 6 ÷ 3 = 2, and 6 ÷ 6 = 1.
When 6 is divided by 1, 2, 3, or 6, the result is a whole number; therefore, the numbers 1, 2, 3, and 6 are factors of 6. However, when 6 is divided by 4 or 5, the result is a decimal. Therefore, 4 and 5 are not factors of 6. Let’s look at an example.
1. Which of the following is a list of all the factors of 18?
A. 1 and 18
B. 1, 3, 6, and 24
C. 1, 2, 3, 6, 9, and 18
D. 1, 2, 3, 4, 6, 9, 12, and 18
Here’s How to Crack It
To find the factors of a number, start with the two obvious factors. The number 1 is a factor of every number as is the number itself. Therefore, 1 and 18 are factors of 18. Now work upward from 1. Is 2 a factor of 18? Since 18 ÷ 2 = 9, 2 is a factor and so is 9. Is 3 a factor of 18? Since 18 ÷ 3 = 6, 3 is a factor and so is 6. Is 4 a factor of 18? Since 18 ÷ 4 is a decimal, it is not. Is 5 a factor of 18? Since 18 ÷ 5 is a decimal, it is not. Is 6 a factor of 18? Remember that 6 is already on the list since 18 ÷ 3 = 6. When you get to a number that’s already on the list, you have all the factors. Therefore, the complete list is 1, 2, 3, 6, 9, and 18. The correct answer is (C).
One concept that is important to factors is that of the greatest common factor (GCF). Consider the numbers 24 and 40. To find the GCF of 24 and 40, find the factors of both numbers. Find the factors of 24 and 40 in pairs as in the problem above. The factors of 24 are 1 and 24, 2 and 12, 3 and 8, and 4 and 6. The factors of 40 are 1 and 40, 2 and 20, 4 and 10, and 5 and 8. The common factors of 24 and 40 are the numbers that are in both lists (regardless of what pairs they’re in). The common factors of 24 and 40 are 1, 2, 4, and 8. The GCF is simply the greatest number of the list of common factors. In this case, the GCF is 8. Let’s look at another example.
2. What is the greatest common factor of 15 and 28?
A. 1
B. 3
C. 4
D. 15
Here’s How to Crack It
Find the factors of each number. The factors of 15 are 1, 3, 5, and 15. The factors of 28 are 1, 2, 4, 7, 14, and 28. The only number that is a factor of both 15 and 28 is 1. Therefore, the GCF of 15 and 28 is 1. The correct answer is (A).
The concept of a factor goes hand in hand with the concept of a multiple. A multiple is a number for which a given number is a factor. Since 1, 2, 3, and 6 are factors of 6, 6 is a multiple of 1, 2, 3, and 6. To find the multiples of a given number, take the number and multiply it by other whole numbers. For example, 6 × 1 = 6, 6 × 2 = 12, 6 × 3 = 18, 6 × 4 = 24, and 6 × 5 = 30, so 6, 12, 18, 24, and 30 are all multiples of 6. Notice that 6 is both a factor and a multiple of itself. This is the case for every number. Also, since 1 is a factor of every number, every number is a multiple of 1.
Another way to think of multiples is as “counting by” a number. To “count by 6,” start with 6 and keep adding 6. Since 6 + 6 = 12, then 12 is a multiple of 6. Since 12 + 6 is 18, then 18 is a multiple of 6. Since 18 + 6 = 24, then 24 is a multiple of 6. Since there is no limit to the number of times you can add 6, there is no limit to the multiples of 6 or any other number.
An important concept of multiples is least common multiple (LCM). For any two numbers, a common multiple is simply a number that is a multiple of both. Consider the numbers 4 and 6. Some of the multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, and 40. Some of the multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, and 60. Therefore, some of the common multiples of 4 and 6 are 12, 24, 36, and 48. The LCM is the smallest number on the list of common multiples. In this case, the LCM of 4 and 6 is 12. Let’s look at another example.
3. What is the least common multiple of 15 and 25?
A. 1
B. 5
C. 75
D. 150
Here’s How to Crack It
To find the LCM of two numbers, list the multiples of one number and stop when one is also a multiple of the other. In this case, find the multiples of 15 by counting by 15 and stopping when one is a multiple of 25. Counting by 15, the multiples of 15 are 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, etc. The numbers 15, 30, 45, and 60 are not multiples of 25, so none of them is the LCM. However, 75 = 25 × 3, so 75 is a common multiple. Since none of the lesser multiples of 15 is a common multiple, 75 must be the least common multiple. The correct answer is (C).
You can check your answers in Part VIII: Answer Key to Drills.
1. List the factors of 36.
2. List the factors of 43.
3. List the factors of 80.
4. List the first 10 positive multiples of 7.
5. List the first 10 positive multiples of 9.
6. What is the greatest common factor of 32 and 80?
7. What is the least common multiple of 7 and 9?
8. What is greatest common factor of 24 and 48?
9. What is the least common multiple of 24 and 48?
A fraction is part of a whole. We write a fraction as 
, in which the top number is the number of parts we are referring to and the bottom number is the total number of parts that make up one whole.
Take a look at the pie below:
This pie has been divided into four equal pieces. Three of the four pieces are shaded. If we wanted to express the part of the pie that is shaded, we would say that 
of the pie is shaded. If we wanted to express the part of the pie that is not shaded, we would say that 
of the pie is not shaded.
A fraction is always a part over a whole.
In the fraction , we have one part out of a total of two equal parts.
In the fraction 
, we have three parts out of a total of seven equal parts.
Another way to think of a fraction is as just another kind of division. The expression means 1 divided by 2. The fraction 
is nothing more than x divided by y. A fraction is made up of a numerator and a denominator. The numerator is on top; the denominator is on the bottom. When a number can be written as a fraction in which both the numerator and denominator are integers (for example, numbers with no fraction or decimal part), then the number is called a rational number.
In math, a number cannot be divided by 0. Therefore, anytime the denominator of a fraction is 0, the fraction is undefined.
Every fraction can be expressed in many different ways:
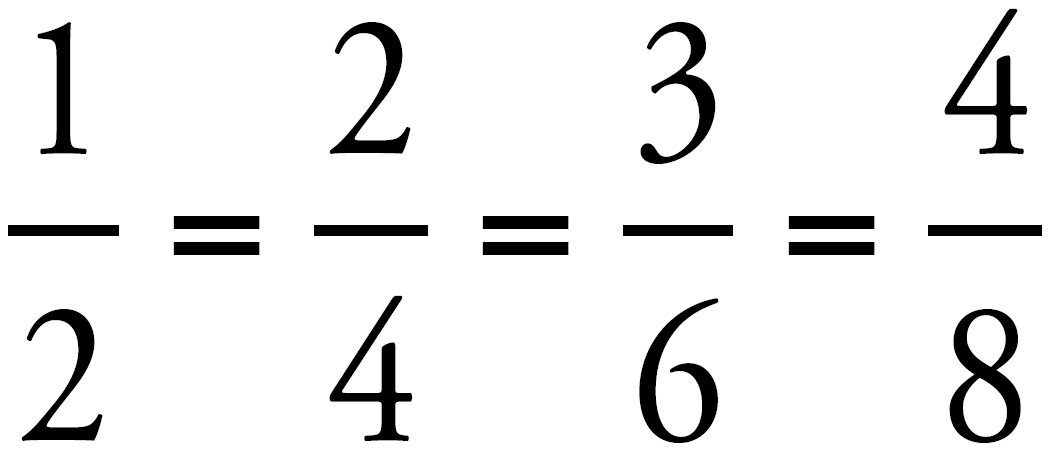…and so on.
Each of these fractions means the same thing. To reduce a fraction with large numbers, see if the numerator and the denominator share a number that divides evenly into both of them. For example, both the numerator and the denominator of 
can be divided by 2, which reduces the fraction to . With larger fractions, it may save time to find the largest number that will divide evenly into both numbers, also known as the greatest common factor (GCF). You can still reduce a fraction using any common (shared) factor, but you will probably have to reduce several times. Using the GCF guarantees that you will have to reduce only once! So how can you find the GCF of your numerator and denominator? Look at the factors of each. Let’s take the fraction 
. What are the different ways to make 8? 1 × 8 = 8 and 2 × 4 = 8.
So the factors of 8 are 1, 2, 4, and 8.
Now, what are the different ways to make 12? 1 × 12 = 12, 2 × 6 = 12, and 3 × 4 = 12.
The factors of 12 are 1, 2, 3, 4, 6, and 12.
To find our GCF, we compare these two lists. What is the largest number that occurs in both? That’s right—4 is your GCF. Now divide both your numerator and denominator by 4 and you have the simplest (most reduced) form of your fraction.
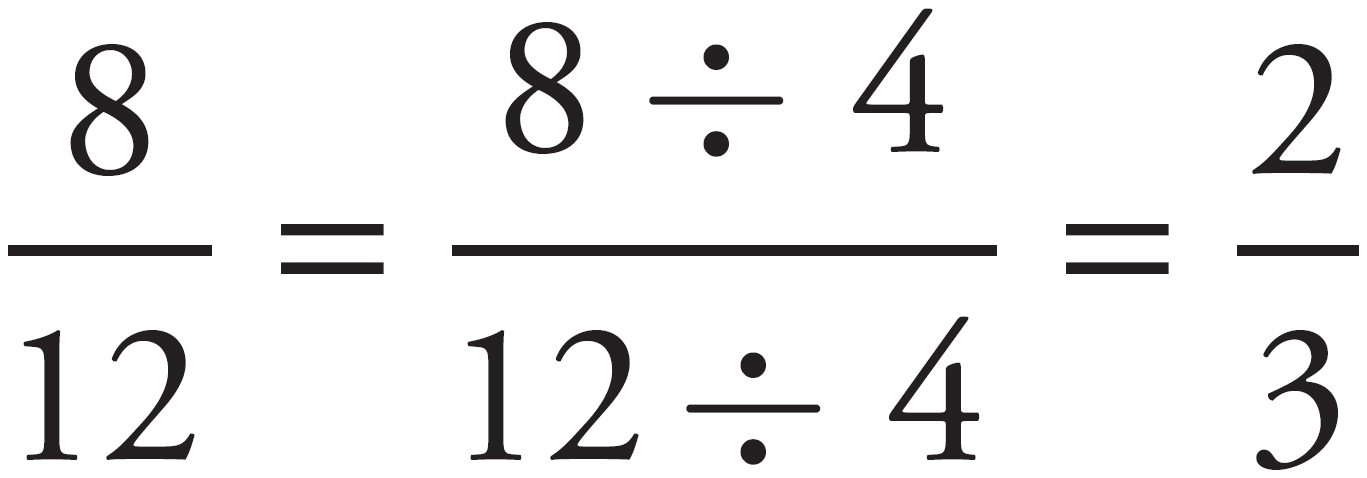
Whenever your answer to a math question is a fraction, make sure to reduce the fraction to its simplest form. The multiple-choice answers will virtually always be fractions in their simplest (most reduced) form.
Reduce the following fractions to their lowest terms. You can check your answers in Part VIII: Answer Key to Drills.
Sometimes a problem will involve deciding which of two fractions is bigger.
Which is bigger, 
or 
? Think of these as parts of a pie. Which is bigger, two parts out of five, or four parts out of five? The fraction is clearly bigger. In this case, it was easy to tell because both fractions had the same whole, the same denominator.
It’s more complicated when the fractions have different denominators. Which is bigger, 
or ? To decide, we need to rewrite the two fractions so that they have the same denominator. How do you decide what your new denominator should be? It’s called the least common denominator (LCD), and is the smallest number that all of your denominators can divide into. How do you find the LCD? Start by listing the multiples of each denominator. Let’s find the LCD of 3 and 7. What are the multiples of 3?
Count by threes: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42,….
Don’t go on forever; just write down a few and if you need to add more later on you can. Now what are the multiples of 7?
Count by sevens: 7, 14, 21, 28, 35, 42, 49,….
Do we have a number that is common to both of these lists? Yes—21 and 42 appear in both lists. But which number is the smaller of the two? The smaller number, 21, is our LCD.
Now we’ll rewrite our two original fractions so they have the same denominator. We’ll change the denominator of into the number 21. To get 3 to equal 21, we have to multiply it by 7. Because we want an equivalent fraction, anything we do to the denominator, we have to do to the numerator, so we also have to multiply the numerator by 7.
The fraction 
still has the same value as (it would reduce to ) because we multiplied the fraction by 
, or one.
Let’s change the denominator of into 21 as well.
The fraction 
still has the same value as (it would reduce to ) because we multiplied the fraction by 
, or one.
Now we can compare the two fractions. Which is bigger, or ? Clearly (or ) is bigger than (or ).
Let’s do it again. Which is bigger, or 
?
First we look at the two denominators, 3 and 5.
The multiples of 3 are 3, 6, 9, 12, 15, 18, 21,….
And the multiples of 5 are 5, 10, 15, 20, 25,….
This time, the least common denominator is 15.
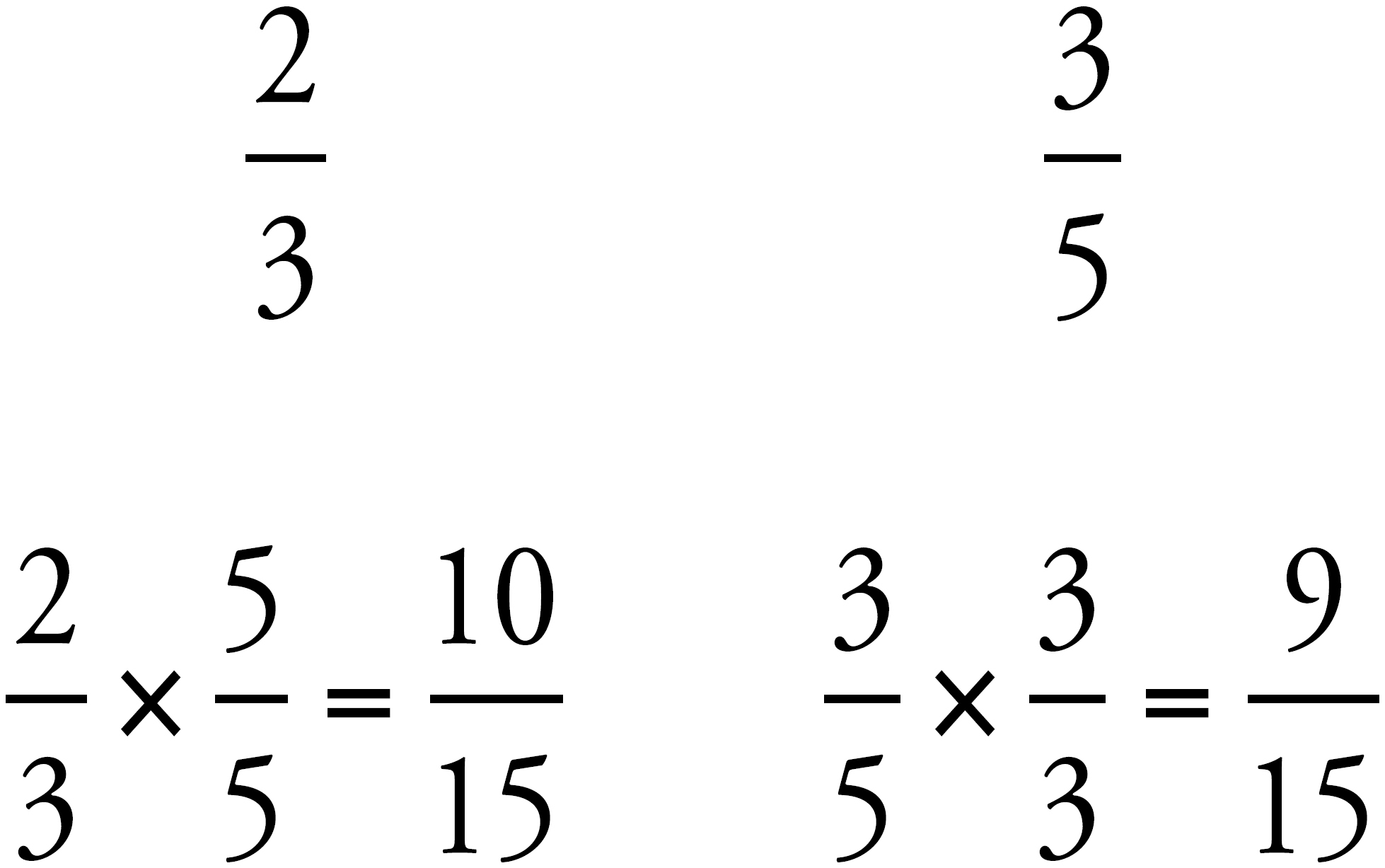
So is bigger than .
or 
?
We have found that a calculator is only of limited use on fraction problems. It can make comparing fractions very easy: simply divide the numerator by the denominator of each fraction and pick the bigger number. If you need your answer in fraction format, the Texas Instruments TI-30XS has a convenient button called the answer toggle. It looks like ◄ ► and is located at the bottom right, just above the enter button. Pressing this button will change a decimal answer into a fraction (or root). If you enter an expression as a fraction, using the 
button, the answer will be automatically given as a fraction. And if you need to change that answer into a decimal, you can press the answer toggle, ◄ ►, button to do so.
The Bowtie is a shortcut that finds a common denominator and converts the numerators for you. Let’s compare the last two fractions again. First, we get the common denominator by multiplying the two denominators together:
Then, we get the new numerators by multiplying using the bowtie-shaped pattern shown below:
Finally, compare the fractions. Once again, we see that 
(or ) is bigger than 
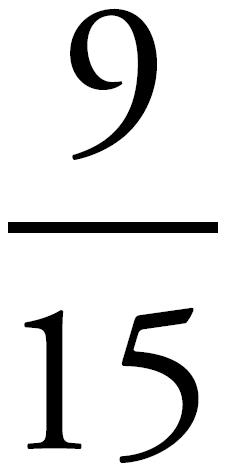(or ).
Whenever you add or subtract fractions, you need the fractions to have a common denominator. You can use the LCD method that we looked at to compare fractions, or you can use the Bowtie method, but you must somehow rewrite the fractions in the problem to those with a common denominator before you add or subtract.
Let’s use the Bowtie to add and .
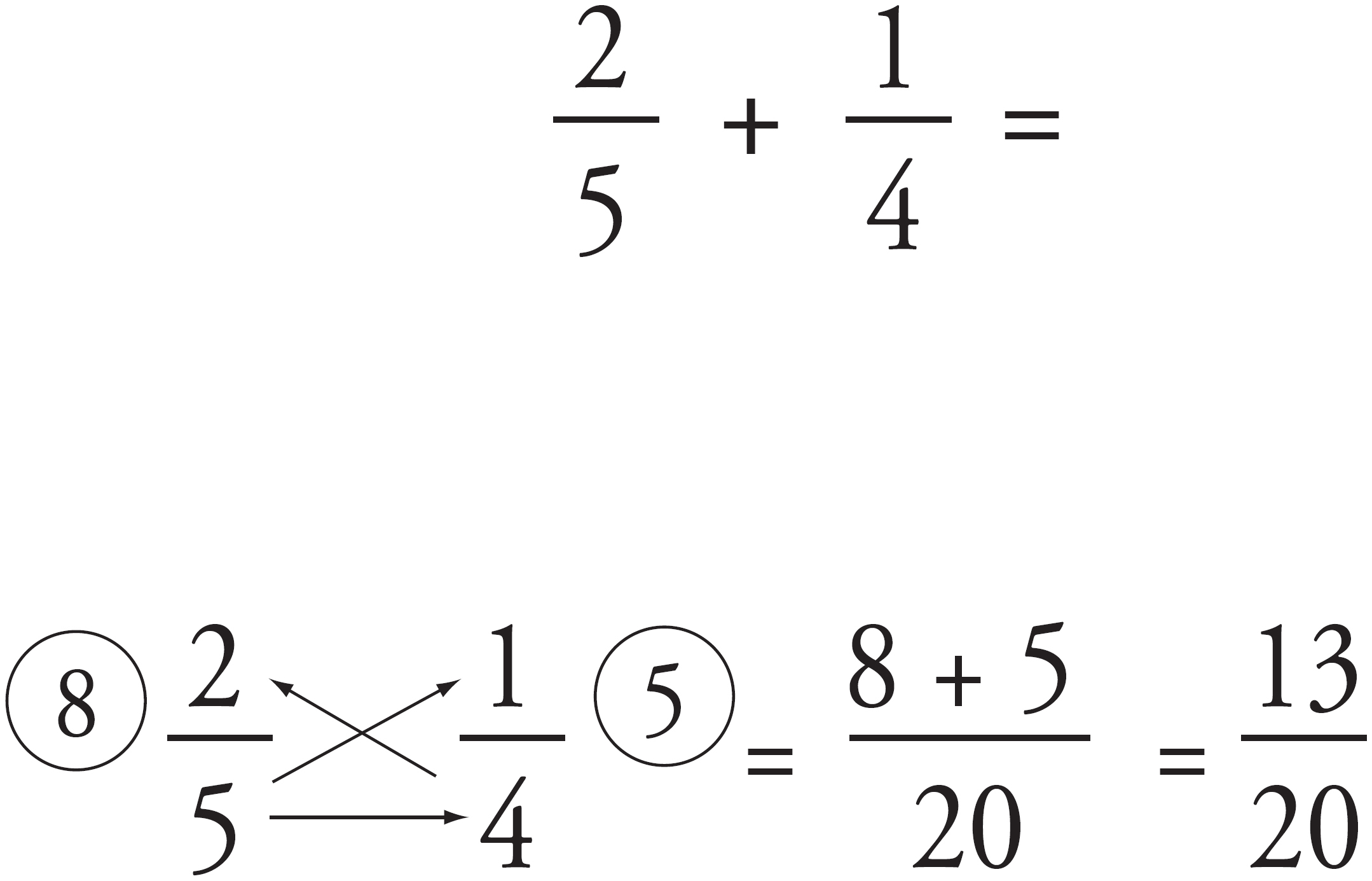
Let’s use the Bowtie to subtract from 
.
You can check your answers in Part VIII: Answer Key to Drills.
To multiply fractions, line them up and multiply straight across.
Was there anything we could have canceled or reduced before we multiplied? You betcha. We could cancel the 5 on top and the 5 on the bottom. What’s left is 
, which reduces to .
Sometimes people think they can cancel or reduce in the same fashion across an equal sign. Consider this example:
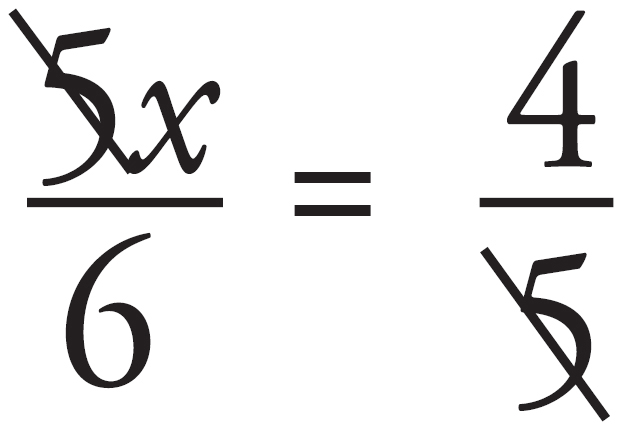No!
You cannot cancel the 5s in this case or reduce the . When there is an equal sign, you have to cross multiply, which you will see more of in Chapter 14.
A: Use the Bowtie! The fraction is bigger than .
To divide one fraction by another, just invert the second fraction and multiply.
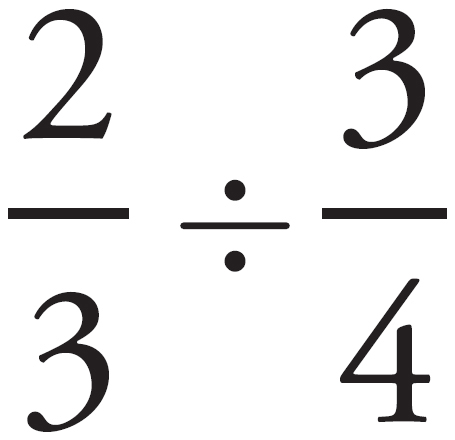is the same thing as 
.
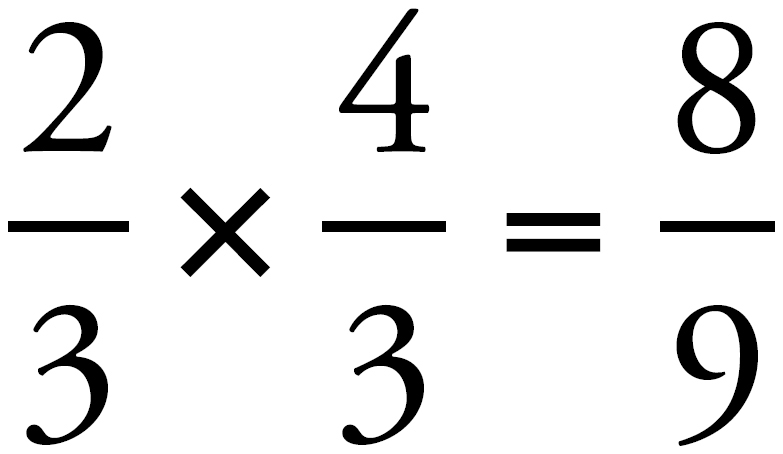You may see this same operation written like this:
Since every fraction is the numerator divided by the denominator, this is the same as divided by . So, just invert and multiply.
Dividing by 6 is the same thing as multiplying by 
.
Try the next example.
Think of 6 as 
, and so we do the same thing.
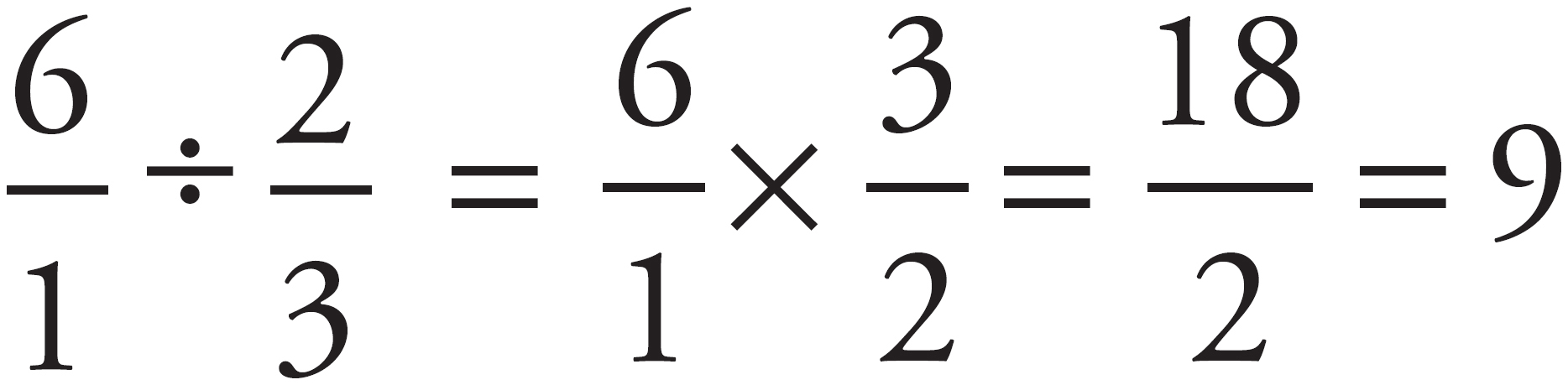
A whole number, such as 8, can always be expressed as a fraction by making that number the numerator and 1 the denominator: 8 = 
.
Sometimes the GED® test gives you numbers that are mixtures of whole numbers and fractions, for example, 3 . These numbers are called mixed fractions (or mixed numbers). It is often easier to work with these numbers by converting them completely into fractions. Here’s how you do it: Because the fraction is expressed in halves, let’s convert the whole number into halves as well: 3 = . Now just add the to the . You get 
.
There is also a shortcut for converting mixed fractions. Multiply the denominator by the whole number, and then add the numerator. This number becomes your new numerator and you keep the original denominator.
Fractions like 
are called improper fractions, because the numerator is larger than the denominator. Despite the name, though, there is nothing wrong with improper fractions. They are much easier to do any operation with than mixed numbers are, so whenever you have to add, subtract, multiply, or divide with mixed numbers, change them to improper fractions.
You can check your answers in Part VIII: Answer Key to Drills.
Now let’s try some fraction problems in the GED® test format.
1. If 
of a group of students say their favorite leisure activity is swimming, and 
of the group say their favorite leisure activity is tennis, what fraction of the group prefers neither swimming nor tennis?
A. 
B.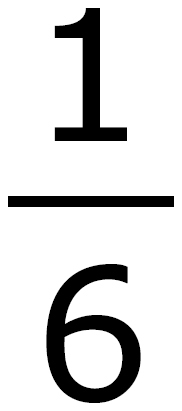 
C.
D. 
Here’s How to Crack It
Test takers are often intimidated by word problems, but you should realize that beneath all those words lies a simple math problem.
Before you even read it, there should be one thing you notice right away: There are fractions in the problem. That can mean only one thing. This is a fraction problem.
On the GED® test, the only things you are ever asked to do with fractions is add them, subtract them, multiply them, divide them, or compare them—and you’ve just learned how to do all those things, if you didn’t know them already.
Let’s read the problem. Half of the students like swimming. One-third like playing tennis. Basically, the question is, who’s left? After we take away the students who like swimming and tennis, what fraction of the students remains?
Before you do any work at all, let’s see if we can ballpark a little. If we add and 
together, that’s quite a lot. There can’t be too much of the whole left over. So do any of the answer choices strike you as unlikely? Choices (C) and (D) are clearly out of the ballpark. Let’s eliminate both of them and now actually solve the problem.
First, let’s use the Bowtie to add up the parts of the whole that we know about.
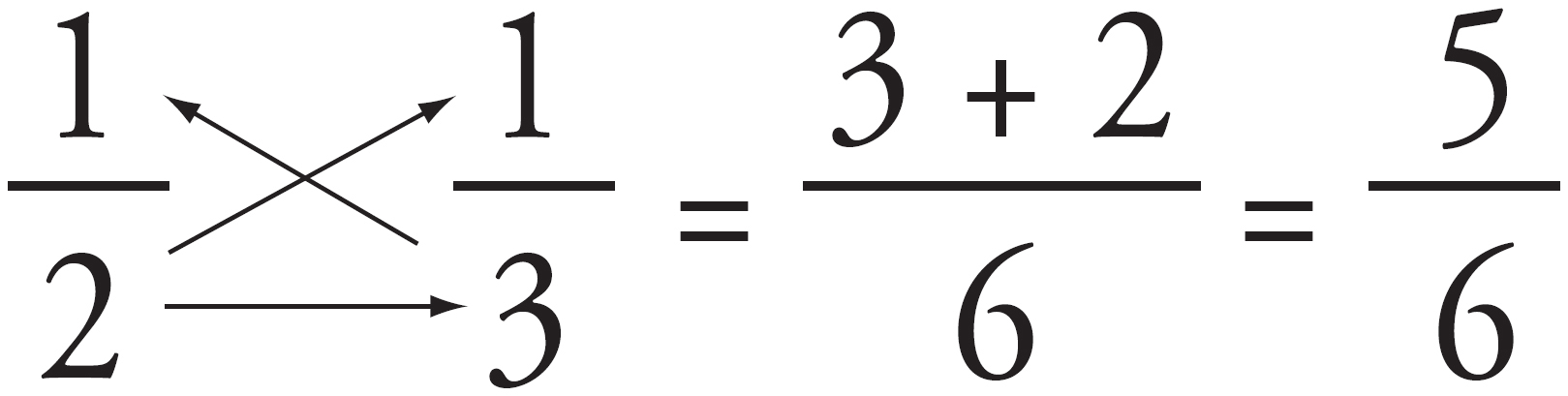
So of the students like either swimming or tennis. Now the big question: What part of the whole remains? That’s right, the answer is 
, and the correct answer is (B). Note that (D), , was a partial answer. It was there for people who were in a hurry and thought they were done when they finished adding and . However, if you read the question carefully and ballparked this problem first, there was no way you were going to fall for that trap. You already knew it was a crazy answer.
Here’s another example:
2. It takes 1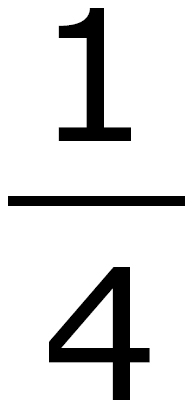 
hours for a factory worker to assemble one television set. How many television sets can be assembled in 17 hours?
Here’s How to Crack It
Again, at first glance, you may feel intimidated by all the words in this problem, but don’t let it fool you. This one’s easy.
As we said earlier, whenever you see mixed numbers, you probably should change them into improper fractions before you do any calculations.
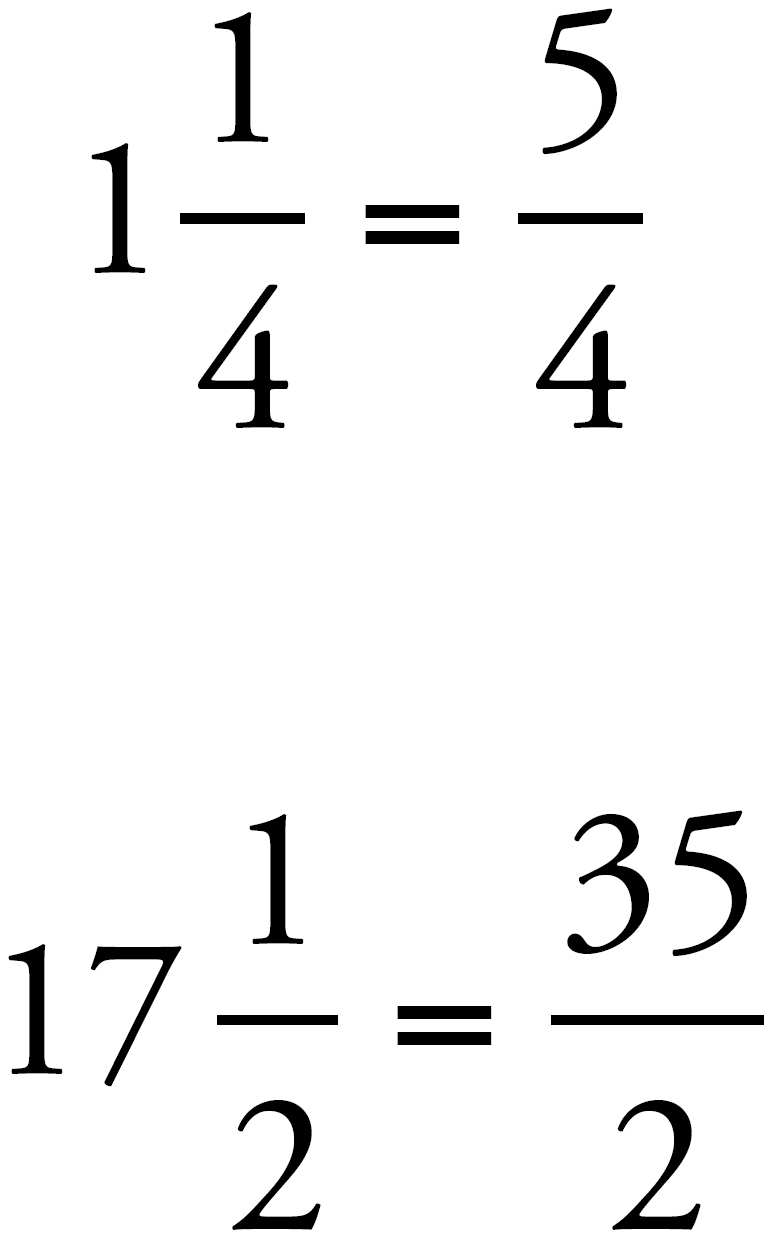
It takes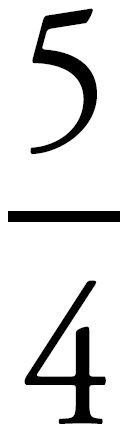 
of an hour to make one TV. How many sets can you make in 
hours? We want to know how many 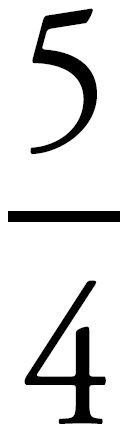s go into , and that just means division.
Let’s do some canceling.
The correct answer is 14.
You can check your answers in Part VIII: Answer Key to Drills.
1. In the town of Arkville, a total of 80 people came in to be tested for Lyme disease. Half of them were found to have the disease. Of those who did not have the disease when first tested, one quarter later developed it. What fraction of the original 80 people got Lyme disease?
A.
B.
C. 
D. 
2. A pie company baked 100 pies in July, as shown in the table below. In August, the company increased production by 
. In September, the pie company again increased production by . Determine the number of pies baked in the months of August and September.
Click on the numbers you want to select and drag them into the table.
3. According to a company survey, of the workers take public transportation to get to work, 
drive cars to work, and the remainder walk to work. What fraction of the workers walk to work?
Fractions can also be expressed as decimals and vice versa. You probably know the decimal equivalent of certain fractions by heart (for example, = 0.5), but you may not know how to convert a fraction into a decimal.
As we said earlier, one way to think of a fraction is just as a division problem.
You can also convert any decimal into a fraction. The first digit to the right of the decimal is the tenths place. The second decimal is the hundredths place. Consider this example:
Calculating with decimals, unlike calculating with fractions, is almost always faster on the calculator. However, because you won’t have the calculator during the first part of the test, it makes sense to practice these both ways. To add or subtract decimals, all you have to do is line up the decimal points and then add or subtract, just as you would any two normal numbers.
If you’re adding or subtracting one number that has fewer digits than another, it helps to add zeros to fill out the decimal places. For example, to subtract 3.26 from 8.4, adding a zero to 8.4 makes the problem easier to see:
The best way to multiply decimals is to ignore the decimal points entirely until after you’ve done the multiplication. For example, let’s multiply 4.3 by 0.5. We’ll start by multiplying 43 by 5:
Now count the total number of digits to the right of the decimal points in the two original numbers you were multiplying. In this case, there were a total of two digits to the right of the decimal points. Therefore, this is the number of digits there should be to the right of the decimal point in your final product. The answer is 2.15. Let’s do another.
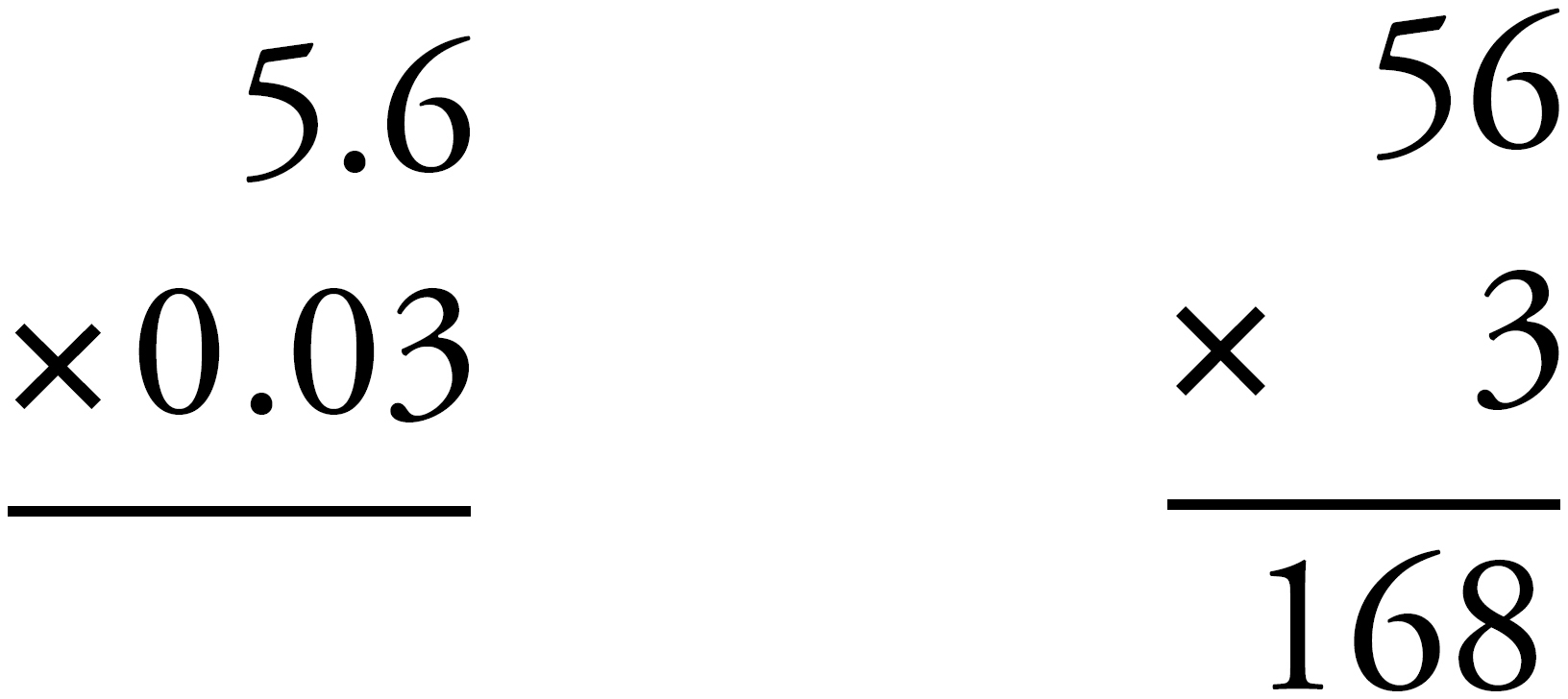
There are a total of three digits to the right of the decimal points in the original numbers, so after multiplying, we place the decimal so that there are three digits to the right in the answer as well. The answer in this case is 0.168.
The best way to divide decimals is first to convert the number you are dividing by (in math terminology, the divisor) into a whole number. You do this simply by moving the decimal point to the right as many places as necessary. This works as long as you remember to move the decimal point in the number that you are dividing (in math terminology, the dividend) the same number of spaces.
For example, to divide 12 by 0.6, set it up the way you would an ordinary division problem:
To make 0.6 (the divisor) a whole number, you simply move the decimal point over one place to the right. You must also move the decimal one place to the right in the dividend. Now the operation looks like this:
Do these problems first on your own. Then, on a separate piece of paper, do them again using your calculator.
You can check your answers in Part VIII: Answer Key to Drills.
A percent is really just a fraction whose denominator happens to be 100.
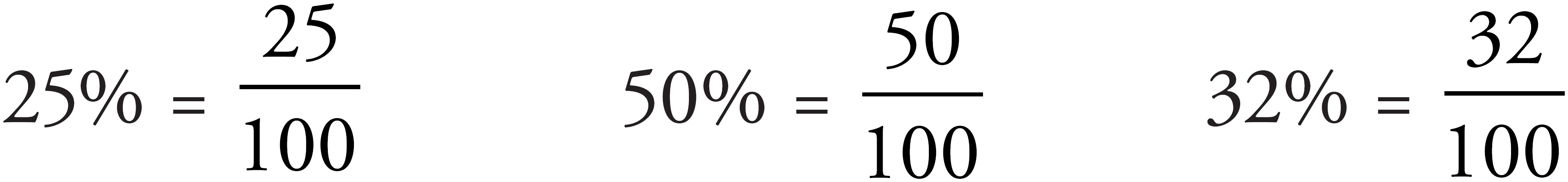
Like any fraction, a percentage can be converted to a decimal and vice versa. Percentage/decimal conversion is even easier than converting a normal fraction because both percentages and decimals are almost invariably already being expressed in hundredths.
To convert a regular fraction into a percent, you can first convert the fraction to a decimal, which, as we just said, is very close to a percentage already. Here are a few examples:
In that last example, you’ll notice that no matter how many places you carry that division to, you will always get a remainder. The fraction produces a decimal that goes on forever. However, if we are going to round to the nearest percent, then it’s 67%.
There are some fractions, decimals, and percentages that come up so often that it’s worth memorizing them. We’ve filled in some for you. Practice your conversions on a separate piece of paper to fill in the remaining boxes. Check your work with a calculator afterward.
Most percent problems on the Mathematical Reasoning test ask you to find a percentage of a larger number. Here’s an example:
1. If 10% of the 3,400 people who enter a sweepstakes won a prize, how many people did NOT win a prize?
A. 34
B. 340
C. 3,060
D. 3,366
We’ll come back to this problem in a minute. But first, we want to show you…
Here’s the way you probably learned percents: A percentage is just a fraction with 100 in the denominator, and the word of always means multiply in math. So when the GED® test asks you to find 20 percent of 400, it can be written this way:
Now you could do some canceling.
While this method will get you the right answer, it can be a long and tedious process when the numbers don’t work out as nicely as the ones we chose for this example. But don’t worry because you are about to learn a more efficient way to approach these problems.
We have a fast, foolproof method for finding percents. This method involves almost no written calculation at all. You can thank us later.
To find 10 percent of any number, all you have to do is move the decimal point of that number over one place to the left.
10% of 4 = 0.4
10% of 30 = 3
10% of 520 = 52
10% of 21 = 2.1
Now, here’s the great part. Ten percent of 30 = 3, right? So how much is 20% of 30? That’s easy. It’s twice as much as 10 percent, or 6. Here are a few examples:
What is 20% of 520?
10% of 520 = 52, so 20% of 520 = 2 × 52 = 104.
What is 20% of 4?
10% of 4 = .4, so 20% of 4 = 2 × 0.4 = 0.8.
What is 30% of 600?
10% of 600 = 60, so 30% of 600 = 3 × 60 = 180.
What is 40% of 500?
10% of 500 = 50, so 40% of 500 = 4 × 50 = 200.
This takes care of a lot of GED® problems right here, but there are some GED® problems that will ask you to find amounts like 15 percent or 27 percent. How do you do this?
To find 1 percent of any number, all you have to do is move the decimal point of that number over two places to the left.
1% of 4 = 0.04
1% of 30 = 0.3
1% of 520 = 5.2
1% of 21 = 0.21
In just the same way that we found 20 percent by doubling 10 percent, we can now find 2 percent by doubling 1 percent.
What is 2% of 500?
1% of 500 = 5, so 2% of 500 = 2 × 5 = 10.
What is 3% of 60?
1% of 60 = 0.6, so 3% of 60 = 3 × 0.6 = 1.8.
Now, here’s the really great part. We can combine these two techniques to find any percentage the test writers can invent.
Let’s find 23% of 600.
Well, 10% of 600 = 60.
So 20% of 600 = 2 × 60 = 120.
And 1% of 600 = 6, so 3% of 600 = 18.
So what is 23% of 600?
20% of 600 = 120
3% of 600 = 18
120 + 18 = 138
Most students find that with a little practice they can do this process in their heads or with minimal scratch work. Which is faster: using this method or using a calculator? Why don’t you try it both ways on the following drill?
Do these problems on your own. Then, on another piece of paper, do them again using your calculator.
You can check your answers in Part VIII: Answer Key to Drills.
1. Find 20% of 83.
2. Find 30% of 15.
3. Find 40% of 720.
4. Find 3% of 70.
5. Find 5% of 180.
6. Find 23% of 500.
7. Find 15% of 98.
8. What is 35% of 140?
9. What is 50% of 62?
10. What is 25% of 144?
(Hint: On the last two problems, remember that 50% = and 25% = .)
Now, let’s go back to the first percentage problem we showed you.
1. If 10% of the 3,400 people who enter a sweepstakes won a prize, how many people did not win a prize?
A. 34
B. 340
C. 3,060
D. 3,366
Here’s How to Crack It
The first thing you see is “10% of 3,400.” At this point, figuring out 10 percent of anything should be second nature to you. Using either Old-Fashioned Percents or The Princeton Review Percents method, we find that 10 percent of 3,400 is 340. But are you done?
Reread the last line of the question. It asks you how many people did not win a prize. You need to take one more step. The total number of people who entered the sweepstakes was 3,400. You now know that 340 of them won a prize. So how many people didn’t? All you have to do is subtract the winners from the entire group. What you’re left with is the number of losers: 3,400 – 340 = 3,060. The correct answer is (C).
If you were really thinking, you could have saved yourself a step by realizing that if 10 percent won, then 90 percent didn’t. You could simply have multiplied 340 (10 percent) by 9 to get 3,060 in one step.
Could you have ballparked this problem? Sure. A careful reading of the question would have told you that the number of people you were looking for was the number who did not win. Because only 10 percent won, you were looking for a large percentage of the people who entered. Which answers didn’t make sense? Choice (A) was ridiculously small. Choice (B) was a partial answer for those who forgot that they were looking for the losers, not the winners. It was easy to pick (B) from a math standpoint, but impossible to pick if you were Ballparking.
Here’s another example:
2. A DVD player is on sale for 20% off its normal price of $400. If the sales tax is 5%, what is the cost of the DVD player?
Here’s How to Crack It
This question requires two separate operations. First, let’s find the sale price of the DVD player.
What is 20% of 400?
10% of 400 = 40
20% of 400 = 2 × 40 = 80
So if the DVD player has been marked down by $80, the sale price is $400 – $80 = $320.
Now let’s find the sales tax. Here’s the tricky part: Is the sales tax on the original $400 or on the sale price of $320? That’s right—it is on the sale price.
What is 5% of $320?
10% of 320 = 32
5% of 320 = × 32 = 16
So what’s the final price?
Sometimes the test writers will ask you a percentage problem backward.
3. If a mailing of 15,000 letters resulted in 3,750 responses, what was the percentage of responses to the mailing?
A. 20%
B. 25%
C. 30%
D. 35%
Here’s How to Crack It
Your old teacher from high school, a gleam in her eye, would be telling you to set up an equation—but there’s a much simpler way. Let’s use POE to get rid of wrong answers.
Start with (A), 20%, and (C), 30%. Both of these are multiple of 10%, and we already know a great trick to find that! Take the 15,000 letters and move the decimal over one place to the left to get 10% = 1,500. Multiply by three to find 30% = 4,500. That’s too big! Now multiply 1,500 by two to get 20% = 3,000. This isn’t big enough.
Do we need to calculate an exact amount for (B), 25%, and (D), 35%? No! If 20% is too small, and 30% is too big, we know our answer must be somewhere in between. The correct answer must be (B), 25%.
You can check your answers in Part VIII: Answer Key to Drills.
1. An investor is deciding between two different investments, X and Y. Investment X is a one-year certificate of deposit that pays 8% in interest, into which the investor would deposit $650. Investment Y is a high-yield savings account that pays 3% in interest, into which the investor would deposit $1,500.
After one year, the amount earned by investment X will be 
the amount earned by investment Y.
2. Janice sells household products door to door. If she must pay her supplier 60% of the money that she takes in, how much would she keep for herself if she took in $1,200?
A. $720.00
B. $560.50
C. $480.00
D. Not enough information is given.
3. A student furnishing his first apartment goes shopping and buys a bed for $120, a sofa for $635, and a lamp for $74. If the sales tax is 9%, how much did the student pay in total for the furniture?
4. Carmen owns a computer store and had $6,750 in sales this May. The year before, she had $8,437.50 in sales in May. If Carmen had a profit of $5,400 this May, what percent of her sales were profits?
A. 36%
B. 60%
C. 64%
D. 80%
Now that you’ve seen the basics of arithmetic one topic at a time, we’re going to give you a drill that mixes up all the different problems we’ve discussed so far. Often, the toughest part of the Mathematical Reasoning test is recognizing what kind of problem you are facing.
As we said at the beginning of this chapter, the last line of a question is usually the key to understanding the entire question. Read the question carefully—you may need to slow down—to ensure you don’t fall for any tricks or traps along the way. And if you are unsure of an answer, flag the question to come back to later with a fresh perspective.
“Standardized” Means Predictable
The nice thing about any standardized test is that each one is very similar to the one before. This means that after you have gone through this book, completed our practice tests, and perhaps taken GED Ready®: The Official Practice Test, you will have seen every type of problem and topic that the test could possibly throw at you at least three or four times each. The GED® test presents percent problems exactly the same way each time. Number line problems employ the same ideas year after year.
This means that it’s important for you to remember the problems you’ve already completed. Math questions that you do in this book should be added to a mental file. Then, when a problem just like one of them surfaces on the real GED® test, instead of staring at it perplexedly, you’ll be saying, “Ah, what an interesting variation on that decimal problem I studied last week.”
You can check your answers in Part VIII: Answer Key to Drills.
1. Which of the following have the same value as 
? Click on the numbers you want to select and drag them into the boxes.
2. Ralph goes out to lunch and receives a bill listing a subtotal of $14.65 and tax of $1.47. Ralph leaves a 20% tip on the total amount. The amount he tips is 
the amount of tax charged.
3. If a boat takes 2 hours to travel 30 miles, how long will it take to travel 72 miles?
A. 1.2 hours
B. 4.0 hours
C. 4.8 hours
D. 6.0 hours
4. Susan did of her homework on Tuesday and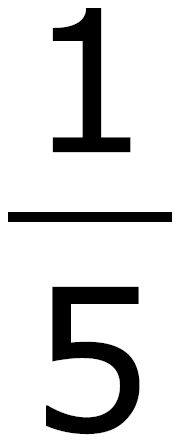 
of her homework on Wednesday. What fraction of her homework remains to be done?
A.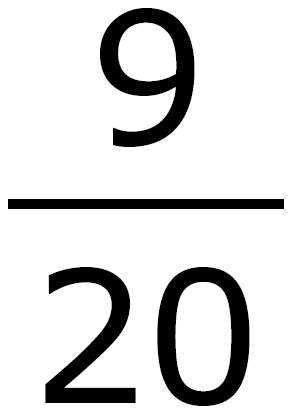 
B.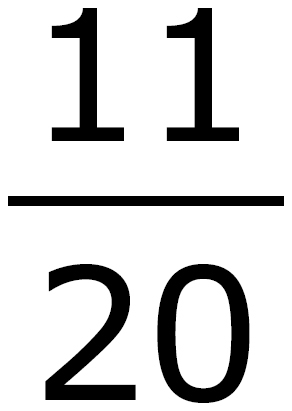 
C. 
D.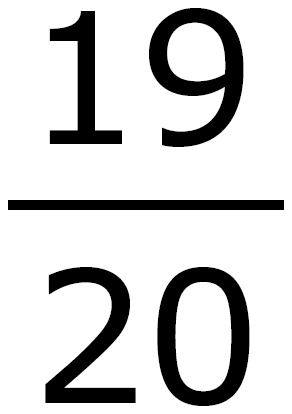 
5. In the figure above, point B represents the number 0. If the midpoint of segment AB is at point –2 on the number line and the midpoint of BC is at point 2 on the number line, then which point represents the midpoint of segment AC?
Click on the number line to plot the point.
6. You are working out a one-year payment plan for a new bicycle. The bicycle costs $275. Tax on the purchase is 11%. You will make 12 equal payments and do not owe any additional interest. How much is each payment, to the nearest dollar?
A. $20.00
B. $23.00
C. $25.00
D. $30.00
7. If 5R – 5S = 35, then what is the value of R – S?
A. 5
B. 6
C. 7
D. Not enough information is given.
8. 5(2 – 4 + 1) + 
(7 – 1) = ?
9. If 30 people in a room of 70 people are smokers, approximately what percent of the people in the room are smokers?
A. 23%
B. 30%
C. 43%
D. 57%
10. A bankrupt company agrees to pay its creditors 80% of what they are actually owed. If the company pays $9,600, what did they originally owe?
A. $7,680
B. $8,000
C. $11,520
D. $12,000
11. Click on the numbers below and drag them into the boxes that represent the appropriate places on the number line.
