In this chapter, we introduce the basics of algebra—plus we’ll show you powerful techniques that make certain types of difficult algebra questions really easy.
Algebra accounts for slightly more than half of the GED® Mathematical Reasoning test. Most people just don’t like algebra, and they never did. Well, we have some good news for you.
You don’t always need to use algebra to solve the algebra problems.
In just a few pages, we’ll show you a great technique that will allow you to do some of the tougher algebra problems without writing equations. However, let’s begin by going over the basics of the easy “solving for x”-type of GED® problems.
If you’ve completed the first two math chapters, then you’ve already been solving simple equations, also known as equalities. Every time you set up a proportion or an average formula, you were using algebra. Here is the most basic type of algebra equation:
1. If 2x – 14 = 10, then x = ?
A. 5
B. 12
C. 15
D. 22
The GED® test writers use some variation of this problem on practically every test. To find the answer to this question, we must “solve for x,” which simply means getting x all alone on one side of the equation, and everything else on the other side. The x is already on the left-hand side of the equals sign in this equation, so let’s try to move the other numbers on the left side over to the right side.
First, let’s tackle the number 14 that is subtracted from 2x. To make this subtraction of 14 disappear, we must add 14 to the left side. This is the concept of inverse operations, because adding is the inverse (opposite) of subtracting. Now, we want both sides to remain equal, so we must then add 14 to the right side of the equation as well, since that’s what we did to the left side.
As long as you add or subtract your number to both sides of the equation, the equation actually stays the same. So now, the equation looks like this:
2x = 24
Now, tackle the number 2, which is being multiplied by x. To make this multiplication of 2 disappear, you must divide by 2 on the left side, since dividing is the inverse of multiplying. As before, you want to avoid unbalancing the equation, so also divide by 2 on the right side.
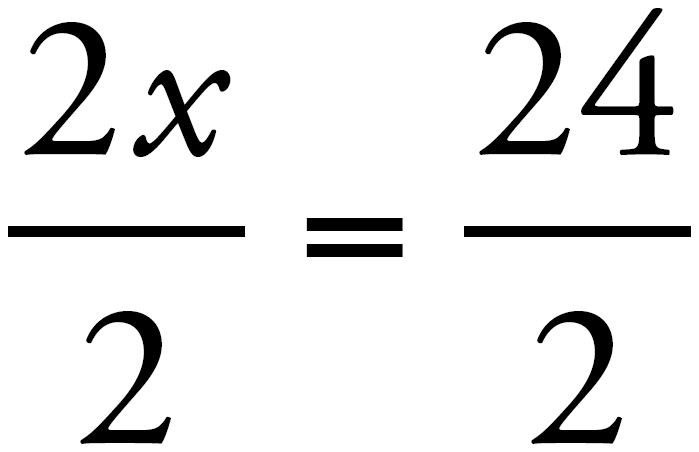
As long as you multiply or divide your number on both sides of the equation, the equation stays proportionately the same. At this point, you can cancel the 2s on the left side and reduce the fraction on the right side as shown:
The correct answer to this question is (B).
Whatever you do to the left side of an equation, you MUST do to the right side as well.
Another kind of algebraic-equation question that comes up fairly often on the GED® test looks like this:
2. Given the formula 2a = 3b(c – 4), find a if b = 5 and c = 6.
A. 30
B. 23
C. 15
D. 9
Here’s How to Crack It
These problems give you an equation and values for two of the three variables. All you have to do is plug the values for the two variables you know into the equation and then solve for the third.
Start by writing the equation on your scratch paper, substituting 5 for b and 6 for c. It should look like this:
2a = (3 × 5)(6 – 4)
2a = (15)(2)
2a = 30
If you were in a hurry, you might now pick (A), 30, but the problem asks for the value of a, not 2a. To solve for a, you must divide both sides by 2. The correct answer is 15, or (C).
You can check your answers in Part VIII: Answer Key to Drills.
While an equality or an equation allows you to solve for x and get one answer, an inequality has a range of answers. For example, in the inequality x > 5, we know that x must be greater than 5, but there is an infinite number of values that x could be. Thus, an inequality defines a range of values for the variable without giving you one specific value. Here are the symbols for inequalities:
|
> |
greater than |
|
< |
less than |
|
≥ |
greater than or equal to |
|
≤ |
less than or equal to |
An inequality is solved in exactly the same way as an equality. Let’s use the same example we used at the beginning of the chapter, with one small change.
1. If 2x – 14 > 10, then which of the following expressions gives all the possible values of x?
A. x > 5
B. x > 12
C. x < 15
D. x < 22
Here’s How to Crack It
Pretend it’s just a normal equality. This is what your work should look like:
So, the correct answer is (B), x > 12.
The only difference between an inequality and an equality occurs when you have to multiply or divide by a negative number.
An inequality is just like an equality EXCEPT when multiplying or dividing by a negative number. In this case, the inequality sign flips!
2. If –3x + 6 < 18, then which of the following expressions gives all the possible values of x?
A. x < 2
B. x < –4
C. x > 2
D. x > –4
Here’s How to Crack It
Until the very last step, this will be just like solving an equality. This is what the work should look like right up until that last step:
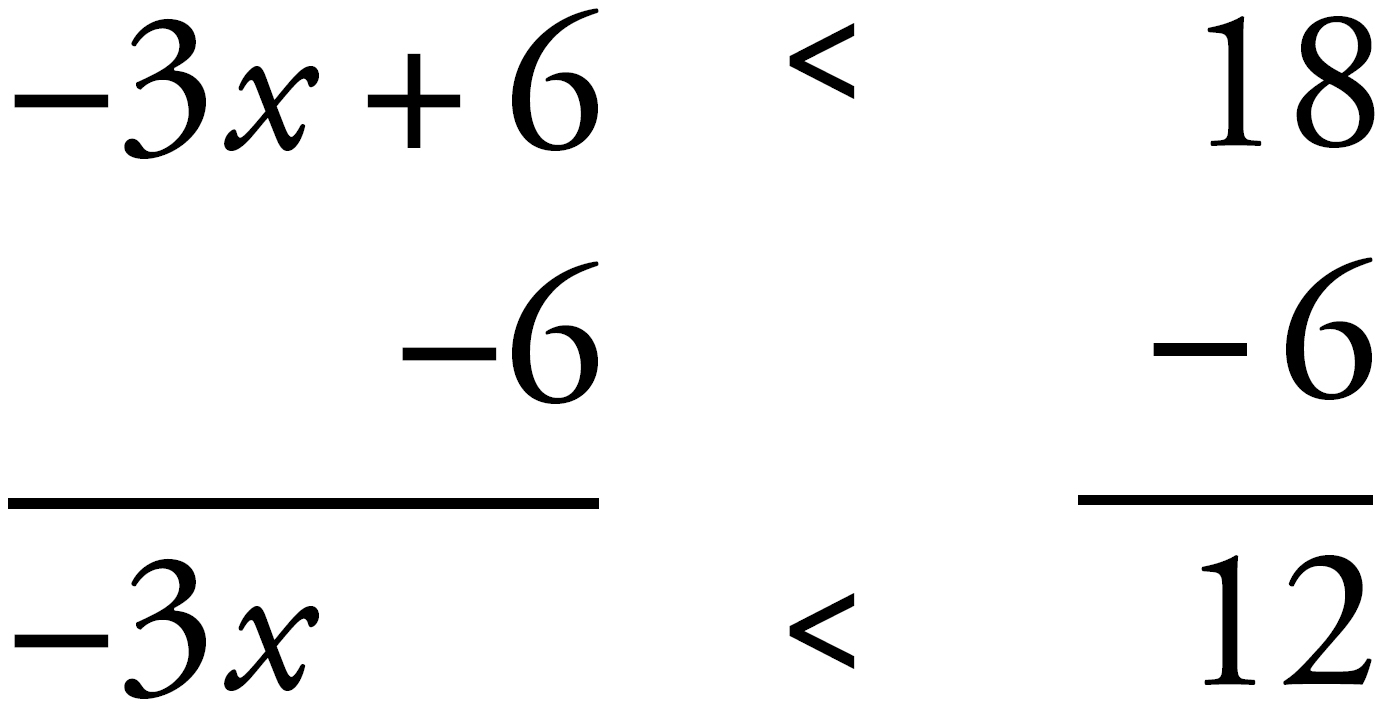
Now, comes the tricky part. When you multiply or divide an inequality by a negative number, the unequal sign flips over (that is, goes from > to <, or vice versa).
In this case, to get x alone on the left side of the equation, you’re going to divide both sides by –3.
But the moment you divide by a negative number, the sign flips over.
x > –4
So, the correct answer to this question is (D).
Take a look at a typical GED® inequality below.
3. For which value of x below is the inequality 4x > 3 true?
A. –4
B. 0
C.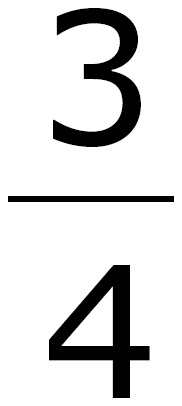 
D. 1
Here’s How to Crack It
You want to isolate x on one side of the equation, so get rid of the 4 by dividing both sides by 4.
So x > 
. When you look at the answer choices, you may be tempted to choose (C), . However, read the question again. “For which value of x below is the inequality…true?” In other words, which of the answer choices is within the range of values expressed by the inequality x > ? Is –4 greater than ? No. Is 0 greater than ? No. Is greater than ? No. Is 1 greater than ? Yes! The correct answer is (D).
You can check your answers in Part VIII: Answer Key to Drills.
1. Freida is not allowed on the roller coaster because she is under the minimum age of 5. Which of the following inequalities expresses all the ages that are allowed on the roller coaster?
A. x < 5
B. x > 5
C. x ≥ 5
D. x > –5
2. If 5x + 3 < 28, then which of the following expressions gives all the possible values of x?
A. x < 5
B. x < –5
C. x > 0
D. x > 5
3. If m is the positive number 4, which of the following inequalities contains the number m?
A. x < 3
B. x > 7
C. 2x > 6
D. 3x ≤ –6
You’ve seen throughout this book that POE—Process of Elimination—can be a very important tool in answering difficult multiple-choice GED® questions. Backsolving is the ultimate extension of POE. Let’s look again at the very first example from this chapter.
1. If 2x – 14 = 10, then x = ?
A. 5
B. 12
C. 15
D. 22
The traditional way to solve this problem is to use algebra to “solve for x.” In fact, this problem is pretty easy, and you will probably want to do it the traditional way (which we just showed you above).
However, there is another way to do this problem, and we’re going to show it to you because this same way can be used to solve many more difficult algebra problems that appear on the Mathematical Reasoning test.
The correct answer is staring you in the face. The problem asks for the value of x and then presents you with four possible answers. In other words, one of those four possibilities is the number you’re looking for.
Well, since one of these four answers is correct, why not try plugging each of them back into the question until we find the one that works?
We’ll start with (C). Let’s suppose for a moment that 15 is the correct answer and plug it into the question.
2(15) – 14 = 10
Is this true? No! 30 – 14 = 16. We’ve just proven that (C) is wrong.
But we’ve done something even better than that. Choice (C) is not just wrong—it’s too big. Do we need to check (D), 22, which is even bigger than (C)?
Just by trying out (C), we eliminated any answers that were bigger. On the Mathematical Reasoning test, multiple-choice math answers are always listed in ascending or descending order. Therefore, every time you try substituting one of the middle answer choices—(B) or (C)—back into the problem, you will eliminate at least one other answer immediately. If the number you get is too big, you can get rid of any choices that are even bigger. If the number you get is too small, you can get rid of any choices that are even smaller.
The only two possibilities left are (A) and (B). Let’s try (B).
2(12) – 14 = 10
Is this true? When we substitute 12 into the equation, we get exactly the correct answer: 24 – 14 = 10. Therefore, the answer to this problem is (B).
This technique is called Backsolving, and while it is probably unnecessary on a simple equation such as this, it will save your life on tougher questions. The method is always exactly the same: Start with one of the middle numbers. Plug it into the equation in the problem. If it makes the equation work, then you’re done; you have the right answer. If the number is too big, eliminate any choices that are bigger, and zero in on the remaining choices. Try one of them. If it’s still too big, then the answer must be the remaining choice. Pick it, and move on.
Let’s try this technique on some more difficult problems.
2. The 8 passengers on a small plane have paid a total of $900 for the flight. If an economy ticket costs $100 and a first-class ticket costs $200, how many first-class tickets were bought?
A. 5
B. 4
C. 2
D. 1
Here’s How to Crack It
At first glance, this may not seem to resemble the equation problem we just finished. This is a word problem, for one thing, and there doesn’t seem to be an equation in the problem at all.
In fact, the words of this problem actually contain an equation. The difficulty is that it’s pretty tricky to translate these words into math. The correct equation that will solve this problem is
200x + [100(8 – x)] = 900
But if you don’t think you could have come up with this, don’t spend any time kicking the ground because you can solve this algebra problem without algebra.
Backsolve! One of those four answers must be correct, so try putting one of them into the problem and see what happens. Which choice do you want to start with? Choice (B) works because it’s in the middle. If (B) is too big, you can eliminate the choice that is even bigger. If (B) is too small, you can eliminate the choices that are even smaller. If (B) is just right, then you can go on to the next problem because you’ll be done.
Choice (B) says that four passengers flew first class. And because there were a total of eight passengers, that means that four passengers flew economy class.
4 × $200 = $800
4 × $100 = $400
If this is the correct answer, the total dollar amount should add up to the total given in the problem: $900. Does it? No, it’s way too big. Which choices can you then eliminate? That’s right: Cross off (A) and (B). The only remaining possibilities are (C) and (D). We’ll try (C) next.
Choice (C) says that two passengers flew first class. And because there were a total of eight passengers, that means that six passengers flew economy class.
2 × $200 = $400
6 × $100 = $600
If this is the correct answer, the total dollar amount should add up to the total given in the problem: $900. Does it? No, but you’re getting warmer; $1,000 is a lot closer to $900 than you were before.
You know the answer is not (A), (B), or (C). Can you guess what the correct answer to this problem is?
Just to be sure, check (D). Choice (D) says that one passenger flew first class. And because there were a total of eight passengers, that means that seven passengers flew economy class.
1 × $200 = $200
7 × $100 = $700
Does this add up to $900? You bet. The correct answer to this tough algebra word problem is (D).
No. Many problems on the GED® test cannot be backsolved because their answer choices contain variables or formulas or because the correct answer choice is the final result of a calculation rather than a missing ingredient in an equation. And, of course, it is impossible to work backward from the answer choices when there are no answer choices. Generally, each GED® test contains as many as three or four problems that can be backsolved. These are frequently considered some of the hardest problems on the test because they involve algebra. Of course, if you backsolve, these problems are actually kind of easy.
Problems that can be backsolved have several characteristics. First, they must be multiple choice; the answer choices are invariably made up of simple numbers (such as 16, 27, or 5) rather than formulas or variables. In addition, the last lines of the problems ask straightforward questions (such as “How many of the workers are women?” or “How many tickets were bought originally?”).
Most important, the best way to spot a backsolve problem is to recognize that the only other way to solve that particular problem—the traditional way—would be to write an algebraic equation. If you need to write an algebraic equation, then you could backsolve instead.
Let’s try another:
3. Forty-two people have signed up for the little league annual dinner. If there are twice as many children as adults signed up, how many children are signed up?
A. 14
B. 20
C. 28
D. 32
Here’s How to Crack It
Is this a Backsolving problem? It certainly has all the earmarks: It is a multiple-choice question, the last line asks a straightforward question, and the answers are simple numbers rather than variables or equations. Most important, the only other way to do this problem would be to write an algebraic equation. And by the way, if you came up with the equation (x + 2x = 42), you could still get the wrong answer because when you solve for x, you get 14—which happens to be (A). Unfortunately, the variable x in this equation represents the number of adults, not the number of children. In this problem, you could have written a perfectly good equation and still have gotten the problem wrong.
Try Backsolving instead. The question asks how many children have signed up for the dinner. One of the answer choices has to be right. Why not start with (B), 20? The problem tells you that there are twice as many children as adults, so if there are 20 children, how many adults can there be? That’s right: 10. If you add the number of children and the number of adults, you are supposed to get the same total number of people as there are in the problem (42 people). Do you? No, you have only 30. Choice (B) is not just the wrong answer—it is too small. So you can eliminate any choices that are smaller than (B), which means (A) bites the dust as well.
The answer is either (C) or (D). Let’s try (C), 28. If there are 28 children and there are twice as many children as adults, that means that there are 14 adults. If you add 28 and 14, you are supposed to get 42. Do you? Yes! The correct answer to this difficult algebra question is (C).
You can check your answers in Part VIII: Answer Key to Drills.
1. Two physical therapists have a total of 16 patients to see in one day. Marcie has to see 2 more patients than Lewis. How many patients will Marcie see?
A. 9
B. 7
C. 5
D. 3
2. Which of the values of m below would make the inequality 3m < 12 true?
A. 7
B. 6
C. 4
D. 2
3. If there are 4 times as many women as men employed by the Ace Insurance Company, then how many of the 75 workers are women?
A. 75
B. 60
C. 45
D. 15
4. If the tax on a $45.00 restaurant check is $4.05, what is the tax rate?
A. 8%
B. 9%
C. 10%
D. 11%
5. If 2x – 7 = 3, then x =
A. 2
B. 3
C. 4
D. 5
Math itself is a kind of language that can be translated into English. For example, when you see 3 + 4 = 7, you automatically translate the symbols on the page into English (three plus four equals seven). A small number of Mathematical Reasoning problems will ask you to do the reverse: translate a word problem from English into algebra. These problems are easy to spot, for the answer choices always contain variables. Here’s an example:
1. Marjorie makes an investment and doubles her money. If she ends up with $480, which equation below could be used to discover the amount of her original investment of x dollars?
A.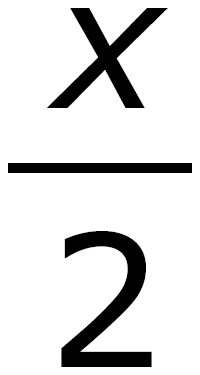 
= 480
B. x – 2 = 480
C. x + 2 = 480
D. 2x = 480
To translate a problem from English to math, you need to know what some English terms mean in math. Here are the terms that come up on the GED® test.
The key to any translation problem is its variable. The variable (x, y, z, or whatever) is always defined for you by the GED® test writers. For example, in the previous problem, the variable represents the original amount of money Marjorie had before the investment. In a translation problem, you have to figure out what to do to this variable to get the final outcome of the problem. Let’s look at Marjorie’s question again.
1. Marjorie makes an investment and doubles her money. If she ends up with $480, which equation below could be used to discover the amount of her original investment of x dollars?
A. 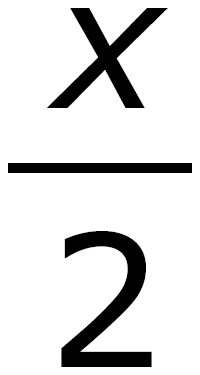= 480
B. x – 2 = 480
C. x + 2 = 480
D. 2x = 480
Here’s How to Crack It
The gist of the problem is this: Marjorie put her nest egg into an investment that doubled her money.
You need to express this in mathematical terms, and the key, as always, is the variable. In this case, the variable x represents the money Marjorie had before she invested. The $480 represents the money she had after she invested. Mathematically, what do you have to do to x in order to double it? That’s right: 2x. (If you aren’t sure of this or any other translation we talk about in the next couple of problems, just look it up on the chart on the previous page.) And after it was doubled, how much money did she have? That’s right: $480. The equation should read:
2x = 480
The correct answer is (D).
Let’s try another one.
2. Sally is three years less than twice the age of her brother Hector. If h represents Hector’s age, which expression shows Sally’s age?
A. h – 3
B. 3 – 2h
C. 2h – 3
D. 3h – 2
Here’s How to Crack It
The variable h represents Hector’s age. What can you do to h in order to get Sally’s age? Let’s translate. She is three years less than (which we know from the chart above means “– 3”) twice Hector’s age (which we know means “2h”).
When you see “three years less than,” leave some space and put – 3 as below.
Then fill this space with whatever follows “than”: in this case “twice the age of her brother Hector.” Since Hector’s age is h and “twice” means two times something, this is 2h. Fill this into the space to get:
2h – 3
The correct answer is (C).
Sometimes, the GED® test writers will require you to translate information in a word problem into a system of equations. Let’s look at an example.
1. A coffee shop sells only large and small lattes. It sells large lattes for $2.50 and small lattes for $1.75. If a group of friends goes into the coffee shop and buys 5 lattes for a total of $10.25, which of the following systems of equations could be used to determine the number of large lattes, L, and the number of small lattes, S, that the group of friends bought.
A. L + S = 5
2.50L + 1.75S = 10.25
B. L + S = 5
1.75L + 2.50S = 10.25
C. L + S = 10.25
1.75L + 2.50S = 5
D. L + S = 10.25
2.50L + 1.75S = 5
Here’s How to Crack It
The question tells you that L and S represent the number of large and small lattes bought, respectively. A total of 5 lattes were bought. Total translates to addition, so L + S = 5. Eliminate any choice that doesn’t include this equation. Eliminate (C) and (D). The total cost is $10.25, so the sum of the cost of the large lattes and the cost of the small lattes is $10.25. Each large latte costs $2.50, so the cost of L large lattes is 2.50L. Each small latte costs 2.50, so the cost of S small lattes is 1.75S. Therefore, 2.50S + 1.75S = 10.25. Eliminate any choice that doesn’t include this equation, so eliminate (B). The correct answer is (A).
You can check your answers in Part VIII: Answer Key to Drills.
1. Sandra weighs 5 pounds more than her younger brother John. If John’s weight is represented by x, what is an expression for the combined weight of the two children?
A. x + 5
B. 2(x + 5)
C. 2x + 5
D. 2(x) + 2(5)
2. The number of rabbits at a zoo doubled in 2000 and rose to five times the original number by the end of 2001. If the original number of rabbits is represented by m, then how many rabbits did the zoo have by the end of 2001?
A. 2m
B. 5m
C. 7m
D. 10m
3. Frank is two years more than three times the age of Sam. If x represents Sam’s age, which expression shows Frank’s age?
A. x + 2
B. 2x – 3
C. 3x + 2
D. 3x – 2
4. Alexis is playing a game in which blue chips are worth 5 points and red chips are worth 3 points. If Alexis has 9 chips for a total of 21 points and the game has no other color chips, then
A. B + R = 21
5B + 3R = 9
B. B + R = 21
3B + 5R = 9
C. B + R = 9
5B + 3R = 21
D. B + R = 9
3B + 5R = 21
A polynomial is an expression that has multiple terms. These terms can include combinations of variables, numbers, and exponents. On the GED® test, you may be asked to simplify a polynomial by combining like terms or to rewrite a polynomial by factoring it. We will start with simplifying a polynomial.
4a – 2b + 2c + a + 8b – 3c2 = ?
First, identify the terms that share the same variable(s). There are six terms in the above expression; each is separated from the others by a + or a – sign.
The terms 4a and a share the same variable, so combine the two to get 5a.
Now let’s combine the terms –2b and 8b to get 6b.
5a + 6b + 2c – 3c2
The only terms left to combine are 2c and –3c2. However, even though both 2c and –3c2 have the same variable c, the different exponents mean that these are not like terms, so the two CANNOT be combined. The simplified version of the original polynomial will look like this:
5a + 6b + 2c – 3c2
Here is another example of simplifying a polynomial:
1. Which expression below is equivalent to 2x2 + 8y – x + 3y – 13 ?
A. x2 + 11y – 13
B. x2 – 2y
C. 2x3 + 11y – 13
D. 2x2 – x + 11y – 13
Here’s How to Crack It
The first term contains the variable x2; are there any other terms that also contain an x2? No. Leave it and move on to the following term, 8y. There is another term that also contains the y variable, 3y. Add the two to get the new y term: 11y.
Look at the third term, –x. Are there any other x terms? No. What about the final term, –13? It does not have a variable, so it cannot be combined with any other variable terms. Leave that one as well.
The correct answer is (D).
Adding and subtracting polynomials simply means combining the like terms.
2. (3z2 – 12z + 7) + (–5z2 + z + 6) =
A. –2z2 –11z + 13
B. 8z2 – 11z + 13
C. –2z2 – 13z + 13
D. 8z2 – 13z + 13
Here’s How to Crack It
Since the polynomials are being added together, simply ignore the parentheses and rewrite like this: 3z2 – 12z + 7 – 5z2 + z + 6. Remember that adding a negative is the same as subtracting. Now combine like terms.
3z2 – 5z2 = –2z2
–12z + z = –11z
7 + 6 = 13
The result is –2z2 –11z + 13, which is (A).
Subtracting polynomials is the same except you have to be careful with the negatives.
3. (–10b2 + 6b + 2) – (–4b + 1) =
A. –10b2 + 2b + 1
B. –10b2 + 10b + 3
C. –10b2 + 2b + 3
D. –10b2 + 10b + 1
Here’s How to Crack It
Again rewrite without the parentheses, but this time the negative must be distributed to every term in the second set of parentheses. Remember that two negatives equal a positive. This looks like –10b2 + 6b + 2 + 4b – 1. Now combine like terms to get –10b2 + 10b + 1, which is (D).
Multiplying polynomials relates to the distributive law from Chapter 13. Remember that
a(b + c) = ab + ac and a(b – c) = ab – ac
The same principle applies to polynomials. Consider (x + 2)(x2 + 3x – 5). The (x + 2) factor distributes to each term of the (x2 + 3x – 5) factor to get (x + 2)(x2) + (x + 2)(3x) – (x + 2)(5). Now apply the distributive law again to each of the resulting terms. Distribute (x2) in (x + 2)(x2) to get (x)(x2) + (2)(x2) = x3 + 2x2. Distribute (3x) in (x + 2)(3x) to get (x)(3x) + (2)(3x) = 3x2 + 6x. Distribute (5) in (x + 2)(5) to get (x)(5) + (2)(5) = 5x + 10. Thus, (x + 2)(x2) + (x + 2)(3x) – (x + 2) (5) = (x3 + 2x2) + (3x2 + 6x) – (5x + 10). Now the problem becomes one of polynomial addition and subtraction. (x3 + 2x2) + (3x2 + 6x) – (5x + 10) = x3 + 2x2 + 3x2 + 6x – 5x – 10 = x3 + 5x2 + x – 10. Let’s look at an example.
4. (x + y)(x – y) = ?
A. 2x – 2y
B. x2 – y2
C. x2 + 2xy + y2
D. x2 – 2xy + y2
Here’s How to Crack It
In the case of multiplying binomials (i.e., polynomials with only two terms), there is a shortcut method. This method is called FOIL (Firsts, Outers, Inners, Lasts). Multiply the FIRST term of each factor by each other: (x)(x) = x2. Then multiply the OUTERMOST terms together: (x)(–y) = –xy. Next, multiply the INNERMOST terms together: (y)(x) = xy. Finally, multiply the LAST terms by each other: (y)(–y) = –y2. Combine the results of these four steps to create the polynomial expression and then simplify: x2 – xy + xy – y2 = x2 – y2. The correct answer is (B).
A polynomial expression can be factored by identifying terms that share factors. For example, let’s factor this expression:
3x + 15
The term 3x factors into 3 times x and the term 15 factors into 3 times 5. Do these two terms share a factor? They both can be factored by 3.
(3)(x) + (3)(5) =
3(x + 5)
Now let’s try a longer polynomial expression:
5. Which of the following is equivalent to the expression 5x – 10 + x2 – 2x ?
A. (5 + x)(x – 2)
B. (5 – x)(x + 2)
C. 2(x + 5)
D. 5(x2 – 2)
Here’s How to Crack It
Look at the first two terms, 5x and –10. They share the factor 5. The last two terms, x2 and –2x, also share a factor, x. Rewrite these two pairs.
5x – 10 + x2 – 2x =
(5)(x) – (5)(2) + (x)(x) – (2)(x) =
5(x – 2) + x(x – 2)
Now you see yet another factor appear, (x – 2). Rewrite the expression again.
5(x – 2) + x(x – 2) =
(x – 2)(5 + x)
The answer is (A). You can also check your answer by using FOIL to arrive at the original polynomial.
Factoring is the key to dividing polynomials. Look at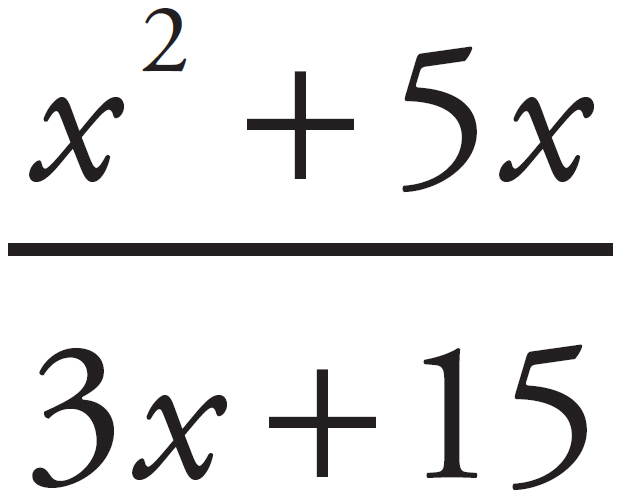 
. Factor x from both terms in the numerator to get x(x + 5), and factor 3 from both terms in the denominator to get 3(x + 5). In the resulting fraction, 
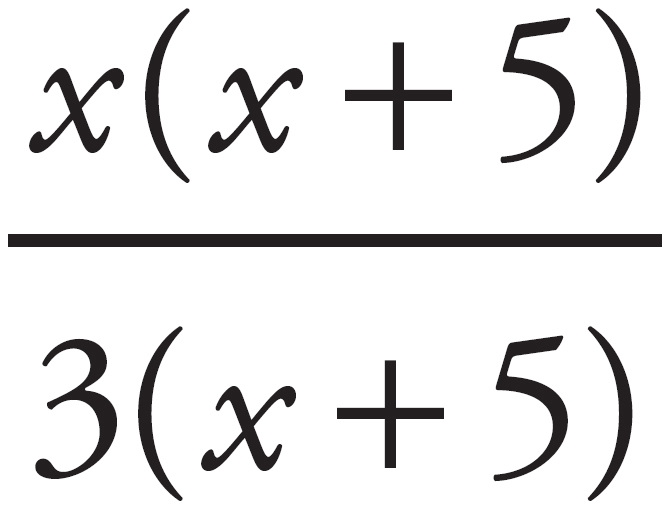, cancel (x + 5) to get 
. Now let’s look at a more complex example.
6. Which of the following expressions is equivalent to 
?
A. 
B.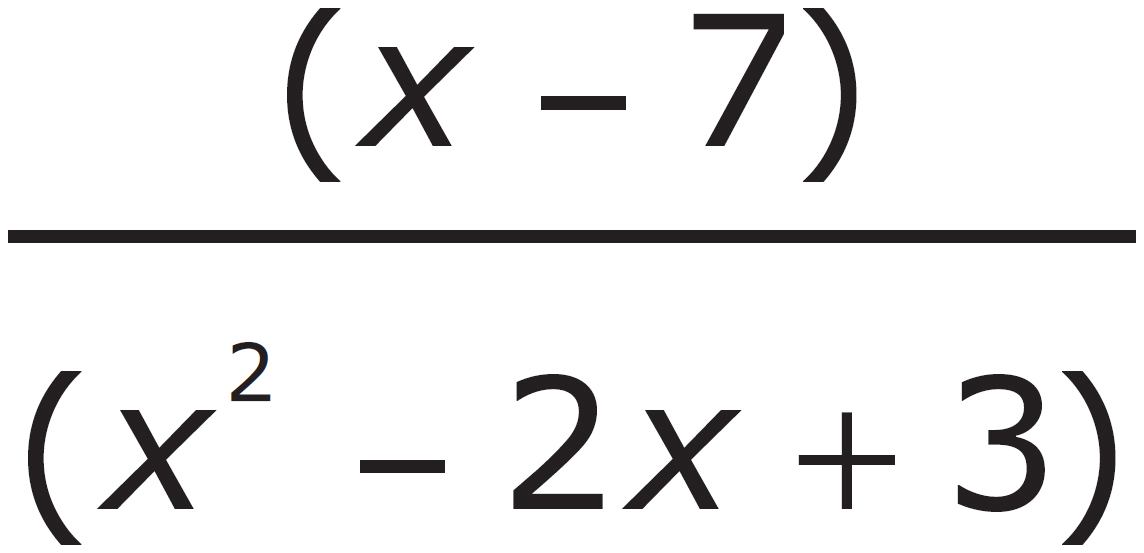 
C. 
D. 
Here’s How to Crack It
Start by factoring the numerator. Factor the x from (x2 – 7x) to get x(x – 7) and –2 from (–2x + 14) to get –2(x – 7), leaving a numerator of x(x – 7) – 2(x – 7). Now factor (x – 7) to get (x – 2)(x – 7). Now factor the denominator. Factor x from (x3 + 2x2 – 3x) to get x(x2 + 2x – 3) and –2 from –2x2 – 4x + 6 to get –2(x2 + 2x – 3), leaving a denominator of x(x2 + 2x – 3) – 2(x2 + 2x – 3) = (x – 2)(x2 + 2x – 3).
From the resulting fraction,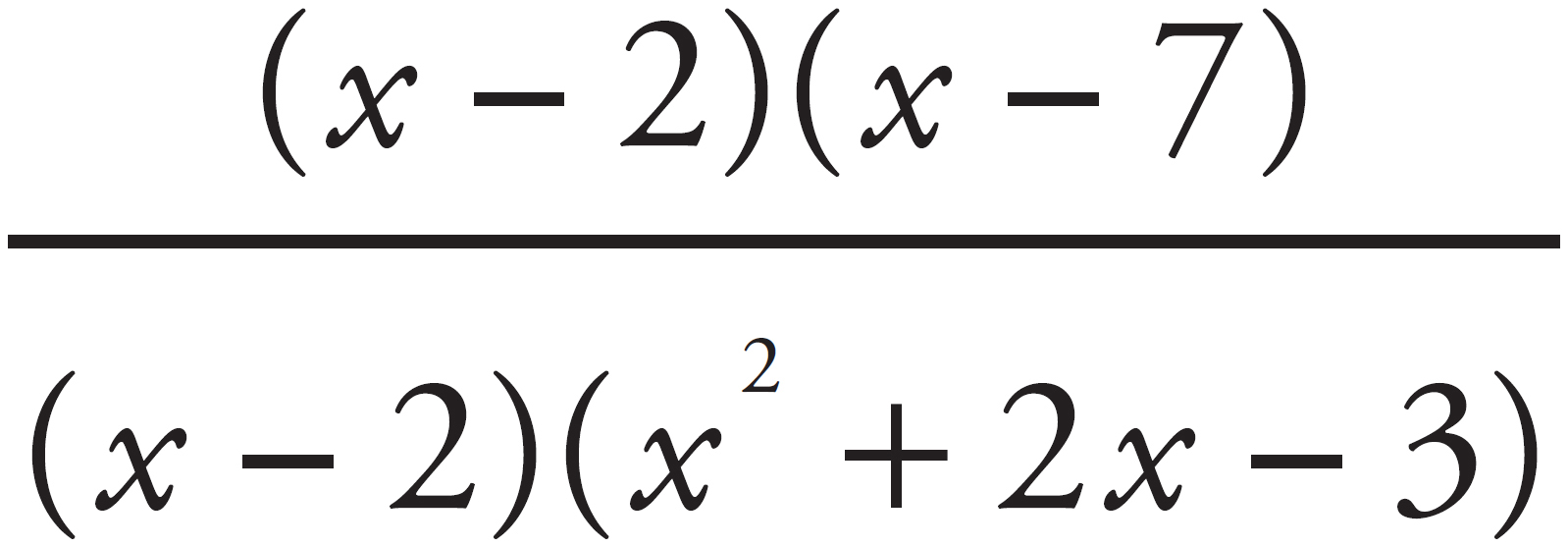 
, cancel (x – 2) to get 
. The correct answer is (D).
Remember the Translation lesson from earlier in the chapter? Sometimes the GED® test will include polynomial word problems. The basic rules of translating still apply to polynomials. For example, if a question were to refer to the sum of the cube of x and the square of the difference between x and 3, what would be the result? Remember that sum refers to addition. What is added? The first term is the cube of x. Since cube refers to raising a number to the third power, the first term is x3. The second term is the square of the difference between x and 3. Break this term into pieces. The difference between x and 3 is (x – 3). The word square refers to raising an expression to the second power so the second term is (x – 3)2. Therefore, the entire expression is x3 + (x – 3)2. Let’s look at another example.
7. When an object is stationary and begins to move at a constant acceleration, the square of the velocity is twice the product of the acceleration and the distance traveled. If an object travels at a constant acceleration of 10 m/s2 for 45 m, what is its velocity, in meters per second?
A. 30
B. 90
C. 450
D. 900
Here’s How to Crack It
First translate the statement: the square of the velocity is twice the product of the acceleration and the distance traveled. Let the velocity be represented by v, the acceleration be represented by a, and the distance be represented by d. Translate this one piece at a time. First, the square of the velocity translates to v2. The word is translates to =. The word twice translates to 2 times whatever follows. What follows is the product of the acceleration and the distance traveled. Since product translates to multiplication, this translates to a × d. Twice this is 2ad. Therefore, the statement translates to v2 = 2ad. The question states that a = 10 and d = 45, so plug in these values to get v2 = 2(10)(45), so v2 = 900. Take the square root of both sides to get v = 30. The correct answer is (A).
You can check your answers in Part VIII: Answer Key to Drills.
1. What is the sum of 5x + 2y + x – 3y?
A. 6x – y
B. 6x + y
C. 5x2 – 6y2
D. 4x – y
2. Which of the following is a factor of x2 – 4x + 3x – 12 ?
A. (x + 4)
B. (x – 4)
C. (x – 3)
D. (x – 2)
3. Which of the following is equivalent to 
?
A. 
B. 
C.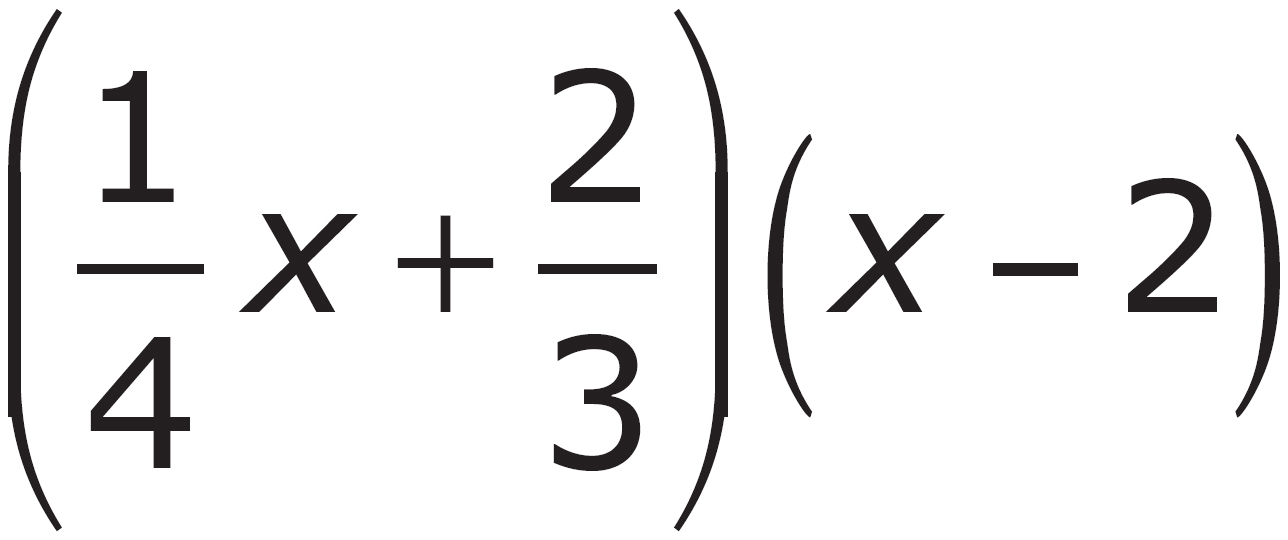 
D.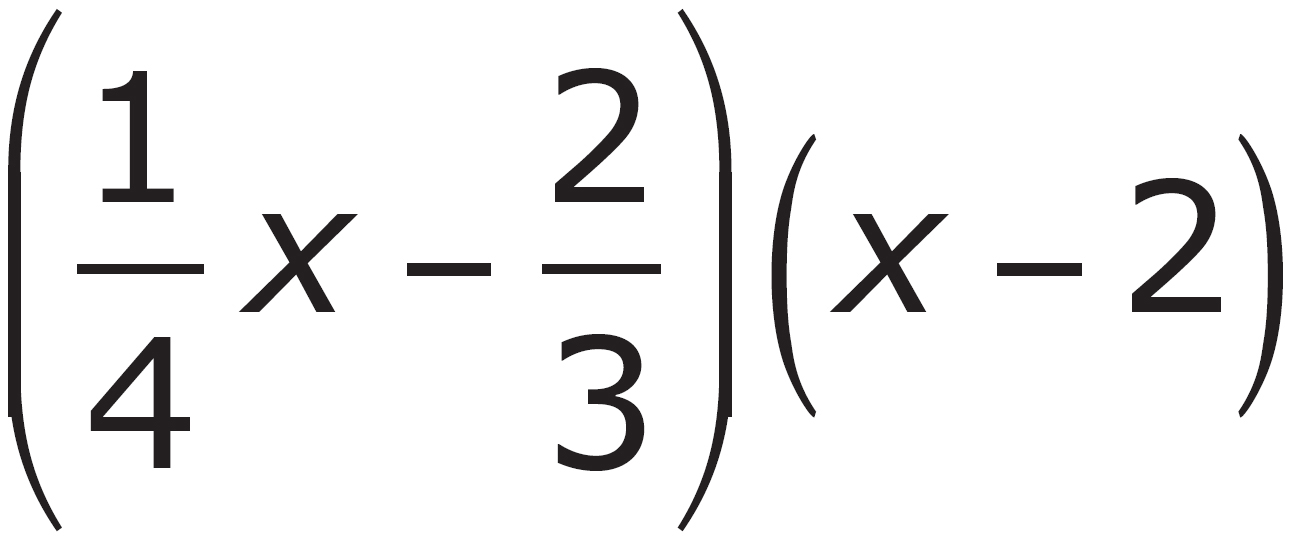 
4. Which of the following is equivalent to (x2 + 2x + 8)(x – 4)?
A. x2 + 2x + 32
B. x2 + 3x + 4
C. x3 – 2x2 – 32
D. x3 + 6x2 + 16x + 32
5. In a certain card game, a deck has cards with integers labeled 1 through 10, and each player has two cards. A player’s score is determined by taking the sum of the squares of the numbers on the two cards. If the numbers on Jennifer’s two cards have a product of 24 and a sum of 11, what is her score?
A. 52
B. 73
C. 148
D. Cannot be determined
A quadratic expression is a polynomial in which the highest exponent is 2. Some quadratic equations are fairly simple. For example, look at this equation:
x2 = 36
This question can be solved by using the inspection method. The inspection method simply involves taking the square root of both sides. The square root of x2 is x and the square root of 36 is 6. However, the answer is not as simple as x = 6. It is true that 62 = 36, so x = 6 is one of the solutions to the equation. However, remember the lesson on multiplying negatives. The product of two negatives is positive. Therefore, (–6)2 = (–6)(–6) = +36, so x = –6 is also a solution to this equation. Quadratic equations will often have two solutions. When an equation is in the form x2 = a, the inspection method will yield the solutions 
.
However, other quadratic equations will be more difficult to solve: in particular, ones that have not only an x2 but also an x term. We already discussed this type of quadratic (although not by name) in the polynomial multiplication lesson. These expressions are often the result of using the FOIL method. Let’s look at an example.
1. Which of the following is equal to x2 + 6x + 8 ?
A. (x + 2)(x + 1)
B. (x – 3)(x + 4)
C. (x + 1)(x – 3)
D. (x + 4)(x + 2)
Here’s How to Crack It
You now know how to FOIL, so you can use the answer choices and FOIL each one to see which one gets the expression that is given. To save some time, though, notice that the number by itself must be 8. The number by itself is represented in the LAST step of FOIL. By multiplying just the LAST numbers in the parentheses, you can see that the LAST term in (A) is going to be 2, in (B) is –12, in (C) is –3, and in (D) is 8. Since (D) is the only one that is 8, it must be the correct answer. If you use FOIL on (D), you multiply the FIRST terms (x and x) to get x2, multiply the OUTSIDE terms (x and 2) to get 2x, multiply the INSIDE terms (4 and x) to get 4x, and multiply the LAST terms (4 and 2) to get 8. The result is x2 + 2x + 4x + 8 = x2 + 6x + 8.
Another way to get the answer to the previous question is by factoring. Factoring is the opposite of using FOIL. It takes a quadratic like the ones you’ve just seen, and puts it into the two sets of parentheses. Let’s take a look at x2 + 6x + 8 again. To factor it, draw two sets of parentheses:
( )( )
The first two terms will usually be x and x. You might sometimes have a number before one or both of them, but in this case there isn’t a number before the x2 so they are both just x.
(x )(x )
Now you need to figure out what the numbers are. The term without a variable in this quadratic is 8. When you FOIL, you get this number by multiplying the “last” terms in the parentheses, so the two numbers in this case must multiply together to equal 8. Think about what has a product of 8: 1 × 8 or 2 × 4. As you saw before, you find the second term in the quadratic, the x, with the “outside” and “inside” terms that are added together after being multiplied. So the two numbers must add or subtract to equal 6 since that is the number before the x in the second term of this quadratic. The numbers 1 and 8 cannot add or subtract to equal 6, but 2 and 4 can if they are added. Thus the parentheses look like this:
(x + 2)(x + 4)
You can and should always use FOIL to check that your factors multiply together to equal what you started with.
Let’s try an example that involves negatives.
x2 – 4x – 12
Start with the parentheses and x in each one:
(x )(x )
Now list the factors of 12: 1 × 12, 2 × 6, and 3 × 4. Ask yourself which one could add or subtract to equal –4. Keep in mind that since they multiply to equal –12, one will be positive and one will be negative because two positives or two negatives multiply together to equal a positive. The only two that could add or subtract to equal –4 are 2 and 6.
(x 2)(x 6)
Now determine which is positive and which is negative. If it is +6 and –2, the sum will be positive 4. It needs to be –4, so that will be –6 and +2. The quadratic factored is as follows:
(x + 2)(x – 6)
One type of question you may see involves an equation, not just an expression like the previous examples. You may have to factor a quadratic and also solve for x. If you use the same example, the problem might look like this:
2. Consider this equation: x2 – 4x – 12 = 0
What is the positive solution in the equation above?
Here’s How to Crack It
Finding the solution to an equation that looks like this always requires factoring first. We’ve already done this above and determined that it was (x + 2)(x – 6) = 0. Don’t forget to write the “= 0” part at the end. Notice now that we have two binomials multiplied together that equal 0. How could this equal 0? Well, a product equals 0 if either of the two factors equals 0, so if the first or the second binomial equaled 0, the whole thing would equal 0. Set the first binomial equal to 0: x + 2 = 0. Now subtract 2 from both sides to get x = –2. This is one solution. Now set the second binomial equal to 0: x – 6 = 0. Add 6 to both sides to get x = 6. The two solutions are x = –2 and x = 6. It is common for quadratic equations to have two solutions as this one does. In this case, the question asks for the positive solution, so you enter 6. You may also see a multiple-choice question that asks for both solutions or it may even ask for something like the sum or the product of the solutions. Regardless, the method is the same.
Note: If the equation doesn’t equal 0 but does involve an x2 term and an x term like the polynomials we’ve seen in this section, be sure to subtract everything from the right side so it equals 0 if you use the factor method.
There are other methods that can be used to solve a quadratic. One is called completing the square. Consider this quadratic equation:
x2 – 6x + 9 = 0
Using the factor method, you need to find a pair of numbers with a sum of –6 and a product of 9. These are –3 and –3, so the equation factors to (x – 3)(x – 3) = 0. Notice that the two factors are the same, so this equation can be rewritten as (x – 3)2 = 0. This looks similar to an equation that can be solved using the inspection method. Take the square root of both sides to get x – 3 = 0. (Remember that ±0 is the same as 0.) Add three to both sides to get x = 3. Now, consider instead this equation:
x2 – 6x + 9 = 4
Again, you can factor the left side to get (x – 3)2 = 4. Take the square root of both sides to get x – 3 = ±2. Consider both x – 3 = 2 and x – 3 = –2. In x – 3 = 2, add three to both sides to get x = 5. In x – 3 = –2, add three to both sides to get x = 1. Therefore the two solutions are x = 1 and x = 5.
This method can be used only when one side of the equation factors into a perfect square. A quadratic expression in the form x2 + bx + c is a perfect square if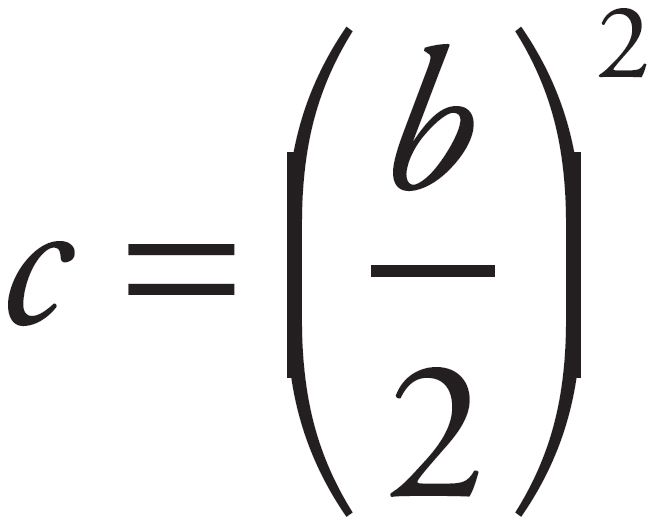 
. (In the case above, b = –6, so 
and 
.) But what if an equation doesn’t have a perfect square? Let’s look at an example.
3. If x2 + 4x – 8 = 13, what are the possible values of x?
Here’s How to Crack It
On the left side of the equation, the coefficient on the x term is 4.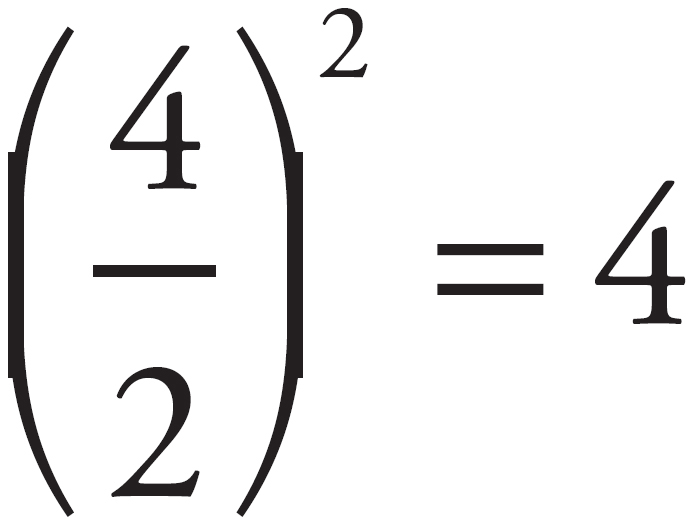 
, so this is not a perfect square. However, you can manipulate the equation to get a perfect square. If you add 12 to both sides, you get x2 + 4x + 4 = 25. Now, the left side is a perfect square. Factor the left side to get (x + 2)2 = 25. Take the square root of both sides to get x + 2 = ±5. If x + 2 = 5, subtract two from both sides to get x = 3. If x + 2 = –5, subtract two from both sides to get x = –7. The correct answers are 3 and –7.
On other equations, it will be more difficult to factor or complete the equation. For example,
3x2 + 9x – 10 = 0
There is no simple way to solve this equation for x by finding factors or by completing the square. However, there is a fall-back plan for quadratics that will work no matter how easy or difficult the equation is. This fall-back plan is called the quadratic formula. For an equation in the form ax2 + bx + c = 0, 
. In the case above, a = 3, b = 9, and c = –10, so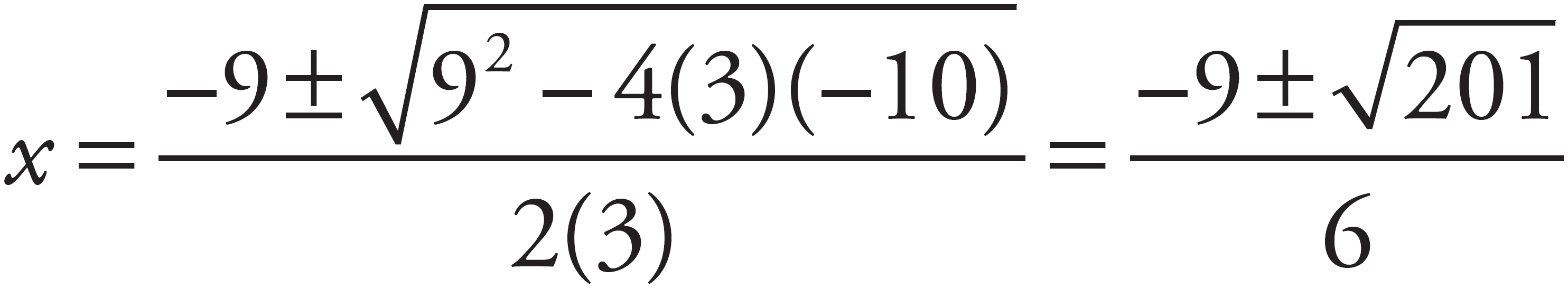 
.
Let’s look at another example.
4. Solve the equation for x.
2x2 – 5x = 4
A. x = 8 and x = –1
B. x = –8 and x = 1
C. 
D.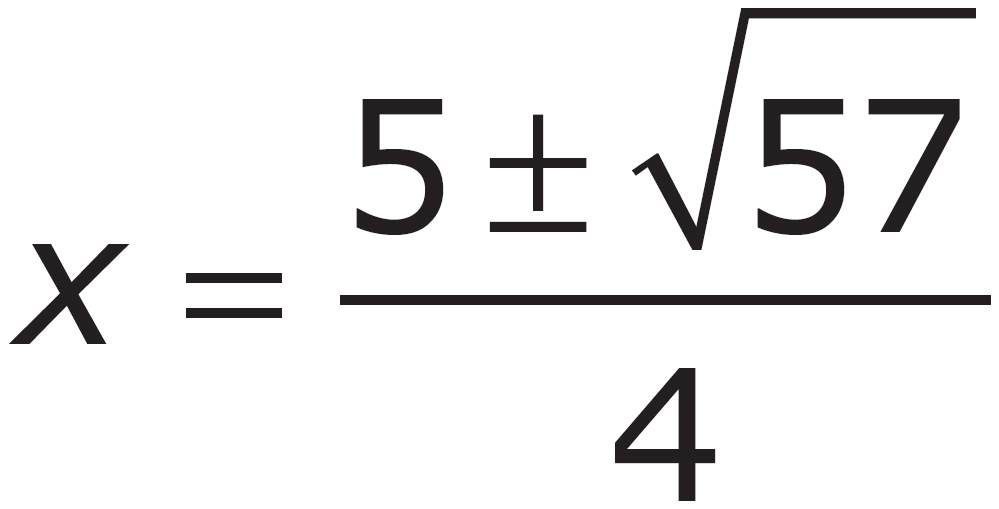 
Here’s How to Crack It
Use the answer choices as a hint that this may be difficult to factor. Use the quadratic equation: 
. However, to use this, the equation must be in the form ax2 + bx + c = 0. Subtract four from both sides to get 2x2 – 5x – 4 = 0, so a = 2, b = –5 and c = –4. Thus, 
. The correct answer is (D).
You can check your answers in Part VIII: Answer Key to Drills.
1. Which of the following are the solutions to the equation x2 – 7x + 12 = 0?
A. x = 3 and x = 4
B. x = 6 and x = 2
C. x = –6 and x = –2
D. x = –3 and x = –4
2. Which of the following equations has the same solutions as x2 – 10x + 16 = 0?
A. (x – 5)2 = 4
B. (x – 5)2 = 9
C. (x + 5)2 = 9
D. (x + 5)2 = 4
3. Which of the following are the solutions to the equation x2 – 8x + 5 = 0?
A.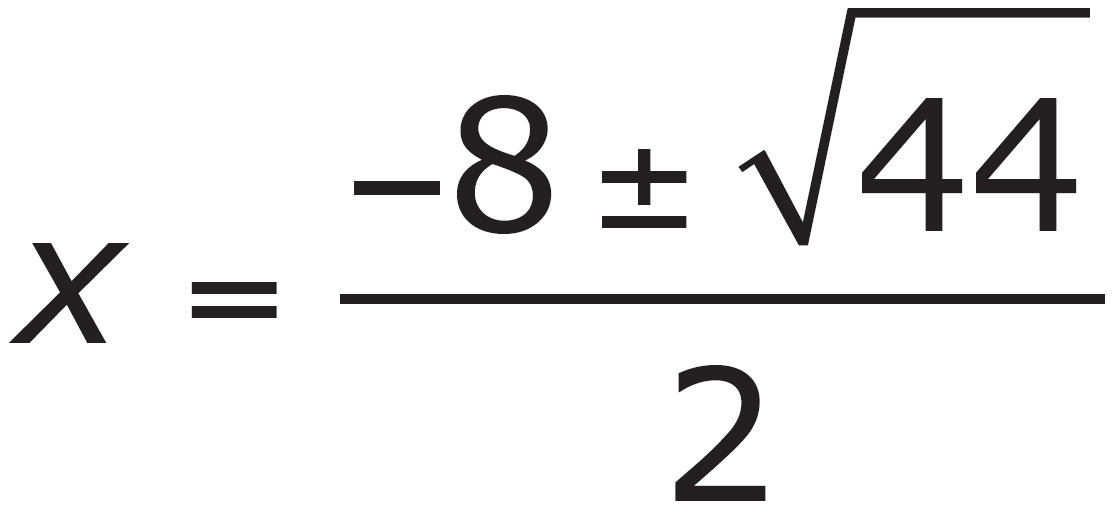 
B.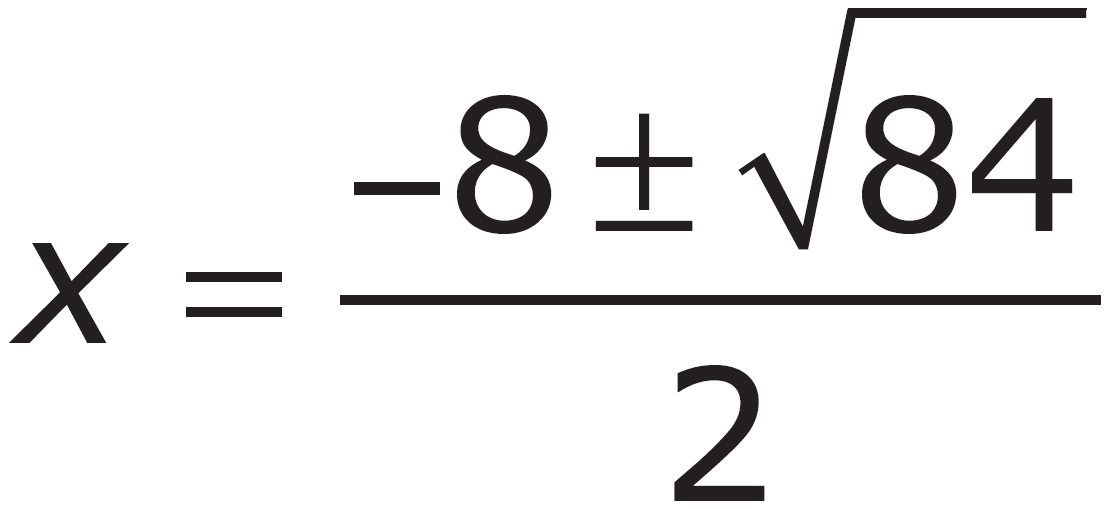 
C. 
D.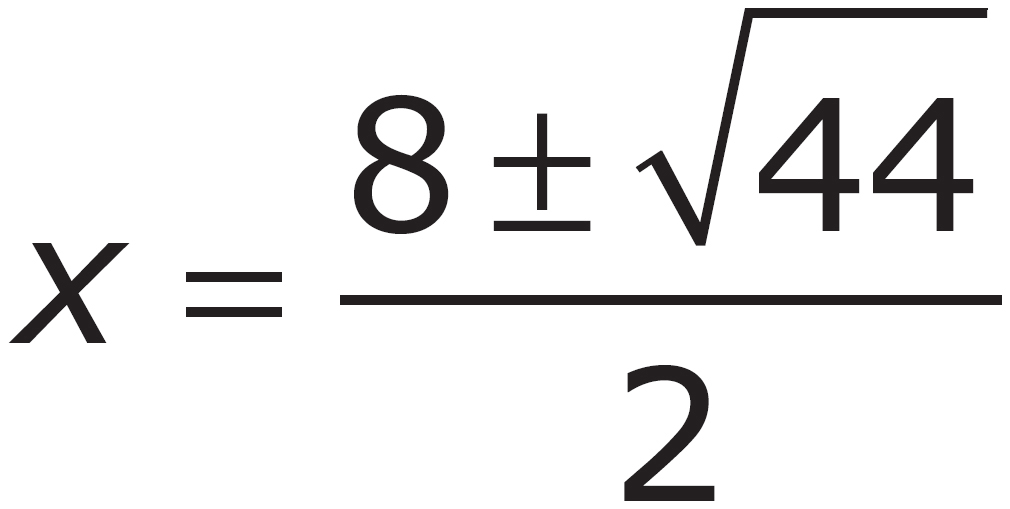 
Rational expressions are fractions made up of polynomials. Because a rational expression is just a type of fraction, the same rules for adding, subtracting, multiplying, and diving fractions still apply.
Remember adding and subtraction fractions from Chapter 13? There were two methods: Bowtie and common denominator. When you’re working with polynomials rather than numbers, the Bowtie may be too cumbersome of a method. However, common denominator works well. Let’s look at an example:
1. Which of the following is equivalent to 
?
A.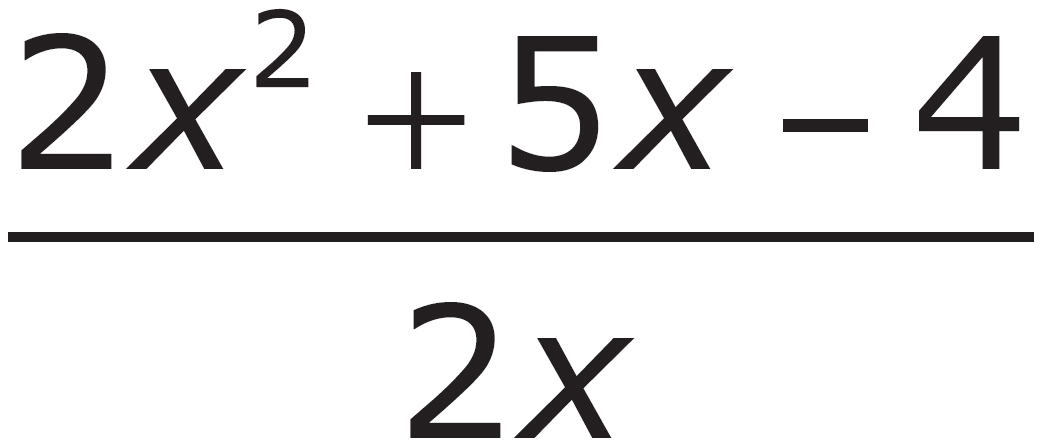 
B.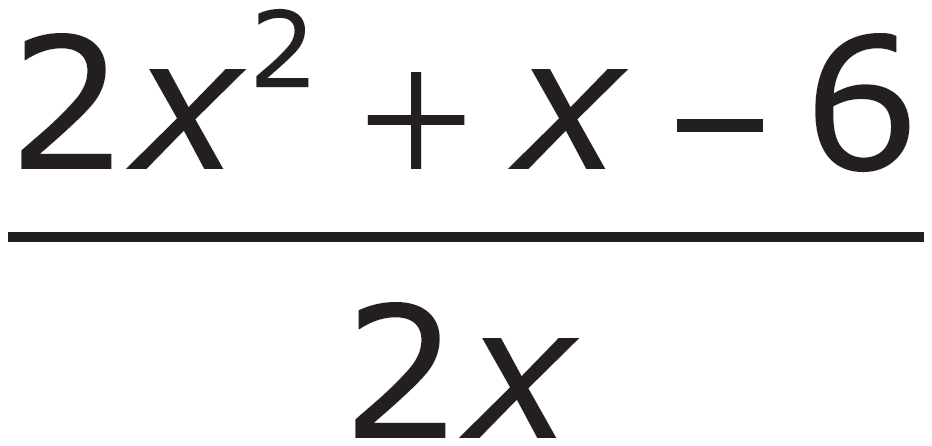 
C. 
D.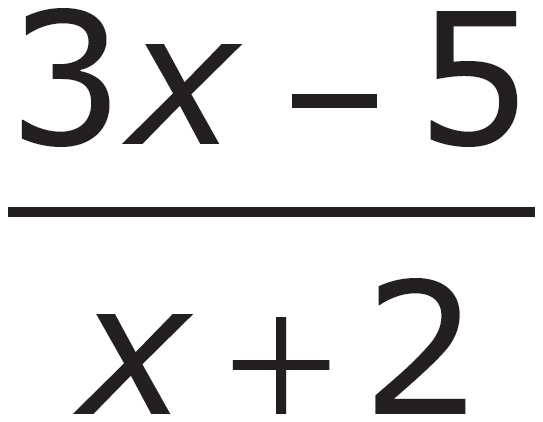 
Here’s How to Crack It
Find the common denominator for the two fractions. The denominators are x and 2. Since these don’t have any common factors, the common denominator is the product 2x. Multiply the first fraction by 
and multiply the second by 
. For the first traction, 
. For the second, 
. Since the denominators are now the same, add the numerators to get 
. Combine like terms in the numerator to get 
. The correct answer is (A).
In the case above, the least common denominator is simply the product of the two denominators. That won’t always be the case.
2. Which of the following is equivalent to 
?
A.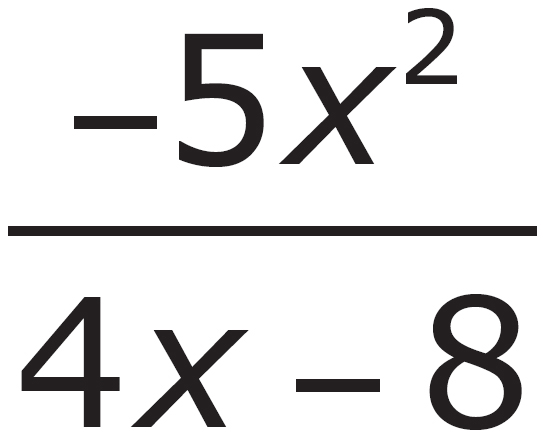 
B.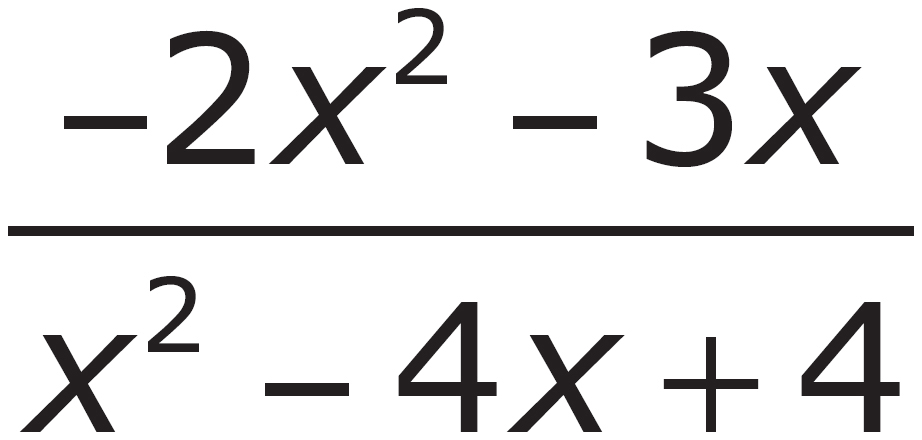 
C. 
D. 
Here’s How to Crack It
The denominators are factorable polynomials, so it’s possible that they have common factors. In the first fraction, (x2 – 4) factors to (x – 2)(x + 2). In the second fraction, (x2 – 4x + 4) factors to (x – 2)2. Since both denominators have a factor of (x – 2), it is only necessary to multiply the first fraction by 
and the second by 
. In the first fraction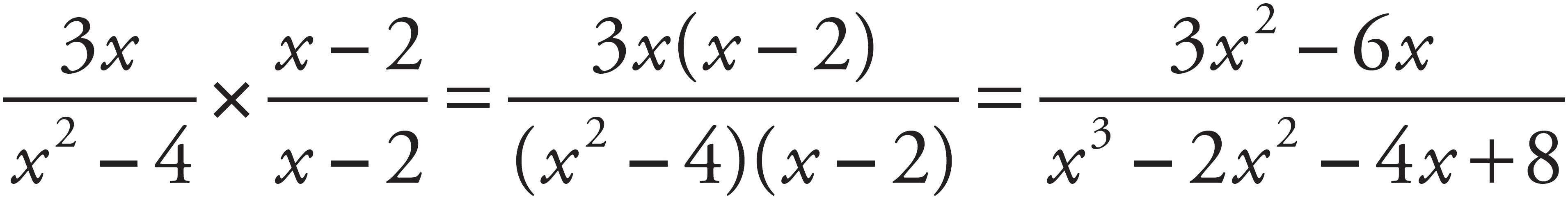 
. In the second, 
. Now that the denominators are the same, subtract the numerators to get 
. The correct answer is (D).
Once again, the rules for multiplying and dividing rational expressions are the same as those for multiplying and dividing fractions. When multiplying rational expressions, there is no need to worry about a common denominator. Just line them up and multiply straight across.
3. Which of the following is equivalent to 
?
A.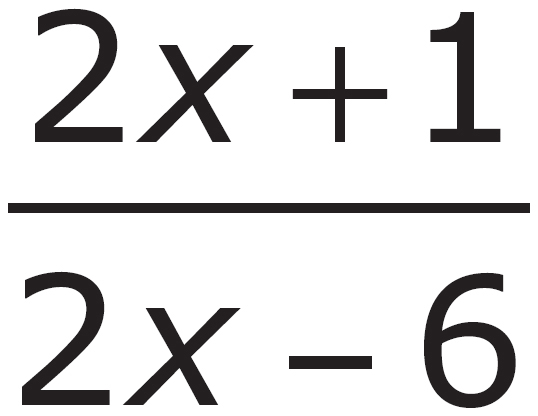 
B. 
C. 
D. 
Here’s How to Crack It
Multiply straight across: Multiply the numerator of the first fraction by the numerator of the second and multiply the denominator of the first fraction by the denominator of the second. For the numerators, (x – 3)(x + 4) = x2 + x – 12. For the denominators, (x + 2)(x – 8) = x2 – 6x – 16. Therefore the product of the fractions is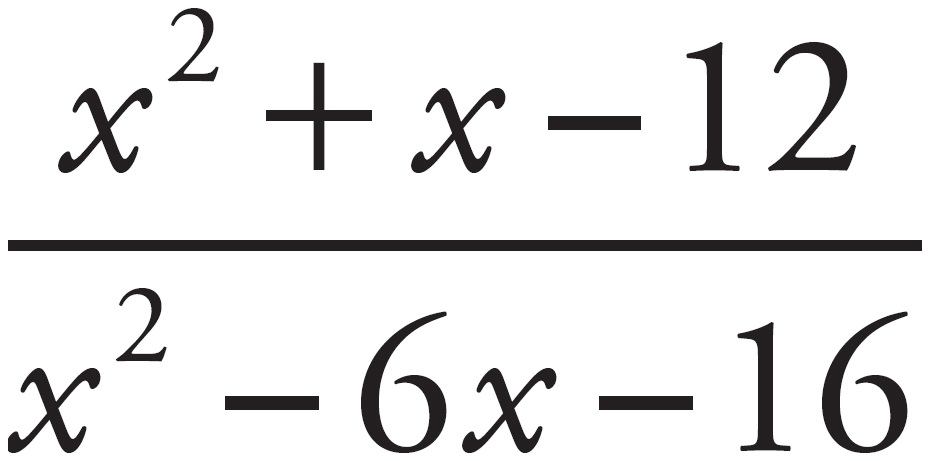 
. The correct answer is (C).
For dividing rational expressions, invert the second fraction and multiply.
4. Which of the following is equivalent to 
?
A. 
B. 
C. 
D. 
Here’s How to Crack It
Since you’re dividing fractions, flip the second and multiply to get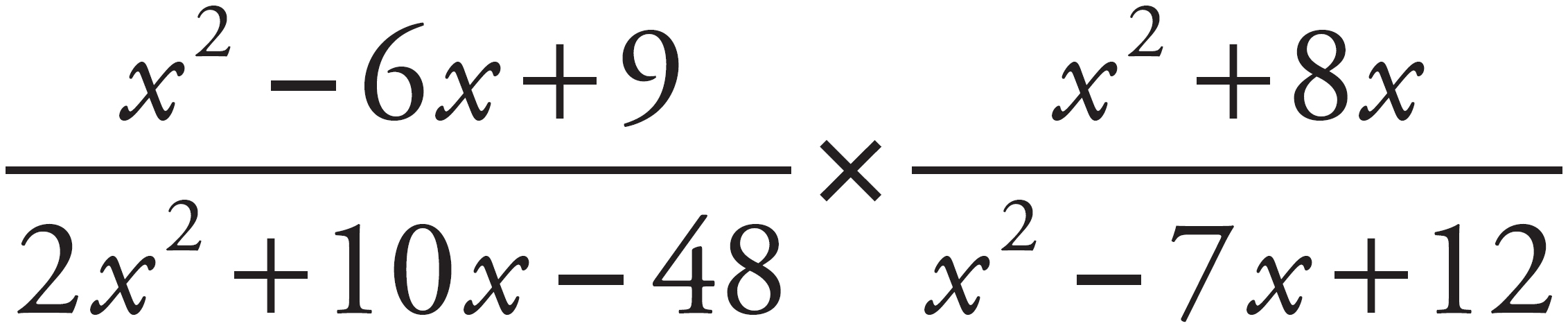 
. This looks painful to multiply, but remember that you can reduce fractions by common factors when you multiply. You can do the same for rational expressions. Factor each polynomial. For the numerator of the first fraction, x2 – 6x +9 factors to (x – 3)2. For the denominator of the first fraction, first notice that 2 is a common factor of all three terms. Therefore, you can factor a 2 to get 2(x2 + 5x – 24). Factor the polynomial inside the parentheses to get 2(x – 3)(x + 8). For the numerator of the second fraction, x2 + 8x factors to x(x + 8). For the denominator of the second fraction, x2 – 7x + 12 factors to (x – 4)(x – 3). Therefore the product becomes 
. Now reduce the fractions. The first fraction can be reduced by (x – 3) to get 
.
Remember that before you multiply, you can reduce fractions diagonally. Therefore, you can cancel a factor of (x – 3) and a factor of (x + 8) to get 
. Multiply straight across to get 
. The correct answer is (B).
You can check your answers in Part VIII: Answer Key to Drills.
1. Which of the following is equivalent to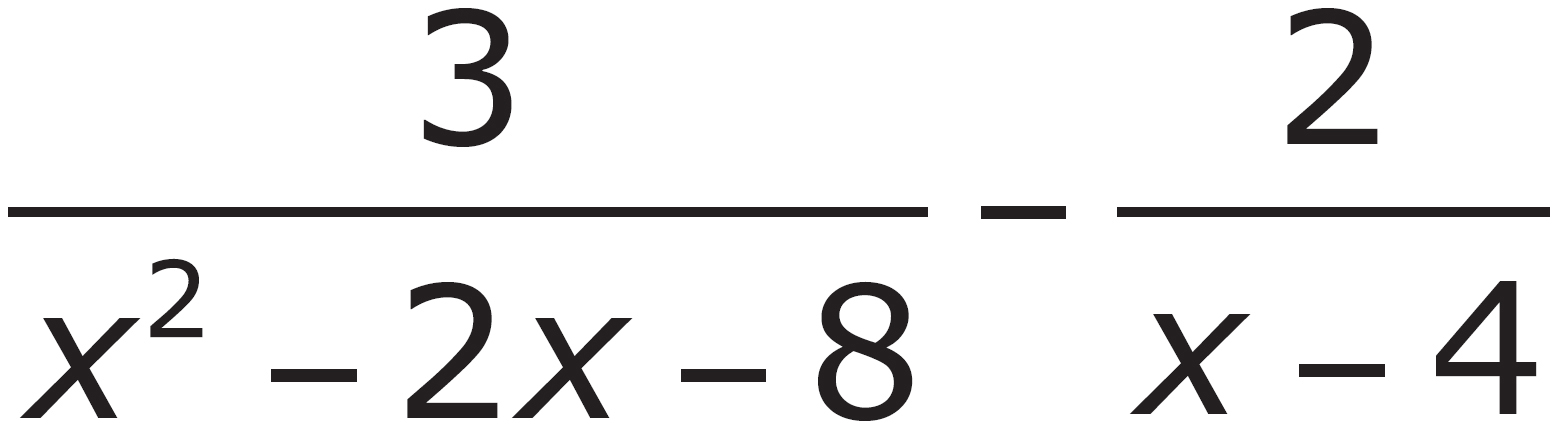 
?
A. 
B.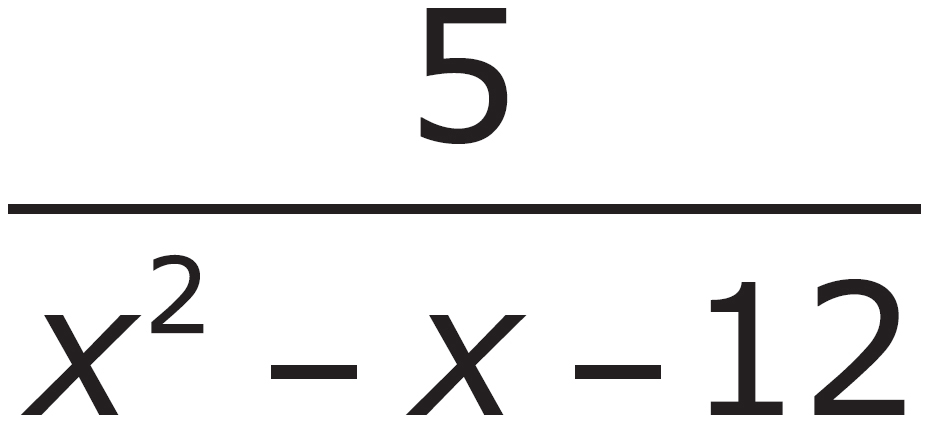 
C. 
D. 
2. Which of the following is equivalent to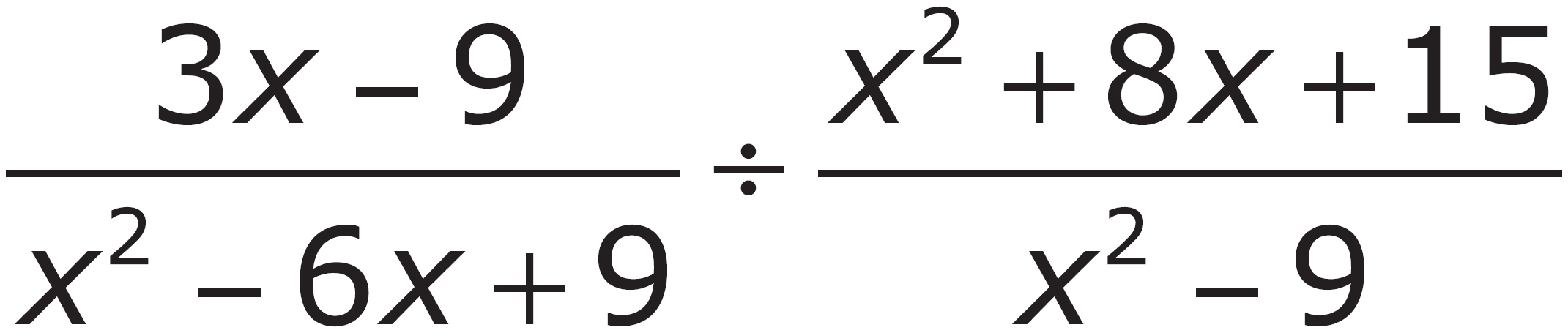 
?
A. 
B.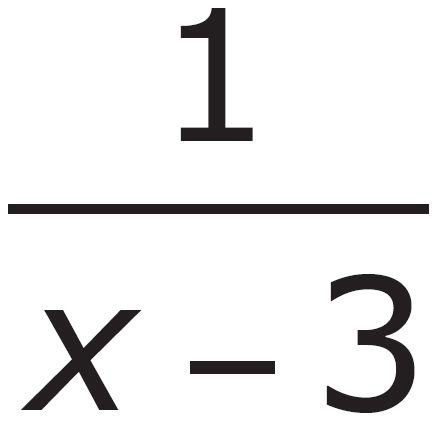 
C. 
D. 
Solving a simple one-variable equation like 3x – 10 = 11 can be done with the method described earlier. However, what if you were given the equation 3x – 10 = y and were asked to come up with a specific value for x? This would be impossible. Different values for y will result in different values for x. However, what if you were also given a second equation like 4x – 17 = y? Although neither equation on its own can determine a value for x, the two of them together can, using a method called the substitution method. Since both equations are isolated for y, set
3x – 10 = 4x – 17
Subtract 3x from both sides to get
–10 = x – 17
Add 17 to both sides to get
7 = x
Need the value of y? Just substitute x = 7 into one of the above equations to get
y = 4(7) – 17 = 28 – 17 = 7
Look at an example.
1. If 3x + 6y = 30 and 2x + 5y = 26, choose two numbers below that are possible values of x and y.
Here’s How to Crack It
There are two equations and two variables. Isolate one of the variables in one of the equations. Take 3x + 6y = 30 and isolate x. Subtract 6y from both sides to get 3x = 30 – 6y. Divide both sides by 3 to get x = 10 – 2y. Now you have an expression for x. Substitute this expression for x into the other equation. 2x + 5y = 26 becomes 2(10 – 2y) + 5y = 26. Distribute 2 to get 20 – 4y + 5y = 26. Combine like terms to get 20 + y = 26. Subtract 20 from both sides to get y = 6. Now, to get x, substitute this value of y into one of the equations. Try the second one. 2x + 5y = 26 becomes 2x + 5(6) = 26 and 2x + 30 = 26. Subtract 30 from both sides to get 2x = –4. Divide both sides by 2 to get x = –2. Therefore, select –2 for x and 6 for y.
There is another method for solving this type of problem, called the linear combination method. Let’s use the equations from the previous question. Stack the two equations as below.
3x + 6y = 30
2x + 5y = 26
To do this method, the first thing you want to do is make sure the coefficients on one of the variables are the same in both equations. In this case, you can multiply the first equation by 2 and the second equation by 3 to get
6x + 12y = 60
6x + 15y = 78
Now, the coefficients on the x variable are the same. Next, subtract the two equations by subtracting the lined up terms to get
Divide both sides by –3 to get y = 6. To get the value of x, substitute this value into one the original equations to get x = –2, just as before.
Try another example.
2. If 4x – 3y = 15 and 5x = 12 – 3y, what is the value of x?
A. –3
B. –1
C. 1
D. 3
Here’s How to Crack It
To solve this using the linear combinations method, first get both equations in the same form. To do this, add 3y to both sides of the second equation to get 5x + 3y = 12. Now line up the two equations to get
4x – 3y = 15
5x + 3y = 12
Notice that the coefficients on the y’s are negation of each other. In this case, you can just add the two equations to get
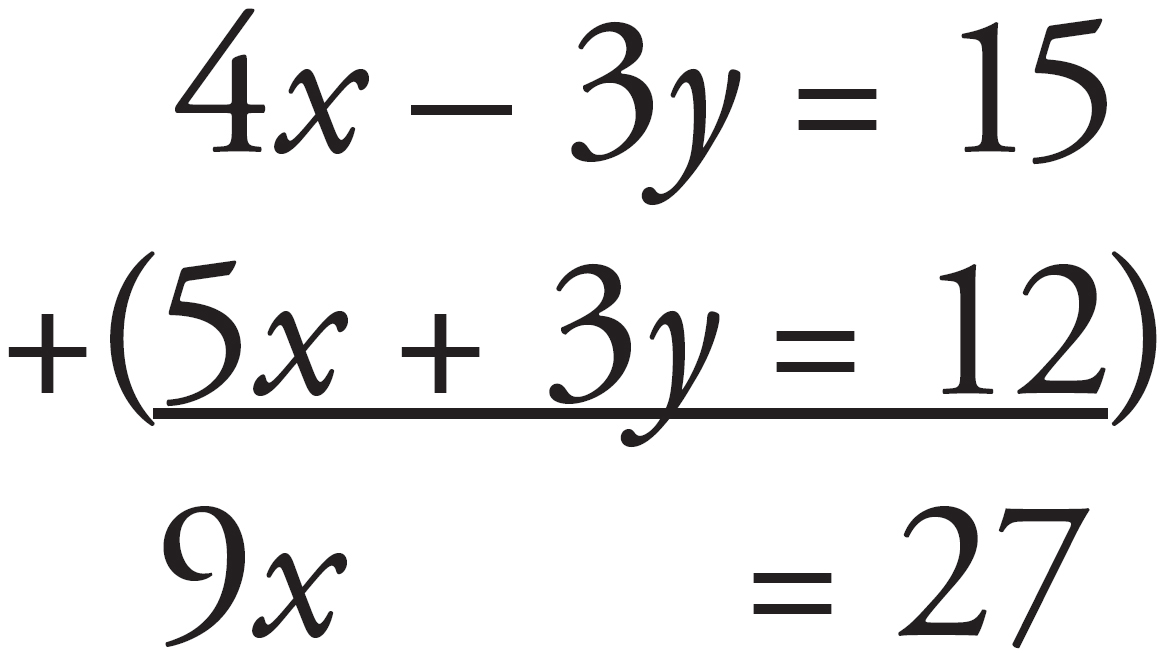
Divide both sides by 9 to get x = 3. The correct answer is (D).
You can check your answers in Part VIII: Answer Key to Drills.
1. If x = 2y + 5 and x = 3y – 6, what is the value of x?
A. 11
B. 22
C. 27
D. 33
2. If 3x + 4y = –5 and –2x – 5y = 8, what is the value of y?
A. –2
B. 1
C. 3
D. 7
3. At a certain fruit stand, apples cost 25 cents and bananas cost 30 cents. If Bill buys a total of 8 apples and bananas for $2.15, how many bananas did Bill buy?
A. 3
B. 4
C. 5
D. 6
Sometimes the GED® test will ask you about relations. A relation is an association between two variables: an input variable called the domain and an output variable called the range. The relations that the GED® test will be most interested in are called functions. Functions are relations in which each member of the domain corresponds to a unique member of the range. Look at the two relations below.
Are these relations functions? When a relation in is table notation, the domain is the variable on the left, in this case x, and the range is the variable on the right, in this case y. For the relation on the left, a member of the domain, 2, goes to two different members of the range, 7 and 1. Therefore, this is not a function. However, in the relation on the right, each member of the domain corresponds with only one member of the range, so this is a function. Does it matter that 2 and 7 from the domain correspond with 4 from the range? No. Each member of the domain has to correspond with a unique member of the range, but each member of the range need not correspond with a unique member of the domain.
Relations can also be put into graphical form.
In the graphical form of a relation, the horizontal axis represents the domain and the vertical axis represents the range. (You’ll see more about graphic functions in the next chapter.) Are these two relations functions? To determine this, use what is called the vertical line test. Since, in a function, every member of the domain corresponds with a unique member of the range, any vertical line drawn on the graph will hit the curve at only one point. If any vertical line touches the curve at more than one point, the relation is not a function. For the graph on the left, multiple vertical lines can be drawn that will touch the curve at more than one point. Therefore, this is not a function. However, for the graph on the right, any vertical line drawn will touch the curve at only one point. Therefore, this relation is a function. This can be seen in the following graphs.
Sometimes the GED® test writers will test your ability to determine whether a relation is a function. Let’s look at an example.
1. Which of the relations below represents a function?
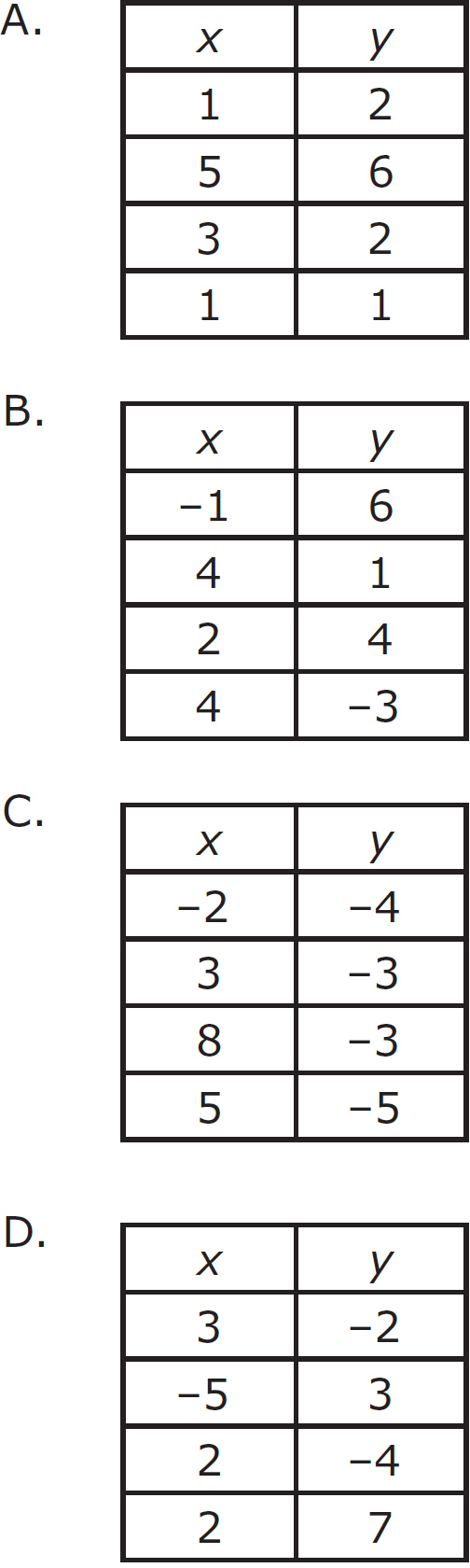
Here’s How to Crack It
In order for a relation to be a function, each member of the domain must correspond with a unique member of the range. In (A), 1 from the domain corresponds with 2 and 1 in the range, so this is not a function. Eliminate (A). In (B), 4 from the domain corresponds with 1 and –3 in the range, so this is not a function. Eliminate (B). In (C), each element of the domain corresponds with only one element from the range. Keep this choice. In (D), 2 from the domain corresponds with –4 and 7 in the range, so this is not a function. Eliminate (D). The correct answer is (C).
Now let’s look at a graphical example.
2. Which of the following graphs does NOT represent a function?
Here’s How to Crack It
Since the question is asking whether graphs represent functions, use the vertical line test. In (A), no vertical line can be drawn that will touch the curve more than once. This represents a function. In (B), no vertical line can be drawn that will touch the curve more than once. This represents a function. In (C), several vertical lines can be drawn that will touch the curve more than once. This does not represent a function. In (D), no vertical line can be drawn that will touch the curve more than once. This represents a function. The only graph that does not represent a function is (C), so the correct answer is (C).
Another way to represent a function is using function notation. This is commonly f(x), though a function could be represented with any letter other than f, as well. f(x) can be stated as “f of x,” “the function of x,” or “f as a function of x.” For example, look at the function f(x) = x2 + 5x. If you were asked for the value of f(3), plug the number inside the parentheses, 3 in this case, in for each appearance of x is the definition of the function. So f(3) = 32 + 5 × 3 = 9 + 15 = 24. If you need f(4), do the same thing. f(4) = 42 + 5 × 4 = 16 + 20 = 36. Let’s look at an example.
|
x |
g(x) |
|
1 |
2 |
|
2 |
6 |
|
3 |
10 |
|
4 |
14 |
3. Which of the following functions could represent the function described in the table above?
A. g(x) = 2x
B. g(x) = 3x – 1
C. g(x) = 4x – 2
D. g(x) = 2x + 4
Here’s How to Crack It
For a question like this, use POE extensively. Start with the first row of the table, which says that g(1) = 2. Go through the answer choices and eliminate any choice for which g(1) does not equal 2. In (A), g(1) = 2 × 1 = 2, so keep this choice. In (B), g(1) = 3 × 1 – 1 = 2, so keep this choice. In (C), g(1) = 4 × 1 – 2 = 2, so keep this choice. In (D), g(1) = 2 × 1 + 4 = 8, so eliminate this choice. Now look at the next row, which says that g(2) = 6, and go through the answer choices, eliminating any choice for which g(2) does not equal 6. In (A), g(2) = 2 × 2 = 4, so eliminate this choice. In (B), g(2) = 3 × 2 – 1 = 5, so eliminate this choice. In (C), g(2) = 4 × 2 – 2 = 6, so keep this choice, which is the only remaining choice. The correct answer is (C).
Some GED® questions will combine functions with translating. Let’s look at an example.
4. A certain fruit stand sells only bananas. The fruit stand earns a profit of five dollars less than 3 dollars for each banana it sells. Which of the following is a function representing the stand’s profits, p, as a function of the number of bananas sold, b?
A. p(b) = 5b – 3
B. p(b) = –2b
C. p(b) = 5 – 3b
D. p(b) = 3b – 5
Here’s How to Crack It
Translate the information in the question into an equation. The profit is p as a function of b, which is written as p(b). The profit is equal to “five dollars less than 3 dollars for each banana it sells.” When you see “five dollars less than,” leave some space and write ______ – 5. Then fill that space with whatever follows “than”: in this case “3 dollars for each banana it sells.” Since this translates to 3b, the function becomes p(b) = 3b –5. The correct answer is (D).
You can check your answers in Part VIII: Answer Key to Drills.
|
x |
h(x) |
|
3 |
–1 |
|
5 |
4 |
|
3 |
y |
|
–2 |
–6 |
1. For which of the following values of y does h(x) represent a function?
A. –6
B. –1
C. 3
D. 4
2. If g(x) = x2 – 6x + 9, which of the following is equal to g(5)?
A. 2
B. 4
C. 5
D. 9
3. Which of the following represents the statement, “The function of x is three times 4 more than the square of x”?
A. f(x) = 3(x2 + 4)
B. f(x) = 3x2 + 4
C. f(x) = 3(x + 4)2
D. f(x) = [3(x – 4)]2
Now that you’ve seen all the elements of algebra separately, we’d like you to try a drill in which they are all mixed together. This will give you practice in recognizing the different types of problems so that you can zero in on exactly which technique you need to solve them quickly. Pay particular attention to spotting Backsolving questions, which our students find takes a bit of practice.
You can check your answers in Part VIII: Answer Key to Drills.
1. If 5x + 9 = 44, then x =
A. 12
B. 10
C. 7
D. 6
2. Laura has $4 more than three times the amount of money Steven has. If x represents the amount of money Steven has, which expression shows how much money Laura has?
A. 3x + 4
B. 3x – 4
C. 4x + 3
D. x + 4(3)
3. Evaluate 5x2 – 4y, if x = 3 and y = 4.
4. The Oakdale Preschool accepts 4-year-olds and 5-year-olds and has a total of 63 students. If the school has 7 more 4-year-olds than 5-year-olds, then how many of the children are 4 years old?
A. 14
B. 28
C. 35
D. 42
5. If 3m + 7 < 28, then which of the following expressions gives all the possible values of m?
A. m < 9
B. m < 7
C. m > –5
D. m > –7
6. What is the sum of 2(x + y) + 3x + 2y?
A. 5x + 3y
B. 6x + 3y
C. 6x + 4y
D. 5x + 4y
7. If p = 4, which of the following inequalities contains the number p?
A. x < 4
B. x > 5
C. 2x < 3
D. x < 5
8. If 36 of the 120 workers in a factory work overtime, what percentage of the workers work overtime?
A. 10%
B. 20%
C. 30%
D. 40%
9. Multiply.
(4x – 8)(x + 2)
A. 4x2 – 16
B. –4x + 2
C. 4x2 + 16x – 16
D. 5x – 6
10. Tony is 4 years older than Heather, and Heather is 5 years younger than Larry. If the sum of their ages is 69, how old is Tony?
A. 18
B. 20
C. 24
D. 25
11. If 3x + 2 = –2y and –x + 3y = –14, what is the value of y ?
A. –4
B. –2
C. 2
D. 4
|
x |
f(x) |
|
–2 |
|
|
1 |
3 |
|
|
19 |
12. If the table above represents the function f(x) = 2x2 + 1, select possible values to complete the table.
