A TRUE MVP
How should we value football team members as players? In this chapter, I argue that we should judge a player's value to his team by comparing how well his team does when he plays and when he doesn't. The notion of a player's value is relevant to various tasks that professional teams engage in, such as drafting, paying, and trading players.
An Illustration: The Most Valuable Player
One area where player value is important is the award for the most valuable player, since the award compares players on the basis of their value. In the NFL, the Associated Press selects the MVP. A nationwide panel of sportswriters and broadcasters who cover the NFL choose the winner. There are other MVP awards, but this one is the most widely recognized and the most prestigious award given to an individual player.
Most of the winners have been running backs and quarterbacks. Players from these positions won the last twenty awards, and forty-six out of fifty since 1957, when the Associate Press MVP award was first given. The winner is usually the statistical leader in an important offensive category such as touchdowns (rushing or passing), yardage (rushing), or effectiveness (passing). Fifteen of the last twenty winners have led in one of these categories. Although the MVP focuses on regular-season performance, the winners are almost always from winning teams. Thirteen out of the last twenty winners were from teams that were in the Super Bowl. The remaining winners came from teams that won 77 percent of their regular season games.
MVP Awards (Associated Press)
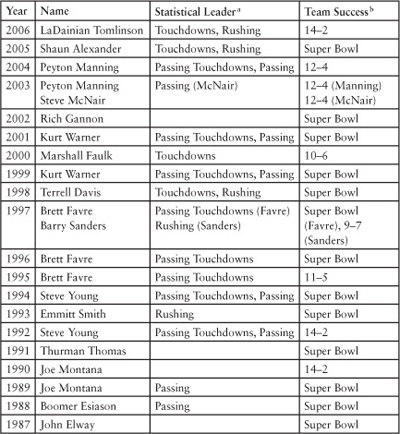
a. The “statistical leader in touchdowns” refers to the number of touchdowns a player ran for. The “statistical leader in rushing” refers to the number of yards the player ran for. The “statistical leader in passing touchdowns” refers to the number of touchdowns the player threw for. The “statistical leader in passing” refers to the player's quarterback rating. This rating is a function of the following factors: completions, touchdowns, yards, attempts, and interceptions.
b. The win-loss record involves the team's regular-season performance. “Super Bowl” refers to the team's presence in the Super Bowl.
There are probably three main reasons that the award has so often been given to these positions. First, how players in these positions perform probably has a greater effect on team success than does the performance of other players. Second, it is easier to measure and compare the statistical performance of players in these positions than in other positions. Third, the viewer's attention naturally tends to focus on these positions so they receive more attention. One reason the MVP is often given to players on a winning team is that a player can be more easily seen to contribute to his team's success when the team actually succeeds.
What Makes a Player Valuable?
This section attempts to provide an analysis of the value of a player. I will adopt parts of an earlier analysis of player value by Neil Feit and myself.1 On this account, player value is concerned with what a player contributes to his team, rather than what he contributes to the average team or the league in general.2 More specifically, one player has more value than a second if and only if he contributes more to his team than other players do to their teams. The underlying idea is that a player can have value to another team (e.g., he keeps on fumbling the ball) or to the league (e.g., he attracts fans), but neither counts as a positive contribution as a player.
Competitive Success as the Ultimate Goal of Competitive Athletics
Since player value to a team exists only in the context of competitive athletics, we need to identify what is valuable in this context. The value to be identified with an activity is a goal that is central to successful participation in it; that is, in virtue of that feature, one achieves excellence with regard to that activity. This goal must be something that acts as the litmus test, so to speak, for excellence in any form that this activity takes.
The distinctive goal of competitive activities, including competitive athletics, is winning. There are other valuable goals—for example, showing respect for others and developing moral character—that can be realized in an athletic context, but there is nothing about these goals that is unique to the athletic realm. They might form a reason for participating in competitive athletics, but they are not the goal of the athletic contest itself. Winning also can occur in nonathletic contexts—for example, war—but only in competitive athletics does it seem to be the central purpose for which persons engage in the activity.
Role- and Team-Based Value
In addition to the analysis of player value in terms of what he contributes to his team's success (that is, winning), a further tightening up of the concept of player value is necessary. Specifically, a player's value comes about via his role as a player. This is opposed to the other roles in which he might serve (e.g., coach, general manager, or owner). That is, the same person might make several kinds of contributions to a team's success, only some of which are relevant to his team's success. On this account, the player-based value might include not only the particular plays he makes but also his role as a mentor, role model, leader, spiritual adviser, or the like, depending on the tasks that constitute being a player. This role specificity rules out contributions such as that of Hall of Fame linebacker Lawrence Taylor, who used to pay prostitutes to keep opposing running backs up all night, thereby reducing their effectiveness.3
Depending on how broadly a player's role is construed, this player-based value might take into account not only a player's performance on the field but also such factors as the player's draft number and pay, since these probably affect who the likely backup is and hence the differential contribution. For example, a player taken at the beginning of the draft restricts his team's ability to obtain other high-quality players in the draft more than if he were picked later in the draft. The same is true with regard to his pay in leagues that cap the overall amount that a team can pay its players. Similar problems arise with regard to team members who both play and make innovative contributions to strategy. For example, Tony Dungy was one of the persons who introduced the modern version of a common NFL defense, the cover two. His formation of the defense came in part when he played in the NFL and in part when he coached in it.4 If Dungy had made his contributions while still playing, then we would have a good test case for what counts as a player-based contribution. Other factors are even less clear, for example, the positive effects a player has on his teammates through humor or friendship. Here we need a theory of whether a player's role includes his effects as a teammate, draftee, collector of salary, strategist, and friend.
Since a role is a set of descriptive conditions that result from the way in which society thinks about the role and since this way of thinking might be indeterminate, role indeterminacy threatens to make player value indeterminate. I think that society views a person's contribution as a player as solely a function of what he does on the field. For example, we might say of a player like Terrell Owens that his media comments so damage team chemistry that they eclipse his tremendous worth as a wide receiver. If this is correct, then the other factors (e.g., draft number, salary, and friendship) are not relevant to a person's contribution as a player. In addition, if on-the-field contribution is determinate, then so is player value.
If this account is correct, then winning is the central goal of competitive athletics and a player's value is a function of the degree to which he contributes to that goal via his on-the-field play. Another way to say this is to say that a player's value is the net benefit that his on-the-field play brings to his team.
Net Benefit to a Team
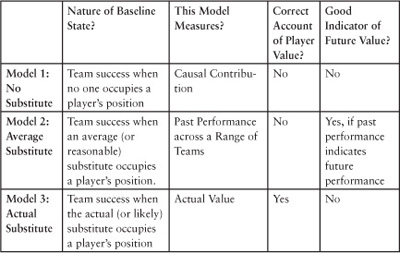
The net benefit is the difference between a player's benefit and cost to his team. The net benefit is measured by comparing the team's performance with the player against some other state in which the player is not present. The latter state is called the “baseline state.” At issue is the nature of the baseline state.
There are three different states that might serve as the relevant baseline state.5 For example, consider the states I might compare to Joe Montana's playing quarterback for the San Francisco 49ers. First, the state might be compared to one in which no one occupies that position (e.g., no one plays quarterback for the 49ers). Second, the state might be compared to one in which a counterfactual player occupies that position. The counterfactual player might be the mean (or perhaps median) backup quarterback. Alternatively, it might be a reasonable backup quarterback. Third, the state might be compared to one in which the actual backup player occupies that position. So, for example, Montana's playing quarterback might be compared to the state in which his actual backup leads the 49er offense. In determining which of these comparative states is relevant to determining a player's value, I shall argue that we will gain a greater understanding of player value.
Model 1: No-Substitute State
The notion behind this model is that it tracks the way in which contribution is normally considered in economics. For example, the marginal benefit of a type of input into production is the additional benefit gained from the last unit of input.6 That is, the marginal benefit of a unit of input involves the comparison of output with the unit and without it. Hence, on this account, to measure a player's net benefit to a team, we compare his team's success when he played and when no one played that position.
One idea that might be seen to motivate this approach is that it measures causal contribution of a thing to an outcome. For example, the causal contribution of an additional acre on which a farmer grows wheat is the comparison of wheat the farmer produces with and without the acre.
The problem with this baseline state is that it fails to track the value of a player because it results in a baseline state involving a game that is very different from the game in which the player in question plays. For example, consider a case in which Drew Bledsoe's net benefit to the New England Patriots is determined by comparing the team's success when he is at quarterback and when no one plays that position. The latter state consists of either the scenario in which the Patriots alone have no quarterback or one in which no team has a quarterback. In the former case, given the centrality of the quarterback to the offense, the Patriots would probably have lost every game. However, even if Drew Bledsoe's play at quarterback contributed to every Patriot win in 2001, this approach overestimates his contribution to his team. This is because the Patriots would likely have won many of the same games were Bledsoe not to play. This is particularly true if he had a particularly talented backup. For example, in the 2001–2002 season, Tom Brady replaced Drew Bledsoe. Brady led the Patriots to three Super Bowls in four years, and during the 2004–2005 season, Brady helped the Patriots set an NFL record with twenty-one straight wins (including the previous year).7 The same is true if we consider other players in the Patriots’ lineup. This results in the team's being unable to win without a number of particular players, because it would be one player short, and this isn't the case. If instead we consider the baseline state to be the one in which no one has a quarterback, the comparative state is so different from the actual state that comparing the two tells us nothing.
In conclusion, the no-substitute baseline fails to provide a proper estimate of player value. It likely tracks causal contribution, and this is not the correct baseline for determining player value.
Model 2: Average-Substitute State
On a second account, the baseline state is one in which a counterfactual player occupies a position. The idea here is that if the player in question (e.g., Drew Bledsoe) doesn't play quarterback, we imagine that some player who might not even be on the Patriots occupies that position, and we compare the Patriots’ success with Bledsoe and the counterfactual player. The counterfactual in this case might vary depending on the particular account.
The counterfactual player might be the average backup player in the league at the time.8 This baseline state is used to measure a player's contribution against a uniform standard across teams. Alternatively, the counterfactual player might be a reasonable backup player in the league at the time. If there is too much talent in the backup for one position (e.g., quarterback) and too little at another (e.g., fullback), the reasonable standard corrects for this maldistribution of talent and thus allows for a better comparison of value across positions. The reasonable backup might vary depending on whether we are comparing players from the same era or from different eras.
This model is useful in measuring the caliber of past performance. For example, in judging a person's performance as a quarterback, this model looks at how well he does in a range of relevant cases. This would allow us to compare performance by screening out the effects of skill differences in backup players and between positions. In principle, we might further tweak the average- or reasonable-player baseline to screen out interteam differences that might come about from factors such as whether the team plays outdoors and the caliber of the surrounding lineup.9 For example, a running back might be more effective when playing with a stellar cast than he would otherwise be. This is because he runs better when given big holes and when the defense has to respect the pass. In measuring past performance, this model likely also gives us a better estimation of future ability than the other two models, at least once we discount age, injury, rule changes, and so on.
An example of a running back with such a stellar cast was Emmitt Smith. Smith, the NFL's leading rusher, gained many of his yards behind arguably the best line ever in the NFL. It included Larry Allen (ten Pro Bowls), Nate Newton (six Pro Bowls), Mark Stepnoski (five Pro Bowls), and Erik Williams (four Pro Bowls). Smith also played with an all-pro quarterback (Troy Aikman, six Pro Bowls), wide receiver (Michael Irvin, five Pro Bowls), and tight end (Jay Novacek, five Pro Bowls) on the team.10 It is unlikely that he would have been as productive surrounded by an ordinary cast.
One problem with this account is that it is not a measure of a player's actual value to his team but his hypothetical value to a range of teams. For example, a player's value to his own team might be negligible, given an unusually talented backup, but for other teams it might be considerable.
A second problem is that the choice of counterfactual player seems arbitrary. The average backup player gets us closer to a player's value to the average team but handicaps comparisons across positions by failing to correct for a maldistribution of talent. In contrast, looking at a reasonable backup player involves the choice of the features of an efficient market that are present in the baseline state. For example, it is not clear if we should take the current crop of players and redistribute them across positions or take into account how more complete information might provide an incentive for other great athletes to enter or leave football. There doesn't seem to be any principled way in which these conditions can be determined. Also, in determining what a reasonable backup player would be like, we would have to determine how much information players, managers, and owners have, the degree to which these persons have rational preferences, and the degree to which there is free entry into and exit from the market. The more we deviate from actual conditions, the less this model measures a player's performance rather than his value to his team.
A third problem concerns the notion of an average backup. Since we are trying to model contribution, it would beg the question to invoke the average contribution to model the backup player. The notion might be filled out in terms of some statistical measure. However, we would need a theory to explain which measure is relevant. To the extent that we cannot find a plausible way to fill out the average backup player, we should reject this model.
In summary, the average-substitution model might be a good measure of a person's past performance but not of a player's value to his own team. Even the former claim isn't obvious, since the notion of an average or reasonable backup player appears to be problematic.
Model 3: Actual-Substitute State
This model focuses on the team's performance with the player in question when compared to its performance when an actual or likely backup plays. On probabilistic accounts, it focuses on the team's performance with the actual player and with each potential backup multiplied by the likelihood of that backup substituting in. It is worth noting that this model takes a perspective similar to that of the team's owner.
This model has an advantage over the first model in that it takes into account the intuition that a player who has the best statistics but who has competitive advantages (e.g., a running back who plays with the best offensive line and an all-pro quarterback) might be less competitive for the MVP than he initially appears. This makes sense on the actual-substitution model, since his replacement would likely have greater success than would replacements on other teams. The actual-substitution model also explains why a great player from a team with a losing record might also be less competitive than he initially appears. His team's lack of effectiveness might lead to less focused and less motivated play from opposing teams, thus making it more likely that his backup would also have greater than average success. The average-substitution model, however, also has these advantages.
There are a number of problems with this approach. First, if a player has a very talented backup, he could have the best statistics and cause the most wins yet fail to have much value. This is because the team would have done nearly as well with his backup. For example, in the late 1980s, Joe Montana was an all-pro quarterback for the San Francisco 49ers. Despite his superb play, he might not have great positive value since his backup was Steve Young, who had the second-highest career passing rating ever and the highest single-season passing rating (Montana was third and second respectively).11 This is counterintuitive.
Second, a player's net benefit to a team is team specific since the comparative states are tied to the performance of a particular team. Thus, it is possible that the same player with the same statistics could have more value than a second player on one team and less on another. Again, this is counterintuitive.
Third, a player whose team doesn't win with him doesn't have much actual value no matter what he contributes. This is because he doesn't bring success to his team.
These problems are not fatal. Consider the first two problems. It is true that a player with the same statistics might be less valuable on one team than another, but this is merely to point out that the contribution a player makes is context dependent. This is no different from the notion that a mediocre doctor in a region of the Congo without any other doctors might make a bigger difference than a superb cardiac surgeon in a large Boston hospital. Statistical measures of performance are also affected by context. For example, a running back's surrounding cast will likely affect his statistics.
Consider the notion that a player didn't bring success to a team that had none. He might make such success more likely, shoulder more than his share of the burden, or be praiseworthy for his efforts, but he doesn't make the team more successful, and, if the above assumptions are true, that is a measure of his value as a player. Here we are interested in actual value, not expected value. The former looks to the past; the latter looks to the future (e.g., it tells us whom to draft and pursue as a free agent).
There is a real-world indicator of a player's net value. On some accounts, the flow of money tends to track contribution to welfare. The assumptions here are that persons spend money in a way that tracks their preferences and that their preferences track contribution to their welfare. If this is correct and if owners pay players to help their team win, players’ salaries will tend to track their net value to their teams. The two will deviate in some cases because economic valuation focuses on expected rather than actual net value.
An objector might note that this view could yield the result that a mediocre player with a terrible backup has more value than any other player. The objector would then assert that this is a knockdown counterexample to the theory. There are two problems with this objection. First, the example is a little hard to imagine, and this may contribute to the oddness of having a mediocre player have the most value. It seems far more likely that a player from another position would be used as a backup or that a decent backup would be obtained via trade or free agency. Second, if the odd scenario obtains, then the player does help his own team more than any other player in the league does, and thus the notion that he has the most value is not so counterintuitive. The mediocre player would also likely be paid the most.
Fitting Actual Value into the Traditional Categories of Value
The table below is a summary of my findings with regard to the three models. In this chapter, I have argued that in the context of team sports the value picked out by the actual-substitute model measures a football player's net value to his team. This claim is based on the assumption that these are the three most plausible models of a player's net value and that the two competitor models fail.
The analysis in this chapter can be applied to issues outside football. It can be used to compare the contributions of different persons to an organization—for example, those of a surgeon and an anesthesiologist to a particular hospital. It is even relevant to broader inquiries such as whether a particular person contributes more to others’ welfare and to making the world a better place when, for example, she becomes a stay-at-home mother rather than an investment banker.
Notes
1. See Stephen Kershnar and Neil Feit, “The Most Valuable Player,” Journal of the Philosophy of Sport 28 (2001): 193–206.
2. The total value of something is the sum of its intrinsic and extrinsic values. Intrinsic value is value that depends on a thing's intrinsic properties. Extrinsic value is value that depends on a thing's extrinsic properties. There is an issue as to whether things are extrinsically valuable only after the intrinsically valuable state has obtained. The idea for this point comes from Toni Ronnow-Rasmussen, “Instrumental Values—Strong and Weak,” Ethical Theory and Moral Practice 5 (2002): 29–32. One concern here is that something might be conducive to bringing about intrinsic value but not actually do so. This concern might be connected to issues regarding whether things exist only in the present and when the future is open. I shall sidestep this issue since my analysis is independent of it. There are two types of extrinsic value: instrumental value (the means to an intrinsically valuable end) and contributory value (the part of an intrinsically valuable whole). In this chapter, I explore different notions that are related to extrinsic value.
3. This comes from an interview of Lawrence Taylor on 60 Minutes, 30 November 2003.
4. Tim Layden, “Two Tough,” Sports Illustrated, 27 November 2006, 48–52, esp. 51.
5. One way to view the choice of baselines is as a way of picking out a thing's extrinsic value. For an account that analyzes extrinsic value in terms of the difference between its total value and its intrinsic value, see Earl Conee, “Pleasure and Intrinsic Goodness” (PhD diss., University of Massachusetts at Amherst 1980), 111, cited in Ben Bradley, “Extrinsic Value,” Philosophical Studies 91 (1998): 113. However, this account doesn't specify the way in which we pick out the baseline account. Ben Bradley argues that the baseline state is context specific. Bradley, “Extrinsic Value,” 109–26. This chapter differs from Bradley's analysis in that it is not trying to analyze extrinsic value but merely trying to identify the type of extrinsic value that we should care about.
6. This definition comes from Steven Landsburg, Price Theory and Applications, 5th ed. (Cincinnati: South-Western, 2002), 120.
7. “Tom Brady,” http://en.wikipedia.org/wiki/Tom_Brady.
8. In baseball, one firm that provides a statistical analysis of baseball analyzes a player's value in term of his value over replacement player (VORP). “VORP” is defined as “the number of runs contributed beyond what a replacement level player would contribute if given the same percentage of team plate appearances.” Stathead. com defines a “replacement level player” as “one who hits far below the league positional average as the league backups do relative to league average, who plays average defense for the position, and is a breakeven base-stealer and baserunner.” Keith Woolner, “Introduction to VORP: Value Over Replacement Player,” http://www.stathead.com/bbeng/woolner/vopdescnew.htm; accessed 13 July 2001.
9. In baseball, for example, one statistic, equivalent average (EqA), is a measure of total offensive value per out. The statistic makes corrections for league offensive level, home park, and team pitching. Baseball Prospectus, “EqA,” http://www.baseballprospectus.com/glossary/index.php?search=EqA; accessed 22 September 2006.
10. “Pro Bowl Index,” http://www.pro-football-reference.com/misc/pbindex.htm; accessed 24 May 2007.
11. “Record and Fact Book: Individual Records—Passing,” NFL.com, http://www.nfl.com/randf/indiv_passing.html; accessed 24 May 2007. A similar thing would likely have been true of Trent Green had he played in 1999. He had a very strong year in 1998 but was in injured in 1999 and replaced by Kurt Warner, who went on to win two MVP awards and is the third-highest-rated quarterback in NFL history. “Kurt Warner,” http://en.wikipedia.org/wiki/Kurt_Warner.