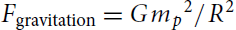2

Gravity is absurdly weak

Gravity and the electric force

Gravity is absurdly weak compared to the electromagnetic force.

How do we compare the relative strength between two forces at the fundamental level? First, a reminder of some basic facts.

We learned about Newton (1642–1726/27)1 and his law of universal gravity in school. It states that the force F of gravitational attraction between a mass M (say, the earth) and a mass m (say, the moon) is equal to a constant G (known as Newton’s gravitational constant) times the product of the two masses (namely, Mm) divided by the square of the distance R separating them. Or, in a more concise language, F = GMm/R².

We also learned about Coulomb’s law. It states that the force F of electric repulsion between two charges, one with charge q₁ and the other with charge q₂, is equal to the product of the two charges (namely, q₁q₂) divided by the square of the distance R separating them. Or, in a more concise language, F = q₁q₂/R².

A striking mystery: the fall-off of the force with increasing distance—the 1/R² inverse square behavior—is the same for gravitation and for the electric force. We will come to the modern understanding of this in due time.

No need to count the number of zeros, we will do it for you

Time out. This is as good a place as any to introduce scientific notation, just in case you do not know it. The ethos behind scientific notation may be expressed as follows: esteemed sir or madam, you don’t have to count the number of zeros, we will do it for you. Thus, 100 is written as 10², 1,000 as 103, 1,000,000 as 10⁶, and so on. The number in the exponent, such as 6 in 10⁶, simply indicates the number of zeros when you write out the number 10⁶ as 1,000,000. It follows that a number such as 149 could be written as 1.49 × 10². The multiplication of large numbers is thus rendered easy: the number of zeros simply add. For example, 100 × 1,000 = 100,000 may then be written as 10² × 10³ = 10²⁺³ = 10⁵. In this notation, 10 may be written as 10¹, and 1 as 10⁰ (since it is equal to 1 with no zero following it).

This explains how to write large numbers. Small numbers are written with a minus sign in the exponent. The logic behind this is as follows. Since, as was just noted, 10^a × 10^b = 10^a+b, on dividing both sides of this equation by 10^a, we obtain 10^b = 10^a+b/10^a and thus, by setting b to −a, we have proved that 10^−a = 10^a−a/10^a = 10⁰/10^a = 1/10^a. For example, let a = 2, and we have 10⁻² = 1/10². In other words, we may write 1/100 (which equals 0. 01 in standard nonscientific notation) as 10⁻² in scientific notation. As another example, 1/10¹⁷ = 10⁻¹⁷ is a very small number, since 10¹⁷ is a very large number.

Comparing gravity to the electromagnetic force

After this notational interlude, we are ready to compare gravity to the electric force. To have a fair comparison, let us consider two protons. The gravitational attraction between them is equal to 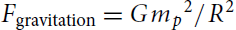, with m_p the mass of the proton. The electric repulsion between them, on the other hand, is equal to F_electric=e²/R², where e denotes the fundamental unit of charge carried by the proton.

Thus, the ratio of the two forces 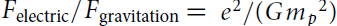. Note that the factors of R² cancel out, so that this ratio is just a number, measured to be about 10³⁶, that is, 1 with 36 zeros after it. This absurdly large number* gives precise meaning to the statement that gravity is absurdly weak compared to electromagnetism. Electromagnetism is stronger than gravity by a factor of 10³⁶.

Note also that before elementary particles, such as protons, and electrons, were known, any proposed comparison between the strengths of gravity and electromagnetism would have been meaningless. What would you use to do the comparison?

Gravity does not know about yin and yang

That gravity is so much weaker than electromagnetism may surprise the unfortunate who has just had a hard fall. The reason is of course that every atom in the unfortunate’s body is being pulled down by every atom in the entire earth. The enormous number of atoms involved more than compensates the teeny number 10⁻³⁶.

A huge difference, and it is huge, as we will see, is that masses are always positive, while charges can be positive or negative. The electric force between a positive and a negative charge then has the opposite sign, namely, it is attractive rather than repulsive. Likes repel, while opposites attract.

Thus, electromagnetism knows about yin and yang. While yin and yang attract, the electric force is repulsive between yin and yin, and between yang and yang.

In contrast, gravity does not know about yin and yang: everybody is gravitationally attracted to everybody else.

I have already alluded to the reason electromagnetism is well hidden in everyday life: common objects contain equal number of positive and negative charges and so are electrically neutral. Whatever force that exists between them is a residual force, left over after the main electric force—namely, the attraction between the protons and electrons, the repulsion between the protons, and the repulsion between the electrons—has been canceled off. It is as if in a financial transaction involving billions rounded off to the nearest dollar, all we get to see is the rounding error of 23 cents.

What electric and magnetic forces we see in everyday life are just the teeny “round off errors.”

A perpetual contest between two forces

An interesting everyday example is the refrigerator magnet. It underlines the enormous strength of the electric force over gravity: the small patch of refrigerator door in contact with the magnet is holding off the entire earth. Furthermore, the magnetic force, caused by the circular motion of the charged particles inside the magnet, is itself much weaker that the electric force.

Once you are alerted to this contest between electromagnetism and gravity, you will start to see it everyday, everywhere. Look at a glass of water. The water molecules hear the incessant siren song of gravity, telling them to lower themselves, to come to the bosom of mother earth. But electromagnetism causes the glass molecules to join hands, forming an interlocking prison through which the water molecules cannot escape. The electric force easily overwhelms the pull of the entire earth.

The escape route is through the top of the glass. Absorbing infrared photons from the environment and hit by air molecules, the water molecules get all agitated and bump into each other in their frenzy. Once in a while, a particular water molecule achieves enough speed—the crowd bumps into him just so—to overcome the downward pull of gravity and shoots to freedom. We call this process evaporation, which leaves us eventually with an empty glass, possibly with some scum in it—the mineral molecules in the scum are too obese to make the getaway.

Or look at a tree. It is desperately pulling up nutrients against gravity. You could surely come up² with many more examples of this never-ending struggle going on all around us between electromagnetism and gravity.

Newton answers your objection

Let’s go back to the refrigerator magnet for a moment. You could have objected that it was not a fair comparison. While the earth is very very large, much of it is also very very far away from the magnet.

Newton was well aware of this problem, and spent almost 20 years proving what he called two “superb theorems.” The magnet is being pulled down by the patch of ground beneath your feet, stuff very close to the magnet but composing a small fraction of the entire earth. The rest of the earth, including the enormous amount of stuff on the other side of the world, is far away. Thus, to apply the law F = GMm/R² to the magnet and the earth, we should mentally cut up the earth into a multitude of infinitesimal pieces, each some distance R from the magnet and each pulling on the magnet, and add up the individual forces.

Newton’s first superb theorem: While the Arctic cap is closest to the apple at the north pole, the equatorial pieces are much more massive. Effectively, the earth pulls on the apple as if the earth’s entire mass is concentrated at its center.

Adapted from Einstein’s Universe: Gravity at Work and Play by A. Zee. Oxford University Press, 1989.

How to do this posed a challenge to Newton, who had to invent integral* calculus to solve this problem (which these days could be given to students as homework). By doing the sum just mentioned, Newton arrived at the remarkable result that the force F exerted on an object of mass m, be it an apple or the refrigerator magnet, by the earth, is as if the entire earth, with mass M, had been shrunk to a point located at the center of the earth. In other words, in his formula F = GMm/R ², we should take for R the radius of the earth.

That Newton took so long to complete his two superb theorems caused one of the most bitter fights in the history of physics. While he was off doing the math, so to speak, his rival, Robert Hooke (1635–1703), also came up with the law of gravitation. Newton, disputing the claim, accused Hooke of not knowing the first superb theorem and thus could not possibly have calculated the force on the proverbial apple.

A famous saying of Newton’s, something like “I could see farther than others because I was able to stand on the shoulders of giants,” often quoted as an indication of his modesty, was apparently a nasty dig at Hooke, who was rather short. This may well be apocryphal, but be that as it may, Sidney Coleman, my PhD advisor, a brilliant but exceedingly arrogant physicist, liked to quip “I could see farther than others because I was able to look over the shoulders of midgets.”

Where is hell?

Before wrapping up this chapter, I cannot resist addressing an issue that may be burning you up. I mentioned that Newton proved two superb theorems but discussed only what is known as the first theorem.

Newton’s second theorem addressed a central mystery of his time: where is hell? While this is no longer a burning question of contemporary physics, we could understand why it would puzzle physicists once upon a time. With a round earth, to imagine heaven localized up above our heads was no longer sensible; heaven would have to be a spherical shell wrapped around the world. It followed that hell must be in the center of a hollow earth. I think that most of my physicist colleagues would agree that this represents the simplest extension of an existing theory. A rudimentary understanding of volcanoes (plus a close reading of the Bible) provided strong observational evidence, confirming the theory for sure.

Furthermore, an erroneous calculation had convinced Newton that the earth was much less dense than the moon, which led his friend Edmond Halley (1656–1742), who, by the way, published Newton’s Principia at his expense, to propose the hollow earth³ theory.4 The idea may seem absurd to us, but not at that time. A location for hell had to be found. Every epoch in physics has it own top ten problems. It is conceivable that future generations would find our desperate attempt to quantize gravity absurd.

So, Newton’s second superb theorem states that there is no gravitation force inside⁵ a spherical shell. You now understand why Newton would even bother to attack this peculiar problem.^*

Either humongous or teeny

If I were a layperson reading popular physics books, I would be confounded by the appearance of numbers that are either humongous or teeny, things are either zillions or zillionths of something. Stars are a zillion times bigger than we are, and we are a zillion times bigger than quarks. And a zillion is always some number beyond all comprehension.

Blame it on the absurd weakness of gravity!

Let us join the movie of the early universe in progress. As the universe expands, it cools. At some point, it has cooled enough for hydrogen atoms to form, consisting of a proton bound with an electron due to their electric attraction for each other. Picture the universe as a diffuse cloud of hydrogen atoms zipping around, a cloud without any structure.

Soon, structures started to emerge, structures that would lead to galaxies, stars, planets, and so on.

The formation of structures, clearly an epochal event in the history of the universe, is based on a commonly observed and easily understood phenomenon: the rich gets richer.

By chance fluctuations, some regions in this primordial gas of hydrogen atoms are denser and some regions are less dense. Thanks to gravity, the denser regions pull hydrogen atoms from the neighboring less-dense regions. The dense regions gets denser, while the less-dense regions gets less dense, in a rapidly accelerating process. Indeed, Newton already understood this consequence of universal gravity and postulated it as the basis for the formation of stars.

Consider a spherical cloud undergoing gravitational collapse and destined to become a star. In modern understanding, eventually the hydrogen atoms are so densely packed that collisions between them strip the electrons off, leaving a gas consisting of protons and electrons. Finally, as the gas becomes even denser, the protons get close enough to each other to initiate nuclear reaction, that is, the strong interaction becomes effective. A star is born!

What could work against gravity? In other words, what must gravity overcome to form structure in the primordial gas of hydrogen atoms? Well, the hydrogen atoms are zipping this way and that way, and some of them are bound to go from the denser region to the less-dense region. Gravity’s job is to pull them back. Clearly, gravity can win if the denser region is massive enough. How much mass do you need? You need a lot, since gravity is so feeble.⁶

In the preceding sections, we measured the feebleness of gravity by comparing it to the electric force and obtained 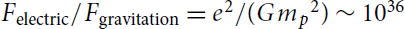. Here the electric force is not in the game, and e² does not enter. So, we should measure the feebleness of gravity by the number 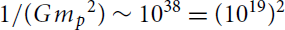. The huge number 10¹⁹, which we might call the Planck7 number, indicates the intrinsic weakness of gravity and plays an important role in contemporary physics, such as in string theory.

In the present context, this number governs the emergence of structure in the universe, and a great deal of astrophysics could be understood in terms of this number. For instance, you could look up that a solar mass is about 2 × 10³⁰ kg and that the proton’s mass is about 1.6 × 10⁻²⁷ kg. Thus, a typical star like the sun contains about 10³⁰/10⁻²⁷ ~ 10⁵⁷ protons.

Where does this humongous number 10⁵⁷, so far out of everyday experience, come from?

An undergraduate level physics exercise (which I won’t go into here8) shows that it comes from the cube of the Planck number: (10¹⁹)³ = 10¹⁹ × 10¹⁹ × 10¹⁹ = 10¹⁹+¹⁹+¹⁹ = 10⁵⁷.

*  Notice that by using two protons to do the comparison, I have biased the result in favor of gravity. Since an electron is about two thousand times less massive than a proton, the ratio of electric to gravitation forces between two electrons would be given by the even larger number 10³⁶ × (2,000)² = 4 × 10⁴².

*  This procedure of cutting up an object into infinitesimal pieces and then adding up the individual forces exerted by the pieces is known as integrating.

*  Incidentally, since there is no gravitation force in hell, the usual portrayal of the leaping flames can’t be right! Flames shoot up because gravity pulls the denser air surrounding the hot gas down.