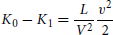
Preface
1. Actually, it weighs less than the classic text by Misner, Thorne, and Wheeler: MTW weighs 5.6 pounds, significantly more than GNut’s paltry 4.6 pounds.
2. Except in passing.
3. Facsimiles of Einstein’s manuscript are available in The Road to Relativity, by H. Gutfreund and J. Renn, Princeton University Press, 2015.
Prologue
1. To set the time scale, dinosaurs roamed about 0.24 billion years ago.
2. See chapter 17.
3. Hence the detection event, the first of its kind, is being cataloged as GW150914.
4. This formula did not appear in Einstein’s original papers on special relativity. Einstein discovered it a few months later, and published it in a 2-page paper, writing
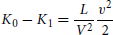
What! It doesn’t look like E = mc2 to you? Einstein is telling us that, when an object moving at velocity v radiates, its kinetic energy K changes by (in modern notation)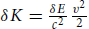 
. (In his paper, L denotes the energy emitted in radiation and V the speed of light.) He then goes on to say, a couple of paragraphs later, “It is not excluded that it will prove possible to test this theory using bodies whose energy content is variable to a high degree (e.g., radium salts).” Einstein wrote to a friend excitedly: “One more consequence of the paper on electrodynamics has also occurred to me…. The argument is amusing and seductive; but for all I know the Lord might be laughing over it and leading me around by the nose.”
As we all know, the Lord did not lead Einstein around by the nose.
Many years later, in 1946, Einstein gave an elegant derivation, which, surprisingly, is omitted from most textbooks (I like Einstein’s 1946 derivation much better than his original 1905 derivation) and so is in danger of being forgotten. See page 232 of GNut. The same derivation was given on page 125 of A. Einstein’s Out of My Later Years, Philosophical Library, 1956.
5. A remarkably modern paper, it derives gravity waves in clear logical steps almost exactly as how a modern textbook would present the subject.
6. This notation was first introduced by Weber and Kohlrausch in 1856, long before Albert was born. By the way, “celeritas,” being Latin, is not related to “celery,” which comes from the Greek word for “parsley.” Meanwhile, “Kohl” means “cabbage” in German.
7. When the rumors of the impending discovery of gravity waves started flying around cyberspace, I emailed my correspondents to name me a theoretical physicist who does not believe in gravity waves. Nobody could come up with a name. Still, it is crucial that physics be based on observational evidence.
8. An extreme example may be the speculation of Democritus (“chosen by the people,” c. 460–c. 370 BC) about atoms. It took over two millennia for it to be verified. In our own times, it is anybody’s guess whether string theory will ever be experimentally verified, and how long it will take.
9. Including my own GNut.
10. Einstein committed a serious error in his 1916 paper, which led the English physicist Arthur Eddington to jest that gravity waves propagate with the speed of thought. Einstein’s 1918 paper, in contrast, contains more or less the essence of the treatment given in modern textbooks.
11. M. Bartusiak, Einstein’s Unfinished Symphony.
12. A. Zee, An Old Man’s Toy (hereafter cited as Toy).
13. It is of course not always American: witness “kiwi” beating out “Chinese gooseberry.”
Chapter 1. A friendly contest between the four interactions
1. See GNut, chapter VIII.2.
2. We still devote one day a week to electromagnetism: Thursday is Thor’s day.
Chapter 2. Gravity is absurdly weak
1. We do know when Newton died; the discrepancy is due to the difference between the Julian and Gregorian calendars.
2. Gravity is responsible for a number of ailments, in particular gout. Molecules of uric acid in the bloodstream are driven downward by gravity and congregate in the lower extremities, typically around the big toes. When the concentration of uric acid reaches a critical value, it can suddenly crystallize, causing excruciating pain.
3. Witness the popularity of the idea in science fiction, notably Jules Verne’s Journey to the Center of the Earth (1864).
4. N. Kollerstrom, “The Hollow World of Edmond Halley,” J. Hist. Astronomy 23 (1992) p. 185.
5. For a popular account, see Toy.
6. The details were worked out by Sir James Jeans (1877–1946). Here is what I just said in more technical language. In stellar physics, the Jeans instability causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent gravitational collapse of a region filled with matter.
7. In honor of Max Planck, who first introduced this number into physics.
8. The curious reader can find this worked out in Zee, Unity of Forces in the Universe (hereafter cited as Unity), volume 2.
Chapter 3. Detection of electromagnetic waves
1. His fundamental contributions range from physics to physiology. During his visit to the United States, Helmholtz was treated like royalty, but on the ship returning to Europe he fell, hit his head, and died soon after. See B. Brown, Planck.
2. Note that this is also the year Maxwell died and Einstein was born. It was also the year the American tycoon and philanthropist John Hertz was born. See a later endnote about him.
3. One of the few examples of an apparatus named after a city rather than a person.
4. With frequency around 100 million hertz (MHz).
5. Look at photos of Hertz’s apparatus, as shown in the text. It would make an easy project for ambitious high school students.
6. Given the role played by electromagnetic waves in our society, I am often astonished that they were discovered a mere 130 years ago.
7. Sadly, the Nazis saw fit to remove Hertz’s portrait from the Hamburg Rathaus, even though his father and paternal grandparents had converted from Judaism to Christianity in the early 19th century. His mother was the daughter of a Lutheran pastor.
8. I was saddened somewhat, but perhaps I shouldn’t have been, that when I searched online for Hertz, a rental car company soundly beat out the person who brought us our electromagnetic age. It is a comment on what is valued in our society. The mogul John Hertz (1879–1961), founder of the rental car company, was actually a remarkable character. Born Sndor Herz in what is now Slovakia, he was five when his family emigrated to Chicago. As a young man, he boxed under the name “Dan Donnelly,” and after winning several championships, eventually fought under his own name. He literally fought his way up in the world.
9. Now discussed in almost any introductory quantum mechanics textbook.
10. In his youth, Planck was much vexed by his inability to obtain a desirable job. Every time such a position opened up, it would be offered to Hertz, with Planck coming in as second choice. See B. Brown, Planck.
11. It still exists in certain areas of physics, but no longer in the so-called Big Science, with the letter “b,” as in a billion dollars.
Chapter 4. From water waves to gravity waves
1. You can see his skull, once housing his big brain, in the Museum of Man in Paris.
2. What this means is the following. Suppose the pond is 13 feet deep. Let us define 1 phathom as 13 feet. Then in terms of phathoms, g is equal to exactly 1 phathom. Historical units such as fathoms, hands, and stones are defined precisely in this spirit.
3. And was written down by Claude-Louis Navier (1785–1836) and George Stokes (1819–1903).
4. The Clay prize; see Wikipedia, for example.
5. For example, the exponential eh is approximately h to leading order.
Chapter 5. Spooky action at a distance
1. I am not sure when gravity was first explicitly recognized as a force. To the ancients, gravity, ubiquitous and ever present, must have been subsumed into a general consciousness of existence.
2. There is perhaps a lesson here for the young theoretical physicists reading this book. Newton was content to postulate the inverse square law and then explore its consequences. He left its dynamical origin to others, like Descartes, whose theory of vortices sweeping the planets along was swept into the dustbin of history. I might call the Descartes approach the “all or nothing approach,” which some theoretical physicists still indulge in. At any stage in the development of physics, certain questions are not appropriate; for instance somebody could always demand of Newton, “Hey Isaac, so why inverse square?”
Chapter 6. Greatness and audacity: Enter the field
1. He has been immortalized in the term “Laplacian,” which physics students mutter all the time.
2. The notation used here is obviously not the one the Marquis used.
3. Physics textbooks tend to introduce Newton’s idea about gravity, work out the moon moving around the earth in a circular orbit, and leave it at that. But if you consider that by then, people had already observed the moon for several millennia, you would realize that a great deal was known about the motion of the moon. There were quite a few discrepancies left unexplained by Newton, which no doubt caused him and his contemporaries and successors some major headaches. (We now know that some of these are due to the pull of the other planets and the sun and to tidal effects.) Well, Laplace thought that if gravity were due to some tiny particles zipping back and forth at the speed cG, the time delay could solve some outstanding puzzles about the moon’s orbit (I am impressed that Laplace’s picture is eerily similar to the modern quantum field theoretic view of the graviton zipping back and forth).
4. Some sort of democratic impulse.
5. This was already mandated by special relativity.
6. But before this understanding, it would seem strange, perhaps even bizarre, that gravity waves and electromagnetic waves would propagate at precisely the same speed c.
7. Those of you who were bottle fed may be excused.
8. Einstein, Out of My Later Years.
9. I must say that the latest and the brashest ideas on the cutting edge of theoretical physics today often seem neither great nor audacious.
10. This passage about Faraday is adapted from my book Fearful.
11. I was amazed when I read this. In more recent times, enemy scientists typically have been captured and interned.
12. My son Max, five as of the writing of this sentence, often asked me to exert the force on him. I would stretch out my hand like the Emperor, and he would grasp his neck and pretend to choke like Luke.
13. A friendly word of advice to those readers of my textbooks who complained on the jungle river that they are not mathematical enough.
14. The American school of theoretical physics by tradition has stressed physical intuition, at the expense of what is sometimes referred to as “fancy shmancy mathematics.” I will refrain from exploring the historical and sociological origins of this emphasis, which has both strengths and weaknesses. Generally speaking, European physicists receive a much more vigorous training in contemporary mathematics than their American counterparts. The French philosophers, now referred to as the French physicists, still are regarded by many Americans as overly mathematical. Of course, what is considered fancy by one generation is often thought basic by the next. The mathematics used by Poisson et al. now looks like child’s play and is familiar to any undergraduate student of physics.
15. Physicists have often used the birth of telecommunications to illustrate the importance of funding basic research. They can easily imagine the Royal Navy official charged with allocating funds to improve communications deciding it would be folly to support these strange types fooling around with wires and frogs’ legs in their gloomy laboratories. Obviously, he might have reasoned, the money would be better spent on breeding a speedier strain of carrier pigeon.
16. QFT Nut.
17. It is actually somewhat more subtle than that, hence my use of the word “almost” twice in this section. The key point, as physics undergrads learn, is that while the static gravitational and electric potential fall off with 1/r, in the propagating wave these potentials fall off like eikr/r.
18. An excellent account, with detailed explanations for the skepticism, has been given by Daniel Kennefick, Traveling at the Speed of Thought.
19. It was during this period, in which general relativity had made relatively little progress, that Richard Feynman participated in a conference on the subject. After hearing some lectures devoted to formalisms, a bored and disgusted Feynman wrote a famous letter to his wife telling her to never allow him to attend a conference on this subject again. Some physicists at the conference tried to convince the others that gravity waves do not exist. In a ludicrously unfair judgment, Feynman referred to the other participants as worms trying to crawl out of a bottle and classified them into six different kinds. I have on occasion classified my Amazon critics using a similar scheme.
20. See J. A. Wheeler, “Superdense Stars,” Annual Review of Astronomy and Astrophysics, vol. 4, 1966, p. 423. See also later work by K. Thorne and A. Campolattaro, Astrophysical Journal, 1967, vol. 149, p. 591.
Chapter 7. Einstein, the exterminator of relativity
1. In German, Einsteinsche Relativittstheorie.
2. P. Galison, Einstein’s Clocks, Poincaré’s Maps.
3. Such as Châtelet Les Halles in Paris.
4. Here we reached this conclusion using Maxwell’s equations. Historically, this was also established empirically by the famous Michelson-Morley experiment.
5. Given that a gravity wave propagates at the speed of light, some wit has suggested that a levity wave should propagate at the speed of dark.
6. Oliver Heaviside in 1893, and independently Henri Poincaré in 1905, anticipated the existence of gravity waves, arguing by analogy with electromagnetic waves. Poincaré understood that Lorentz invariance is a property of spacetime, not solely of electromagnetism, and thus even stated that gravity waves propagated with the speed of light. But only Einstein had the actual relativistic theory of gravity, and so only he was able to determine the properties of gravity waves.
Chapter 8. Einstein’s idea: Spacetime becomes curved
1. I am abusing geography slightly.
2. This celebrated experiment was also performed by Simon Stevins of Bruges.
3. Newtonian physics cannot entertain the existence of massless particles.
4. As to what type of blonde, see the classification and scholarly study Blonde Like Me by Natalia Ilyin.
5. See https://www.npl.washington.edu/eotwash/node/1.
6. If the gravitational mass were not equal to the inertial mass, this would correspond to, in our analogy, different airplanes seeing a different curvature of the earth.
7. Staircase wit, l’esprit d’escalier, Treppenwitz, firing the cannon after the cavalry has already charged by you.
8. Einstein fastened on the universality of gravity as the one essential fact. A priori, it was certainly not clear, out of the known facts about gravity, which one we should fasten onto. When I first learned about gravity, I wondered about the inverse square law, why it was the square of the distance and not the cube, say. No doubt many students have had the same thought. That it is inverse square is now understood in quantum field theory as due to the masslessness of the photon and of the graviton. In fact, one could have started with the masslessness of the graviton and, knowing how it couples to mass in Newtonian gravity, recovered Einstein gravity. But that’s another story for another evening. See GNut, chapter IX.5
9. See Box 1 in the article about Wheeler by C. Misner, K. Thorne, and W. Zurek: http://authors.library.caltech.edu/15184/1/Misner2009p1638PhysToday.pdf. Note that according to this article, Wheeler was not the first to come up with the term “black hole.” Incidentally, reference 14 in this article contains a description of my work mentioned in an earlier endnote.
10. One reason I went to Princeton was because I had read about John Wheeler. I learned physics from him starting on day one, until the end of my junior year, when Murph Goldberger told me that I had better abandon gravity and study something more interesting called quantum field theory instead. And so I devoted the entire summer learning quantum field theory. Then I spent my senior year working with Arthur Wightman on his particular approach, known as axiomatic field theory, complete with theorems, proofs, and all that kind of stuff. I remember Goldberger saying to Sam Treiman in my presence, “I saved the kid from Wheeler’s clutches only to see him fall into a worse trap.” When it came time for graduate studies, I went to Wheeler for advice, and he was gracious enough to pick up the phone and got me into the appropriate school.
11. Readers who wish to feast on these niceties could read GNut. It is explained in detail there how g blossoms into ten different functions.
Chapter 9. How to detect something as ethereal as ripples in spacetime
1. I recommend getting the history of LIGO from one of its founders, Rainer Weiss. See http://news.mit.edu/2016/rainer-weiss-ligo-origins-0211.
2. With this kind of time and cost involved, the reader can readily surmise that considerable infighting has occurred, with one scientist after another outsted from the project. For a short book like this, I have to assume that the reader is not terribly interested in gossipy details. More important, the question of which institution deserves the most recognition might occur. For this, I refer the reader to the actual press release: http://ligo.org/detections/GW150914/press-release/english.pdf. I quote two passages here:
The discovery … was made by the LIGO Scientific Collaboration (which includes the GEO Collaboration and the Australian Consortium for Interferometric Gravitational Astronomy) and the Virgo Collaboration using data from the two LIGO detectors.
The discovery was made possible by the enhanced capabilities of Advanced LIGO, a major upgrade…. The US National Science Foundation leads in financial support for Advanced LIGO. Funding organizations in Germany (Max Planck Society), the U.K. (Science and Technology Facilities Council, STFC) and Australia (Australian Research Council) also have made significant commitments to the project. Several of the key technologies that made Advanced LIGO so much more sensitive have been developed and tested by the German-UK GEO collaboration. Significant computer resources have been contributed by the AEI Hannover Atlas Cluster, the LIGO Laboratory, Syracuse University, and the University of Wisconsin Milwaukee. Several universities designed, built, and tested key components for Advanced LIGO: The Australian National University, the University of Adelaide, the University of Florida, Stanford University, Columbia University in the City of New York, and Louisiana State University.
3. In physics, wave interference has played—and continues to play—a crucial role. The phenomenon, characteristic of waves, was used in a crucial experiment by Thomas Young (1773–1829) to establish that light was a wave. By the way, the breadth of Young’s interests was such that he was referred to as “the last man who knew everything.”
4. Interestingly, each detector is conceptually similar to the famous Michelson-Morley interferometer that established special relativity. In that case, the experiment was to see whether the speed of light was different in the two arms.
5. The word “exactly” is of course a mathematical abstraction and is used here to simplify the discussion. Two kilometers-long arms could hardly be built to have “exactly” the same length, but the slight difference in lengths can be adjusted for.
6. QFT Nut, chapter N.1.
7. In fact, much of this modeling can also be done analytically using the perturbation theory first developed by S. Chandrasekhar.
8. The masses of the two black holes involved surprised astrophysicists somewhat. The black holes are considerably more massive than the stellar-mass black holes that should result when massive stars die, but are many orders of magnitude less massive than the million- to billion-solar-mass giant black hole that is expected to sit at the center of each galaxy.
9. The merger radiated away 3 solar masses worth of energy in gravity waves, resulting in a black hole with 29 + 36 − 3 = 62 times the mass of the sun.
10. In a later edition, the title was changed to Einstein’s Universe by a new publisher.
11. M. Bartusiak, Einstein’s Unfinished Symphony.
12. Kennefick, Traveling at the Speed of Thought.
13. See also H. Collins, Gravity’s Ghost. Note especially the reference to the “Italians,” a codeword that may or may not refer to people born in Italy.
14. The Perils of Pauline is an American melodrama film serial shown in 1914 in weekly installments, featuring a damsel named Pauline in constant distress and always saved at the last minute.
15. Richard Garwin, one ofWeber’s most vocal critics, simply built a replica of Weber’s detector and showed that he could not pick up any signal. At a physics conference, Garwin and Weber almost came to blows.
16. For example, in recent times, the TAMA 300 in Japan, the GEO 600 in Germany, and Virgo in Italy. In fact, members of the Virgo team worked on LIGO and were listed on the discovery paper.
Chapter 10. Getting the best possible deal
1. R. P. Feynman, QED, with a new introduction by A. Zee.
2. Babies have no need for Euclid; as soon as they can crawl, they move toward the obscure objects of their desire along a straight line.
3. The bitter academic controversy over Fermat’s birth year stems from his father marrying twice and naming two sons from two different wives both Pierre. K. Barner, NTM, 2001, vol. 9, no. 4, p. 209.
4. Historians have fun exploring counterfactual histories. See Cowley, What If?
5. Two small stories about two towering figures connected with the action principle: Lagrange and Feynman.
Starting when he was 18, Joseph Louis, the Comte de Lagrange (1736–1813), (who, by the way, was born Giuseppe Lodovico Lagrangia before the term “Italian” existed), worked on the problem of the tautochrone, which nowadays we would describe as the problem of finding the extremum of functionals. A year or so later, he sent a letter to Leonhard Euler (1707–1783), the leading mathematician of the time, to say that he had solved the isoperimetrical problem: for curves of a given perimeter, find the one that would maximize the area enclosed. Euler had been struggling with the same problem, but he generously gave the teenager full credit. Later, he recommended that Lagrange should succeed him as the director of mathematics at the Prussian Academy of Sciences.
Richard Feynman (1918–1988) recalled that when he first learned of the action principle, he was blown away. Indeed, the action principle underlies some of Feynman’s deepest contributions to theoretical physics. In particular, his formulation of quantum mechanics depends very much on the action.
6. The reader should not confuse extremization of the action with the everyday observation that matter likes to minimize energy, which is just the principle of “water always flows downhill” and “a couch potato will stay on the couch.” Throw a child’s marble into a bowl. Come back later, and you would be astonished if it is not resting at the bottom of the bowl. The marble has minimized its total energy by setting its kinetic energy to zero and lowering its potential energy as much as possible. (Occasionally, a bright student might wonder if this minimization of energy contradicts the conservation of energy. In fact, while the latter is absolute and sacred to physicists, the former is merely apparent because we choose to ignore other forms of energy. By rattling in the bowl, the marble has generated sound and heat, both of which escaped into the environment.)
7. I consider this to be one of the great triumphs of quantum physics: the explanation of why the action is extremized, rather than minimized or maximized.
8. I must emphasize that the action principle of mechanics says no more, and no less, than Newton’s laws of motion. The action formulation, although more compact and aesthetically more appealing, is physically entirely equivalent to Newton’s formulation.
The outlook, however, is quite different in the two formulations. In the action formulation, one takes a structural view, comparing different ways by which the particle could have gotten from here to there.
To the 17th- and 18th- century mind, the least time and least action principles provided comforting evidence of Divine guidance. A voice told each particle in the universe to follow the most advantageous path and history. Not surprisingly, the least action principle has inspired a considerable amount of quasi-philosophical, quasi-theological writing, a body of writing, which, while intriguing, proves to be sterile ultimately. Nowadays, physicists generally adopt the conservative, pragmatic position that the least action principle is simply a more compact way to formulate physics, and that the quasi-theological interpretation suggested by it is neither admissible nor relevant.
Next time you are invited to a dinner party at the home of a philosophy professor, say the word “teleological” in the middle of the main course. After these guys have stopped clawing at each other, utter, with nonchalant total self-assurance, “the ontological is distinct from the epistemological, while the tautological is antithetical to the logical,” and watch the fun start again. That statement is of course what is known in polite circles as “utter nonsense” and in less polite circles as total BS, but it gives you an idea of how some academics talk.
The philosophy-R-us version, which I could give you for no charge, is that things are teleological if they have a purpose, or at least act as if they have a purpose. That’s a big no-no in modern science. You see that Fermat’s least time principle (incidentally, if it ever comes to a priority dispute, Fermat would have to cede to Heron of Alexandria, circa AD 65) has a strongly teleological flavor—that light, and particularly, daylight, somehow knows how to save time—a flavor totally distasteful to the post rational palate. In contrast, at the time of Fermat, there was lots of quasi-theological talk about Divine Providence and Harmonious Nature, so no one questioned that light would be guided to follow the most prudent path.
9. The title of this section is my reminder to the author to keep this book brief.
10. In the differential formulation, we specify the initial position and velocity of a particle and ask where it will be at a later time T and how fast it will be moving then. In the action formulation, we specify the initial position of a particle and its final position at some time T. Note that the initial velocity is not specified as in the differential formulation; rather, the initial velocity is to be determined by the action principle. The particle has to “find” the initial velocity needed to get it to the specified final position at time T, sort of like the protagonist in the Western 3:10 to Yuma.
11. Newton’s equation of motion is described as “local” in time: it tells us what is going to happen in the next instant. In contrast, the action principle is “global”: one integrates over various possible trajectories and chooses the best one. While the two formulations are mathematically entirely equivalent, the action principle offers numerous advantages over the equation of motion approach. For example, the action leads directly to an understanding of quantum mechanics via the so-called Dirac-Feynman path integral formulation. Indeed, the discussion here gives a premonition of the emergence of probability in the quantum world. Which path will the particle choose? Betting odds, anybody? See, for example, R. P. Feynman and A. R. Hibbs, Quantum Mechanics and Path Integrals; also, QFT Nut, chapter I.2.
Chapter 11. Symmetry: Physics must not depend on the physicist
1. Fearful.
Chapter 12. Yes, I want the best deal, but what is the deal?
1. For the curious reader, here is the action governing the electromagnetic field: S = ∫d4xF2. That’s it. Simple, eh? By extremizing this action, we obtain Maxwell’s equations for the electromagnetic field.
I can deconstruct the action for you. Actions are traditionally denoted by capital S; the integral sign is ∫ known to students of calculus; the symbol d4x indicates that the integration is over spacetime, with the 4 saying that spacetime is 4-dimentional in the sense of Minkowski. The hard part is F2: F is actually a tensor denoting the electromagnetic field. For this, you will have to get a textbook on electromagnetism at the appropriate level and self-study—believe me, it’s not that hard (so I say, having learned it decades ago)—or pay tuition at an institution of learning to have it explained to you.
2. By the way, this follows from high school level dimensional analysis.
3. The astute reader might worry about massless particles, such as the photon. See GNut for details.
4. Specifically, R the scalar curvature. There are other measures of curvature, known as the Riemann curvature tensor and the Ricci tensor, but the requirement that the action be invariant picks out the scalar curvature.
5. GNut, page 390.
6. For details, see GNut, chapter IV.2.…
7. The so-called Bianchi identities.
8. The material here is adapted from my book GNut. See p. 396.
9. I am reminded of a New Yorker cartoon showing a hapless employee standing before the boss’s big desk, with the boss saying “Yes, it was your idea, but I am the one who recognized that it was a good idea.”
Chapter 14. It must be
1. I can now explain the error in Einstein’s 1916 paper, which I mentioned in the prologue. Some physical properties of gravity waves deduced by Einstein were not invariant. In other words, they depended on the coordinates used to describe them and so could not be physical.
2. Strictly speaking, the scalar curvature mentioned in an earlier endnote in chapter 12 is an invariant.
3. Some readers may wonder why other geometrical invariants besides Λ and R are not included in the action. Surely, if R is invariant, then R2, for example, will also be invariant. The answer is that in modern formulation of quantum field theory, possible terms are ordered according to how important they are expected to be over long distances in spacetime. These other terms you might worry about are all (expected to be) negligible compared to Λ and R. See GNut, chapter X.3.
4. By Abraham Pais, the leading biographer of Einstein.
Chapter 15. From frozen star to black hole
1. Hence the warning against firing guns in the air in celebration in certain countries.
2. Back in chapter 2, I stated that the gravitational attraction between two objects, of mass M and m, is equal to GMm/R2 with R the distance between the two objects. When applied to the earth and the moon, since the sizes of the earth and of the moon are both tiny compared to the distance between them, it is clear what R means. But when Newton applied his law to the gravitation attraction between the earth and the apple, what should he have taken for R? Should R have been the height of the apple tree? In fact, as was explained in chapter 2 Newton spent years proving that R should be the distance between the apple and the center of the earth. Since the height of the apple tree is completely negligible compared to the radius of the earth, R is equal to the radius of the earth. Similarly here, R should be taken to be the radius of the planet.
3. Interestingly, Laplace removed this speculation from later editions of his book.
4. For a modern treatment of black hole, see GNut, Part VII.
5. Furthermore, this often-cited argument actually does not establish the existence of a black hole defined as an object from which nothing can escape. The escape velocity refers to the initial speed with which we attempt to fling something into outer space. In a Newtonian world, we could certainly escape from any massive planet in a rocket with a powerful enough engine.
6. See p. 432 of GNut for a more technical reason, pointed out by D. Marolf, for objecting to this analogy.
Chapter 16. The quantum world and Hawking radiation
1. We already met the Planck number in chapter 2. For a fascinating biography of Max Planck, see B. Brown, Planck.
2. It has been done; the key is of course to repeat this theft for millions of accounts.
3. The use of that particular word is consonant with its use in everyday parlance. But considering that air contains zillions of molecules to begin with, the vacua produced by even the best commercially available pump will still have quite a few molecules in them. A quantum field theorist simply conceptualizes a quantum state with nothing in it.
4. For the interested reader who already knows some quantum mechanics and special relativity, many textbooks stand ready to teach you quantum field theory. In particular, see QFT Nut.
Chapter 17. Gravitons and the nature of gravity
1. Which naturally does not inhibit people from writing about it. Quite to the contrary.
2. In a vague sense, but only in a vague sense, you could say that Newton’s corpuscles never went away.
3. This picture is somewhat oversimplified, but is, however, adequate for our purposes here.
4. This type of problem has given birth to a new area of physics known as “numerical relativity.”
5. For more, see Toy, p. 203 and subsequent pages. For a technical, yet more or less accessible account, see QFTNut, chapter III.2, and GNut, chapter X.8.
6. Notably, non-abelian gauge theories. You can think of the begetting in these theories as being more restrained than in Einstein gravity.
7. Can’t resist a truly sophomoric nod to quantum gravydynamics, especially as I am writing this shortly after Thanksgiving, when I had a discussion with a French friend on the role of gravy in French cuisine, as distinct from sauce.
8. See QFTNut, chapter I.5 and I.7.
9. See Fearful p. 164.
10. Notably, Freeman Dyson of the Institute for Advanced Study in Princeton. For further discussion of the struggle to quantize gravity, see chapter X.8 of GNut.
Chapter 18. Mysterious messages from the dark side
1. I actually saw this at a playground in Paris. A couple of big kids, perhaps aged nine or ten, came over and spun the merry-go-round hard. All the little kids aged five or less went flying off and started crying like crazy. You can imagine the parents dropping their cell phones and rushing over.
2. An early suggestion was by Jacobus Kapteyn, later confirmed by Jan Oort.
3. A cantankerous character, Zwicky also invented the term “spherical bastards” to describe his colleagues who were bastards no matter how he looked at them.
4. As I was working on the final draft of this chapter, the sad news came that Vera Rubin had died at the age of 88. See http://www.latimes.com/local/obituaries/lame-vera-rubin-20161226-story.html.
5. Note that it is not necessary to resolve the motion of individual stars, of which there are zillions.
6. Astronomers have also discovered some extremely diffuse galaxies containing almost no stars, which may be composed entirely of dark matter.
7. For more, see chapters 10 and 11 of Toy.
8. This proposal goes by the acronym MOND for modified Newtonian dynamics.
9. See GNut, p. 495, and chapter VIII.2.
10. This person is hardly mythical, because, as I said in the preface to this book and in the preface to GNut, more than once I have taught Einstein gravity as an advanced undergraduate course.
11. I am aware that a vast literature exists out there, but given the size and nature of this book, I must refrain from further comment.
12. See, for example, QFT Nut or GNut.
13. On some scale that theoretical physicists are very fond of. See QFTNut, p. 449, and GNut, p.746
14. Photons and neutrinos contribute negligibly.
15. For a cartoon depiction of the situation in the late 1980s, see p. 185 of Toy.
Chapter 19. A new window to the cosmos
1. See Bartusiak, Einstein’s Unfinished Symphony.
2. Shimon Kolkowitz, Igor Pikovski, Nicholas Langellier, Mikhail D. Lukin, Ronald L. Walsworth, Jun Ye, “Gravitational Wave Detection with Optical Lattice Atomic Clocks,” arXiv:1606.01859. See this article for references to other proposals as well.
3. Ashes, ashes, we all fall down!
4. I was tempted to invite Darwin to join the panel also. Charles Darwin: There used to be apples that fell down and others that flew up into outer space. Those that flew up did not get to reproduce. So apples evolved to fall down. I am not a geologist and so I don’t know about rocks.
Appendix: What does curved spacetime mean?
1. When I was in high school, I got the erroneous impression that the notion of coordinates originated with Descartes. In fact, by the time of Ptolemy, astronomers in the West certainly had defined latitudes and longitudes. In China, Chang Heng, roughly a contemporary of Ptolemy, was said to have derived, by watching a woman weaving, a system of coordinates to map heaven and earth. The Chinese words for “latitudes” and “longitudes,” “jing” and “wei,” are just the terms for warp and weft in weaving.
2. For those readers who know calculus, “very small” means so small that it actually approaches zero.
3. Actually also known in several other ancient civilizations, including those of Babylonia, China, and Egypt.
4. Of course, the French had insisted that φP should be set to 0, but unfortunately for them, the Brits were more powerful when these things were determined.
5. I am not worrying about the additional technicality that dθ might be negative, while distance is usually understood to be positive. This problem is taken care of, because all the terms appear as squares in the generalized Pythagorean formula given later in this appendix.
6. For the mathematically sophisticated reader, f (θ) = cos θ, with θ defined to be 0 at the equator and π/2 at the north pole.
7. If you are at all into math, you will have fun figuring out the properties of the spaces described by various metrics. For example, consider ds2 = (dx2 + dy2)/y2 with y > 0. The space it describes is called the Poincaré half plane and has some weird properties. See GNut, p.67.
8. Note that dy dx is the same as dx dy and should not be counted separately.
9. That’s the hard part, but still not that hard. It is easily mastered by undergrads. I should know, since I have taught it to undergrads.
10. Seriously. I kid you not: way way easier than learning quantum mechanics. The math involved only goes a bit beyond what is discussed here.
11. See Fearful, QFT Nut, and GNut.
12. Historically, the time coordinate t was written as x4, but later it was realized that it was more sensibly written as x0.
13. There are ten terms altogether but I have not bothered to write them all out; the ones I did not write out are indicated by dots.
14. I say “structurally,” because there are clearly some difference in the details. For one thing, gμV (x) consists of ten functions, instead of the one function g (t, x, y). For another, x is now a compact notation denoting (t, x, y, z), but that is just because we live in 3-dimensional space, while the surface of the lake is 2-dimensional.
15. See GNut, p.6 and p.77.
16. I mention this to encourage you. If you feel that you are comparable to a bright undergrad at a large American state university, then for sure you can learn how to derive the Riemann curvature tensor. That is an experimentally established fact.