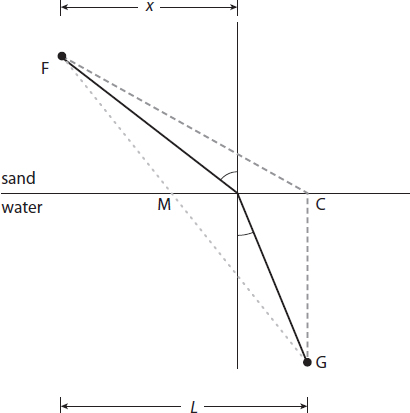
Figure 1. The best possible path for Feynman to follow to get to the drowning girl is along the solid lines from F to G.
From Einstein Gravity in a Nutshell by A. Zee. Copyright ©2013 by Princeton University Press.
Getting the best possible deal
To say what everyone else has already said, but better
In science, one tries to say what no one else has ever said before. In poetry, one tries to say what everyone else has already said, but better. This explains, in essence, why good poetry is as rare as good science.
It would appear that science and poetry are in extreme contrast to each other. However, some theoretical physicists, like poets, do devote their creative energies to saying what has already been said, but in a different way. Their work is often dismissed by more pragmatic physicists for essentially the same reason that poetry sometimes is dismissed. A body of physics is reformulated, but the new formulation does not advance our knowledge one whit. In the vast majority of cases, in poetry as in theoretical physics, the rude dismissal is perfectly justified. The new version is more convoluted and turgid than the old. But once in a while, a poem, compact in structure and eloquent in cadence, manages to illuminate a theme more lucidly than ever before. In physics, too, formulations more in tune with the inner logic of Nature emerge from time to time. Perhaps the best example is the so-called action formulation, developed in the 18th century as an alternative to Newton’s differential formulation of physics.
In Newton’s view of motion, one focuses on the moving particle at every instant in time. A force acting on the particle causes the particle’s velocity to change according to Newton’s law, F = ma. Knowing the particle’s acceleration a allows us to determine the particle’s velocity at the next instant, and then, the particle’s position at an instant after that. By repeating this procedure, one determines the position and velocity of the particle in the future. This, in short, is the standard formulation with which every beginning student of physics has to grapple. The formulation is called “differential,” since one focuses on differences in physical quantities from one instant to the next. The equations describing these changes are known as “equations of motion.”
With the action formulation, in contrast, one takes an overall view of the path followed by the particle and asks for the criterion the particle “used” in choosing that particular path rather than some other path. As we have already seen in chapter 8, and as we will see in chapter 11, this notion will come to the fore when we talk about curved spacetime.
The drowning beauty and the scrawny lifeguard
So, the action formulation. But first, a story about Richard Feynman,1 likely apocryphal but possibly true.
The movie opens on a gorgeous Southern California beach. We zoom in on a lifeguard, noticeably scrawnier than the other lifeguards. However, we soon discover that he is considerably smarter. Egads, it is Dick Feynman, in the days before Baywatch! Perched on his high chair, he has been watching an attractive swimmer with great interest, plotting how he might win the young woman’s affection, all the while solving a field theory problem in his head. Suddenly, he notices that she is splashing about frantically. She is going under! Must be a cramp! An action hero is as an action hero does: Feynman jumps down from his lookout and goes into action.

Figure 1. The best possible path for Feynman to follow to get to the drowning girl is along the solid lines from F to G.
From Einstein Gravity in a Nutshell by A. Zee. Copyright ©2013 by Princeton University Press.
Euclid2 long ago proclaimed that the shortest path between two points is a straight line. Ergo, if you are in a hurry to get from one point to another, you would want to go in a straight line. So, the other lifeguards are already proceeding in a straight line (starting from point F, the lifeguard station, in figure 1, going along the dotted line) toward the girl (at point G). That would be the path of least distance.
But no, Feynman has already calculated the path that would allow him to reach the girl in the least amount of time. Time counts more than space here: least time trumps least distance. Our hero, as any other human for that matter, can run much faster, even on a soft sandy beach, than he can swim. So the rescuer should spend more time running before plunging into the sea. A simple high school level calculation shows Feynman the best path to take (see the solid line in figure 1). Our hero beats the other guys and gets to the eternally grateful young woman (or so he hopes) first!
Figure 2. A light ray goes from the swimmer’s toes T to the observer’s eye E. Light “chooses” the path that enables it to get to its destination in the least amount of time. Since light moves faster in air than in water, the path TAE is chosen rather than the straight line path TBE. The observer’s brain, judging the direction from which the light ray comes, decides that it came from the point T′. Then to the observer, the toe T appears to be at T′. Therefore, the swimmer’s legs look shorter than normal. Surely you have noticed, traveling by car on a hot day, that the highway beneath a distant car often appears to be wet. But by the time you get to that spot, the road surface is in fact bone dry. This common mirage is explained in figure 3. That light is in a hurry also accounts for the observation that the air around a hot object appears to shimmer.
From Fearful Symmetry: The Search for Beauty in Modern Physics by A. Zee. Copyright ©1986 by A. Zee. Princeton University Press.
But you don’t have to calculate to see that there is an optimal path. Clearly, only a cretin would follow the third path (the dashed line) shown in figure 1.
Light in a hurry
We all know that light travels in a straight line, but we also notice that when light enters water from air, it bends. You can easily observe this by sticking a spoon in a glass of water. Indeed, that explains why people standing in swimming pools appear to have comically short legs. See figure 2.
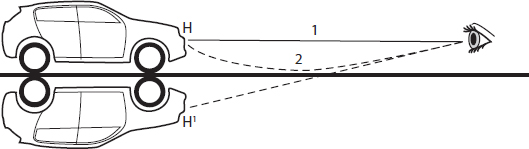
Figure 3. Summer mirage: A light ray leaving the hood H and headed downward encounters a layer of hot air near the road surface and bends upward. It ends up following Path 2 to the observer’s eye. The observer’s brain, judging the direction from which the light ray comes, concludes that it came from H′. Another light ray goes directly from H to the eye, following Path 1. This is repeated for light rays leaving every point on the car, causing a reflection of the car to be seen. The brain — what a marvelous organ — deduces that the road must be wet. By the way, some readers may see that this example shows that light only cares about the local, not the global, minimum time of transit.
From Fearful Symmetry: The Search for Beauty in Modern Physics by A. Zee. Copyright ©1986 by A. Zee. Princeton University Press.
Fermat’s least time principle for light
As our parable showed, the bending of light as it enters water from air can be explained if light moves more slowly in water than in air and if light is always in a hurry to get to where it is going. Light would not be so stupid as not to follow Feynman’s path, like the other lifeguards.
The great mathematician Pierre Fermat (1601 or 1607/ 08?–1665)3, he of the “last theorem,” proposed, in the year of his death, precisely this least time principle for light.
That light bends is of course not just for laughs around swimming pools, but crucial for a pleasant life. To read these very words, you have (or rather your saintly mother has) cleverly positioned in your eyes a blob of watery substance (known to the cognoscenti as a lens), which you squeeze just so using tiny muscles, in order to bend light to your advantage and bring the ambient light bouncing off these words on the printed page into focus. Your mother, as the product of eons of evolution, was oh so clever giving you eyes. As we speak, you are using precisely this phenomenon of light bending to save the light entering your eyes some time (a phenomenon known as refraction) to gain yourself some knowledge about physics and the universe, an activity that evolution applauds: reading this book could conceivably boost your reproductive advantage.
Material particles
After the success of the least time principle for light, physicists naturally wanted to find a similar principle for material particles. Something is minimized, but what?
Matter behaves quite differently from light. For one thing, material particles do not travel at a constant speed. If a particle starts out faster, it gets to its destination faster. So a least time principle certainly does not apply.
It took physicists quite a while to arrive at the correct principle, now known as the action principle. To explain this, I will invoke yet another great name, Humpty Dumpty. When Dumpty falls, he starts out at a leisurely pace, and then goes faster and faster. Not even all the King’s men and horses could make him start out fast and then slow down as he approaches the ground.
A record of where Dumpty is and how fast he is falling at any instant in time is known to theoretical physicists as a history. An infinite number of histories could be contemplated (such as Napoleon defeating Wellington),4 but somehow only one history is actually realized. From everyday observation, Dumpty never starts falling fast and then slows down as if in fear of his imminent crack-up.
Choice of history: The action principle
What principle dictates Dumpty’s choice of history? Indeed, this is the question at the heart of physics. How does anything choose its history? Fermat answered it for light.
At any instant during Dumpty’s fall, he has both kinetic and potential energy. Allow me to remind you that, in Newtonian mechanics, the kinetic energy is simply the energy associated with the movement of the particle, while the potential energy is a kind of “stored” energy that is available for conversion into kinetic energy. For example, an object near the surface of the earth has potential energy because of the earth’s gravitational pull. The higher the object is from the ground, the more potential energy it possesses. The total energy, given by the sum of kinetic energy and potential energy, is conserved; that is, it does not change. As the object falls, its potential energy decreases, while its kinetic energy increases, keeping the sum of the two constant. In other words, potential energy is converted into kinetic energy. When we go downhill skiing, we pay the lift operator to provide us with lots of potential energy, which we then convert into kinetic energy.
As mentioned above, physicists had to struggle to figure out an analog of the least time principle for material particles. It turns out that the correct principle is formulated in terms of a fundamental quantity known as the action. At any instant, subtract the potential energy from the kinetic energy and call the resulting quantity the Lagrangian.5 The action is then the result of adding up the Lagrangians from the start time to the end time. (In our example, these two times would be, respectively, the time Dumpty leaves the security of the wall and the time when he spills his yolk on the ground.)
Readers with a nodding acquaintance of calculus would know that “adding up” is calledy* “integrating.” The resulting sum is called an “integral,” denoted by the symbol, which you could see is a distorted S representing the word “sum.” The action is equal to the integral of the Lagrangian over time.*
The action principle states that a material particle (as distinct from light) “chooses” the path that either maximizes or minimizes the action.6
A technical aside that most readers can simply ignore: Fermat tells us that light minimizes travel time. It turns out that in some circumstances, material particles minimize the action, as we might have guessed, but in other circumstances, they maximize the action. Physicists have coined the word “extremize” to cover both “minimize” and “maximize.” That the action principle is an extremal principle, rather than a simple minimal principle like Fermat’s, remained a mystery until the advent of quantum physics.7
Catch me if you can
The computation of the action is similar to that done by an accountant determining the total profit of a business for any given production strategy. She subtracts the total cost of production from the gross income on a weekly basis and then sums this quantity over the 52 weeks in the fiscal year. The businessperson naturally tries to maximize the total profit by following the most advantageous history.
Just like the businessperson maximizing profit, Dumpty chooses the history that would minimize his action. Since the action is equal to the kinetic energy minus the potential energy summed over the duration of the fall, and since the potential energy increases with the distance from the ground, it clearly pays to spend more time high above the ground, so that a larger potential energy could be subtracted off.
In everyday life, a falling object, especially if it is fragile and valuable, appears to hesitate for a moment or so (almost as if it is saying “Catch me if you can!”) before gathering speed and crashing to the floor. That’s Galileo’s law of acceleration in action, of course. From the action point of view, we can understand what went on as follows. The object, by staying at high altitude for “as long as possible,” maximizes its potential energy and thus lowers the action. But then it has to rush at the end to get to the floor in the allotted time, and hence pays the price of a larger kinetic energy.
Dumpty, therefore, starts slowly and then accelerates. With the help of elementary mathematics, one can show that the best strategy for Dumpty is to accelerate at a constant rate.8
The reader may feel that, in this case, the action formulation actually is more convoluted than the differential formulation, and indeed it is. In the latter formulation, Dumpty’s acceleration is determined immediately by Newton’s law. However, as knowledge of physics progressed beyond Newtonian mechanics, the superiority* of the action formulation became more apparent, as will be indicated below.
Brevity is the soul of wit
For a long time, the action formulation was regarded as nothing more than an elegant alternative.9 Meanwhile, physics continued to be formulated largely in terms of differential equations of motion.10 However, theoretical physicists working on fundamental issues have gradually embraced the action formulation and jilted the differential formulation.11
All physical theories established since Newton may be formulated in terms of an action. The fundamental interactions we know about, the strong, weak, electromagnetic, and gravitational, can all be described by the action principle.*
The action formulation is elegantly concise. For instance, Maxwell’s eight electromagnetic equations are replaced by a single action, specifying a single number for each possible history describing how the electromagnetic field changes.
In Einstein’s theory, ten equations describing how the graviton field changes are summarized in a single action. The point is, while the equations of motion may be complicated and numerous, the action is given by a single expression. Believe me, it is much much easier to find the action, one single expression, than the ten equations of motion, as Einstein was to find out through much pain and suffering. See chapter 12.
Our analogy may be helpful here. The best deal (corresponding to the action) may be easy to state, but the strategy (the equations of motion) needed to nab the best deal might be complicated to describe.
A series of ever better actions
Some books describe the history of physics as a series of revolutions. I don’t like the word “revolution,” as it suggests the overthrow of the previous regime. Einstein did not show that Newton was wrong. Newtonian physics is perfectly correct when applied to objects moving slowly compared to the almost fantastic speed of light.
What actually happens is that the action describing Newtonian physics has to be modified and extended. It is replaced by an Einsteinian action, which is, however, required to reduce to the Newtonian action when describing slowly moving objects.
I prefer to think of the history of physics as a series of ever better, ever sexier actions. Often physicists simply add to an existing action. For example, in the 19th century, Maxwell’s action for electromagnetism had to be added to the Newtonian action. It is the incompatibility between the two terms in the action that led to Einstein’s special relativity, in which the Newtonian action was modified, as was just mentioned.
* In math symbols, S = ∫dtL. Traditionally, the letter S is used for the action, and L for the Lagrangian.
* These days, fundamental physics is largely formulated using the action principle.
* Why this should be so represents a profound mystery. We can certainly conceive of equations of motion that do not follow from extremizing an action.