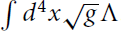. As explained in the appendix, this is equal to the volume of spacetime multiplied by an unknown constant, called the “cosmological constant” and denoted by the capital Greek letter Ʌ. More later.It must be
An extremely tight theory
The fabric of modern theories of physics is tightly woven: deep, underlying symmetries mandate the design and structure of these theories. Physicists revere Einstein’s theory because it is so tight.
Einstein’s theory is required to respect the constraint, almost self-evident in hindsight, that the action must not depend on the coordinates we choose to describe spacetime. (This requirement may be called “general coordinate invariance,” more commonly known as general covariance when referring to the resulting equations of motion.)
To explain what this means, I appeal again to an analogy mentioned in chapter 8. In the Mercator projection, Greenland looks bigger than China, but in some other projection, it does not. But the area of Greenland and of China could not possibly depend on whether we use Mercator or some other projection. Area is an example of what mathematicians call a “geometric invariant,” meaning something which does not depend on the coordinates used.1
Similarly, curvature2 is a geometric invariant.
In short, Einstein gravity is what physicists call a geometrical theory. The action is to be constructed of geometrical invariants.3
The Einstein-Hilbert action displayed in chapter 12 is definitely geometrical. But now, given our discussion about area being a geometrical invariant, a lightbulb clicks on, and you realize that there exists another term that we could add to the action, namely, something like the area of spacetime. And here everyday language fails us. Area is a concept applied to 2-dimensional spaces, and here we are talking about 4-dimensional spacetime. Well, physicists call the relevant quantity the “volume of spacetime,” for lack of a better term. Thus, we could add to the Einstein-Hilbert action the term 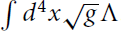. As explained in the appendix, this is equal to the volume of spacetime multiplied by an unknown constant, called the “cosmological constant” and denoted by the capital Greek letter Ʌ. More later.
Einstein and Beethoven.
From Fearful Symmetry: The Search for Beauty in Modern Physics by A. Zee. Copyright ©1986 by A. Zee. Princeton University Press.
The rise of gravity: The paradigm for fundamental physics
Symmetry dictates design. Once the symmetry underlying gravity was discerned, physics was literally forced to Einstein’s theory. Einstein’s theory of gravity carries with it a sense of the inevitable.
The notion that a particular theory is the only one possible was new to physics. For instance, Newton’s pronouncement that the gravitational attraction decreases as the square of the distance between two bodies appears quite arbitrary from a purely logical point of view. Why doesn’t the force decrease as the distance, or as the cube of the distance? Newton would have regarded this question as unanswerable. He presents his law simply as a statement whose consequences accord with the real world. In contrast, once Einstein understood the symmetry underlying gravity, the theory of gravity was fixed. The inverse square law pops out.
When I first encountered Einstein’s theory of gravity, I marveled at how cleverly it is put together. With deeper understanding, I came to understand that it is essentially inevitable.
It has been aptly remarked4 that Einstein’s theory of gravity has the full force of a Beethoven opus. The last movement of Beethoven’s Opus 135 carries the motto “Muss es sein? Es muss sein!” (Must it be? It must be.)
Art in its perfection must be a necessity.