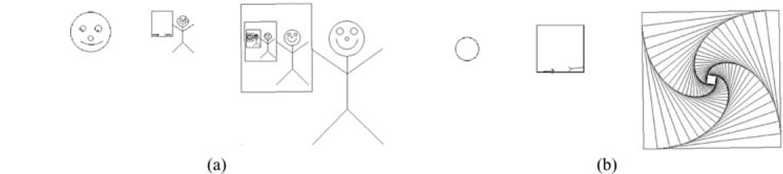
Figure 11.1: (a) Man recursively framed; (b) rotating square.
Recursion can be used to construct very complex and beautiful pictures. We begin by combining the same two fixed images recursively over and over again. This produces fractal-like images whose substructures are identical to the whole. Next we will generate random mazes by using randomness to slightly modify these two images so that the substructures are not identical.
Drawing an Image: An image is specified by a set of lines, circles, and arcs and by two points A and B that are referred to as the handles. Before such an image can be drawn on the screen, its location, size, and orientation on the screen need to be specified. We will do this by specifying two points A and B on the screen. Then a simple program can translate, rotate, scale, and draw the image on the screen in such a way that the two handle points of the image land on these two specified points on the screen.
Specifying a Recursive Image: A recursive image is specified by the following:
1. a base case image
2. a recurse image
3. a set of places within the recurse image to recurse
4. the two points A and B on the screen at which the recursive image should be drawn.
5. an integer n.
The Base Case: If n = 1, then the base case image is drawn.
Recursing: If n > 1, then the recursive image is drawn on the screen at the location specified. Included in the recursive image are a number of places to recurse. These are each depicted by an arrow, —> >—. When the recursive image is translated, rotated, scaled, and drawn on the screen, these arrows are located somewhere on the screen. The arrows themselves are not drawn. Instead, the same picture is drawn recursively at these locations, but with the value n − 1.
Examples:
Man Recursively Framed: See Figure 11.1.a. The base case for this construction consists of a happy face. When n = 1, this face is drawn. The recursive image consists of a man holding a frame. There is one place to recurse within the frame. Hence, when n = 2, this man is drawn with the n = 1 happy face inside it. For n = 3, the man is holding a frame containing the n = 2 image of a man holding a framed n = 1 happy face. The recursive image provided is with n = 5. It consists of a man holding a picture of a man holding a picture of a man holding a picture of . . . a face. In general, the recursive image for n contains R(n) = R(n − 1) + 1 = n − 1 men and B(n) = B(n − 1) = 1 happy faces.
Rotating Square: See Figure 11.1.b. This image is constructed similarly to the previous one. Here, however, the n = 1 base case consists of a circle. The recursive image consists of a single square with the n − 1 image shrunk and rotated within it. The squares continue to spiral inward until the base case is reached.
Birthday Cake: See Figure 11.2. The birthday cake recursive image is different in that it recurses in two places. The n = 1 base case consists of a single circle. The recursive image consists of a single line with two smaller copies of the n − 1 image drawn above it. In general, the recursive image for n contains R(n) = 2R(n − 1) + 1 = 2n−1 − 1 lines from the recursive image and B(n) = 2B(n − 1) = 2n−1 circles from the base case image.
Figure 11.1: (a) Man recursively framed; (b) rotating square.
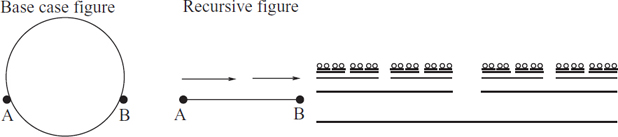
Figure 11.2: Birthday cake.
Leaf: See Figure 11.3. A leaf consists of a single stem plus eight subleaves along it. Each subleaf is an n − 1 leaf. The base case image is empty, and the recursive image consists of the stem plus the eight places to recurse. Hence, the n = 1 image is blank. The n = 2 image consists of a lone stem. The n = 3 image is a stem with eight stems for leaves, and so on. In general, the recursive image for n contains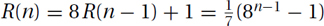 
stems from the recursive image.
Fractal: See Figure 11.4. This recursive image is a classic. The base case is a single line. The recursive image is empty except for four places to recurse. Hence, n = 1 consists of the line, n = 2 consists of four lines, forming a line with an equilateral triangle jutting out of it. As n becomes large, the image becomes a snowflake. It is a fractal in that every piece of it looks like a copy of the whole.
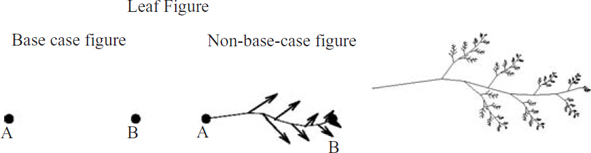
Figure 11.3: Leaf.
The classic way to construct it is slightly different than done here. In the classical method, we are allowed the following operation. Given a line, divide it into three equal parts. Replace the middle part with the two equal-length lines forming an equilateral triangle. Starting with a single line, construct the fractal by repeatedly applying this operation to all the lines that appear.
In general, the recursive image for n contains B(n) = 4B(n − 1) = 4n−1 base case lines. The length of each of these lines is 
. The total length of all these lines is 
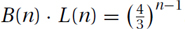. As n approaches infinity, the fractal becomes a curve of infinite length.
Figure 11.4: Fractal.
EXERCISE 11.1.1 (See solution in Part Five.) See Figure 11.5.a. Construct the recursive image that arises from the base case and recursive image for some large n. Describe what is happening.
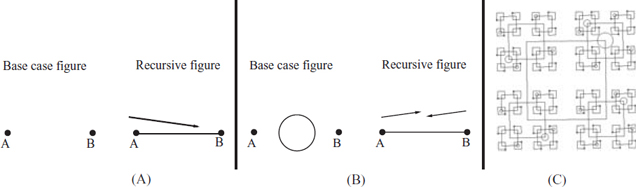
Figure 11.5: Three more examples.
EXERCISE 11.1.2 (See solution in Part Five.) See Figure 11.5.b. Construct the recursive image that arises from the base case and recursive image for some large n. Note that one of the places to recurse is pointing opposite the other. To line the image up with these arrows, the image must be rotated 180°. The image cannot be flipped.
EXERCISE 11.1.3 See Figure 11.5.c. This construction looks simple enough. The difficulty is keeping track of at which corners the circle is. Construct the base case and the recursive image from which the given recursive image arises. Describe what is happening.
We will use similar methods to generate a random maze. The maze M will be represented by an n × m two-dimensional array with entries from {brick, floor, cheese}. Walls consist of lines of bricks. A mouse will be able to move along floor squares in any of the eight directions. The maze generated will not contain corridors as such, but only many small rectangular rooms. Each room will either have one door in one corner of the room or two doors in opposite corners. The cheese will be placed in a room that is chosen randomly from among the rooms that are far enough from the start location.
Precondition: The routine AddWalls is passed a matrix representing the maze as constructed so far and the coordinates of a room within it. The room will have a surrounding wall except for one door in one of its corners. The room will be empty of walls. The routine is also passed a flag indicating whether or not cheese should be added somewhere in the room.
Postcondition: The output is the same maze with a randomly chosen submaze added within the indicated room and cheese added as appropriate.
Initial Conditions: To meet the preconditions of AddWalls, the main routine first constructs the four outer walls with the top right corner square left as a floor tile to act as a door into the maze and as the start square for the mouse. Calling AddWalls on this single room completes the maze.
Subinstances: If the indicated room has height and width of at least 3, then the routine AddWalls will choose a single location (i, j) uniformly at random from all those in the room that are not right next to one of its outer walls. (The (i, j) chosen by the top stack frame in Figure 11.6 is indicated.) A wall is added within the room all the way across row i and all the way down column j, subdividing the room into four smaller rooms. To act as a door connecting these four rooms, the square at location (i, j) remains a floor tile. See Figure 11.7. Then four friends are asked to fill a maze into each of these four smaller rooms. If our room is to have cheese, then one of the three rooms not containing the door to our room is selected to contain the cheese.
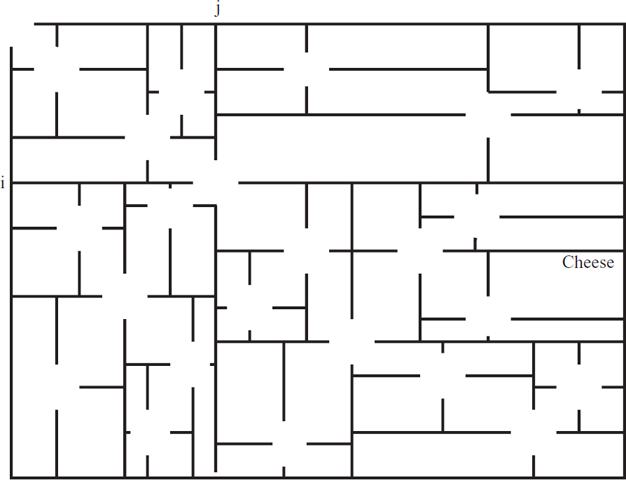
Figure 11.6: A maze containing cheese.
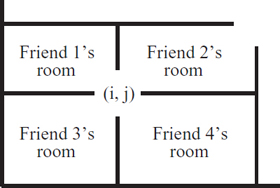
Figure 11.7: Partitioning a room of the maze.
Running Time: The time required to construct an n × n maze is Θ(n2). This can be seen two ways. For the easy way, note that a brick is added at most once to any entry of the matrix and that there are Θ(n2) entries. The hard way solves the recurrence relation T(n) = 4T(n/2) + Θ(n) = Θ(n2).
Searching the Maze: One way of representing a maze is by a graph. Chapter 14 presents a number of iterative algorithms for searching a graph. Section 14.5 presents the recursive version of the depth-first search algorithm. All of these could be used by a mouse to find the cheese.
EXERCISE 11.2.1 Write the code for generating a maze of rooms.
EXERCISE 11.2.2 Tiling: The precondition to the problem is that you are given three integers 
n, i, j
, where i and j are in the range 1 to 2n. You have a 2n by 2n square board of squares. You have a sufficient number of tiles each with the shape 
. Your goal is to place nonoverlapping tiles on the board to cover each of the 2n × 2n tiles except for the single square at location i, j. Give a recursive algorithm for this problem in which you place one tile yourself and then have four friends help you. What is your base case?