Iterative algorithms start at the beginning and take one step at a time towards the final destination. Another technique used in many algorithms is to slice the given task into a number of disjoint pieces, solve each of these separately, and then combine these answers into an answer for the original task. This is the divide-and-conquer method. When the subtasks are different, it leads to different subroutines. When they are instances of the original problem, it leads to recursive algorithms.
People often find recursive algorithms very difficult. To understand them, it is important to have a good solid understanding of the theory and techniques presented in this chapter.
There are a number of ways to view a recursive algorithm. Though the resulting algorithm is the same, having the different paradigms at your disposal can be helpful.
Code: Code is useful for implementing an algorithm on a computer. It is precise and succinct. However, code is prone to bugs, is language-dependent, and often lacks higher levels of intuition.
Stack of Stack Frames: Recursive algorithms are executed using a stack of stack frames. See Section 8.6. Though this should be understood, tracing out such an execution is painful.
Tree of Stack Frames: This is a useful way of viewing the entire computation at once. It is particularly useful when computing the running time of the algorithm. However, the structure of the computation tree may be very complex and difficult to understand all at once.
Friends, on Strong Induction: The easiest method is to focus on one step at a time. Suppose that someone gives you an instance of the computational problem. You solve it as follows. If it is sufficiently small, solve it yourself. Otherwise, you have a number of friends to help you. You construct for each friend an instance of the same computational problem that is smaller then your own. We refer to these as subinstances. Your friends magically provide you with the solutions to these. You then combine these subsolutions into a solution for your original instance.
I refer to this as the friends level of abstraction. If you prefer, you can call it the strong induction level of abstraction and use the word “recursion" instead of “friend.” Either way, the key is that you concern yourself only about your task. Do not worry about how your friends solve the subinstances that you assigned them. Similarly, do not worry about whoever gave you your instance and what he does with your answer. Leave these things up to him. Trust your friends.
Use It: I strongly recommend using this method when designing, understanding, and describing a recursive algorithm.
Faith in the Method: As with the loop invariant method, you do not want to be rethinking the issue of whether or not you should steal every time you walk into a store. It is better to have some general principles with which to work. You do not want to be rethinking the issue of whether or not you believe in recursion every time you consider a hard algorithm. Understanding the algorithm itself will be hard enough. While reading this chapter you should once and for all come to understand and believe how the following steps are sufficient to describing a recursive algorithm. Doing this can be difficult. It requires a whole new way of looking at algorithms. However, at least for now, adopt this as something that you believe in.
Circular Argument? Recursion involves designing an algorithm by using it as if it already exists. At first this looks paradoxical. Suppose, for example, the key to the house that you want to get into is in that same house. If you could get in, you could get the key. Then you could open the door, so that you could get in. This is a circular argument. It is not a legal recursive program because the subinstance is not smaller.
One Problem and a Row of Instances: Consider a row of houses. Each house is bigger than the next. Your task is to get into the biggest one. You are locked out of all the houses. The key to each house is locked in the house of the next smaller size. The recursive problem consists in getting into any specified house. Each house in the row is a separate instance of this problem.
The Algorithm: The smallest house is small enough that one can use brute force to get in. For example, one could simply lift off the roof. Once in this house, we can get the key to the next house, which is then easily opened. Within this house, we can get the key to the house after that, and so on. Eventually, we are in the largest house as required.
Focus on One Step: Though this algorithm is quite simple to understand, more complex algorithms are harder to understand all at once. Instead we focus on one step at a time. Here, one step consists in opening house i. We ask a friend to open house i − 1, out of which we take the key with which we open house i. We do not worry about how to open house i − 1.
Working Forward vs. Backward: An iterative algorithm works forward. It knows about house i − 1. It uses a loop invariant to show that this house has been opened. It searches this house and learns that the key within it is that for house i. Because of this, it decides that house i would be a good one to go to next.
A recursion algorithm works backward. It knows about house i. It wants to get it open. It determines that the key for house i is contained in house i − 1. Hence, opening house i − 1 is a subtask that needs to be accomplished.
There are two advantages of recursive algorithms over iterative ones. The first is that sometimes it is easier to work backward than forward. The second is that a recursive algorithm is allowed to have more than one subtask to be solved. This forms a tree of houses to open instead of a row of houses.
Do Not Trace: When designing a recursive algorithm it is tempting to trace out the entire computation. “I must open house n, so I must open house n − 1,.… The smallest house I rip the roof off. I get the key for house 1 and open it. I get the key for house 2 and open it. . . . I get the key for house n and open it.” Such an explanation is complicated and unnecessary.
Solving Only Your Instance: An important quality of any leader is knowing how to delegate. Your job is to open house i. Delegate to a friend the task of opening house i − 1. Trust him, and leave the responsibility to him.
The following are the steps to follow when developing a recursive algorithm within the friends level of abstraction.
Specifications: Carefully write the specifications for the problem.
Preconditions: The preconditions state any assumptions that must be true about the input instance for the algorithm to operate correctly.
Postconditions: The postconditions are statements about the output that must be true when the algorithm returns.
This step is even more important for recursive algorithms than for other algorithms, because there must be tight agreement between what is expected from you in terms of pre- and postconditions and what is expected from your friends.
Size: Devise a measure of the size of each instance. This measure can be anything you like and corresponds to the measure of progress within the loop invariant level of abstraction.
General Input: Consider a large and general instance of the problem.
Magic: Assume that by magic a friend is able to provide the solution to any instance of your problem as long as the instance is strictly smaller than the current instance (according to your measure of size). More specifically, if the instance that you give the friend meets the stated preconditions, then her solution will meet the stated postconditions. Do not, however, expect your friend to accomplish more than this. (In reality, the friend is simply a mirror image of yourself.)
Subinstances: From the original instance, construct one or more subinstances, which are smaller instances of the same problem. Be sure that the preconditions are met for these smaller instances. Do not refer to these as “subproblems.” The problem does not change, just the input instance to the problem.
Subsolutions: Ask your friend to (recursively) provide solutions for each of these subinstances. We refer to these as subsolutions even though it is not the solution, but the instance, that is smaller.
Solution: Combine these subsolutions into a solution for the original instance.
Generalizing the Problem: Sometimes a subinstance you would like your friend to solve is not a legal instance according to the preconditions. In such a case, start over, redefining the preconditions in order to allow such instances. Note, however, that now you too must be able to handle these extra instances. Similarly, the solution provided by your friend may not provide enough information about the subinstance for you to be able to solve the original problem. In such a case, start over, redefining the postcondition by increasing the amount of information that your friend provides. Again, you must now also provide this extra information. See Section 10.3.
Natural Pre- and Postconditions: On the other hand, have the more generalized problem still be a natural problem. Do not attempt to pass it lots of extra information about your instance. For the very first call (or stack frame) of the computation to pass a value through the chain of recursive calls is a type of globalvariable “cheat.” It also makes it look like you are micromanaging your friends. Similarly, a stack frame (friend) should not know what level of recursion it is on.
Both the Pre- and the Postconditions Act as Loop Invariants: The loop invariant in an iterative algorithm states what is maintained as the control gets passed from iteration to iteration. It provides a picture of what you want to be true in the middle of this computation. With recursion, however, there are two directions. The precondition states what you want to be true halfway down the recursion tree. The postcondition states what you want to be true halfway back up the recursion tree.
Minimizing the Number of Cases: You must ensure that the algorithm that you develop works for every valid input instance. To achieve this, the algorithm will often require many separate pieces of code to handle inputs of different types. Ideally, the algorithm developed has as few such cases as possible. One way to help you minimize the number of cases needed is as follows. Initially, consider an instance that is as large and as general as possible. If there are a number of different types of instances, choose one whose type is as general as possible. Design an algorithm that works for this instance. Afterwards, if there is another type of instance that you have not yet considered, consider a general instance of this type. Before designing a separate algorithm for this new instance, try executing your existing algorithm on it. You may be surprised to find that it works. If, on the other hand, it fails to work for this instance, then repeat the above steps to develop a separate algorithm for this case. You may need to repeat this process a number of times.
For example, suppose that the input consists of a binary tree. You may well find that the algorithm designed for a tree with a full left child and a full right child also works for a tree with a missing child and even for a child consisting of only a single node. The only remaining case maybe the empty tree.
Base Cases: When all the remaining unsolved instances are sufficiently small, solve them in a brute force way.
Running Time: Use a recurrence relation or a tree of stack frames to estimate the running time.
A Link to the Techniques for Iterative Algorithms: The techniques that often arise in iterative algorithms also arise in recursive algorithms, though sometimes in a slightly different form.
More of the Input: When the input includes n objects, this technique for iterative algorithms extends (for i = 1, . . . , n − 1) a solution for the first i − 1 objects into a solution for the first i. This same technique also can be used for recursive algorithms. Your friend provides you a solution for the first n − 1 objects in your instance, and then you extend this to a solution to your entire instance. This iterative algorithm and this recursive algorithm would be two implementations of the same algorithm. The recursion is more interesting when one friend can provide you a solution for the first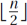 
objects in your instance, another friend can provide a solution for the next 
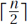objects, and you combine them into a solution for the whole.
More of the Output: This technique for iterative algorithms builds the output one piece at a time. Again a recursive algorithm could have a friend build all but the last piece and have you add the last piece. However, it is better to have one friend build the first half of the output, another the second half, and you combine them somehow.
Narrowing the Search Space: Some iterative algorithms repeatedly narrow the search space in which to look for something. Instead, a recursive algorithm may split the search space in half and have a friend search each half.
Case Analysis: Instead of trying each of the cases oneself, one could give one case to each friend.
Work Done: Work does not accumulate in recursive algorithms as it does in iterative algorithms. We get each friend to do some work, and then we do some work, ourselves to combine these solution.
The towers of Hanoi is a classic puzzle for which the only possible way of solving it is to think recursively.
Specification: The puzzle consists of three poles and a stack of N disks of different sizes.
Precondition: All the disks are on the first of the three poles.
Postcondition: The goal is to move the stack over to the last pole. See the first and the last parts of Figure 8.1.
Figure 8.1: The towers of Hanoi problem.
You are only allowed to take one disk from the top of the stack on one pole and place it on the top of the stack on another pole. Another rule is that no disk can be placed on top of a smaller disk.
Lost with First Step: The first step must be to move the smallest disk. But it is by no means clear whether to move it to the middle or to the last pole.
Divide: Jump into the middle of the computation. One thing that is clear is that at some point, you must move the biggest disk from the first pole to the last. In order to do this, there can be no other disks on either the first or the last pole. Hence, all the other disks need to be stacked on the middle pole. See the second and the third parts of Figure 8.1. This point in the computation splits the problem into two subproblems that must be solved. The first is how to move all the disks except the largest from the first pole to the middle. See the first and second parts of Figure 8.1. The second is how to move these same disks from the middle pole to the last. See the third and fourth parts of Figure 8.1.
Conquer: Together these steps solve the entire problem. Starting with all disks on the first pole, somehow move all but the largest to the second pole. Then, in one step, move the largest from the first to the third pole. Finally, somehow move all but the largest from the second to the third pole.
Magic: In order to make a clear separation between task of solving the entire problem and that of solving each of the subproblems, I like to say that we delegate to one friend the task of solving one of the subproblems and delegate to another friend the other.
More General Specification: The subproblem of moving all but the largest disk from the first to the middle pole is very similar to original towers of Hanoi problem. However, it is an instance of a slightly more general problem, because not all of the disks are moved. To include this as an instance of our problem, we generalize the problem as follows.
Precondition: The input specifies the number n of disks to be moved and the roles of the three poles. These three roles for poles are polesource, poledestination, and polespare. The precondition requires that the smallest n disks be currently on polesource. It does not care where the larger disks are.
Postcondition: The goal is to move these smallest n disks to poledestination. Pole polespare is available to be used temporarily. The larger disks are not moved.
Subinstance: Our task is to move all the disks from the first to the last pole. This is specified by giving n = N, polesource = first, poledestination = last, and polespare = middle. We will get one friend to move all but the largest disk from the first to the middle pole. This is specified by giving n = N − 1, polesource = first, poledestination = middle, and polespare = last. On our own, we move the largest disk from the first to the last disk. Finally, we will get another friend to move all but the largest disk from the middle to the last pole. This is specified by giving n = N − 1, polesource = middle, poledestination = last, and polespare = first.
Code:
Running Time: Let T(n) be the time to move n disks. Clearly, T(1) = 1 and T(n) = 2 · T(n − 1) + 1. Solving this gives T(n) = 2n − 1.
Writing a recursive algorithm is surprisingly hard when you are first starting out and surprisingly easy when you get it. This section contains a list of things to think about to make sure that you do not make any of the common mistakes.
0) The Code Structure: The code does not need to be much more complex than the following.
1) Specifications: You must clearly define what the algorithm is supposed to do.
2) Variables: A great deal is understood about an algorithm by understanding its variables. As in any algorithm, you want variables to be well documented and to have meaningful names. It is also important to carefully check that you give variables values of the correct type, e.g., k is an integer, G is a graph, and so on. Moreover, with recursive programs there are variables that play specific roles and should be used in specific ways. This can be a source of many confusions and mistakes. Hence, I outline these carefully here.
2.1.) Your Input: Your mission, if you are to accept it, is received through your inputs. The first line of your code, algorithm Alg(a, b, c), specifies both the name Alg of the routine and the names of its inputs. Here 
a, b, c
is the input instance that you need to find a solution for. I sometimes use Alg(a, b, c) because it emphasizes the viewpoint that we are receiving one instance, even if that instance might be composed of a tuple of things. Your preconditions must clearly specify what each of these components a, b, and c are and any restrictions on their values. You must be able to handle any instance that meets these conditions.
2.2.) Your Output: You must return a solution x, y, z to your instance a, b, c through a return statement return(x, y, z). Your postconditions must clearly specify what each of the components x, y, and z of your solution are and their required relation to the input instance a, b, c.
2.2.1.) Every Path: Given any instance meeting the precondition, you must return a correct solution. Hence, if your code has if or loop statements, then every path through the code must end with a return statement.
2.2.2.) Type of Output: Each return statement must return a solution x, y, z of the right type. The one partial exception to this is: if the postcondition leaves open the possibility that a solution does not exist, then some paths through the code may end with the statement return("no solution exists").
2.3.) Your Friend’s Input: To get help from friends, you must create a subinstance asub, bsub, csub for each friend. You pass this to a friend by recursing with Alg(asub, bsub, csub). To be able to give a subinstance to a friend, it needs to meet the preconditions of your problem. Do not recurse with Alg(asub, bsub).
2.4.) Your Friend’s Output: You can trust that each friend will give you a correct solution xsub, ysub, zsub to the subinstance asub, bsub, csub that you give her. Be sure to save her result in variables of the correct type, using the code xsub, ysub, zsub = Alg(asub, bsub, csub). In contrast, the code Alg(asub, bsub, csub) as a line by itself is insulting to your friend, because you got her to do all of this work and then you dropped her result in the garbage.
2.5.) Rarely Need New Inputs or Outputs: I did speak of the need to generalize the problem by adding new inputs and/or outputs. This, however, is needed far less often than people think. Try hard to solve the problem using the friend analogy without extra variables. Only add them if absolutely necessary. If you do add extra inputs or outputs, clearly specify in the pre- and postconditions what they are for. Do not have inputs or outputs that are not explained.
2.6.) No Global Variables or Global Effects: When you recurse with the line xsub, ysub, zsub = Alg(asub, bsub, csub), the only thing that should happen is that your friend passes back a correct solution xsub, ysub, zsub to the subinstance asub, bsub, csub that you gave her. If the code has a local variable n, then your variable n is completely different than your friend’s. (They are stored in different stack frames. See Section 8.6.) If you set your variable n to 5 and then recurse, your friend’s variable n will not have this value. If you want him to have a 5, you must pass it in as part of his subinstance asub, 5, csub. Similarly, if your friend sets his variable n to 6 and then returns, your variable n will not have this value, but will still have the value 5. If you want him to give you a 6, he must return it as part of his solution xsub, 6, zsub.
I often suspect that people intend for a parameter in their algorithm’s arguments to both pass a value in and pass a value out. Though I know there are programming languages that allow this, I strongly recommend not doing this. The code xsub, ysub, zsub = Alg(asub, bsub, csub) does not change the values of asub, bsub, or csub.
I have seen lots of code that loops n times recursing Alg(asub, bsub, csub) on the exact same subinstance asub, bsub, csub. One definition of insanity is repeating the same thing over and over and expecting to get a different result. Your friend on the same subinstance will give you the same solution. Do not waste her time.
It is tempting to use a global variable that everyone has access too. However, this is very bad form, mainly because it is very prone to errors and side effects that you did not expect.
Similarly, you can have no global returns. For example, suppose your friend’s friend’s friend’s friend finds something that you are looking for. It needs to be passed back friend to friend, because things returned by your friends do not get returned to your boss unless you do the returning.
2.7.) Few Local Variables: An iterative algorithm consists of a big loop with a set of local variables holding the current state. Each iteration these variables get updated. Because thinking iteratively comes more naturally to people, they want to do this with recursive algorithms. Don’t. Generally there is no need for a loop in a recursive algorithm unless you require the immediate help of many friends and you loop through them, creating subinstances for each and considering their subsolutions. In fact, despite the name “variable,” rarely is there a need to change the value of a variable once initially set. For example, the variables a, b, c storing your instance are sacred. This is the instance you must solve. Why ever change it? You must construct a solution x, y, z. Create it and return it. Why ever change it? Similarly for what you give asub, bsub, csub and receive xsub, ysub, zsub from each friend. Other local variables are rarely needed. If you do need them, be sure to document what they are for.
3) Tasks to Complete: Your mission, given an arbitrary instance a, b, c meeting the preconditions, is to construct and return a solution x, y, z that meets the post-condition. The following are the only steps that you should be following towards this goal.
3.1.) Accept Your Mission: Imagine that you have an a, b, c meeting the preconditions. Know the range of things that your instance might be. For example, if the input instance is a binary tree, make sure that your program works for a general tree with big left and right subtrees, a tree with big left and empty right, a tree with empty left and big right, and the empty tree. Also know what is require of your output.
3.2.) Construct Subinstances: For each friend, construct from your instance a, b, c a subinstance asub, bsub, csub to give this friend. Sometimes this requires a block of code. Sometimes it happens right in place. For example, if your instance is a1, a2, . . . , an, b, c, you might construct the subinstance a1, a2, . . . , an−1, b − 5, leftSub(c) for your friend by stripping the last object off the tuple a, subtracting 5 from the integer b, and taking the left subtree of the tree c. This subinstance can be constructed and passed to your friend in the one line
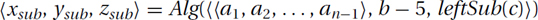
3.2.1.) Valid Subinstance: Be sure that the subinstance asub, bsub, csub that you give your friend meets the preconditions.
3.2.2.) Smaller Subinstance: Be sure that the subinstance asub, bsub, csub that you give your friend is smaller in some way than your own subinstance a, b, c.
3.3.) Trust Your Friend: Focus on only your mission. Trust your friend to give you a correct solution xsub, ysub, zsub to the instance asub, bsub, csub that you give her. Do not worry about how she gets her answer. Do not trace through the entire computation. Do not talk of your friends' friends' friends. I cannot emphasize this enough. Time and time again, I see students not trusting. It causes them no end of trouble until they finally see the light and let go.
3.4.) Construct Your Solution: Using the solutions xsub, ysub, zsub provided by your friends for your subinstances asub, bsub, csub, your next task is to construct a solution x, y, z for your subinstance a, b, c. This generally requires a block of code, but sometimes it can be contained in a single line. For example, if the only output is a single integer x, then the one line of code return(Alg(asub1, bsub1, csub1) + Alg(asub2, bsub2, csub2)) combines the friends' solutions xsub1 and xsub2 to give your solution x = xsub1 + xsub2 and returns it.
3.5.) Base Cases: Consider which instance get solved by your program. For those that don’t, either add more cases to solve them recursively or add base cases to solve them in a brute force way. If your input instance is sufficiently small according to your definition of size then you must solve it yourself as a base case.
This is all that you need to do. Do not do more.
EXERCISE 8.5.1 You are now the professor. Which of the above steps to develop a recursive algorithm did the students fail to do correctly in the following code? How? How would you fix it? See Exercise 10.3.1 for corrrect code for this problem.
EXERCISE 8.5.2 (See solution in Part Five.) In the friends level of abstracting recursion, you can give your friend any legal instance that is smaller than yours according to some measure as long as you solve in your own any instance that is sufficiently small. For which of these algorithms has this been done? If so, what is your measure of the size of the instance? On input instance n, m, either bound the depth to which the algorithm recurses as a function of n and m, or prove that there is at least one path down the recursion tree that is infinite.
Tree of Stack Frames: Tracing out the entire computation of a recursive algorithm, one line of code at a time, can get incredibly complex. This is why the friends level of abstraction, which considers one stack frame at a time, is the best way to understand, explain, and design a recursive algorithm. However, it is also useful to have some picture of the entire computation. For this, the tree-of-stack-frames level of abstraction is best.
The key thing to understand is the difference between a particular routine and a particular execution of a routine on a particular input instance. A single routine can at one moment in time have many executions going on. Each such execution is referred to as a stack frame. You can think of each as the task given to a separate friend. Even though each friend may be executing exactly the same routine, each execution may currently be on a different line of code and have different values for the local variables.
If each routine makes a number of subroutine calls (recursive or not), then the stack frames that get executed form a tree. In the example in Figure 8.2, instance A is called first. It executes for a while and at some point recursively calls B. When B returns, A then executes for a while longer before calling H. When H returns, A executes for a while before completing. We have skipped over the details of the execution of B. Let’s go back to when instance A calls B. Then B calls C, which calls D. D completes; then C calls E. After E, C completes. Then B calls F, which calls G. Then G completes, F completes, B completes, and A goes on to call H. It does get complicated.
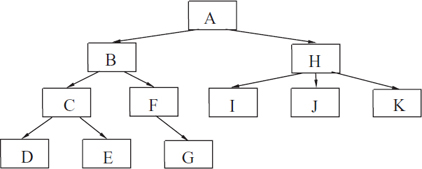
Figure 8.2: Tree of stack frames.
Stack of Stack Frames: The algorithm is actually implemented on a computer by a stack of stack frames. What is stored in the computer memory at any given point in time is only a single path down the tree. The tree represents what occurs throughout time. In Figure 8.2, when instance G is active, A, B, F, and G are in the stack. C, D, and E have been removed from memory as these have completed. H, I, J, and K have not been started yet. Although we speak of many separate stack frames executing on the computer, the computer is not a parallel machine. Only the top stack frame G is actively being executed. The other instances are on hold, waiting for the return of a subroutine call that it made.
Memory: Here is how memory is managed for the simultaneous execution of many instances of the same routine. The routine itself is described only once, by a block of code that appears in static memory. This code declares a set of variables. On the other hand, each instance of this routine that is currently being executed may be storing different values in these variables and hence needs to have its own separate copy of these variables. The memory requirements of each of these instances are stored in a separate stack frame. These frames are stacked on top of each other within stack memory.
Using a Stack Frame: Recall that a stack is a data structure in which either a new element is pushed onto the top or the last element to have been added is popped off (Section 3.1). Let us denote the top stack frame by A. When the execution of A makes a subroutine call to a routine with some input values, a stack frame is created for this new instance. This frame denoted B is pushed onto the stack after that for A. In addition to a separate copy of the local variables for the routine, it contains a pointer to the next line of code that A must execute when B returns. When B returns, its stack frame is popped, and A continues to execute at the line of code that had been indicated within B. When A completes, it too is popped off the stack.
Silly Example: This example demonstrates how difficult it is to trace out the full stack-frame tree, yet how easy it is to determine the output using the friends (strong-induction) method:
EXERCISE 8.6.1 Attempt to trace out the tree of stack frames for the silly example Fun(5).
EXERCISE 8.6.2 (See solution in Part Five.) Now try the following simpler approach. What is the output of Fun(1)? What is the output of Fun(2)? Trust the answers to all previous questions; do not recalculate them. (Assume a trusted friend gave you the answer.) Now, what is the output of Fun(3)? Repeat this approach for n = 4, 5, and 6.
Whether you give your subinstances to friends or you recurse on them, this level of abstraction considers only the algorithm for the top stack frame. We must now prove that this suffices to produce an algorithm that successfully solves the problem for every input instance. When proving this, it is tempting to talk about stack frames. This stack frame calls this one, which calls that one, until you hit the base case. Then the solutions bubble back up to the surface. These proofs tend to make little sense. Instead, we use strong induction to prove formally that the friends level of abstraction works.
Strong Induction: Strong induction is similar to induction, except that instead of assuming only S(n − 1) to prove S(n), you must assume all of S(0), S(1), S(2), . . . , S(n − 1).
A Statement for Each n: For each value of n ≥ 0, let S(n) represent a Boolean statement. For some values of n this statement may be true, and for others it may be false.
Goal: Our goal is to prove that it is true for every value of n, namely that ∀n ≥ 0, S(n).
Proof Outline: Proof by strong induction on n.
Induction Hypothesis: For each n ≥ 0, let S(n) be the statement that . . . . (It is important to state this clearly.)
Base Case: Prove that the statement S(0) is true.
Induction Step: For each n ≥ 0, prove S(0), S(1), S(2), . . . , S(n − 1) ⇒ S(n).
Conclusion: By way of induction, we can conclude that ∀n ≥ 0, S(n).
See Exercises 8.7.1 and 8.7.2.
Proving the Recursive Algorithm Works:
Induction Hypothesis: For each n ≥ 0, let S(n) be the statement “The recursive algorithm works for every instance of size n."
Goal: Our goal is to prove that ∀n ≥ 0, S(n), i.e. that the recursive algorithm works for every instance.
Proof Outline: The proof is by strong induction on n.
Base Case: Proving S(0) involves showing that the algorithm works for the base cases of size n = 0.
Induction Step: The statement S(0), S(1), S(2), . . . , S(n − 1) ⇒ S(n) is proved as follows. First assume that the algorithm works for every instance of size strictly smaller than n, and then prove that it works for every instance of size n. This mirrors exactly what we do on the friends level of abstraction. To prove that the algorithm works for every instance of size n, consider an arbitrary instance of size n. The algorithm constructs subinstances that are strictly smaller. By our induction hypothesis we know that our algorithm works for these. Hence, the recursive calls return the correct solutions. On the friends level of abstraction, we proved that the algorithm constructs the correct solutions to our instance from the correct solutions to the subinstances. Hence, the algorithm works for this arbitrary instance of size n. The S(n) follows.
Conclusion: By way of strong induction, we can conclude that ∀n ≥ 0, S(n), i.e., the recursive algorithm works for every instance.
EXERCISE 8.7.1 Give the process of strong induction as we did for regular induction.
EXERCISE 8.7.2 (See solution in Part Five.) As a formal statement, the base case can be eliminated in strong induction because it is included in the formal induction step. How is this? (In practice, the base cases are still proved separately.)