2 Steps
More than a hundred years ago, artists such as Georges Seurat and Paul Signac began to experiment with using small dots of pure color to create an image. The descendants of this technique—television and digital displays of all kinds—are now so common that it’s hard to remember that there was a time when people never looked at visual representations made of little dots.
In modern technical terminology, we refer to those dots as pixels (a contraction of “picture element”). Now that such fields of pixels are used widely for all sorts of purposes, many people have experienced the related phenomenon of pixelation, when some limitation of the display system makes the pixels weirdly big and blocky, rendering some or all of the image “chunky.” Those moments reveal the underlying representation of the image as a collection of discrete pieces rather than the continuous smooth image we might prefer to see. An interesting philosophical question is this: what if the world itself were actually made of very small discrete pieces? How would our experiences be different, and would we be able to tell?
The term digital is commonly heard as a description of various kinds of computer or media systems with these “stepped” or “chunky” characteristics. The meaning of “digital” is an important foundation for our upcoming explorations of computation. We can rephrase our philosophical question about a world made of small pieces by asking, What does it mean to be digital? Whatever “digital” is, it underpins all the systems we examine later in this book. Its properties will accordingly constrain what those systems can be.
Our fingers are also called our digits, and they give their name to whatever is called digital. Counting on fingers is probably everyone’s first experience of a digital system. We teach children to count integers “1, 2, 3…” holding up one, then two, then three fingers. When we’re choosing to count fingers, we have a shared understanding that fingers only “count” when they are clearly “up” or clearly “down.”
Despite that convention, your hand is perfectly capable of adopting intermediate positions. If we ask a question about what number is represented by such an intermediate position, the usual answer is something like “I don’t know” or “nothing.” In terms of the integer-counting scheme we learn on our fingers, we can produce only integer-valued answers—it doesn’t “make sense” to answer with “2½” or “2.16.”
Another kind of digital system in everyday life is a stair. A stair divides the vertical space between two levels into several distinct levels. It’s useful to contrast a stair with a simple ramp that leads between the same two levels. On a ramp we can take small moves horizontally—in fact, those moves can be as small as we choose—and for each small change in horizontal distance there is a corresponding small change in vertical distance (and vice versa). That’s different from what happens on a stair. There, a small change in one direction doesn’t always produce a small change in the other direction. In particular, the edge of a stair step produces a sharp difference in vertical distance for only a small change in horizontal distance.
Let’s assume for a moment that the stair and the ramp have the same slope (see figure 2.1). In the real world, such matching slopes almost never happen: such an alignment means that either the ramp is dangerously steep or the stair is frustratingly shallow. But it’s useful for our purposes, because we are just trying to understand the characteristics of each.
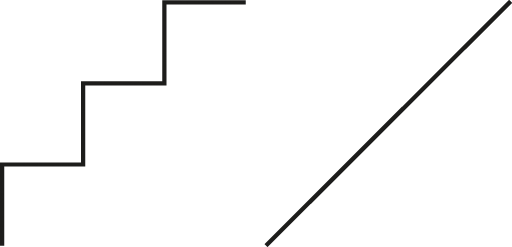
A stair and a ramp with the same slope.
There are three common ways of relating the stair to the ramp (see figure 2.2). One possibility is that the stair is just below the ramp, so that the “outermost” parts of the treads coincide with the ramp.

Different relationships between ramp and stair.
The opposite possibility is that the stair is just above the ramp, so that the “innermost” parts of the treads coincide with the ramp. And a third possibility is halfway between the first two approaches, which makes it so that the center of each tread coincides with the ramp.
We’ll choose to talk about the first structure, because the associated physical experiences and intuitions are a little easier to explain. But it’s important to observe that it doesn’t actually matter which structure is used: we’ll be talking about the nature and size of the gaps between stair and ramp. No matter how we align the stair and the ramp, those gaps still have the same total size.
When the stair and ramp have the same slope but the ramp is aligned with the outermost part of the treads, most positions on the ramp are slightly above the corresponding vertically aligned position on the flat part of the stair. If we put a foot anywhere onto the ramp, it rests solidly on the ramp; if we put a foot into the exact same position while using the stair, the foot does not rest solidly on anything—instead, it falls a short distance to the lower position on the step, where it does rest solidly. If we believed that we were walking up a smooth ramp, these repeated drops down to the stairs could be quite jarring. We would experience them as errors, lumpiness, or roughness in the “ramp-ness” that we were expecting. Most people have had the experience of momentary disorientation or discomfort when they miss a step of a stair; this “missing the ramp” would likely feel quite similar, but with the added problem of repeating.
We can reduce the gap between the “ramp experience” and the “stair experience” by making the stairs smaller (see figure 2.3).

Making steps smaller.
Very, very small stairs are indistinguishable from a ramp. In fact, if we look at any real physical ramp in microscopic detail, we’ll find that it’s not anything like a perfectly straight line connecting the two levels. Instead, it is a bumpy collection of level changes of varying slopes and heights. However, that microscopic bumpiness doesn’t matter for our typical uses of the ramp; we can simply treat it as though it were smooth.
In general, a system can have steps or it can be smoothly varying. The technical term for a stepped system is digital, and the technical term for a smooth unstepped system is analog. Sometimes analog and digital aspects can be found together in the same system. The crucial insight is that digital and analog are simply models. When it is useful to notice and work with discrete separated levels (like the stairs) we call that system “digital.” When it is useful to ignore lumpiness and sharp changes in favor of having as many intermediate levels as might ever be needed—like the ramp—we call that system “analog.” But just as we can choose to see a stair as a bumpy ramp or to see a ramp as if it has microscopic steps, there is no way in which any system is “really digital” or “really analog.”
Our focus in the remainder of the book will be on systems that are digital in two distinct ways. Computation is about “doing,” and it’s also about “stuff.” Usually we are concerned about their combination, “doing something with stuff,” but it’s useful at the beginning to separate these. In the rest of this chapter, we focus on “stuff”—what a computer scientist would refer to as digital data. In the next chapter, we focus on “doing”—what a computer scientist would refer to as processes.
Bits
What is digital data? All of our “stuff” is represented as a collection of bits. Each bit is valued either 0 or 1, like a switch that is either off or on. There are no other, intermediate values: just 0 or 1, but lots of them! Once we have a “single step” from 0 to 1 and back to 0, we can combine those to build as elaborate a stair as we want. We’ll see a little later that we can use these simple building blocks to represent all kinds of bizarre wiggly curves.
Before we do that, it’s worth asking, What’s good about digital? Why is it interesting or useful to build systems around digital data?
If we need to store or transmit data, we typically care about reliability (we consider reliability more carefully later in chapter 16). If we are storing or transmitting something important, then we want to be sure that we get out exactly what we put in. We don’t want to lose anything, and we don’t want any distortions. That’s true regardless of whether we’re talking about a voice, a written message, a photograph, or a movie, and it’s true whether we’re talking about sending those to another person or storing them so we can retrieve them later.
A digital system is attractive because typically it’s easier to achieve a given level of reliability with a digital system than with an analog system. That’s not to say that a digital system is necessarily easier to build, but that it’s easier to get good results with a digital system.
Noise
The enemy to be defeated in any kind of storage or transmission system is noise. Noise in this sense is not loud or distracting sound—instead, it’s low-level “fuzz” that creeps into every stage of transmission or storage. This kind of noise is hard to eliminate entirely, since it often arises from thermal processes—that is, the random vibrations of the molecules in any physical material, including the atmosphere.
In an analog system, it is hard to distinguish added noise from a small fluctuation in the signal. After all, the signal (like an audio recording) may well have some small fluctuations in its original form, which ideally should be captured and retained. So we can’t simply declare that all small fluctuations in the signal are noise and should be eliminated.
In figure 2.4, we have a complex “wiggly” analog signal at the left and some lower-intensity noise being added in the middle. The resulting signal is subtly distorted compared to the original: if you look closely, you can see it’s not the exact same shape. Unfortunately, when we look at only the result, it’s not obvious which of the small wiggles are noise—some of them were in the original signal. It’s not clear how we can improve the result to get rid of the noise and recover the original signal.

Noise added into an analog signal is hard to separate out.
In contrast, figure 2.5 shows a digital signal and the same low-intensity noise as in the previous analog example. The result is again a distorted signal, but now we know that the digital signal consists of only the “high” and “low” values, and any wiggles are just noise. We can filter out the wiggles and recover the original digital signal in a way that wasn’t possible with the analog signal.

Noise added into a digital signal is easier to separate out.
A digital system can be built so that small fluctuations in the signal are not meaningful—the transitions from 0 to 1 or from 1 to 0 can be much larger than the small changes caused by noise processes. Accordingly, the system can successfully extract a clean, noise-free signal by successfully mapping each slightly distorted element back to its original bit value.
Is Computation Physical?
In the world of computation, if we’re given a bit pattern in some particular physical form, what matters is the bit pattern, not the physical form. We might draw an analogy to a knot, which is another kind of pattern. If we take a particular knot—for example, a so-called square knot—it doesn’t matter if it’s tied in a thin cord or a thick rope, it’s still a square knot. It likewise doesn’t matter if the material is nylon, polyester, or hemp, or what the color is—the knot is the same knot regardless. In fact, if we have a single rope that is made up of different colors, thicknesses, and/or materials joined seamlessly end to end, we can take a single knot and slide it along that rope. It’s really the same knot, even though it’s composed of different materials at different times.
Likewise, we can see that a page of text (like a page of this book) is the same in its information properties if we photocopy the page onto a different color paper, or a different thickness of paper, or even if we copy the page by hand-painting letters on a wall. Other aspects of the text will change—how easy it is to read, how easy it is to carry—but there is a kind of “textness” that is shared by all the different versions, a kind of Platonic form that we can discern behind the surface variations.
A bit pattern is the same bit pattern whether it’s represented as fluctuations in magnetization, charge in a semiconductor, black marks printed as a barcode on paper, or a sequence of blinking lights. The physical characteristics of the storage and computing mechanisms can have a large impact in terms of the possible speeds, capacities, and reliability, but “bits are bits”—there’s nothing about a “magnetic bit” (for example) that makes it better or worse than any other bit.
Thus, what matters in computation is not physical, but that doesn’t mean that computation is imaginary or fantasy. Computation is real, and tangible realizations of computation are physical—but what matters about computation is not physical. The nonphysical character of computation is challenging for people who equate “real” with “physical.” Entertainingly, computation resembles magic, something that is itself distinct from the “ordinary stuff” of the world but that nonetheless has the ability to affect the world.
Weighing Programs
In one joke about the nonphysical nature of computation, we see a NASA technician in the early days of the space program trying to calculate the total weight of the rocket to be launched. He goes to the leader of the programming team and asks for the weight of the programs.
“Nothing,” replies the programmer.
“No, I really need you to tell me the weight of the programs or else I won’t have an accurate total,” says the technician.
“I told you, it’s nothing!” the programmer insists.
Feeling like he is being brushed off, the technician goes to fetch one of the large decks of punched cards that were used for programming in those days. He drops the heavy box in the programmer’s lap.
“There’s a program, and it weighs more than nothing!” the technician proclaims.
The programmer quietly replies, “No, the program is the holes.”
Analog/Digital Conversion
If we’re starting with some smoothly varying analog data, it might seem that we have to stick with a smoothly varying analog representation—but actually, we can migrate between the analog and digital worlds. The key is the observation we made about small stairs starting to resemble a ramp: we can make a digital representation resemble an analog representation by making the steps small enough. That same principle applies not only to ramps but also to any analog shape. Better yet, the connection between digital and analog can be cast in terms of rules: we can work out how small we have to make the steps so that we can represent a given set of analog data.
Let’s assume that the data of interest is the sound of some music that is being played. Physically, that sound consists of complex sequences of air pressure changes. If we could see the music as it goes through the air, we’d see the air behaving a little bit like ocean waves. Analog techniques like magnetic recording and phonographs produce copies of those complex waves in different media—magnetic particles on tape or grooves in vinyl. A version of the sound waves is actually visible if we look closely at the grooves on a record.
So we can make an analog representation by effectively copying the shapes in a different analog medium. Our challenge is to somehow represent the waves as a series of steps instead. Two handy pieces of engineering knowledge are relevant to our quest to represent the sound in digital form.
Our first handy piece of knowledge is that any complicated back-and-forth wave shape can be approximated by a sum of sine waves. Figure 2.6 is a picture of a sine wave. Although all sine waves have a similar shape, they can differ in their frequency (how close together the peaks are) and their amplitude (how tall the peaks are). A single sine wave on its own sounds like a pure tone—at a single pitch and without any complexity to the sound.
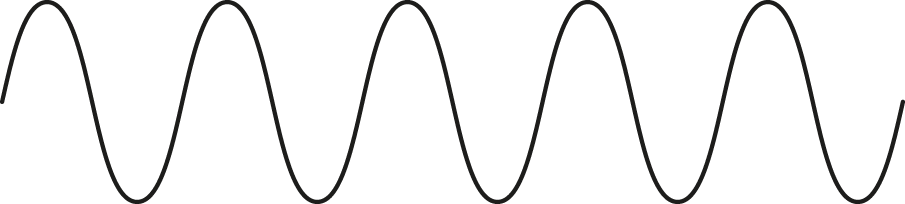
A sine wave.
Surprising as it may seem, even the messiest wave can be approximated by some number of different sine waves. Figure 2.7 shows an example of how three simple sine waves at the top add together to produce the much-more-complex form at the bottom. Although it’s not obvious from this simple example, the reverse process also works—given a wildly complex periodically repeating wave, we can figure out a collection of sine waves that add up to produce the complex shape. Now, this business of adding up sine waves is not guaranteed to be perfect. Instead, as we add more and more component waves into the mix, we come closer and closer to an exact match … but may not ever reach it. But we can pick some threshold at which we say that the match is “close enough,” and declare victory.
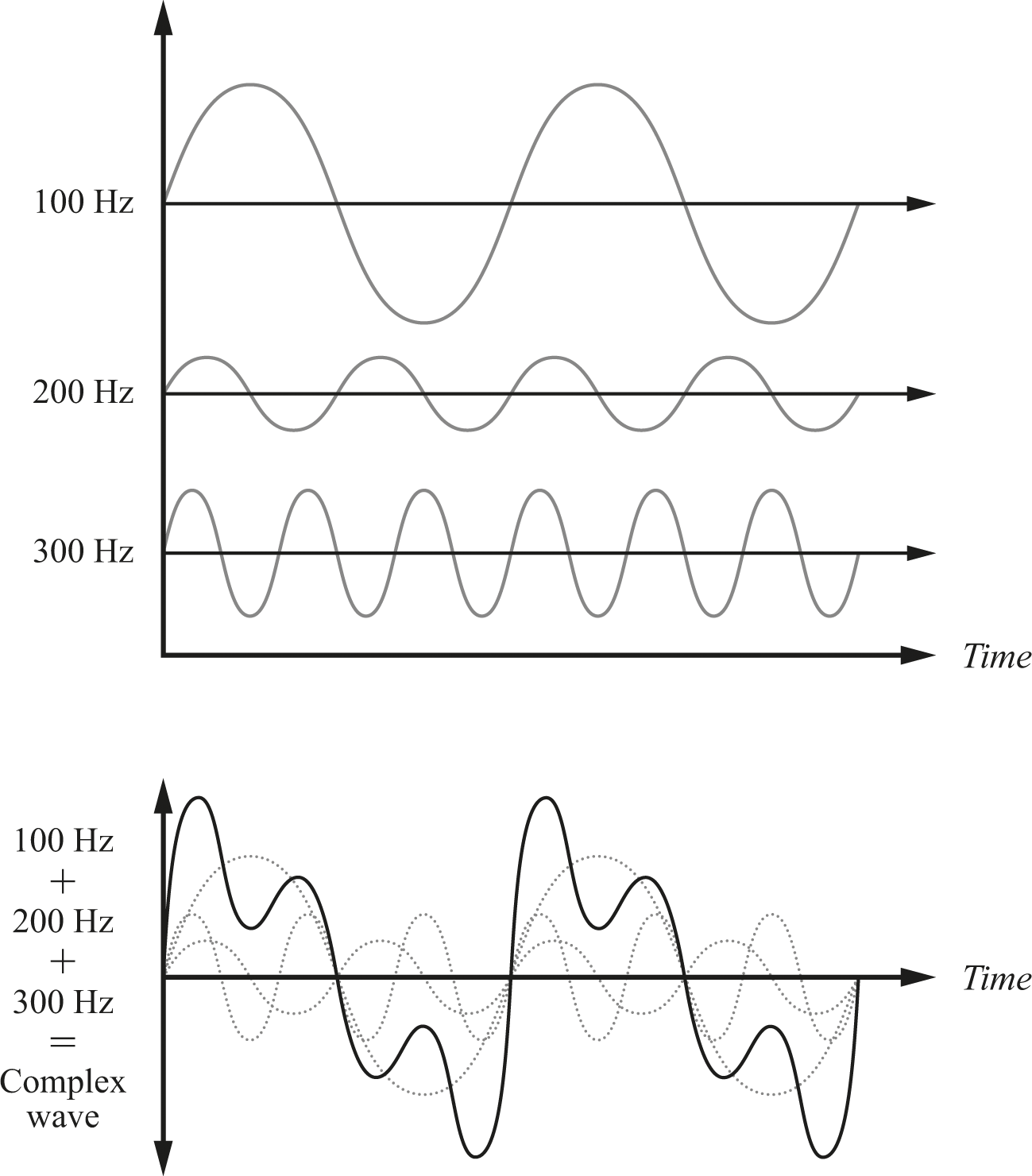
Adding together multiple sine waves for a more complex wave.
The second handy piece of knowledge is that if we have any kind of repeating wave, we can copy it perfectly if we sample at the right speed. Sampling here means that we are doing incomplete measurement—rather than measure continuously, we measure occasionally but regularly. Effectively, sampling is a kind of “stepped” or intermittent measurement. Figure 2.8 shows the way that samples let us reconstruct a signal. The more samples, the better the reconstruction.

Increasing sample frequency produces a more accurate reconstruction.
The right speed to sample is at least twice the frequency of the wave. Sampling more often is okay, but if we want to make a perfect copy, we have to sample twice as fast as the rate at which anything is changing in the wave we’re trying to copy. Why twice as fast? The underlying math is a little complicated, but the physical intuition is that if you’re sampling at least twice as fast as anything happening in the wave, you never miss anything—you catch every meaningful change in the wave’s behavior.
For example, you probably know that household electricity in a wall socket is a kind of wave. In the United States, this “electric wave” wiggles back and forth 60 times each second (or, we can say, the frequency is 60 Hz). So if our wave is one of these U.S. alternating-current waves at 60 Hz, we can sample it 120 times each second and be confident we can reassemble those readings into a perfect copy. Engineers talk about this reassembly from samples as reconstructing the wave.
As we mentioned, the sounds you hear are the result of waves in the air reaching your ear. Let’s pick some particular musical note as an example. If you know music, then you will understand a description like “the A three octaves above middle C.” If you don’t know music, we’re just picking some note, and it doesn’t much matter which one it is. That particular note (the A three octaves above middle C) happens to have a frequency of 3520 Hz. So if we sample it at twice that frequency (that is, 7040 times each second) we can reconstruct it perfectly.
Both the alternating current wave and the pure musical tone are sine waves, but this frequency-doubling technique doesn’t require sine waves—sampling at twice the wave’s frequency is sufficient to reconstruct waves that don’t look even a little bit like sine waves. And again, let’s emphasize that this is a perfect reconstruction of the wave—as long as the wave repeats exactly at the stated frequency. (In the real world, lots of complex sounds actually grow, decay, or change in various ways rather than being strictly repeating in this sense.)
Let’s recap the two techniques we’ve examined. The first, “adding-waves” technique lets us take apart even nonrepeating waves into collections of repeating sine waves. When the collection of sine waves is added together, the result is approximately the same as the original wave. In a complementary fashion, the second, “sampling” technique lets us perfectly reconstruct any repeating wave from only a sample of the points.
The great thing is that we can use these ideas together: we can take any wave apart into lots of repeating waves, which we can then represent perfectly with sampled measurements. In combination, these two techniques mean that we should be able to perfectly represent any sound by taking digital samples. We just have to be sure that we sample twice as fast as the frequency of the highest-frequency wave in the collection.
In practice, there are some problems with this approach. One problem has to do with determining what is the highest frequency that matters. If human perception is involved (as it often is), we have the challenge of whether this “perfect representation” really has to be perfect for all people, or just apparently perfect for the vast majority. Some unusual individuals can see or hear much better than almost all other people; building systems to accommodate their special talents makes everything considerably more expensive while delivering no value for that vast majority.
Accordingly, most digital audio and video systems involve trade-offs that produce visible or audible “glitches” for some but are undetectable for most people. Your friend who complains about the sound quality of some recording may really be able to hear things that you can’t.
Born Digital
Do we need to worry about these sampling and reconstruction issues for everything of interest? No. Recall that some items of interest are most usefully understood as digital representations already. For example, this book was written as a series of characters inserted into a word-processor file stored on a laptop. It was “born digital.” Although it’s possible to identify analog elements of the writing process (the movements of the author’s fingers to press keys; the specific shapes of letters and spaces between letters as visible on the laptop’s screen), those are not the elements that were crucial and selected for storage. None of those analog aspects affected the version that has passed down through multiple stages of editing and production to be read by you now. All that really mattered in that first act of writing was the selection and storage of a particular sequence of characters—and a sequence of discrete characters is a fine example of something that has an obvious digital representation.
We can contrast that writing process with what would have been required if the author had written the original manuscript with a fountain pen. At some point the original handwritten text would need to be typed up, a kind of digitization process with some of the same hazards that we’ve identified for music.
To summarize:
• We can use digital representations for both digital and analog data.
• Digital data is easy to store and transmit correctly.
Together, these characteristics help explain why it is appealing to digitize all forms of media.
In addition, digital storage costs have dropped dramatically over time—a phenomenon that we’ll examine in the next chapter. Those cost reductions provide an additional incentive for the widespread transition to digital representations.