23 Secrets
So far, all of our discussion about enforcing trust has assumed that the problem is local. When we are dealing with a single step-taking machine, we can build trust mechanisms that are based on some aspect of that machine’s physical implementation. For example, we have described ways in which an interrupt causes the execution of a particular piece of (local) trusted interrupt-handling code (chapter 11). It’s also possible to load trusted programs into a particular part of the computer’s (local) storage, so that attempts to write into that trusted area are very carefully checked. It’s still not possible to avoid all attacks—for example, we have mentioned problems like viruses (chapter 21) and Thompson’s hack (chapter 22)—but when everything is local, it is at least easy to distinguish the privileged operating system from an unprivileged ordinary application.
As we know from chapter 13, distributed systems create new problems for functionality, correctness, performance, and fault-tolerance. So it’s really no surprise that distributed systems also create new problems relating to trust. In the world of distributed systems, there is nothing that corresponds to a privileged address or privileged section of memory. Instead, we have different entities separated by distance, operating autonomously, and communicating only in terms of messages.
Within any one of those messages, there are numbers (network addresses) that identify different machines for communication. It would be easy—but incorrect!—to think that those network-addressing numbers are like the memory-addressing numbers that identify different storage locations within a single machine. The difference is in how easy it is to forge network addresses. As received in a network message, each network address is just another kind of data. There is nothing to stop a rogue computer from forging those network addresses. So even if we were to decide that a particular unique machine would be the only one we would trust to give us special commands, we don’t yet have any way to keep an attacker from pretending to be that special machine. In contrast, if an attacker tries to forge a special memory address, the local operating system’s memory protection causes an interrupt (chapter 11).
Within a single machine, the hardware can actually enforce the meaning of an address and prevent certain kinds of misuse. The operating system doesn’t need to prove its identity and its privileges to the programs that it is supporting, because it controls every aspect of the physical machine where it runs. (This total control is part of what makes it challenging to write a hypervisor for virtualizing the machine, as we mentioned in chapter 12.) In contrast, there is nothing in a network message that prevents the misuse or abuse of addressing information. The receiving operating system does not control any aspect of how the sender operates. Any machine can construct any message that it wants to, including intentional frauds and forgeries intended to deceive the recipient.
Recall that each remote communicating party is autonomous. Even if our local machine is secure, the remote machine may be subverted or controlled by an attacker. A remote communicating party is also distant—and therefore not subject to physical controls or inspections like the ones possible on a local machine. As a result of autonomy and distance, the receiver cannot rely on the local operating system or the physical hardware to enforce trust relationships. Instead, trust mechanisms in a distributed system depend on two parts:
- 1. The receiver has to make sure that the messages received are really coming from a specific party, not an impostor.
- 2. The receiver has to make sure that the specific party is actually one that it wants to trust.
It’s important to keep in mind that both parts are crucial, and that neither part on its own solves the other problem:
• If messages are invulnerable to interception or tampering, but we don’t know whether we’re communicating with the right party, we could easily have a high-quality channel directly to the attacker.
• If we’re highly confident that we are communicating with the right party, but our messages are subject to interception or tampering, then it’s easy for an attacker to rearrange the conversation.
Secrets Are the Solution
Since we can’t depend on hardware mechanisms, how can we have any kind of trust enforcement in a distributed system? In a distributed system, trust depends on secrets. It is possible to determine that a message is really from the right party, but they have to include some information that is known only to you and them.
The sender and receiver are collectively the defenders. The sender is trying to send a message to the receiver despite the efforts of the attacker. The defenders succeed if three conditions are all true:
- 1. the receiver receives the sender’s message;
- 2. the receiver understands that received message identically to how it was sent; and
- 3. the attacker does not understand the message (possibly because the attacker never sees it).
The defenders fail whenever one or more of these conditions is not true. So it’s a failure if the receiver never gets a message; or if the receiver gets a wrong version of the sender’s message because of the attacker’s efforts; or if the attacker can read the message.
The message as originally produced by the sender and ultimately consumed by the receiver is called plaintext. The plaintext is the original form of the message, before anyone has done any “secrecy work” on it. The plaintext is also the final form of the message, after all of the transformations have been performed. In contrast to the plaintext, the message in its protected, hidden form is called ciphertext.
These terms—attacker, defender, plaintext, and ciphertext—give us the vocabulary to talk more carefully about some of the different ways to protect information.
To support secrecy, we want to somehow have problems that are expensive for attackers but cheap for defenders. Fortunately, it turns out that there are many different kinds of problems where finding the solution is hard, but checking a possible solution is easy.
For example, if we are given a large collection of cities and distances between them, it’s hard to come up with an itinerary that goes through all the cities and is the shortest possible—there are so many choices, and it’s not obvious which one is right. But it’s easy if we have a current “best” solution to see whether a new proposed solution is better: we just check whether the new solution is shorter and whether it still goes through all the cities.
Something of the same spirit is involved in secrecy mechanisms. The attacker has to do a lot of work (ideally, an infeasible amount of work)—as in the problem of finding the shortest possible route. Meanwhile, the defender has only a modest amount of work—as in checking a new possible route.
Steganography
The first possibility we consider is a situation where the defenders are sneaky and hide even the existence of the information. In such an arrangement, the defenders (sender and receiver) are trying to conceal their roles, as well as the existence of the ciphertext. The sender might physically conceal the message, or embed it in some other, more innocent-looking information. All of these kinds of games go by the technical term of steganography, or “concealed writing.”
What does it mean to conceal the information? Consider the possibilities of secret messaging via junk mail delivery. Most households receive a postal delivery each day, and among the letters and bills are items that are advertisements or solicitations of various kinds. These are intended to grab attention, but they are frequently ignored or discarded. The junk mail itself is a carrier of visible information, although it is not considered very high-value information (thus the term “junk” is applied). But consider the possibility of the postal service conveying numeric information secretly via junk mail. It would be easy to convey a number between zero and five each day by supplying or suppressing pieces of junk mail, so that the number of pieces of junk mail delivered corresponds to the number being signaled. Of course, this example leaves open the question of what we would want to signal in this way, but it does convey the essence of how we could hide information inside another communication mechanism.
There are two primary drawbacks to this sneaky approach. The first problem is that it depends on the defenders having shared understanding. So it won’t work between defenders who have never met before, and it can’t readily adapt to a situation in which the scheme needs to be changed (perhaps because an attacker has discovered it). The other problem is that being sneaky implies low data rates. The more information you need to convey, the harder it is to hide its existence. By analogy, we can think of the problem that old-school spies could have when using microdots—tiny micrographic photo-reductions of graphical information. It might be easy for a spy to hide one microdot containing a small set of plans, perhaps by pasting it under a postage stamp or sneaking it under the jewel of a ring. But if you want to communicate a whole encyclopedia, and it turns into 500 microdots, suddenly it’s much harder to avoid discovery.
Cryptography
Instead of hiding the existence of the message, the opposite extreme is to use some very well-known technique to obscure the content of the message. In this approach the ciphertext is readily available to the attacker, but its form is nevertheless unintelligible. The technical term for this approach is cryptography. There is some kind of “machinery” for transforming between plaintext and ciphertext, usually a program but sometimes a hardware/software combination. Whereas steganography tried to hide the existence of the message entirely, cryptography allows much more to be known. Apart from the plaintext itself, the only item kept away from the attacker is the secret used to drive the transformation from plaintext to ciphertext. That transformation-driving secret is called a key.
Usually a good key will be a random string of bits. The length of the key is determined by the encryption scheme, and in general a longer key corresponds to stronger (harder to attack) encryption. Unfortunately, keys for sensible-quality encryption are already much longer than people can remember (anywhere from 128 to 512 bits, at this writing). Keys of that length in turn require some kind of key-management system so that people can generate, store, and supply these long keys as required without needing to write them down or otherwise disclose them. Typically, the key-management system encrypts the key using a shorter password that is possible for a person to remember (this is a sort of recursive use of encryption!). Users employ a short password to send or receive encrypted data, but there is an intermediate step in which they have supplied a longer key that is used for the real encryption/decryption task.
One drawback to all of this machination is that each step, and each new level of complexity, offers another opportunity for attack. There is both a human system and a technical system involved in trust; often attackers succeed not by breaking the sophisticated mathematics of an encryption system, but simply by stealing or guessing passwords from careless users.
“Security through Obscurity”
As we have noted, a sensible implementation of cryptography assumes that the attacker already knows how the encryption machinery works. However, we should also mention another less wise implementation possibility: sometimes people advocate using a secret technique to transform the message, instead of a well-known technique. Intuitively, it seems like a secret technique should be even better protection than using a well-known technique; but this is one of those places where intuition is misleading. Although it’s common for people to convince themselves that this approach is a good idea, it’s not.
Why not? In practice, it’s hard to limit knowledge of implementation techniques to only the two communicating parties. It’s particularly hard to limit this knowledge if many users share the implementation: for example, in widely used operating systems and applications. In such cases, the supposedly secret implementation is unlikely to really be secret; instead, it’s likely to be exposed in the worst-possible way, in which attackers know everything about it, but defenders are in the dark about its potential vulnerabilities.
In contrast, if defenders use a publicly known mechanism, then much less needs to be kept secret. Indeed, only the keys themselves need to be well-guarded. Both attackers and defenders have equal access to analyzing the implementation, which increases the likelihood that weaknesses will be identified and fixed by the defenders.
The overall approach of using secret implementations is sometimes summarized as “security by obscurity.” It’s important to be aware that this is a derisive slogan, not a desirable condition. If you encounter someone who is touting their use of security through obscurity, run away!
In the rest of the chapter, we’ll focus instead on the right kind of solution: publicly known encryption systems, where the only secrets are keys.
Shared Secrets and One-Time Pads
If the encrypted message is readily available, and the mechanism is well known, then the only thing protecting the data is the cost of undoing the encryption. In general, the only advantage of the defenders is knowledge of the secret key. The attackers may well be able to use more computers, and they may also be willing to spend a long time in attacking a particular message. In a properly functioning encryption system, it is very easy for the defenders to encrypt and decrypt messages because they have the necessary key(s), but it is essentially impossible for an attacker to do likewise.
So far we’ve assumed that the defenders share secret keys. For thousands of years, the sharing of secret keys was a requirement for encryption to work. One of the most important—and possibly surprising—aspects of the computer age is that it led to an entirely different approach to secret communication.
First, let’s understand the older approach and its limitations. There is a kind of “chicken-and-egg” problem for shared-secret communication: it’s possible to have very secure communication between the defenders, but only if they can somehow first establish secure communication (oops!).
In shared-secret communication, the best security comes from using a one-time pad. Think of a one-time pad as a notepad where each sheet has a key printed on it. The communicating parties start with identical one-time pads. When communicating, they use the one-time pad for each new message by tearing off the top sheet (with the last-used key) and then using the key printed on the revealed sheet to send the new message. Of course, a software implementation doesn’t use pads of paper or tear anything off. Instead, the “pad” is just a series of different keys, each used only once and then discarded. Because no key is ever reused, it doesn’t matter if the attackers collect the encrypted messages and try to find common patterns. The attackers won’t find any common patterns related to the keys that were used, because each message was encrypted with a different key—one from each “page” of the one-time pad. As long as the defenders can keep their use of the keys synchronized, and they change keys more frequently than attackers can analyze their traffic, this is an essentially unbreakable scheme. In particular, when the keys are truly random numbers and are the same length as the text being sent, then it’s provably impossible to break the code.
But there are two serious problems with a one-time pad:
- 1. If the defenders fall out of sync, communication breaks down. Such a problem can happen if a defender loses their one-time pad, or has lost track of which key they should be using. For example, if you start to encrypt a message but then change your mind, you really should “go back”—perhaps paste the page back on that you tore off. This is particularly hard to get right if the reason you didn’t finish encrypting the message is that your machine crashed.
- 2. The scheme isn’t relevant for parties that are never able to establish a secure connection by some other means. If we imagine that the defenders meet in person, they can arrange to use identical pads and then they “only” have the synchronization problem. But that doesn’t help defenders who are physically far away from each other and unable to meet in person. They can use some other secret communication technique, but that won’t be as secure as a one-time pad.
It’s not OK to transmit the one-time pad via an insecure technique. Unless the one-time pad is communicated securely, an attacker may have also intercepted the one-time pad. A one-time pad that might be known by the attacker is of little value to the defenders.
Key Exchange
A notable step forward came with the idea of key exchange (a computer scientist would call it Diffie-Hellman-Merkle key exchange, after the inventors). At the end of a key exchange, two parties end up knowing the same shared secret, and no one else knows it. In terms of what the defenders know vs. what the attacker knows, that result can be as good as a one-time pad. But in contrast to a one-time pad, key exchange happens by public interactions: the two defenders don’t need to already have a secure channel. So key exchange gets us partway out of the chicken-and-egg problem of needing secrecy before we can have secrecy.
The underlying mechanism, as with most aspects of cryptography, is mathematical, but we can understand the principles in terms of paint mixing. Mixing two colors of paint together is easy, but separating a mixed paint into its original component colors is hard. If we mix the same proportions of three paint colors together, it doesn’t matter the order in which we do the mixing: the color will end up the same.
Let’s assume that Alice has a secret color a. Correspondingly, Bob has a secret color b. There is a single public color P chosen by some arbitrary method for this particular exchange. P is publicly visible, and so known to the attacker. Here’s how key exchange works in terms of paint mixing:
- 1. Bob and Alice each mix their secret color with the public color, so Alice produces a mixture of (a + P) while Bob produces a mixture of (b + P).
- 2. Next, each party provides that mixture to the other party. That doesn’t disclose the secret color of either party, because it’s visible only in the mixture. Alice winds up holding the (b + P) mixture received from Bob, while Bob winds up holding the (a + P) mixture from Alice. They’re each holding a mixture containing the other party’s secret color.
- 3. Finally, they each mix in their own secret color to the mixture received. Alice winds up with (b + P + a), while Bob has (a + P + b). We know those are the same mixture, and thus the same color. Alice and Bob now have a shared secret but have never revealed their unique secret colors.
Even if the attacker mixes together everything he or she has seen in different combinations, the shared secret color can’t be constructed. The attacker will always have too much P. Because separating paint is hard, it doesn’t even matter that the attacker knows that’s the problem.
Key exchange is a neat trick, but unfortunately it doesn’t address the question of how Alice and Bob know that they are communicating with the right party. As previously noted, we don’t really want to work out a shared secret with an attacker, and there’s nothing about key exchange that lets Alice know that “her Bob” is the intended Bob.
Public Key
A group of computer science researchers revolutionized the practice of secret-keeping with two related inventions. The first is public-key cryptography. (The second is the key distribution center, which we’ll take up in the next chapter.)
Public-key cryptography changes the nature of the key in secret communication. In the shared-secret cryptography that we described in the previous sections, the key is secret and known only to the two communicating parties.
Figure 23.1 shows how a key works for shared-secret cryptography between two defenders, with an attacker shown below. The practical challenge in these systems is that the two defenders have to find a way to share the secret key while still keeping it from the attacker. Although it is possible to be quite ingenious about this, there is an intrinsic problem: since the defenders have to share, that sharing might be subverted to also share the same data with an attacker.

Key in shared-secret cryptography.
Public-key cryptography changes the structure of the sharing that’s needed. In public-key cryptography, the key is no longer secret; instead, it’s partly public and partly secret, with the secret part known only by one party.
Figure 23.2 shows the exact same defenders and the exact same attacker, but now using a public-key system. The keys have become quite a bit more complicated: where there used to be a single key, there are now four. However, the sharing situation has become quite a bit easier. There are two public keys, freely known to all. The defenders don’t care if the attacker has the public keys. There are also two private keys that are completely unshared—in the diagram they are “locked away” in heavy boxes. Because the defenders don’t need to share these private keys with each other, those keys are much easier to defend against the efforts of the attacker to find them.
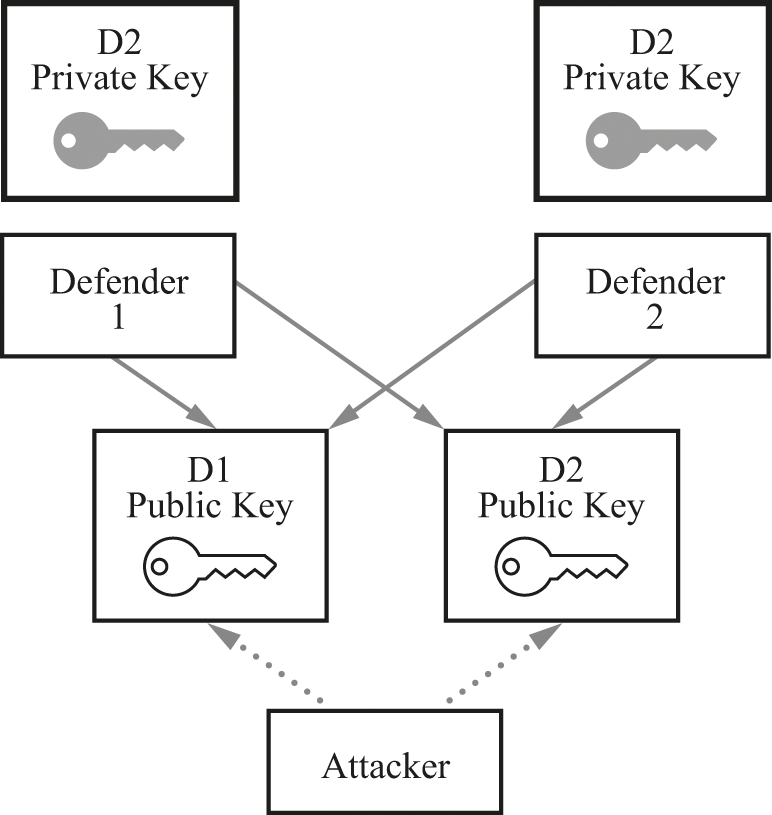
Keys in public-key cryptography.
In contrast to a public-key system, a shared-secret system has the problem that the key must be shared with “only the right people.” A public-key system does away with that problem entirely. In a public-key system, a key can be public and shared with absolutely anyone else; or a key can be private and shared with absolutely no one else.
It’s easy to see that key management would be easier in a public-key system. However, we don’t yet know how such a system can work. The keys come in public/private pairs. The two parts of the pair have a mathematical relationship that is “easy to check but hard to generate.” Recall that our plan here is to exploit that difference to protect secrets by ensuring that the defenders get the easy task while the attackers have the hard task.
Multiplying and Factoring
To get a flavor of the math involved, we’ll look at multiplying and factoring. These operations are opposites (what a mathematician would call inverses). Everyone learns in elementary school that multiplication combines two or more numbers into a single result. Meanwhile, factoring reverses that operation, dividing a single number into two or more numbers that can be combined via multiplication to yield the original single number.
You probably learned in elementary mathematics that a prime number is one that does not allow even division except by itself and 1. So, for example, 2, 3, 5, 7, and 11 are some examples of prime numbers, while 4, 6, 8, 9, and 10 are not. The numbers in the second group are not prime because 4 has 2 as a factor; 6 has 2 and 3 as factors; 8 has 2 as a factor; 9 has 3 as a factor; and finally, 10 has 2 and 5 as factors.
Assume now that we are given a larger number—say, 920,639—and asked to produce two prime factors. It’s a hard problem to solve by hand. It’s not obvious to most people what its factors are, and it’s very tedious to start trying different possibilities to figure it out. However, if we are given the two numbers 929 and 991 and asked to check whether they work, that is a relatively easy problem to solve. We simply perform the multiplication (929 × 991) and confirm that the result is 920,639. We might look at that multiplication problem and say that’s not easy—but it’s much easier than the factoring problem. Even with pencil and paper, it’s only a few straightforward steps to multiply two given three-digit numbers together; it’s much more daunting (and many more steps) to determine the prime factors of a six-digit number. Multiplication effectively discards information about the original prime factors, and that information is hard to recover. If you don’t already know what the prime factors are, it’s a hard process to figure them out.
Messages via Multiplication
So multiplying is easier than factoring—so what? This particular trio of numbers (929; 991; and 920,639) is not actually useful for keeping secrets. All of the numbers would have to be much larger for a comparable level of difficulty when using computers, because computers are so much faster at arithmetic operations than people are. Fortunately, each time we make a number just one bit larger we’re doubling the size of number that can be represented—and repeated doubling quickly makes numbers really big, as we learned earlier with the chessboard story (chapter 6). Even if the numbers get to be incomprehensibly huge, the principles are the same.
A more significant problem with our discussion so far is that even though we’ve pointed out a difference in effort between multiplication and factoring, we haven’t really explained how to exploit that difference when there is an actual message involved. To remedy that deficiency, let’s work through an example of transmitting a message in this scheme. Keep in mind that this is emphatically not a real public-key scheme—we’re just trying to capture some of the flavor of multiplication vs. factoring in the context of transmitting information.
Suppose that our “message” is a number. Let’s first look at how Alice sends the value 49 to Bob. To use the scheme for sending information, each defender has one of the small numbers and also knows the big number. Let’s assume that Alice’s small number is 929 while Bob’s small number is 991. To transmit 49, Alice multiplies 49 × 929 = 45521. Our “ciphertext” 45521 doesn’t look very much like the original “plaintext” 49, so in a very crude way the encryption seems to be effective.
On the receiving side, Bob multiplies the received message by 991 and divides the result by 920,639. 45521 × 991 = 45,111,311 / 920,639 = 49, so Bob successfully recovers Alice’s message.
Now Bob wants to send back the number 81. Bob multiplies 81 × 991 to get 80271. That ciphertext 80271 again doesn’t resemble the plaintext 81; nor does it resemble the previous ciphertext transmitted from Alice to Bob.
On the receiving side Alice (who was the previous sender of 49) multiplies the received message by 929 and divides by 920,639. 80271 × 929 = 74,571,759 / 920,639 = 81, so again the receiver successfully recovers the sender’s message.
An attacker watching this interaction sees only 45521 in one direction and 80271 in the other direction, as well as possibly knowing the “public key” 920639. Those numbers don’t have any obvious relationship. The defenders do a single multiplication followed by a single division, both with numbers they already know. Meanwhile, any attacker can only proceed by trial and error to figure out the missing numbers so that it all works out. The attacker’s task can be made much harder by making the numbers bigger, and by using a more sophisticated operation than a single multiplication.
This simple scheme takes advantage of a handy property of multiplication, which you probably know but might take for granted. It doesn’t matter whether we multiply 929 × 991 or the other way around. In fact, when we have three numbers multiplied together, it doesn’t matter in which order we multiply them; we still get the same result.
This example of factoring vs. multiplication is just providing an intuition of how we can build encryption with “one-way” functions: operations that are easy to carry out but hard to reverse. For our purposes, what matters is only that the right kind of math exists. We don’t need to be able to construct these things ourselves. We just need to understand that they exist, we can use them, and they aren’t magic—even though their properties are quite amazing. With public-key encryption, we are exploiting specific properties of particular mathematical “materials.”
Proving Identity Remotely
We’ll assume for now that we can somehow get the right keys in the right places. With that assumption, public-key cryptography does a nice job of giving the easy work to defenders and the hard work to attackers. After we look at how a public-key system works when we just assume that everyone has the right keys, chapter 24 will explain how to get the keys in the right places.
Let’s assume that Alice wants to communicate with Bob using public-key cryptography. Both Alice and Bob have key pairs, which each consist of a private key and a public key. Alice keeps her private key to herself, but can freely share the matching public key. Likewise, Bob never shares his private key, but can freely distribute the matching public key.
Because we’re assuming that we can get all the right keys in the right places, Alice has Bob’s public key, and Bob has Alice’s public key. The main problem we are ignoring for the moment is how Alice knows that her “Bob public key” is really the public key for the Bob she wants to communicate with; we are simply assuming that she has somehow found the right key. Likewise for the reverse case, we are simply assuming that Bob somehow possesses the right public key for the Alice of interest.
With this configuration, suppose that Bob receives a message from Alice that says she’d like to set up a secure communication channel. How can Bob know that the message is really from Alice? He really can’t, at least not yet. But Bob can challenge the sender of the message to prove that they are really Alice. How can he do that? By having that sender demonstrate that they have Alice’s private key. One way to do that would be to just ask for Alice’s private key—but that would be foolish for two reasons: first, if Alice shares her private key with Bob it isn’t private anymore; and second, Bob can’t tell from looking at it whether it’s Alice’s private key or not. The only way that Bob can verify that it’s really Alice’s private key is by seeing if it’s the matching key to Alice’s public key—which Bob already has.
That is, verifying Alice’s identity is not so much a matter of what Alice’s private key is but more a matter of what the key can do. With that insight, it becomes apparent that Alice can prove her identity by responding to a challenge from Bob: essentially Bob says, “encrypt this!” and Alice responds. If Alice’s response is one that only Alice could construct, then Bob knows he’s dealing with the real Alice.
Figure 23.3 illustrates the stages of the exchange. In the first part, Bob is sending Alice the challenge “?” and asking her to respond with an encrypted version.
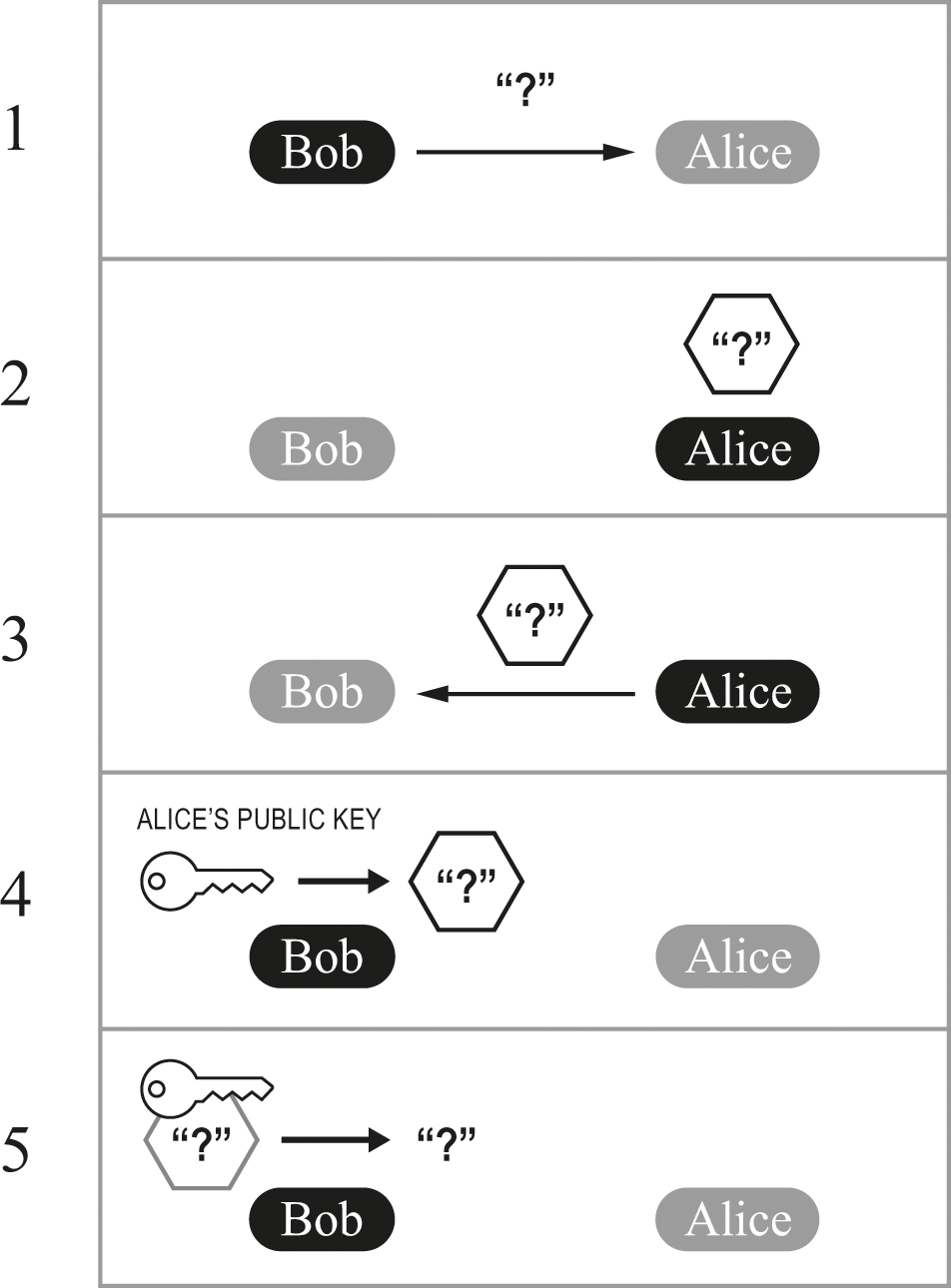
Alice proves her identity to Bob.
In the next part, Alice has constructed an obscuring “container” around the challenge, using her private key. In the third part, she sends this encrypted challenge back to Bob.
After receiving the encrypted challenge, Bob decrypts it in the fourth part. In the fifth part, Bob is applying Alice’s public key to the encrypted “package” he received from Alice. Finally, in the last part, Bob applies Alice’s public key to the encrypted reply, revealing that it contains “?”—which Bob knows is what he sent to Alice.
Correctly encrypting the challenge so that it’s decrypted by Alice’s public key must mean that it was encrypted by Alice’s private key. Whoever can do that must be Alice (at least as far as we can tell from public-key cryptography).
If some attacker Eve were trying to pretend to be Alice but didn’t have Alice’s private key, Eve would not be able to construct an encrypted package that behaves the right way. Applying Alice’s public key to Eve’s fake package would either yield an answer other than “?” or would fail.
What should Bob ask Alice to encrypt? It should be something that an attacker wouldn’t be able to guess, so choosing a large number at random should work. So Bob chooses a random number, then both remembers it and sends it to Alice. When (if?) a reply comes back, Bob uses Alice’s public key to decrypt it; if the decrypted value matches what he sent to Alice, then Bob can be pretty sure that the other party really is Alice. Because of the mathematics of public-key cryptography, we’re pretty sure that the only likely way to get the right kind of reply is to actually use Alice’s private key. So if Bob gets the right kind of reply, that most likely means that someone with Alice’s private key did the relatively easy work to produce it.
The short summary, then, is that this scheme lets Bob be sure that Alice is the party with whom he’s communicating. It’s worth noting some footnotes or disclaimers to that broad claim:
• There is a small chance that someone without Alice’s private key did the very hard work to produce the right kind of reply.
• There is also a small chance that Alice lost control of her private key, so that someone else is replying.
Those two unlikely issues are not easily fixed, so we’ll just have to live with them. However, there is one additional weakness in this first simple scheme that is fixable: if Bob and Alice have had many previous conversations, it’s a little too easy for an attacker to take advantage of that. We’ll fix that weakness in the next chapter.