24 Secure Channel, Key Distribution, and Certificates
In the previous chapter, we were considering how Bob can determine whether he’s really communicating with Alice. Although Alice initiated the communication by sending a message to Bob, she has the mirror-image problem: she doesn’t (yet) know that she’s really talking with Bob. She knows that she’s sending messages to Bob’s address, but let’s be paranoid for a minute. What if an attacker is intercepting those messages and sending back the attacker’s version of the replies? Is there a way to rule out that possibility?
In the previous chapter, we saw how Bob can test Alice’s identity. Alice can use the same approach, asking Bob to encrypt a random number. Alice remembers her choice of random number, and compares it to Bob’s reply. So Alice’s “hello, I’d like to talk” message needs to contain a little additional information. That initiating message includes a random number for Bob to encrypt using his private key and send back to Alice in his “OK” reply. Alice decrypts alleged-Bob’s reply using real-Bob’s public key and compares it to the number that she sent. If it matches, she can be pretty sure that the real Bob really encrypted it.
In this chapter we will outline the full recipe for Alice and Bob to communicate securely. To do that, we need to introduce some abbreviations. Although these details help illuminate the issues that need to be covered to make communication secure, you can skip them without missing the main point. So if the recipes and notation start to seem unhelpful, feel free to skip on to the section about “Key Distribution Center (KDC).”
When we write
[X]y
that means the plaintext X encrypted with the key y. We can also write the reverse operation, as
{Z}a
meaning the ciphertext Z decrypted with the key a. Notice that encryption hides information and uses square brackets while decryption exposes information and uses curly brackets.
We’ll also use these abbreviations:
• B for Bob’s public key
• b for Bob’s private (secret) key
Using these abbreviations, we can say that we ought to be able to get any message X back after we encrypt with public-key and decrypt with secret-key:
{[X]B}b = X
It all works likewise for the reversed situation. We get the same message X back after we encrypt with secret-key and decrypt with public-key:
{[X]b}B = X
As you can see, these lines can quickly look impressively complex, but the actual transformations are not hard to understand.
With these abbreviations to assist, here’s the seven-step outline for how the mutual identity-verification works so far:
- 1. Alice sends: Alice sends a request to talk to Bob, including a random number Na that she remembers. (The “a” in “Na” is for “Alice.”)
- 2. Bob replies: Bob sends a reply to Alice. His reply includes Alice’s number encrypted by his private key: [Na]b. He also sends a random number Nb that he remembers. (The “b” in “Nb” is for “Bob.”)
- 3. Alice decodes: The message as received by Alice consists of an obscure element X (unintelligible due to Bob’s encryption) as well as the random number Nb. Alice uses Bob’s public key on the obscure element X, which we could write as {X}B. That decrypts what Bob encrypted because {X}B ={[Na]b}B, and we know from our preceding “equations” that {[Na]b}B = Na.
- 4. Alice knows: Since Alice recovers Na and this number matches the one that she sent, she now knows that this message really came from Bob.
- 5. Alice replies: Alice replies to Bob including Bob’s number encrypted by her private key: [Nb]a.
- 6. Bob decodes: The message as received by Bob consists of an obscure element Y (unintelligible due to Alice’s encryption). Bob uses Alice’s public key on the obscure element Y, which we could write as {Y}A. That decrypts what Alice encrypted because {Y}A = {[Nb]a}A, and we know from our “equations” above that {[Nb]a}A = Nb.
- 7. Bob knows: Since Bob recovers Nb and this number matches the one that he sent, he now knows that this message really came from Alice.
This is not the whole scheme we will end up using. We’re going to add a further refinement. But it’s already enough to get a flavor of how this works.
Why Is This Worthwhile?
It is reasonable to think this scheme is already a crazily complicated way of communicating, and we should step back to remember why it’s worth bothering. Despite operating in an anarchic world of data communication where anyone can pretend to be anyone else, we are nevertheless quite close to having a scheme that lets us be sure that we’re not being cheated. Considering that this approach lets us go from a zero-trust free-for-all to a high degree of confidence that we’re talking to the right party, this is not such a bad deal. There are two remaining problems. First, this scheme is not quite strong enough yet to keep from being fooled by bad guys; and second, this scheme depends on Alice knowing Bob’s public key B and Bob knowing Alice’s public key A. We’ll fix the first problem in the next section, and after that we’ll fix the second problem by explaining key distribution.
Before we proceed, it’s also worth reexamining the foundation of the security we’re achieving, so we can understand what might go wrong. The security of this communication scheme depends on random numbers, public-key math, and secrecy of private keys. Let’s consider each of those elements in turn.
Random numbers: Alice and Bob both need to use random numbers that are not easily guessed. For example, if Alice has a really bad random-number generator that always picks 42, it’s easy for an attacker to reuse a previous Bob answer to substitute themselves for Bob. Alice simply won’t be able to tell the difference. Both Alice and Bob need to have random-number generators that are good: unpredictable, nonrepeating.
Public-key math: The public and private keys must have certain properties, specifically
• the public key easily decrypts what is encrypted by the private key and vice versa;
• the private key is not easily derived from the public key; and
• the plaintext is not easily derived from a ciphertext in the absence of a matching key.
If any of these properties is missing, then we can’t expect to achieve secure communication with the scheme we outlined.
Secrecy of private keys: When using a public-key scheme, “identity” is no more and no less than the use of a particular private key. If Alice lets someone else use her private key, that someone will appear completely identical to the “real” Alice. Indeed, from a cryptographic perspective that other person is the real Alice. Accordingly, we have to keep in mind that the scheme actually determines whether parties possess particular private keys—not any other concept of identity or authority.
Secure Channel, Refined
Now, let’s refine our system to fix one problem we mentioned. In this fix, we still assume that Alice and Bob magically have each other’s public keys. In the next section, we’ll show how to solve that key-distribution problem.
The refinement we now add is to hide the random numbers that Alice and Bob are using to challenge each other. Alice and Bob don’t want to show a possible attacker any more information than they have to. For example, it’s possible that a randomly chosen number will (purely by chance) coincide with a number that one party sent previously—it’s unlikely, but possible. We need to be concerned about an attacker who is watching and recording everything. Such an attacker might take advantage of any repetition: When the attacker sees a previously used number sent as a challenge, the attacker may be able to substitute a previously recorded response to that challenge and thereby hijack the conversation.
The fix is easy enough. Instead of simply sending a random number that the attacker could read, the sender should encrypt the random number before sending it. How should the sender encrypt the random number? Ideally, it should be encrypted in a way so that only the recipient can read it. We can achieve that if both parties send their random-number challenge encrypted by the other party’s public key. In fact, each side will encrypt the entire message containing the random number (including the response to the other party’s challenge). The result is that an attacker can’t see any other elements of the conversation.
With those changes, here’s how the conversation works. It’s basically the same structure as before, but the steps have become a little more elaborate, and there are now eight of them:
- 1. Alice sends: Alice sends a request to talk to Bob, including a random number Na that she remembers. Alice encrypts the request before sending it, using Bob’s public key. So what Alice sends is [Na]B.
- 2. Bob decodes: Bob receives the obscured information, which we’ll call Q, and decrypts it with his private key: {Q}b. Because Q = [Na]B, this is the same as {[Na]B}b; and we know that {[Na]B}b = Na. Bob has now extracted Na, which is Alice’s randomly chosen challenge..
- 3. Bob replies: Bob sends a reply to Alice. His reply includes Alice’s same number Na, but now reencrypted using Bob’s private key: [Na]b. Bob also sends a random number Nb that he remembers. Bob’s reply thus contains two data items: the reply to Alice’s original challenge, and Bob’s new challenge to purported-Alice. Bob encrypts both elements, using Alice’s public key: [[Na]b, Nb]A. Notice the nested item: it’s the number Na that Alice sent originally. It has one “inner layer” of encryption to demonstrate that it was sent from Bob, and an “outer layer” of encryption to protect it from being read by anyone except Alice.
- 4. Alice decodes: Alice receives the obscured information, which we’ll call R. She decrypts it with her private key: {R}a. We know (because we saw Bob encrypt it) that R consists of some stuff (that we’ll call S) encrypted by A: [S]A. Accordingly, when Alice decrypts it, {[S]A}a = S, she recovers whatever stuff S was originally encrypted. There are two items in S. The second item is simply a number (in fact, it’s Nb), but the first item is at this point just another obscure object that we’ll call T. So now Alice has some obscure object T, and she knows Bob’s challenge number Nb. Alice knows that T is Bob’s response to her challenge. Alice then uses Bob’s public key and decrypts the part that Bob encrypted: {T}B = {[Na]b}B = Na. Through this process she recovers Na.
- 5. Alice knows: Since the number Na matches the one she previously sent in step 1, she now knows that this message came from Bob. We could say that Bob has met her challenge.
- 6. Alice replies: Alice replies to Bob’s challenge by including Bob’s number Nb that she extracted in step 4. Alice encrypts that number using her private key: [Nb]a. This step of encryption is needed so that Bob will know the message came from Alice. Then to protect it from being read en route, she hides that result with another layer of encryption using Bob’s public key: [[Nb]a]B. This second layer of encryption ensures that no one except Bob can read Alice’s response to Bob’s challenge.
- 7. Bob decodes: Bob receives an obscure object, which we’ll call U. He decrypts it using his private key: {U}b = {[V]B}b = V. So he extracts another obscure object, which we’ll call V, as Alice’s response. Bob then uses Alice’s public key and decrypts Alice’s response V: {V}A = {[Nb]a}A = Nb.
- 8. Bob knows: Bob has now recovered Nb; since this number matches the one he originally sent in step 3, he now knows that this message really came from Alice. We can say that Alice has also met Bob’s challenge.
That might seem like a lot of steps with a lot of complexity—and it is—but let’s keep in mind what it accomplishes. If we assume for a moment that all the mathematical constraints related to public-key systems work out, and that Alice and Bob have each other’s public keys, this exchange means that Alice and Bob can set up a secure channel to each other: they each know that the other party is the one they want to talk to, and they know that no one else can see what they are discussing. That’s pretty impressive. And remember, for all the history of secret codes in all of civilization before the late twentieth century, this particular result was impossible!
Key Distribution Center (KDC)
The eight-step conversation we have outlined lets the parties set up a secure channel, assuming that Alice already had Bob’s public key (and vice versa). At some level that assumption is not much better than assuming that Alice and Bob each have the same one-time pad, unknown to anyone else. It’s an assumption that allows for great security, but it seems hard or impossible to accomplish if you don’t already have great security.
So in some respects the most impressive part of public-key cryptography is not the message exchange itself, but the key distribution. How can you get an authentic public key for someone whose public key you don’t already have?
Conceptually, it’s pretty simple to solve the problem of trustworthy distribution of public keys. We assume that there’s a key distribution center (KDC) that establishes individual trust relationships with individual key holders (see figure 24.1). The KDC knows who Alice is and who Bob is, and knows both of their public keys; in addition, both Alice and Bob know the KDC and know its public key.

A key distribution center (KDC).
Alice and Bob don’t need to know each other (or all the many other parties who each have an individual relationship with the KDC). The one relationship each has with the KDC is sufficient for Alice and Bob to get each other’s public keys, even though they may not know or trust each other initially.
You might be wondering, why doesn’t Alice just contact Bob and ask for his public key? That can work in some special cases, but in general it doesn’t get us past that frustrating chicken-and-egg problem: how do you know it’s really the right Bob if you have never contacted him before? In general, you will be depending on some mutual acquaintance whom you already trust to introduce you or to confirm that you have the right person. The KDC takes that same idea and makes it a simple general mechanism.
We start with Alice and the KDC knowing each other’s public keys by some reliable mechanism. That mechanism most likely involves some kind of non-computer, non-network interaction, probably completely unrelated to public-key cryptography. For example, Alice might go to a local office of the KDC organization and speak to an employee of that organization, presenting some physical evidence of her identity. Similarly, Bob and the KDC know each other’s public keys, again perhaps via a “real-world” interaction.
So the KDC knows Alice’s public key and Bob’s public key. In addition, Alice and Bob both know the KDC’s public key. However, Alice and Bob don’t know each other’s public key. What we want is that Alice and Bob should be able to learn each other’s public keys in a way that is not vulnerable to an attacker.
Fortunately, we already know how to establish a secure channel between two parties who know each other’s public keys, as we developed in the previous section. So Alice simply establishes a secure channel to the KDC and asks for Bob’s public key. The use of a secure channel means that Alice knows she’s talking to the KDC, and the KDC knows it’s talking to Alice. Accordingly, when Alice asks the KDC for Bob’s public key, she can trust that the data she receives is actually Bob’s public key (as known to the KDC), not some attacker’s substitute.
Likewise, when Bob wants Alice’s public key, he can simply ask the KDC over a secure channel. Since Bob knows he’s talking to the KDC and trusts the KDC, he can be sure that he’s getting Alice’s public key and not some other key.
This seems like a pretty easy solution to the problem, and it just reuses what we previously developed to perform secure communication. So what justifies our previous claim that this function was impossible without an important invention?
Scaling up Key Distribution
The KDC we’re describing works at small scale, but has some problems if we try to scale it up. It’s not clear how to have a simple system where anyone can find the key of anyone else they might want to reach. Likewise, it’s not clear it’s feasible—or even desirable—for everyone in the world to have a trust relationship with one single KDC. So while this simple system is a good starting point for thinking about how we can get secure communication in general, the scheme we’ve presented isn’t very practical.
To get a more practical system, we want to solve the key-distribution problem without depending on a single central source of knowledge. We notice that the KDC is serving two roles: it links names with public keys, and it is the trusted source of those linkages. We can instead think of these as two distinct functions: we can have one mechanism that links names with public keys and another mechanism that establishes which of those linkages is trustworthy.
Accordingly, we will make two major changes from the simple KDC approach:
- 1. Instead of having the KDC distribute the public keys over secure connections, we wrap each public key in a certificate signed by the KDC. A certificate simply links a name to a public key. Because the signatures can’t be forged, we know that the linkage is a valid one, at least to the extent that we trust the signer. We explain more about certificates in the next section.
- 2. We organize the signing of certificates into hierarchies of certificate authorities (CAs). A CA is composed of both a technical mechanism that performs the signing, and a human process that determines which certificates to sign or not sign. Each CA is testifying to the trustworthiness of certificates it signs. We explain more about CAs later in the chapter.
With these changes, we have the essential elements of the commonly used internet trust infrastructure.
Certificates
Each certificate links a specific name to a specific public key, in a way that we can check easily. Certificates are useful because they are signed. Without signatures, it would be easy to substitute different names or keys in the certificate, and we would have no reason to trust the linkage between name and key. But a signed certificate makes a package: name, key, and signature are tied together so that any tampering will be detectable. For the moment we’ll just assume that signatures are possible and consider why they allow a better solution; then we’ll look a little more closely at how they work.
A signed certificate is what it is—its merit (or lack of merit) is not determined by who gave it to us. In this “inherent trust” approach, a certificate works like cash: it doesn’t matter whether we receive a $20 bill from someone we trust or someone we distrust—as long as it’s a real $20 bill, it’s still valuable and useful. Likewise, a properly signed certificate provides a trusted linkage between name and key, regardless of who gives us the certificate. The signature, not the source, is what determines trustworthiness.
Using certificates is a significant improvement over the KDC as we first presented it, because that first KDC required secure connections to the particular single central service. Now, instead of trying to build a single highly available central service as a KDC, we can think of having a “sea” of duplicate certificates available from many different servers. Those servers don’t need to worry about secure channels. In fact, they don’t even need to take special steps to protect the certificates, because the certificates have built-in mechanisms to detect tampering. An attacker can’t keep us from learning the right public key by taking down the KDC service, because there may be many possible alternative sources for a copy of the relevant certificate.
Cryptography for Integrity
Signatures are different from the secret-keeping we’ve considered previously. We were previously using cryptographic techniques for secrecy, but with signatures, we’re using cryptographic techniques for integrity. Using cryptographic techniques but not trying to hide data can seem weird, so let’s look at a non-cryptographic example of a signature to be sure we have that clear.
Consider playing chess against an opponent you don’t trust. You need to leave the room. Especially if you aren’t a very good chess player, you probably won’t notice if your opponent moves a piece or two into positions that help the opponent. Even if you do notice, it might be hard to make the case that the opponent is cheating. In this situation you can take a quick digital photograph of the board (probably using your mobile phone) as a kind of signature. The board is not hidden, and it’s still vulnerable to manipulation by the untrustworthy opponent. But now there’s a clear mechanism to verify that things are unchanged, by comparing the board with the photo. If the photo and board don’t match, then we know the opponent has changed the board.
Cryptographic signing works a little differently from this conceptual “photographic signing.” As used for certificates, signing combines a chunk of data with a private key to produce a signature block. The signature and the data together are “signed data.”
In figure 24.2, the signed data has an appended block of some additional bits that were computed by the signing mechanism. The signing mechanism computed those bits by somehow combining the original data with the private key. The signed data (original data + block) can be checked to ensure that no tampering has occurred, as we will shortly see.
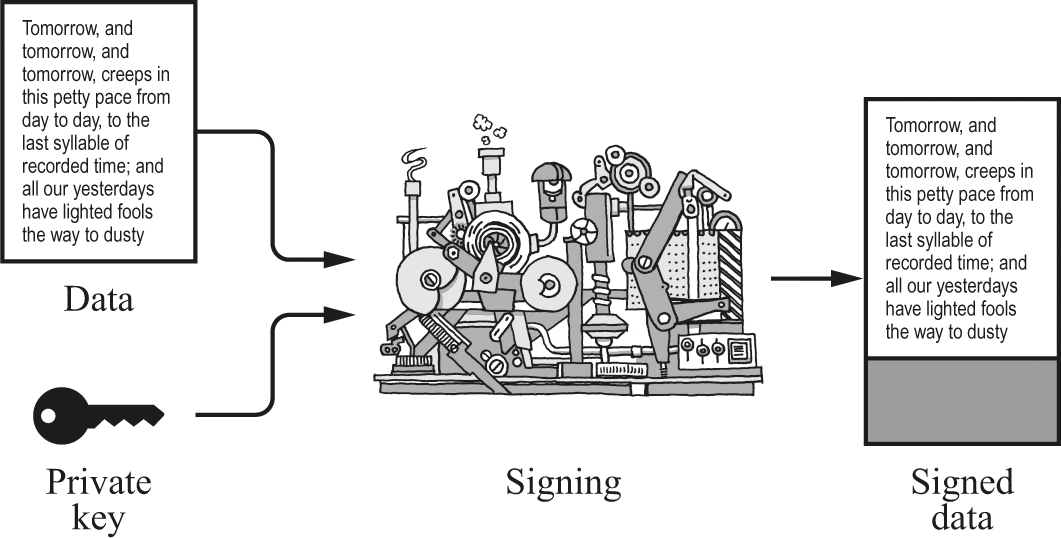
Signing data.
In figure 24.3, we’re checking the signed data by using the public key. The computation either says the signed data is OK (the attached block is the one that matches the original data and private key) or says that something is wrong:
• the signature doesn’t match the data, or
• the public key doesn’t match the private key.

Checking the validity of signed data.
Notice that we don’t necessarily know exactly what’s wrong—we can just tell that something is not right.
What are the necessary properties for this kind of signing and validation?
- 1. The signature block has to be obscure, so the attacker can’t easily tell how to change it to match a change in the signed data. The only way to produce a valid signature for changed data must be to sign it again with the relevant key. Again, this obscurity of the signature does not mean that we’re hiding the original data. For signing purposes, it’s fine to leave the original data as unchanged plaintext; signing just provides another (checkable) element that goes with that original data.
- 2. The signature block also has to be sensitive, so that even the tiniest change to the original data (one bit flipped) produces a different value for the signature block. This requirement means that even the smallest change to the signed data “breaks” the signature.
As with other aspects of public-key cryptography, these requirements can seem like unreasonable demands. But marvelously, there are mathematical mechanisms with the right properties. Once again, we won’t try to explain how or why signatures work mathematically; we’ll just take advantage of their properties.
Signed Certificates
Signatures let us distinguish between good and bad certificates. Let’s assume that we have a certificate in hand that we’ve somehow found or received. (Recall at this stage that we’re still assuming that everyone knows the KDC’s public key somehow. In a later section we’ll get rid of that dependence on a single KDC.) For that certificate to be authentic, it must have been signed by the KDC.
So we can make a certificate that links a name to a public key, have the KDC sign that certificate, and then make as many copies of that certificate as we like. Every one of the certificates is equally valid and equally useful for the purpose of learning the public key linked to a name. Anyone who has a copy of the certificate no longer needs to contact the KDC to get the public key linked to that name. We can distribute and share name/key pairs without requiring the KDC to be involved—we have eliminated the need for the KDC to be some kind of super service that’s always available and always correct.
Revocation
Unfortunately, there is a new drawback that comes along with this new benefit. With all these certificates potentially floating around, it’s somewhere between hard and impossible to undo a name/key linkage. For example, suppose that Dennis realizes that his private key has been compromised—a bad guy has stolen it, or Dennis is just not sure any more whether someone might have a copy of it. Meanwhile Alice may well have a certificate, duly signed by the KDC, binding the name “Dennis” to what is now the wrong public key. Dennis really doesn’t want Alice to trust that public key to protect interactions with him, because some attacker may use the corresponding (compromised) private key to pretend to be Dennis.
What can Dennis do to improve the situation? He can certainly get a new pair of corresponding private and public keys, replacing the old bad ones. And Dennis can certainly get the KDC to sign a new certificate that binds “Dennis” to the new correct public key. But there’s not much that Dennis can do about the old bad certificate that Alice is using. After all, Dennis and Alice may not know each other at all before Alice attempts to contact Dennis via the information in the certificate—that is a part of what we wanted to enable with a certificate-based system.
What we see here is the problem of revocation. A certificate establishes a linkage between a name and a public key in a way that can’t be tampered with, but it’s hard to correct that linkage—for example, if there has been a security breach or even if there’s something more innocent that changed the name/key linkage, like a reconfiguration or upgrade.
Given that a certificate is a freely distributable, freestanding object, how can we eliminate old obsolete certificates? One answer is to have a certificate revocation list (CRL). Entities wanting to invalidate a certificate add it to the CRL, and entities using certificates then check the CRL to see if the certificate has been revoked. Although this works in principle, in practice a CRL has rarely been successful. In some ways the CRL is the KDC all over again: we have to have a trusted source for the CRL to ensure that our certificates aren’t undercut by an attacker, and unfortunately, it’s hard to scale up that kind of service.
In practice, the scope of certificates is limited primarily by expiration—that is, each certificate is valid only until a particular date and time, after which it is no longer trustworthy. Organizations can trade off the expense of more frequent renewal and replacement of expired certificates vs. the longer time of exposure after a security breach with less frequent renewal and replacement.
Unfortunately, the expiration mechanism is clumsy. All too often, the expiration of a batch of certificates requires a flurry of pointless bookkeeping work to replace them. Meanwhile, people often continue to use certificates beyond their stated expiration dates. In most people’s experience, an expired certificate is usually an innocent housekeeping oversight—an annoyance rather than a bona fide security problem.
Certificate Authorities (CAs)
In the previous section, we used certificates to get away from the need to interact with a single KDC service, but we still used a single KDC as the basis for all the signatures. As we mentioned previously, the other half of the solution is to allow more than one entity to sign certificates. In computer science terms, we move from a single certificate authority (CA) to having multiple CAs.
Any CA can sign a certificate, but a certificate signed by an unknown or untrusted CA is no better than an unsigned one. If we look back at the two previous KDC schemes (without certificates, then with certificates), we can say that the single, central KDC was the single common trusted entity in both schemes. Every user has to trust the KDC, and as a result every user can trust any certificate signed by the KDC. There are two different ways of moving from a single CA to multiple CAs, and they are both useful in practical systems. One approach is to have multiple independent sources of trust, and the other approach is to delegate trust.
Root CAs and Hierarchies
If we consider multiple independent sources of trust, then we shift from talking about the single KDC to talking about root CAs. A root CA plays much the same role that the single KDC did in our earlier explanation: It is a trusted entity, with the trust relationship established by some mechanism unrelated to signing and certificates. A root CA signing certificates is a little like a sovereign country issuing passports. Although you might well be prepared to accept a lot of different passports, you won’t want to accept just anything that claims to be a passport. Passports from France and Germany are probably OK, but a passport from Upper Voltonia probably isn’t.
How do you know the public key of a root CA? You find it in a “self-signed” certificate from that same root CA. Some of those root CA certificates are actually built into browsers so that your browser can easily validate certificates signed by those popular root CAs. If you choose to trust a root CA that isn’t already built into your browser, you can manually add its certificate to your browser. And just as it’s possible to add certificates to indicate that you trust the corresponding CAs as root CAs, it’s typically also possible to do the reverse—remove certificates if the user or organization chooses not to trust some or all of those corresponding CAs.
Having multiple independent root CAs offers one kind of scale: multiple diverse unrelated entities that we would expect to fail independently. But the use of multiple root CAs doesn’t really address the other scaling question: how to support a larger, more reliable workload of signing for a particular single CA. Rather than requiring the single CA to do all signing work, we put mechanisms in place that allow the delegation of signing work, in a hierarchy of trust. This approach is like a sovereign country allowing multiple offices and embassies to issue its passports. The authority all eventually hinges on the root, but the root doesn’t have to do all of the work. In a hierarchy of trust, a well-known CA can sign a certificate that names another CA. So now a CA is not just providing reassurance about the name/key binding for a communicating party like Alice or Bob: it’s also potentially providing reassurance about the name/key binding for another CA.
So now suppose that we encounter a certificate from an unknown CA. If the unknown CA’s certificate is signed by a known (and trusted) CA, the known CA is indicating that the unknown CA can itself be trusted. The trust hierarchy has many of the same merits that we already saw when we looked at DNS (chapter 15) and when we looked at making better servers (chapter 20). In particular, in the same way that DNS let names be “owned” by subordinate directories, a trust hierarchy lets certificate signing be “owned” by subordinate CAs. Just as we don’t want to try to implement a global search service or a global name service with a single server, we don’t want to implement a global signing service with a single server. Instead, we gain capacity, fault-tolerance, and responsiveness by allowing the signing to take place at multiple, separately administered, globally distributed CAs.
In such a hierarchical system, checking on a single name/key correspondence may well require checking a sequence of certificates. If we don’t already know and trust the CA signing a particular certificate, we shift to examining that CA’s certificate. If we don’t know the CA that signed that first CA’s certificate, we shift to examining the second CA’s certificate. We follow a chain of certificates until we either find a CA that we trust or we reach the end of the chain.
If we encounter a CA that we trust, then we can believe the name/key binding in the first certificate considered. However, we might end this process by finding that there is no CA in the certificate’s chain that we trust. If we follow the whole chain to the root CA without finding a CA we trust, we have no basis for believing that the name/key binding is correct. We also don’t know for sure that it’s wrong. Nor do we know that there’s an attack or an attacker. Failing to find a trusted CA is a problem, but not necessarily a cause for alarm; we just don’t know whether the key in that first certificate is trustworthy.
Trust Problems
We previously mentioned that there are both technical and nontechnical (human) aspects to trust systems. That’s still true—and a potential source of vulnerability—regardless of whether we use certificate hierarchies and multiple CAs. In particular, we need to be aware that a person or organization can choose to accept a certificate that later turns out to be bogus: the certificate appears to be valid, and in narrow technical terms is completely fine. Nevertheless, something in the trust system has broken down. For example, if an attacker successfully commits fraud in the process of obtaining a certificate from a CA, the legitimate signature of that CA won’t somehow overcome the fraudulent information in the certificate.
For a concrete example, assume that attacker Eve has convinced a legitimate CA to issue her a private/public key pair, and that same CA has issued a certificate that ties Eve’s public key to Alice’s name. Now anyone who relies on that certificate believes that they are interacting with Alice, but they are actually interacting with Eve. There is nothing wrong with the certificates or keys that would allow an automatic warning of potential harm, even though this is clearly a bad situation. Even when certificates appear to be working correctly, communicating parties need to be alert for other possible signs of attacks or misbehavior.
An even worse problem is that an entire CA—not just one certificate—can turn out to be bogus. Why is that worse? Because, as we just learned, trusting a CA implies trusting all of the certificates signed by it: that’s what a trust hierarchy means. So trusting a bogus CA not only means accepting everything directly signed by that CA; it also means accepting all of the certificates signed by any other CAs to which the bogus CA delegated trust.
What causes a CA to fail in this way? Unfortunately, even a legitimate CA making good-faith efforts can have these kinds of problems. For example, some CAs have suffered security lapses and lost control of their private keys. If an attacker controls a CA’s private key, then everyone trusting that CA is vulnerable to apparently good but actually fake certificates.
It’s worth underscoring that “everyone trusting them” includes everyone interacting with the signed certificates. There’s an obvious harm for the users whose certificates that turn out to not be very convincing, but there’s also a subtler harm for anyone who is trying to validate a certificate. Many users of a certificate are only seeking to determine if it is correct; as we’ve noted, part of the attraction of a certificate scheme is that such validation can be performed locally, without needing to contact the issuer. These “ordinary users” of certificates may not see themselves as customers of a particular CA, and indeed have no business relationship with that CA. However, they are just as vulnerable to the subversion of a CA as the people who obtained certificates. Anyone who pays a CA for signing certificates is clearly harmed when the CA endorsement turns out to be dubious—but so is everyone using any certificate that came from the problematic CA.
We already saw that there is no effective way to recall bad certificates. Accordingly, we can see that the first trust failure of a CA is also, in some ways, its last: a CA that has been compromised cannot really be repaired. Since we know from previous chapters that failures do occur in systems, it’s unfortunate that the CAs are so fragile; and doubly unfortunate that CA failure affects so many parties, many of whom are not even known to the CA. This alarming fragility is somewhat mitigated by the presence of multiple independent root CAs, which we expect to fail independently. However, that is not especially comforting. If you are personally affected by one of these trust failures, you are unlikely to feel much better knowing that most other parts of the internet are unaffected.