26 Bitcoin Mechanisms
In chapter 25 we laid out goals for Bitcoin and summarized it as a shared extensible recordkeeping system for a community of untrusting participants. In this chapter we consider how the system is actually constructed so that it works that way.
Some systems achieve a stable permanent record by using physical irreversibility. For example, archival storage media such as write-once optical disks are designed so they cannot be altered once data is written onto them: there is simply no way to erase or rewrite them. When we describe the consensus view among Bitcoin participants, it’s worth noting that its stability is not enforced by any physical mechanism. At the physical level, Bitcoin records can be completely reversible and rewritable—all of the history in the ledger could be changed if a large enough group of attackers performs that attack. The stability of the agreed sequence results from the efforts of the defenders.
What are these efforts of the defenders? Each participant operates independently in making its decisions about whether to join or leave and in deciding what to accept or reject from other participants. A participant has to be prepared to incorporate genuine updates into its local version of the ledger, while rejecting any bogus updates.
Suppose that Charlie is a cheater and Victor is his intended victim. Charlie could insert bogus records showing that he has received money and then send those updates to Victor. An alternative way of committing the same kind of fraud is that Charlie could receive legitimate updates showing that he has spent money, but then suppresses them. Rather than forward them on to Victor, Charlie could delete the records showing that he has spent money.
With either kind of cheating, Charlie can potentially fool Victor. Victor receives updates showing that Charlie has more money than he really has, or fails to receive updates showing Charlie has less money than he claims. In turn, Victor might be convinced to sell something valuable to Charlie in exchange for that (actually nonexistent) money. We need to find a way to protect Victor from Charlie. We may not have any good way to prevent cheaters from trying to fake the log, but we can make sure that they don’t succeed.
There are four different aspects of Bitcoin that make life hard for a cheater:
- 1. Each individual transaction is hard to forge or modify.
- 2. Adding a new item at the tail end of the sequence is somewhat challenging. Furthermore, the difficulty of modification increases with distance from the tail, so older transactions are harder to change.
- 3. Participants compete to be allowed to add an update at the tail of the sequence, and cheaters can’t be sure that they will win.
- 4. It’s not enough to win the competition to add an update at the tail of the sequence—in addition, most of the community must accept that update.
We’ll examine each of these aspects in turn. Let’s first consider how to make an individual transaction hard to forge.
Unforgeable Transactions
If each entry in the sequence were actually represented in the way that we showed in the earlier diagram, such as “Alice: $6,” then it would be easy to forge entries. If we saw some updated state such as “Alice: $4,” we wouldn’t know whether it was a real change or a fake change. It doesn’t matter whether the recorded items are balances (as in this example) or changes like “Decrement Alice’s account by $2” or transfers like “Move $2 from Alice’s account to Bob’s account.” The problem isn’t in the form of the record, it’s that we have no idea whether to believe it or not.
Fortunately, we already know a way to protect against spoofing and forgery. We have already seen a similar problem of distinguishing trusted information from untrusted information, when we wanted to distribute public keys (chapter 25). There, we were interested in finding the public key that is linked to a particular name. The hazard that we had to overcome was that an attacker might fake such a linkage and fool us.
The solution there was to use a signed certificate for each name/key pair. The signing establishes both that the information is from a trusted party, and also that the information is unchanged from what the trusted party published. Because of the mathematical properties of the signatures, we are confident that an attacker can’t simply substitute different data.
In a similar fashion, Alice can sign a transaction with her private key. That signature allows anyone to check the signed transaction for validity. If it passes the validity check, that means both that
• the signed transaction was really signed by Alice, and also
• it hasn’t been altered from what Alice signed.
However, if the signed transaction fails the validity check, it’s meaningless; there’s no way of knowing whether it wasn’t really signed by Alice or whether it was signed by Alice and subsequently altered. But either way, it’s not a transaction to use.
In fact, Bitcoin goes a little further than this. Although we can talk about “Alice’s public key,” the underlying technical reality in Bitcoin is that “Alice” is identical to her public/private key pair within the payment system. Anyone who knows Alice’s private key essentially is Alice. We noted this characteristic when we first looked at public-key cryptography (chapter 24), but it’s more noticeable in Bitcoin.
Bitcoin transactions take place between “wallets” that are identified by special addresses. These addresses are derived from public keys, and for our purposes they’re basically the same as public keys—it’s just inconvenient to use the public keys directly. In contrast to what we saw when we were concerned with certificates, Bitcoin intentionally does not have any means to match people to particular addresses or public keys. This unusual structure is part of why descriptions of Bitcoin sometimes call it “anonymous,” which is technically incorrect. Bitcoin indeed does not have any personal names, but the wallet addresses are pseudonyms, so using Bitcoin is like publishing articles and books under a pen name. If Bitcoin were really anonymous, there would be a total lack of identifying information, and thus a lack of traceability. In fact, the wallet addresses are identities, and the transactions are easy to trace between those identities. If any wallet address can be tied to a particular person, that person is in turn tied to all of the transactions relating to that wallet.
By analogy, we can imagine a world in which every cash transaction involves recording the serial numbers on the bills being used, with those serial numbers then being posted on websites along with date/time/location information. In such a world, cash transactions would still be anonymous in the sense that the convenience-store clerk wouldn’t know your name as you bought a soda but it would be easy for authorities to figure out where money went to or where it came from, in a way that’s usually impossible for cash transactions.
A person who is concerned about Bitcoin traceability can use multiple addresses in an effort to reduce their exposure, but it’s hard to be sure you’ve covered your tracks. Investigators have already been successful at learning many interesting patterns of spending among Bitcoin users, and prosecuting criminals based on records of Bitcoin payments.
Unforgeable History
So far we’ve figured out only how to make each individual item hard to forge, but that doesn’t necessarily prevent an attacker from deleting one or more whole items, or reordering the items. Let’s next consider how to make the sequence hard to modify. When we first get a copy of the sequence, we may well need to validate every item in it to make sure it’s all OK; but we don’t want to revalidate every individual item in the sequence every time we read or modify the sequence. Instead, we want something that is cheaper to check.
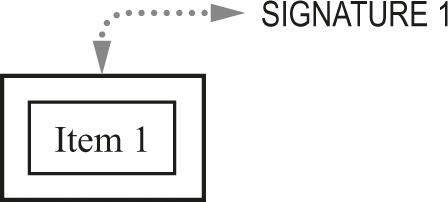
One possible solution is to use a digital signature that covers the whole log. Figure 26.1 shows a single signature protecting a two-item log. Such a signature means that not even one bit of either item can be changed without breaking the matching signature.

Whole-log signature, two-item log.
We can then add an item and protect the new three-item log with a new signature (figure 26.2).

Whole-log signature, three-item log.
Although the new signature ensures that the three signed items are not changed subsequently, the transition from a two-item list to a three-item list was essentially unprotected: There’s nothing stopping the substitution or alteration of item 1 or item 2 after signature A is removed and before signature B is applied. Figure 26.3 shows the problem.

Altering the log while it’s unprotected.
At the top of the diagram, we have the two-item sequence, and we want to add a third item. In the second line, we have to remove signature A to add the third item—just adding in the third item would break the existing signature, which isn’t what we want. But while the signature is absent, an attacker replaces item 2 with X. We then add in our item 3 and sign the three-item sequence, even though the second item was corrupted.
The signature scheme here clearly isn’t working correctly, because removing and replacing the signature left a vulnerability. So we’d instead prefer a scheme in which we sign an item once and then leave the signature alone.
What about signing the whole log all over again every time an item is added?
Figure 26.4 shows a one-item log and its associated signature. Figure 26.5 shows a two-item log and its associated signature.
Nested signatures, one-item log.

Nested signatures, two-item log.
The second item is just appended to the first item with its signature, and the whole pile is then signed.
In principle, this looks like a success. In practice, there will be problems if each change has to sign the whole log again. The log just keeps getting longer, and there is always some per-bit cost for any signing mechanism; so the cost of signing the whole log just keeps growing. A potential hazard is that the system can eventually get to a point where it takes a long time just to read all the bits that need to be signed, without even considering the time it takes to actually do the signing computation as well. A successful long-running system sows the seeds of its own failure; as the number of bits grows, the system becomes ever slower. We don’t really want to build a “success disaster” system, where successful operation of the system guarantees that it just gets slower and slower over time. So we’d prefer to build a system where the cost of signing stays roughly the same, no matter how long the log is.
Fortunately, we don’t have to sign the entire log. All that we really need to do is to ensure that there’s an unforgeable way of adding in each new entry. We can think about simply chaining together two entries:
- 1. the signature of the last entry, and
- 2. the new entry.
Recall that computing a signature over some piece of data means that the signed piece of data can’t be changed by even a single bit. Even a one-bit change will “break” the associated signature—that is, the signature will fail if we test its validity for the changed data. So computing a signature over both the last signature and the new entry means that not even a single bit of either one can be changed.
As with our previous scheme, figure 26.6 shows a single-item log with a corresponding signature. But adding a new element now doesn’t involve all of the earlier items. Instead, the new signature only covers the old last signature and the new item (figure 26.7).

Chained signatures, one-item log.
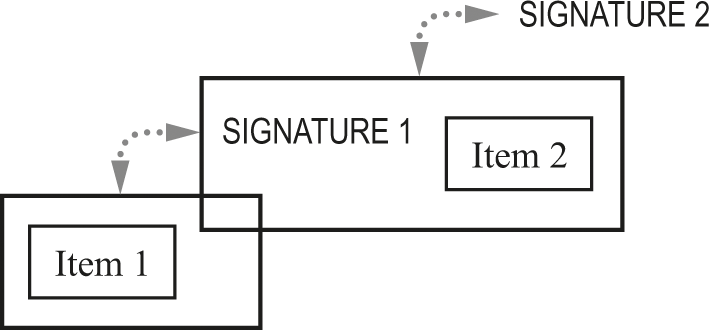
Chained signatures, two-item log.
Even though the signature doesn’t cover the whole log, it still has very similar behavior. In the chain, if even a single bit of item 1 is changed, the corresponding signature breaks.
In figure 26.8, there is a small dot that is different in item 1. As a result, signature 1 no longer matches item 1, as indicated by the large exclamation point.

Single-bit change in item 1 breaks signature 1.
Fixing such a break requires recomputing the relevant signature. In figure 26.9, we’ve repaired the mismatch between the modified item 1 and signature 1, by computing a new signature: signature 1′. But changing signature 1 to signature 1′ in turn breaks the following signature. In the same diagram, signature 2 has broken (as indicated by the large exclamation point). So changing even a single bit somewhere inside the chain ripples down the chain from there, breaking all of the following signatures. Although it’s possible to “fix up” the chain so that it once again contains all correct signatures, such a fix requires recomputing all of the chained signatures after the point of the change.
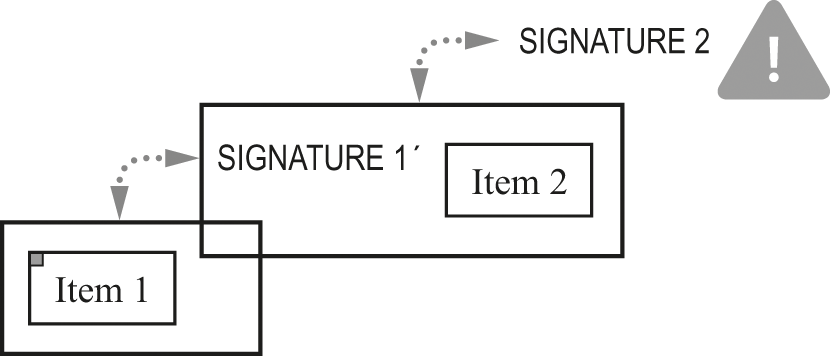
Recomputed signature 1 breaks signature 2.
With this chained-signature scheme, we can now have an extensible sequence of items that’s hard to forge. Attackers can’t simply delete an item, insert an item, or modify an existing item, because any of those changes will break signatures that are expensive to recompute.
Bitcoin Puzzles
The Bitcoin ledger goes a step further than simply chaining entries so they can’t be split apart. There are also limits on what kind of an entry can be added. To understand those limits, we can start by thinking about a large collection of Lego blocks, all the same size, but various different colors. The signature mechanism that we’ve described so far is a little bit like putting blocks together, and using a strong glue to keep them connected. The longer the glue has dried, the harder it is to pry the blocks apart; but we haven’t yet had any limitations on what colors can be added in what order. But let’s assume that we now have a rule that says the blocks have to go in rainbow order: red, orange, yellow, green, blue, indigo, violet, then red again, orange again, and so on. That means it won’t be enough to just have the end of the chain and the glue ready when we want to add a block—we’ll also have to find a block that’s the right color. If the last block of the chain is green, it doesn’t matter if we have lots of red blocks handy; the next block we need has to be blue.
We described this constraint in terms of a well-known fixed sequence of colors. Our next step toward the actual Bitcoin arrangement is to think about a table to let us determine the next color from the current color. For the seven colors of the rainbow, that table may not be necessary if we are pretty good at remembering the colors. But if there were a much larger number of colors and we insisted on particular sequences (“mango” after “fuchsia,” say), then we would have to use a table to keep track of what the next allowed color is.
In Bitcoin, there is a similar kind of constraint in terms of what kind of element can follow another one, but it’s actually even more complicated than a big table of allowed colors. A Lego block has both “bumps” on top and “hollows” below. A single piece both fits onto the piece before it and defines the place where the next piece will fit. In a somewhat similar fashion, in Bitcoin the last element of the sequence is both a solution to the previous puzzle and a new puzzle to be solved. What kind of puzzle is it? In chapter 24, we saw the problem of factoring numbers as an example of a problem that’s hard to solve but easy to check. If you or someone you know likes Sudoku puzzles, those also have the same characteristic. The specific puzzle to be solved in extending the Bitcoin ledger is neither a factoring problem nor a Sudoku, but it shares those characteristics: it’s mathematical, it’s hard to solve, but it’s easy to check.
So instead of having a sequence of Lego blocks where each color determines the following color, Bitcoin has a sequence of puzzle solutions where each solution determines the next solution. A rather elegant aspect of Bitcoin is that the puzzle to be solved hinges on the same kind of mathematical characteristics that we already exploit for signatures, but turned “backwards.” To understand that, we’ll first look inside signatures to examine hash functions.
Hash Functions
A hash function takes an input value and produces a very different output value. It metaphorically “hashes it up.” Typically the hashing-up happens by various transformations on the bits of the input value, but we’re not going to look any further at exactly how any particular hash function works. Instead, we’ll just consider a physical (if crazy) way to build a hash function. Suppose that you have a collection of 1,000 small boxes, each of which has a different output value from 0 to 999 written inside. You take the boxes to some suitable open space like a field or a gymnasium, and you scatter them around and mix them up, so that they are all in random unordered positions. Then you gather them together—still in that random order—and write a sequence of input values from 0 to 999 on the outside of each box. This is now your hash function: to “hash” a number like 72, you just find the box with 72 written on the outside and open it up (to find a value like 381).
This “box-based” hash function is special in two ways: First, the input values have the same range as the output values (both of them run from 0 to 999). Second, every input value maps to a single output value and vice versa. Hashing is actually much more general than this particular field of boxes, but it’s not hard to adapt the field-of-boxes metaphor for more general cases. For example, if two or more different input values can hash to the same output value, that just means that a single box might have more than one number written on the outside.
Now consider how this field-of-boxes works if we want to run the hash function in reverse. We won’t worry yet about why we would want to do such a thing. We’re just looking at how it would work.
Let’s say that the goal is to find the input value whose output value is 42. Naturally, we don’t just go over to the box labeled 42, because that’s an input value—we need the output value (the one written inside the box) to be 42. Instead, we have to open one box after another until we find the one that has 42 inside. It doesn’t much matter whether we open the boxes sequentially or randomly, because we don’t have any way of knowing the fastest way of finding the box that contains 42. However, as soon as we find the box that contains 42, we can easily yell out to any others around what the number is on the outside of the box (say, 89). Anyone who’s skeptical can easily walk over and pick up the 89 box for themselves and verify that it has 42 inside.
Hashing Data
The actual Bitcoin puzzle is like this reverse hash, but it uses much larger numbers than this example. In fact, the input value for the Bitcoin hash is the chunk of new information that we want to add to the distributed ledger. We don’t ordinarily think of a chunk of information—a pile of names, numbers, data structures—as a number. But for any chunk of information in the digital world, we can also look at it as just a string of bits and treat it as a really long number.
So now let’s revisit the situation with much bigger numbers and a much bigger hash function. We won’t try to sustain the field-of-boxes metaphor, just relying instead on the intuition we’ve developed about a forward-hash being easy (opening a single box) while a reverse-hash is hard (opening many boxes in the quest for a particular value).
But wait, there’s more! We don’t just use the chunk of data as the input value to the hash function. The new wrinkle in the Bitcoin puzzle is that the chunk of data we’re adding to the ledger has one part that is adjustable. In that place, we can put any number that we want. That means that we can produce a whole series of different numbers to try with the hash function.
With this arrangement, we can produce lots of different numbers. Can we produce any possible number? No. Even with an adjustable part of the chunk, we can’t produce every possible number. After all, we do still have some unchanging data in the chunk. The situation with these chunks-that-can-be-numbers is a little like being told that the input values have to be of the form 429XXX387, where each of the X’s can be any value from 0 to 9. There’s some variability or freedom, but there are also limits. We can produce 429000387 or 429924387 or 429888387, but there’s simply no way we can adjust those X’s to produce a number like 333333, for example.
Does it matter that we can’t produce every possible number? Not really. In our earlier example of running the hash function backward, we were looking for the single value 42. We might be in trouble if we had to find a single output value now, since we know we can’t produce every possible input value. Fortunately, that’s not an issue for the Bitcoin puzzle. The limits are OK, because we aren’t looking for only a single matching value. Instead, we are looking for any number with a particular “shape.” When thinking about decimal numbers—not the way the real Bitcoin puzzle works—the rule might be that any number ending in three zeroes is acceptable. So that means we don’t care if the number found is 1000, 2000, 10000, or 48290302000—only that it has to have (at least) three zeroes at the end. The real Bitcoin puzzle is like this, but it works in terms of having a certain number of bits being zero.
By trying different values in the adjustable part of the chunk, we can produce different input values for the Bitcoin hash function. For each different try, we then treat the chunk as a number and “look inside the corresponding box” (run the hash function) to see if the number inside has enough zeroes at the end. As soon as we have a winner, we can publish the winning chunk—including the “right” value for the adjustable part. Everyone else can readily verify that the winning chunk does indeed achieve the right “shape” value for the hash function.
Because the hash function is intentionally complex and unpredictable, the only way to find the right input is to proceed by trial and error. Once the solution is found, it’s obvious to all that it does indeed fit; until it’s found, no one knows who will find it first. There are no shortcuts to finding the right solution.
A correctly formed puzzle solution is called a block; not surprisingly, the chain of blocks that the participants collectively build is called a blockchain.
Moving Time Forward
We’ve now seen three of the ways that the blockchain is protected against forgery:
• Each wallet-related item in a block is signed to avoid fake transactions.
• A chain of signatures helps ensure that it’s hard for an attacker to change any item of the blockchain.
• Extending the chain only by solving an unpredictable puzzle both makes it hard for an attacker to change the chain and makes it hard for any attacker to monopolize the process of adding updates to the chain.
These techniques already mean that it would be expensive to forge a different version of the blockchain: it would require recomputing lots of signatures, and again solving lots of trial-and-error puzzles.
However, we still have to be concerned that a well-equipped attacker could invest a lot of time and resources in just such a brute-force approach. We know that the cost of altering the chain increases with every block following the point of change; accordingly, we would expect a brute-force attacker to focus on something that’s newly added to the chain. Can the participants discourage such an attack? Yes, thanks to an additional part of the system: The blockchain does not simply sit idle, waiting for new items to be added. Instead, there is an ongoing process whereby participants are always trying to add more blocks to the shared chain. The participants are in a perpetual churn of working to lengthen the chain, even if there’s no new information to add to the ledger.
Why is it useful to have all this logically unneeded work of chain-lengthening, even if the ledger’s content is not otherwise changing? We can see it as imposing a kind of deadline. Suppose that we are given a hard puzzle to solve, and without a deadline it would usually take us a month to solve it. That puzzle becomes harder if we impose a deadline of solving it in an hour or less, even though the puzzle itself is identical. In a roughly similar fashion, if the chain were static, then it might not matter that the chain is expensive to forge—because a determined attacker could choose to spend whatever time was required to forge it. However, there’s a deadline because the puzzle keeps changing. The blockchain combines both an expensive-to-forge representation and a “now” that is constantly moving forward. That combination makes it hard to forge a replacement log.
The Crowd Foils Cheating
What if attackers simply assert that they have solved the necessary puzzle when they really haven’t? Remember that the puzzle solutions are easy to check, even though the puzzle is hard to solve. Each participant maintains his or her own local view of the chain, with his or her own local decision about whether a block can be added at the end of the chain. A correctly functioning participant (defender) who receives a failed puzzle solution simply ignores it. If most of the community does likewise, then the collective view of the chain is not fooled by the attempt to cheat.
What about the inverse problem, where a cheater ignores a correct solution? The cheater’s local view of the chain would no longer match what others have; in particular, the cheater would still be working on solving the problem of adding to the “old” tail of the chain while everyone else has moved on to a new problem. Ignoring a correct solution hurts only the cheater.
Informally, we can argue that successful cheating requires that the cheater(s) have far more computing power than everyone else. With completely dominant computing power, it would be possible to find solutions faster than anyone else. After enough time, it would be possible to build up a completely bogus ledger so that it was the longest chain, and accepted by the wider community. However, if computing power is divided among participants with diverse interests, the overall system will still function properly even if some of those participants try to cheat. Notice that we can also turn that reasoning around to produce a caution: if some participant or group of participants can amass a majority of the available computing power, they will be able to cheat.
Rewards via Mining
As we have noted, the Bitcoin system depends on convincing participants to spend their resources on producing new elements of the blockchain. In fact, it’s not enough to just have some participants working on that task—to beat an attacker, the defenders need to ensure that more resources are spent extending the blockchain than any attacker can use. How is that possible? The answer is surprisingly simple: Participants are paid for successfully extending the chain. Every successful addition to the blockchain also produces a small amount of new bitcoins, credited to the participant that successfully solved the relevant puzzle. How do the new bitcoins appear? There’s just an entry in the distributed ledger, like any other entry describing a transfer; we can think of it as a reserved entry in each block that is filled in with the identity of the participant, and thus becomes part of the chain if that participant solves the problem first. The process of adding blocks to the chain is often called mining.
Let’s compare bitcoin mining to gold mining. Mining for bitcoin is like mining for gold in that a lot of effort and machinery are used in the pursuit of unpredictable rewards. In the case of bitcoin mining, all of the effort and machinery is computational—but overall, the analogy still works. Whereas a gold miner is handling a large volume of low-value minerals to find a small volume of gold, a bitcoin miner is handling a large volume of failed puzzle solutions to find a small volume of correct puzzle solutions.
However, the analogy has its limits. A notable contrast to gold mining is that there are no richer or poorer veins of the desired reward. All the bitcoin miners are effectively competing within one single mine, as defined by mathematical properties of the universe. In fact, they’re all working at the very same “mine face” within that single mine.
Another notable contrast is that speed is essential to miners—a puzzle solution is only valuable if immediately published, beating all the competitors who are also looking for the next solution. That’s not like gold mining, where once you have the gold it’s yours regardless of whether anyone else knows about it. In some ways, bitcoin mining is more like staking claims than like mining—if there are competing claims to the same property, the winner is the one who gets the paperwork filed first.
Also in contrast to gold mining, the productivity of bitcoin mining is controlled by an automatic feedback process. When bitcoins are being produced too quickly, mining them becomes harder. When bitcoins are being produced too slowly, mining them becomes easier. The system includes a well-known limit to the number of bitcoins that can ever be mined, so eventually mining will end. Until then, the bitcoin “mine” never gets “worked out” like a gold mine—but it also never hits rich new veins like the ones a gold mine might have.
Pollution and Bitcoin
Although it might sound very clean and environmentally friendly to perform mathematical puzzle-solving at high speed, the ugly reality of fast computing is that it requires energy. Bitcoin miners compete with each other in terms of their ingenuity and engineering for who can most effectively convert energy into new blocks on the blockchain; however, the blockchain itself is indifferent to everything except the mathematics of the puzzle-solving. Accordingly, it’s often economically attractive to use lots of cheap energy, rather than being sophisticated about energy usage. At this writing, bitcoin mining is dominated by miners in China, who achieve their advantage primarily through the use of highly polluting (but cheap) coal to generate the electricity used.
Even if we were using energy to provide a direct benefit to people in the form of heat or electricity, increasing the consumption of “bad” energy sources seems like a poor choice. Such a choice of harmful energy sources seems especially dubious when the growth in pollution and heat generation is simply driving a kind of computational treadmill. Although that activity might be worthwhile to keep people from cheating on Bitcoin transactions, it doesn’t seem like it should be a high priority if it’s damaging the environment.
The Bitcoin system structure is elegant if all miners are using similar sources of energy, but this “race to the bottom” for the cheapest, nastiest energy is a serious drawback. It will be interesting to see whether this situation can be improved: perhaps in a future evolution of Bitcoin, or perhaps a different competing approach to building a distributed ledger.
Mining and Value
The community of miners is not fixed. Instead, each individual participant is free to join or leave the community of miners at any time. Indeed, if you are so inclined, you can personally acquire the equipment and knowledge required to mine bitcoin—part of its appeal is that there are no gatekeepers to judge your worthiness to join the community. That community is the engine powering the blockchain, and the community’s efforts are an important component of how well the system can defend against cheating. So it’s worth looking a little closer at what prompts a participant to join or leave the group of miners.
Being a miner means that you have some step-taking machinery at your disposal, and you choose to perform the mining computations: the puzzle-solving task that allows an update to be added to the chain. If there are no other miners, the analysis of rewards vs. effort is easy: the sole miner reaps all the rewards. As soon as there are any other miners, there are no guarantees of rewards; instead, it’s a little like buying lottery tickets.
In a lottery, the odds are arranged so that the players lose on average. Bitcoin miners are more calculating than lottery players—they want to “play” only when they will win. Each participant “plays” when they expect their reward to exceed their costs. If any participant expects to lose in this exchange, they will stop mining. But this simple formulation leaves us with the question of what makes the exchange attractive or unattractive at any particular point in time. The decision is necessarily a matter of judgment—the exchange is between the likely cost of “winning” the next block on the chain and the next expected reward. We could pursue this analysis in some detail, but we wouldn’t really learn anything more about Bitcoin as a system. We can simply wind up our examination of the join-or-leave decision by observing that it’s impossible to get it exactly right—between the unpredictability of rewards, the unknown behavior of other players, and the volatile “real-world” value of bitcoins, there’s too much noise in the system to make precise reliable rules. It’s worth underscoring this point: Although parts of the Bitcoin system are encoded as programs and very mechanical, each participant’s decision to mine or stop mining necessarily depends on human judgment.
Bootstrapping Value
Bitcoin links economic incentives to a desired system behavior. The system rewards miners for their work by providing them with bitcoins. This approach is great if you can get it to work, but there is a bootstrapping problem: what makes the reward valuable? A number of Bitcoin variants and derivatives have been created, which shouldn’t be surprising—after all, once you realize that it’s possible to create a money system without government involvement, why stop at just one? But each such new currency creates again the chicken-and-egg problem that afflicted Bitcoin in its early days: to be valuable, a currency needs to be widely accepted; to be widely accepted, a currency needs to be valuable.
For a concrete example, imagine that Bob wants to create a new currency called Bobcoin. It’s easy for Bob to just set up the system and start mining bobcoin, awarding himself bobcoins every time that he extends the blockchain. But the bobcoins don’t have any value as long as he’s the only one who has them, and it’s not clear what anyone else gains from joining with Bob in the Bobcoin world.
These kinds of currencies have intriguing analogies to a startup company. In both cases, there is a step that seems like the creation of something potentially valuable from nothing at all: the mining of coins in one case, the issuance of stock in the other. But in both cases the “something” that’s created is best understood as a share of something aspirational.
Why do people accept payment in shares of a startup company? Because they believe it will be worth more in the future; because they believe in the future of the company. Likewise, why would early adopters accept a reward of bitcoins? Because they believed that reward would be worth more in the future.
Bitcoin and Governance
Bitcoin is an ingenious system. However, its origins can prompt some understandable concern. The system was invented and published by “Satoshi Nakomoto.” At this writing, no one has satisfactorily connected a real person or group to that name. Since no one knows for sure who invented the scheme, it’s hard to judge their motivations. It’s entirely possible that there are hidden conflicts of interest or outright cheating that should affect our willingness to use the system.
The Snowden revelations about activities of the U.S. National Security Agency (NSA) included some surprising efforts by the NSA to subvert cryptographic standards. It’s entirely conceivable that some actor—not necessarily the NSA, not necessarily any U.S. agency—is doing something similar with Bitcoin. Unfortunately, it’s not even clear whether such subversion would be undercutting Bitcoin (to cheat in the future) or whether Bitcoin itself is a big subversion (to avoid a better, less traceable cryptocurrency). These suspicions will necessarily endure as long as the origins of the system remain obscure, and to be fair, there will probably be some concerns about the nature of Bitcoin even if all of its origins and early history are completely revealed.
For partly related reasons, governance of the Bitcoin system is problematic. The problems don’t affect the minute-to-minute, day-to-day behavior: the ordinary operations of recording transactions in the blockchain seem to be quite reliable. Despite a variety of attacks and errors, at this writing the Bitcoin system itself is still running. If some participants take actions that cause the state of the system to be split or unclear, the participants with the most computational power eventually win; the ongoing operation of the system resolves the conflict. That part of the Bitcoin experiment can probably be deemed a success.
Although the features that let Bitcoin work are powerful and interesting, they should not be oversold as somehow providing new ways to organize society. Indeed, there is at least anecdotal evidence in the opposite direction: that Bitcoin needs more “political” elements to thrive. Although the day-to-day operation of the system works surprisingly well, there are serious problems whenever that operational system encounters its own design limits or flaws. Bitcoin is not perfect, and sometimes the imperfections become serious obstacles to continued operation of the system. At such a point it becomes apparent that Nakomoto’s design did not include any reliable mechanism to choose among competing versions of how the blockchain mechanisms should evolve. We might say that the system’s operations work acceptably, but in contrast its “meta-operations” are not adequate. In some ways Bitcoin is like a constitution that does not include an amendment process.
Naturally, it’s difficult to establish trust in a system intended for use among mutually untrusting participants. However, experience with Bitcoin suggests that evolving systems inevitably encounter some situations that are difficult to handle without any trust. In certain kinds of decisions, resolution is easier if at least some of the participants trust each other—accepting a temporary loss of control or power, in the expectation that there will be a better eventual result.
Significance of Bitcoin
What is the significance of Bitcoin? The system serves as a useful demonstration that it’s possible to build a distributed ledger that works, even when some people are trying to cheat. That demonstration is valuable regardless of how Bitcoin succeeds or fails subsequently. Whether Bitcoin supersedes the payment systems of the world or collapses due to governance failures, it will have been a valuable experiment and will have accomplished more than many people thought was possible when it started.
Bitcoin is potentially important to the world at large. We can see in it the seeds of a next wave of digital revolution. We have seen textual information become digital and then networked. After that, we’ve seen audio and video became digital and then networked. In Bitcoin we can see ways in which various kinds of financial entities—money, commitments, contracts, and escrow—become digital and then networked.
What if we narrow our interest to the focus of this book? What is Bitcoin’s significance as a computational system? Bitcoin comes closer than any other system we’ve examined to substituting mathematics for trust. That capability of achieving something useful for a group, with others whom you don’t know (or perhaps even know and actively distrust) is very interesting. Bitcoin is powered by an intriguing combination of self-interest and mathematics.