3 Processes
In the previous chapter, we looked at the idea of stair steps as the “digitized” version of a ramp. We compared stairs to ramps as a way of getting a perspective on what it means to be digital versus analog. Now let’s consider the idea of moving forward in discrete steps—not necessarily on a stairway, but just as separate and distinguishable steps. These are the kind of “digital actions” that make up the behavior of software. In the same way that we wondered in the previous chapter about a pixelated world around us, now we will consider what it would mean to have all activities (ours and others’) similarly “pixelated.” In the course of the chapter, we’ll work our way down from abstract ideas of steps to some very concrete characteristics of computing hardware.
Our first steps of interest are like a person walking deliberately, not walking quickly or running. Each step is either yet-to-be-taken (has not yet had any effect) or has-been-taken (has had its effect). We are moving from one stable standing position to another, with the move caused by a single step. We said previously that we don’t assign a distinct meaning to partly raised fingers when we’re counting on our fingers; likewise, we don’t see any “partial” steps, any “halfway” results, or the like.
A step is the smallest indivisible atom, and everything is built up from there. This approach contrasts with everyday intuitions about time: we tend to assume that time can be divided as finely as we want. Our best available stopwatch may be unable to measure a unit of time smaller than a hundredth of a second, but we nevertheless believe that there are smaller intervals of time that could (in principle) be perceived or measured with more elaborate instruments. In contrast, in this world of steps, there is nothing smaller than the smallest step size.
Reading as a Process
With the simple definition of process as “sequence of steps,” we can see processes everywhere. For example, consider reading a book—as you are doing now! Scientists have learned that reading is a startlingly complex process when examined in terms of its physiological/neurological/psychological mechanisms. We won’t try to cover all of those details. Instead, we’ll focus on the experience of reading and pick out elements that help us build up more general ideas of how processes work.
We can see reading as a process with each page read being a different step, starting at the first page and ending at the last page. Or we can see reading as a process with each sentence read being a different step, or each word, or each letter.
As shown in figure 3.1, we can think of reading an excerpt from a book as reading a sequence of pages, or reading a sequence of sentences. Notice that the sentence boundaries do not coincide with the page boundaries, so a step at one level may not correspond exactly to a step at another level.

Pages and sentences.
Similarly, in figure 3.2, we can think of reading a section of text as reading a sequence of sentences, or reading a sequence of words. Since it’s not possible for a single word to be split across sentences, it’s possible to find an exact word boundary for every sentence boundary (but not necessarily the other way around).

Sentences and words.
All of these different kinds of steps are acceptable as descriptions of some kind of process. We could even get sophisticated and combine these descriptions, so as to capture the relationships: pages contain words, which contain letters, while sentences also contain words, which contain letters; but sentences often cross page boundaries, so it wouldn’t be correct to claim that a page contains only whole sentences.
There is a potential source of confusion here, because there are some circumstances in which we will be dealing with something that seems like a partially taken step. As in the case of letters, pages, words, and sentences, it is sometimes useful to build smaller steps into sequences of steps, and then treat such a sequence as a single larger step. Sometimes that sequence will fail to act like a single step and will be prone to partial completion, partial changes, and the like. However, that difficulty doesn’t change the nature of the digital model. If we look inside a partially completed step, we’ll find smaller steps being grouped together. Somewhere, down low enough, is some kind of indivisible step. The bottom layer of the system is some kind of machinery that accomplishes a single step cleanly, indivisibly, repeatedly.
For the sake of generality, we will sometimes talk about a lower layer as the “step-taking machinery.” That term can certainly refer to a “computer” as it is commonly understood: readily purchasable hardware. When we look carefully at one of those computers, we see an electrical device. We have to plug it in or provide battery power for it to work. If we open it up, we see various chips and widgets that perform electronic or magnetic tricks, powered by the electricity. It’s easy to think that the electricity and the exotic parts are required for computation. But actually, none of that is really essential except for its being an extremely fast step-taking machine. Even if we think of some bizarre future or alternative computer with no electricity, electronics, or magnetic components involved, our ideas here will still be relevant as long as it’s a step-taking machine.
Turing Machines
There is a simple model of this generic step-taking machine. It consists of two elements: a kind of “cheat sheet” and a kind of “scratch pad,” as shown in figure 3.3.
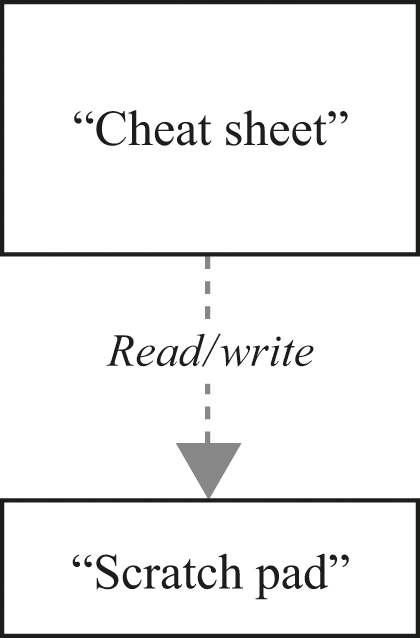
Cheat sheet and scratch pad.
The cheat sheet is like a specialized, customized dictionary. However, the details are a little different from a dictionary: instead of looking up the definition that corresponds to a particular word, the machinery uses the cheat sheet to determine what it should do next. So the machine’s actions are completely determined at each step by the combination of what’s on the scratch pad and what’s on the cheat sheet. For a given machine, we can set up its cheat sheet however we want, but the machine doesn’t modify that cheat sheet once it starts running. In contrast, the machine does modify the scratch pad. The machine has a simple repeating cycle: it looks at what’s on the scratch pad, then looks up the corresponding behavior on the cheat sheet, then writes something on the scratch pad. Surprising as it might seem, this arrangement is basically a computer.
The scratch pad is actually a little more structured and a little more limited than you might think from the preceding brief description. First, the scratch pad is divided into discrete areas arranged in a row. Conventionally, these areas are cells big enough to write a single character, but they could be small enough that you could only write 0 or 1, or (in principle) big enough to write a novel. It’s crucial that there should be clear boundaries between the cells (so there’s no confusing one of them with another). It’s also crucial that a cell’s contents should be recognizable in a single machine step—this is the reason why people don’t actually make the cells big enough for a novel. Finally, there have to be enough of these cells that we don’t worry about running out. To save ourselves any concerns about having enough cells, we just say that there are always more cells available—an infinite number of cells, if necessary.
The step-taking machine has one particular cell that is its current focus: the machine reads or writes only the current cell. The machine can also change the current cell, but it does so only by shifting its focus one cell left or one cell right.
This machine takes steps: one step at a time, repeatedly. From one point of view, every step is identical: it consists of reading the current cell, looking up the corresponding entry in the cheat sheet, writing the current cell, and moving left or right to a new cell. From another point of view, every step is different:
• Whatever is read in the current cell may be something that’s never been read before in this computation;
• the action to be taken may be something that’s never been found before on the cheat sheet in this computation; and/or
• whatever is written into the current cell may be something that’s never been written before in this computation.
So even though the outline or structure of every step is identical, the detailed content of any particular step—its inputs, actions, outputs—may be unique.
A computer scientist would refer to this step-taking machine as a Turing machine (see figure 3.4). It is named for its inventor, mathematician Alan Turing. The computer-science name for the cheat sheet is a finite state machine. In Turing’s original formulation and most other descriptions, the part we have called a scratch pad is described as a kind of tape.
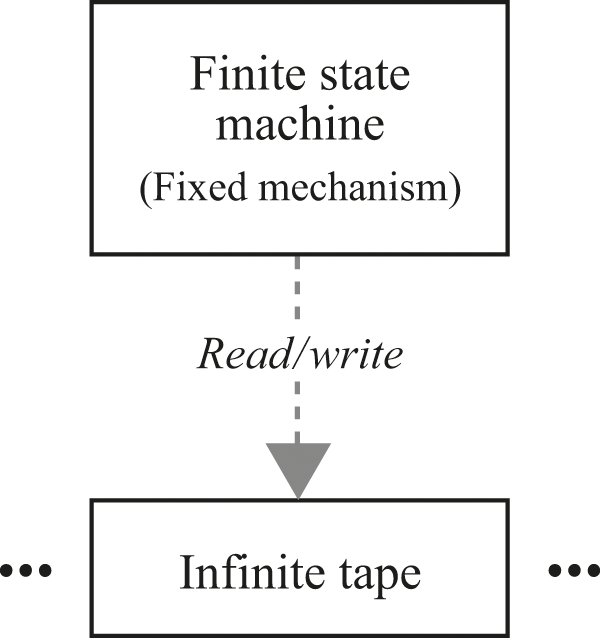
Turing machine.
Rather surprisingly, this odd combination of cheat sheet, scratch pad, and repetitive simple steps turns out to be enough to represent any computation.
You can see the shadow of a Turing machine if you look the right way at a modern computer. A modern computer has some hardware with a fixed set of repetitive functions, like the cheat sheet/state machine of the Turing machine. A modern computer repeatedly performs a cycle of fetching the next instruction and performing its corresponding actions, in much the same way that a Turing machine repeats its simple read/lookup/write behavior. And a modern computer can read and/or write to any of a large collection of locations in memory or on disk, in much the same way that a Turing machine can read and/or write to any of the infinite number of cells on its scratch pad/tape.
A modern jet airliner has nothing specific in common with the first powered airplane flown by the Wright brothers, yet we can still recognize the common features. In much the same way, a modern computer is far more sophisticated and capable for practical computations than is a Turing machine, but we can still see the family resemblance.
Infinite Processes
Reading a book is typically a process with an identifiable beginning and end. Most often the process starts at the first page and ends at the last page. But sometimes reading is an unending process. For example, some people adopt a routine of reading a few verses of the Bible each day. When they reach the end of the book, they restart from the beginning.
In talking about these issues, it’s helpful to separate specification from behavior. A specification is a higher-level description of what we want to happen, whereas the behavior is what actually happens. Once we separate specification from behavior, we see that it is possible to have a compact specification whose corresponding behavior is very noncompact—long in time, massive in space. An easy example is a process that simply prints “Hi,” then pauses a second and repeats (see figure 3.5).
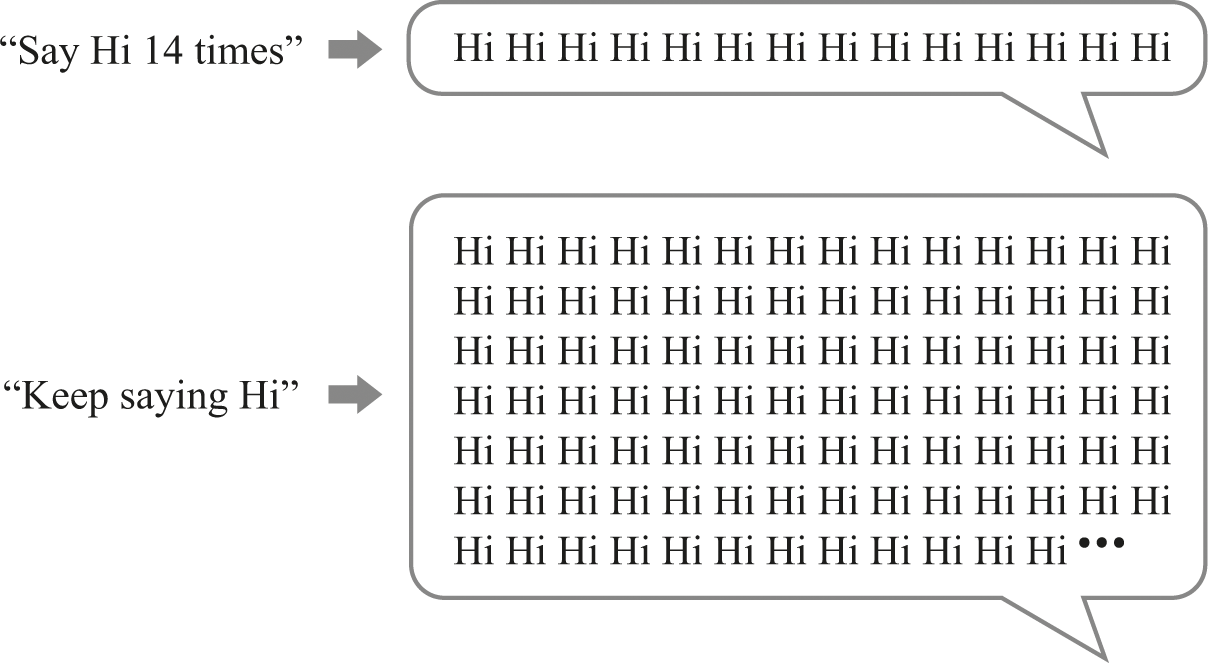
A finite process and an infinite process.
It’s not very useful, but it does make the point: its description is short, its activity goes on without end, and the number of times it will print “Hi” is unbounded. We might refer to the description/specification here as a program, although it’s a very informal kind of program. As we see with this example, a small program can specify a process that continues endlessly.
Execution
What happens in a process—its actual behavior—is also referred to as the execution of a process. The execution of a given process (for example, one of the reading processes) depends on something taking steps, supplying the energy to proceed. In the case of our example reading process, the reader is supplying the energy to go to the next step. In the case of a computer program, ultimately it’s the hardware that supplies the energy. Indeed, that’s what a computer ultimately is: something that transforms energy into steps.
On one hand, the process is something real that can accomplish effects in the world; on the other hand, it is just the shadow cast by the step-taking machinery as driven by some program. To shine a different light on execution, we can ask, What is the relationship between a reel of movie film and the movie projected on the screen? Or, What is the relationship between a phonograph record and the music coming from the speakers? To a computer scientist, these are both analog versions of the relationship between program and process. The reel of film and the record are both like programs, while the projected movie and the playing music are both like processes. The movie projector and record player are both machines for this transformation, like the step-taking machinery we have described.
We can say that a program is a static description of what a process does, or we can say that a process is a dynamic realization of what a program describes. Either way, it’s important to see that program and process are at one level alternative descriptions of the same thing, and at another level are completely different from each other.
Both movie film and phonograph records are like programs in that they are mechanically interpreted—we place an emphasis on their consistent playback, and great effort goes into ensuring accuracy of reproduction. There is a looser analogy to programs and processes when we consider the relationship of a musical score to an orchestral performance, or the relationship of a recipe to a cooked dish. Although there is the same sense that the score and performance are closely related but different kinds of entities, and that the recipe and dish have a comparable relationship, we expect that the interpretation of the “program” in these cases is not achievable by pure mechanics. Indeed, many observers would judge a “mechanical” interpretation in these domains to be of low quality. Investing effort in greater fidelity of reproduction in these domains would seem to be missing the point.
Because movies and recorded music are mechanically reproducible and place an emphasis on fidelity, they have rapidly shifted away from analog media to digital media. In a few years, perhaps, most readers won’t really understand the point of our analogy to film and records, because those artifacts will be so unfamiliar, completely replaced by digital versions.
Now that we understand something about what these “action steps” are, we should consider in some more detail how to realize them in practice. That means understanding something about both what is involved in making a program and what is involved in making the step-taking machinery that can execute that program.
Effective Construction
Programs are examples of what computer scientists would call effective constructions: things that we can actually understand how to build.
In contrast, mathematics doesn’t require effective constructions. Mathematically, there’s nothing wrong with assuming conditions that we don’t know how to achieve, as in the old joke about a mathematician hired to increase milk production who starts the presentation by saying, “Assume a spherical cow.” Similarly, there’s nothing mathematically wrong with the following technique for finding the weight of an average grain of sand:
- 1. Weigh beach to determine total weight
- 2. Count grains of sand to determine total number of grains
- 3. Divide total weight by total number to determined average weight
However, we can recognize that this is not an achievable or sensible procedure: it’s not clear what it really means to “weigh a beach,” or what apparatus we would use. Likewise, although it might be possible to count all the grains of sand on a beach, it seems like a poor way of spending one’s resources. This “beach-weighing” approach is a handy counterexample to what programmers do. For computation, each step must be effective—we have to have some means of actually performing it, not just conceptualizing or imagining it.
Hardware vs. Software
In principle, we don’t need any machinery to execute a program. Indeed, the earliest use of the term “computer” was for people who performed calculations. If we were so inclined, we could always just work through the step-by-step execution of a program by hand. But execution by hand is slow, error-prone, and excruciatingly tedious. So we’re almost always more interested in using some step-taking machinery to do the work.
In the terminology of computer scientists, the step-taking machinery is usually referred to as hardware, while the programs being executed are software. A handy way of making the distinction is to think about whether the item of interest could somehow be transmitted via telephone. So the design of a physical computer (its specifications and drawings) can be seen as a form of software, but the device itself isn’t.
So far, we have talked about the hardware as though it is fixed, and only the software is dynamic or changeable. But this is not an accurate summary of the situation. In fact, hardware is itself an engineered artifact, and so hardware is subject to revision, redesign, and adaptation. Just as it’s possible to build better programs and processes, it’s possible to build better hardware. And it’s even possible to take a holistic view of software and hardware, with the idea that the hardware/software boundary is subject to movement and redesign.
Further blurring the issue is the possibility of using customizable hardware. One example is a technology called field-programmable gate arrays (FPGA). An FPGA consists of a large collection of small, simple hardware resources whose interconnections can be arranged to better match the structure of the problem to be solved. Viewed in one way, such an FPGA is hardware; viewed another way, it’s software.
When we can take a holistic view, it is often useful to move functionality from software into hardware to speed it up, or to move functionality from hardware into software to increase flexibility. It’s possible to think in terms of a total system design approach, in which we start with all software and “crystallize” the lowest levels into faster hardware. Alternatively, we can think of starting with all hardware and then “vaporize” the higher levels into more-flexible software. Our overall goal is to strike the right balance between speed and flexibility.
The tricky part of this trade-off is that putting too much functionality into hardware can actually decrease the overall speed possible. So although a naïve view is that “hardware is fast,” one has to be careful not to pursue this blindly. Instead, it’s more accurate to say that “simple hardware is fast.”
Uniformity Gives Speed
To understand why not all hardware is equally fast, consider running a warehouse that stores cans of soup for a single product line of a single manufacturer. At one level you may be handling a tremendous variety of merchandise—perhaps there are hundreds of different kinds of soup. However, at the level of handling the goods in the warehouse, all of those different kinds of soup are basically alike: they come in the same size cans, the cans are packed in the same size cases, the barcodes are in the same places on the cans. There is a lot of uniformity, and accordingly your shelving and machinery can be optimized around that uniformity.
Suppose that your success at soup-handling gives you a reputation for running a fast and efficient warehouse, and other manufacturers start to ask you to handle their warehousing. Some of their goods are different sizes from soup cans. Even when you consider only the other soup manufacturers, they don’t use the exact same cans or boxes or barcode placements as the single manufacturer you worked with before. Inevitably, the reduction in uniformity makes the operation less efficient: there’s now a need for more-expensive infrastructure, and any given set of operations probably takes longer.
Similar issues arise when building a step-taking machine. The more alike the operations are, the more efficient the execution of those operations can be. The more different kinds of operations we ask the step-taking machinery to do, the more uniformity decreases and costs rise.
Moore’s Law and Uniformity
There is potentially an additional level of cost from nonuniformity. We can see this additional cost most clearly if the warehousing industry as a whole is focused primarily on soup cans. If there are competitive suppliers of shelving and automation, and most are delivering soup-can handling systems, we expect that there will be steady improvements in those areas—and as consumers of those systems, we expect to reap those benefits. In contrast, consider what happens if we are building our own nonuniform systems that are very different from what the industry as a whole is building. We may benefit from having a very different market niche, but we will be unable to benefit from those soup-can-focused improvements that the industry is delivering.
Likewise when we apply this thinking to computers, we can see that it’s possible to build custom hardware of various kinds to address particular computational problems. That custom hardware yields benefits in the near term, but we lose out in the longer term to the continuing process improvements driven by mainstream computing.
This observation leads us to recognize that there is a significant economic element at work here. In 1965, Gordon Moore published a paper about the trend of transistor density in the semiconductor products we’ve come to call “chips,” but which are technically called integrated circuits. Moore observed that in the period from 1958 to 1965 this density had doubled every year, and that the trend was likely to continue for a number of years to come. The increased density means both more devices and faster devices for a constant amount of money. In line with Moore’s observation—subsequently dubbed Moore’s law—computing devices have had many years of dramatic improvements in their cost and performance.
Moore’s law is often cited as an amazing and counterintuitive aspect of the modern development of computing, and it is indeed remarkable to see the way in which speeds and storage capacities have expanded while costs have declined. A common way of capturing the extreme nature of these improvements is to recast them into another domain, like transportation, and ask people to consider what it would be like if a modern commercial aircraft only cost $500, circled the world in 20 minutes, and used only 5 gallons of fuel to do so. Because of this dramatic history of improvement, people sometimes invoke Moore’s law as though it will solve all problems of having enough computation within another few years. The reality is a little more complex. In the rest of this chapter we’ll work out what Moore’s law really says. A later chapter will explain why even the startling improvements from Moore’s law do not overcome the costs of some computational problems.
Moore’s law is a statement about the rate at which hardware improves over time. When you get into the details, there are actually multiple slightly different versions of Moore’s law—so it’s not as lawlike as its name would suggest. For our purposes, we’ll treat Moore’s law as saying that the density of transistors on chips roughly doubles every 18 months.
An important qualification to Moore’s law, frequently overlooked, is that it applies to what might be described as the mainstream of computing. The computing tasks and computing machines that are of the most interest to the most people receive the most attention from engineers, and are the areas of keenest competition. So in addition to our observation that “simple hardware is fast” we also need to be aware that “common hardware is fast.” This principle is a little counterintuitive, so it’s worth explaining carefully.
Moore’s law is a special version of a more general economic principle. In any manufacturing business, we expect that we will benefit from economies of scale—if we can sell more identical copies of the widget we produce, we will be spreading our fixed costs across more sales, lowering our overall costs. In addition, larger-scale production typically benefits from more attention by smart people concerned with lowering manufacturing costs. This can lead to a virtuous cycle in which customers are attracted to these bigger-selling widgets because they are cheaper than alternatives.
Moore’s law is really about the rate of improvement in the most popular choice(s), and its underlying engine is this virtuous manufacturing cycle. The further removed we are from the most popular family of products, the less we benefit from Moore’s law. Although it’s often presented as though it were related to electronics or computers in general, Moore’s law is really more about the progress of the technological mainstream.
Even without the benefit of any further improvement from Moore’s law, the modern world contains amazing step-taking machinery that is readily available to us. We have devices that can execute literally billions of (simple) steps each second, with the cheapest such devices costing only pennies.