It was the mathematician Hermann Minkowski who joined space and time together in his 1908 talk to the 80th Assembly of German Natural Scientists and Physicians stating that “Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” Interestingly enough, Einstein was not initially comfortable with the reformulation of special relativity by Minkowski, his former teacher, into fourdimensional spacetime. Let us begin with this union of space and time.
In Euclidean space, which has a positive definite metric, the time coordinate has the same status as the space coordinates; in relativity theory, the time coordinate has a special status due to the indefinite metric of Einstein spacetime. The most important thing to remember is that, just like the space coordinates, the time coordinate itself is not associated with a “flow” in any particular time direction. It does not have an intrinsic orientation, asymmetry, or arrow associated with it. Put another way, there is no “arrow of time” associated with the time coordinate itself except for what we give it for illustrative purposes.
The concept of “time” has multiple meanings: there is the coordinate itself; and there is the asymmetry of time in our three-dimensional space — which never changes its direction of flow; thermodynamic time, associated with the increase of entropy; psychological time, which each of us experiences as a present moment moving into the future; and finally, the concept of “cosmic time” associated with the expansion of the universe. Although these different concepts may be related, they are not identical and should not be confused.
The Minkowski diagrams of special relativity are made up of a continuum of space-like three-dimensional hypersurfaces along the time axis and perpendicular to it. The general view of time is that if one were to travel backwards in time one would see, for example, a sphere representing a propagating light pulse getting smaller and taking the size it had at an earlier time. That is, moving backward in time takes one to a three-dimensional space as it was in the past with the configuration of matter being what it was at each instant of past time. In this conception of time, three-dimensional hypersurfaces continue to exist in the sense that moving backward in time, were that possible, recapitulates threedimensional space exactly as it was in the past. This concept of time leads to the usual conundrum that one could go back in time and murder one’s grandfather. There is an even deeper problem.
The Einstein field equations of general relativity (the theory of gravity) have solutions that apply to objects like the earth or sun or to the universe as a whole. In the case of objects like the earth or the strong gravitational fields of massive neutron stars, these solutions have been tested to a very great accuracy. But the field equations also have perfectly good solutions, such as the infamous Gödel solution, that allow closed time curves.1 Not only does this solution allow closed time curves, but in addition, closed timelike curves pass through every point of this spacetime, and even more problematic is that there exists no embedded threedimensional spaces without boundary that are spacelike everywhere, nor does a global Cauchy hypersurface exist.2 Under the usual conception of time, moving in one direction along closed timelike curves is the equivalent to traveling backwards in time in that one may not only eventually arrive at the time when one began, but the configurations of three-dimensional space repeat themselves over and over again.
The Gödel solution and others like it are generally dismissed as being non-physical, but that simply begs the problem raised by their existence. The famous Kerr solution, representing the spacetime around a rotating mass, and which has no known interior solution — unlike the static Schwarzschild solution for a non-rotating mass — also has closed timelike curves if the angular momentum in appropriate units is greater than the mass, and one passes through the ring singularity. Yet, this solution is not dismissed as being non-physical.
Stephen Hawking has tried to get around the problem of closed time curves by introducing what he called the chronology protection conjecture: “The laws of physics do not allow the appearance of closed timelike curves.” But thus far there has been no proof of this conjecture. Einstein’s field equations alone, being partial differential equations, only tell us about the value of a function and its derivatives in an arbitrarily small neighborhood of a point. Whether closed time curves exist or not is a global question that may also depend on the topology of the spacetime. Some things about closed time lines are known. For example, for asymptotically flat spacetimes, if certain energy conditions are satisfied, closed timelike curves can only occur if spacetime singularities are present.
If a signal may be sent between two points in spacetime only if the points can be joined by a non-spacelike curve, then the signal is said to be causal (this type of formulation allows for the possibility that the two points can only be joined by light rays). The spacetime will be causal if there are no closed non-spacelike curves. The non-rotating solutions to Einstein’s field equations, such as the Schwarzschild and Friedman–Robertson–Walker cosmological solutions are causally simple. For most “physically realistic” solutions it has been shown that the chronology condition — that there are no closed timelike curves — is equivalent to the causality condition stating that there are no closed non-spacelike curves.3
More generally, the Einstein field equations belong to a class of partial differential equations known as symmetric hyperbolic systems.4 Such equations have an initial-value formulation in the sense that once initial data are specified on a spacelike hypersurface, the subsequent time evolution follows from this data. Unlike the Gödel solution, where a global Cauchy hypersurface does not exist, if a Cauchy surface does exist, and initial conditions are imposed on it for its future evolution governed by the Einstein field equations, closed timelines — the equivalent of a “time machine” — cannot occur. As put by Geroch, “. . . there exist solutions of Einstein’s equation in general relativity that manifest closed causal curves. But we do not, in light of this circumstance, allow observers to build time-machines at their pleasure. Instead, we permit observers to construct initial conditions — and then we require that they live with the consequences of those conditions. It turns out that a ‘timemachine’ is never a consequence, in this sense, of the equations of general relativity, . . .”5
The usual conception of time, with its past three-dimensional hypersurfaces that continue to exist, imposes itself on our own psychological sense of time. But while we can remember and think of how things were in the past, this does not mean that the physical past continues to exist.
Another reason that the past, as conceived generally, does not exist has to do with microreversibility — the symmetry under time reversal — of the wavefunction given by Schrödinger's equation. For a system of particles, this symmetry is generally broken; i.e., the equation of motion describes the possible future evolution that a system may follow, but the time-reversal of the actual evolution of the system will not in general follow the same path backwards in time.
As pointed out earlier, just like spatial coordinates, the time coordinate itself is not associated with a “flow” in any particular time direction. If we measure the time distance around a closed timelike curve, there is no prima facie reason to expect the answer to be modulo the circumference.
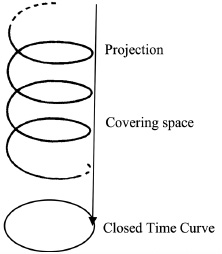
Instead, one may think of the evolution of time as being a onedimensional covering space over the original closed timelike curve as shown in Fig. A.1 below.6 It is not necessary to identify the covering space as being the actual time curve in our universe since causality violations occur only if past three-dimensional hypersurfaces continue to exist. With this conception of time, one could go around a closed time curve many times without a causality violation. The need for Hawking’s chronology protection conjecture is eliminated.
Fig. A.1. Closed time curve with a covering space. The original closed curve can be thought of as a projection of an infinite spiral over the closed time curve. Time changes monotonically in the covering space as one loops around the closed time curve.
Time and the Expansion of the Universe
The Friedmann–Lemaître spacetimes thought to represent our universe have exact spherical symmetry about every point, which implies that the spacetime is spatially homogeneous and isotropic, admitting a sixparameter group of isometries whose orbits are space-like three-surfaces (constant time) of constant curvature (positive, negative, or flat). One may choose the coordinates such that the line element has the form ds2 = dt2 − R2(t)dl2, where dl2 is the line element of a time-independent Riemannian three-space of constant curvature, be it positive, negative, or flat, and R(t) is the expansion function. What this form of the metric tells us is that the proper physical distance dl between a pair of comoving galaxies scales with time as l(t) ∝ R(t) . For flat three-dimensional space, now believed to represent the actual universe, the function R(t) monotonically increases with time.7 One can readily show from the form of the metric that the velocity of separation of two comoving galaxies, V, is given by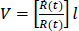 
, where the “dot” means the derivative with respect to time. This is the origin of the cosmological red shift. Thus, if R(t) is constant, V = 0, and motion freezes.
The parameter t of the Friedmann–Lemaître spacetimes is explicitly identified with the time parameter used to express physical relationships such as in Newton’s and Maxwell’s equations. This implies that if the time is set equal to a constant number so that the universe freezes at some radius, the time associated with physical processes also freezes — nothing can propagate or change in three-dimensional space. Motion and the flow of time are inexplicably linked, as originally pointed out by Hermann Weyl. This would also be true in more general spacetimes where time may pass at different rates depending on the local massenergy concentration. Thus, identification of the Friedmann–Lemaître time parameter (often called cosmic time) with physical time implies that the “flow” of time in three-dimensional space is due to the expansion of the universe.
The connection would seem to be even deeper. These spacetimes begin with an initial singularity — the term being used loosely. This means space and time came into being together and, in the real as opposed to mathematical world, may not be able to exist independently. This is an obvious point: without time, there would be no space since expansion after the initial singularity would not be possible; and the expansion of space from the initial singularity implicitly introduces time and induces a time asymmetry in three-dimensional space.
This induced cosmic time is quite distinct from the thermodynamic time direction arising from increasing entropy when matter is present. It is also different from time as measured by “clocks” whose rate will vary according to both special and general relativity, but always in the implicit time direction induced in three-dimensional space by its expansion.
The Friedmann–Lemaître spacetimes can also have spatial sections that have positive curvature so that R(t) is a cyclic function of time; i.e., the universe expands and then contracts (Fig. A.2). But time is not reversed during the contraction phase; the initial asymmetry in time persists.8 Thus, either the expansion or contraction of the universe leads to a time asymmetry in the same direction. The term “expansion” alone will continue to be used here since the real universe appears to be flat.
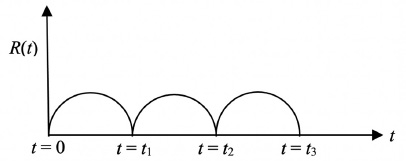
Fig. A.2. The Cyclic Friedmann–Lemaître spacetime with positive curvature that first expands from an initial singularity and then contracts to a singularity. The equation for R(t) is a cycloid.
If the singularities at the times indicated in Fig. A.2 are identified so that one has a closed time curve and the time asymmetry persists in the same direction as indicated in the figure, then time could increase monotonically through the cycles (see Fig. A.1 and associated discussion).
There is one additional point that should be made. The cosmological solutions to the Einstein field equations discussed above all have an initial singularity where spacetime itself is generally assumed to have come into being. The Einstein field equations themselves, however, do not inform us about what if anything existed “before” the initial singularity. The existence of the singularity simply indicates the limits of applicability of the field equations. In particular, these equations do not rule out the existence of some form of space or spacetime before the initial singularity. Most theoreticians assume that some form of quantum gravity will illuminate this issue. Unfortunately, current attempts in this direction — as exemplified by some forms of string theory, loop quantum gravity, non-commutative geometries, etc., have not had any convincing success. Also, to state a heretical view, there is no experimental evidence that space, time, or spacetime is quantized or that it need be quantized.9 The desire to do so is primarily a matter of esthetics. It is based on the idea that because spacetime is a dynamical entity in its own right — due to its interactions with matter and energy — spacetime should in some sense be quantized.
The Asymmetry of Time
The standard “big bang” model of cosmology assumes that at the very beginning of the universe, there was no matter present but only energy in the form of enormously hot thermal radiation. The actual nature of this radiation, associated with a temperature similar to 1032 °K at the Planck time of 10-24 sec, is not really known, although it is generally characterized as thermal radiation, which is, of course, of electromagnetic origin. The extremely hot origin of the universe is confirmed by the existence of the isotropic 3 °K background radiation. The conversion of this early radiation into particle-antiparticle pairs, as the expanding universe cooled through a series of phase changes, is widely believed to be the source of the matter that exists today. The 3 °K background radiation itself comes from a time about half a million years after the initial singularity, by which time the plasma of ions (primarily hydrogen and helium, as well as electrons and photons) had formed and cooled to the point where it became a transparent gas. But there is a fundamental problem with this scenario that has not yet been resolved.
Consider the baryons (particles like neutrons and protons). From the observed ratio of the number of baryons to the number of photons in the background radiation — something like 10-9 — it is apparent that only a small fraction of the matter survived the annihilation of the particleantiparticle pairs. This means that somehow there must have been a small excess of matter over antimatter before the annihilation occurred. For this to be the case, the symmetry between baryons and antibaryons must be broken. Baryon number conservation must be violated so that the various allowed decay schemes resulting in baryons can lead to a difference between the number of baryons and anti-baryons. The criteria for breaking this symmetry was established by Sakharov10 quite some time ago: both C and CP invariance must be violated, or otherwise for each process that generates a baryon-antibaryon asymmetry there would be a C or CP conjugate process that would eliminate the possibility of a net asymmetry; and there must be a departure from thermal equilibrium, or CPT invariance — which must hold for any local, relativistic field theory — implying that there would be a balance between processes increasing and decreasing baryon number. There is some confusion in the literature about the meaning of the last requirement with regard to “time”.
For example, Börner 11 states that, “Loosely speaking, the CPTinvariance of local, relativistic field theories and thermodynamic equilibrium imply the invariance under CP, because in thermodynamic equilibrium there is no arrow of time.” Grotz and Klapdor12 state that only if there is a departure from thermodynamic equilibrium will CP-violating interactions permit “. . . the rates of reactions which lead to the formation of baryons, to be larger than the rates of reactions which lead to antibaryons, but in thermodynamic equilibrium, no time direction is given, and the same would also apply to the inverse reactions.”
Both statements argue that in thermodynamic equilibrium there is no Arrow of Time; i.e., no time direction is given. As it stands, this is certainly true, but as shown below in the discussion of thermodynamic time, this Arrow of Time has no relation to the kinematic time reversal transformation (see the book by Sachs referenced below). There is often confusion between the Arrow of Time and T-violation. As put by Sean Carroll in November 20, 2012 “blog” of the popular magazine Discover, referring to the recent results from BaBar on T violation, “. . . the entire phenomenon of T violation — has absolutely nothing to do with that arrow of time [emphasis in the original].”
With regard to Sakharov’s requirement that there be a departure from thermodynamic equilibrium, Kolb and Turner 13 argue that, “The necessary non-equilibrium condition is provided by the expansion of the Universe. . . . if the expansion rate is faster than key particle interaction rates, departures from equilibrium can result.” Calculations by Kolb and Turner show that only a very small C and CP violation can result in the necessary baryon-antibaryon asymmetry.
Systems in thermodynamic equilibrium (while they do not have an Arrow of Time) called “thermodynamic time” in this book, in the hopes of avoiding the kind of confusion found in the literature, do of course move through time in a direction given by the time asymmetry in the three-dimensional space within which we live.
Because of CPT conservation, it is clear that CP violation means that T-invariance is also violated. Now these symmetry violations are generally discussed in the context of particle decays. For example, the decay of the K-meson tells us that the violation of T-symmetry is very small. But no matter how small the breaking of time reversal invariance, the fact that it exists at all implies that there is a direction of time in particle physics; i.e., a time asymmetry, which — to reiterate it once again — has nothing to do with the thermodynamic Arrow of Time.
Before beginning the discussion of the asymmetry of time in quantum mechanics, we turn to thermodynamic time so as to both complete the discussion above and introduce the Poincaré recurrence theorem.
Thermodynamic Time
Thermodynamic time has to do with the increase of entropy.14 To begin with, the Poincaré recurrence theorem,15 associated with thermodynamic and classical systems in general, states that for an isolated and bounded non-dissipative system, any particular state will be revisited arbitrarily closely; for macroscopic systems composed of many particles, the recurrence time will be very, very large. A simple example is a perfect gas confined to one side of a chamber by a membrane with the other side of the chamber being evacuated. If a hole in the membrane is opened, the gas will flow into the vacuum side; but ultimately all the gas will return to its original configuration after the Poincaré recurrence time has elapsed. From the point of view of thermodynamic time, it is possible to return to where the physical configuration of matter is arbitrarily close to its original configuration provided the assumptions given above on the nature of the system hold. What has been called cosmic time above always increases monotonically into the future even for such systems.
Let us explore this issue more quantitatively. Consider a onedimensional lattice of N particles of mass m elastically coupled to their nearest neighbors by springs with a force constant K, and let one particle have a mass M ≫ m, which at t = 0 is given some velocity, the other particles being at rest. Rubin16 computed the subsequent motion of the lattice and for large N found that the motion of the single particle with mass M was damped nearly exponentially. But the time symmetry is preserved and after a time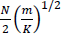 
the lattice system completes a Poincaré cycle and returns to the original configuration at t = 0. A similar effect occurs with quantum systems as will be shown later in this book.
While a bounded system may therefore return to its initial state, there is no asymmetry in time involved. Nonetheless, one often hears of the “thermodynamic arrow of time” established by the second law of thermodynamics and the increase of entropy. The situation with thermodynamic time is quite murky. As put by Brown and Uffink,17 “All traditional formulations of the Second Law presuppose the distinction between past and future (or ‘earlier’ and ‘later’, or ‘initial’ and ‘final’). To which pre-thermodynamic arrow(s) of time were the founding fathers of thermodynamics implicitly referring? It is not clear whether this was a question they asked themselves, or whether, if pushed, they would not have fallen back on psychological time.”
The idea that the thermodynamic arrow of time coincides with the psychological arrow of time led Hawking to observe that “. . . the second law of thermodynamics is really a tautology. Entropy increases with time, because we define the direction of time to be that in which entropy increases.” 18 There has been some objection to this pithy characterization of the second law, but it suffices for our purposes. The connection between the thermodynamic arrow of time and the physics of time reversal has been put quite succinctly by Sachs, “. . . the Arrow of Time has little to do with the time variable as measured by physicists. In particular, it has no bearing on the physics of time reversal.”19 The thermodynamic arrow of time will play no further role here. On the other hand, the Poincaré recurrence theorem will appear again in the next section.
Time Asymmetry in Quantum Mechanics
Below, in discussing Feynman’s picture of the scattering of the Dirac wavefunction by a potential, waves will be allowed to travel backwards in time. These waves correspond to the negative energy states of the Dirac equation. That is, positrons may be interpreted as electrons propagating backwards in time. This may be explicitly shown by the transformation properties of the Dirac equation under the combination of parity, charge conjugation, and time reversal.
The Feynman interpretation of a positron as a backward-in-time moving electron is not inconsistent with the interpretation of time given above where past three-dimensional spacelike hypersurfaces do not continue to exist. The propagation into the past is very limited and the Feynman interpretation only applies to elementary particles. One way to accommodate this is to think of the three-dimensional space or hypersurface within which we live with a very small thickness in the time dimension.20
To simplify the discussion of time asymmetry in quantum mechanics, let us consider the Schrödinger equation H|Ψ⟩ = i∂t|Ψ⟩. Like the Dirac equation, the probability amplitude Ψ is invariant under the T operator so that the physical content of the theory is unchanged. What will now be shown is that even though the physical content of quantum mechanics is preserved under time reversal (micro-reversibility under the T operator), when one considers multiple systems, an asymmetry in time results. The discussion here follows that given by Davies.21
The Poincaré recurrence theorem associated with thermodynamic and classical systems that was discussed above has a quantum mechanical analog: Consider a collection of systems having only a ground state and one excited state whose energy can vary with the system. Now assume all systems are in their ground states save for one that is in its excited state. Assume further that all the systems are coupled by an interaction Hamiltonian Hint. After some time passes, there is a probability that the original excited system is in its ground state and one of the other systems is in its excited state. Davies finds that for two identical coupled systems, the Schrödinger equation gives a probability amplitude for the original excited system of cos2( |Hint|t). Here the Poincaré recurrence period is 2π⁄|Hint|. On the other hand, for a large number of systems, the probability amplitude for the original excited system is e-2π|Hint|2t/∆E, where ΔE-1 is the density of states available. This is the usual time asymmetrical decay of an excited state with a half-life of ∆E/2π|Hint|2. As the number of systems increases, the density of states available goes to zero and the probability of the original state returning to its original excited state tends to zero.
While quantum mechanics satisfies what is known as the principle of micro-reversibility, processes that appear asymmetric in time are related to special initial conditions and the openness of the system, a good example being radioactive decay.
When we say we are “understanding” something, we generally mean we can relate it to something simpler that we already understand; and in the case of spacetime, this usually means quantum mechanics. And many attempts have been made to do this, none with outstanding success. All are based on the idea that general relativity tells us that spacetime is a dynamical entity, while quantum mechanics tells us that a dynamical entity has quanta associated with it, and consequently this entity can be in a superposition of quantum states. The implication is that there are “quanta” of space and time. But what does this mean? Does it mean that space is made up of elemental little parcels of three-dimensional space? What role would time play with such parcels? Are there four-dimensional parcels of spacetime? Is time itself infinitely divisible? If not, is it made up of minimal steps? Is the ordering of such steps fixed?
The usual approach to quantum gravity is to treat the dynamical variable as being the spacetime metric gij(X). Then the usual procedure of quantization leads to the infamous Wheeler–DeWitt equation, which DeWitt was known to refer to as “that damned equation”. The Wheeler–DeWitt equation is essentially the Schrödinger equation for the gravitational field, and its wavefunction, Ψ[gij(X)] , is the “wavefunction of the universe”. Time does not explicitly appear in the equation and there are conceptual problems with regard to the definition of probability, not to speak of the fact that the resulting theory is not renormalizable.
An analogy that may help with regard to these questions is to represent spacetime as a piece of cloth: from a distance, it is quite smooth, but as one comes closer, it begins to show the structure of its weave. The argument is made that if we look at space and time at the Planck distance and time, it would show a structure that we could understand and use to explain the nature of spacetime. It is string theory and loop quantum gravity that attempt to address these questions.
Some Metaphysical Thoughts
Notwithstanding the discussion above, there is little that is really known about the empty spacetime continuum itself — or the vacuum in the context of quantum field theory — except for what hints we have from special and general relativity, and those given by the Standard Model of particle physics. Unfortunately, the greatest fundamental conceptual issue with the Standard Model is that its redefinition of the vacuum begins to make it look like some form of æther, albeit a relativistic one! This results from the imposition of analogies from condensed matter physics, and in particular, superconductivity. Surely these analogies should not be taken literally. The fact that they “work” should only be taken as a hint about the real nature of the vacuum.
• • •
In the end, there could be limitations to the phenomenological approach of science to addressing epistemological or metaphysical issues. The situation with regard to our current understanding of space and time may, perhaps, be characterized by a portion of the ~1959 lecture of Professor Walter von der Vogelweide:22
Introduction: “And now, ladies and gentlemen, Professor Walter von der Vogelweide will present A Short Talk on The Universe:
Now, why, you will ask me, have I chosen to speak on the Universe rather than some other topic. Well, it’s very simple. There isn’t anything else!
Now, in the universe we have time, space, motion, and thought. Now, you will ask me, what is this thing called time? [several second pause] THAT is time.
Now, you will ask me, what is space? Now this over here — this is some space. However, this is not all space. However, when I said that was time that was all the time there was anywhere in the universe — at that time. Now, if you were to take all of the space that there is in the universe and CRAM it into this little tiny place, this would be ALL the space there was! Unless of course, some leaked out. Which it could. And did! Hence the universe!”
____________________________________
1 This solution caused enormous ferment in physics and philosophical circles. See: P. Yourgrau, Gödel Meets Einstein: Time Travel in the Gödel Universe (Open Court, Chicago, 1999); A World Without Time: The Forgotten Legacy of Gödel and Einstein (Basic Books, Cambridge, MA, 2005).
2 A global Cauchy surface is a spacelike hypersurface such that every non-spacelike curve intersects it only once.
3 While there is no need to discuss the time orientability of a spacetime here, it might be useful to give an example of a non-orientable spacetime. If one draws a circle representing the space axis along a Möbius strip and imposes a time direction perpendicular to the circle, after starting at any point and traversing the circle so as to return to the same point (on the other side of the strip of a paper model — a real Möbius strip only has one side), the time direction will be reversed. Such behavior implies that this (1 + 1) dimensional spacetime is not time orientable. While a spacetime that is non-orientable has a double covering space, which is orientable, that does not eliminate the problem in the underlying base space. Covering spaces are very useful in mathematics, but in terms of the physics, it does not seem to be possible to jump between the two spaces. Either the base space or the covering space must be chosen as representing physical spacetime.
4 R. Geroch, “Partial differential equations of physics,” arXiv:gr-qc/9602055v1 (27 Feb 1996).
5 R. Geroch, Advances in Lorentzian Geometry: Proceedings of the Lorentzian Geometry Conference in Berlin, M. Plaue, A. Rendall, and M. Scherfner (Eds.) (American Mathematical Society, 2011), p. 59. arXive: gr-qc/1005.1614v1.
6 A relevant concept is called “unwrapping”: S. Slobodov, “Unwrapping closed timelike curves,” Found. Phys. 38 (2008), 1082. Unfortunately, the process of extending a spacetime containing closed timelike curves generally introduces other pathologies.
7 The flatness of three-dimensional space does not necessarily imply that the full spacetime is flat.
8 In this connection, I should mention the work of Hawking who considered quantum gravity and metrics that are compact and without boundary. He showed that the observed asymmetry of time defined by the direction of entropy increase is related to the cosmological arrow of time defined by the expansion of the universe. S. W. Hawking, “Arrow of time in cosmology,” Phys. Rev. D 32 (1985), 259.
9 One often hears Heisenberg’s uncertainty relations incorrectly raised in this context. But they have to do with the theory of measurement in quantum mechanics and are directly derivable from classical wave theory and the relations E = ℎv and pλ = ℎ. They do not apply to the fundamental limits of spacetime itself.
10 A. D. Sakharov, Pisma Zh. Eksp. Teor. Fiz. 5 (1967), 32 [JETP Lett. 5 (1967), 24] [Sov. Phys. Usp. 34 (1991), 392] [Usp. Fiz. Nauk 161 (1991), 61]. Here C, P, and T are the discrete symmetries associated with charge, parity, and time respectively.
11 G. Börner, The Early Universe (Springer-Verlag, Berlin, 1993).
12 K. Grotz and H. V. Klapdor, The Weak Interaction in Nuclear, Particle and Astrophysics (Adam Hilger, Bristol, 1990).
13 E. W. Kolb and M. S. Turner, The Early Universe (Addison-Wesley, New York, 1990).
14 An extensive and interesting discussion of time and entropy is contained in I. Prigogine, From Being to Becoming: Time and Complexity in the Physical Sciences (W. H. Freeman and Company, 1980).
15 A clear and elegant proof of this theorem has been given by V. I. Arnold, Mathematical Methods of Classical Mechanics (Springer-Verlag, New York, 1989), p. 72.
16 R. J. Rubin, J. Amer. Chem. Soc. 90 (1968), 3061.
17 H. R. Brown and J. Uffink, Stud. Hist. Phil. Mod. Phys. 32 (2001), 525–538.
18 S. Hawking, The No Boundary Condition And The Arrow Of Time, in J. J. Halliwell, J. Pérez-Mercador, and W. H. Zurek, (eds), Physical Origins of Time Asymmetry (Cambridge University Press, Cambridge, 1994).
19 R. G. Sachs, op. cit.
20 R. P. Feynman, Quantum Electrodynamics (W. A. Benjamin, Inc., New York, 1962), pp. 84–85.
21 P. C. W. Davies, The Physics of Time Asymmetry (University of California Press, Berkeley, 1977), § 6.1.
22 From Severn Darden’s A Short Talk on the Universe. This portion of professor von der Vogelweide’s talk can be heard by clicking on http://www.gemarsh.com/wp-content/uploads/SpaceTimeM.mp3. The kind of improvisation that this slightly edited extract comes from began in the back of a bar called the Compass in Chicago’s Hyde Park neighborhood near the University of Chicago campus. The Compass Players, including Mike Nichols, Elaine May, Shelley Berman, and Severn Darden, performed in Hyde Park from 1955–1958 and several of the members went on to form The Second City Theater in 1959.